mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-08-02 20:28:28 +08:00
930 lines
30 KiB
Markdown
930 lines
30 KiB
Markdown
|
||
<p align="center"><strong><a href="./qita/join.md">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!</strong></p>
|
||
|
||
# dijkstra(堆优化版)精讲
|
||
|
||
[卡码网:47. 参加科学大会](https://kamacoder.com/problempage.php?pid=1047)
|
||
|
||
【题目描述】
|
||
|
||
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。
|
||
|
||
小明的起点是第一个车站,终点是最后一个车站。然而,途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素(如天气变化)等不同,这些因素都会影响每条路径的通行时间。
|
||
|
||
小明希望能选择一条花费时间最少的路线,以确保他能够尽快到达目的地。
|
||
|
||
【输入描述】
|
||
|
||
第一行包含两个正整数,第一个正整数 N 表示一共有 N 个公共汽车站,第二个正整数 M 表示有 M 条公路。
|
||
|
||
接下来为 M 行,每行包括三个整数,S、E 和 V,代表了从 S 车站可以单向直达 E 车站,并且需要花费 V 单位的时间。
|
||
|
||
【输出描述】
|
||
|
||
输出一个整数,代表小明从起点到终点所花费的最小时间。
|
||
|
||
输入示例
|
||
|
||
```
|
||
7 9
|
||
1 2 1
|
||
1 3 4
|
||
2 3 2
|
||
2 4 5
|
||
3 4 2
|
||
4 5 3
|
||
2 6 4
|
||
5 7 4
|
||
6 7 9
|
||
```
|
||
|
||
输出示例:12
|
||
|
||
【提示信息】
|
||
|
||
能够到达的情况:
|
||
|
||
如下图所示,起始车站为 1 号车站,终点车站为 7 号车站,绿色路线为最短的路线,路线总长度为 12,则输出 12。
|
||
|
||

|
||
|
||
不能到达的情况:
|
||
|
||
如下图所示,当从起始车站不能到达终点车站时,则输出 -1。
|
||
|
||

|
||
|
||
数据范围:
|
||
|
||
1 <= N <= 500;
|
||
1 <= M <= 5000;
|
||
|
||
|
||
## 思路
|
||
|
||
> 本篇我们来讲解 堆优化版dijkstra,看本篇之前,一定要先看 我讲解的 朴素版dijkstra,否则本篇会有部分内容看不懂。
|
||
|
||
在上一篇中,我们讲解了朴素版的dijkstra,该解法的时间复杂度为 O(n^2),可以看出时间复杂度 只和 n (节点数量)有关系。
|
||
|
||
如果n很大的话,我们可以换一个角度来优先性能。
|
||
|
||
在 讲解 最小生成树的时候,我们 讲了两个算法,[prim算法](./0053.寻宝-prim.md)(从点的角度来求最小生成树)、[Kruskal算法](./0053.寻宝-Kruskal.md)(从边的角度来求最小生成树)
|
||
|
||
这么在n 很大的时候,也有另一个思考维度,即:从边的数量出发。
|
||
|
||
当 n 很大,边 的数量 也很多的时候(稠密图),那么 上述解法没问题。
|
||
|
||
但 n 很大,边 的数量 很小的时候(稀疏图),是不是可以换成从边的角度来求最短路呢?
|
||
|
||
毕竟边的数量少。
|
||
|
||
有的录友可能会想,n (节点数量)很大,边不就多吗? 怎么会边的数量少呢?
|
||
|
||
别忘了,谁也没有规定 节点之间一定要有边连接着,例如有一万个节点,只有一条边,这也是一张图。
|
||
|
||
了解背景之后,再来看 解法思路。
|
||
|
||
### 图的存储
|
||
|
||
首先是 图的存储。
|
||
|
||
关于图的存储 主流有两种方式: 邻接矩阵和邻接表
|
||
|
||
#### 邻接矩阵
|
||
|
||
邻接矩阵 使用 二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图,有多少节点就申请多大的二维数组。
|
||
|
||
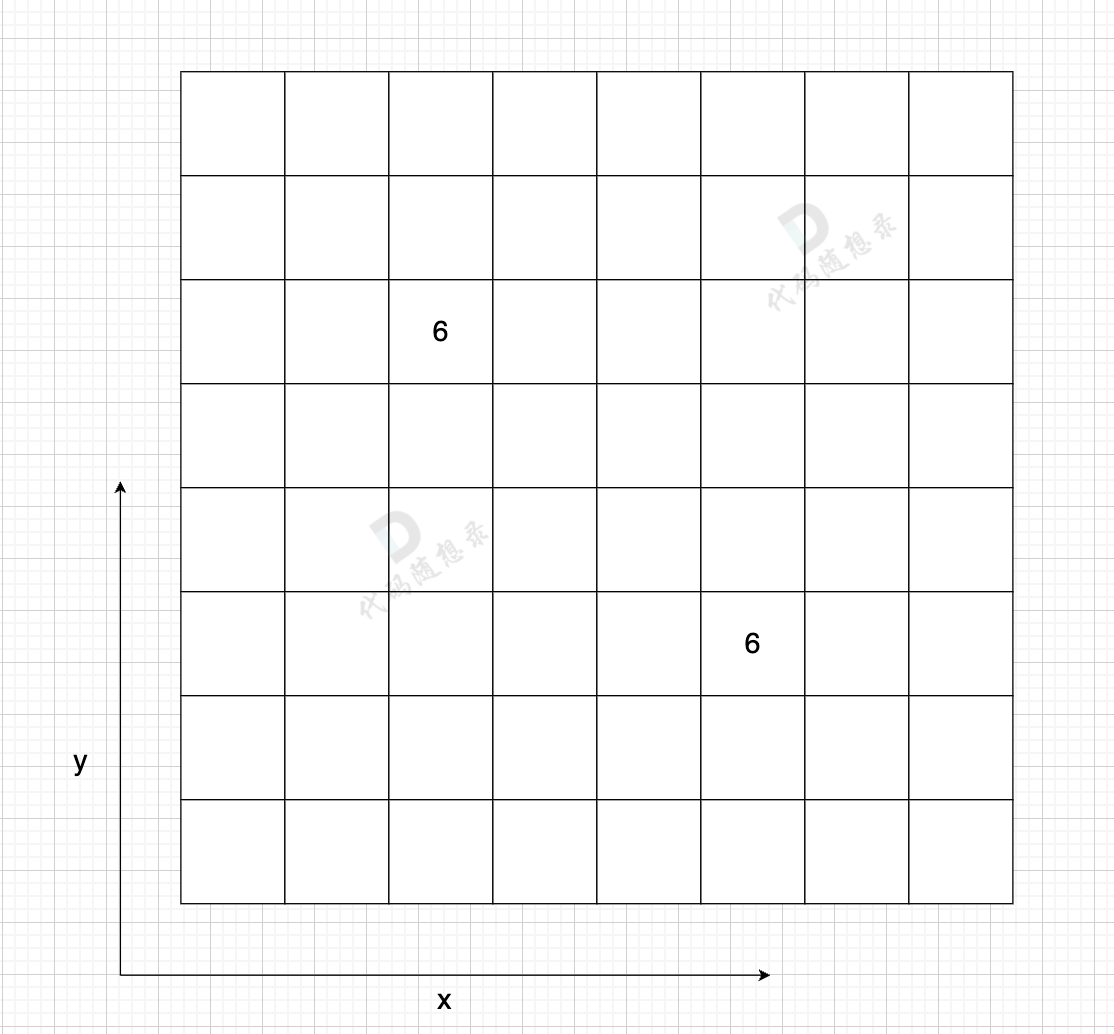
例如: grid[2][5] = 6,表示 节点 2 链接 节点5 为有向图,节点2 指向 节点5,边的权值为6 (套在题意里,可能是距离为6 或者 消耗为6 等等)
|
||
|
||
如果想表示无向图,即:grid[2][5] = 6,grid[5][2] = 6,表示节点2 与 节点5 相互连通,权值为6。
|
||
|
||
|
||
如图:
|
||
|
||
|
||
|
||
在一个 n (节点数)为8 的图中,就需要申请 8 * 8 这么大的空间,有一条双向边,即:grid[2][5] = 6,grid[5][2] = 6
|
||
|
||
这种表达方式(邻接矩阵) 在 边少,节点多的情况下,会导致申请过大的二维数组,造成空间浪费。
|
||
|
||
而且在寻找节点链接情况的时候,需要遍历整个矩阵,即 n * n 的时间复杂度,同样造成时间浪费。
|
||
|
||
邻接矩阵的优点:
|
||
|
||
* 表达方式简单,易于理解
|
||
* 检查任意两个顶点间是否存在边的操作非常快
|
||
* 适合稠密图,在边数接近顶点数平方的图中,邻接矩阵是一种空间效率较高的表示方法。
|
||
|
||
缺点:
|
||
|
||
* 遇到稀疏图,会导致申请过大的二维数组造成空间浪费 且遍历 边 的时候需要遍历整个n * n矩阵,造成时间浪费
|
||
|
||
#### 邻接表
|
||
|
||
邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图,有多少边 才会申请对应大小的链表。
|
||
|
||
邻接表的构造如图:
|
||
|
||

|
||
|
||
这里表达的图是:
|
||
|
||
* 节点1 指向 节点3 和 节点5
|
||
* 节点2 指向 节点4、节点3、节点5
|
||
* 节点3 指向 节点4,节点4指向节点1。
|
||
|
||
有多少边 邻接表才会申请多少个对应的链表节点。
|
||
|
||
从图中可以直观看出 使用 数组 + 链表 来表达 边的链接情况 。
|
||
|
||
邻接表的优点:
|
||
|
||
* 对于稀疏图的存储,只需要存储边,空间利用率高
|
||
* 遍历节点链接情况相对容易
|
||
|
||
缺点:
|
||
|
||
* 检查任意两个节点间是否存在边,效率相对低,需要 O(V)时间,V表示某节点链接其他节点的数量。
|
||
* 实现相对复杂,不易理解
|
||
|
||
#### 本题图的存储
|
||
|
||
接下来我们继续按照稀疏图的角度来分析本题。
|
||
|
||
在第一个版本的实现思路中,我们提到了三部曲:
|
||
|
||
1. 第一步,选源点到哪个节点近且该节点未被访问过
|
||
2. 第二步,该最近节点被标记访问过
|
||
3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
|
||
|
||
在第一个版本的代码中,这三部曲是套在一个 for 循环里,为什么?
|
||
|
||
因为我们是从节点的角度来解决问题。
|
||
|
||
三部曲中第一步(选源点到哪个节点近且该节点未被访问过),这个操作本身需要for循环遍历 minDist 来寻找最近的节点。
|
||
|
||
同时我们需要 遍历所有 未访问过的节点,所以 我们从 节点角度出发,代码会有两层for循环,代码是这样的: (注意代码中的注释,标记两层for循环的用处)
|
||
|
||
```CPP
|
||
|
||
for (int i = 1; i <= n; i++) { // 遍历所有节点,第一层for循环
|
||
|
||
int minVal = INT_MAX;
|
||
int cur = 1;
|
||
|
||
// 1、选距离源点最近且未访问过的节点 , 第二层for循环
|
||
for (int v = 1; v <= n; ++v) {
|
||
if (!visited[v] && minDist[v] < minVal) {
|
||
minVal = minDist[v];
|
||
cur = v;
|
||
}
|
||
}
|
||
|
||
visited[cur] = true; // 2、标记该节点已被访问
|
||
|
||
// 3、第三步,更新非访问节点到源点的距离(即更新minDist数组)
|
||
for (int v = 1; v <= n; v++) {
|
||
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
|
||
minDist[v] = minDist[cur] + grid[cur][v];
|
||
}
|
||
}
|
||
|
||
}
|
||
```
|
||
|
||
那么当从 边 的角度出发, 在处理 三部曲里的第一步(选源点到哪个节点近且该节点未被访问过)的时候 ,我们可以不用去遍历所有节点了。
|
||
|
||
而且 直接把 边(带权值)加入到 小顶堆(利用堆来自动排序),那么每次我们从 堆顶里 取出 边 自然就是 距离源点最近的节点所在的边。
|
||
|
||
这样我们就不需要两层for循环来寻找最近的节点了。
|
||
|
||
了解了大体思路,我们再来看代码实现。
|
||
|
||
首先是 如何使用 邻接表来表述图结构,这是摆在很多录友面前的第一个难题。
|
||
|
||
邻接表用 数组+链表 来表示,代码如下:(C++中 vector 为数组,list 为链表, 定义了 n+1 这么大的数组空间)
|
||
|
||
```CPP
|
||
vector<list<int>> grid(n + 1);
|
||
```
|
||
|
||
不少录友,不知道 如何定义的数据结构,怎么表示邻接表的,我来给大家画一个图:
|
||
|
||

|
||
|
||
图中邻接表表示:
|
||
|
||
* 节点1 指向 节点3 和 节点5
|
||
* 节点2 指向 节点4、节点3、节点5
|
||
* 节点3 指向 节点4
|
||
* 节点4 指向 节点1
|
||
|
||
大家发现图中的边没有权值,而本题中 我们的边是有权值的,权值怎么表示?在哪里表示?
|
||
|
||
所以 在`vector<list<int>> grid(n + 1);` 中 就不能使用int了,而是需要一个键值对 来存两个数字,一个数表示节点,一个数表示 指向该节点的这条边的权值。
|
||
|
||
那么 代码可以改成这样: (pair 为键值对,可以存放两个int)
|
||
|
||
```CPP
|
||
vector<list<pair<int,int>>> grid(n + 1);
|
||
```
|
||
|
||
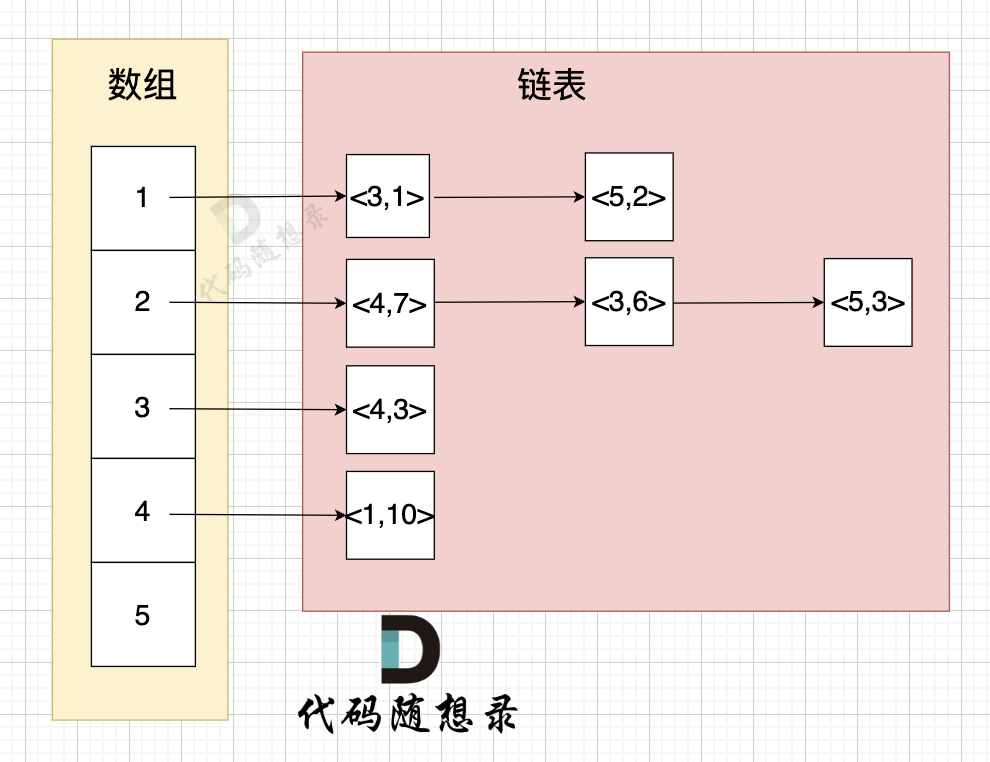
举例来给大家展示 该代码表达的数据 如下:
|
||
|
||
|
||
|
||
* 节点1 指向 节点3 权值为 1
|
||
* 节点1 指向 节点5 权值为 2
|
||
* 节点2 指向 节点4 权值为 7
|
||
* 节点2 指向 节点3 权值为 6
|
||
* 节点2 指向 节点5 权值为 3
|
||
* 节点3 指向 节点4 权值为 3
|
||
* 节点5 指向 节点1 权值为 10
|
||
|
||
这样 我们就把图中权值表示出来了。
|
||
|
||
但是在代码中 使用 `pair<int, int>` 很容易让我们搞混了,第一个int 表示什么,第二个int表示什么,导致代码可读性很差,或者说别人看你的代码看不懂。
|
||
|
||
那么 可以 定一个类 来取代 `pair<int, int>`
|
||
|
||
类(或者说是结构体)定义如下:
|
||
|
||
```CPP
|
||
struct Edge {
|
||
int to; // 邻接顶点
|
||
int val; // 边的权重
|
||
|
||
Edge(int t, int w): to(t), val(w) {} // 构造函数
|
||
};
|
||
```
|
||
|
||
这个类里有两个成员变量,有对应的命名,这样不容易搞混 两个int的含义。
|
||
|
||
所以 本题中邻接表的定义如下:
|
||
|
||
```CPP
|
||
struct Edge {
|
||
int to; // 链接的节点
|
||
int val; // 边的权重
|
||
|
||
Edge(int t, int w): to(t), val(w) {} // 构造函数
|
||
};
|
||
|
||
vector<list<Edge>> grid(n + 1); // 邻接表
|
||
|
||
```
|
||
|
||
(我们在下面的讲解中会直接使用这个邻接表的代码表示方式)
|
||
|
||
### 堆优化细节
|
||
|
||
其实思路依然是 dijkstra 三部曲:
|
||
|
||
1. 第一步,选源点到哪个节点近且该节点未被访问过
|
||
2. 第二步,该最近节点被标记访问过
|
||
3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
|
||
|
||
只不过之前是 通过遍历节点来遍历边,通过两层for循环来寻找距离源点最近节点。 这次我们直接遍历边,且通过堆来对边进行排序,达到直接选择距离源点最近节点。
|
||
|
||
先来看一下针对这三部曲,如果用 堆来优化。
|
||
|
||
那么三部曲中的第一步(选源点到哪个节点近且该节点未被访问过),我们如何选?
|
||
|
||
我们要选择距离源点近的节点(即:该边的权值最小),所以 我们需要一个 小顶堆 来帮我们对边的权值排序,每次从小顶堆堆顶 取边就是权值最小的边。
|
||
|
||
C++定义小顶堆,可以用优先级队列实现,代码如下:
|
||
|
||
```CPP
|
||
// 小顶堆
|
||
class mycomparison {
|
||
public:
|
||
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
|
||
return lhs.second > rhs.second;
|
||
}
|
||
};
|
||
// 优先队列中存放 pair<节点编号,源点到该节点的权值>
|
||
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;
|
||
```
|
||
|
||
(`pair<int, int>`中 第二个int 为什么要存 源点到该节点的权值,因为 这个小顶堆需要按照权值来排序)
|
||
|
||
|
||
有了小顶堆自动对边的权值排序,那我们只需要直接从 堆里取堆顶元素(小顶堆中,最小的权值在上面),就可以取到离源点最近的节点了 (未访问过的节点,不会加到堆里进行排序)
|
||
|
||
所以三部曲中的第一步,我们不用 for循环去遍历,直接取堆顶元素:
|
||
|
||
```CPP
|
||
// pair<节点编号,源点到该节点的权值>
|
||
pair<int, int> cur = pq.top(); pq.pop();
|
||
|
||
```
|
||
|
||
第二步(该最近节点被标记访问过) 这个就是将 节点做访问标记,和 朴素dijkstra 一样 ,代码如下:
|
||
|
||
```CPP
|
||
// 2. 第二步,该最近节点被标记访问过
|
||
visited[cur.first] = true;
|
||
|
||
```
|
||
|
||
(`cur.first` 是指取 `pair<int, int>` 里的第一个int,即节点编号 )
|
||
|
||
第三步(更新非访问节点到源点的距离),这里的思路 也是 和朴素dijkstra一样的。
|
||
|
||
但很多录友对这里是最懵的,主要是因为两点:
|
||
|
||
* 没有理解透彻 dijkstra 的思路
|
||
* 没有理解 邻接表的表达方式
|
||
|
||
我们来回顾一下 朴素dijkstra 在这一步的代码和思路(如果没看过我讲解的朴素版dijkstra,这里会看不懂)
|
||
|
||
```CPP
|
||
|
||
// 3、第三步,更新非访问节点到源点的距离(即更新minDist数组)
|
||
for (int v = 1; v <= n; v++) {
|
||
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
|
||
minDist[v] = minDist[cur] + grid[cur][v];
|
||
}
|
||
}
|
||
```
|
||
|
||
其中 for循环是用来做什么的? 是为了 找到 节点cur 链接指向了哪些节点,因为使用邻接矩阵的表达方式 所以把所有节点遍历一遍。
|
||
|
||
而在邻接表中,我们可以以相对高效的方式知道一个节点链接指向哪些节点。
|
||
|
||
再回顾一下邻接表的构造(数组 + 链表):
|
||
|
||

|
||
|
||
假如 加入的cur 是节点 2, 那么 grid[2] 表示的就是图中第二行链表。 (grid数组的构造我们在 上面 「图的存储」中讲过)
|
||
|
||
所以在邻接表中,我们要获取 节点cur 链接指向哪些节点,就是遍历 grid[cur节点编号] 这个链表。
|
||
|
||
这个遍历方式,C++代码如下:
|
||
|
||
```CPP
|
||
for (Edge edge : grid[cur.first])
|
||
```
|
||
|
||
(如果不知道 Edge 是什么,看上面「图的存储」中邻接表的讲解)
|
||
|
||
`cur.first` 就是cur节点编号, 参考上面pair的定义: pair<节点编号,源点到该节点的权值>
|
||
|
||
接下来就是更新 非访问节点到源点的距离,代码实现和 朴素dijkstra 是一样的,代码如下:
|
||
|
||
```CPP
|
||
// 3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
|
||
for (Edge edge : grid[cur.first]) { // 遍历 cur指向的节点,cur指向的节点为 edge
|
||
// cur指向的节点edge.to,这条边的权值为 edge.val
|
||
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
|
||
minDist[edge.to] = minDist[cur.first] + edge.val;
|
||
pq.push(pair<int, int>(edge.to, minDist[edge.to]));
|
||
}
|
||
}
|
||
```
|
||
|
||
但为什么思路一样,有的录友能写出朴素dijkstra,但堆优化这里的逻辑就是写不出来呢?
|
||
|
||
**主要就是因为对邻接表的表达方式不熟悉**!
|
||
|
||
以上代码中,cur 链接指向的节点编号 为 edge.to, 这条边的权值为 edge.val ,如果对这里模糊的就再回顾一下 Edge的定义:
|
||
|
||
```CPP
|
||
struct Edge {
|
||
int to; // 邻接顶点
|
||
int val; // 边的权重
|
||
|
||
Edge(int t, int w): to(t), val(w) {} // 构造函数
|
||
};
|
||
```
|
||
|
||
确定该节点没有被访问过,`!visited[edge.to]` , 目前 源点到cur.first的最短距离(minDist) + cur.first 到 edge.to 的距离 (edge.val) 是否 小于 minDist已经记录的 源点到 edge.to 的距离 (minDist[edge.to])
|
||
|
||
如果是的话,就开始更新操作。
|
||
|
||
即:
|
||
|
||
```CPP
|
||
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
|
||
minDist[edge.to] = minDist[cur.first] + edge.val;
|
||
pq.push(pair<int, int>(edge.to, minDist[edge.to])); // 由于cur节点的加入,而新链接的边,加入到优先级队里中
|
||
}
|
||
|
||
```
|
||
|
||
同时,由于cur节点的加入,源点又有可以新链接到的边,将这些边加入到优先级队里中。
|
||
|
||
|
||
以上代码思路 和 朴素版dijkstra 是一样一样的,主要区别是两点:
|
||
|
||
* 邻接表的表示方式不同
|
||
* 使用优先级队列(小顶堆)来对新链接的边排序
|
||
|
||
### 代码实现
|
||
|
||
堆优化dijkstra完整代码如下:
|
||
|
||
```CPP
|
||
#include <iostream>
|
||
#include <vector>
|
||
#include <list>
|
||
#include <queue>
|
||
#include <climits>
|
||
using namespace std;
|
||
// 小顶堆
|
||
class mycomparison {
|
||
public:
|
||
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
|
||
return lhs.second > rhs.second;
|
||
}
|
||
};
|
||
// 定义一个结构体来表示带权重的边
|
||
struct Edge {
|
||
int to; // 邻接顶点
|
||
int val; // 边的权重
|
||
|
||
Edge(int t, int w): to(t), val(w) {} // 构造函数
|
||
};
|
||
|
||
int main() {
|
||
int n, m, p1, p2, val;
|
||
cin >> n >> m;
|
||
|
||
vector<list<Edge>> grid(n + 1);
|
||
|
||
for(int i = 0; i < m; i++){
|
||
cin >> p1 >> p2 >> val;
|
||
// p1 指向 p2,权值为 val
|
||
grid[p1].push_back(Edge(p2, val));
|
||
|
||
}
|
||
|
||
int start = 1; // 起点
|
||
int end = n; // 终点
|
||
|
||
// 存储从源点到每个节点的最短距离
|
||
std::vector<int> minDist(n + 1, INT_MAX);
|
||
|
||
// 记录顶点是否被访问过
|
||
std::vector<bool> visited(n + 1, false);
|
||
|
||
// 优先队列中存放 pair<节点,源点到该节点的权值>
|
||
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;
|
||
|
||
|
||
// 初始化队列,源点到源点的距离为0,所以初始为0
|
||
pq.push(pair<int, int>(start, 0));
|
||
|
||
minDist[start] = 0; // 起始点到自身的距离为0
|
||
|
||
while (!pq.empty()) {
|
||
// 1. 第一步,选源点到哪个节点近且该节点未被访问过 (通过优先级队列来实现)
|
||
// <节点, 源点到该节点的距离>
|
||
pair<int, int> cur = pq.top(); pq.pop();
|
||
|
||
if (visited[cur.first]) continue;
|
||
|
||
// 2. 第二步,该最近节点被标记访问过
|
||
visited[cur.first] = true;
|
||
|
||
// 3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
|
||
for (Edge edge : grid[cur.first]) { // 遍历 cur指向的节点,cur指向的节点为 edge
|
||
// cur指向的节点edge.to,这条边的权值为 edge.val
|
||
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
|
||
minDist[edge.to] = minDist[cur.first] + edge.val;
|
||
pq.push(pair<int, int>(edge.to, minDist[edge.to]));
|
||
}
|
||
}
|
||
|
||
}
|
||
|
||
if (minDist[end] == INT_MAX) cout << -1 << endl; // 不能到达终点
|
||
else cout << minDist[end] << endl; // 到达终点最短路径
|
||
}
|
||
|
||
```
|
||
|
||
* 时间复杂度:O(ElogE) E 为边的数量
|
||
* 空间复杂度:O(N + E) N 为节点的数量
|
||
|
||
堆优化的时间复杂度 只和边的数量有关 和节点数无关,在 优先级队列中 放的也是边。
|
||
|
||
以上代码中,`while (!pq.empty())` 里套了 `for (Edge edge : grid[cur.first])`
|
||
|
||
`for` 里 遍历的是 当前节点 cur 所连接边。
|
||
|
||
那 当前节点cur 所连接的边 也是不固定的, 这就让大家分不清,这时间复杂度究竟是多少?
|
||
|
||
其实 `for (Edge edge : grid[cur.first])` 里最终的数据走向 是 给队列里添加边。
|
||
|
||
那么跳出局部代码,整个队列 一定是 所有边添加了一次,同时也弹出了一次。
|
||
|
||
所以边添加一次时间复杂度是 O(E), `while (!pq.empty())` 里每次都要弹出一个边来进行操作,在优先级队列(小顶堆)中 弹出一个元素的时间复杂度是 O(logE) ,这是堆排序的时间复杂度。
|
||
|
||
(当然小顶堆里 是 添加元素的时候 排序,还是 取数元素的时候排序,这个无所谓,时间复杂度都是O(E),总之是一定要排序的,而小顶堆里也不会滞留元素,有多少元素添加 一定就有多少元素弹出)
|
||
|
||
所以 该算法整体时间复杂度为 O(ElogE)
|
||
|
||
网上的不少分析 会把 n (节点的数量)算进来,这个分析是有问题的,举一个极端例子,在n 为 10000,且是有一条边的 图里,以上代码,大家感觉执行了多少次?
|
||
|
||
`while (!pq.empty())` 中的 pq 存的是边,其实只执行了一次。
|
||
|
||
所以该算法时间复杂度 和 节点没有关系。
|
||
|
||
至于空间复杂度,邻接表是 数组 + 链表 数组的空间 是 N ,有E条边 就申请对应多少个链表节点,所以是 复杂度是 N + E
|
||
|
||
## 拓展
|
||
|
||
当然也有录友可能想 堆优化dijkstra 中 我为什么一定要用邻接表呢,我就用邻接矩阵 行不行 ?
|
||
|
||
也行的。
|
||
|
||
但 正是因为稀疏图,所以我们使用堆优化的思路, 如果我们还用 邻接矩阵 去表达这个图的话,就是 **一个高效的算法 使用了低效的数据结构,那么 整体算法效率 依然是低的**。
|
||
|
||
如果还不清楚为什么要使用 邻接表,可以再看看上面 我在 「图的存储」标题下的讲解。
|
||
|
||
这里我也给出 邻接矩阵版本的堆优化dijkstra代码:
|
||
|
||
```CPP
|
||
#include <iostream>
|
||
#include <vector>
|
||
#include <list>
|
||
#include <climits>
|
||
using namespace std;
|
||
// 小顶堆
|
||
class mycomparison {
|
||
public:
|
||
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
|
||
return lhs.second > rhs.second;
|
||
}
|
||
};
|
||
|
||
int main() {
|
||
int n, m, p1, p2, val;
|
||
cin >> n >> m;
|
||
|
||
vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));
|
||
|
||
for(int i = 0; i < m; i++){
|
||
cin >> p1 >> p2 >> val;
|
||
// p1 指向 p2,权值为 val
|
||
grid[p1][p2] = val;
|
||
}
|
||
|
||
int start = 1; // 起点
|
||
int end = n; // 终点
|
||
|
||
// 存储从源点到每个节点的最短距离
|
||
std::vector<int> minDist(n + 1, INT_MAX);
|
||
|
||
// 记录顶点是否被访问过
|
||
std::vector<bool> visited(n + 1, false);
|
||
|
||
// 优先队列中存放 pair<节点,源点到该节点的距离>
|
||
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;
|
||
|
||
|
||
// 初始化队列,源点到源点的距离为0,所以初始为0
|
||
pq.push(pair<int, int>(start, 0));
|
||
|
||
minDist[start] = 0; // 起始点到自身的距离为0
|
||
|
||
while (!pq.empty()) {
|
||
// <节点, 源点到该节点的距离>
|
||
// 1、选距离源点最近且未访问过的节点
|
||
pair<int, int> cur = pq.top(); pq.pop();
|
||
|
||
if (visited[cur.first]) continue;
|
||
|
||
visited[cur.first] = true; // 2、标记该节点已被访问
|
||
|
||
// 3、第三步,更新非访问节点到源点的距离(即更新minDist数组)
|
||
for (int j = 1; j <= n; j++) {
|
||
if (!visited[j] && grid[cur.first][j] != INT_MAX && (minDist[cur.first] + grid[cur.first][j] < minDist[j])) {
|
||
minDist[j] = minDist[cur.first] + grid[cur.first][j];
|
||
pq.push(pair<int, int>(j, minDist[j]));
|
||
}
|
||
}
|
||
}
|
||
|
||
if (minDist[end] == INT_MAX) cout << -1 << endl; // 不能到达终点
|
||
else cout << minDist[end] << endl; // 到达终点最短路径
|
||
|
||
}
|
||
|
||
```
|
||
|
||
* 时间复杂度:O(E * (N + logE)) E为边的数量,N为节点数量
|
||
* 空间复杂度:O(log(N^2))
|
||
|
||
`while (!pq.empty())` 时间复杂度为 E ,while 里面 每次取元素 时间复杂度 为 logE,和 一个for循环 时间复杂度 为 N 。
|
||
|
||
所以整体是 E * (N + logE)
|
||
|
||
|
||
## 总结
|
||
|
||
在学习一种优化思路的时候,首先就要知道为什么要优化,遇到了什么问题。
|
||
|
||
正如我在开篇就给大家交代清楚 堆优化方式的背景。
|
||
|
||
堆优化的整体思路和 朴素版是大体一样的,区别是 堆优化从边的角度出发且利用堆来排序。
|
||
|
||
很多录友别说写堆优化 就是看 堆优化的代码也看的很懵。
|
||
|
||
主要是因为两点:
|
||
|
||
* 不熟悉邻接表的表达方式
|
||
* 对dijkstra的实现思路还是不熟
|
||
|
||
这是我为什么 本篇花了大力气来讲解 图的存储,就是为了让大家彻底理解邻接表以及邻接表的代码写法。
|
||
|
||
至于 dijkstra的实现思路 ,朴素版 和 堆优化版本 都是 按照 dijkstra 三部曲来的。
|
||
|
||
理解了三部曲,dijkstra 的思路就是清晰的。
|
||
|
||
针对邻接表版本代码 我做了详细的 时间复杂度分析,也让录友们清楚,相对于 朴素版,时间都优化到哪了。
|
||
|
||
最后 我也给出了 邻接矩阵的版本代码,分析了这一版本的必要性以及时间复杂度。
|
||
|
||
至此通过 两篇dijkstra的文章,终于把 dijkstra 讲完了,如果大家对我讲解里所涉及的内容都吃透的话,详细对 dijkstra 算法也就理解到位了。
|
||
|
||
|
||
|
||
## 其他语言版本
|
||
|
||
### Java
|
||
|
||
```Java
|
||
|
||
import java.util.*;
|
||
|
||
class Edge {
|
||
int to; // 邻接顶点
|
||
int val; // 边的权重
|
||
|
||
Edge(int to, int val) {
|
||
this.to = to;
|
||
this.val = val;
|
||
}
|
||
}
|
||
|
||
class MyComparison implements Comparator<Pair<Integer, Integer>> {
|
||
@Override
|
||
public int compare(Pair<Integer, Integer> lhs, Pair<Integer, Integer> rhs) {
|
||
return Integer.compare(lhs.second, rhs.second);
|
||
}
|
||
}
|
||
|
||
class Pair<U, V> {
|
||
public final U first;
|
||
public final V second;
|
||
|
||
public Pair(U first, V second) {
|
||
this.first = first;
|
||
this.second = second;
|
||
}
|
||
}
|
||
|
||
public class Main {
|
||
public static void main(String[] args) {
|
||
Scanner scanner = new Scanner(System.in);
|
||
int n = scanner.nextInt();
|
||
int m = scanner.nextInt();
|
||
|
||
List<List<Edge>> grid = new ArrayList<>(n + 1);
|
||
for (int i = 0; i <= n; i++) {
|
||
grid.add(new ArrayList<>());
|
||
}
|
||
|
||
for (int i = 0; i < m; i++) {
|
||
int p1 = scanner.nextInt();
|
||
int p2 = scanner.nextInt();
|
||
int val = scanner.nextInt();
|
||
grid.get(p1).add(new Edge(p2, val));
|
||
}
|
||
|
||
int start = 1; // 起点
|
||
int end = n; // 终点
|
||
|
||
// 存储从源点到每个节点的最短距离
|
||
int[] minDist = new int[n + 1];
|
||
Arrays.fill(minDist, Integer.MAX_VALUE);
|
||
|
||
// 记录顶点是否被访问过
|
||
boolean[] visited = new boolean[n + 1];
|
||
|
||
// 优先队列中存放 Pair<节点,源点到该节点的权值>
|
||
PriorityQueue<Pair<Integer, Integer>> pq = new PriorityQueue<>(new MyComparison());
|
||
|
||
// 初始化队列,源点到源点的距离为0,所以初始为0
|
||
pq.add(new Pair<>(start, 0));
|
||
|
||
minDist[start] = 0; // 起始点到自身的距离为0
|
||
|
||
while (!pq.isEmpty()) {
|
||
// 1. 第一步,选源点到哪个节点近且该节点未被访问过(通过优先级队列来实现)
|
||
// <节点, 源点到该节点的距离>
|
||
Pair<Integer, Integer> cur = pq.poll();
|
||
|
||
if (visited[cur.first]) continue;
|
||
|
||
// 2. 第二步,该最近节点被标记访问过
|
||
visited[cur.first] = true;
|
||
|
||
// 3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
|
||
for (Edge edge : grid.get(cur.first)) { // 遍历 cur指向的节点,cur指向的节点为 edge
|
||
// cur指向的节点edge.to,这条边的权值为 edge.val
|
||
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
|
||
minDist[edge.to] = minDist[cur.first] + edge.val;
|
||
pq.add(new Pair<>(edge.to, minDist[edge.to]));
|
||
}
|
||
}
|
||
}
|
||
|
||
if (minDist[end] == Integer.MAX_VALUE) {
|
||
System.out.println(-1); // 不能到达终点
|
||
} else {
|
||
System.out.println(minDist[end]); // 到达终点最短路径
|
||
}
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
|
||
### Python
|
||
|
||
```python
|
||
import heapq
|
||
|
||
class Edge:
|
||
def __init__(self, to, val):
|
||
self.to = to
|
||
self.val = val
|
||
|
||
def dijkstra(n, m, edges, start, end):
|
||
grid = [[] for _ in range(n + 1)]
|
||
|
||
for p1, p2, val in edges:
|
||
grid[p1].append(Edge(p2, val))
|
||
|
||
minDist = [float('inf')] * (n + 1)
|
||
visited = [False] * (n + 1)
|
||
|
||
pq = []
|
||
heapq.heappush(pq, (0, start))
|
||
minDist[start] = 0
|
||
|
||
while pq:
|
||
cur_dist, cur_node = heapq.heappop(pq)
|
||
|
||
if visited[cur_node]:
|
||
continue
|
||
|
||
visited[cur_node] = True
|
||
|
||
for edge in grid[cur_node]:
|
||
if not visited[edge.to] and cur_dist + edge.val < minDist[edge.to]:
|
||
minDist[edge.to] = cur_dist + edge.val
|
||
heapq.heappush(pq, (minDist[edge.to], edge.to))
|
||
|
||
return -1 if minDist[end] == float('inf') else minDist[end]
|
||
|
||
# 输入
|
||
n, m = map(int, input().split())
|
||
edges = [tuple(map(int, input().split())) for _ in range(m)]
|
||
start = 1 # 起点
|
||
end = n # 终点
|
||
|
||
# 运行算法并输出结果
|
||
result = dijkstra(n, m, edges, start, end)
|
||
print(result)
|
||
|
||
```
|
||
|
||
### Go
|
||
|
||
```go
|
||
package main
|
||
|
||
import (
|
||
"container/heap"
|
||
"fmt"
|
||
"math"
|
||
)
|
||
|
||
// Edge 表示带权重的边
|
||
type Edge struct {
|
||
to, val int
|
||
}
|
||
|
||
// PriorityQueue 实现一个小顶堆
|
||
type Item struct {
|
||
node, dist int
|
||
}
|
||
|
||
type PriorityQueue []*Item
|
||
|
||
func (pq PriorityQueue) Len() int { return len(pq) }
|
||
|
||
func (pq PriorityQueue) Less(i, j int) bool {
|
||
return pq[i].dist < pq[j].dist
|
||
}
|
||
|
||
func (pq PriorityQueue) Swap(i, j int) {
|
||
pq[i], pq[j] = pq[j], pq[i]
|
||
}
|
||
|
||
func (pq *PriorityQueue) Push(x interface{}) {
|
||
*pq = append(*pq, x.(*Item))
|
||
}
|
||
|
||
func (pq *PriorityQueue) Pop() interface{} {
|
||
old := *pq
|
||
n := len(old)
|
||
item := old[n-1]
|
||
*pq = old[0 : n-1]
|
||
return item
|
||
}
|
||
|
||
func dijkstra(n, m int, edges [][]int, start, end int) int {
|
||
grid := make([][]Edge, n+1)
|
||
for _, edge := range edges {
|
||
p1, p2, val := edge[0], edge[1], edge[2]
|
||
grid[p1] = append(grid[p1], Edge{to: p2, val: val})
|
||
}
|
||
|
||
minDist := make([]int, n+1)
|
||
for i := range minDist {
|
||
minDist[i] = math.MaxInt64
|
||
}
|
||
visited := make([]bool, n+1)
|
||
|
||
pq := &PriorityQueue{}
|
||
heap.Init(pq)
|
||
heap.Push(pq, &Item{node: start, dist: 0})
|
||
minDist[start] = 0
|
||
|
||
for pq.Len() > 0 {
|
||
cur := heap.Pop(pq).(*Item)
|
||
|
||
if visited[cur.node] {
|
||
continue
|
||
}
|
||
|
||
visited[cur.node] = true
|
||
|
||
for _, edge := range grid[cur.node] {
|
||
if !visited[edge.to] && minDist[cur.node]+edge.val < minDist[edge.to] {
|
||
minDist[edge.to] = minDist[cur.node] + edge.val
|
||
heap.Push(pq, &Item{node: edge.to, dist: minDist[edge.to]})
|
||
}
|
||
}
|
||
}
|
||
|
||
if minDist[end] == math.MaxInt64 {
|
||
return -1
|
||
}
|
||
return minDist[end]
|
||
}
|
||
|
||
func main() {
|
||
var n, m int
|
||
fmt.Scan(&n, &m)
|
||
|
||
edges := make([][]int, m)
|
||
for i := 0; i < m; i++ {
|
||
var p1, p2, val int
|
||
fmt.Scan(&p1, &p2, &val)
|
||
edges[i] = []int{p1, p2, val}
|
||
}
|
||
|
||
start := 1 // 起点
|
||
end := n // 终点
|
||
|
||
result := dijkstra(n, m, edges, start, end)
|
||
fmt.Println(result)
|
||
}
|
||
|
||
```
|
||
|
||
### Rust
|
||
|
||
### Javascript
|
||
|
||
### TypeScript
|
||
|
||
### PhP
|
||
|
||
### Swift
|
||
|
||
### Scala
|
||
|
||
### C#
|
||
|
||
### Dart
|
||
|
||
### C
|
||
|