algorithm/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2025-07-05 14:46:51 +08:00
Code Issues Packages Projects Releases Wiki Activity

Update

Browse Source
This commit is contained in:
programmercarl
2024-07-15 16:49:16 +08:00
parent 918590614e
commit 2c32229383
24 changed files with 1996 additions and 122 deletions
Download Patch File Download Diff File Expand all files Collapse all files

1
README.md
View File

@ -105,6 +105,7 @@
3. [数组：27.移除元素](./problems/0027.移除元素.md)
4. [数组：977.有序数组的平方](./problems/0977.有序数组的平方.md)
5. [数组：209.长度最小的子数组](./problems/0209.长度最小的子数组.md)
6. [数组：区间和](./problems/kamacoder/0058.区间和.md)
6. [数组：59.螺旋矩阵II](./problems/0059.螺旋矩阵II.md)
7. [数组：总结篇](./problems/数组总结篇.md)

386
problems/kamacoder/0044.开发商购买土地.md Normal file
View File

@ -0,0 +1,386 @@
# 44. 开发商购买土地
【题目描述】
在一个城市区域内，被划分成了n * m个连续的区块，每个区块都拥有不同的权值，代表着其土地价值。目前，有两家开发公司，A 公司和 B 公司，希望购买这个城市区域的土地。
现在，需要将这个城市区域的所有区块分配给 A 公司和 B 公司。
然而，由于城市规划的限制，只允许将区域按横向或纵向划分成两个子区域，而且每个子区域都必须包含一个或多个区块。
为了确保公平竞争，你需要找到一种分配方式，使得 A 公司和 B 公司各自的子区域内的土地总价值之差最小。
注意：区块不可再分。
【输入描述】
第一行输入两个正整数，代表 n 和 m。
接下来的 n 行，每行输出 m 个正整数。
输出描述
请输出一个整数，代表两个子区域内土地总价值之间的最小差距。
【输入示例】
3 3
1 2 3
2 1 3
1 2 3
【输出示例】
0
【提示信息】
如果将区域按照如下方式划分：
1 2 | 3
2 1 | 3
1 2 | 3
两个子区域内土地总价值之间的最小差距可以达到 0。
【数据范围】：
* 1 <= n, m <= 100；
* n 和 m 不同时为 1。
## 思路
看到本题，大家如果想暴力求解，应该是 n^3 的时间复杂度，
一个 for 枚举分割线， 嵌套 两个for 去累加区间里的和。
如果本题要求 任何两个行（或者列）之间的数值总和，大家在[0058.区间和](./0058.区间和.md) 的基础上 应该知道怎么求。
就是前缀和的思路，先统计好，前n行的和 q[n]，如果要求矩阵 a 行到 b行 之间的总和，那么就 q[b] - q[a - 1]就好。
至于为什么是 a - 1，大家去看 [0058.区间和](./0058.区间和.md) 的分析，使用 前缀和 要注意 区间左右边的开闭情况。
本题也可以使用 前缀和的思路来求解，先将 行方向，和 列方向的和求出来，这样可以方便知道 划分的两个区间的和。
代码如下：
```CPP
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main () {
int n, m;
cin >> n >> m;
int sum = 0;
vector<vector<int>> vec(n, vector<int>(m, 0)) ;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> vec[i][j];
sum += vec[i][j];
}
}
// 统计横向
vector<int> horizontal(n, 0);
for (int i = 0; i < n; i++) {
for (int j = 0 ; j < m; j++) {
horizontal[i] += vec[i][j];
}
}
// 统计纵向
vector<int> vertical(m , 0);
for (int j = 0; j < m; j++) {
for (int i = 0 ; i < n; i++) {
vertical[j] += vec[i][j];
}
}
int result = INT_MAX;
int horizontalCut = 0;
for (int i = 0 ; i < n; i++) {
horizontalCut += horizontal[i];
result = min(result, abs(sum - horizontalCut - horizontalCut));
}
int verticalCut = 0;
for (int j = 0; j < m; j++) {
verticalCut += vertical[j];
result = min(result, abs(sum - verticalCut - verticalCut));
}
cout << result << endl;
}
```
时间复杂度： O(n^2)
其实本题可以在暴力求解的基础上，优化一下，就不用前缀和了，在行向遍历的时候，遇到行末尾就统一一下， 在列向遍历的时候，遇到列末尾就统计一下。
时间复杂度也是 O(n^2)
代码如下：
```CPP
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main () {
int n, m;
cin >> n >> m;
int sum = 0;
vector<vector<int>> vec(n, vector<int>(m, 0)) ;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> vec[i][j];
sum += vec[i][j];
}
}
int result = INT_MAX;
int count = 0; // 统计遍历过的行
for (int i = 0; i < n; i++) {
for (int j = 0 ; j < m; j++) {
count += vec[i][j];
// 遍历到行末尾时候开始统计
if (j == m - 1) result = min (result, abs(sum - count - count));
}
}
count = 0; // 统计遍历过的列
for (int j = 0; j < m; j++) {
for (int i = 0 ; i < n; i++) {
count += vec[i][j];
// 遍历到列末尾的时候开始统计
if (i == n - 1) result = min (result, abs(sum - count - count));
}
}
cout << result << endl;
}
```
## 其他语言版本
### Java
前缀和
```Java
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int sum = 0;
int[][] vec = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
vec[i][j] = scanner.nextInt();
sum += vec[i][j];
}
}
// 统计横向
int[] horizontal = new int[n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
horizontal[i] += vec[i][j];
}
}
// 统计纵向
int[] vertical = new int[m];
for (int j = 0; j < m; j++) {
for (int i = 0; i < n; i++) {
vertical[j] += vec[i][j];
}
}
int result = Integer.MAX_VALUE;
int horizontalCut = 0;
for (int i = 0; i < n; i++) {
horizontalCut += horizontal[i];
result = Math.min(result, Math.abs(sum - 2 * horizontalCut));
}
int verticalCut = 0;
for (int j = 0; j < m; j++) {
verticalCut += vertical[j];
result = Math.min(result, Math.abs(sum - 2 * verticalCut));
}
System.out.println(result);
scanner.close();
}
}
```
优化暴力
```Java
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int sum = 0;
int[][] vec = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
vec[i][j] = scanner.nextInt();
sum += vec[i][j];
}
}
int result = Integer.MAX_VALUE;
int count = 0; // 统计遍历过的行
// 行切分
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
count += vec[i][j];
// 遍历到行末尾时候开始统计
if (j == m - 1) {
result = Math.min(result, Math.abs(sum - 2 * count));
}
}
}
count = 0;
// 列切分
for (int j = 0; j < m; j++) {
for (int i = 0; i < n; i++) {
count += vec[i][j];
// 遍历到列末尾时候开始统计
if (i == n - 1) {
result = Math.min(result, Math.abs(sum - 2 * count));
}
}
}
System.out.println(result);
scanner.close();
}
}
```
### python
前缀和
```python
def main():
import sys
input = sys.stdin.read
data = input().split()
idx = 0
n = int(data[idx])
idx += 1
m = int(data[idx])
idx += 1
sum = 0
vec = []
for i in range(n):
row = []
for j in range(m):
num = int(data[idx])
idx += 1
row.append(num)
sum += num
vec.append(row)
# 统计横向
horizontal = [0] * n
for i in range(n):
for j in range(m):
horizontal[i] += vec[i][j]
# 统计纵向
vertical = [0] * m
for j in range(m):
for i in range(n):
vertical[j] += vec[i][j]
result = float('inf')
horizontalCut = 0
for i in range(n):
horizontalCut += horizontal[i]
result = min(result, abs(sum - 2 * horizontalCut))
verticalCut = 0
for j in range(m):
verticalCut += vertical[j]
result = min(result, abs(sum - 2 * verticalCut))
print(result)
if __name__ == "__main__":
main()
```
优化暴力
```python
def main():
import sys
input = sys.stdin.read
data = input().split()
idx = 0
n = int(data[idx])
idx += 1
m = int(data[idx])
idx += 1
sum = 0
vec = []
for i in range(n):
row = []
for j in range(m):
num = int(data[idx])
idx += 1
row.append(num)
sum += num
vec.append(row)
result = float('inf')
count = 0
# 行切分
for i in range(n):
for j in range(m):
count += vec[i][j]
# 遍历到行末尾时候开始统计
if j == m - 1:
result = min(result, abs(sum - 2 * count))
count = 0
# 列切分
for j in range(m):
for i in range(n):
count += vec[i][j]
# 遍历到列末尾时候开始统计
if i == n - 1:
result = min(result, abs(sum - 2 * count))
print(result)
if __name__ == "__main__":
main()
```

152
problems/kamacoder/0047.参会dijkstra堆.md
View File

@ -755,8 +755,160 @@ public class Main {
### Python
```python
import heapq
class Edge:
def __init__(self, to, val):
self.to = to
self.val = val
def dijkstra(n, m, edges, start, end):
grid = [[] for _ in range(n + 1)]
for p1, p2, val in edges:
grid[p1].append(Edge(p2, val))
minDist = [float('inf')] * (n + 1)
visited = [False] * (n + 1)
pq = []
heapq.heappush(pq, (0, start))
minDist[start] = 0
while pq:
cur_dist, cur_node = heapq.heappop(pq)
if visited[cur_node]:
continue
visited[cur_node] = True
for edge in grid[cur_node]:
if not visited[edge.to] and cur_dist + edge.val < minDist[edge.to]:
minDist[edge.to] = cur_dist + edge.val
heapq.heappush(pq, (minDist[edge.to], edge.to))
return -1 if minDist[end] == float('inf') else minDist[end]
# 输入
n, m = map(int, input().split())
edges = [tuple(map(int, input().split())) for _ in range(m)]
start = 1 # 起点
end = n # 终点
# 运行算法并输出结果
result = dijkstra(n, m, edges, start, end)
print(result)
```
### Go
```go
package main
import (
"container/heap"
"fmt"
"math"
)
// Edge 表示带权重的边
type Edge struct {
to, val int
}
// PriorityQueue 实现一个小顶堆
type Item struct {
node, dist int
}
type PriorityQueue []*Item
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].dist < pq[j].dist
}
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
}
func (pq *PriorityQueue) Push(x interface{}) {
*pq = append(*pq, x.(*Item))
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
item := old[n-1]
*pq = old[0 : n-1]
return item
}
func dijkstra(n, m int, edges [][]int, start, end int) int {
grid := make([][]Edge, n+1)
for _, edge := range edges {
p1, p2, val := edge[0], edge[1], edge[2]
grid[p1] = append(grid[p1], Edge{to: p2, val: val})
}
minDist := make([]int, n+1)
for i := range minDist {
minDist[i] = math.MaxInt64
}
visited := make([]bool, n+1)
pq := &PriorityQueue{}
heap.Init(pq)
heap.Push(pq, &Item{node: start, dist: 0})
minDist[start] = 0
for pq.Len() > 0 {
cur := heap.Pop(pq).(*Item)
if visited[cur.node] {
continue
}
visited[cur.node] = true
for _, edge := range grid[cur.node] {
if !visited[edge.to] && minDist[cur.node]+edge.val < minDist[edge.to] {
minDist[edge.to] = minDist[cur.node] + edge.val
heap.Push(pq, &Item{node: edge.to, dist: minDist[edge.to]})
}
}
}
if minDist[end] == math.MaxInt64 {
return -1
}
return minDist[end]
}
func main() {
var n, m int
fmt.Scan(&n, &m)
edges := make([][]int, m)
for i := 0; i < m; i++ {
var p1, p2, val int
fmt.Scan(&p1, &p2, &val)
edges[i] = []int{p1, p2, val}
}
start := 1 // 起点
end := n // 终点
result := dijkstra(n, m, edges, start, end)
fmt.Println(result)
}
```
### Rust
### Javascript

57
problems/kamacoder/0047.参会dijkstra朴素.md
View File

@ -806,6 +806,63 @@ public class Main {
### Python
```
import sys
def dijkstra(n, m, edges, start, end):
# 初始化邻接矩阵
grid = [[float('inf')] * (n + 1) for _ in range(n + 1)]
for p1, p2, val in edges:
grid[p1][p2] = val
# 初始化距离数组和访问数组
minDist = [float('inf')] * (n + 1)
visited = [False] * (n + 1)
minDist[start] = 0 # 起始点到自身的距离为0
for _ in range(1, n + 1): # 遍历所有节点
minVal = float('inf')
cur = -1
# 选择距离源点最近且未访问过的节点
for v in range(1, n + 1):
if not visited[v] and minDist[v] < minVal:
minVal = minDist[v]
cur = v
if cur == -1: # 如果找不到未访问过的节点，提前结束
break
visited[cur] = True # 标记该节点已被访问
# 更新未访问节点到源点的距离
for v in range(1, n + 1):
if not visited[v] and grid[cur][v] != float('inf') and minDist[cur] + grid[cur][v] < minDist[v]:
minDist[v] = minDist[cur] + grid[cur][v]
return -1 if minDist[end] == float('inf') else minDist[end]
if __name__ == "__main__":
input = sys.stdin.read
data = input().split()
n, m = int(data[0]), int(data[1])
edges = []
index = 2
for _ in range(m):
p1 = int(data[index])
p2 = int(data[index + 1])
val = int(data[index + 2])
edges.append((p1, p2, val))
index += 3
start = 1 # 起点
end = n # 终点
result = dijkstra(n, m, edges, start, end)
print(result)
```
### Go
### Rust

137
problems/kamacoder/0053.寻宝-Kruskal.md
View File

@ -404,8 +404,145 @@ Kruskal算法 时间复杂度 为 nlogn，其中n 为边的数量，适用稀疏
### Java
```Java
import java.util.*;
class Edge {
int l, r, val;
Edge(int l, int r, int val) {
this.l = l;
this.r = r;
this.val = val;
}
}
public class Main {
private static int n = 10001;
private static int[] father = new int[n];
// 并查集初始化
public static void init() {
for (int i = 0; i < n; i++) {
father[i] = i;
}
}
// 并查集的查找操作
public static int find(int u) {
if (u == father[u]) return u;
return father[u] = find(father[u]);
}
// 并查集的加入集合
public static void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return;
father[v] = u;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int v = scanner.nextInt();
int e = scanner.nextInt();
List<Edge> edges = new ArrayList<>();
int result_val = 0;
for (int i = 0; i < e; i++) {
int v1 = scanner.nextInt();
int v2 = scanner.nextInt();
int val = scanner.nextInt();
edges.add(new Edge(v1, v2, val));
}
// 执行Kruskal算法
edges.sort(Comparator.comparingInt(edge -> edge.val));
// 并查集初始化
init();
// 从头开始遍历边
for (Edge edge : edges) {
int x = find(edge.l);
int y = find(edge.r);
if (x != y) {
result_val += edge.val;
join(x, y);
}
}
System.out.println(result_val);
scanner.close();
}
}
```
### Python
```python
class Edge:
def __init__(self, l, r, val):
self.l = l
self.r = r
self.val = val
n = 10001
father = list(range(n))
def init():
global father
father = list(range(n))
def find(u):
if u != father[u]:
father[u] = find(father[u])
return father[u]
def join(u, v):
u = find(u)
v = find(v)
if u != v:
father[v] = u
def kruskal(v, edges):
edges.sort(key=lambda edge: edge.val)
init()
result_val = 0
for edge in edges:
x = find(edge.l)
y = find(edge.r)
if x != y:
result_val += edge.val
join(x, y)
return result_val
if __name__ == "__main__":
import sys
input = sys.stdin.read
data = input().split()
v = int(data[0])
e = int(data[1])
edges = []
index = 2
for _ in range(e):
v1 = int(data[index])
v2 = int(data[index + 1])
val = int(data[index + 2])
edges.append(Edge(v1, v2, val))
index += 3
result_val = kruskal(v, edges)
print(result_val)
```
### Go
### Rust

132
problems/kamacoder/0053.寻宝-prim.md
View File

@ -520,8 +520,140 @@ int main() {
### Java
```Java
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int v = scanner.nextInt();
int e = scanner.nextInt();
// 初始化邻接矩阵，所有值初始化为一个大值，表示无穷大
int[][] grid = new int[v + 1][v + 1];
for (int i = 0; i <= v; i++) {
Arrays.fill(grid[i], 10001);
}
// 读取边的信息并填充邻接矩阵
for (int i = 0; i < e; i++) {
int x = scanner.nextInt();
int y = scanner.nextInt();
int k = scanner.nextInt();
grid[x][y] = k;
grid[y][x] = k;
}
// 所有节点到最小生成树的最小距离
int[] minDist = new int[v + 1];
Arrays.fill(minDist, 10001);
// 记录节点是否在树里
boolean[] isInTree = new boolean[v + 1];
// Prim算法主循环
for (int i = 1; i < v; i++) {
int cur = -1;
int minVal = Integer.MAX_VALUE;
// 选择距离生成树最近的节点
for (int j = 1; j <= v; j++) {
if (!isInTree[j] && minDist[j] < minVal) {
minVal = minDist[j];
cur = j;
}
}
// 将最近的节点加入生成树
isInTree[cur] = true;
// 更新非生成树节点到生成树的距离
for (int j = 1; j <= v; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
}
}
}
// 统计结果
int result = 0;
for (int i = 2; i <= v; i++) {
result += minDist[i];
}
System.out.println(result);
scanner.close();
}
}
```
### Python
```python
def prim(v, e, edges):
import sys
import heapq
# 初始化邻接矩阵，所有值初始化为一个大值，表示无穷大
grid = [[10001] * (v + 1) for _ in range(v + 1)]
# 读取边的信息并填充邻接矩阵
for edge in edges:
x, y, k = edge
grid[x][y] = k
grid[y][x] = k
# 所有节点到最小生成树的最小距离
minDist = [10001] * (v + 1)
# 记录节点是否在树里
isInTree = [False] * (v + 1)
# Prim算法主循环
for i in range(1, v):
cur = -1
minVal = sys.maxsize
# 选择距离生成树最近的节点
for j in range(1, v + 1):
if not isInTree[j] and minDist[j] < minVal:
minVal = minDist[j]
cur = j
# 将最近的节点加入生成树
isInTree[cur] = True
# 更新非生成树节点到生成树的距离
for j in range(1, v + 1):
if not isInTree[j] and grid[cur][j] < minDist[j]:
minDist[j] = grid[cur][j]
# 统计结果
result = sum(minDist[2:v+1])
return result
if __name__ == "__main__":
import sys
input = sys.stdin.read
data = input().split()
v = int(data[0])
e = int(data[1])
edges = []
index = 2
for _ in range(e):
x = int(data[index])
y = int(data[index + 1])
k = int(data[index + 2])
edges.append((x, y, k))
index += 3
result = prim(v, e, edges)
print(result)
```
### Go
### Rust

104
problems/kamacoder/0058.区间和.md
View File

@ -93,7 +93,6 @@ int main() {
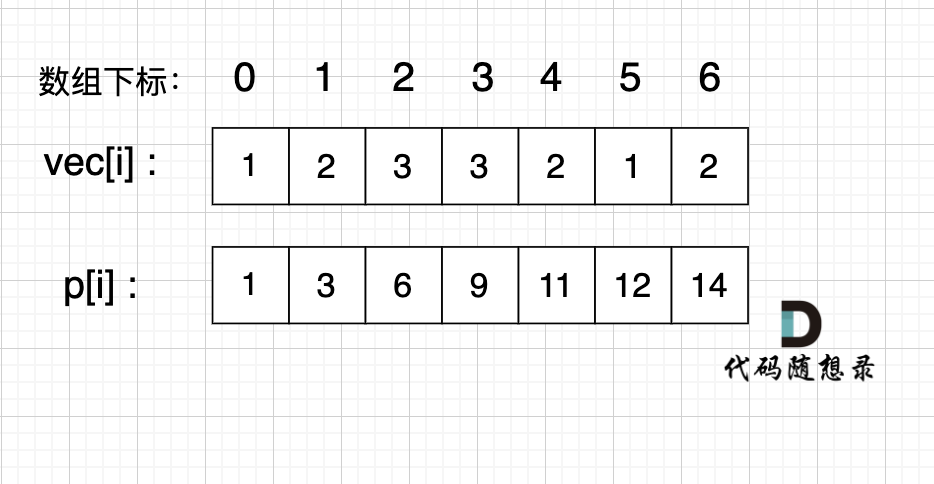
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240627110604.png)
如果，我们想统计，在vec数组上 下标 2 到下标 5 之间的累加和，那是不是就用 p[5] - p[1] 就可以了。
为什么呢？
@ -114,7 +113,11 @@ p[5] - p[1] 就是 红色部分的区间和。
而 p 数组是我们之前就计算好的累加和，所以后面每次求区间和的之后 我们只需要 O(1)的操作。
**特别注意**： 在使用前缀和求解的时候，要特别注意 求解区间。
如上图，如果我们要求 区间下标 [2, 5] 的区间和，那么应该是 p[5] - p[1]，而不是 p[5] - p[2]。
很多录友在使用前缀和的时候，分不清前缀和的区间，建议画一画图，模拟一下 思路会更清晰。
```CPP
#include <iostream>
@ -142,6 +145,8 @@ int main() {
```
C++ 代码 面对大量数据 读取 输出操作，最好用scanf 和 printf，耗时会小很多：
```CPP
#include <iostream>
#include <vector>
@ -168,24 +173,89 @@ int main() {
```
```CPP
## 其他语言版本
#include<bits/stdc++.h>
using namespace std;
### Java
```Java
int main(){
int n, a, b;
cin >> n;
vector<int> vec(n + 1);
vector<int> p(n + 1, 0);
for(int i = 1; i <= n; i++) {
scanf("%d", &vec[i]);
p[i] = p[i - 1] + vec[i];
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int[] vec = new int[n];
int[] p = new int[n];
int presum = 0;
for (int i = 0; i < n; i++) {
vec[i] = scanner.nextInt();
presum += vec[i];
p[i] = presum;
}
while (scanner.hasNextInt()) {
int a = scanner.nextInt();
int b = scanner.nextInt();
int sum;
if (a == 0) {
sum = p[b];
} else {
sum = p[b] - p[a - 1];
}
System.out.println(sum);
}
scanner.close();
}
while(~scanf("%d%d", &a, &b)){
printf("%d\n", p[b + 1] - p[a]);
}
return 0;
}
}
```
### Python
```python
import sys
input = sys.stdin.read
def main():
data = input().split()
index = 0
n = int(data[index])
index += 1
vec = []
for i in range(n):
vec.append(int(data[index + i]))
index += n
p = [0] * n
presum = 0
for i in range(n):
presum += vec[i]
p[i] = presum
results = []
while index < len(data):
a = int(data[index])
b = int(data[index + 1])
index += 2
if a == 0:
sum_value = p[b]
else:
sum_value = p[b] - p[a - 1]
results.append(sum_value)
for result in results:
print(result)
if __name__ == "__main__":
main()
```

2
problems/kamacoder/0095.城市间货物运输II.md
View File

@ -78,7 +78,7 @@ circle
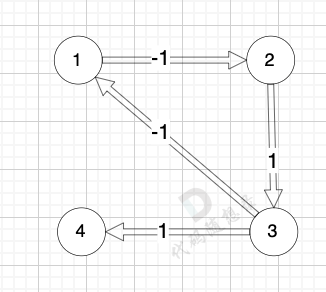
我们拿题目中示例来画一个图：
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240402103135.png)
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240705161426.png)
图中 节点1 到 节点4 的最短路径是多少（题目中的最低运输成本） （注意边可以为负数的）

2
problems/kamacoder/0096.城市间货物运输III.md
View File

@ -65,7 +65,7 @@
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240402115614.png)
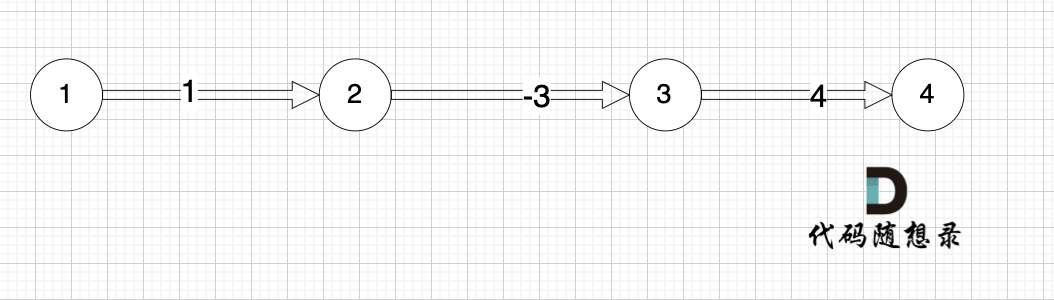
图中，节点2 最多已经经过2个节点 到达节点4，那么中间是有多少条边呢，是 3 条边对吧。
图中，节点1 最多已经经过2个节点 到达节点4，那么中间是有多少条边呢，是 3 条边对吧。
所以本题就是求：起点最多经过k + 1 条边到达终点的最短距离。

2
problems/kamacoder/0098.所有可达路径.md
View File

@ -83,7 +83,7 @@
如果笔试的时候出一道原题 （笔试都是ACM模式，部分面试也是ACM模式），不少熟练刷力扣的录友都难住了，因为不知道图应该怎么存，也不知道自己存的图如何去遍历。
所以这也是为什么我要让大家练习 ACM模式
所以这也是为什么我要让大家练习 ACM模式，也是我为什么 在代码随想录图论讲解中，不惜自己亲自出题，让大家统一练习ACM模式。
--------

10
problems/kamacoder/0105.有向图的完全可达性.md
View File

@ -114,11 +114,11 @@ void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
```C++
// 写法二：处理下一个要访问的节点
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
list<int> keys = rooms[key];
list<int> keys = graph[key];
for (int key : keys) {
if (visited[key] == false) { // 确认下一个是没访问过的节点
visited[key] = true;
dfs(rooms, key, visited);
dfs(graph, key, visited);
}
}
}
@ -202,11 +202,11 @@ int main() {
using namespace std;
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
list<int> keys = rooms[key];
list<int> keys = graph[key];
for (int key : keys) {
if (visited[key] == false) { // 确认下一个是没访问过的节点
visited[key] = true;
dfs(rooms, key, visited);
dfs(graph, key, visited);
}
}
}
@ -223,7 +223,7 @@ int main() {
}
vector<bool> visited(n + 1, false);
visited[0] = true; // 节点1 预先处理
visited[1] = true; // 节点1 预先处理
dfs(graph, 1, visited);
for (int i = 1; i <= n; i++) {

147
problems/kamacoder/0135.获取连通的相邻节点列表.md Normal file
View File

@ -0,0 +1,147 @@
# 135. 获取连通的相邻节点列表
本题是一个 “阅读理解”题，其实题目的算法很简单，但理解题意很费劲。
题目描述中的【提示信息】 是我后加上去了，华为笔试的时候没有这个 【提示信息】。
相信没有 【提示信息】大家理解题意 平均要多用半个小时。
思路：
1. 将第一行数据加入set中
2. 后面输出数据，判断是否在 set里
3. 最后把结果排个序
```CPP
#include <iostream>
#include <vector>
#include <algorithm>
#include <unordered_set>
using namespace std;
int main() {
unordered_set<int> uset;
int n, a;
cin >> n;
while (n--) {
cin >> a;
uset.insert(a);
}
int m, x, vlan_id;
long long tb;
vector<long long> vecTB;
cin >> m;
while(m--) {
cin >> tb;
cin >> x;
vector<long long> vecVlan_id(x);
for (int i = 0; i < x; i++) {
cin >> vecVlan_id[i];
}
for (int i = 0; i < x; i++) {
if (uset.find(vecVlan_id[i]) != uset.end()) {
vecTB.push_back(tb);
break;
}
}
}
cout << vecTB.size() << endl;
if (vecTB.size() != 0) {
sort(vecTB.begin(), vecTB.end());
for (int i = 0; i < vecTB.size() ; i++) cout << vecTB[i] << " ";
}
}
```
## 其他语言版本
### Java
```Java
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
Set<Integer> uset = new HashSet<>();
int n = scanner.nextInt();
while (n-- > 0) {
int a = scanner.nextInt();
uset.add(a);
}
int m = scanner.nextInt();
List<Long> vecTB = new ArrayList<>();
while (m-- > 0) {
long tb = scanner.nextLong();
int x = scanner.nextInt();
List<Integer> vecVlan_id = new ArrayList<>();
for (int i = 0; i < x; i++) {
vecVlan_id.add(scanner.nextInt());
}
for (int vlanId : vecVlan_id) {
if (uset.contains(vlanId)) {
vecTB.add(tb);
break;
}
}
}
System.out.println(vecTB.size());
if (!vecTB.isEmpty()) {
Collections.sort(vecTB);
for (long tb : vecTB) {
System.out.print(tb + " ");
}
}
}
}
```
### Python
```python
def main():
import sys
input = sys.stdin.read
data = input().split()
index = 0
n = int(data[index])
index += 1
uset = set()
for _ in range(n):
a = int(data[index])
index += 1
uset.add(a)
m = int(data[index])
index += 1
vecTB = []
while m > 0:
tb = int(data[index])
index += 1
x = int(data[index])
index += 1
vecVlan_id = []
for _ in range(x):
vecVlan_id.append(int(data[index]))
index += 1
for vlan_id in vecVlan_id:
if vlan_id in uset:
vecTB.append(tb)
break
m -= 1
print(len(vecTB))
if vecTB:
vecTB.sort()
print(" ".join(map(str, vecTB)))
if __name__ == "__main__":
main()
```

148
problems/kamacoder/0136.字符串处理器.md Normal file
View File

@ -0,0 +1,148 @@
# 字符串处理器
纯模拟，但情况比较多，非常容易 空指针异常。
大家要注意，边界问题 以及 负数问题。
整体代码如下：
```CPP
#include<bits/stdc++.h>
using namespace std;
int main() {
int index = 0;
long long optNum;
string s;
string cmd;
while(cin >> cmd){
//cout << s << endl;
if(cmd == "insert") {
string buff;
cin >> buff;
s.insert(index, buff);
index += buff.size();
}
else if(cmd == "move") {
cin >> optNum;
if(optNum > 0 && index + optNum <= s.size()) index += optNum;
if(optNum < 0 && index >= -optNum) index += optNum;
}
else if(cmd == "delete") {
cin >> optNum;
if(index >= optNum && optNum > 0){
s.erase(index - optNum, optNum);
index -= optNum;
}
}
else if(cmd == "copy") {
if(index > 0) {
string tmp = s.substr(0, index);
s.insert(index, tmp);
}
}
else if(cmd == "end") {
for(int i = 0; i < index; i++) {
cout << s[i];
}
cout << '|';
for(int i = index; i < s.size(); i++) cout << s[i];
break;
}
}
return 0;
}
```
## 其他语言版本
### Java
```Java
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
StringBuilder s = new StringBuilder();
int index = 0;
int optNum;
while (true) {
String cmd = scanner.next();
if (cmd.equals("insert")) {
String buff = scanner.next();
s.insert(index, buff);
index += buff.length();
} else if (cmd.equals("move")) {
optNum = scanner.nextInt();
if (optNum > 0 && index + optNum <= s.length()) index += optNum;
if (optNum < 0 && index >= -optNum) index += optNum;
} else if (cmd.equals("delete")) {
optNum = scanner.nextInt();
if (index >= optNum && optNum > 0) {
s.delete(index - optNum, index);
index -= optNum;
}
} else if (cmd.equals("copy")) {
if (index > 0) {
String tmp = s.substring(0, index);
s.insert(index, tmp);
}
} else if (cmd.equals("end")) {
System.out.print(s.substring(0, index) + '|' + s.substring(index));
break;
}
}
scanner.close();
}
}
```
### Python
```python
def main():
import sys
input = sys.stdin.read
data = input().split()
s = ""
index = 0
i = 0
while i < len(data):
cmd = data[i]
i += 1
if cmd == "insert":
buff = data[i]
i += 1
s = s[:index] + buff + s[index:]
index += len(buff)
elif cmd == "move":
optNum = int(data[i])
i += 1
if optNum > 0 and index + optNum <= len(s):
index += optNum
elif optNum < 0 and index >= -optNum:
index += optNum
elif cmd == "delete":
optNum = int(data[i])
i += 1
if index >= optNum and optNum > 0:
s = s[:index - optNum] + s[index:]
index -= optNum
elif cmd == "copy":
if index > 0:
tmp = s[:index]
s = s[:index] + tmp + s[index:]
elif cmd == "end":
print(s[:index] + '|' + s[index:])
break
if __name__ == "__main__":
main()
```

192
problems/kamacoder/0137.消息传输.md Normal file
View File

@ -0,0 +1,192 @@
# 137. 消息传输
这道题目，普通广搜就可以解决。
这里说一下几点注意事项：
1、 题目描述中，注意 n 是列数，m是行数
这是造成很多录友周赛的时候提交 返回 【运行错误】的罪魁祸首，如果 输入用例是 正方形，那没问题，如果后台输入用例是矩形， n 和 m 搞反了，就会数组越界。
矩阵是 m * n ，但输入的顺序却是 先输入n 再输入 m。
这会让很多人把矩阵的 n 和 m 搞反。
其实规范出题，就应该是n 行，m列，然后 先输入n，在输入m。
只能说 大厂出题的人，也不是专业出题的，所以会在 非算法方面一不小心留下很多 “bug”，消耗大家的精力。
2、再写广搜的时候，可能担心会无限循环
即 A 走到 B，B又走到A，A又走到B ，这种情况，一般来说 广搜都是用一个 visit数组来标记的。
但本题不用，因为 不会重复走的，题图里的信号都是正数，根据距离判断大小 可以保证不走回头路。
```CPP
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
const int inf = 1e6;
int main () {
int n, m, startx, starty;
cin >> n >> m;
cin >> startx >> starty;
vector<vector<int>> grid(m, vector<int>(n));
vector<vector<int>> dis(m, vector<int>(n, inf));
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
cin >> grid[i][j];
}
}
queue<pair<int, int>> que;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
que.push(pair<int, int>(startx, starty));
dis[startx][starty] = 0;
while(!que.empty()) {
pair<int, int> cur = que.front(); que.pop();
for (int i = 0; i < 4; i++) {
int newx = cur.first + dir[i][1];
int newy = cur.second + dir[i][0];
if (newx < 0 || newx >= m || newy < 0 || newy >= n || grid[cur.first][cur.second] == 0) continue;
if (dis[newx][newy] > dis[cur.first][cur.second] + grid[cur.first][cur.second]) {
dis[newx][newy] = dis[cur.first][cur.second] + grid[cur.first][cur.second];
que.push(pair<int, int>(newx, newy));
}
}
}
int result = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (dis[i][j] == inf) {
cout << -1 << endl;
return 0;
}
result = max(result, dis[i][j]);
}
}
cout << result << endl;
}
```
## 其他语言版本
### Java
```Java
import java.util.*;
public class Main {
static final int INF = 1000000;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int startX = scanner.nextInt();
int startY = scanner.nextInt();
int[][] grid = new int[m][n];
int[][] dis = new int[m][n];
for (int i = 0; i < m; i++) {
Arrays.fill(dis[i], INF);
for (int j = 0; j < n; j++) {
grid[i][j] = scanner.nextInt();
}
}
Queue<int[]> queue = new LinkedList<>();
int[][] directions = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};
queue.add(new int[]{startX, startY});
dis[startX][startY] = 0;
while (!queue.isEmpty()) {
int[] current = queue.poll();
for (int[] dir : directions) {
int newX = current[0] + dir[0];
int newY = current[1] + dir[1];
if (newX >= 0 && newX < m && newY >= 0 && newY < n && grid[current[0]][current[1]] != 0) {
if (dis[newX][newY] > dis[current[0]][current[1]] + grid[current[0]][current[1]]) {
dis[newX][newY] = dis[current[0]][current[1]] + grid[current[0]][current[1]];
queue.add(new int[]{newX, newY});
}
}
}
}
int result = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (dis[i][j] == INF) {
System.out.println(-1);
return;
}
result = Math.max(result, dis[i][j]);
}
}
System.out.println(result);
scanner.close();
}
}
```
### Python
```Python
from collections import deque
inf = 1000000
def main():
import sys
input = sys.stdin.read
data = input().split()
index = 0
n = int(data[index])
m = int(data[index+1])
startx = int(data[index+2])
starty = int(data[index+3])
index += 4
grid = []
dis = [[inf] * n for _ in range(m)]
for i in range(m):
grid.append([int(data[index+j]) for j in range(n)])
index += n
directions = [(0, 1), (1, 0), (-1, 0), (0, -1)]
queue = deque()
queue.append((startx, starty))
dis[startx][starty] = 0
while queue:
curx, cury = queue.popleft()
for dx, dy in directions:
newx, newy = curx + dx, cury + dy
if 0 <= newx < m and 0 <= newy < n and grid[curx][cury] != 0:
if dis[newx][newy] > dis[curx][cury] + grid[curx][cury]:
dis[newx][newy] = dis[curx][cury] + grid[curx][cury]
queue.append((newx, newy))
result = 0
for i in range(m):
for j in range(n):
if dis[i][j] == inf:
print(-1)
return
result = max(result, dis[i][j])
print(result)
if __name__ == "__main__":
main()
```

101
problems/kamacoder/0139.可爱串.md Normal file
View File

@ -0,0 +1,101 @@
# 可爱串
整体思路，就含有 子序列的字符串数量 减去 含有子串的字符串数量。
因为子序列数量已经是包含子串数量的。 剩下的就是 只有子序列 且没有子串的 字符串数量。
需要注意我们求的不是 长度为 i 的字符串里有多少个 red 子序列。
**而是 可以有多少个 长度为i 的字符串 含有子序列 red**
同理，可以有多少个长度为i的字符串含有 red 子串
认清这一点很重要！
### 求子串
dp2[i][3] 长度为i 且 含有子串 red 的字符串数量 有多少
dp2[i][2] 长度为i 且 含有子串 re 的字符串数量有多少
dp2[i][1] 长度为 i 且 含有子串 r 的字符串数量有多少
dp2[1][0] 长度为 i 且 含有 只有 de, ee , e, d的字符串的字符串数量有多少。
```CPP
// 求子串
dp2[0][0] = 1;
for(int i = 1;i <= n; i++) {
dp2[i][0] = (dp2[i - 1][2] + dp2[i - 1][1] + dp2[i - 1][0] * 2) % mod; // 含有 re 的可以把 r改成d， 含有r 的可以改成
dp2[i][1] = (dp2[i - 1][2] + dp2[i - 1][1] + dp2[i - 1][0]) % mod;
dp2[i][2] = (dp2[i - 1][1]);
dp2[i][3] = (dp2[i - 1][3] * 3 + dp2[i - 1][2]) % mod;
}
``
### 求子序列
dp1[i][3] 长度为i 且 含有子序列 red 的字符串数量 有多少
dp2[i][2] 长度为i 且 含有子序列 re 的字符串数量有多少
dp2[i][1] 长度为 i 且 含有子序列 r 的字符串数量有多少
dp2[1][0] 长度为 i 且 含有 只含有 e 和 d 的字符串的字符串数量有多少。
```CPP
// 求子序列
dp1[0][0]=1;
for(int i=1;i<=n;i++)
{
dp1[i][0] = (dp1[i - 1][0] * 2) % mod;
dp1[i][1] = (dp1[i - 1][0] + dp1[i - 1][1] * 2) % mod;
dp1[i][2] = (dp1[i - 1][1] + dp1[i - 1][2] * 2) % mod;
dp1[i][3] = (dp1[i - 1][2] + dp1[i - 1][3] * 3) % mod;
}
```
```CPP
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
const int mod=1e9+7;
int main()
{
int n;
cin>>n;
vector<vector<ll>> dp1(n + 1,vector<ll> (4,0));
vector<vector<ll>> dp2(n + 1,vector<ll> (4,0));
// 求子串
dp2[0][0] = 1;
for(int i = 1;i <= n; i++) {
dp2[i][0] = (dp2[i - 1][2] + dp2[i - 1][1] + dp2[i - 1][0] * 2) % mod;
dp2[i][1] = (dp2[i - 1][2] + dp2[i - 1][1] + dp2[i - 1][0]) % mod;
dp2[i][2] = (dp2[i - 1][1]);
dp2[i][3] = (dp2[i - 1][3] * 3 + dp2[i - 1][2]) % mod;
}
// 求子序列
dp1[0][0]=1;
for(int i=1;i<=n;i++)
{
dp1[i][0] = (dp1[i - 1][0] * 2) % mod;
dp1[i][1] = (dp1[i - 1][0] + dp1[i - 1][1] * 2) % mod;
dp1[i][2] = (dp1[i - 1][1] + dp1[i - 1][2] * 2) % mod;
dp1[i][3] = (dp1[i - 1][2] + dp1[i - 1][3] * 3) % mod;
}
cout<<(dp1[n][3] - dp2[n][3])%mod;
}
```

30
problems/kamacoder/两个字符串的最小ASCII删除总和.md Normal file
View File

@ -0,0 +1,30 @@
本题和[代码随想录：两个字符串的删除操作](https://www.programmercarl.com/0583.%E4%B8%A4%E4%B8%AA%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%88%A0%E9%99%A4%E6%93%8D%E4%BD%9C.html) 思路基本是一样的。
```CPP
#include <iostream>
#include <vector>
using namespace std;
int main() {
string s1, s2;
cin >> s1 >> s2;
vector<vector<int>> dp(s1.size() + 1, vector<int>(s2.size() + 1, 0));
// s1 如果变成空串的最小删除ASCLL值综合
for (int i = 1; i <= s1.size(); i++) dp[i][0] = dp[i - 1][0] + s1[i - 1];
// s2 如果变成空串的最小删除ASCLL值综合
for (int j = 1; j <= s2.size(); j++) dp[0][j] = dp[0][j - 1] + s2[j - 1];
for (int i = 1; i <= s1.size(); i++) {
for (int j = 1; j <= s2.size(); j++) {
if (s1[i - 1] == s2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
else dp[i][j] = min(dp[i - 1][j] + s1[i - 1], dp[i][j - 1] + s2[j - 1]);
}
}
cout << dp[s1.size()][s2.size()] << endl;
}
```

93
problems/kamacoder/图论为什么用ACM模式.md Normal file
View File

@ -0,0 +1,93 @@
# 图论为什么统一使用ACM模式
代码随想录图论章节给大家统一换成ACM输入输出模式。
图论是在笔试还有面试中，通常都是以ACM模式来考察大家，而大家习惯在力扣刷题（核心代码模式），核心代码模式对图的存储和输出都隐藏了。
而图论题目的输出输出 相对其他类型题目来说是最难处理的。
ACM模式是最考察候选人对代码细节把控程度的， 图的构成，图的输出，这些只有ACM输入输出模式才能体现出来。
### 输入的细节
图论的输入难在 图的存储结构，**如果没有练习过 邻接表和邻接矩阵 ，很多录友是写不出来的**。
而力扣上是直接给好现成的 数据结构，可以直接用，所以练习不到图的输入，也练习不到邻接表和邻接矩阵。
**如果连邻接表 和 邻接矩阵都不知道或者写不出来的话，可以说 图论没有入门**。
举个例子，对于力扣 [797.所有可能的路径](https://leetcode.cn/problems/all-paths-from-source-to-target/description/) ，录友了解深度优先搜索之后，这道题目就是模板题，是送分题。
如果面试的时候出一道原题 （笔试都是ACM模式，部分面试也是ACM模式），不少熟练刷力扣的录友都难住了，**因为不知道图应该怎么存，也不知道自己存的图如何去遍历**。
即使面试的时候，有的面试官，让你用核心代码模式做题，当你写出代码后，**面试官补充一句：这个图 你是怎么存的**？
难道和面试官说：我只知道图的算法，但我不知道图怎么存。
后面大家在刷 代码随想录图论第一题[98. 所有可达路径](./0098.所有可达路径.md) 的时候，就可以感受到图存储的难点所在。
所以这也是为什么我要让大家练习 ACM模式，也是我为什么 在代码随想录图论讲解中，不惜自己亲自出题，让大家统一练习ACM模式。
### 输出的细节
同样，图论的输出也有细节，例如 求节点1 到节点5的所有路径， 输出可能是：
```
1 2 4 5
1 3 5
```
表示有两条路可以到节点5， 那储存这个结果需要二维数组，最后在一起输出，力扣是直接return数组就好了，但 ACM模式要求我们自己输出，这里有就细节了。
就拿 只输出一行数据，输出 `1 2 4 5` 来说，
很多录友代码可能直接就这么写了：
```CPP
for (int i = 0 ; i < result.size(); i++) {
cout << result[i] << " ";
}
```
这么写输出的结果是 `1 2 4 5 `， 发现结果是对的，一提交，发现OJ返回 格式错误 或者 结果错误。
如果没练习过这种输出方式的录友，就开始怀疑了，这结果一样一样的，怎么就不对，我在力扣上提交都是对的！
**大家要注意，5 后面要不要有空格**！
上面这段代码输出，5后面是加上了空格了，如果判题机判断 结果的长度，标准答案`1 2 4 5`长度是7，而上面代码输出的长度是 8，很明显就是不对的。
所以正确的写法应该是：
```CPP
for (int i = 0 ; i < result.size() - 1; i++) {
cout << result[i] << " ";
}
cout << result[result.size() - 1];
```
这么写，最后一个元素后面就没有空格了。
这是很多录友经常疏忽的，也是大家刷习惯了 力扣（核心代码模式）根本不会注意到的细节。
**同样在工程开发中，这些细节都是影响系统稳定运行的因素之一**。
**ACM模式 除了考验算法思路，也考验 大家对 代码的把控力度**， 而 核心代码模式 只注重算法的解题思路，所以输入输出这些就省略掉了。
### 其他
**大家如果熟练ACM模式，那么核心代码模式没问题，但反过来就不一定了**。
而且我在讲解图论的时候，最头疼的就是找题，在力扣上 找题总是找不到符合思路且来完整表达算法精髓的题目。
特别是最短路算法相关的题目，例如 Bellman_ford系列 ，Floyd ，A * 等等总是找不到符合思路的题目。
索性统一我自己来出题，这其中也是巨大的工作量。为了给大家带来极致的学习体验，我在很多细节上都下了功夫。
等大家将图论刷完，就会感受到我的良苦用心。加油

2
problems/kamacoder/图论理论基础.md
View File

@ -3,6 +3,8 @@
这一篇我们正式开始图论！
代码随想录图论中的算法题目将统一使用ACM模式，[为什么要使用ACM模式](./图论为什么用ACM模式.md)
## 图的基本概念
二维坐标中，两点可以连成线，多个点连成的线就构成了图。

104
problems/kamacoder/好二叉树.md Normal file
View File

@ -0,0 +1,104 @@
本题和 [96.不同的二叉搜索树](https://www.programmercarl.com/0096.%E4%B8%8D%E5%90%8C%E7%9A%84%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91.html) 比较像
* 取模这里很容易出错
* 过程中所用到的数值都有可能超过int，所以要改用longlong
```CPP
#include <iostream>
#include <vector>
using namespace std;
long long mod = 1e9 + 7;
long long dp(int t, vector<long long>& memory) {
if (t % 2 == 0) return 0;
if (t == 1) return 1;
if (memory[t] != -1) return memory[t];
long long result = 0;
// 枚举左右子树节点的数量
for (int i = 1; i < t; i += 2) {
long long leftNum = dp(i, memory); // 左子树节点数量为i
long long rightNum = dp(t - i - 1, memory); // 右子树节点数量为t - i - 1
result += (leftNum * rightNum) % mod; // 注意这里是乘的关系
result %= mod;
}
memory[t] = result;
return result;
}
int main() {
int n;
cin >> n;
vector<long long> memory(n + 1, -1);
cout << dp(n, memory) << endl;
}
```
```CPP
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
const int MOD = 1000000007;
int main() {
int num;
cin >> num;
if (num % 2 == 0) {
cout << 0 << endl;
return 0;
}
vector<long long> dp(num + 1, 0);
dp[1] = 1;
for (int i = 3; i <= num; i += 2) {
for (int j = 1; j <= i - 2; j += 2) {
dp[i] = (dp[i] + dp[j] * dp[i - 1 - j]) % MOD;
}
}
cout << dp[num] << endl;
return 0;
}
```
第二题的代码
#include <bits/stdc++.h>
using namespace std;
long fastexp(long base,long n,long mod){
long answer = 1;
while(n > 0){
if(n % 2 == 1){
answer = (answer * base) % mod;
}
base = (base * base) % mod;
n /= 2;
}
return answer;
}
int kawaiiStrings(int n) {
// write code here
std::vector<long> f(n + 1), g(n + 1), h(n + 1);
long mod = 1000000007;
for (long i = 2; i <= n; i++) g[i] = (g[i - 1] * 2 + (i - 1) * fastexp(2,i-2,mod)) % mod;
for (long i = 3; i <= n; i++) f[i] = ((f[i - 1] * 3) % mod + g[i - 1]) % mod;
for (long i = 3; i <= n; i++) h[i] = (fastexp(3, i - 3, mod) + h[i - 1] * 3 - h[i - 3]) % mod;
return (f[n]-h[n]+mod)%mod;
}
int main(){
int n;
cin >> n;
cout << kawaiiStrings(n) << endl;
return 0;
}

50
problems/kamacoder/字符串处理器.md
View File

@ -1,50 +0,0 @@
```CPP
#include<bits/stdc++.h>
using namespace std;
int main() {
int index = 0;
long long optNum;
string s;
string cmd;
while(cin >> cmd){
//cout << s << endl;
if(cmd == "insert"){
string buff;
cin >> buff;
s.insert(index, buff);
index += buff.size();
}
else if(cmd == "move"){
cin >> optNum;
if(optNum > 0 && index + optNum <= s.size()) index += optNum;
if(optNum < 0 && index >= -optNum) index += optNum;
}
else if(cmd == "delete"){
cin >> optNum;
if(index >= optNum && optNum != 0){
s.erase(index - optNum, optNum);
index -= optNum;
}
}
else if(cmd == "copy"){
if(index > 0) {
string tmp = s.substr(0, index);
s.insert(index, tmp);
}
}
else if(cmd == "end"){
for(int i = 0; i < index; i++) {
cout << s[i];
}
cout << '|';
for(int i = index; i < s.size(); i++){
cout << s[i];
}
break;
}
}
return 0;
}
```

29
problems/kamacoder/完美数.md Normal file
View File

@ -0,0 +1,29 @@
```CPP
#include <iostream>
#include <vector>
using namespace std;
int countOnes(long long num) {
int zeroCount = 0;
while (num > 0) {
if (num % 10 != 0) { // 检查最低位是否为0
zeroCount++;
}
num /= 10; // 移除最低位
}
return zeroCount;
}
int main() {
int n;
cin >> n;
vector<int> vec(n);
for (int i = 0; i < n; i++) cin >> vec[i];
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (countOnes(vec[i] * vec[j]) == 1) result++;
}
}
cout << result << endl;
}
```

109
problems/kamacoder/小红的区间翻转.md Normal file
View File

@ -0,0 +1,109 @@
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] a = new int[n];
int[] b = new int[n];
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
for (int i = 0; i < n; i++) {
b[i] = sc.nextInt();
}
int p = -1, s = -1;
for (int i = 0; i < n; i++) {
if (a[i] == b[i]) p = i;
else break;
}
for (int j = n - 1 ; j >= 0 ; j--) {
if (a[j] == b[j]) s = j;
else break;
}
boolean[][] dp = new boolean[n][n];
int res = 0;
for (int j = 0; j < n; j++) {
for (int i = j ; i >= 0 ; i--) {
if (i == j) dp[i][j] = a[i] == b[i];
else if (i + 1 == j) dp[i][j] = (a[i] == b[j] && a[j] == b[i]);
else {
dp[i][j] = dp[i+1][j-1] && (a[i] == b[j] && a[j] == b[i]);
}
if (dp[i][j] && (i == 0 || p >= i-1) && (j == n - 1 || j+1 >= s)) res++;
}
}
System.out.println(res);
}
}
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] a = new int[n];
int[] b = new int[n];
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
for (int i = 0; i < n; i++) {
b[i] = sc.nextInt();
}
int count = 0;
// 遍历所有可能的区间
for (int left = 0; left < n; left++) {
for (int right = left; right < n; right++) {
// 检查翻转区间 [left, right] 后，a 是否可以变成 b
if (canTransform(a, b, left, right)) {
count++;
}
}
}
System.out.println(count);
}
private static boolean canTransform(int[] a, int[] b, int left, int right) {
// 提前检查翻转区间的值是否可以匹配
for (int i = left, j = right; i <= right; i++, j--) {
if (a[i] != b[j]) {
return false;
}
}
// 检查翻转区间外的值是否匹配
for (int i = 0; i < left; i++) {
if (a[i] != b[i]) {
return false;
}
}
for (int i = right + 1; i < a.length; i++) {
if (a[i] != b[i]) {
return false;
}
}
return true;
}
}

81
problems/kamacoder/最长同值路径.md Normal file
View File

@ -0,0 +1,81 @@
```CPP
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
// 定义二叉树节点结构
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
// 根据层序遍历数组构建二叉树
TreeNode* constructBinaryTree(const vector<string>& levelOrder) {
if (levelOrder.empty()) return NULL;
TreeNode* root = new TreeNode(stoi(levelOrder[0]));
queue<TreeNode*> q;
q.push(root);
int i = 1;
while (!q.empty() && i < levelOrder.size()) {
TreeNode* current = q.front();
q.pop();
if (i < levelOrder.size() && levelOrder[i] != "null") {
current->left = new TreeNode(stoi(levelOrder[i]));
q.push(current->left);
}
i++;
if (i < levelOrder.size() && levelOrder[i] != "null") {
current->right = new TreeNode(stoi(levelOrder[i]));
q.push(current->right);
}
i++;
}
return root;
}
int result = 0;
int dfs(TreeNode* node) {
if (node == NULL) return 0;
int leftPath = dfs(node->left);
int rightPath = dfs(node->right);
int leftNum = 0, rightNum = 0;
if (node->left != NULL && node->left->val == node->val) {
leftNum = leftPath + 1;
}
if (node->right != NULL && node->right->val == node->val) {
rightNum = rightPath + 1;
}
result = max(result, leftNum + rightNum);
return max(leftNum, rightNum);
}
int main() {
int n;
cin >> n;
vector<string> levelOrder(n);
for (int i = 0; i < n ; i++) cin >> levelOrder[i];
TreeNode* root = constructBinaryTree(levelOrder);
dfs(root);
cout << result << endl;
return 0;
}
```

47
problems/kamacoder/获取连通的相邻节点列表.md
View File

@ -1,47 +0,0 @@
```CPP
#include <iostream>
#include <vector>
#include <algorithm>
#include <unordered_set>
using namespace std;
int main() {
unordered_set<int> uset;
int n, a;
cin >> n;
while (n--) {
cin >> a;
uset.insert(a);
}
int m, x, vlan_id;
long long tb;
vector<long long> vecTB;
cin >> m;
while(m--) {
cin >> tb;
cin >> x;
vector<long long> vecVlan_id(x);
for (int i = 0; i < x; i++) {
cin >> vecVlan_id[i];
}
for (int i = 0; i < x; i++) {
if (uset.find(vecVlan_id[i]) != uset.end()) {
vecTB.push_back(tb);
break;
}
}
}
cout << vecTB.size() << endl;
if (vecTB.size() != 0) {
sort(vecTB.begin(), vecTB.end());
for (int i = 0; i < vecTB.size() ; i++) cout << vecTB[i] << " ";
}
}
```