Update

2025-07-09 11:34:46 +08:00 · 2021-07-26 11:18:29 +08:00
parent bafa3da280
commit f1b862c814
10 changed files with 490 additions and 74 deletions
--- a/problems/0042.接雨水.md
+++ b/problems/0042.接雨水.md
@ -364,6 +364,14 @@ public:

 ## 其他语言版本 

+Java: 
+
+Python:
+
+Go:
+
+JavaScript:
+

 -----------------------
 * 作者微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
--- a/problems/0101.对称二叉树.md
+++ b/problems/0101.对称二叉树.md
@ -7,7 +7,7 @@
 <p align="center"><strong>欢迎大家<a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>


-## 101. 对称二叉树
+# 101. 对称二叉树

 题目地址：https://leetcode-cn.com/problems/symmetric-tree/

@ -15,7 +15,7 @@

 ![101. 对称二叉树](https://img-blog.csdnimg.cn/20210203144607387.png)

-## 思路
+# 思路

 **首先想清楚，判断对称二叉树要比较的是哪两个节点，要比较的可不是左右节点！**

@ -73,7 +73,7 @@ bool compare(TreeNode* left, TreeNode* right)
 此时左右节点不为空，且数值也不相同的情况我们也处理了。

 代码如下：
-```
+```C++
 if (left == NULL && right != NULL) return false;
 else if (left != NULL && right == NULL) return false;
 else if (left == NULL && right == NULL) return true;
@ -84,7 +84,7 @@ else if (left->val != right->val) return false; // 注意这里我没有

 3.  确定单层递归的逻辑

-此时才进入单层递归的逻辑，单层递归的逻辑就是处理 右节点都不为空，且数值相同的情况。
+此时才进入单层递归的逻辑，单层递归的逻辑就是处理 左右节点都不为空，且数值相同的情况。


 * 比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
@ -93,7 +93,7 @@ else if (left->val != right->val) return false; // 注意这里我没有

 代码如下：

-```
+```C++
 bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右
 bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左
 bool isSame = outside && inside;                    // 左子树：中、 右子树：中（逻辑处理）
@ -104,7 +104,7 @@ return isSame;

 最后递归的C++整体代码如下：

-```
+```C++
 class Solution {
 public:
    bool compare(TreeNode* left, TreeNode* right) {
@ -137,7 +137,7 @@ public:
 **盲目的照着抄，结果就是：发现这是一道“简单题”，稀里糊涂的就过了，但是真正的每一步判断逻辑未必想到清楚。**

 当然我可以把如上代码整理如下：
-```
+```C++
 class Solution {
 public:
    bool compare(TreeNode* left, TreeNode* right) {
@ -177,7 +177,7 @@ public:

 代码如下：

-```
+```C++
 class Solution {
 public:
    bool isSymmetric(TreeNode* root) {
@ -212,7 +212,7 @@ public:

 只要把队列原封不动的改成栈就可以了，我下面也给出了代码。

-```
+```C++
 class Solution {
 public:
    bool isSymmetric(TreeNode* root) {
@ -239,7 +239,7 @@ public:
 };
 ```

-## 总结
+# 总结

 这次我们又深度剖析了一道二叉树的“简单题”，大家会发现，真正的把题目搞清楚其实并不简单，leetcode上accept了和真正掌握了还是有距离的。

@ -249,11 +249,14 @@ public:

 如果已经做过这道题目的同学，读完文章可以再去看看这道题目，思考一下，会有不一样的发现！

+# 相关题目推荐

+* 100.相同的树
+* 572.另一个树的子树

-## 其他语言版本
+# 其他语言版本

-Java：
+## Java

 ```Java
    /**
@ -358,9 +361,9 @@ Java：

 ```

-Python：
+## Python

-> 递归法
+递归法:
 ```python
 class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
@ -384,7 +387,7 @@ class Solution:
        return isSame
 ```

-> 迭代法： 使用队列
+迭代法： 使用队列
 ```python
 import collections
 class Solution:
@ -410,7 +413,7 @@ class Solution:
        return True
 ```

-> 迭代法：使用栈
+迭代法：使用栈
 ```python
 class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
@ -433,7 +436,7 @@ class Solution:
        return True
 ```

-Go：
+## Go

 ```go
 /**
@ -484,22 +487,7 @@ func isSymmetric(root *TreeNode) bool {
 ```


-JavaScript
-```javascript
-var isSymmetric = function(root) {
-    return check(root, root)
-};
-
-const check = (leftPtr, rightPtr) => {
-    // 如果只有根节点，返回true
-    if (!leftPtr && !rightPtr) return true
-    // 如果左右节点只存在一个，则返回false
-    if (!leftPtr || !rightPtr) return false
-    
-    return leftPtr.val === rightPtr.val && check(leftPtr.left, rightPtr.right) && check(leftPtr.right, rightPtr.left)
-}
-```
-JavaScript:
+## JavaScript

 递归判断是否为对称二叉树：
 ```javascript
@ -526,6 +514,7 @@ var isSymmetric = function(root) {
    return compareNode(root.left,root.right);
 };
 ```
+
 队列实现迭代判断是否为对称二叉树：
 ```javascript
 var isSymmetric = function(root) {
@ -554,6 +543,7 @@ var isSymmetric = function(root) {
  return true;
 };
 ```
+
 栈实现迭代判断是否为对称二叉树：
 ```javascript
 var isSymmetric = function(root) {
--- a/problems/0104.二叉树的最大深度.md
+++ b/problems/0104.二叉树的最大深度.md
@ -30,9 +30,13 @@

 ### 递归法

-本题其实也要后序遍历（左右中），依然是因为要通过递归函数的返回值做计算树的高度。
+本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。

-按照递归三部曲，来看看如何来写。
+**而根节点的高度就是二叉树的最大深度**，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。
+
+这一点其实是很多同学没有想清楚的，很多题解同样没有讲清楚。
+
+我先用后序遍历（左右中）来计算树的高度。

 1. 确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。

@ -92,6 +96,66 @@ public:
 **精简之后的代码根本看不出是哪种遍历方式，也看不出递归三部曲的步骤，所以如果对二叉树的操作还不熟练，尽量不要直接照着精简代码来学。**


+本题当然也可以使用前序，代码如下：(**充分表现出求深度回溯的过程**)
+
+```C++
+class Solution {
+public:
+    int result;
+    void getDepth(TreeNode* node, int depth) {
+        result = depth > result ? depth : result; // 中
+
+        if (node->left == NULL && node->right == NULL) return ;
+
+        if (node->left) { // 左
+            depth++;    // 深度+1
+            getDepth(node->left, depth);
+            depth--;    // 回溯，深度-1
+        }
+        if (node->right) { // 右
+            depth++;    // 深度+1
+            getDepth(node->right, depth);
+            depth--;    // 回溯，深度-1
+        }
+        return ;
+    }
+    int maxDepth(TreeNode* root) {
+        result = 0;
+        if (root == 0) return result;
+        getDepth(root, 1);
+        return result;
+    }
+};
+``` 
+
+**可以看出使用了前序（中左右）的遍历顺序，这才是真正求深度的逻辑！**
+
+注意以上代码是为了把细节体现出来，简化一下代码如下：
+
+```C++
+class Solution {
+public:
+    int result;
+    void getDepth(TreeNode* node, int depth) {
+        result = depth > result ? depth : result; // 中
+        if (node->left == NULL && node->right == NULL) return ;
+        if (node->left) { // 左
+            getDepth(node->left, depth + 1);
+        }
+        if (node->right) { // 右
+            getDepth(node->right, depth + 1);
+        }
+        return ;
+    }
+    int maxDepth(TreeNode* root) {
+        result = 0;
+        if (root == 0) return result;
+        getDepth(root, 1);
+        return result;
+    }
+};
+```
+
 ### 迭代法

 使用迭代法的话，使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。
--- a/problems/0129.求根到叶子节点数字之和.md
+++ b/problems/0129.求根到叶子节点数字之和.md
@ -1,10 +1,9 @@
-
-## 链接
+## 链接 
 https://leetcode-cn.com/problems/sum-root-to-leaf-numbers/

 ## 思路

-本题和[113.路径总和II](https://github.com/youngyangyang04/leetcode-master/blob/master/problems/0113.%E8%B7%AF%E5%BE%84%E6%80%BB%E5%92%8CII.md)是类似的思路，做完这道题，可以顺便把[113.路径总和II](https://github.com/youngyangyang04/leetcode-master/blob/master/problems/0113.%E8%B7%AF%E5%BE%84%E6%80%BB%E5%92%8CII.md) 和 [112.路径总和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0112.路径总和.md) 做了。
+本题和[113.路径总和II](https://mp.weixin.qq.com/s/6TWAVjxQ34kVqROWgcRFOg)是类似的思路，做完这道题，可以顺便把[113.路径总和II](https://mp.weixin.qq.com/s/6TWAVjxQ34kVqROWgcRFOg) 和 [112.路径总和](https://mp.weixin.qq.com/s/6TWAVjxQ34kVqROWgcRFOg) 做了。

 结合112.路径总和 和 113.路径总和II，我在讲了[二叉树：递归函数究竟什么时候需要返回值，什么时候不要返回值？](https://mp.weixin.qq.com/s/6TWAVjxQ34kVqROWgcRFOg)，如果大家对二叉树递归函数什么时候需要返回值很迷茫，可以看一下。

@ -26,19 +25,19 @@ https://leetcode-cn.com/problems/sum-root-to-leaf-numbers/

 参数只需要把根节点传入，此时还需要定义两个全局遍历，一个是result，记录最终结果，一个是vector<int> path。

-**为什么用vector类型（就是数组）呢？ 因为用vector方便我们做回溯！**
+**为什么用vector类型（就是数组）呢？ 因为用vector方便我们做回溯！** 

 所以代码如下：

 ```
 int result;
 vector<int> path;
-void traversal(TreeNode* cur)
+void traversal(TreeNode* cur) 
 ```

-* 确定终止条件
+* 确定终止条件 

-递归什么时候终止呢？
+递归什么时候终止呢？ 

 当然是遇到叶子节点，此时要收集结果了，通知返回本层递归，因为单条路径的结果使用vector，我们需要一个函数vectorToInt把vector转成int。

@ -154,12 +153,13 @@ public:
 };
 ```

-## 总结
+# 总结

 过于简洁的代码，很容易让初学者忽视了本题中回溯的精髓，甚至作者本身都没有想清楚自己用了回溯。

 **我这里提供的代码把整个回溯过程充分体现出来，希望可以帮助大家看的明明白白！**

+
 ## 其他语言版本

 Java： 
--- a/problems/1365.有多少小于当前数字的数字.md
+++ b/problems/1365.有多少小于当前数字的数字.md
@ -0,0 +1,146 @@
+
+
+
+# 1365.有多少小于当前数字的数字
+
+题目链接：https://leetcode-cn.com/problems/sort-integers-by-the-number-of-1-bits/
+
+给你一个数组 nums，对于其中每个元素 nums[i]，请你统计数组中比它小的所有数字的数目。
+
+换而言之，对于每个 nums[i] 你必须计算出有效的 j 的数量，其中 j 满足 j != i 且 nums[j] < nums[i] 。
+
+以数组形式返回答案。
+ 
+
+示例 1：
+* 输入：nums = [8,1,2,2,3]     
+* 输出：[4,0,1,1,3] 
+* 解释：
+对于 nums[0]=8 存在四个比它小的数字：（1，2，2 和 3）。        
+对于 nums[1]=1 不存在比它小的数字。        
+对于 nums[2]=2 存在一个比它小的数字：（1）。       
+对于 nums[3]=2 存在一个比它小的数字：（1）。       
+对于 nums[4]=3 存在三个比它小的数字：（1，2 和 2）。      
+
+示例 2：
+* 输入：nums = [6,5,4,8]
+* 输出：[2,1,0,3]
+
+示例 3：
+* 输入：nums = [7,7,7,7]
+* 输出：[0,0,0,0]
+ 
+提示：
+* 2 <= nums.length <= 500
+* 0 <= nums[i] <= 100
+
+# 思路
+
+两层for循环暴力查找，时间复杂度明显为O(n^2)。
+
+那么我们来看一下如何优化。
+
+首先要找小于当前数字的数字，那么从小到大排序之后，该数字之前的数字就都是比它小的了。
+
+所以可以定义一个新数组，将数组排个序。
+
+**排序之后，其实每一个数值的下标就代表这前面有几个比它小的了**。
+
+代码如下：
+
+```
+vector<int> vec = nums;
+sort(vec.begin(), vec.end()); // 从小到大排序之后，元素下标就是小于当前数字的数字
+```
+
+用一个哈希表hash（本题可以就用一个数组）来做数值和下标的映射。这样就可以通过数值快速知道下标（也就是前面有几个比它小的）。
+
+此时有一个情况，就是数值相同怎么办？
+
+例如，数组：1 2 3 4 4 4 ，第一个数值4的下标是3，第二个数值4的下标是4了。
+
+这里就需要一个技巧了，**在构造数组hash的时候，从后向前遍历，这样hash里存放的就是相同元素最左面的数值和下标了**。
+代码如下：
+
+```C++
+int hash[101];
+for (int i = vec.size() - 1; i >= 0; i--) { // 从后向前，记录 vec[i] 对应的下标
+    hash[vec[i]] = i;
+}
+```
+
+最后在遍历原数组nums，用hash快速找到每一个数值 对应的 小于这个数值的个数。存放在将结果存放在另一个数组中。
+
+代码如下：
+
+```C++
+// 此时hash里保存的每一个元素数值 对应的 小于这个数值的个数
+for (int i = 0; i < nums.size(); i++) {
+    vec[i] = hash[nums[i]];
+}
+```
+
+流程如图：
+
+<img src='https://code-thinking.cdn.bcebos.com/pics/1365.有多少小于当前数字的数字.png' width=600> </img></div>
+
+关键地方讲完了，整体C++代码如下：
+
+```C++
+class Solution {
+public:
+    vector<int> smallerNumbersThanCurrent(vector<int>& nums) {
+        vector<int> vec = nums;
+        sort(vec.begin(), vec.end()); // 从小到大排序之后，元素下标就是小于当前数字的数字
+        int hash[101];
+        for (int i = vec.size() - 1; i >= 0; i--) { // 从后向前，记录 vec[i] 对应的下标
+            hash[vec[i]] = i;
+        }
+        // 此时hash里保存的每一个元素数值 对应的 小于这个数值的个数
+        for (int i = 0; i < nums.size(); i++) {
+            vec[i] = hash[nums[i]];
+        }
+        return vec;
+    }
+};
+```
+
+可以排序之后加哈希，时间复杂度为O(nlogn)
+
+
+# 其他语言版本
+
+Java： 
+
+```Java 
+public int[] smallerNumbersThanCurrent(int[] nums) {
+        Map<Integer, Integer> map = new HashMap<>(); // 记录数字 nums[i] 有多少个比它小的数字
+        int[] res = Arrays.copyOf(nums, nums.length);
+        Arrays.sort(res);
+        for (int i = 0; i < res.length; i++) {
+            if (!map.containsKey(res[i])) { // 遇到了相同的数字，那么不需要更新该 number 的情况
+                map.put(res[i], i);
+            }
+        }
+
+        for (int i = 0; i < nums.length; i++) {
+            res[i] = map.get(nums[i]);
+        }
+
+        return res;
+    }
+```
+
+Python：
+
+Go：
+
+JavaScript：
+
+
+
+-----------------------
+* 作者微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
+* B站视频：[代码随想录](https://space.bilibili.com/525438321)
+* 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
+<div align="center"><img src=../pics/公众号.png width=450 alt=> </img></div>
--- a/problems/前序/程序员简历.md
+++ b/problems/前序/程序员简历.md
@ -10,7 +10,6 @@

 # 程序员的简历应该这么写！！（附简历模板）

-> Carl多年积累的简历技巧都在这里了

 Carl校招社招都拿过大厂的offer，同时也看过很多应聘者的简历，这里把自己总结的简历技巧以及常见问题给大家梳理一下。

--- a/problems/周总结/20200927二叉树周末总结.md
+++ b/problems/周总结/20200927二叉树周末总结.md
@ -13,7 +13,7 @@

 对于二叉树节点的定义，C++代码如下：

-```
+```C++
 struct TreeNode {
    int val;
    TreeNode *left;
@ -35,7 +35,7 @@ TreeNode* a = new TreeNode(9);

 没有构造函数的话就要这么写：

-```
+```C++
 TreeNode* a = new TreeNode();
 a->val = 9;
 a->left = NULL;
@ -60,11 +60,35 @@ morris遍历是二叉树遍历算法的超强进阶算法，morris遍历可以

 在[二叉树：听说递归能做的，栈也能做！](https://mp.weixin.qq.com/s/c_zCrGHIVlBjUH_hJtghCg)中我们开始用栈来实现递归的写法，也就是所谓的迭代法。

-细心的同学发现文中前后序遍历空节点是入栈的，其实空节点入不入栈都差不多，但感觉空节点不入栈确实清晰一些，符合文中动画的演示。
+细心的同学发现文中前后序遍历空节点是否入栈写法是不同的

-前序遍历空节点不入栈的代码：（注意注释部分，和文章中的区别）
+其实空节点入不入栈都差不多，但感觉空节点不入栈确实清晰一些，符合文中动画的演示。

+拿前序遍历来举例，空节点入栈：
+
+```C++
+class Solution {
+public:
+    vector<int> preorderTraversal(TreeNode* root) {
+        stack<TreeNode*> st;
+        vector<int> result;
+        st.push(root);
+        while (!st.empty()) {
+            TreeNode* node = st.top();                      // 中
+            st.pop();
+            if (node != NULL) result.push_back(node->val);
+            else continue;
+            st.push(node->right);                           // 右
+            st.push(node->left);                            // 左
+        }
+        return result;
+    }
+};
 ```
+
+前序遍历空节点不入栈的代码：（注意注释部分和上文的区别）
+
+```C++
 class Solution {
 public:
    vector<int> preorderTraversal(TreeNode* root) {
@ -82,32 +106,8 @@ public:
        return result;
    }
 };
-
 ```

-后序遍历空节点不入栈的代码：（注意注释部分，和文章中的区别）
-
-```
-class Solution {
-public:
-    vector<int> postorderTraversal(TreeNode* root) {
-        stack<TreeNode*> st;
-        vector<int> result;
-        if (root == NULL) return result;
-        st.push(root);
-        while (!st.empty()) {
-            TreeNode* node = st.top();
-            st.pop();
-            result.push_back(node->val);
-            if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
-            if (node->right) st.push(node->right); // 空节点不入栈
-        }
-        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
-        return result;
-    }
-};
-
-```

 在实现迭代法的过程中，有同学问了：递归与迭代究竟谁优谁劣呢？

--- a/problems/周总结/二叉树阶段总结系列一.md
+++ b/problems/周总结/二叉树阶段总结系列一.md
@ -0,0 +1,209 @@
+# 本周小结！（二叉树）
+
+**周日我做一个针对本周的打卡留言疑问以及在刷题群里的讨论内容做一下梳理吧。**，这样也有助于大家补一补本周的内容，消化消化。
+
+**注意这个周末总结和系列总结还是不一样的（二叉树还远没有结束），这个总结是针对留言疑问以及刷题群里讨论内容的归纳。**
+
+1. [关于二叉树，你该了解这些！](https://mp.weixin.qq.com/s/q_eKfL8vmSbSFcptZ3aeRA)
+2. [二叉树：一入递归深似海，从此offer是路人](https://mp.weixin.qq.com/s/Ww60X5mIKWdMQV4cN3ejOA)
+3. [二叉树：听说递归能做的，栈也能做！](https://mp.weixin.qq.com/s/OH7aCVJ5-Gi32PkNCoZk4A)
+4. [二叉树：前中后序迭代方式的写法就不能统一一下么？](https://mp.weixin.qq.com/s/ATQMPCpBlaAgrqdLDMVPZA)
+5. [二叉树：层序遍历登场！](https://mp.weixin.qq.com/s/4-bDKi7SdwfBGRm9FYduiA)
+6. [二叉树：你真的会翻转二叉树么？](https://mp.weixin.qq.com/s/jG0MgYR9DoUMYcRRF7magw)
+
+
+## [关于二叉树，你该了解这些！](https://mp.weixin.qq.com/s/q_eKfL8vmSbSFcptZ3aeRA)
+
+有同学会把红黑树和二叉平衡搜索树弄分开了，其实红黑树就是一种二叉平衡搜索树，这两个树不是独立的，所以C++中map、multimap、set、multiset的底层实现机制是二叉平衡搜索树，再具体一点是红黑树。
+
+对于二叉树节点的定义，C++代码如下：
+
+```C++
+struct TreeNode {
+    int val;
+    TreeNode *left;
+    TreeNode *right;
+    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
+};
+```
+对于这个定义中`TreeNode(int x) : val(x), left(NULL), right(NULL) {}` 有同学不清楚干什么的。
+
+这是构造函数，这么说吧C语言中的结构体是C++中类的祖先，所以C++结构体也可以有构造函数。
+
+构造函数也可以不写，但是new一个新的节点的时候就比较麻烦。
+
+例如有构造函数，定义初始值为9的节点：
+
+```
+TreeNode* a = new TreeNode(9);
+```
+
+没有构造函数的话就要这么写：
+
+```C++
+TreeNode* a = new TreeNode();
+a->val = 9;
+a->left = NULL;
+a->right = NULL;
+```
+
+在介绍前中后序遍历的时候，有递归和迭代（非递归），还有一种牛逼的遍历方式：morris遍历。
+
+morris遍历是二叉树遍历算法的超强进阶算法，morris遍历可以将非递归遍历中的空间复杂度降为O(1)，感兴趣大家就去查一查学习学习，比较小众，面试几乎不会考。我其实也没有研究过，就不做过多介绍了。
+
+## [二叉树的递归遍历](https://mp.weixin.qq.com/s/Ww60X5mIKWdMQV4cN3ejOA)
+
+在[二叉树：一入递归深似海，从此offer是路人](https://mp.weixin.qq.com/s/Ww60X5mIKWdMQV4cN3ejOA)中讲到了递归三要素，以及前中后序的递归写法。
+
+文章中我给出了leetcode上三道二叉树的前中后序题目，但是看完[二叉树：一入递归深似海，从此offer是路人](https://mp.weixin.qq.com/s/Ww60X5mIKWdMQV4cN3ejOA)，依然可以解决n叉树的前后序遍历，在leetcode上分别是
+
+* 589. N叉树的前序遍历
+* 590. N叉树的后序遍历
+
+大家可以再去把这两道题目做了。
+
+## [二叉树的非递归遍历](https://mp.weixin.qq.com/s/OH7aCVJ5-Gi32PkNCoZk4A)
+
+细心的同学发现文中前后序遍历空节点是入栈的，其实空节点入不入栈都差不多，但感觉空节点不入栈确实清晰一些，符合文中动画的演示。
+
+前序遍历空节点不入栈的代码：（注意注释部分，和文章中的区别）
+
+```C++
+class Solution {
+public:
+    vector<int> preorderTraversal(TreeNode* root) {
+        stack<TreeNode*> st;
+        vector<int> result;
+        if (root == NULL) return result;
+        st.push(root);
+        while (!st.empty()) {
+            TreeNode* node = st.top();                       // 中
+            st.pop();
+            result.push_back(node->val);
+            if (node->right) st.push(node->right);           // 右（空节点不入栈）
+            if (node->left) st.push(node->left);             // 左（空节点不入栈）
+        }
+        return result;
+    }
+};
+
+```
+
+后序遍历空节点不入栈的代码：（注意注释部分，和文章中的区别）
+
+```C++
+class Solution {
+public:
+    vector<int> postorderTraversal(TreeNode* root) {
+        stack<TreeNode*> st;
+        vector<int> result;
+        if (root == NULL) return result;
+        st.push(root);
+        while (!st.empty()) {
+            TreeNode* node = st.top();
+            st.pop();
+            result.push_back(node->val);
+            if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
+            if (node->right) st.push(node->right); // 空节点不入栈
+        }
+        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
+        return result;
+    }
+};
+
+```
+
+在实现迭代法的过程中，有同学问了：递归与迭代究竟谁优谁劣呢？
+
+从时间复杂度上其实迭代法和递归法差不多（在不考虑函数调用开销和函数调用产生的堆栈开销），但是空间复杂度上，递归开销会大一些，因为递归需要系统堆栈存参数返回值等等。
+
+递归更容易让程序员理解，但收敛不好，容易栈溢出。
+
+这么说吧，递归是方便了程序员，难为了机器（各种保存参数，各种进栈出栈）。
+
+**在实际项目开发的过程中我们是要尽量避免递归！因为项目代码参数、调用关系都比较复杂，不容易控制递归深度，甚至会栈溢出。**
+
+## 周四
+
+在[二叉树：前中后序迭代方式的写法就不能统一一下么？](https://mp.weixin.qq.com/s/WKg0Ty1_3SZkztpHubZPRg)中我们使用空节点作为标记，给出了统一的前中后序迭代法。
+
+此时又多了一种前中后序的迭代写法，那么有同学问了：前中后序迭代法是不是一定要统一来写，这样才算是规范。
+
+其实没必要，还是自己感觉哪一种更好记就用哪种。
+
+但是**一定要掌握前中后序一种迭代的写法，并不因为某种场景的题目一定要用迭代，而是现场面试的时候，面试官看你顺畅的写出了递归，一般会进一步考察能不能写出相应的迭代。**
+
+## 周五
+
+在[二叉树：层序遍历登场！](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)中我们介绍了二叉树的另一种遍历方式（图论中广度优先搜索在二叉树上的应用）即：层序遍历。
+
+看完这篇文章，去leetcode上怒刷五题，文章中 编号107题目的样例图放错了（原谅我匆忙之间总是手抖），但不影响大家理解。
+
+只有同学发现leetcode上“515. 在每个树行中找最大值”，也是层序遍历的应用，依然可以分分钟解决，所以就是一鼓作气解决六道了，哈哈。
+
+**层序遍历遍历相对容易一些，只要掌握基本写法（也就是框架模板），剩下的就是在二叉树每一行遍历的时候做做逻辑修改。**
+
+## 周六
+
+在[二叉树：你真的会翻转二叉树么？](https://mp.weixin.qq.com/s/6gY1MiXrnm-khAAJiIb5Bg)中我们把翻转二叉树这么一道简单又经典的问题，充分的剖析了一波，相信就算做过这道题目的同学，看完本篇之后依然有所收获！
+
+
+**文中我指的是递归的中序遍历是不行的，因为使用递归的中序遍历，某些节点的左右孩子会翻转两次。**
+
+如果非要使用递归中序的方式写，也可以，如下代码就可以避免节点左右孩子翻转两次的情况：
+
+```
+class Solution {
+public:
+    TreeNode* invertTree(TreeNode* root) {
+        if (root == NULL) return root;
+        invertTree(root->left);         // 左
+        swap(root->left, root->right);  // 中
+        invertTree(root->left);         // 注意 这里依然要遍历左孩子，因为中间节点已经翻转了
+        return root;
+    }
+};
+```
+
+代码虽然可以，但这毕竟不是真正的递归中序遍历了。
+
+但使用迭代方式统一写法的中序是可以的。
+
+代码如下：
+
+```
+class Solution {
+public:
+    TreeNode* invertTree(TreeNode* root) {
+        stack<TreeNode*> st;
+        if (root != NULL) st.push(root);
+        while (!st.empty()) {
+            TreeNode* node = st.top();
+            if (node != NULL) {
+                st.pop();
+                if (node->right) st.push(node->right);  // 右
+                st.push(node);                          // 中
+                st.push(NULL);
+                if (node->left) st.push(node->left);    // 左
+
+            } else {
+                st.pop();
+                node = st.top();
+                st.pop();
+                swap(node->left, node->right);          // 节点处理逻辑
+            }
+        }
+        return root;
+    }
+};
+
+
+```
+
+为什么这个中序就是可以的呢，因为这是用栈来遍历，而不是靠指针来遍历，避免了递归法中翻转了两次的情况，大家可以画图理解一下，这里有点意思的。
+
+## 总结
+
+**本周我们都是讲解了二叉树，从理论基础到遍历方式，从递归到迭代，从深度遍历到广度遍历，最后再用了一个翻转二叉树的题目把我们之前讲过的遍历方式都串了起来。**
+
+
--- a/problems/背包理论基础01背包-1.md
+++ b/problems/背包理论基础01背包-1.md
@ -190,7 +190,7 @@ for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量

 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。

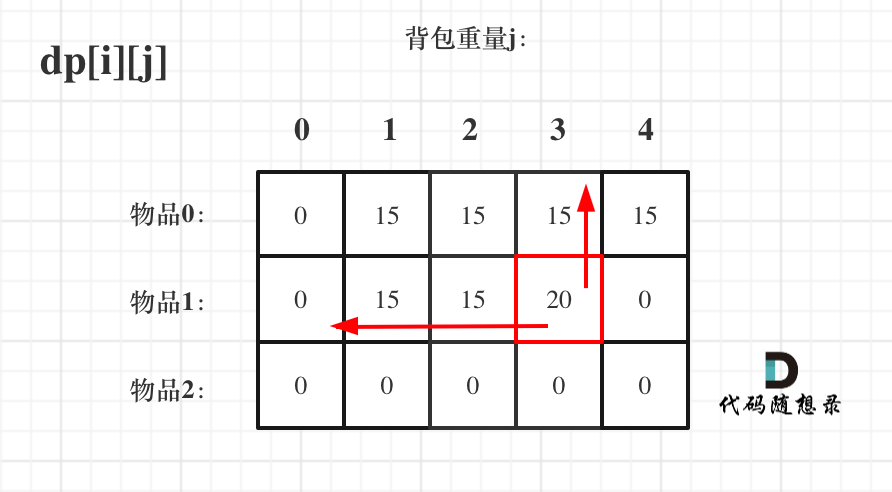
-dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向（包括正左和正上两个方向），那么先遍历物品，再遍历背包的过程如图所示：
+dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向（包括正上方向），那么先遍历物品，再遍历背包的过程如图所示：

 ![动态规划-背包问题5](https://img-blog.csdnimg.cn/202101101032124.png)

--- a/problems/背包理论基础01背包-2.md
+++ b/problems/背包理论基础01背包-2.md
@ -80,7 +80,7 @@ dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，

 看一下递归公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

-dp数组在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了，如果题目给的价值有负数，那么非0下标就要初始化为负无穷。
+dp数组在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。

 **这样才能让dp数组在递归公式的过程中取的最大的价值，而不是被初始值覆盖了**。