mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-08 08:50:15 +08:00
docs: 股票的最佳时机二添加视频链接跳转
This commit is contained in:
@ -4,43 +4,49 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
# 122.买卖股票的最佳时机II
|
||||
# 122.买卖股票的最佳时机 II
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/)
|
||||
|
||||
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
|
||||
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
|
||||
|
||||
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
|
||||
|
||||
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
|
||||
|
||||
|
||||
示例 1:
|
||||
* 输入: [7,1,5,3,6,4]
|
||||
* 输出: 7
|
||||
* 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
|
||||
|
||||
- 输入: [7,1,5,3,6,4]
|
||||
- 输出: 7
|
||||
- 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
|
||||
|
||||
示例 2:
|
||||
* 输入: [1,2,3,4,5]
|
||||
* 输出: 4
|
||||
* 解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
|
||||
|
||||
示例 3:
|
||||
* 输入: [7,6,4,3,1]
|
||||
* 输出: 0
|
||||
* 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
|
||||
- 输入: [1,2,3,4,5]
|
||||
- 输出: 4
|
||||
- 解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
|
||||
|
||||
示例 3:
|
||||
|
||||
- 输入: [7,6,4,3,1]
|
||||
- 输出: 0
|
||||
- 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
|
||||
|
||||
提示:
|
||||
* 1 <= prices.length <= 3 * 10 ^ 4
|
||||
* 0 <= prices[i] <= 10 ^ 4
|
||||
|
||||
- 1 <= prices.length <= 3 \* 10 ^ 4
|
||||
- 0 <= prices[i] <= 10 ^ 4
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法也能解决股票问题!LeetCode:122.买卖股票最佳时机 II](https://www.bilibili.com/video/BV1ev4y1C7na),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
本题首先要清楚两点:
|
||||
|
||||
* 只有一只股票!
|
||||
* 当前只有买股票或者卖股票的操作
|
||||
- 只有一只股票!
|
||||
- 当前只有买股票或者卖股票的操作
|
||||
|
||||
想获得利润至少要两天为一个交易单元。
|
||||
|
||||
@ -52,17 +58,16 @@
|
||||
|
||||
如何分解呢?
|
||||
|
||||
假如第0天买入,第3天卖出,那么利润为:prices[3] - prices[0]。
|
||||
假如第 0 天买入,第 3 天卖出,那么利润为:prices[3] - prices[0]。
|
||||
|
||||
相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。
|
||||
|
||||
**此时就是把利润分解为每天为单位的维度,而不是从0天到第3天整体去考虑!**
|
||||
**此时就是把利润分解为每天为单位的维度,而不是从 0 天到第 3 天整体去考虑!**
|
||||
|
||||
那么根据prices可以得到每天的利润序列:(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。
|
||||
那么根据 prices 可以得到每天的利润序列:(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
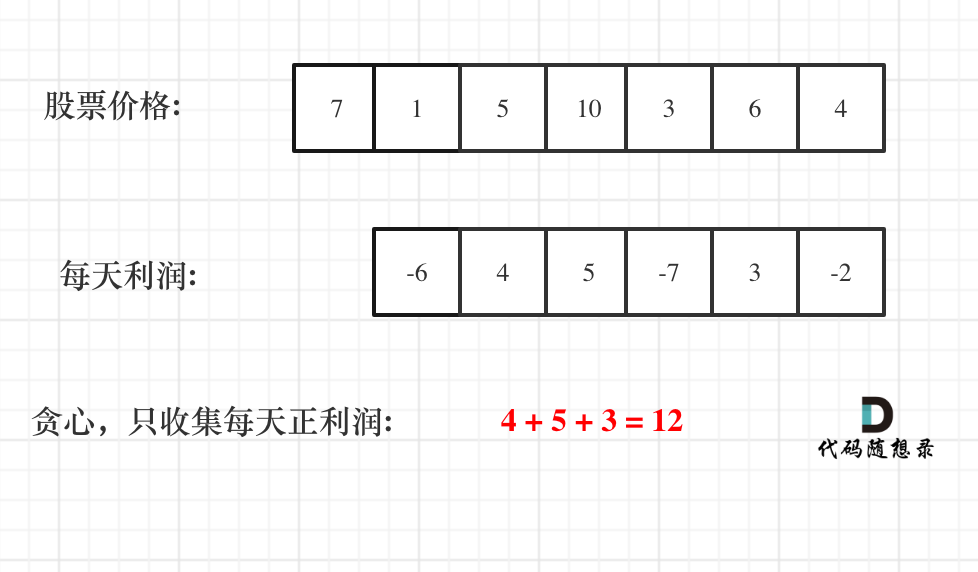
|
||||
|
||||
一些同学陷入:第一天怎么就没有利润呢,第一天到底算不算的困惑中。
|
||||
@ -77,7 +82,7 @@
|
||||
|
||||
局部最优可以推出全局最优,找不出反例,试一试贪心!
|
||||
|
||||
对应C++代码如下:
|
||||
对应 C++代码如下:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -92,12 +97,12 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1)
|
||||
- 时间复杂度:O(n)
|
||||
- 空间复杂度:O(1)
|
||||
|
||||
### 动态规划
|
||||
|
||||
动态规划将在下一个系列详细讲解,本题解先给出我的C++代码(带详细注释),感兴趣的同学可以自己先学习一下。
|
||||
动态规划将在下一个系列详细讲解,本题解先给出我的 C++代码(带详细注释),感兴趣的同学可以自己先学习一下。
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -119,8 +124,8 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:$O(n)$
|
||||
* 空间复杂度:$O(n)$
|
||||
- 时间复杂度:$O(n)$
|
||||
- 空间复杂度:$O(n)$
|
||||
|
||||
## 总结
|
||||
|
||||
@ -134,9 +139,10 @@ public:
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java:
|
||||
### Java:
|
||||
|
||||
贪心:
|
||||
|
||||
```java
|
||||
// 贪心思路
|
||||
class Solution {
|
||||
@ -151,6 +157,7 @@ class Solution {
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```java
|
||||
class Solution { // 动态规划
|
||||
public int maxProfit(int[] prices) {
|
||||
@ -172,8 +179,10 @@ class Solution { // 动态规划
|
||||
}
|
||||
```
|
||||
|
||||
### Python:
|
||||
### Python:
|
||||
|
||||
贪心:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def maxProfit(self, prices: List[int]) -> int:
|
||||
@ -184,6 +193,7 @@ class Solution:
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def maxProfit(self, prices: List[int]) -> int:
|
||||
@ -200,6 +210,7 @@ class Solution:
|
||||
### Go:
|
||||
|
||||
贪心算法
|
||||
|
||||
```go
|
||||
func maxProfit(prices []int) int {
|
||||
var sum int
|
||||
@ -212,7 +223,9 @@ func maxProfit(prices []int) int {
|
||||
return sum
|
||||
}
|
||||
```
|
||||
|
||||
动态规划
|
||||
|
||||
```go
|
||||
func maxProfit(prices []int) int {
|
||||
dp := make([][]int, len(prices))
|
||||
@ -226,7 +239,7 @@ func maxProfit(prices []int) int {
|
||||
dp[i][1] = max(dp[i-1][0] - prices[i], dp[i-1][1])
|
||||
}
|
||||
return dp[len(prices)-1][0]
|
||||
|
||||
|
||||
}
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
@ -239,6 +252,7 @@ func max(a, b int) int {
|
||||
### Javascript:
|
||||
|
||||
贪心
|
||||
|
||||
```Javascript
|
||||
var maxProfit = function(prices) {
|
||||
let result = 0
|
||||
@ -249,27 +263,28 @@ var maxProfit = function(prices) {
|
||||
};
|
||||
```
|
||||
|
||||
动态规划
|
||||
动态规划
|
||||
|
||||
```javascript
|
||||
const maxProfit = (prices) => {
|
||||
let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
|
||||
// dp[i][0] 表示第i天持有股票所得现金。
|
||||
// dp[i][1] 表示第i天不持有股票所得最多现金
|
||||
dp[0][0] = 0 - prices[0];
|
||||
dp[0][1] = 0;
|
||||
for(let i = 1; i < prices.length; i++) {
|
||||
// 如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
|
||||
// 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
|
||||
// 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
|
||||
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] - prices[i]);
|
||||
|
||||
// 在来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
|
||||
// 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
|
||||
// 第i天卖出股票,所得现金就是按照今天股票佳价格卖出后所得现金即:prices[i] + dp[i - 1][0]
|
||||
dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i]);
|
||||
}
|
||||
let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
|
||||
// dp[i][0] 表示第i天持有股票所得现金。
|
||||
// dp[i][1] 表示第i天不持有股票所得最多现金
|
||||
dp[0][0] = 0 - prices[0];
|
||||
dp[0][1] = 0;
|
||||
for (let i = 1; i < prices.length; i++) {
|
||||
// 如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
|
||||
// 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
|
||||
// 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
|
||||
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
|
||||
|
||||
return dp[prices.length -1][1];
|
||||
// 在来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
|
||||
// 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
|
||||
// 第i天卖出股票,所得现金就是按照今天股票佳价格卖出后所得现金即:prices[i] + dp[i - 1][0]
|
||||
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
|
||||
}
|
||||
|
||||
return dp[prices.length - 1][1];
|
||||
};
|
||||
```
|
||||
|
||||
@ -277,17 +292,18 @@ const maxProfit = (prices) => {
|
||||
|
||||
```typescript
|
||||
function maxProfit(prices: number[]): number {
|
||||
let resProfit: number = 0;
|
||||
for (let i = 1, length = prices.length; i < length; i++) {
|
||||
resProfit += Math.max(prices[i] - prices[i - 1], 0);
|
||||
}
|
||||
return resProfit;
|
||||
};
|
||||
let resProfit: number = 0;
|
||||
for (let i = 1, length = prices.length; i < length; i++) {
|
||||
resProfit += Math.max(prices[i] - prices[i - 1], 0);
|
||||
}
|
||||
return resProfit;
|
||||
}
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
贪心:
|
||||
|
||||
```Rust
|
||||
impl Solution {
|
||||
fn max(a: i32, b: i32) -> i32 {
|
||||
@ -304,6 +320,7 @@ impl Solution {
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```Rust
|
||||
impl Solution {
|
||||
fn max(a: i32, b: i32) -> i32 {
|
||||
@ -323,7 +340,9 @@ impl Solution {
|
||||
```
|
||||
|
||||
### C:
|
||||
|
||||
贪心:
|
||||
|
||||
```c
|
||||
int maxProfit(int* prices, int pricesSize){
|
||||
int result = 0;
|
||||
@ -339,6 +358,7 @@ int maxProfit(int* prices, int pricesSize){
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```c
|
||||
#define max(a, b) (((a) > (b)) ? (a) : (b))
|
||||
|
||||
@ -363,6 +383,7 @@ int maxProfit(int* prices, int pricesSize){
|
||||
### Scala
|
||||
|
||||
贪心:
|
||||
|
||||
```scala
|
||||
object Solution {
|
||||
def maxProfit(prices: Array[Int]): Int = {
|
||||
|
||||
Reference in New Issue
Block a user