Update

README.md

@@ -10,7 +10,7 @@
 
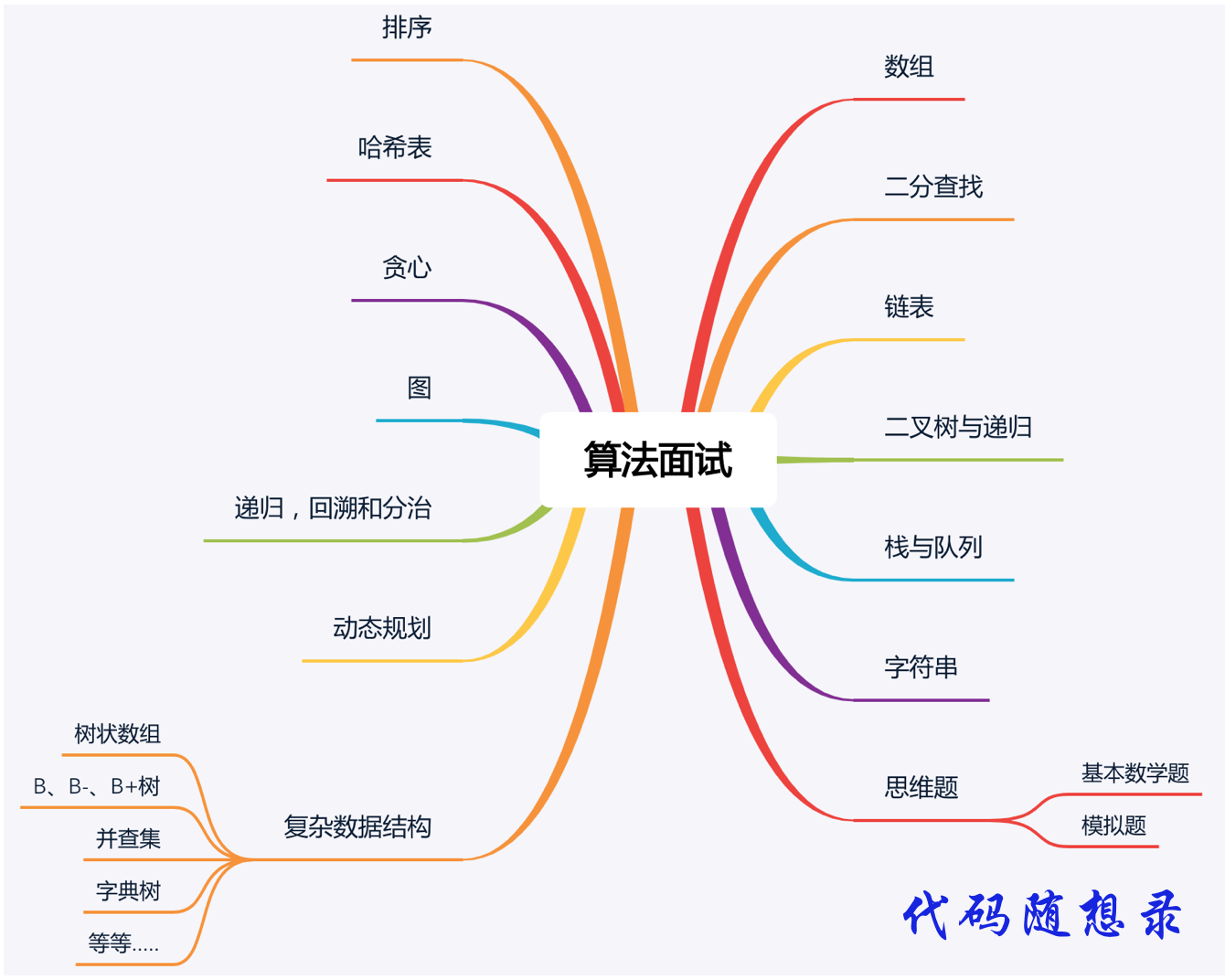
 # 算法面试思维导图
 
-![算法面试知识大纲](https://img-blog.csdnimg.cn/20200811091858722.png)
+![算法面试知识大纲](https://img-blog.csdnimg.cn/20200729181420491.png)
 
 # 算法文章精选
 

problems/0404.左叶子之和.md

@@ -0,0 +1,77 @@
+## 题目地址 
+https://leetcode-cn.com/problems/sum-of-left-leaves/
+
+## 思路 
+
+首先要注意是判断左叶子呢，不是左子树，不要上来想着层序遍历。
+
+因为题目中其实没有说清楚左叶子究竟是什么节点，那么我来给出左叶子的明确定义：**如果左节点不为空，且左节点没有左右孩子，那么这个节点就是左叶子**
+
+大家思考一下如下图中二叉树，左叶子之和究竟是多少？
+
+<img src='../pics/404.左叶子之和.png' width=600> </img></div>
+
+**其实是0，因为这棵树根本没有左叶子！**
+
+那么判断左叶子，如果**判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。**
+
+判断的根据如下：
+
+```
+    if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
+        sum = node->left->val;
+    }
+```
+
+递归写法代码如下：
+
+## 递归C++代码
+
+```
+class Solution {
+public:
+    int sumOfLeftLeaves(TreeNode* root) {
+        if (root == NULL) return 0;
+        int sum = 0;
+        if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) {
+            sum = root->left->val;
+        }
+        return sum + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
+    }
+};
+```
+
+递归的过程其实就是二叉树的前序遍历，那么写过二叉树的同学都知道，既然是二叉树的前序遍历，能写出递归，就能写出非递归。
+
+如果对二叉树的各种递归和非递归的写法不熟悉，可以看我的这个题解：
+[彻底吃透二叉树的前中后序递归法和迭代法！！](https://leetcode-cn.com/problems/binary-tree-inorder-traversal/solution/che-di-chi-tou-er-cha-shu-de-qian-zhong-hou-xu-d-2/)
+
+那么非递归版本善良登场，判断条件都是一样的
+
+## 非递归C++代码
+
+```
+
+class Solution {
+public:
+    int sumOfLeftLeaves(TreeNode* root) {
+        stack<TreeNode*> st;
+        if (root == NULL) return 0;
+        st.push(root);
+        int result = 0;
+        while (!st.empty()) {
+            TreeNode* node = st.top();
+            st.pop();
+            if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
+                result += node->left->val;
+            }
+            if (node->right) st.push(node->right);
+            if (node->left) st.push(node->left);
+        }
+        return result;
+    }
+
+
+};
+```
+

problems/栈与队列总结.md

@@ -0,0 +1,156 @@
+
+> 学习不总结等于白学
+
+# 栈与队列的理论基础
+
+首先我们在[栈与队列：来看看栈和队列不为人知的一面](https://mp.weixin.qq.com/s/VZRjOccyE09aE-MgLbCMjQ)中讲解了栈和队列的理论基础。
+
+里面提到了灵魂四问：
+
+1. C++中stack，queue 是容器么？
+2. 我们使用的stack，queue是属于那个版本的STL？
+3. 我们使用的STL中stack，queue是如何实现的？
+4. stack，queue 提供迭代器来遍历空间么？
+
+相信不仅仅是C++中有这些问题，那么大家使用其他编程语言，也可以考虑一下这四个问题，栈和队列是如何实现的。
+
+栈与队列是我们熟悉的不能再熟悉的数据结构，但它们的底层实现，很多同学都比较模糊，这其实就是基础所在。
+
+可以出一道面试题：栈里面的元素在内存中是连续分布的么？ 
+
+这个问题有两个陷阱：
+
+* 陷阱1：栈是容器适配器，底层容器使用不同的容器，导致栈内数据在内存中是不是连续分布。
+* 陷阱2：缺省情况下，默认底层容器是deque，那么deque的在内存中的数据分布是什么样的呢？ 答案是：不连续的，下文也会提到deque。
+
+所以这就是考察候选者基础知识扎不扎实的好问题。
+
+大家还是要多多重视起来！
+
+了解了栈与队列基础之后，那么可以用[栈与队列：栈实现队列](https://mp.weixin.qq.com/s/P6tupDwRFi6Ay-L7DT4NVg) 和 [栈与队列：队列实现栈](https://mp.weixin.qq.com/s/yzn6ktUlL-vRG3-m5a8_Yw) 来练习一下栈与队列的基本操作。
+
+值得一提的是，用[栈与队列：用队列实现栈还有点别扭](https://mp.weixin.qq.com/s/yzn6ktUlL-vRG3-m5a8_Yw)中，其实只用一个队列就够了。
+
+**一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外） 重新添加到队列尾部，此时在去弹出元素就是栈的顺序了。** 
+
+# 栈经典题目
+
+## 栈在系统中的应用
+
+如果还记得编译原理的话，编译器在 词法分析的过程中处理括号、花括号等这个符号的逻辑，就是使用了栈这种数据结构。
+
+再举个例子，linux系统中，cd这个进入目录的命令我们应该再熟悉不过了。
+
+```
+cd a/b/c/../../
+```
+
+这个命令最后进入a目录，系统是如何知道进入了a目录呢 ，这就是栈的应用。**这在leetcode上也是一道题目，编号：71. 简化路径，大家有空可以做一下。**
+
+**递归的实现是栈：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中**，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。
+
+所以栈在计算机领域中应用是非常广泛的。 
+
+有的同学经常会想学的这些数据结构有什么用，也开发不了什么软件，大多数同学说的软件应该都是可视化的软件例如APP、网站之类的，那都是非常上层的应用了，底层很多功能的实现都是基础的数据结构和算法。 
+
+**所以数据结构与算法的应用往往隐藏在我们看不到的地方！**
+
+## 括号匹配问题
+
+在[栈与队列：系统中处处都是栈的应用](https://mp.weixin.qq.com/s/nLlmPMsDCIWSqAtr0jbrpQ)中我们讲解了括号匹配问题。
+
+**括号匹配是使用栈解决的经典问题。**
+
+建议要写代码之前要分析好有哪几种不匹配的情况，如果不动手之前分析好，写出的代码也会有很多问题。 
+
+先来分析一下 这里有三种不匹配的情况，
+
+1. 第一种情况，字符串里左方向的括号多余了 ，所以不匹配。
+2. 第二种情况，括号没有多余，但是 括号的类型没有匹配上。
+3. 第三种情况，字符串里右方向的括号多余了，所以不匹配。
+
+这里还有一些技巧，在匹配左括号的时候，右括号先入栈，就只需要比较当前元素和栈顶相不相等就可以了，比左括号先入栈代码实现要简单的多了！
+
+## 字符串去重问题
+
+在[栈与队列：匹配问题都是栈的强项](https://mp.weixin.qq.com/s/eynAEbUbZoAWrk0ZlEugqg)中讲解了字符串去重问题。
+1047. 删除字符串中的所有相邻重复项
+
+思路就是可以把字符串顺序放到一个栈中，然后如果相同的话 栈就弹出，这样最后栈里剩下的元素都是相邻不相同的元素了。
+
+## 逆波兰表达式问题 
+
+在[栈与队列：有没有想过计算机是如何处理表达式的？](https://mp.weixin.qq.com/s/hneh2nnLT91rR8ms2fm_kw)中讲解了求逆波兰表达式。
+
+本题中每一个子表达式要得出一个结果，然后拿这个结果再进行运算，那么**这岂不就是一个相邻字符串消除的过程，和[栈与队列：匹配问题都是栈的强项](https://mp.weixin.qq.com/s/eynAEbUbZoAWrk0ZlEugqg)中的对对碰游戏是不是就非常像了。** 
+
+
+# 队列的经典题目 
+
+## 滑动窗口最大值问题
+
+在[栈与队列：滑动窗口里求最大值引出一个重要数据结构](https://mp.weixin.qq.com/s/8c6l2bO74xyMjph09gQtpA)中讲解了一种数据结构：单调队列。
+
+这道题目还是比较绕的，如果第一次遇到这种题目，需要反复琢磨琢磨
+
+主要思想是**队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。** 
+
+那么这个维护元素单调递减的队列就叫做**单调队列，即单调递减或单调递增的队列。C++中没有直接支持单调队列，需要我们自己来一个单调队列**
+
+而且**不要以为实现的单调队列就是 对窗口里面的数进行排序，如果排序的话，那和优先级队列又有什么区别了呢。**
+
+设计单调队列的时候，pop，和push操作要保持如下规则：
+
+1. pop(value)：如果窗口移除的元素value等于单调队列的出口元素，那么队列弹出元素，否则不用任何操作
+2. push(value)：如果push的元素value大于入口元素的数值，那么就将队列出口的元素弹出，直到push元素的数值小于等于队列入口元素的数值为止 
+
+保持如上规则，每次窗口移动的时候，只要问que.front()就可以返回当前窗口的最大值。
+
+一些同学还会对单调队列都有一些困惑，首先要明确的是，**题解中单调队列里的pop和push接口，仅适用于本题。**
+
+**单调队列不是一成不变的，而是不同场景不同写法**，总之要保证队列里单调递减或递增的原则，所以叫做单调队列。 
+
+**不要以为本地中的单调队列实现就是固定的写法。**  
+
+我们用deque作为单调队列的底层数据结构，C++中deque是stack和queue默认的底层实现容器（这个我们之前已经讲过），deque是可以两边扩展的，而且deque里元素并不是严格的连续分布的。
+
+
+## 求前 K 个高频元素 
+
+在[栈与队列：求前 K 个高频元素和队列有啥关系？](https://mp.weixin.qq.com/s/8hMwxoE_BQRbzCc7CA8rng)中讲解了求前 K 个高频元素。
+
+通过求前 K 个高频元素，引出另一种队列就是**优先级队列**。 
+
+什么是优先级队列呢？ 
+
+其实**就是一个披着队列外衣的堆**，因为优先级队列对外接口只是从队头取元素，从队尾添加元素，再无其他取元素的方式，看起来就是一个队列。
+
+而且优先级队列内部元素是自动依照元素的权值排列。那么它是如何有序排列的呢？
+
+缺省情况下priority_queue利用max-heap（大顶堆）完成对元素的排序，这个大顶堆是以vector为表现形式的complete binary tree（完全二叉树）。
+
+什么是堆呢？ 
+
+**堆是一颗完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。** 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。 
+
+所以大家经常说的大顶堆（堆头是最大元素），小顶堆（堆头是最小元素），如果懒得自己实现的话，就直接用priority_queue（优先级队列）就可以了，底层实现都是一样的，从小到大排就是小顶堆，从大到小排就是大顶堆。
+
+本题就要**使用优先级队列来对部分频率进行排序。**  注意这里是对部分数据进行排序而不需要对所有数据排序！
+
+所以排序的过程的时间复杂度是O(logk)，整个算法的时间复杂度是O(nlogk)。
+
+# 总结
+
+在栈与队列系列中，我们强调栈与队列的基础，也是很多同学容易忽视的点。
+
+使用抽象程度越高的语言，越容易忽视其底层实现，而C++相对来说是比较接近底层的语言。
+
+我们用栈实现队列，用队列实现栈来掌握的栈与队列的基本操作。
+
+接着，通过括号匹配问题、字符串去重问题、逆波兰表达式问题来系统讲解了栈在系统中的应用，以及使用技巧。
+
+通过求滑动窗口最大值，以及前K个高频元素介绍了两种队列：单调队列和优先级队列，这是特殊场景解决问题的利器，是一定要掌握的。
+
+好了，栈与队列我们就总结到这里了，接下来Carl就要带大家开启新的篇章了，大家加油！
+
+