mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-06 23:28:29 +08:00
Update
This commit is contained in:
51
problems/0207.课程表.md
Normal file
51
problems/0207.课程表.md
Normal file
@ -0,0 +1,51 @@
|
||||
|
||||
拓扑排序指的是一种 解决问题的大体思路, 而具体算法,可能是 广搜 可能是深搜。
|
||||
|
||||
大家可能发现 各式各样的解法,纠结哪个是拓扑排序?
|
||||
|
||||
只要能在把 有向无环图 进行线性排序 的算法 都可以叫做 拓扑排序。
|
||||
|
||||
引用与任务调度,课程安排等等。
|
||||
|
||||
为什么
|
||||
|
||||
|
||||
-----
|
||||
|
||||
「拓扑排序」是专门应用于有向图的算法;
|
||||
|
||||
把一个 有向无环图 转成 线性的排序 就叫 拓扑排序。
|
||||
|
||||
拓扑排序(Kahn 算法,其实就是广度优先遍历的思路)
|
||||
|
||||
这道题的做法同样适用于第 210 题。
|
||||
|
||||
------------------
|
||||
|
||||
```
|
||||
vector<int> inDegree(numCourses);
|
||||
unordered_map<int, vector<int>> map;
|
||||
for (int i = 0; i < prerequisites.size(); i++) {
|
||||
inDegree[prerequisites[i][0]]++;//当前课程入度值+1
|
||||
map[prerequisites[i][1]].push_back(prerequisites[i][0]);//添加依赖他的后续课
|
||||
}
|
||||
queue<int> Qu;
|
||||
for (int i = 0; i < numCourses; i++) {
|
||||
if (inDegree[i] == 0) Qu.push(i);//所有入度为0的课入列
|
||||
}
|
||||
int count = 0;
|
||||
while (Qu.size()) {
|
||||
int selected = Qu.front(); //当前选的课
|
||||
Qu.pop();//出列
|
||||
count++;//选课数+1
|
||||
vector<int> toEnQueue = map[selected];//获取这门课对应的后续课
|
||||
if (toEnQueue.size()) { //确实有后续课
|
||||
for (int i = 0; i < toEnQueue.size(); i++) {
|
||||
inDegree[toEnQueue[i]]--; //依赖它的后续课的入度-1
|
||||
if (inDegree[toEnQueue[i]] == 0) Qu.push(toEnQueue[i]); //如果因此减为0,入列
|
||||
}
|
||||
}
|
||||
}
|
||||
if (count == numCourses) return true;
|
||||
return false;
|
||||
```
|
||||
@ -1194,8 +1194,7 @@ public:
|
||||
|
||||
至此通过 两篇dijkstra的文章,终于把 dijkstra 讲完了,如果大家对我讲解里所涉及的内容都吃透的话,详细对 dijkstra 算法也就理解到位了。
|
||||
|
||||
|
||||
# Bellman_ford
|
||||
这里在给出本题的Bellman_ford解法,关于 Bellman_ford ,后面我会专门来讲解的,Bellman_ford 有其独特的应用场景
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -1204,27 +1203,25 @@ public:
|
||||
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
|
||||
vector<int> minDist(n + 1 , INT_MAX/2);
|
||||
minDist[k] = 0;
|
||||
vector<int> minDist_copy(n); // 用来记录每一次遍历的结果
|
||||
//vector<int> minDist_copy(n); // 用来记录每一次遍历的结果
|
||||
for (int i = 1; i <= n + 1; i++) {
|
||||
minDist_copy = minDist; // 获取上一次计算的结果
|
||||
//minDist_copy = minDist; // 获取上一次计算的结果
|
||||
for (auto &f : times) {
|
||||
int from = f[0];
|
||||
int to = f[1];
|
||||
int price = f[2];
|
||||
if (minDist[to] > minDist_copy[from] + price) minDist[to] = minDist_copy[from] + price;
|
||||
}
|
||||
int price = f[2];
|
||||
if (minDist[to] > minDist[from] + price) minDist[to] = minDist[from] + price;
|
||||
}
|
||||
|
||||
}
|
||||
int result = 0;
|
||||
int result = 0;
|
||||
for (int i = 1;i <= n; i++) {
|
||||
if (minDist[i] == INT_MAX/2) return -1;// 没有路径
|
||||
result = max(minDist[i], result);
|
||||
}
|
||||
|
||||
return result;
|
||||
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
|
||||
@ -1,4 +1,21 @@
|
||||
|
||||
# 787. K 站中转内最便宜的航班
|
||||
|
||||
有 n 个城市通过一些航班连接。给你一个数组 flights ,其中 flights[i] = [fromi, toi, pricei] ,表示该航班都从城市 fromi 开始,以价格 pricei 抵达 toi。
|
||||
|
||||
现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到出一条最多经过 k 站中转的路线,使得从 src 到 dst 的 价格最便宜 ,并返回该价格。 如果不存在这样的路线,则输出 -1。
|
||||
|
||||
|
||||

|
||||
|
||||
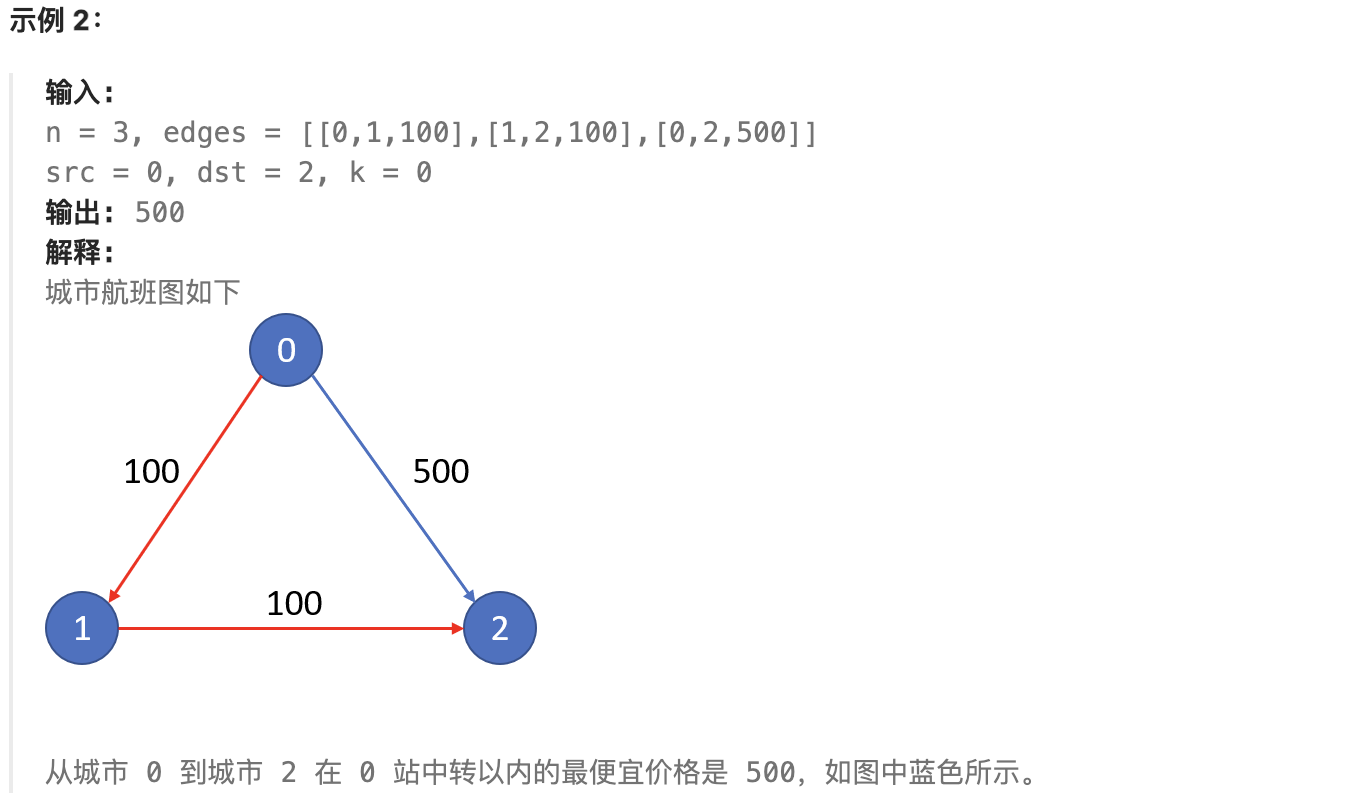
|
||||
|
||||

|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -13,7 +30,8 @@ public:
|
||||
int from = f[0];
|
||||
int to = f[1];
|
||||
int price = f[2];
|
||||
if (minDist[to] > minDist_copy[from] + price) minDist[to] = minDist_copy[from] + price;
|
||||
minDist[to] = min(minDist_copy[from] + price, minDist[to]);
|
||||
// if (minDist[to] > minDist_copy[from] + price) minDist[to] = minDist_copy[from] + price;
|
||||
}
|
||||
|
||||
}
|
||||
@ -23,6 +41,8 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
下面是典型的错误写法
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
@ -42,3 +62,117 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
-----------
|
||||
|
||||
SPFA
|
||||
|
||||
|
||||
class Solution {
|
||||
struct Edge {
|
||||
int to; // 链接的节点
|
||||
int val; // 边的权重
|
||||
|
||||
Edge(int t, int w): to(t), val(w) {} // 构造函数
|
||||
};
|
||||
|
||||
public:
|
||||
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
|
||||
vector<int> minDist(n , INT_MAX/2);
|
||||
vector<list<Edge>> grid(n + 1); // 邻接表
|
||||
for (auto &f : flights) {
|
||||
int from = f[0];
|
||||
int to = f[1];
|
||||
int price = f[2];
|
||||
grid[from].push_back(Edge(to, price));
|
||||
|
||||
}
|
||||
minDist[src] = 0;
|
||||
vector<int> minDist_copy(n); // 用来记录每一次遍历的结果
|
||||
k++;
|
||||
queue<int> que;
|
||||
que.push(src);
|
||||
std::vector<bool> visited(n + 1, false); // 可加,可不加,加了效率高一些,防止重复访问
|
||||
int que_size;
|
||||
while (k-- && !que.empty()) {
|
||||
|
||||
minDist_copy = minDist; // 获取上一次计算的结果
|
||||
que_size = que.size();
|
||||
while (que_size--) { // 这个while循环的设计实在是妙啊
|
||||
int node = que.front(); que.pop();
|
||||
for (Edge edge : grid[node]) {
|
||||
int from = node;
|
||||
int to = edge.to;
|
||||
int price = edge.val;
|
||||
if (minDist[to] > minDist_copy[from] + price) {
|
||||
minDist[to] = minDist_copy[from] + price;
|
||||
que.push(to);
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
}
|
||||
int result = minDist[dst] == INT_MAX/2 ? -1 : minDist[dst];
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
|
||||
-----------------
|
||||
|
||||
队列加上 visited 不能重复访问
|
||||
|
||||
class Solution {
|
||||
struct Edge {
|
||||
int to; // 链接的节点
|
||||
int val; // 边的权重
|
||||
|
||||
Edge(int t, int w): to(t), val(w) {} // 构造函数
|
||||
};
|
||||
|
||||
public:
|
||||
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
|
||||
vector<int> minDist(n , INT_MAX/2);
|
||||
vector<list<Edge>> grid(n + 1); // 邻接表
|
||||
for (auto &f : flights) {
|
||||
int from = f[0];
|
||||
int to = f[1];
|
||||
int price = f[2];
|
||||
grid[from].push_back(Edge(to, price));
|
||||
|
||||
}
|
||||
minDist[src] = 0;
|
||||
vector<int> minDist_copy(n); // 用来记录每一次遍历的结果
|
||||
k++;
|
||||
queue<int> que;
|
||||
que.push(src);
|
||||
int que_size;
|
||||
while (k-- && !que.empty()) {
|
||||
// 注意这个数组放的位置
|
||||
vector<bool> visited(n + 1, false); // 可加,可不加,加了效率高一些,防止队列里重复访问,其数值已经算过了
|
||||
minDist_copy = minDist; // 获取上一次计算的结果
|
||||
que_size = que.size();
|
||||
while (que_size--) {
|
||||
int node = que.front(); que.pop();
|
||||
for (Edge edge : grid[node]) {
|
||||
int from = node;
|
||||
int to = edge.to;
|
||||
int price = edge.val;
|
||||
if (minDist[to] > minDist_copy[from] + price) {
|
||||
minDist[to] = minDist_copy[from] + price;
|
||||
if(visited[to]) continue; // 不用重复放入队列,但需要重复计算,所以放在这里位置
|
||||
visited[to] = true;
|
||||
que.push(to);
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
}
|
||||
int result = minDist[dst] == INT_MAX/2 ? -1 : minDist[dst];
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
|
||||
|
||||
|
||||
46
problems/1334.阈值距离内邻居最少的城市.md
Normal file
46
problems/1334.阈值距离内邻居最少的城市.md
Normal file
@ -0,0 +1,46 @@
|
||||
|
||||
floyd
|
||||
|
||||
|
||||
class Solution {
|
||||
public:
|
||||
int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
|
||||
vector<vector<int>> grid(n, vector<int>(n, 10005)); // 因为边的最大距离是10^4
|
||||
|
||||
// 节点到自己的距离为0
|
||||
for (int i = 0; i < n; i++) grid[i][i] = 0;
|
||||
// 构造邻接矩阵
|
||||
for (const vector<int>& e : edges) {
|
||||
int from = e[0];
|
||||
int to = e[1];
|
||||
int val = e[2];
|
||||
grid[from][to] = val;
|
||||
grid[to][from] = val; // 注意这里是双向图
|
||||
}
|
||||
|
||||
// 开始 floyd
|
||||
// 思考 为什么 p 要放在最外面一层
|
||||
for (int p = 0; p < n; p++) {
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
grid[i][j] = min(grid[i][j], grid[i][p] + grid[p][j]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
int result = 0;
|
||||
int count = n + 10; // 记录所有城市在范围内连接的最小城市数量
|
||||
for (int i = 0; i < n; i++) {
|
||||
int curCount = 0; // 统计一个城市在范围内可以连接几个城市
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (i != j && grid[i][j] <= distanceThreshold) curCount++;
|
||||
// cout << "i:" << i << ", j:" << j << ", val: " << grid[i][j] << endl;
|
||||
}
|
||||
if (curCount <= count) { // 注意这里是 <=
|
||||
count = curCount;
|
||||
result = i;
|
||||
}
|
||||
}
|
||||
return result;
|
||||
}
|
||||
};
|
||||
371
problems/kama94.城市间货物运输I.md
Normal file
371
problems/kama94.城市间货物运输I.md
Normal file
@ -0,0 +1,371 @@
|
||||
|
||||
# 94. 城市间货物运输 I
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1152)
|
||||
|
||||
题目描述
|
||||
|
||||
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
|
||||
|
||||
|
||||
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
|
||||
|
||||
|
||||
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。如果最低运输成本是一个负数,它表示在遵循最优路径的情况下,运输过程中反而能够实现盈利。
|
||||
|
||||
|
||||
城市 1 到城市 n 之间可能会出现没有路径的情况,同时保证道路网络中不存在任何负权回路。
|
||||
|
||||
输入描述
|
||||
|
||||
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
|
||||
|
||||
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v(单向图)。
|
||||
|
||||
输出描述
|
||||
|
||||
如果能够从城市 1 到连通到城市 n, 请输出一个整数,表示运输成本。如果该整数是负数,则表示实现了盈利。如果从城市 1 没有路径可达城市 n,请输出 "unconnected"。
|
||||
|
||||
输入示例:
|
||||
|
||||
```
|
||||
6 7
|
||||
5 6 -2
|
||||
1 2 1
|
||||
5 3 1
|
||||
2 5 2
|
||||
2 4 -3
|
||||
4 6 4
|
||||
1 3 5
|
||||
```
|
||||
|
||||
## 思路
|
||||
|
||||
本题依然是最短路问题,求 从 节点1 到节点n 的最小费用。 但本题不同之处在于 边的权值是有负数的。
|
||||
|
||||
从 节点1 到节点n 的最小费用也可以是负数,费用如果是负数 则表示 运输的过程中 政府补贴大于运输成本。
|
||||
|
||||
在求单源最短路的方法中,使用dijkstra 的话,则要求图中边的权值都为正数。
|
||||
|
||||
我们在 [kama47.参会dijkstra朴素](./kama47.参会dijkstra朴素.md) 中专门有讲解,为什么有边为负数 使用dijkstra就不行了。
|
||||
|
||||
本题是经典的带负权值的单源最短路问题,此时就轮到Bellman_ford登场了,接下来我们来详细介绍Bellman_ford 算法 如何解决这类问题。
|
||||
|
||||
> 该算法是由 R.Bellman 和L.Ford 在20世纪50年代末期发明的算法,故称为Bellman_ford算法。
|
||||
|
||||
**Bellman_ford算法的核心思想是 对所有边进行松弛n-1次操作(n为节点数量),从而求得目标最短路**。
|
||||
|
||||
|
||||
看到这里,估计大家都比较晕了,为什么是 n-1 次,那“松弛”这两个字究竟是个啥意思?
|
||||
|
||||
我们先来说什么是 “松弛”。
|
||||
|
||||
《算法四》里面把这个操作叫做 “放松”, 英文版里叫做 “relax the edge”
|
||||
|
||||
所以大家翻译过来,就是 “放松” 或者 “松弛” 。
|
||||
|
||||
但《算法四》没有具体去讲这个 “放松” 究竟是个啥? 网上的题解也没有讲题解里的 “松弛这条边,松弛所有边”等等 里面的 “松弛” 究竟是什么意思?
|
||||
|
||||
这里我给大家举一个例子,每条边有起点、终点和边的权值。例如一条边,节点A 到 节点B 权值为value,如图:
|
||||
|
||||
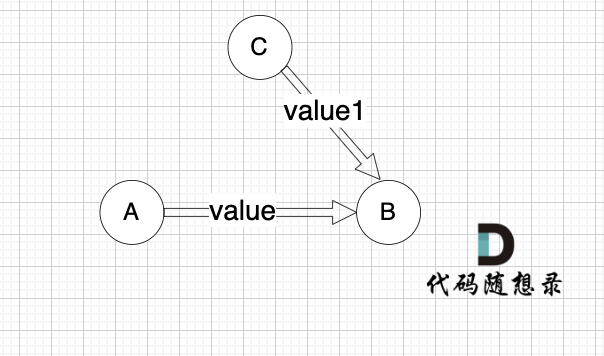
|
||||
|
||||
minDist[B] 表示 到达B节点 最小权值,minDist[B] 有哪些状态可以推出来?
|
||||
|
||||
状态一: minDist[A] + value 可以推出 minDist[B]
|
||||
状态二: minDist[B]本身就有权值 (可能是其他边链接的节点B 例如节点C,以至于 dp[B]记录了其他边到dp[B]的权值)
|
||||
|
||||
那么minDist[B] 应为如何取舍。
|
||||
|
||||
本题我们要求最小权值,那么 这两个状态我们就取最小的
|
||||
|
||||
```
|
||||
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
|
||||
|
||||
```
|
||||
|
||||
也就是说,如果 通过 A 到 B 这条边可以获得更短的到达B节点的路径,即如果 `minDist[B] > minDist[A] + value`,那么我们就更新 `minDist[B] = minDist[A] + value` ,**这个过程就叫做 “松弛**” 。
|
||||
|
||||
以上讲了这么多,其实都是围绕以下这句代码展开:
|
||||
|
||||
```
|
||||
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
|
||||
|
||||
```
|
||||
|
||||
**这句代码就是 Bellman_ford算法的核心操作**。
|
||||
|
||||
以上代码也可以这么写:`minDist[B] = min(minDist[A] + value, minDist[B]) `
|
||||
|
||||
如果大家看过代码随想录的动态规划章节,会发现 无论是背包问题还是子序列问题,这段代码(递推公式)出现频率非常高的。
|
||||
|
||||
其实 Bellman_ford算法 也是采用了动态规划的思想,即:将一个问题分解成多个决策阶段,通过状态之间的递归关系最后计算出全局最优解。
|
||||
|
||||
(如果理解不了动态规划的思想也无所谓,理解我上面讲的松弛操作就好)
|
||||
|
||||
**那么为什么是 n - 1次 松弛呢**?
|
||||
|
||||
这里要给大家模拟一遍 Bellman_ford 的算法才行,接下来我们来看看对所有边松弛 n -1 次的操作是什么样的。
|
||||
|
||||
我们依然使用**minDist数组来表达 起点到各个节点的最短距离**,例如minDist[3] = 5 表示起点到达节点3 的最小距离为5
|
||||
|
||||
### 模拟过程
|
||||
|
||||
初始化过程。
|
||||
|
||||
起点为节点1, 起点到起点的距离为0,所以 minDist[1] 初始化为0
|
||||
|
||||
如图:
|
||||
|
||||
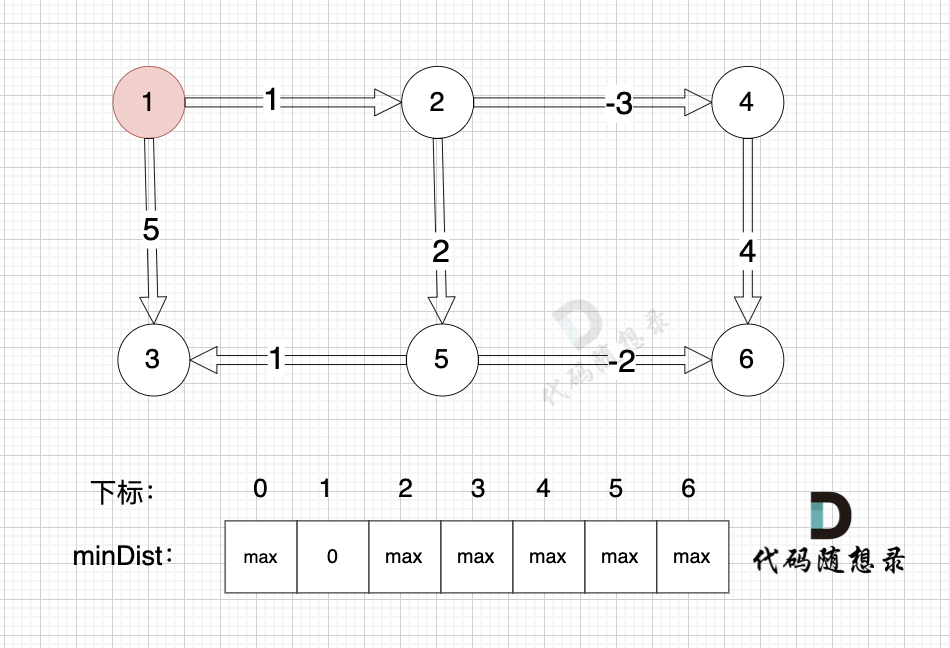
|
||||
|
||||
其他节点对应的minDist初始化为max,因为我们要求最小距离,那么还没有计算过的节点 默认是一个最大数,这样才能更新最小距离。
|
||||
|
||||
|
||||
对所有边 进行第一次松弛: (什么是松弛,在上面我已经详细讲过)
|
||||
|
||||
以示例给出的所有边为例:
|
||||
|
||||
```
|
||||
5 6 -2
|
||||
1 2 1
|
||||
5 3 1
|
||||
2 5 2
|
||||
2 4 -3
|
||||
4 6 4
|
||||
1 3 5
|
||||
```
|
||||
|
||||
接下来我们来松弛一遍所有的边。
|
||||
|
||||
边:节点5 -> 节点6,权值为-2 ,minDist[5] 还是默认数值max,所以不能基于 节点5 去更新节点6,如图:
|
||||
|
||||
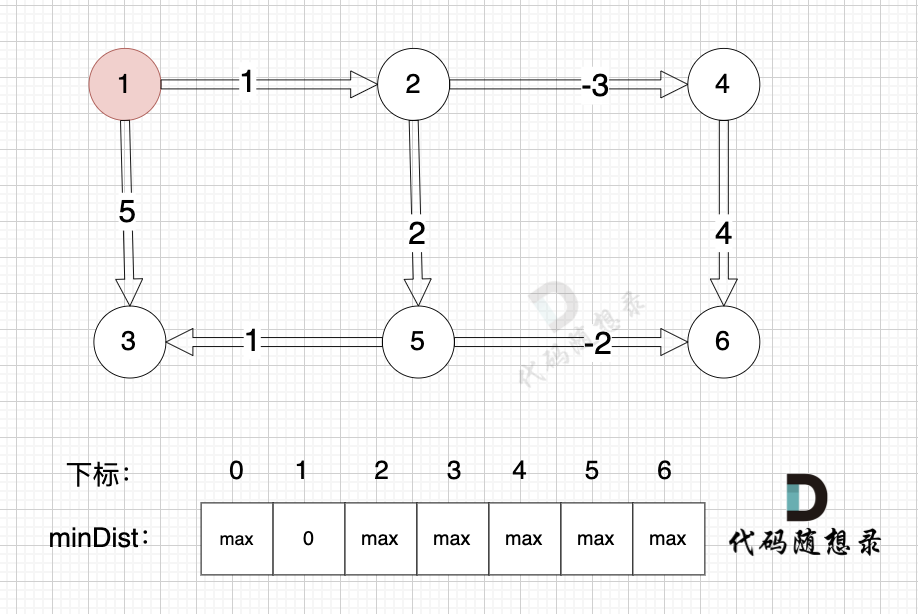
|
||||
|
||||
(在复习一下,minDist[5] 表示起点到节点5的最短距离)
|
||||
|
||||
|
||||
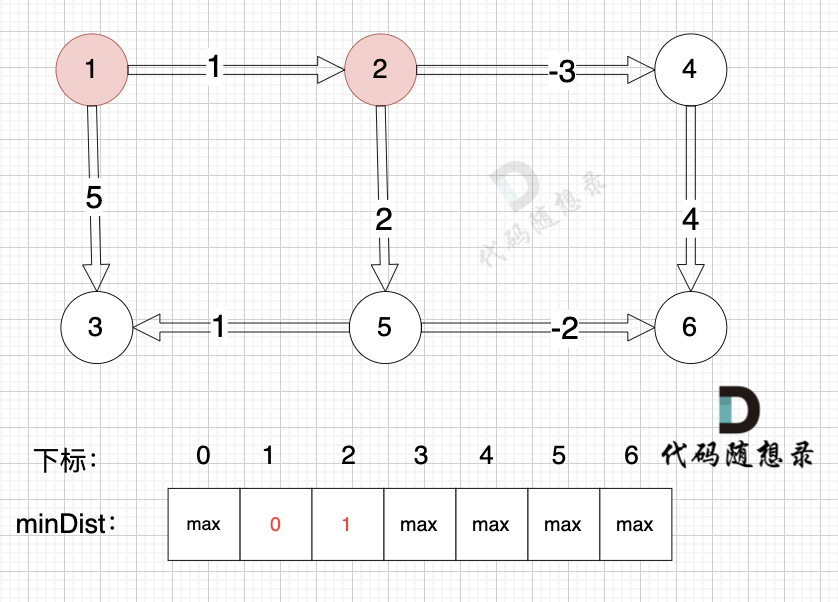
边:节点1 -> 节点2,权值为1 ,minDist[2] > minDist[1] + 1 ,更新 minDist[2] = minDist[1] + 1 = 0 + 1 = 1 ,如图:
|
||||
|
||||
|
||||
|
||||
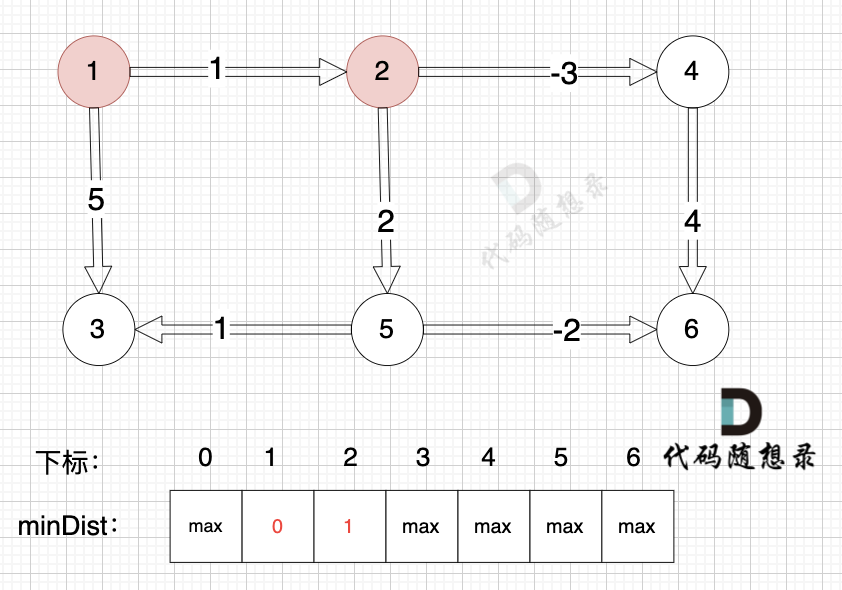
边:节点5 -> 节点3,权值为1 ,minDist[5] 还是默认数值max,所以不能基于节点5去更新节点3 如图:
|
||||
|
||||
|
||||
|
||||
|
||||
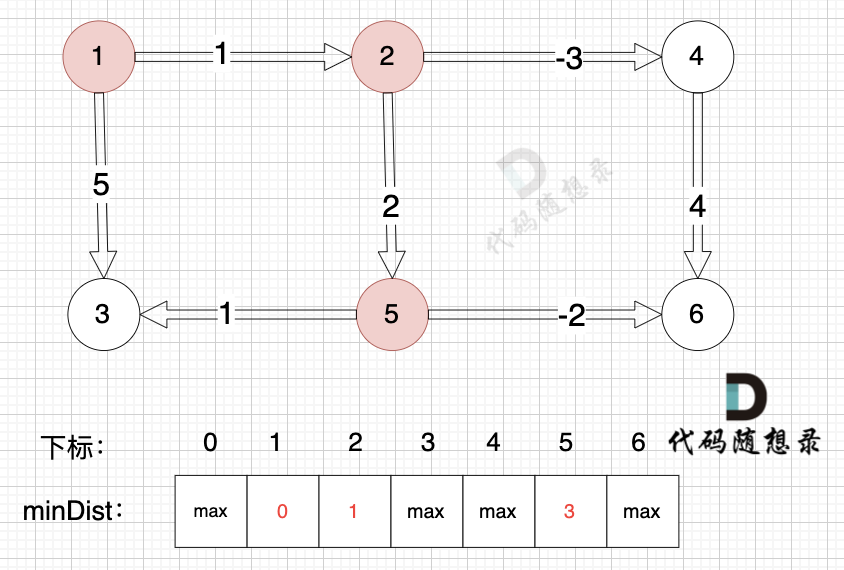
边:节点2 -> 节点5,权值为2 ,minDist[5] > minDist[2] + 2 (经过上面的计算minDist[2]已经不是默认值,而是 1),更新 minDist[5] = minDist[2] + 2 = 1 + 2 = 3 ,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
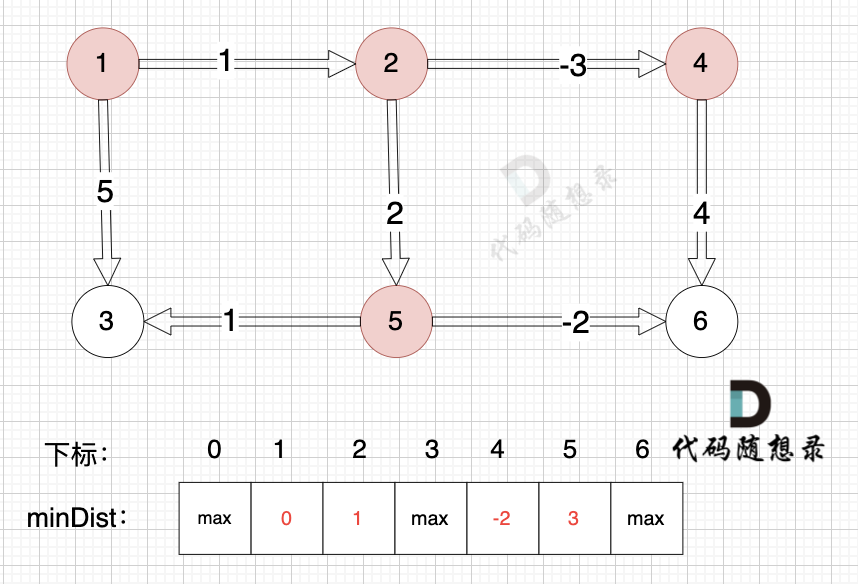
边:节点2 -> 节点4,权值为-3 ,minDist[4] > minDist[2] + 2,更新 minDist[4] = minDist[2] + (-3) = 1 + (-3) = -2 ,如图:
|
||||
|
||||
|
||||
|
||||
边:节点4 -> 节点6,权值为4 ,minDist[6] > minDist[4] + 4,更新 minDist[6] = minDist[4] + 4 = -2 + 4 = 2
|
||||
|
||||
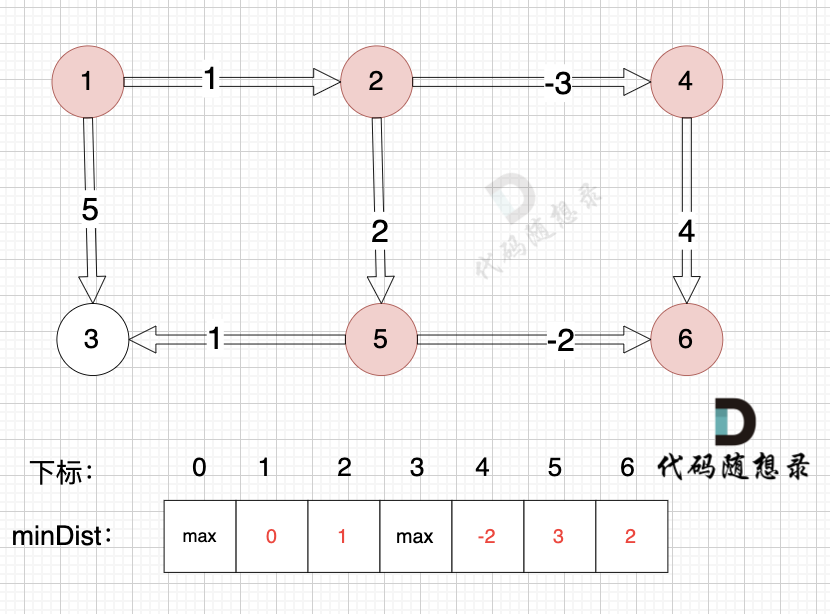
|
||||
|
||||
边:节点1 -> 节点3,权值为5 ,minDist[3] > minDist[1] + 5,更新 minDist[3] = minDist[1] + 5 = 0 + 5 = 5 ,如图:
|
||||
|
||||
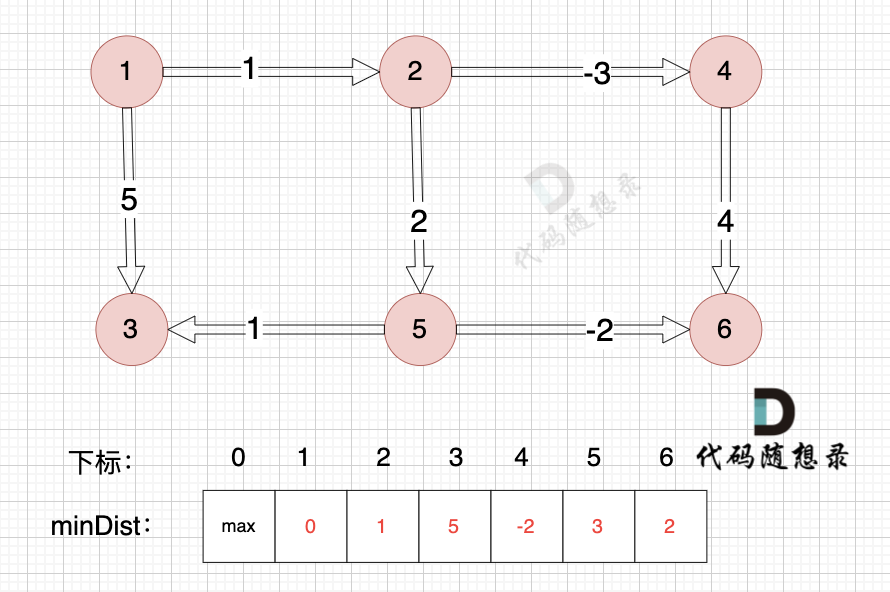
|
||||
|
||||
--------
|
||||
|
||||
以上是对所有边进行一次松弛之后的结果。
|
||||
|
||||
那么需要对所有边松弛几次才能得到 起点(节点1) 到终点(节点6)的最短距离呢?
|
||||
|
||||
**对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离**。
|
||||
|
||||
上面的距离中,我们得到里 起点达到 与起点一条边相邻的节点2 和 节点3 的最短距离,分别是 minDist[2] 和 minDist[3]
|
||||
|
||||
这里有录友疑惑了 minDist[3] = 5,分明不是 起点到达 节点3 的最短距离,节点1 -> 节点2 -> 节点5 -> 节点3 这条路线 距离才是4。
|
||||
|
||||
注意我上面讲的是 **对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离**,这里 说的是 一条边相连的节点。
|
||||
|
||||
与起点(节点1)一条边相邻的节点,到达节点2 最短距离是 1,到达节点3 最短距离是5。
|
||||
|
||||
而 节点1 -> 节点2 -> 节点5 -> 节点3 这条路线 是 与起点 三条边相连的路线了。
|
||||
|
||||
所以对所有边松弛一次 能得到 与起点 一条边相连的节点最短距离。
|
||||
|
||||
那对所有边松弛两次 可以得到与起点 两条边相连的节点的最短距离。
|
||||
|
||||
那对所有边松弛三次 可以得到与起点 三条边相连的节点的最短距离,这个时候,我们就能得到到达节点3真正的最短距离,也就是 节点1 -> 节点2 -> 节点5 -> 节点3 这条路线。
|
||||
|
||||
那么再回归刚刚的问题,**需要对所有边松弛几次才能得到 起点(节点1) 到终点(节点6)的最短距离呢**?
|
||||
|
||||
节点数量为n,那么起点到终点,最多是 n-1 条边相连。
|
||||
|
||||
那么无论图是什么样的,边是什么样的顺序,我们对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。
|
||||
|
||||
其实也同时计算出了,起点 到达 所有节点的最短距离,因为所有节点与起点连接的变数最多也就是 n-1条边。
|
||||
|
||||
截止到这里,Bellman_ford 的核心算法思路,大家就了解的差不多了。
|
||||
|
||||
共有两个关键点。
|
||||
|
||||
* “松弛”究竟是个啥
|
||||
* 为什么要对所有边松弛 n - 1 次 (n为节点个数)
|
||||
|
||||
那么Bellman_ford的解题解题过程其实就是对所有边松弛 n-1 次,然后得出得到终点的最短路径。
|
||||
|
||||
|
||||
|
||||
### 代码
|
||||
|
||||
理解上面讲解的内容,代码就更容易写了,本题代码如下:(详细注释)
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <list>
|
||||
#include <climits>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int n, m, p1, p2, val;
|
||||
cin >> n >> m;
|
||||
|
||||
vector<vector<int>> grid;
|
||||
|
||||
// 将所有边保存起来
|
||||
for(int i = 0; i < m; i++){
|
||||
cin >> p1 >> p2 >> val;
|
||||
// p1 指向 p2,权值为 val
|
||||
grid.push_back({p1, p2, val});
|
||||
|
||||
}
|
||||
int start = 1; // 起点
|
||||
int end = n; // 终点
|
||||
|
||||
vector<int> minDist(n + 1 , INT_MAX);
|
||||
minDist[start] = 0;
|
||||
for (int i = 1; i < n; i++) { // 对所有边 松弛 n-1 次
|
||||
for (vector<int> &side : grid) { // 每一次松弛,都是对所有边进行松弛
|
||||
int from = side[0]; // 边的出发点
|
||||
int to = side[1]; // 边的到达点
|
||||
int price = side[2]; // 边的权值
|
||||
// 松弛操作
|
||||
// minDist[from] != INT_MAX 防止从未计算过的节点出发
|
||||
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) {
|
||||
minDist[to] = minDist[from] + price;
|
||||
}
|
||||
}
|
||||
}
|
||||
if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
|
||||
else cout << minDist[end] << endl; // 到达终点最短路径
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
### 拓展
|
||||
|
||||
有录友可能会想,那我 松弛 n 次,松弛 n + 1次,松弛 2 * n 次会怎么样?
|
||||
|
||||
其实没啥影响,结果不会变的,因为 题目中说了 “同时保证道路网络中不存在任何负权回路” 也就是图中没有 负权回路(在有向图中出现有向环 且环的总权值为负数)。
|
||||
|
||||
那么我们只要松弛 n - 1次 就一定能得到结果,没必要在松弛更多次了。
|
||||
|
||||
这里有疑惑的录友,可以加上打印 minDist数组 的日志,尝试一下,看看松弛 n 次会怎么样。
|
||||
你会发现 松弛 大于 n - 1次,minDist数组 就不会变化了。
|
||||
|
||||
这里我给出打印日志的代码:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <list>
|
||||
#include <climits>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int n, m, p1, p2, val;
|
||||
cin >> n >> m;
|
||||
|
||||
vector<vector<int>> grid;
|
||||
|
||||
// 将所有边保存起来
|
||||
for(int i = 0; i < m; i++){
|
||||
cin >> p1 >> p2 >> val;
|
||||
// p1 指向 p2,权值为 val
|
||||
grid.push_back({p1, p2, val});
|
||||
|
||||
}
|
||||
int start = 1; // 起点
|
||||
int end = n; // 终点
|
||||
|
||||
vector<int> minDist(n + 1 , INT_MAX);
|
||||
minDist[start] = 0;
|
||||
for (int i = 1; i < n; i++) { // 对所有边 松弛 n-1 次
|
||||
for (vector<int> &side : grid) { // 每一次松弛,都是对所有边进行松弛
|
||||
int from = side[0]; // 边的出发点
|
||||
int to = side[1]; // 边的到达点
|
||||
int price = side[2]; // 边的权值
|
||||
// 松弛操作
|
||||
// minDist[from] != INT_MAX 防止从未计算过的节点出发
|
||||
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) {
|
||||
minDist[to] = minDist[from] + price;
|
||||
}
|
||||
}
|
||||
cout << "对所有边松弛 " << i << "次" << endl;
|
||||
for (int k = 1; k <= n; k++) {
|
||||
cout << minDist[k] << " ";
|
||||
}
|
||||
cout << endl;
|
||||
}
|
||||
if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
|
||||
else cout << minDist[end] << endl; // 到达终点最短路径
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
通过打日志,大家发现,怎么对所有边进行第二次松弛以后结果就 不再变化了,那根本就不用松弛 n - 1啊?
|
||||
|
||||
这是本题的样例的特殊性, 松弛 n-1次 是保证对任何图 都能最后求得到终点的最小距离。
|
||||
|
||||
如果还想不明白 我再举一个例子,用以下测试用例再跑一下。
|
||||
|
||||
|
||||
```
|
||||
6 5
|
||||
5 6 1
|
||||
4 5 1
|
||||
3 4 1
|
||||
2 3 1
|
||||
1 2 1
|
||||
```
|
||||
|
||||
打印结果:
|
||||
|
||||
```
|
||||
对所有边松弛 1次
|
||||
0 1 2147483647 2147483647 2147483647 2147483647
|
||||
对所有边松弛 2次
|
||||
0 1 2 2147483647 2147483647 2147483647
|
||||
对所有边松弛 3次
|
||||
0 1 2 3 2147483647 2147483647
|
||||
对所有边松弛 4次
|
||||
0 1 2 3 4 2147483647
|
||||
对所有边松弛 5次
|
||||
0 1 2 3 4 5
|
||||
```
|
||||
|
||||
你会发现到 n-1 次 打印出最后的最短路结果。
|
||||
|
||||
关于上面的讲解,大家已经要多写代码去实验,验证自己的想法。
|
||||
|
||||
至于 负权回路 ,我在下一篇会专门讲解这种情况,大家有个印象就好。
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
Bellman_ford 是可以计算 负权值的单源最短路算法。
|
||||
|
||||
其算法核心思路是对 所有边进行 n-1 次 松弛。
|
||||
|
||||
弄清楚 什么是 松弛? 为什么要 n-1 次? 对理解Bellman_ford 非常重要。
|
||||
|
||||
150
problems/kama95.城市间货物运输II.md
Normal file
150
problems/kama95.城市间货物运输II.md
Normal file
@ -0,0 +1,150 @@
|
||||
|
||||
# 95. 城市间货物运输 II
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1153)
|
||||
|
||||
【题目描述】
|
||||
|
||||
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
|
||||
|
||||
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;
|
||||
|
||||
权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
|
||||
|
||||
然而,在评估从城市 1 到城市 n 的所有可能路径中综合政府补贴后的最低运输成本时,存在一种情况:图中可能出现负权回路。
|
||||
|
||||
负权回路是指一系列道路的总权值为负,这样的回路使得通过反复经过回路中的道路,理论上可以无限地减少总成本或无限地增加总收益。
|
||||
|
||||
为了避免货物运输商采用负权回路这种情况无限的赚取政府补贴,算法还需检测这种特殊情况。
|
||||
|
||||
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。同时能够检测并适当处理负权回路的存在。
|
||||
|
||||
城市 1 到城市 n 之间可能会出现没有路径的情况
|
||||
|
||||
【输入描述】
|
||||
|
||||
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
|
||||
|
||||
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
|
||||
|
||||
【输出描述】
|
||||
|
||||
如果没有发现负权回路,则输出一个整数,表示从城市 1 到城市 n 的最低运输成本(包括政府补贴)。
|
||||
|
||||
如果该整数是负数,则表示实现了盈利。如果发现了负权回路的存在,则输出 "circle"。如果从城市 1 无法到达城市 n,则输出 "unconnected"。
|
||||
|
||||
|
||||
输入示例
|
||||
|
||||
```
|
||||
4 4
|
||||
1 2 -1
|
||||
2 3 1
|
||||
3 1 -1
|
||||
3 4 1
|
||||
```
|
||||
|
||||
输出示例
|
||||
|
||||
```
|
||||
circle
|
||||
```
|
||||
|
||||
## 思路
|
||||
|
||||
本题是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 延伸题目。
|
||||
|
||||
本题是要我们判断 负权回路,也就是图中出现环且环上的边总权值为负数。
|
||||
|
||||
如果在这样的图中求最短路的话, 就会在这个环里无限循环 (也是负数+负数 只会越来越小),无法求出最短路径。
|
||||
|
||||
所以对于 在有负权值的图中求最短路,都需要先看看这个图里有没有负权回路。
|
||||
|
||||
接下来我们来看 如何使用 bellman_ford 算法来判断 负权回路。
|
||||
|
||||
在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 中 我们讲了 bellman_ford 算法的核心就是一句话:对 所有边 进行 n-1 次松弛。 同时文中的 【拓展】部分, 我们也讲了 松弛n次以上 会怎么样?
|
||||
|
||||
在没有负权回路的图中,松弛 n 次以上 ,结果不会有变化。
|
||||
|
||||
但本题有 负权回路,如果松弛 n 次,结果就会有变化了,因为 有负权回路 就是可以无限最短路径(一直绕圈,就可以一直得到无限小的最短距离)。
|
||||
|
||||
那么每松弛一次,都会更新最短路径,所以结果会一直有变化。
|
||||
|
||||
(如果对于 bellman_ford 不了解的录友,建议详细看这里:[kama94.城市间货物运输I](./kama94.城市间货物运输I.md))
|
||||
|
||||
以上为理论分析,接下来我们再画图举例。
|
||||
|
||||
我们拿题目中示例来画一个图:
|
||||
|
||||

|
||||
|
||||
图中 节点1 到 节点4 的最短路径是多少(题目中的最低运输成本) (注意边可以为负数的)
|
||||
|
||||
节点1 -> 节点2 -> 节点3 -> 节点4,这样的路径总成本为 -1 + 1 + 1 = 1
|
||||
|
||||
而图中有负权回路:
|
||||
|
||||
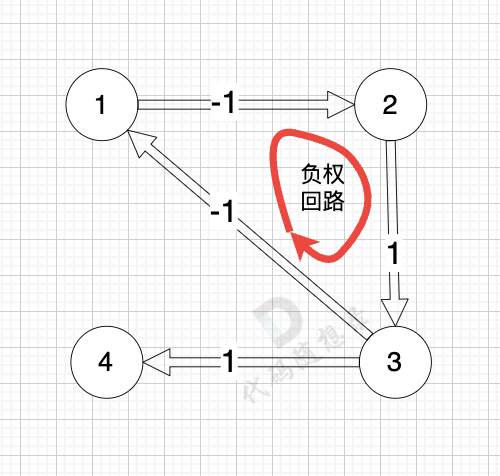
|
||||
|
||||
那么我们在负权回路中多绕一圈,我们的最短路径 是不是就更小了 (也就是更低的运输成本)
|
||||
|
||||
节点1 -> 节点2 -> 节点3 -> 节点1 -> 节点2 -> 节点3 -> 节点4,这样的路径总成本 (-1) + 1 + (-1) + (-1) + 1 + (-1) + 1 = -1
|
||||
|
||||
如果在负权回路多绕两圈,三圈,无穷圈,那么我们的总成本就会无限小, 如果要求最小成本的话,你会发现本题就无解了。
|
||||
|
||||
在 bellman_ford 算法中,松弛 n-1 次所有的边 就可以求得 起点到任何节点的最短路径,松弛 n 次以上,minDist数组(记录起到到其他节点的最短距离)中的结果也不会有改变 (如果对 bellman_ford 算法 不了解,也不知道 minDist 是什么,建议详看上篇讲解[kama94.城市间货物运输I](./kama94.城市间货物运输I.md))
|
||||
|
||||
而本题有负权回路的情况下,一直都会有更短的最短路,所以 松弛 第n次,minDist数组 也会发生改变。
|
||||
|
||||
那么解决本题的 核心思路,就是在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 的基础上,再多松弛一次,看minDist数组 是否发生变化。
|
||||
|
||||
代码和 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 基本是一样的,如下:(关键地方已注释)
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <list>
|
||||
#include <climits>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int n, m, p1, p2, val;
|
||||
cin >> n >> m;
|
||||
|
||||
vector<vector<int>> grid;
|
||||
|
||||
for(int i = 0; i < m; i++){
|
||||
cin >> p1 >> p2 >> val;
|
||||
// p1 指向 p2,权值为 val
|
||||
grid.push_back({p1, p2, val});
|
||||
|
||||
}
|
||||
int start = 1; // 起点
|
||||
int end = n; // 终点
|
||||
|
||||
vector<int> minDist(n + 1 , INT_MAX);
|
||||
minDist[start] = 0;
|
||||
bool flag = false;
|
||||
for (int i = 1; i <= n; i++) { // 这里我们松弛n次,最后一次判断负权回路
|
||||
for (vector<int> &side : grid) {
|
||||
int from = side[0];
|
||||
int to = side[1];
|
||||
int price = side[2];
|
||||
if (i < n) {
|
||||
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) minDist[to] = minDist[from] + price;
|
||||
} else { // 多加一次松弛判断负权回路
|
||||
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) flag = true;
|
||||
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
if (flag) cout << "circle" << endl;
|
||||
else if (minDist[end] == INT_MAX) {
|
||||
cout << "unconnected" << endl;
|
||||
} else {
|
||||
cout << minDist[end] << endl;
|
||||
}
|
||||
}
|
||||
```
|
||||
125
problems/kama96.城市间货物运输III.md
Normal file
125
problems/kama96.城市间货物运输III.md
Normal file
@ -0,0 +1,125 @@
|
||||
|
||||
# 96. 城市间货物运输 III
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1154)
|
||||
|
||||
【题目描述】
|
||||
|
||||
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
|
||||
|
||||
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。
|
||||
|
||||
权值为正表示扣除了政府补贴后运输货物仍需支付的费用;
|
||||
|
||||
权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
|
||||
|
||||
请计算在最多经过 k 个城市的条件下,从城市 src 到城市 dst 的最低运输成本。
|
||||
|
||||
【输入描述】
|
||||
|
||||
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
|
||||
|
||||
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
|
||||
|
||||
最后一行包含三个正整数,src、dst、和 k,src 和 dst 为城市编号,从 src 到 dst 经过的城市数量限制。
|
||||
|
||||
【输出描述】
|
||||
|
||||
输出一个整数,表示从城市 src 到城市 dst 的最低运输成本,如果无法在给定经过城市数量限制下找到从 src 到 dst 的路径,则输出 "unreachable",表示不存在符合条件的运输方案。
|
||||
|
||||
输入示例:
|
||||
|
||||
```
|
||||
6 7
|
||||
1 2 1
|
||||
2 4 -3
|
||||
2 5 2
|
||||
1 3 5
|
||||
3 5 1
|
||||
4 6 4
|
||||
5 6 -2
|
||||
2 6 1
|
||||
```
|
||||
|
||||
输出示例:
|
||||
|
||||
```
|
||||
0
|
||||
```
|
||||
|
||||
## 思路
|
||||
|
||||
本题为单源有限最短路问题,同样是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 延伸题目。
|
||||
|
||||
在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 中我们讲了:**对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离**。
|
||||
|
||||
节点数量为n,那么起点到终点,最多是 n-1 条边相连。 那么对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。
|
||||
|
||||
(如果对以上讲解看不懂,建议详看 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) )
|
||||
|
||||
本题是最多经过 k 个城市, 那么是 k + 1条边相连的节点。 这里可能有录友想不懂为什么是k + 1,来看这个图:
|
||||
|
||||
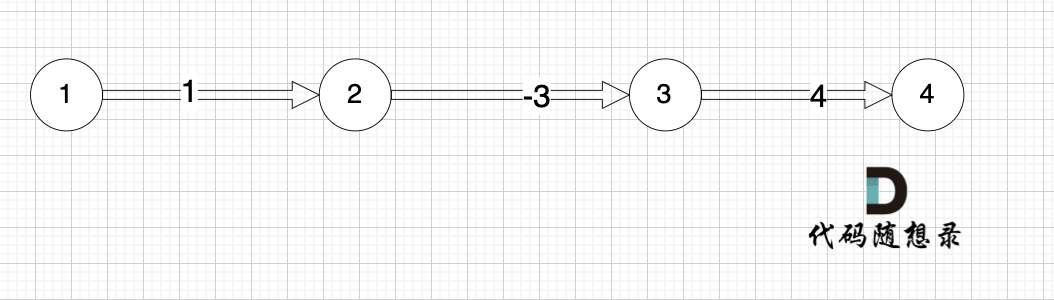
|
||||
|
||||
图中,节点2 最多已经经过2个节点 到达节点4,那么中间是有多少条边呢,是 3 条边对吧。
|
||||
|
||||
所以本题就是求,起点最多经过k + 1 条边到达终点的最短距离。
|
||||
|
||||
|
||||
对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离,那么对所有边松弛 k + 1次,就是求 起点到达 与起点k + 1条边相连的节点的 最短距离。
|
||||
|
||||
如果 终点数值没有被计算覆盖,那就是无法到达。
|
||||
|
||||
**注意**: 本题是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 的拓展题,如果对 bellman_ford 没有深入了解,强烈建议先看 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 再做本题。
|
||||
|
||||
理解以上内容,其实本题代码就很容易了,bellman_ford 标准写法是松弛 n-1 次,本题就松弛 k + 1次就好。
|
||||
|
||||
如果大家理解后,建议先自己写写代码,提交一下看看,因为 这里还有一个坑,如果不自己去试试,体会就不够深刻了。
|
||||
|
||||
|
||||
|
||||
代码如下: (关键地方详细注释)
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <list>
|
||||
#include <climits>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int src, dst,k ,p1, p2, val ,m , n;
|
||||
|
||||
cin >> n >> m;
|
||||
|
||||
vector<vector<int>> grid;
|
||||
|
||||
for(int i = 0; i < m; i++){
|
||||
cin >> p1 >> p2 >> val;
|
||||
// p1 指向 p2,权值为 val
|
||||
grid.push_back({p1, p2, val});
|
||||
}
|
||||
|
||||
cin >> src >> dst >> k;
|
||||
|
||||
vector<int> minDist(n + 1 , INT_MAX);
|
||||
minDist[src] = 0;
|
||||
vector<int> minDist_copy(n + 1); // 用来记录每一次遍历的结果
|
||||
for (int i = 1; i <= k + 1; i++) {
|
||||
minDist_copy = minDist; // 获取上一次计算的结果
|
||||
for (vector<int> &side : grid) {
|
||||
int from = side[0];
|
||||
int to = side[1];
|
||||
int price = side[2];
|
||||
//cout << f[0] << " " << f[1] << " " << f[2] << endl;
|
||||
if (minDist_copy[from] != INT_MAX && minDist[to] > minDist_copy[from] + price) minDist[to] = minDist_copy[from] + price;
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
if (minDist[dst] == INT_MAX) cout << "unreachable" << endl; // 不能到达终点
|
||||
else cout << minDist[dst] << endl; // 到达终点最短路径
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
@ -99,7 +99,7 @@ Carl校招社招都拿过大厂的offer,同时也看过很多应聘者的简
|
||||
|
||||
面试只有短短的30分钟或者一个小时,如何把自己掌握的技术更好的展现给面试官呢,博客、github都是很好的选择,如果把这些放在简历上,面试官一定会看的,这都是加分项。
|
||||
|
||||
## 简历模板
|
||||
## 领取方式
|
||||
|
||||
最后福利,把我的简历模板贡献出来!如下图所示。
|
||||
|
||||
@ -107,7 +107,11 @@ Carl校招社招都拿过大厂的offer,同时也看过很多应聘者的简
|
||||
|
||||
这里是简历模板中Markdown的代码:[https://github.com/youngyangyang04/Markdown-Resume-Template](https://github.com/youngyangyang04/Markdown-Resume-Template) ,可以fork到自己Github仓库上,按照这个模板来修改自己的简历。
|
||||
|
||||
**Word版本的简历,大家可以在公众号「代码随想录」后台回复:简历模板,就可以获取!**
|
||||
**Word版本的简历,添加如下企业微信,通过之后就会发你word版本**。
|
||||
|
||||
<div align="center"><img src="https://code-thinking-1253855093.file.myqcloud.com/pics/20240328164645.png" data-img="1" width="200" height="200"></img></div>
|
||||
|
||||
如果已经有我的企业微信,直接回复:简历模板,就可以了。
|
||||
|
||||
## 总结
|
||||
|
||||
|
||||
Reference in New Issue
Block a user