mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-08 00:43:04 +08:00
Update
This commit is contained in:
155
problems/kama53.寻宝.md
Normal file
155
problems/kama53.寻宝.md
Normal file
@ -0,0 +1,155 @@
|
||||
|
||||
|
||||
如果你的图相对较小且比较密集,而且你更注重简单性和空间效率,数组实现可能更合适。
|
||||
|
||||
如果你的图规模较大,尤其是在稀疏图中,而且你更注重时间效率和通用性,优先级队列实现可能更合适。
|
||||
|
||||
其关键 在于弄清楚 minDist 的定义
|
||||
|
||||
```CPP
|
||||
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <queue>
|
||||
#include <climits>
|
||||
|
||||
using namespace std;
|
||||
|
||||
// 定义图的邻接矩阵表示
|
||||
const int INF = INT_MAX; // 表示无穷大
|
||||
typedef vector<vector<int>> Graph;
|
||||
|
||||
// 使用Prim算法找到最小生成树
|
||||
void primMST(const Graph& graph, int startVertex) {
|
||||
int V = graph.size();
|
||||
|
||||
// 存储顶点是否在最小生成树中
|
||||
vector<bool> inMST(V, false);
|
||||
|
||||
// 存储最小生成树的边权重
|
||||
vector<int> key(V, INF);
|
||||
|
||||
// 优先队列,存储边权重和目标顶点
|
||||
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
|
||||
|
||||
// 初始顶点的权重设为0,加入优先队列
|
||||
key[startVertex] = 0;
|
||||
pq.push({0, startVertex});
|
||||
|
||||
while (!pq.empty()) {
|
||||
// 从优先队列中取出权重最小的边
|
||||
int u = pq.top().second;
|
||||
pq.pop();
|
||||
|
||||
// 将顶点u标记为在最小生成树中
|
||||
inMST[u] = true;
|
||||
|
||||
// 遍历u的所有邻居
|
||||
for (int v = 0; v < V; ++v) {
|
||||
// 如果v未在最小生成树中,且u到v的权重小于v的当前权重
|
||||
if (!inMST[v] && graph[u][v] < key[v]) {
|
||||
// 更新v的权重为u到v的权重
|
||||
key[v] = graph[u][v];
|
||||
// 将(u, v)添加到最小生成树
|
||||
pq.push({key[v], v});
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 输出最小生成树的边
|
||||
cout << "Edges in the Minimum Spanning Tree:\n";
|
||||
for (int i = 1; i < V; ++i) {
|
||||
cout << i << " - " << key[i] << " - " << i << "\n";
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
// 例子:无向图的邻接矩阵表示
|
||||
Graph graph = {
|
||||
{0, 2, 0, 6, 0},
|
||||
{2, 0, 3, 8, 5},
|
||||
{0, 3, 0, 0, 7},
|
||||
{6, 8, 0, 0, 9},
|
||||
{0, 5, 7, 9, 0}
|
||||
};
|
||||
|
||||
// 从顶点0开始运行Prim算法
|
||||
primMST(graph, 0);
|
||||
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <climits>
|
||||
|
||||
using namespace std;
|
||||
|
||||
// 定义图的邻接矩阵表示
|
||||
const int INF = INT_MAX; // 表示无穷大
|
||||
typedef vector<vector<int>> Graph;
|
||||
|
||||
// 使用Prim算法找到最小生成树
|
||||
void primMST(const Graph& graph, int startVertex) {
|
||||
int V = graph.size();
|
||||
|
||||
// 存储顶点是否在最小生成树中
|
||||
vector<bool> inMST(V, false);
|
||||
|
||||
// 存储每个顶点的权重
|
||||
vector<int> key(V, INF);
|
||||
|
||||
// 初始化起始顶点的权重为0
|
||||
key[startVertex] = 0;
|
||||
|
||||
// 存储最小生成树的边权重
|
||||
vector<int> parent(V, -1);
|
||||
|
||||
// 构建最小生成树
|
||||
for (int count = 0; count < V - 1; ++count) {
|
||||
// 从未在最小生成树中的顶点中找到权重最小的顶点
|
||||
int u = -1;
|
||||
for (int v = 0; v < V; ++v) {
|
||||
if (!inMST[v] && (u == -1 || key[v] < key[u])) {
|
||||
u = v;
|
||||
}
|
||||
}
|
||||
|
||||
// 将顶点u标记为在最小生成树中
|
||||
inMST[u] = true;
|
||||
|
||||
// 更新u的邻居的权重和父节点
|
||||
for (int v = 0; v < V; ++v) {
|
||||
if (graph[u][v] != 0 && !inMST[v] && graph[u][v] < key[v]) {
|
||||
key[v] = graph[u][v];
|
||||
parent[v] = u;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 输出最小生成树的边
|
||||
cout << "Edges in the Minimum Spanning Tree:\n";
|
||||
for (int i = 1; i < V; ++i) {
|
||||
cout << parent[i] << " - " << key[i] << " - " << i << "\n";
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
// 例子:无向图的邻接矩阵表示
|
||||
Graph graph = {
|
||||
{0, 2, 0, 6, 0},
|
||||
{2, 0, 3, 8, 5},
|
||||
{0, 3, 0, 0, 7},
|
||||
{6, 8, 0, 0, 9},
|
||||
{0, 5, 7, 9, 0}
|
||||
};
|
||||
|
||||
// 从顶点0开始运行Prim算法
|
||||
primMST(graph, 0);
|
||||
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
@ -42,7 +42,7 @@
|
||||
|
||||
如果hashCode得到的数值大于 哈希表的大小了,也就是大于tableSize了,怎么办呢?
|
||||
|
||||
此时为了保证映射出来的索引数值都落在哈希表上,我们会在再次对数值做一个取模的操作,就要我们就保证了学生姓名一定可以映射到哈希表上了。
|
||||
此时为了保证映射出来的索引数值都落在哈希表上,我们会在再次对数值做一个取模的操作,这样我们就保证了学生姓名一定可以映射到哈希表上了。
|
||||
|
||||
此时问题又来了,哈希表我们刚刚说过,就是一个数组。
|
||||
|
||||
|
||||
@ -274,27 +274,53 @@ join(3, 2);
|
||||
|
||||
通过以上讲解之后,我在带大家一步一步去画一下,并查集内部数据连接方式。
|
||||
|
||||
注意:为了让录友们了解基础并查集的操作,不至于混乱,**以下模拟过程中不考虑路径压缩的过程**,了解基础并查集操作后,路径压缩也很容易理解。
|
||||
1、`join(1, 8);`
|
||||
|
||||
我们先通过一些列的join操作,将两两元素分别放入同一个集合中。
|
||||
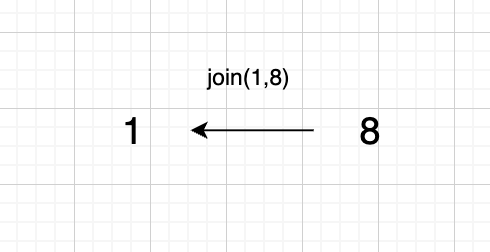
|
||||
|
||||
```CPP
|
||||
join(1, 8);
|
||||
join(3, 8);
|
||||
join(1, 7);
|
||||
join(8, 5);
|
||||
join(2, 9);
|
||||
join(6, 2);
|
||||
```
|
||||
|
||||
此时我们生成的的有向图为:
|
||||
2、`join(3, 8);`
|
||||
|
||||

|
||||
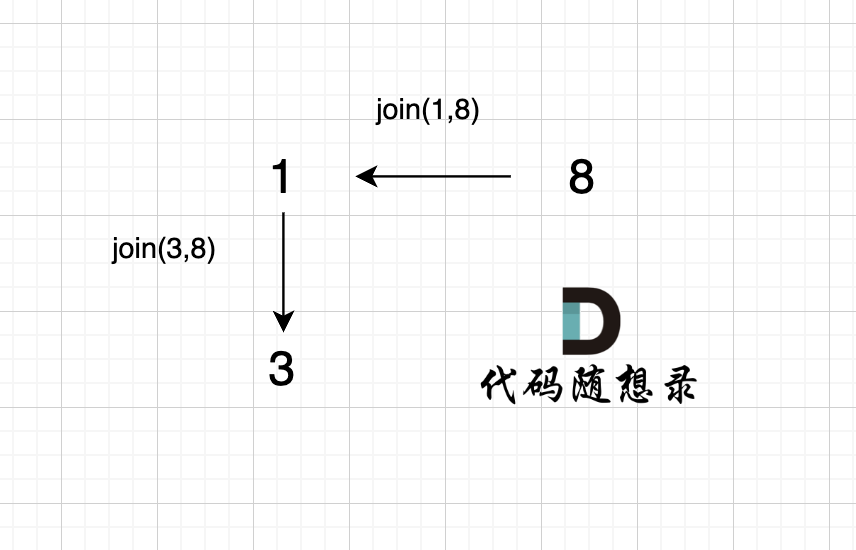
|
||||
|
||||
有录友可能想,`join(3, 8)` 在图中为什么 将 元素1 连向元素 3 而不是将 元素 8 连向 元素 3 呢?
|
||||
|
||||
这一点 我在 「常见误区」标题下已经详细讲解了,因为在`join(int u, int v)`函数里 要分别对 u 和 v 寻根之后再进行关联。
|
||||
|
||||
3、`join(1, 7);`
|
||||
|
||||
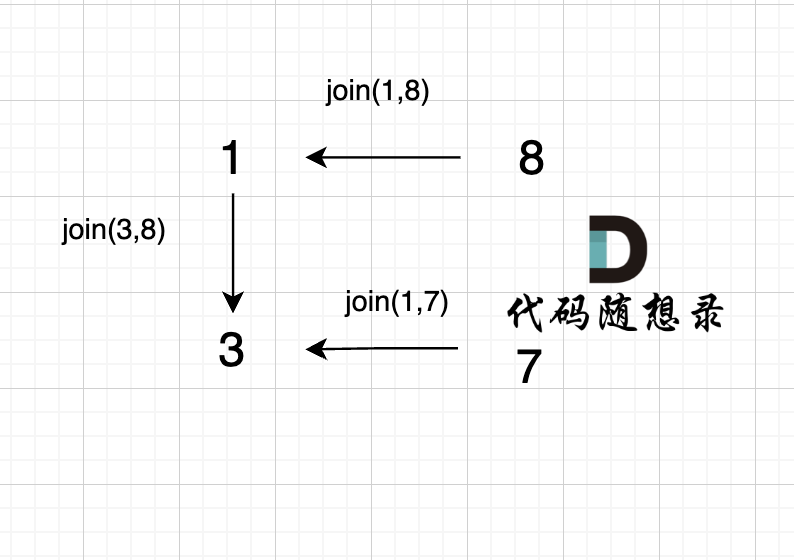
|
||||
|
||||
|
||||
4、`join(8, 5);`
|
||||
|
||||
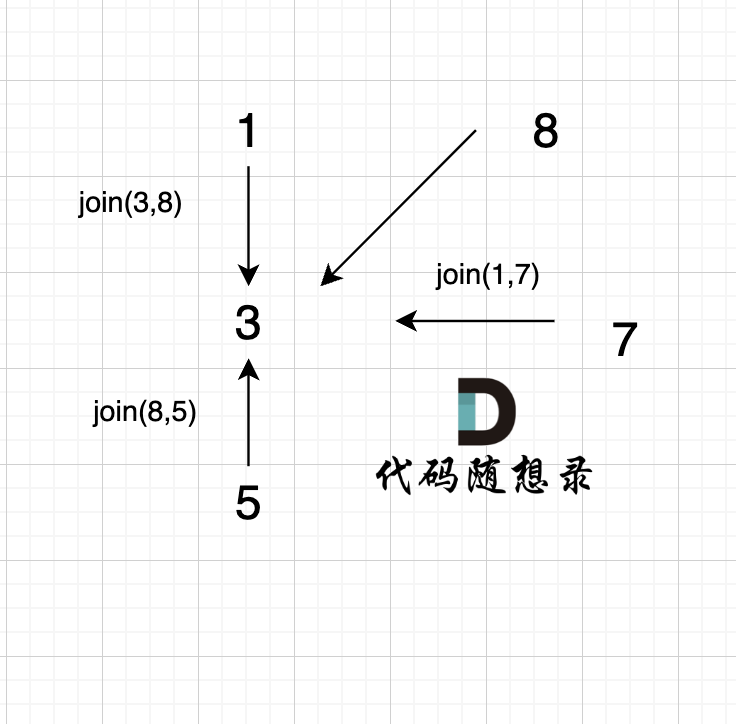
|
||||
|
||||
这里8的根是3,那么 5 应该指向 8 的根 3,这里的原因,我们在上面「常见误区」已经讲过了。 但 为什么 图中 8 又直接指向了 3 了呢?
|
||||
|
||||
**因为路经压缩了**
|
||||
|
||||
即如下代码在寻找跟的过程中,会有路径压缩,减少 下次查询的路径长度。
|
||||
|
||||
```
|
||||
// 并查集里寻根的过程
|
||||
int find(int u) {
|
||||
return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
|
||||
}
|
||||
```
|
||||
|
||||
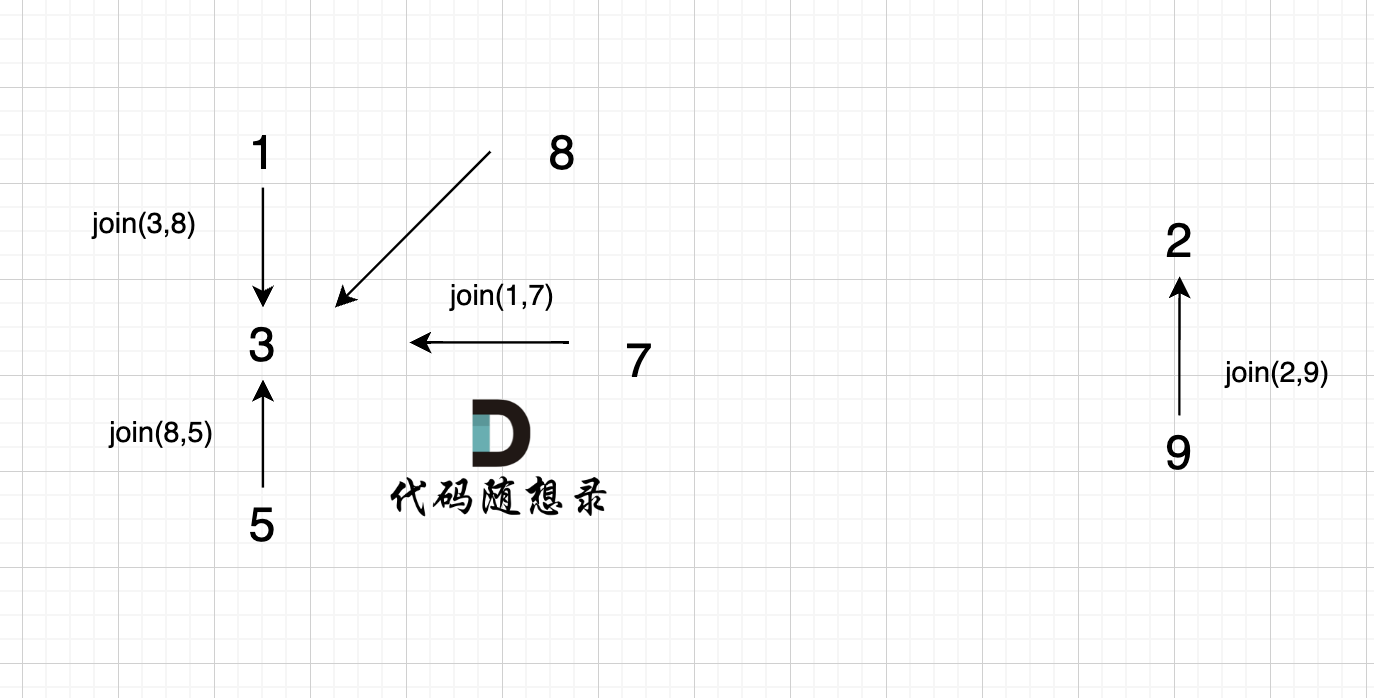
5、`join(2, 9);`
|
||||
|
||||
|
||||
|
||||
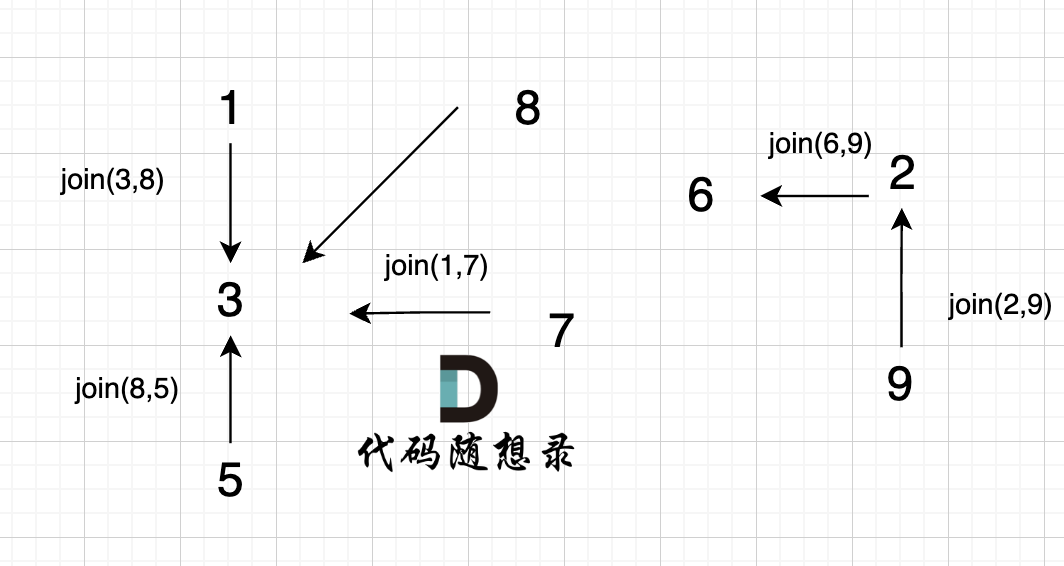
6、`join(6, 9);`
|
||||
|
||||
|
||||
|
||||
这里为什么是 2 指向了 6,因为 9的根为 2,所以用2指向6。
|
||||
|
||||
|
||||
|
||||
大家看懂这个有向图后,相信应该知道如下函数的返回值了。
|
||||
|
||||
```CPP
|
||||
@ -309,6 +335,8 @@ true
|
||||
false
|
||||
```
|
||||
|
||||
|
||||
|
||||
## 拓展
|
||||
|
||||
|
||||
|
||||
Reference in New Issue
Block a user