mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-08 16:54:50 +08:00
Update
This commit is contained in:
@ -42,7 +42,7 @@
|
||||
|
||||
删除过程如下:
|
||||
|
||||

|
||||

|
||||
|
||||
很明显暴力解法的时间复杂度是O(n^2),这道题目暴力解法在leetcode上是可以过的。
|
||||
|
||||
@ -86,7 +86,7 @@ public:
|
||||
|
||||
删除过程如下:
|
||||
|
||||

|
||||

|
||||
|
||||
很多同学不了解
|
||||
|
||||
|
||||
@ -16,31 +16,39 @@
|
||||
candidates 中的每个数字在每个组合中只能使用一次。
|
||||
|
||||
说明:
|
||||
所有数字(包括目标数)都是正整数。
|
||||
解集不能包含重复的组合。
|
||||
所有数字(包括目标数)都是正整数。解集不能包含重复的组合。
|
||||
|
||||
示例 1:
|
||||
输入: candidates = [10,1,2,7,6,1,5], target = 8,
|
||||
所求解集为:
|
||||
* 示例 1:
|
||||
* 输入: candidates = [10,1,2,7,6,1,5], target = 8,
|
||||
* 所求解集为:
|
||||
```
|
||||
[
|
||||
[1, 7],
|
||||
[1, 2, 5],
|
||||
[2, 6],
|
||||
[1, 1, 6]
|
||||
]
|
||||
```
|
||||
|
||||
示例 2:
|
||||
输入: candidates = [2,5,2,1,2], target = 5,
|
||||
所求解集为:
|
||||
* 示例 2:
|
||||
* 输入: candidates = [2,5,2,1,2], target = 5,
|
||||
* 所求解集为:
|
||||
|
||||
```
|
||||
[
|
||||
[1,2,2],
|
||||
[5]
|
||||
]
|
||||
```
|
||||
|
||||
# 算法公开课
|
||||
|
||||
**《代码随想录》算法视频公开课:[回溯算法中的去重,树层去重树枝去重,你弄清楚了没?| LeetCode:40.组合总和II](https://www.bilibili.com/video/BV12V4y1V73A),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
|
||||
# 思路
|
||||
|
||||
**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/)** 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
|
||||
|
||||
|
||||
这道题目和[39.组合总和](https://programmercarl.com/0039.组合总和.html)如下区别:
|
||||
|
||||
|
||||
@ -16,24 +16,28 @@
|
||||
* 删除一个字符
|
||||
* 替换一个字符
|
||||
|
||||
示例 1:
|
||||
输入:word1 = "horse", word2 = "ros"
|
||||
输出:3
|
||||
解释:
|
||||
* 示例 1:
|
||||
* 输入:word1 = "horse", word2 = "ros"
|
||||
* 输出:3
|
||||
* 解释:
|
||||
```
|
||||
horse -> rorse (将 'h' 替换为 'r')
|
||||
rorse -> rose (删除 'r')
|
||||
rose -> ros (删除 'e')
|
||||
``
|
||||
|
||||
示例 2:
|
||||
输入:word1 = "intention", word2 = "execution"
|
||||
输出:5
|
||||
解释:
|
||||
|
||||
* 示例 2:
|
||||
* 输入:word1 = "intention", word2 = "execution"
|
||||
* 输出:5
|
||||
* 解释:
|
||||
```
|
||||
intention -> inention (删除 't')
|
||||
inention -> enention (将 'i' 替换为 'e')
|
||||
enention -> exention (将 'n' 替换为 'x')
|
||||
exention -> exection (将 'n' 替换为 'c')
|
||||
exection -> execution (插入 'u')
|
||||
|
||||
```
|
||||
|
||||
提示:
|
||||
|
||||
@ -54,10 +58,11 @@ exection -> execution (插入 'u')
|
||||
|
||||
**dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]**。
|
||||
|
||||
这里在强调一下:为啥要表示下标i-1为结尾的字符串呢,为啥不表示下标i为结尾的字符串呢?
|
||||
有同学问了,为啥要表示下标i-1为结尾的字符串呢,为啥不表示下标i为结尾的字符串呢?
|
||||
|
||||
用i来表示也可以! 但我统一以下标i-1为结尾的字符串,在下面的递归公式中会容易理解一点。
|
||||
为什么这么定义我在 [718. 最长重复子数组](https://programmercarl.com/0718.最长重复子数组.html) 中做了详细的讲解。
|
||||
|
||||
其实用i来表示也可以! 用i-1就是为了方便后面dp数组初始化的。
|
||||
|
||||
### 2. 确定递推公式
|
||||
|
||||
@ -111,9 +116,13 @@ if (word1[i - 1] != word2[j - 1])
|
||||
+-----+-----+
|
||||
```
|
||||
|
||||
操作三:替换元素,`word1`替换`word1[i - 1]`,使其与`word2[j - 1]`相同,此时不用增加元素,那么以下标`i-2`为结尾的`word1` 与 `j-2`为结尾的`word2`的最近编辑距离 加上一个替换元素的操作。
|
||||
操作三:替换元素,`word1`替换`word1[i - 1]`,使其与`word2[j - 1]`相同,此时不用增删加元素。
|
||||
|
||||
即 `dp[i][j] = dp[i - 1][j - 1] + 1;`
|
||||
可以回顾一下,`if (word1[i - 1] == word2[j - 1])`的时候我们的操作 是 `dp[i][j] = dp[i - 1][j - 1]` 对吧。
|
||||
|
||||
那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。
|
||||
|
||||
所以 `dp[i][j] = dp[i - 1][j - 1] + 1;`
|
||||
|
||||
综上,当 `if (word1[i - 1] != word2[j - 1])` 时取最小的,即:`dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;`
|
||||
|
||||
|
||||
@ -169,7 +169,7 @@ public:
|
||||
|
||||
通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等,如动画所示:
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
|
||||
|
||||
@ -23,7 +23,7 @@
|
||||
* 111.二叉树的最小深度
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
|
||||
@ -53,7 +53,7 @@
|
||||
|
||||
使用队列实现二叉树广度优先遍历,动画如下:
|
||||
|
||||

|
||||

|
||||
|
||||
这样就实现了层序从左到右遍历二叉树。
|
||||
|
||||
|
||||
@ -23,11 +23,13 @@
|
||||
["a","a","b"]
|
||||
]
|
||||
|
||||
# 算法公开课
|
||||
|
||||
**《代码随想录》算法视频公开课:[131.分割回文串](https://www.bilibili.com/video/BV1c54y1e7k6),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
# 思路
|
||||
|
||||
关于本题,大家也可以看我在B站的视频讲解:[131.分割回文串(B站视频)](https://www.bilibili.com/video/BV1c54y1e7k6)
|
||||
|
||||
本题这涉及到两个关键问题:
|
||||
|
||||
1. 切割问题,有不同的切割方式
|
||||
|
||||
@ -40,7 +40,7 @@ fast和slow各自再走一步, fast和slow就相遇了
|
||||
动画如下:
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
C++代码如下
|
||||
@ -64,7 +64,7 @@ public:
|
||||
|
||||
## 扩展
|
||||
|
||||
做完这道题目,可以在做做[142.环形链表II](https://mp.weixin.qq.com/s/gt_VH3hQTqNxyWcl1ECSbQ),不仅仅要找环,还要找环的入口。
|
||||
做完这道题目,可以在做做[142.环形链表II](https://programmercarl.com/0142.%E7%8E%AF%E5%BD%A2%E9%93%BE%E8%A1%A8II.html),不仅仅要找环,还要找环的入口。
|
||||
|
||||
|
||||
|
||||
|
||||
@ -57,7 +57,7 @@ fast和slow各自再走一步, fast和slow就相遇了
|
||||
|
||||
动画如下:
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
### 如果有环,如何找到这个环的入口
|
||||
@ -101,7 +101,7 @@ fast指针走过的节点数:` x + y + n (y + z)`,n为fast指针在环内走
|
||||
|
||||
动画如下:
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
那么 n如果大于1是什么情况呢,就是fast指针在环形转n圈之后才遇到 slow指针。
|
||||
|
||||
@ -103,7 +103,7 @@ void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y
|
||||
}
|
||||
```
|
||||
|
||||
以上两个版本其实,其实只有细微区别,就是 `visited[x][y] = true;` 放在的地方,着去取决于我们对 代码中队列的定义,队列中的节点就表示已经走过的节点。 **所以只要加入队列,理解标记该节点走过**。
|
||||
以上两个版本其实,其实只有细微区别,就是 `visited[x][y] = true;` 放在的地方,着去取决于我们对 代码中队列的定义,队列中的节点就表示已经走过的节点。 **所以只要加入队列,立即标记该节点走过**。
|
||||
|
||||
本题完整广搜代码:
|
||||
|
||||
|
||||
@ -33,7 +33,7 @@
|
||||
|
||||
我们拿有示例中的链表来举例,如动画所示:(纠正:动画应该是先移动pre,在移动cur)
|
||||
|
||||

|
||||

|
||||
|
||||
首先定义一个cur指针,指向头结点,再定义一个pre指针,初始化为null。
|
||||
|
||||
|
||||
@ -53,7 +53,7 @@
|
||||
|
||||
我们下文以前序遍历为例,通过动画来看一下翻转的过程:
|
||||
|
||||

|
||||

|
||||
|
||||
我们来看一下递归三部曲:
|
||||
|
||||
|
||||
@ -43,7 +43,7 @@
|
||||
|
||||
操作动画如下:
|
||||
|
||||

|
||||

|
||||
|
||||
定义一个数组叫做record用来上记录字符串s里字符出现的次数。
|
||||
|
||||
|
||||
@ -36,7 +36,7 @@
|
||||
|
||||
如动画所示:
|
||||
|
||||

|
||||

|
||||
|
||||
C++代码如下:
|
||||
|
||||
|
||||
@ -69,7 +69,7 @@
|
||||
|
||||
以字符串`hello`为例,过程如下:
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
不难写出如下C++代码:
|
||||
|
||||
@ -68,7 +68,7 @@ if (root == nullptr) return root;
|
||||
|
||||
第五种情况有点难以理解,看下面动画:
|
||||
|
||||

|
||||

|
||||
|
||||
动画中的二叉搜索树中,删除元素7, 那么删除节点(元素7)的左孩子就是5,删除节点(元素7)的右子树的最左面节点是元素8。
|
||||
|
||||
|
||||
@ -56,7 +56,7 @@
|
||||
|
||||
(如果这里看不懂,回忆一下dp[i][j]的定义)
|
||||
|
||||
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子串的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
|
||||
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
|
||||
|
||||
加入s[j]的回文子序列长度为dp[i + 1][j]。
|
||||
|
||||
@ -91,13 +91,13 @@ for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
|
||||
|
||||
4. 确定遍历顺序
|
||||
|
||||
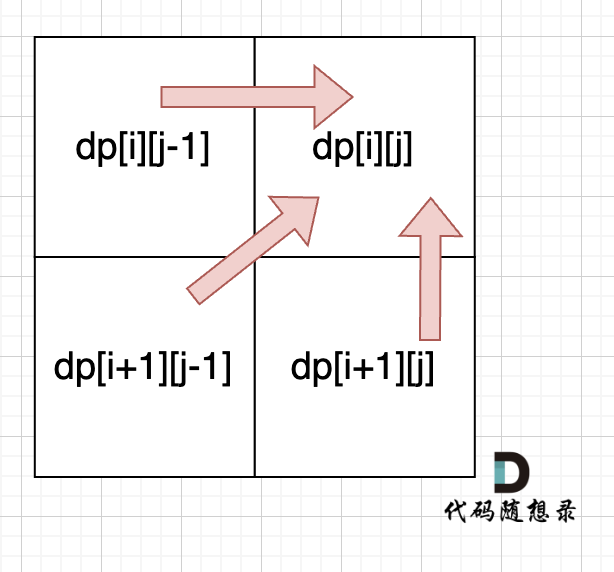
从递推公式dp[i][j] = dp[i + 1][j - 1] + 2 和 dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]) 可以看出,dp[i][j]是依赖于dp[i + 1][j - 1] 和 dp[i + 1][j],
|
||||
从递归公式中,可以看出,dp[i][j] 依赖于 dp[i + 1][j - 1] ,dp[i + 1][j] 和 dp[i][j - 1],如图:
|
||||
|
||||
也就是从矩阵的角度来说,dp[i][j] 下一行的数据。 **所以遍历i的时候一定要从下到上遍历,这样才能保证,下一行的数据是经过计算的**。
|
||||
|
||||
|
||||
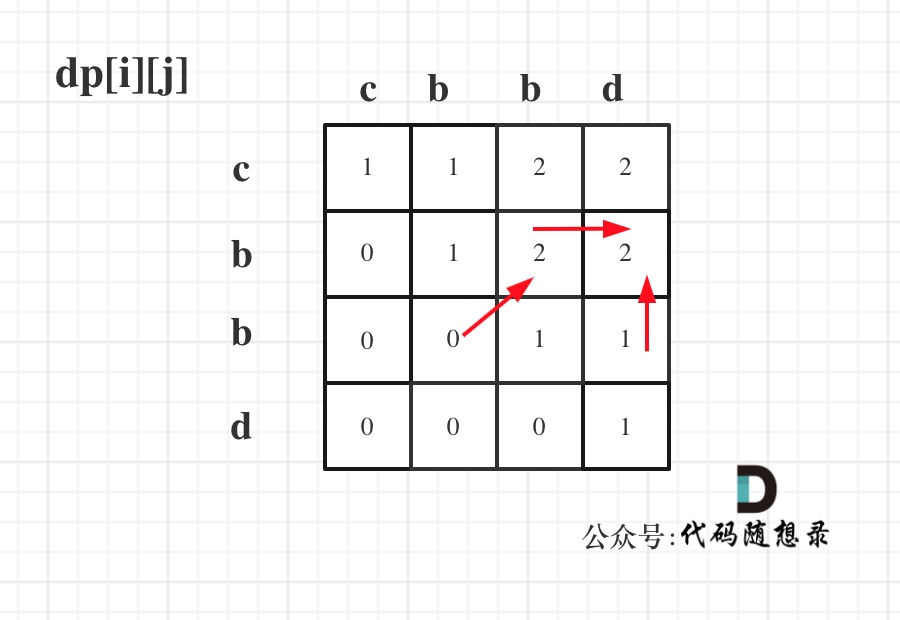
递推公式:dp[i][j] = dp[i + 1][j - 1] + 2,dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]) 分别对应着下图中的红色箭头方向,如图:
|
||||
**所以遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的**。
|
||||
|
||||
|
||||
j的话,可以正常从左向右遍历。
|
||||
|
||||
代码如下:
|
||||
|
||||
|
||||
@ -12,9 +12,9 @@
|
||||
|
||||
示例:
|
||||
|
||||
输入: "sea", "eat"
|
||||
输出: 2
|
||||
解释: 第一步将"sea"变为"ea",第二步将"eat"变为"ea"
|
||||
* 输入: "sea", "eat"
|
||||
* 输出: 2
|
||||
* 解释: 第一步将"sea"变为"ea",第二步将"eat"变为"ea"
|
||||
|
||||
## 思路
|
||||
|
||||
@ -47,7 +47,10 @@ dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word
|
||||
|
||||
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
|
||||
|
||||
因为dp[i - 1][j - 1] + 1等于 dp[i - 1][j] 或 dp[i][j - 1],所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
|
||||
|
||||
因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
|
||||
|
||||
这里可能不少录友有点迷糊,从字面上理解 就是 当 同时删word1[i - 1]和word2[j - 1],dp[i][j-1] 本来就不考虑 word2[j - 1]了,那么我在删 word1[i - 1],是不是就达到两个元素都删除的效果,即 dp[i][j-1] + 1。
|
||||
|
||||
|
||||
3. dp数组如何初始化
|
||||
|
||||
@ -40,7 +40,7 @@
|
||||
|
||||
动画如下:
|
||||
|
||||

|
||||

|
||||
|
||||
那么我们来按照递归三部曲来解决:
|
||||
|
||||
|
||||
@ -14,25 +14,21 @@
|
||||
|
||||
示例 1:
|
||||
|
||||
输入:"abc"
|
||||
输出:3
|
||||
解释:三个回文子串: "a", "b", "c"
|
||||
* 输入:"abc"
|
||||
* 输出:3
|
||||
* 解释:三个回文子串: "a", "b", "c"
|
||||
|
||||
示例 2:
|
||||
|
||||
输入:"aaa"
|
||||
输出:6
|
||||
解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
|
||||
* 输入:"aaa"
|
||||
* 输出:6
|
||||
* 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
|
||||
|
||||
提示:
|
||||
|
||||
输入的字符串长度不会超过 1000 。
|
||||
提示:输入的字符串长度不会超过 1000 。
|
||||
|
||||
## 暴力解法
|
||||
|
||||
两层for循环,遍历区间起始位置和终止位置,然后判断这个区间是不是回文。
|
||||
|
||||
时间复杂度:O(n^3)
|
||||
两层for循环,遍历区间起始位置和终止位置,然后还需要一层遍历判断这个区间是不是回文。所以时间复杂度:O(n^3)
|
||||
|
||||
## 动态规划
|
||||
|
||||
@ -40,6 +36,23 @@
|
||||
|
||||
1. 确定dp数组(dp table)以及下标的含义
|
||||
|
||||
如果大家做了很多这种子序列相关的题目,在定义dp数组的时候 很自然就会想题目求什么,我们就如何定义dp数组。
|
||||
|
||||
绝大多数题目确实是这样,不过本题如果我们定义,dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话,我们会发现很难找到递归关系。
|
||||
|
||||
dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系。
|
||||
|
||||
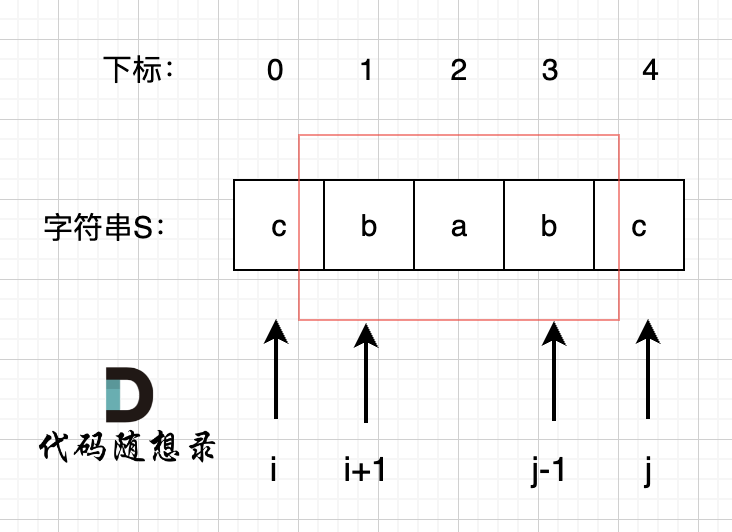
所以我们要看回文串的性质。 如图:
|
||||
|
||||
|
||||
|
||||
我们在判断字符串S是否是回文,那么如果我们知道 s[1],s[2],s[3] 这个子串是回文的,那么只需要比较 s[0]和s[4]这两个元素是否相同,如果相同的话,这个字符串s 就是回文串。
|
||||
|
||||
|
||||
那么此时我们是不是能找到一种递归关系,也就是判断一个子字符串(字符串的下表范围[i,j])是否回文,依赖于,子字符串(下表范围[i + 1, j - 1])) 是否是回文。
|
||||
|
||||
所以为了明确这种递归关系,我们的dp数组是要定义成一位二维dp数组。
|
||||
|
||||
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
|
||||
|
||||
|
||||
|
||||
@ -34,7 +34,7 @@
|
||||
|
||||
最大二叉树的构建过程如下:
|
||||
|
||||

|
||||

|
||||
|
||||
构造树一般采用的是前序遍历,因为先构造中间节点,然后递归构造左子树和右子树。
|
||||
|
||||
|
||||
@ -3,8 +3,11 @@
|
||||
<img src="../pics/训练营.png" width="1000"/>
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
# 695. 岛屿的最大面积
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/max-area-of-island/)
|
||||
|
||||
给你一个大小为 m x n 的二进制矩阵 grid 。
|
||||
|
||||
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
|
||||
@ -15,9 +18,9 @@
|
||||
|
||||
|
||||
|
||||
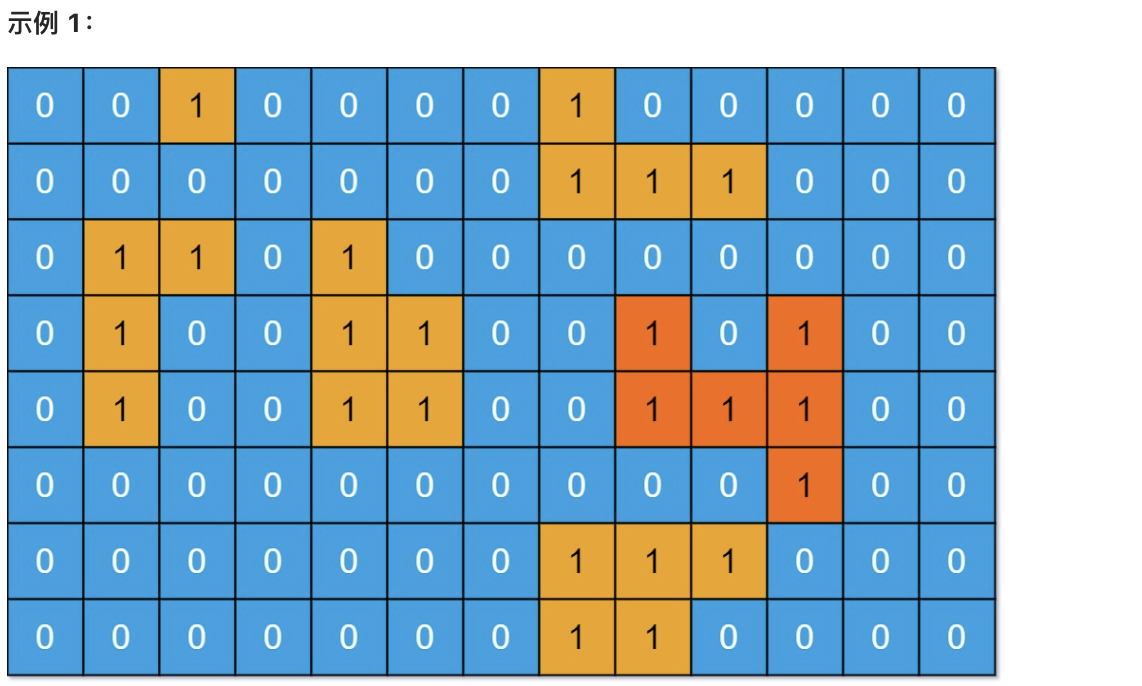
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
|
||||
输出:6
|
||||
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
|
||||
* 输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
|
||||
* 输出:6
|
||||
* 解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
|
||||
|
||||
# 思路
|
||||
|
||||
@ -28,18 +31,23 @@
|
||||
|
||||

|
||||
|
||||
这道题目也是 dfs bfs基础类题目。
|
||||
这道题目也是 dfs bfs基础类题目,就是搜索每个岛屿上“1”的数量,然后取一个最大的。
|
||||
|
||||
本题思路上比较简单,难点其实都是 dfs 和 bfs的理论基础,关于理论基础我在这里都有详细讲解 :
|
||||
|
||||
* [DFS理论基础](https://leetcode.cn/problems/all-paths-from-source-to-target/solution/by-carlsun-2-66pf/)
|
||||
* [BFS理论基础](https://leetcode.cn/circle/discuss/V3FulB/)
|
||||
|
||||
## DFS
|
||||
|
||||
很多同学,写dfs其实也是凭感觉来,有的时候dfs函数中写终止条件才能过,有的时候 dfs函数不写终止添加也能过!
|
||||
|
||||
这里其实涉及到dfs的两种写法,
|
||||
这里其实涉及到dfs的两种写法。
|
||||
|
||||
以下代码使用dfs实现,如果对dfs不太了解的话,建议先看这篇题解:[797.所有可能的路径](https://leetcode.cn/problems/all-paths-from-source-to-target/solution/by-carlsun-2-66pf/),
|
||||
写法一,dfs只处理下一个节点,即在主函数遇到岛屿就计数为1,dfs处理接下来的相邻陆地
|
||||
|
||||
写法一,dfs只处理下一个节点
|
||||
```CPP
|
||||
// 版本一
|
||||
class Solution {
|
||||
private:
|
||||
int count;
|
||||
@ -67,7 +75,7 @@ public:
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (!visited[i][j] && grid[i][j] == 1) {
|
||||
count = 1;
|
||||
count = 1; // 因为dfs处理下一个节点,所以这里遇到陆地了就先计数,dfs处理接下来的相邻陆地
|
||||
visited[i][j] = true;
|
||||
dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
|
||||
result = max(result, count);
|
||||
@ -79,9 +87,11 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
写法二,dfs处理当前节点
|
||||
写法二,dfs处理当前节点,即即在主函数遇到岛屿就计数为0,dfs处理接下来的全部陆地
|
||||
|
||||
dfs
|
||||
```CPP
|
||||
// 版本二
|
||||
class Solution {
|
||||
private:
|
||||
int count;
|
||||
@ -106,7 +116,7 @@ public:
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (!visited[i][j] && grid[i][j] == 1) {
|
||||
count = 0;
|
||||
count = 0; // 因为dfs处理当前节点,所以遇到陆地计数为0,进dfs之后在开始从1计数
|
||||
dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
|
||||
result = max(result, count);
|
||||
}
|
||||
@ -117,8 +127,13 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
大家通过注释可以发现,两种写法,版本一,在主函数遇到陆地就计数为1,接下来的相邻陆地都在dfs中计算。 版本二 在主函数遇到陆地 计数为0,也就是不计数,陆地数量都去dfs里做计算。
|
||||
|
||||
这也是为什么大家看了很多,dfs的写法,发现写法怎么都不一样呢? 其实这就是根本原因。
|
||||
|
||||
以上两种写法的区别,我在题解: [DFS,BDF 你没注意的细节都给你列出来了!LeetCode:200. 岛屿数量](https://leetcode.cn/problems/number-of-islands/solution/by-carlsun-2-n72a/)做了详细介绍。
|
||||
|
||||
|
||||
## BFS
|
||||
|
||||
关于广度优先搜索,如果大家还不了解的话,看这里:[广度优先搜索精讲](https://leetcode.cn/circle/discuss/V3FulB/)
|
||||
|
||||
@ -34,7 +34,7 @@
|
||||
|
||||
如下演示视频中可以看出:只要按照二叉搜索树的规则去遍历,遇到空节点就插入节点就可以了。
|
||||
|
||||

|
||||

|
||||
|
||||
例如插入元素10 ,需要找到末尾节点插入便可,一样的道理来插入元素15,插入元素0,插入元素6,**需要调整二叉树的结构么? 并不需要。**。
|
||||
|
||||
|
||||
@ -63,7 +63,7 @@ public:
|
||||
|
||||
看代码有点抽象我们来看一下动画(中序遍历):
|
||||
|
||||

|
||||

|
||||
|
||||
动画中,result数组就是最终结果集。
|
||||
|
||||
|
||||
@ -37,7 +37,7 @@
|
||||
|
||||
动画如下:
|
||||
|
||||

|
||||

|
||||
|
||||
不难写出如下代码: (**注意代码中空节点不入栈**)
|
||||
|
||||
@ -84,7 +84,7 @@ public:
|
||||
|
||||
动画如下:
|
||||
|
||||

|
||||

|
||||
|
||||
**中序遍历,可以写出如下代码:**
|
||||
|
||||
|
||||
@ -25,7 +25,7 @@
|
||||
|
||||
i指向新长度的末尾,j指向旧长度的末尾。
|
||||
|
||||

|
||||

|
||||
|
||||
有同学问了,为什么要从后向前填充,从前向后填充不行么?
|
||||
|
||||
|
||||
@ -26,6 +26,7 @@
|
||||
|
||||
再举一个例子如果是 有一堆盒子,你有一个背包体积为n,如何把背包尽可能装满,如果还每次选最大的盒子,就不行了。这时候就需要动态规划。动态规划的问题在下一个系列会详细讲解。
|
||||
|
||||
|
||||
## 贪心的套路(什么时候用贪心)
|
||||
|
||||
很多同学做贪心的题目的时候,想不出来是贪心,想知道有没有什么套路可以一看就看出来是贪心。
|
||||
@ -74,7 +75,10 @@
|
||||
* 求解每一个子问题的最优解
|
||||
* 将局部最优解堆叠成全局最优解
|
||||
|
||||
其实这个分的有点细了,真正做题的时候很难分出这么详细的解题步骤,可能就是因为贪心的题目往往还和其他方面的知识混在一起。
|
||||
这个四步其实过于理论化了,我们平时在做贪心类的题目 很难去按照这四步去思考,真是有点“鸡肋”。
|
||||
|
||||
做题的时候,只要想清楚 局部最优 是什么,如果推导出全局最优,其实就够了。
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
@ -84,9 +88,6 @@
|
||||
|
||||
最后给出贪心的一般解题步骤,大家可以发现这个解题步骤也是比较抽象的,不像是二叉树,回溯算法,给出了那么具体的解题套路和模板。
|
||||
|
||||
本篇没有配图,其实可以找一些动漫周边或者搞笑的图配一配(符合大多数公众号文章的作风),但这不是我的风格,所以本篇文字描述足以!
|
||||
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
|
||||
Reference in New Issue
Block a user