mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-06 15:09:40 +08:00
Update
This commit is contained in:
@ -295,7 +295,7 @@
|
||||
21. [本周小结!(贪心算法系列四)](./problems/周总结/20201224贪心周末总结.md)
|
||||
22. [贪心算法:738.单调递增的数字](./problems/0738.单调递增的数字.md)
|
||||
23. [贪心算法:968.监控二叉树](./problems/0968.监控二叉树.md)
|
||||
24. [贪心算法:714.买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费.md)
|
||||
<!-- 24. [贪心算法:714.买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费.md) -->
|
||||
25. [贪心算法:总结篇!(每逢总结必经典)](./problems/贪心算法总结篇.md)
|
||||
|
||||
## 动态规划
|
||||
|
||||
@ -85,7 +85,8 @@ map目的用来存放我们访问过的元素,因为遍历数组的时候,
|
||||
|
||||
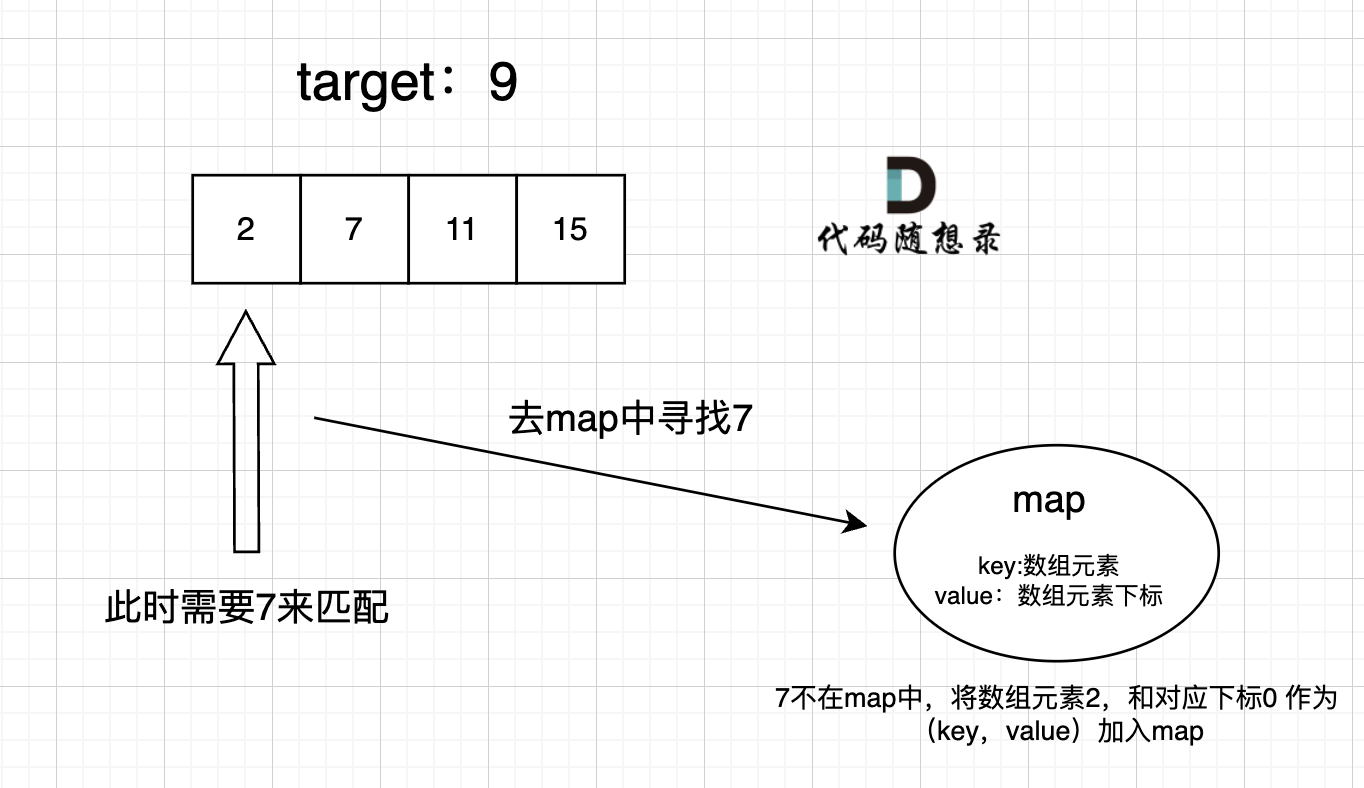
|
||||
|
||||
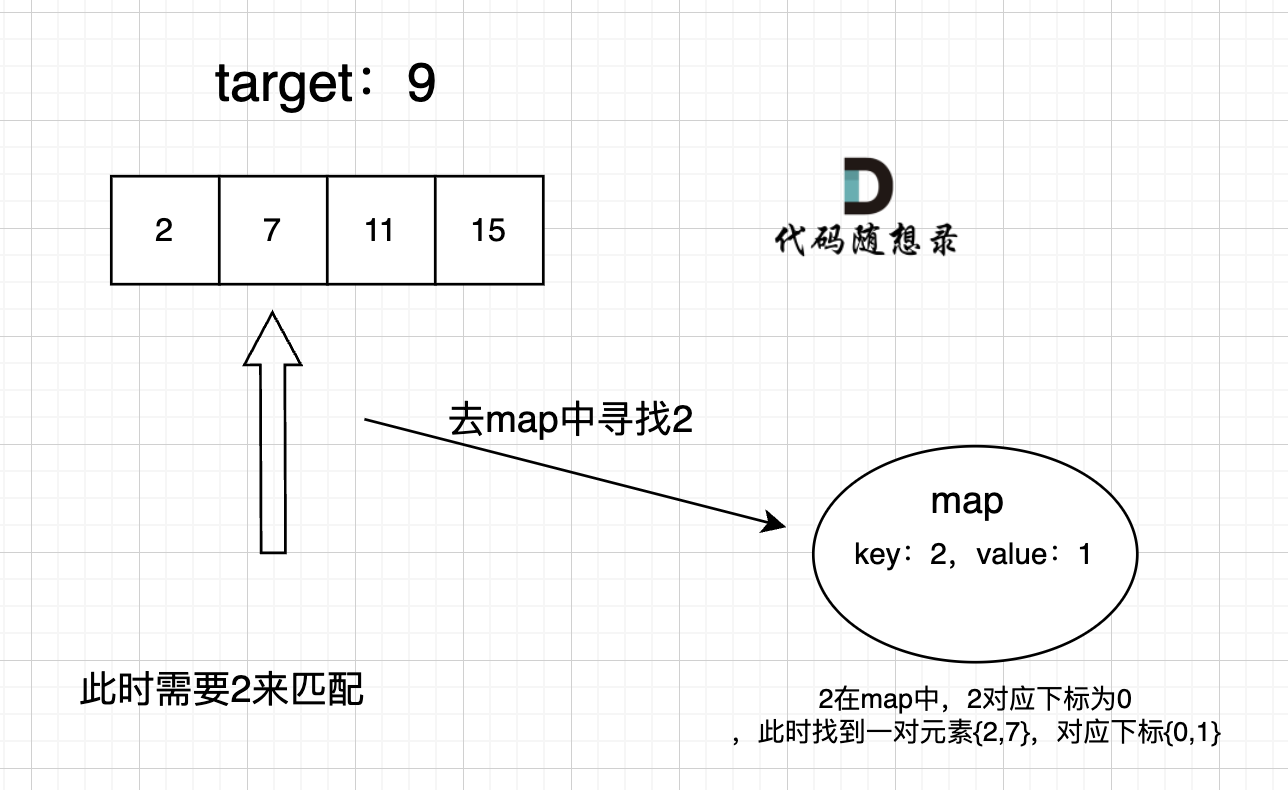
|
||||
|
||||
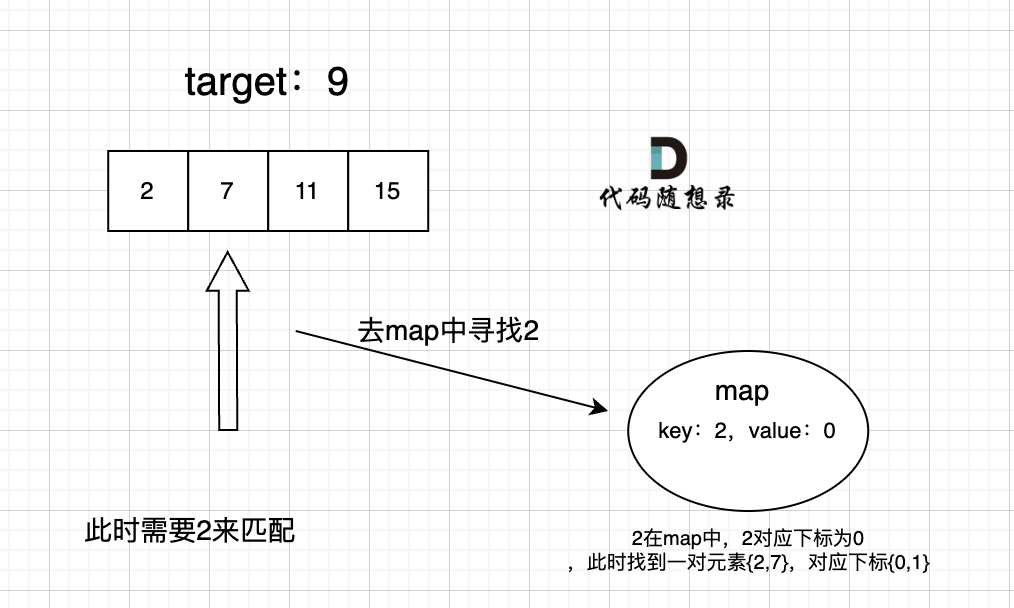
|
||||
|
||||
C++代码:
|
||||
|
||||
|
||||
@ -17,6 +17,8 @@
|
||||
|
||||
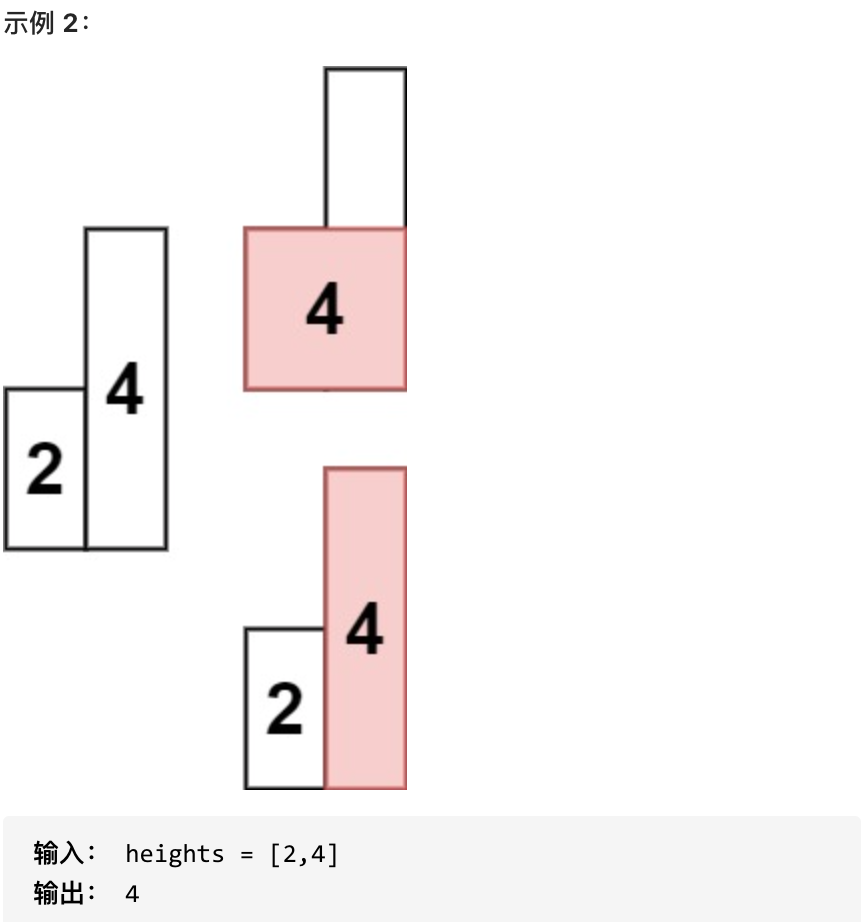
|
||||
|
||||
* 1 <= heights.length <=10^5
|
||||
* 0 <= heights[i] <= 10^4
|
||||
|
||||
# 思路
|
||||
|
||||
@ -24,9 +26,9 @@
|
||||
|
||||
其实这两道题目先做那一道都可以,但我先写的42.接雨水的题解,所以如果没做过接雨水的话,建议先做一做接雨水,可以参考我的题解:[42. 接雨水](https://programmercarl.com/0042.接雨水.html)
|
||||
|
||||
我们先来看一下双指针的解法:
|
||||
我们先来看一下暴力解法的解法:
|
||||
|
||||
## 双指针解法
|
||||
## 暴力解法
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -53,9 +55,9 @@ public:
|
||||
|
||||
如上代码并不能通过leetcode,超时了,因为时间复杂度是$O(n^2)$。
|
||||
|
||||
## 动态规划
|
||||
## 双指针解法
|
||||
|
||||
本题动态规划的写法整体思路和[42. 接雨水](https://programmercarl.com/0042.接雨水.html)是一致的,但要比[42. 接雨水](https://programmercarl.com/0042.接雨水.html)难一些。
|
||||
本题双指针的写法整体思路和[42. 接雨水](https://programmercarl.com/0042.接雨水.html)是一致的,但要比[42. 接雨水](https://programmercarl.com/0042.接雨水.html)难一些。
|
||||
|
||||
难就难在本题要记录记录每个柱子 左边第一个小于该柱子的下标,而不是左边第一个小于该柱子的高度。
|
||||
|
||||
@ -110,7 +112,7 @@ public:
|
||||
|
||||
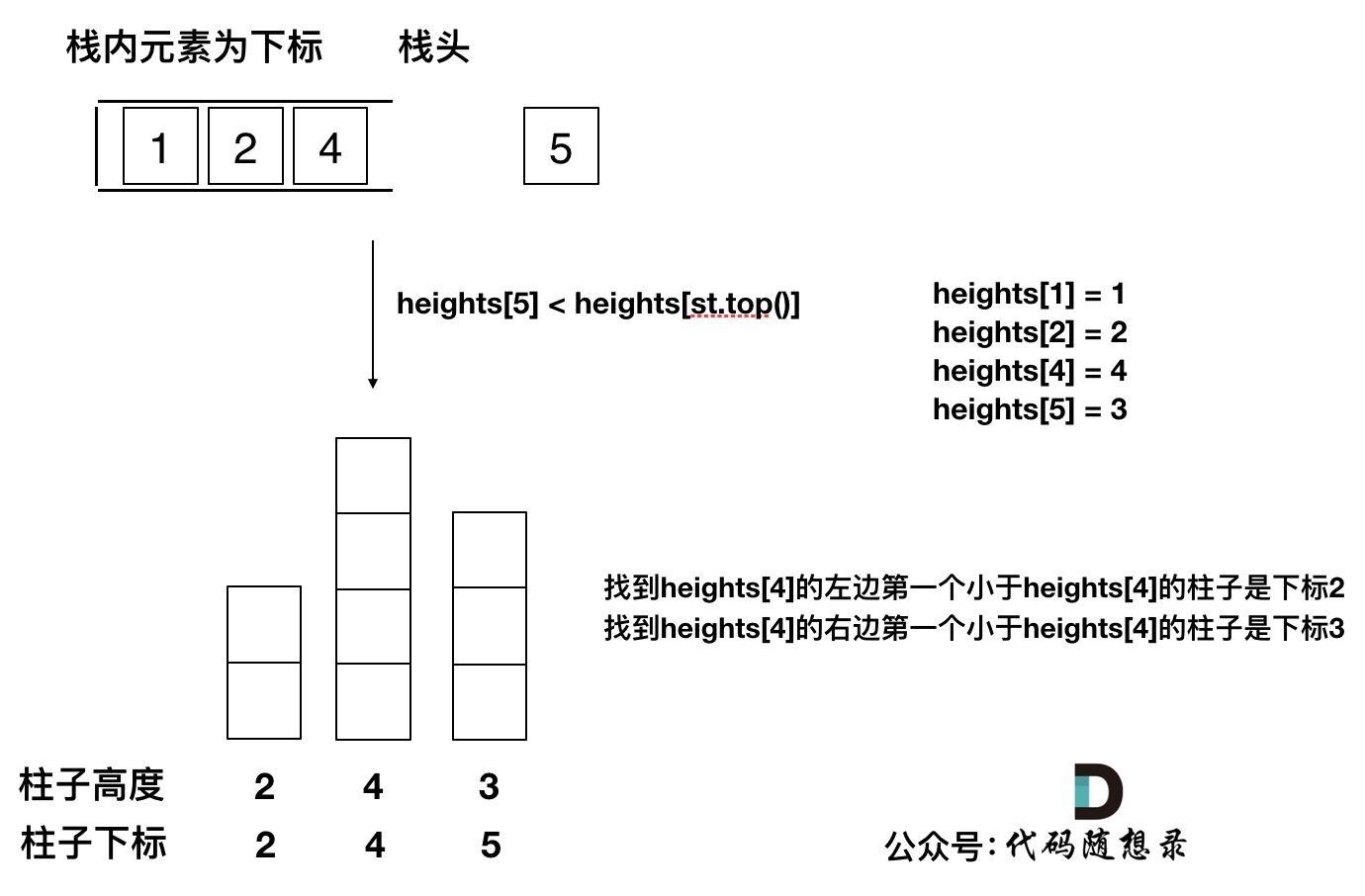
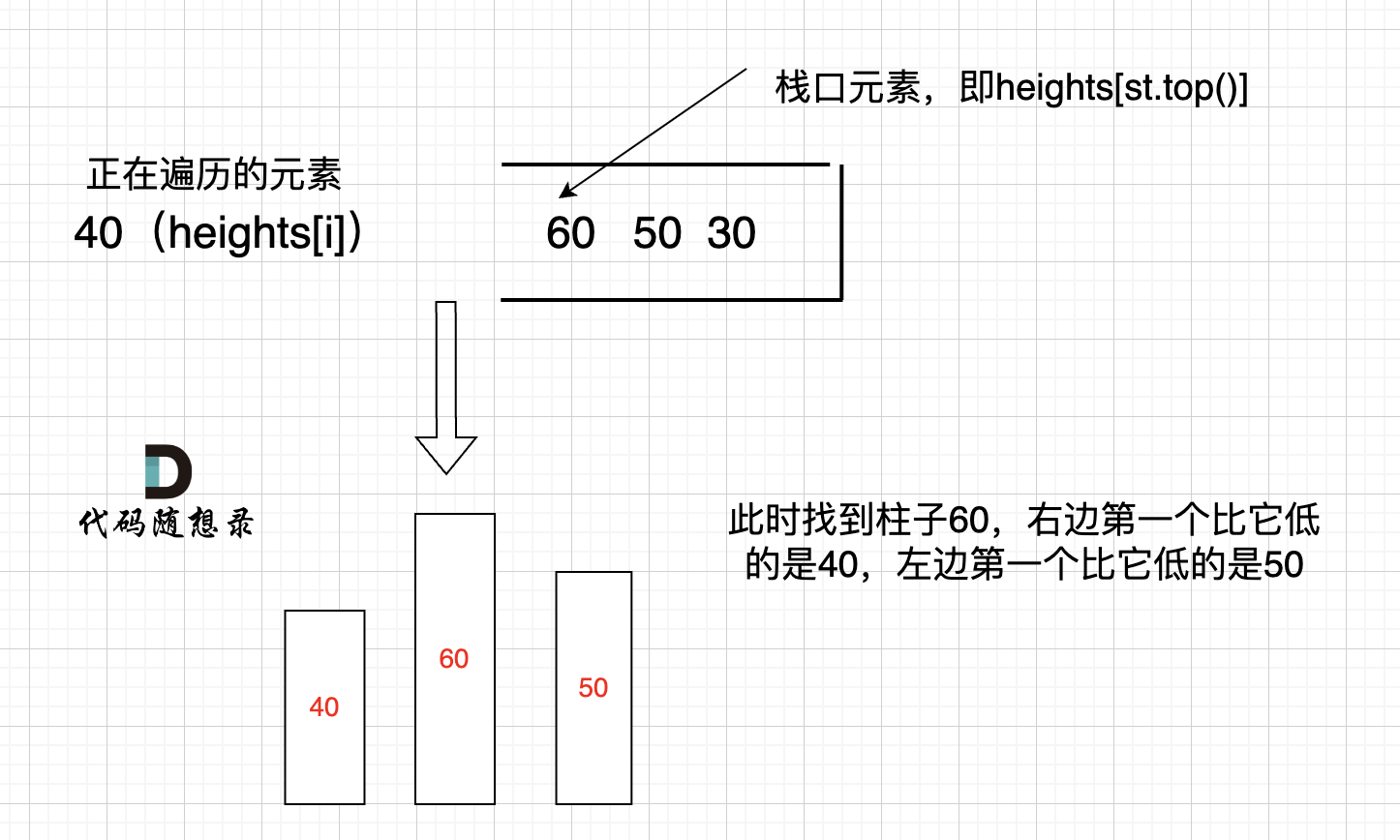
我来举一个例子,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
只有栈里从大到小的顺序,才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子。
|
||||
|
||||
@ -122,11 +124,11 @@ public:
|
||||
|
||||
除了栈内元素顺序和接雨水不同,剩下的逻辑就都差不多了,在题解[42. 接雨水](https://programmercarl.com/0042.接雨水.html)我已经对单调栈的各个方面做了详细讲解,这里就不赘述了。
|
||||
|
||||
剩下就是分析清楚如下三种情况:
|
||||
主要就是分析清楚如下三种情况:
|
||||
|
||||
* 情况一:当前遍历的元素heights[i]小于栈顶元素heights[st.top()]的情况
|
||||
* 情况一:当前遍历的元素heights[i]大于栈顶元素heights[st.top()]的情况
|
||||
* 情况二:当前遍历的元素heights[i]等于栈顶元素heights[st.top()]的情况
|
||||
* 情况三:当前遍历的元素heights[i]大于栈顶元素heights[st.top()]的情况
|
||||
* 情况三:当前遍历的元素heights[i]小于栈顶元素heights[st.top()]的情况
|
||||
|
||||
C++代码如下:
|
||||
|
||||
@ -135,28 +137,30 @@ C++代码如下:
|
||||
class Solution {
|
||||
public:
|
||||
int largestRectangleArea(vector<int>& heights) {
|
||||
int result = 0;
|
||||
stack<int> st;
|
||||
heights.insert(heights.begin(), 0); // 数组头部加入元素0
|
||||
heights.push_back(0); // 数组尾部加入元素0
|
||||
st.push(0);
|
||||
int result = 0;
|
||||
|
||||
// 第一个元素已经入栈,从下标1开始
|
||||
for (int i = 1; i < heights.size(); i++) {
|
||||
// 注意heights[i] 是和heights[st.top()] 比较 ,st.top()是下标
|
||||
if (heights[i] > heights[st.top()]) {
|
||||
if (heights[i] > heights[st.top()]) { // 情况一
|
||||
st.push(i);
|
||||
} else if (heights[i] == heights[st.top()]) {
|
||||
} else if (heights[i] == heights[st.top()]) { // 情况二
|
||||
st.pop(); // 这个可以加,可以不加,效果一样,思路不同
|
||||
st.push(i);
|
||||
} else {
|
||||
while (heights[i] < heights[st.top()]) { // 注意是while
|
||||
} else { // 情况三
|
||||
while (!st.empty() && heights[i] < heights[st.top()]) { // 注意是while
|
||||
int mid = st.top();
|
||||
st.pop();
|
||||
int left = st.top();
|
||||
int right = i;
|
||||
int w = right - left - 1;
|
||||
int h = heights[mid];
|
||||
result = max(result, w * h);
|
||||
if (!st.empty()) {
|
||||
int left = st.top();
|
||||
int right = i;
|
||||
int w = right - left - 1;
|
||||
int h = heights[mid];
|
||||
result = max(result, w * h);
|
||||
}
|
||||
}
|
||||
st.push(i);
|
||||
}
|
||||
@ -165,9 +169,36 @@ public:
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
```
|
||||
|
||||
代码精简之后:
|
||||
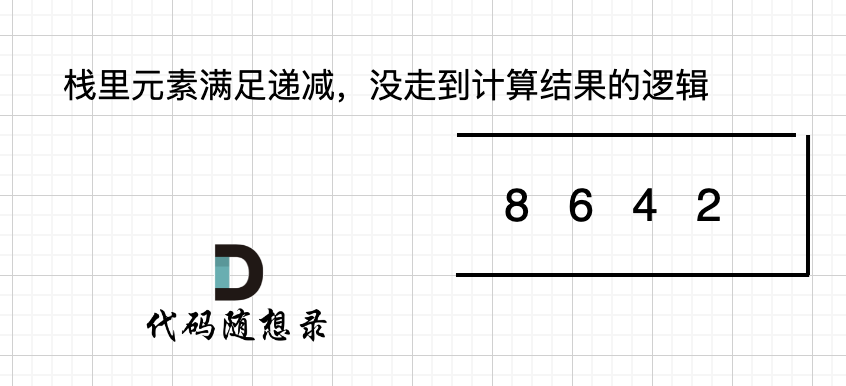
细心的录友会发现,我在 height数组上后,都加了一个元素0, 为什么这么做呢?
|
||||
|
||||
首先来说末尾为什么要加元素0?
|
||||
|
||||
如果数组本身就是升序的,例如[2,4,6,8],那么入栈之后 都是单调递减,一直都没有走 情况三 计算结果的哪一步,所以最后输出的就是0了。 如图:
|
||||
|
||||
|
||||
|
||||
那么结尾加一个0,就会让栈里的所有元素,走到情况三的逻辑。
|
||||
|
||||
|
||||
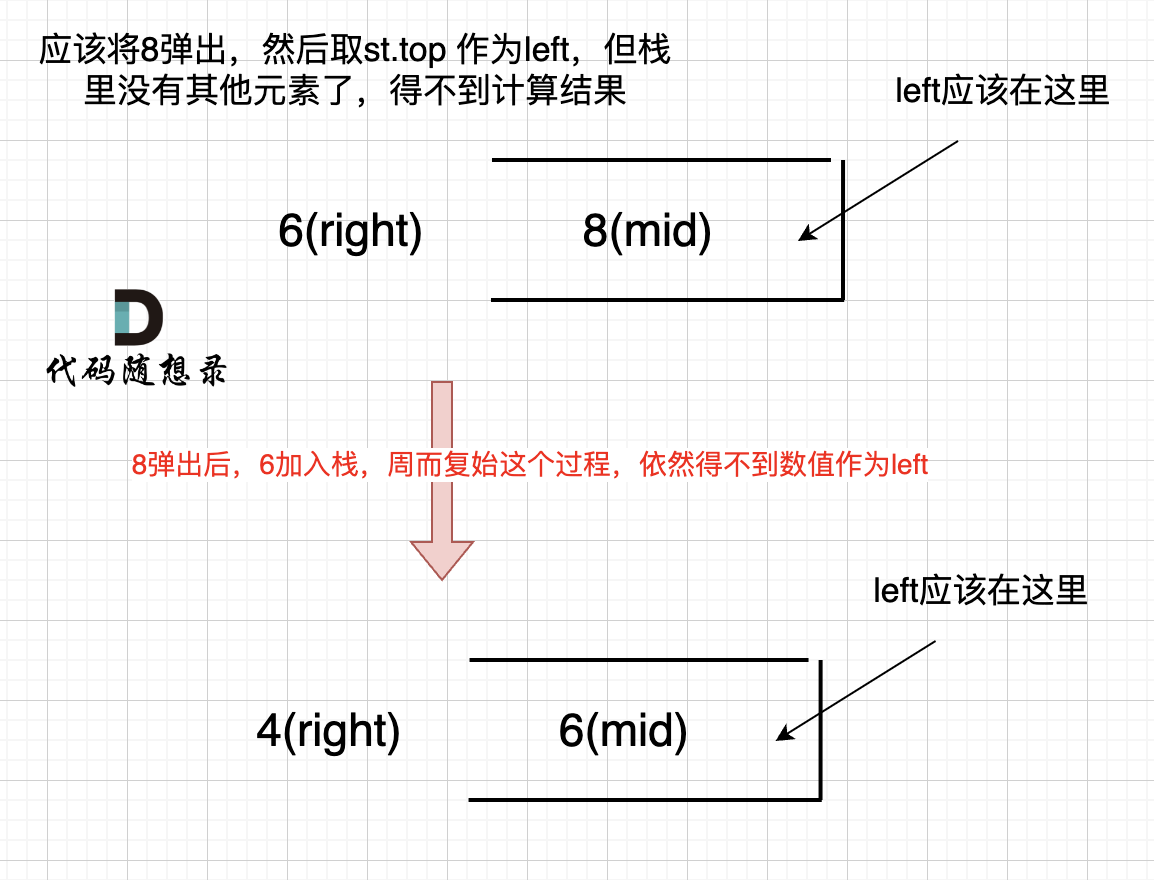
开头为什么要加元素0?
|
||||
|
||||
如果数组本身是降序的,例如 [8,6,4,2],在 8 入栈后,6 开始与8 进行比较,此时我们得到 mid(8),rigt(6),但是得不到 left。
|
||||
|
||||
(mid、left,right 都是对应版本一里的逻辑)
|
||||
|
||||
因为 将 8 弹出之后,栈里没有元素了,那么为了避免空栈取值,直接跳过了计算结果的逻辑。
|
||||
|
||||
之后又将6 加入栈(此时8已经弹出了),然后 就是 4 与 栈口元素 8 进行比较,周而复始,那么计算的最后结果resutl就是0。 如图所示:
|
||||
|
||||
|
||||
|
||||
所以我们需要在 height数组前后各加一个元素0。
|
||||
|
||||
|
||||
|
||||
版本一代码精简之后:
|
||||
|
||||
```CPP
|
||||
// 版本二
|
||||
@ -200,7 +231,7 @@ public:
|
||||
|
||||
Java:
|
||||
|
||||
动态规划
|
||||
暴力解法:
|
||||
```java
|
||||
class Solution {
|
||||
public int largestRectangleArea(int[] heights) {
|
||||
@ -233,7 +264,7 @@ class Solution {
|
||||
}
|
||||
```
|
||||
|
||||
单调栈
|
||||
单调栈:
|
||||
```java
|
||||
class Solution {
|
||||
int largestRectangleArea(int[] heights) {
|
||||
@ -281,7 +312,7 @@ Python3:
|
||||
|
||||
```python
|
||||
|
||||
# 双指针;暴力解法(leetcode超时)
|
||||
# 暴力解法(leetcode超时)
|
||||
class Solution:
|
||||
def largestRectangleArea(self, heights: List[int]) -> int:
|
||||
# 从左向右遍历:以每一根柱子为主心骨(当前轮最高的参照物),迭代直到找到左侧和右侧各第一个矮一级的柱子
|
||||
@ -307,7 +338,7 @@ class Solution:
|
||||
|
||||
return res
|
||||
|
||||
# DP动态规划
|
||||
# 双指针
|
||||
class Solution:
|
||||
def largestRectangleArea(self, heights: List[int]) -> int:
|
||||
size = len(heights)
|
||||
@ -450,7 +481,7 @@ func largestRectangleArea(heights []int) int {
|
||||
|
||||
JavaScript:
|
||||
```javascript
|
||||
//动态规划 js中运行速度最快
|
||||
//双指针 js中运行速度最快
|
||||
var largestRectangleArea = function(heights) {
|
||||
const len = heights.length;
|
||||
const minLeftIndex = new Array(len);
|
||||
@ -525,7 +556,7 @@ var largestRectangleArea = function(heights) {
|
||||
```
|
||||
TypeScript:
|
||||
|
||||
> 双指针法(会超时):
|
||||
> 暴力法(会超时):
|
||||
|
||||
```typescript
|
||||
function largestRectangleArea(heights: number[]): number {
|
||||
@ -546,7 +577,7 @@ function largestRectangleArea(heights: number[]): number {
|
||||
};
|
||||
```
|
||||
|
||||
> 动态规划预处理:
|
||||
> 双指针预处理:
|
||||
|
||||
```typescript
|
||||
function largestRectangleArea(heights: number[]): number {
|
||||
|
||||
@ -73,7 +73,7 @@ Carl个人认为:如果找出局部最优并可以推出全局最优,就是
|
||||
大家都知道股票系列问题是动规的专长,其实用贪心也可以解决,而且还不止就这两道题目,但这两道比较典型,我就拿来单独说一说
|
||||
|
||||
* [贪心算法:买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II.html)
|
||||
* [贪心算法:买卖股票的最佳时机含手续费](https://programmercarl.com/0714.买卖股票的最佳时机含手续费.html) 本题使用贪心算法比较绕,建议理解动态规划就好
|
||||
* [贪心算法:买卖股票的最佳时机含手续费](https://programmercarl.com/0714.买卖股票的最佳时机含手续费.html) 本题使用贪心算法比较绕,建议后面学习动态规划章节的时候,理解动规就好
|
||||
|
||||
### 两个维度权衡问题
|
||||
|
||||
|
||||
Reference in New Issue
Block a user