Merge branch 'master' of github.com:youngyangyang04/leetcode-master

problems/0019.删除链表的倒数第N个节点.md

@@ -105,8 +105,8 @@ public ListNode removeNthFromEnd(ListNode head, int n){
     ListNode fastIndex = dummyNode;
     ListNode slowIndex = dummyNode;
 
-    //只要快慢指针相差 n 个结点即可
-    for (int i = 0; i < n  ; i++){
+    // 只要快慢指针相差 n 个结点即可
+    for (int i = 0; i <= n  ; i++){ 
         fastIndex = fastIndex.next;
     }
 

problems/0028.实现strStr.md

@@ -207,7 +207,7 @@ next数组就是一个前缀表（prefix table）。
 
 ### 前缀表与next数组
 
-很多KMP算法的时间都是使用next数组来做回退操作，那么next数组与前缀表有什么关系呢？
+很多KMP算法的实现都是使用next数组来做回退操作，那么next数组与前缀表有什么关系呢？
 
 next数组就可以是前缀表，但是很多实现都是把前缀表统一减一（右移一位，初始位置为-1）之后作为next数组。
 

problems/0034.在排序数组中查找元素的第一个和最后一个位置.md

@@ -329,6 +329,67 @@ class Solution {
 }
 ```
 
+### C#
+
+```c#
+public int[] SearchRange(int[] nums, int target) {
+
+	var leftBorder = GetLeftBorder(nums, target);
+	var rightBorder = GetRightBorder(nums, target);
+	
+	if (leftBorder == -2 || rightBorder == -2) {
+		return new int[] {-1, -1};
+	}
+	
+	if (rightBorder - leftBorder >=2) {
+		return new int[] {leftBorder + 1, rightBorder - 1};
+	}
+	
+	return new int[] {-1, -1};
+
+}
+
+public int GetLeftBorder(int[] nums, int target){
+	var left = 0;
+	var right = nums.Length - 1;
+	var leftBorder = -2;
+	
+	while (left <= right) {
+		var mid = (left + right) / 2;
+		
+		if (target <= nums[mid]) {
+			right = mid - 1;
+			leftBorder = right;
+		}
+		else {
+			left = mid + 1;
+		}
+	}
+	
+	return leftBorder;
+}
+
+public int GetRightBorder(int[] nums, int target){
+	var left = 0;
+	var right = nums.Length - 1;
+	var rightBorder = -2;
+	
+	while (left <= right) {
+		var mid = (left + right) / 2;
+		
+		if (target >= nums[mid]) {
+			left = mid + 1;
+			rightBorder = left;
+		}
+		else {
+			right = mid - 1;
+		}
+	}
+	
+	return rightBorder;
+}
+```
+
 
 
 ### Python

problems/0035.搜索插入位置.md

@@ -258,6 +258,37 @@ public int searchInsert(int[] nums, int target) {
 
 
 
+### C#
+
+```go
+public int SearchInsert(int[] nums, int target) {
+	
+	var left = 0;
+	var right = nums.Length - 1;
+
+	while (left <= right) {
+		
+		var curr = (left + right) / 2;
+		
+		if (nums[curr] == target)
+		{
+			return curr;	
+		}
+		
+		if (target > nums[curr]) {
+			left = curr + 1;
+		}
+		else {
+			right = curr - 1;
+		}
+	}
+	
+	return left;
+}
+```
+
+
+
 ### Golang
 
 ```go
@@ -500,3 +531,4 @@ int searchInsert(int* nums, int numsSize, int target){
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
 </a>
+

problems/0042.接雨水.md

@@ -704,6 +704,45 @@ func min(x, y int) int {
 }
 ```
 
+单调栈压缩版：
+
+```go
+func trap(height []int) int {
+    stack := make([]int, 0)
+    res := 0
+
+    // 无需事先将第一个柱子的坐标入栈，因为它会在该for循环的最后入栈
+    for i := 0; i < len(height); i ++ {
+        // 满足栈不为空并且当前柱子高度大于栈顶对应的柱子高度的情况时
+        for len(stack) > 0 && height[stack[len(stack) - 1]] < height[i] {
+            // 获得凹槽高度
+            mid := height[stack[len(stack) - 1]]
+            // 凹槽坐标出栈
+            stack = stack[: len(stack) - 1]
+
+            // 如果栈不为空则此时栈顶元素为左侧柱子坐标
+            if len(stack) > 0 {
+                // 求得雨水高度
+                h := min(height[i], height[stack[len(stack) - 1]]) - mid
+                // 求得雨水宽度
+                w := i - stack[len(stack) - 1] - 1
+                res += h * w
+            }
+        }
+        // 如果栈为空或者当前柱子高度小于等于栈顶对应的柱子高度时入栈
+        stack = append(stack, i)
+    }
+    return res
+}
+
+func min(x, y int) int {
+    if x < y {
+        return x
+    }
+    return y
+}
+```
+
 ### JavaScript:
 
 ```javascript

problems/0084.柱状图中最大的矩形.md

@@ -478,36 +478,34 @@ class Solution:
 
 ```go
 func largestRectangleArea(heights []int) int {
- // 声明max并初始化为0
- max := 0
- // 使用切片实现栈
- stack := make([]int, 0)
- // 数组头部加入0
- heights = append([]int{0}, heights...)
- // 数组尾部加入0
- heights = append(heights, 0)
- // 初始化栈，序号从0开始
- stack = append(stack, 0)
- for i := 1; i < len(heights); i++ {
-  // 结束循环条件为：当即将入栈元素>top元素，也就是形成非单调递增的趋势
-  for heights[stack[len(stack)-1]] > heights[i] {
-   // mid 是top
-   mid := stack[len(stack)-1]
-   // 出栈
-   stack = stack[0 : len(stack)-1]
-   // left是top的下一位元素，i是将要入栈的元素
-   left := stack[len(stack)-1]
-   // 高度x宽度
-   tmp := heights[mid] * (i - left - 1)
-   if tmp > max {
-    max = tmp
-   }
-  }
-  stack = append(stack, i)
- }
- return max
+    max := 0
+    // 使用切片实现栈
+    stack := make([]int, 0)
+    // 数组头部加入0
+    heights = append([]int{0}, heights...)
+    // 数组尾部加入0
+    heights = append(heights, 0)
+    // 初始化栈，序号从0开始
+    stack = append(stack, 0)
+    for i := 1; i < len(heights); i ++ {
+        // 结束循环条件为：当即将入栈元素>top元素，也就是形成非单调递增的趋势
+        for heights[stack[len(stack) - 1]] > heights[i] {
+            // mid 是top
+            mid := stack[len(stack) - 1]
+            // 出栈
+            stack = stack[0 : len(stack) - 1]
+            // left是top的下一位元素，i是将要入栈的元素
+            left := stack[len(stack) - 1]
+            // 高度x宽度
+            tmp := heights[mid] * (i - left - 1)
+            if tmp > max {
+                max = tmp
+            }
+        }
+        stack = append(stack, i)
+    }
+    return max
 }
-
 ```
 
 ### JavaScript:

problems/0111.二叉树的最小深度.md

@@ -173,12 +173,12 @@ private:
     int result;
     void getdepth(TreeNode* node, int depth) {
         // 函数递归终止条件
-        if (root == nullptr) {
+        if (node == nullptr) {
             return;
         }
         // 中，处理逻辑：判断是不是叶子结点
-        if (root -> left == nullptr && root->right == nullptr) {
-            res = min(res, depth);
+        if (node -> left == nullptr && node->right == nullptr) {
+            result = min(result, depth);
         }
         if (node->left) { // 左
             getdepth(node->left, depth + 1);

problems/0235.二叉搜索树的最近公共祖先.md

@@ -50,15 +50,15 @@
 
 因为是有序树，所有 如果 中间节点是 q 和 p 的公共祖先，那么 中节点的数组 一定是在 [p, q]区间的。即 中节点 > p && 中节点 < q   或者 中节点 > q && 中节点 < p。 
 
-那么只要从上到下去遍历，遇到 cur节点是数值在[p, q]区间中则一定可以说明该节点cur就是q 和 p的公共祖先。 那问题来了，**一定是最近公共祖先吗**？
+那么只要从上到下去遍历，遇到 cur节点是数值在[p, q]区间中则一定可以说明该节点cur就是p 和 q的公共祖先。 那问题来了，**一定是最近公共祖先吗**？
 
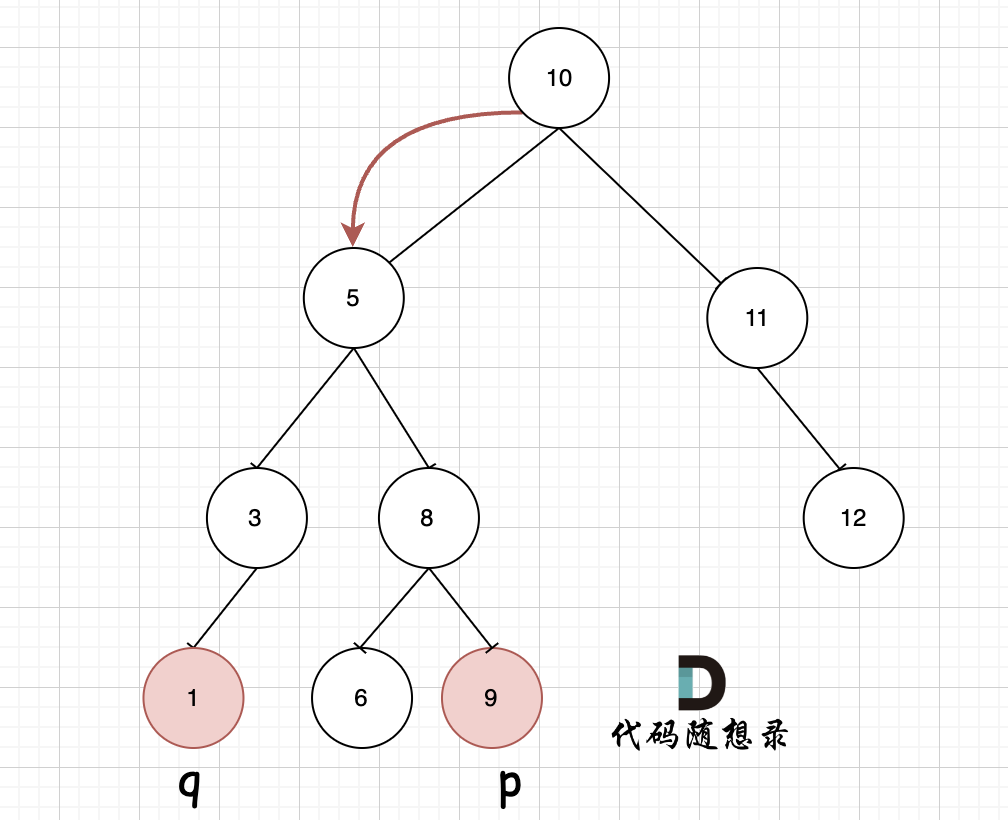
-如图，我们从根节点搜索，第一次遇到 cur节点是数值在[p, q]区间中，即 节点5，此时可以说明 p 和 q 一定分别存在于 节点 5的左子树，和右子树中。 
+如图，我们从根节点搜索，第一次遇到 cur节点是数值在[q, p]区间中，即 节点5，此时可以说明 q 和 p 一定分别存在于 节点 5的左子树，和右子树中。 
 
 ![235.二叉搜索树的最近公共祖先](https://code-thinking-1253855093.file.myqcloud.com/pics/20220926164214.png)
 
-此时节点5是不是最近公共祖先？ 如果 从节点5继续向左遍历，那么将错过成为q的祖先， 如果从节点5继续向右遍历则错过成为p的祖先。 
+此时节点5是不是最近公共祖先？ 如果 从节点5继续向左遍历，那么将错过成为p的祖先， 如果从节点5继续向右遍历则错过成为q的祖先。 
 
-所以当我们从上向下去递归遍历，第一次遇到 cur节点是数值在[p, q]区间中，那么cur就是 p和q的最近公共祖先。
+所以当我们从上向下去递归遍历，第一次遇到 cur节点是数值在[q, p]区间中，那么cur就是 q和p的最近公共祖先。
 
 理解这一点，本题就很好解了。
 

problems/0343.整数拆分.md

@@ -469,6 +469,34 @@ object Solution {
 }
 ```
 
+
+### PHP
+```php
+class Solution {
+
+    /**
+     * @param Integer $n
+     * @return Integer
+     */
+    function integerBreak($n) {
+        if($n == 0 || $n == 1) return 0;
+        if($n == 2) return 1;
+
+        $dp = [];
+        $dp[0] = 0;
+        $dp[1] = 0;
+        $dp[2] = 1;
+        for($i=3;$i<=$n;$i++){
+            for($j = 1;$j <= $i/2; $j++){
+                $dp[$i] = max(($i-$j)*$j, $dp[$i-$j]*$j, $dp[$i]);
+            }
+        }
+
+        return $dp[$n];
+    }
+}
+```
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/0503.下一个更大元素II.md

@@ -207,7 +207,7 @@ class Solution:
 ```go
 func nextGreaterElements(nums []int) []int {
     length := len(nums)
-    result := make([]int,length,length)
+    result := make([]int,length)
     for i:=0;i<len(result);i++{
         result[i] = -1
     }

problems/0684.冗余连接.md

@@ -256,6 +256,23 @@ class Solution:
         return []
 ```
 
+### Python简洁写法：
+
+```python
+class Solution:
+    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
+        n = len(edges)
+        p = [i for i in range(n+1)]
+        def find(i):
+            if p[i] != i:
+                p[i] = find(p[i])
+            return p[i]
+        for u, v in edges:
+            if p[find(u)] == find(v):
+                return [u, v]
+            p[find(u)] = find(v)
+```
+
 ### Go
 
 ```go

problems/0841.钥匙和房间.md

@@ -324,7 +324,7 @@ class Solution {
 ### python3
 
 ```python
-
+# 深度搜索优先
 class Solution:
     def dfs(self, key: int, rooms: List[List[int]]  , visited : List[bool] ) :
         if visited[key] :
@@ -346,6 +346,31 @@ class Solution:
                 return False
         return True
 
+# 广度搜索优先
+class Solution:
+    def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:
+        visited = [False] * len(rooms)
+        self.bfs(rooms, 0, visited)
+        
+        for room in visited:
+            if room == False:
+                return False
+        
+        return True
+    
+    def bfs(self, rooms, index, visited):
+        q = collections.deque()
+        q.append(index)
+
+        visited[0] = True
+
+        while len(q) != 0:
+            index = q.popleft()
+            for nextIndex in rooms[index]:
+                if visited[nextIndex] == False:
+                    q.append(nextIndex)
+                    visited[nextIndex] = True
+
 ```
 
 

problems/1971.寻找图中是否存在路径.md

@@ -134,6 +134,22 @@ public:
     }
 };
 ```
+
+PYTHON并查集解法如下：
+```PYTHON
+class Solution:
+    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
+        p = [i for i in range(n)]
+        def find(i):
+            if p[i] != i:
+                p[i] = find(p[i])
+            return p[i]
+        for u, v in edges:
+            p[find(u)] = find(v)
+        return find(source) == find(destination)
+```
+
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/qita/acm.md

@@ -1,5 +1,5 @@
 
-# 如何练习ACM模式输入输入模式 | 如何准备笔试 | 卡码网
+# 如何练习ACM模式输入输出模式 | 如何准备笔试 | 卡码网
 
 卡码网地址：[https://kamacoder.com](https://kamacoder.com)
 

problems/图论广搜理论基础.md

@@ -9,7 +9,7 @@
 
 在[深度优先搜索](https://programmercarl.com/图论深搜理论基础.html)的讲解中，我们就讲过深度优先搜索和广度优先搜索的区别。
 
-广搜（bfs）是一圈一圈的搜索过程，和深搜（dfs）是一条路跑到黑然后在回溯。
+广搜（bfs）是一圈一圈的搜索过程，和深搜（dfs）是一条路跑到黑然后再回溯。
 
 ## 广搜的使用场景