diff --git a/problems/0019.删除链表的倒数第N个节点.md b/problems/0019.删除链表的倒数第N个节点.md
index 1c95ad5b..dbd053d1 100644
--- a/problems/0019.删除链表的倒数第N个节点.md
+++ b/problems/0019.删除链表的倒数第N个节点.md
@@ -105,8 +105,8 @@ public ListNode removeNthFromEnd(ListNode head, int n){
ListNode fastIndex = dummyNode;
ListNode slowIndex = dummyNode;
- //只要快慢指针相差 n 个结点即可
- for (int i = 0; i < n ; i++){
+ // 只要快慢指针相差 n 个结点即可
+ for (int i = 0; i <= n ; i++){
fastIndex = fastIndex.next;
}
diff --git a/problems/0028.实现strStr.md b/problems/0028.实现strStr.md
index 207a047d..629ff014 100644
--- a/problems/0028.实现strStr.md
+++ b/problems/0028.实现strStr.md
@@ -207,7 +207,7 @@ next数组就是一个前缀表（prefix table）。
### 前缀表与next数组
-很多KMP算法的时间都是使用next数组来做回退操作，那么next数组与前缀表有什么关系呢？
+很多KMP算法的实现都是使用next数组来做回退操作，那么next数组与前缀表有什么关系呢？
next数组就可以是前缀表，但是很多实现都是把前缀表统一减一（右移一位，初始位置为-1）之后作为next数组。
diff --git a/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md b/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
index b4128166..3bf90e3b 100644
--- a/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
+++ b/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
@@ -329,6 +329,67 @@ class Solution {
}
```
+### C#
+
+```c#
+public int[] SearchRange(int[] nums, int target) {
+
+ var leftBorder = GetLeftBorder(nums, target);
+ var rightBorder = GetRightBorder(nums, target);
+
+ if (leftBorder == -2 || rightBorder == -2) {
+ return new int[] {-1, -1};
+ }
+
+ if (rightBorder - leftBorder >=2) {
+ return new int[] {leftBorder + 1, rightBorder - 1};
+ }
+
+ return new int[] {-1, -1};
+
+}
+
+public int GetLeftBorder(int[] nums, int target){
+ var left = 0;
+ var right = nums.Length - 1;
+ var leftBorder = -2;
+
+ while (left <= right) {
+ var mid = (left + right) / 2;
+
+ if (target <= nums[mid]) {
+ right = mid - 1;
+ leftBorder = right;
+ }
+ else {
+ left = mid + 1;
+ }
+ }
+
+ return leftBorder;
+}
+
+public int GetRightBorder(int[] nums, int target){
+ var left = 0;
+ var right = nums.Length - 1;
+ var rightBorder = -2;
+
+ while (left <= right) {
+ var mid = (left + right) / 2;
+
+ if (target >= nums[mid]) {
+ left = mid + 1;
+ rightBorder = left;
+ }
+ else {
+ right = mid - 1;
+ }
+ }
+
+ return rightBorder;
+}
+```
+
### Python
diff --git a/problems/0035.搜索插入位置.md b/problems/0035.搜索插入位置.md
index 04dd0cac..80b7e40e 100644
--- a/problems/0035.搜索插入位置.md
+++ b/problems/0035.搜索插入位置.md
@@ -258,6 +258,37 @@ public int searchInsert(int[] nums, int target) {
+### C#
+
+```go
+public int SearchInsert(int[] nums, int target) {
+
+ var left = 0;
+ var right = nums.Length - 1;
+
+ while (left <= right) {
+
+ var curr = (left + right) / 2;
+
+ if (nums[curr] == target)
+ {
+ return curr;
+ }
+
+ if (target > nums[curr]) {
+ left = curr + 1;
+ }
+ else {
+ right = curr - 1;
+ }
+ }
+
+ return left;
+}
+```
+
+
+
### Golang
```go
@@ -500,3 +531,4 @@ int searchInsert(int* nums, int numsSize, int target){
+
diff --git a/problems/0042.接雨水.md b/problems/0042.接雨水.md
index 1090467d..73d787b1 100644
--- a/problems/0042.接雨水.md
+++ b/problems/0042.接雨水.md
@@ -704,6 +704,45 @@ func min(x, y int) int {
}
```
+单调栈压缩版：
+
+```go
+func trap(height []int) int {
+ stack := make([]int, 0)
+ res := 0
+
+ // 无需事先将第一个柱子的坐标入栈，因为它会在该for循环的最后入栈
+ for i := 0; i < len(height); i ++ {
+ // 满足栈不为空并且当前柱子高度大于栈顶对应的柱子高度的情况时
+ for len(stack) > 0 && height[stack[len(stack) - 1]] < height[i] {
+ // 获得凹槽高度
+ mid := height[stack[len(stack) - 1]]
+ // 凹槽坐标出栈
+ stack = stack[: len(stack) - 1]
+
+ // 如果栈不为空则此时栈顶元素为左侧柱子坐标
+ if len(stack) > 0 {
+ // 求得雨水高度
+ h := min(height[i], height[stack[len(stack) - 1]]) - mid
+ // 求得雨水宽度
+ w := i - stack[len(stack) - 1] - 1
+ res += h * w
+ }
+ }
+ // 如果栈为空或者当前柱子高度小于等于栈顶对应的柱子高度时入栈
+ stack = append(stack, i)
+ }
+ return res
+}
+
+func min(x, y int) int {
+ if x < y {
+ return x
+ }
+ return y
+}
+```
+
### JavaScript:
```javascript
diff --git a/problems/0084.柱状图中最大的矩形.md b/problems/0084.柱状图中最大的矩形.md
index b54429ed..97dab4f3 100644
--- a/problems/0084.柱状图中最大的矩形.md
+++ b/problems/0084.柱状图中最大的矩形.md
@@ -478,36 +478,34 @@ class Solution:
```go
func largestRectangleArea(heights []int) int {
- // 声明max并初始化为0
- max := 0
- // 使用切片实现栈
- stack := make([]int, 0)
- // 数组头部加入0
- heights = append([]int{0}, heights...)
- // 数组尾部加入0
- heights = append(heights, 0)
- // 初始化栈，序号从0开始
- stack = append(stack, 0)
- for i := 1; i < len(heights); i++ {
- // 结束循环条件为：当即将入栈元素>top元素，也就是形成非单调递增的趋势
- for heights[stack[len(stack)-1]] > heights[i] {
- // mid 是top
- mid := stack[len(stack)-1]
- // 出栈
- stack = stack[0 : len(stack)-1]
- // left是top的下一位元素，i是将要入栈的元素
- left := stack[len(stack)-1]
- // 高度x宽度
- tmp := heights[mid] * (i - left - 1)
- if tmp > max {
- max = tmp
- }
- }
- stack = append(stack, i)
- }
- return max
+ max := 0
+ // 使用切片实现栈
+ stack := make([]int, 0)
+ // 数组头部加入0
+ heights = append([]int{0}, heights...)
+ // 数组尾部加入0
+ heights = append(heights, 0)
+ // 初始化栈，序号从0开始
+ stack = append(stack, 0)
+ for i := 1; i < len(heights); i ++ {
+ // 结束循环条件为：当即将入栈元素>top元素，也就是形成非单调递增的趋势
+ for heights[stack[len(stack) - 1]] > heights[i] {
+ // mid 是top
+ mid := stack[len(stack) - 1]
+ // 出栈
+ stack = stack[0 : len(stack) - 1]
+ // left是top的下一位元素，i是将要入栈的元素
+ left := stack[len(stack) - 1]
+ // 高度x宽度
+ tmp := heights[mid] * (i - left - 1)
+ if tmp > max {
+ max = tmp
+ }
+ }
+ stack = append(stack, i)
+ }
+ return max
}
-
```
### JavaScript:
diff --git a/problems/0111.二叉树的最小深度.md b/problems/0111.二叉树的最小深度.md
index 61f9beb7..8b9d92e6 100644
--- a/problems/0111.二叉树的最小深度.md
+++ b/problems/0111.二叉树的最小深度.md
@@ -173,12 +173,12 @@ private:
int result;
void getdepth(TreeNode* node, int depth) {
// 函数递归终止条件
- if (root == nullptr) {
+ if (node == nullptr) {
return;
}
// 中，处理逻辑：判断是不是叶子结点
- if (root -> left == nullptr && root->right == nullptr) {
- res = min(res, depth);
+ if (node -> left == nullptr && node->right == nullptr) {
+ result = min(result, depth);
}
if (node->left) { // 左
getdepth(node->left, depth + 1);
diff --git a/problems/0235.二叉搜索树的最近公共祖先.md b/problems/0235.二叉搜索树的最近公共祖先.md
index 2b8af060..b7e92e4e 100644
--- a/problems/0235.二叉搜索树的最近公共祖先.md
+++ b/problems/0235.二叉搜索树的最近公共祖先.md
@@ -50,15 +50,15 @@
因为是有序树，所有 如果 中间节点是 q 和 p 的公共祖先，那么 中节点的数组 一定是在 [p, q]区间的。即 中节点 > p && 中节点 < q 或者 中节点 > q && 中节点 < p。
-那么只要从上到下去遍历，遇到 cur节点是数值在[p, q]区间中则一定可以说明该节点cur就是q 和 p的公共祖先。 那问题来了，**一定是最近公共祖先吗**？
+那么只要从上到下去遍历，遇到 cur节点是数值在[p, q]区间中则一定可以说明该节点cur就是p 和 q的公共祖先。 那问题来了，**一定是最近公共祖先吗**？
-如图，我们从根节点搜索，第一次遇到 cur节点是数值在[p, q]区间中，即 节点5，此时可以说明 p 和 q 一定分别存在于 节点 5的左子树，和右子树中。
+如图，我们从根节点搜索，第一次遇到 cur节点是数值在[q, p]区间中，即 节点5，此时可以说明 q 和 p 一定分别存在于 节点 5的左子树，和右子树中。
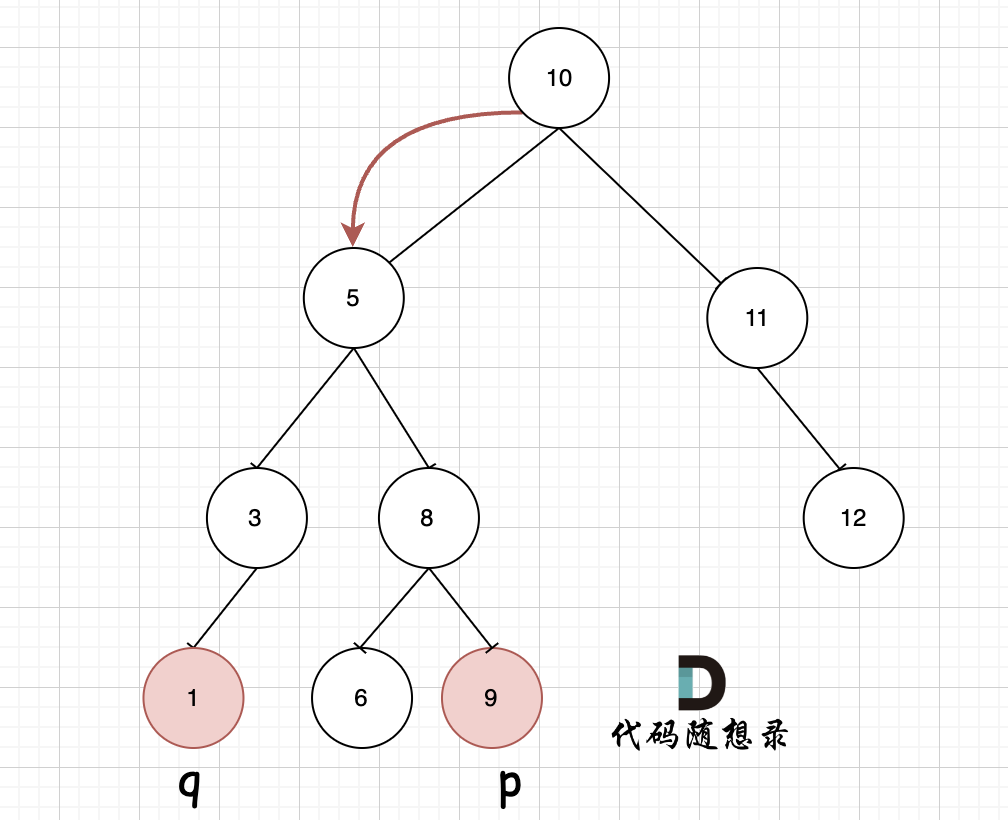
-此时节点5是不是最近公共祖先？ 如果 从节点5继续向左遍历，那么将错过成为q的祖先， 如果从节点5继续向右遍历则错过成为p的祖先。
+此时节点5是不是最近公共祖先？ 如果 从节点5继续向左遍历，那么将错过成为p的祖先， 如果从节点5继续向右遍历则错过成为q的祖先。
-所以当我们从上向下去递归遍历，第一次遇到 cur节点是数值在[p, q]区间中，那么cur就是 p和q的最近公共祖先。
+所以当我们从上向下去递归遍历，第一次遇到 cur节点是数值在[q, p]区间中，那么cur就是 q和p的最近公共祖先。
理解这一点，本题就很好解了。
diff --git a/problems/0343.整数拆分.md b/problems/0343.整数拆分.md
index cba82f6c..2e17caf5 100644
--- a/problems/0343.整数拆分.md
+++ b/problems/0343.整数拆分.md
@@ -469,6 +469,34 @@ object Solution {
}
```
+
+### PHP
+```php
+class Solution {
+
+ /**
+ * @param Integer $n
+ * @return Integer
+ */
+ function integerBreak($n) {
+ if($n == 0 || $n == 1) return 0;
+ if($n == 2) return 1;
+
+ $dp = [];
+ $dp[0] = 0;
+ $dp[1] = 0;
+ $dp[2] = 1;
+ for($i=3;$i<=$n;$i++){
+ for($j = 1;$j <= $i/2; $j++){
+ $dp[$i] = max(($i-$j)*$j, $dp[$i-$j]*$j, $dp[$i]);
+ }
+ }
+
+ return $dp[$n];
+ }
+}
+```
+
diff --git a/problems/0503.下一个更大元素II.md b/problems/0503.下一个更大元素II.md
index c001df50..b788968c 100644
--- a/problems/0503.下一个更大元素II.md
+++ b/problems/0503.下一个更大元素II.md
@@ -207,7 +207,7 @@ class Solution:
```go
func nextGreaterElements(nums []int) []int {
length := len(nums)
- result := make([]int,length,length)
+ result := make([]int,length)
for i:=0;i List[int]:
+ n = len(edges)
+ p = [i for i in range(n+1)]
+ def find(i):
+ if p[i] != i:
+ p[i] = find(p[i])
+ return p[i]
+ for u, v in edges:
+ if p[find(u)] == find(v):
+ return [u, v]
+ p[find(u)] = find(v)
+```
+
### Go
```go
diff --git a/problems/0841.钥匙和房间.md b/problems/0841.钥匙和房间.md
index 00156d4e..b4785d1b 100644
--- a/problems/0841.钥匙和房间.md
+++ b/problems/0841.钥匙和房间.md
@@ -324,7 +324,7 @@ class Solution {
### python3
```python
-
+# 深度搜索优先
class Solution:
def dfs(self, key: int, rooms: List[List[int]] , visited : List[bool] ) :
if visited[key] :
@@ -346,6 +346,31 @@ class Solution:
return False
return True
+# 广度搜索优先
+class Solution:
+ def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:
+ visited = [False] * len(rooms)
+ self.bfs(rooms, 0, visited)
+
+ for room in visited:
+ if room == False:
+ return False
+
+ return True
+
+ def bfs(self, rooms, index, visited):
+ q = collections.deque()
+ q.append(index)
+
+ visited[0] = True
+
+ while len(q) != 0:
+ index = q.popleft()
+ for nextIndex in rooms[index]:
+ if visited[nextIndex] == False:
+ q.append(nextIndex)
+ visited[nextIndex] = True
+
```
diff --git a/problems/1971.寻找图中是否存在路径.md b/problems/1971.寻找图中是否存在路径.md
index 29e50ab8..5660233c 100644
--- a/problems/1971.寻找图中是否存在路径.md
+++ b/problems/1971.寻找图中是否存在路径.md
@@ -134,6 +134,22 @@ public:
}
};
```
+
+PYTHON并查集解法如下：
+```PYTHON
+class Solution:
+ def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
+ p = [i for i in range(n)]
+ def find(i):
+ if p[i] != i:
+ p[i] = find(p[i])
+ return p[i]
+ for u, v in edges:
+ p[find(u)] = find(v)
+ return find(source) == find(destination)
+```
+
+
diff --git a/problems/qita/acm.md b/problems/qita/acm.md
index 1be0e924..99928356 100644
--- a/problems/qita/acm.md
+++ b/problems/qita/acm.md
@@ -1,5 +1,5 @@
-# 如何练习ACM模式输入输入模式 | 如何准备笔试 | 卡码网
+# 如何练习ACM模式输入输出模式 | 如何准备笔试 | 卡码网
卡码网地址：[https://kamacoder.com](https://kamacoder.com)
diff --git a/problems/图论广搜理论基础.md b/problems/图论广搜理论基础.md
index 64ca181b..1174e239 100644
--- a/problems/图论广搜理论基础.md
+++ b/problems/图论广搜理论基础.md
@@ -9,7 +9,7 @@
在[深度优先搜索](https://programmercarl.com/图论深搜理论基础.html)的讲解中，我们就讲过深度优先搜索和广度优先搜索的区别。
-广搜（bfs）是一圈一圈的搜索过程，和深搜（dfs）是一条路跑到黑然后在回溯。
+广搜（bfs）是一圈一圈的搜索过程，和深搜（dfs）是一条路跑到黑然后再回溯。
## 广搜的使用场景