mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-05 22:59:31 +08:00
Update
This commit is contained in:
@ -74,6 +74,7 @@
|
||||
|
||||
* 编程语言
|
||||
* [C++面试&C++学习指南知识点整理](https://github.com/youngyangyang04/TechCPP)
|
||||
* [C++语言基础课](https://kamacoder.com/course.php?course_id=1)
|
||||
|
||||
* 项目
|
||||
* [基于跳表的轻量级KV存储引擎](https://github.com/youngyangyang04/Skiplist-CPP)
|
||||
|
||||
@ -31,7 +31,7 @@ for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target;
|
||||
|
||||
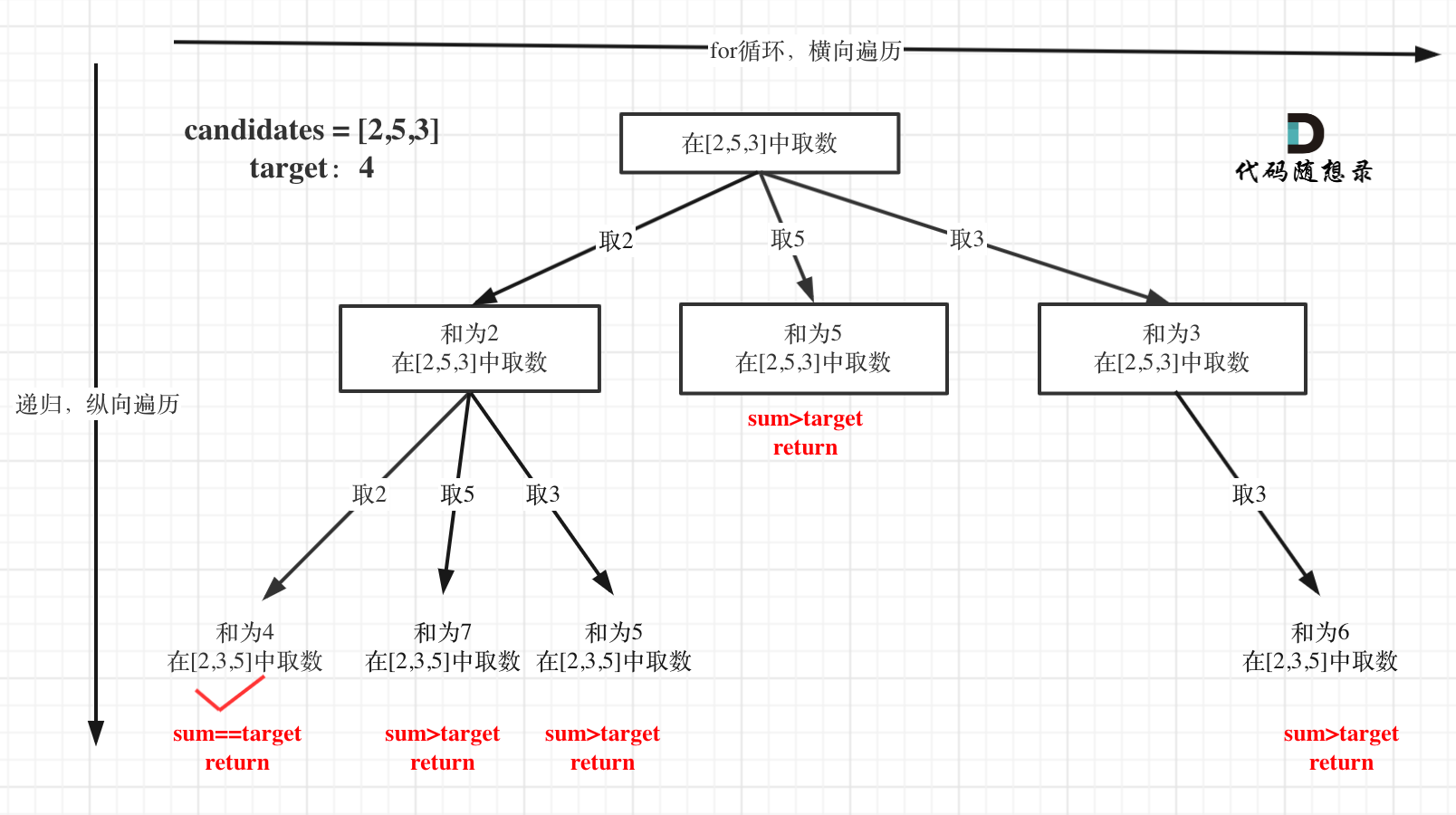
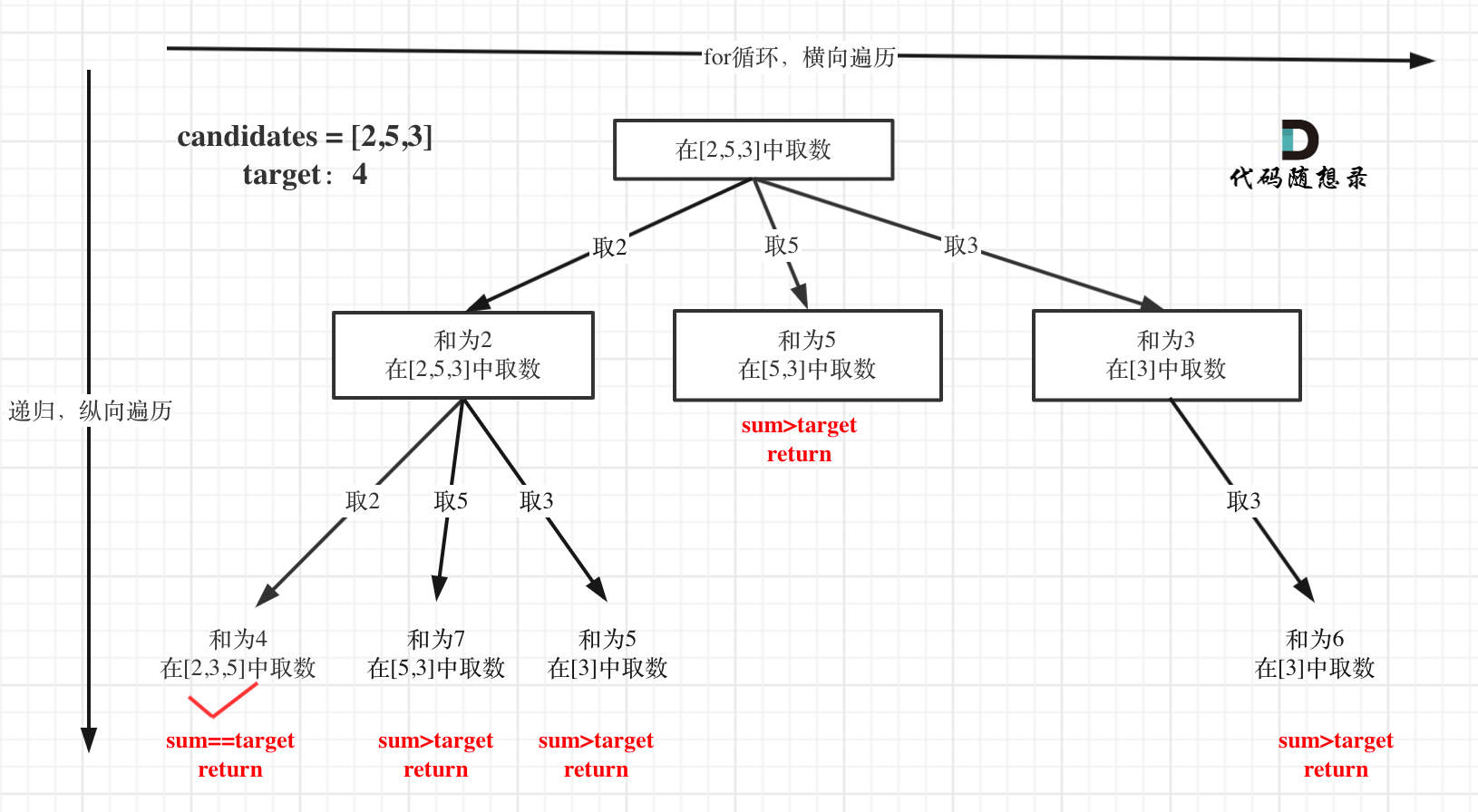
在[回溯算法:求组合总和(二)](https://programmercarl.com/0039.组合总和.html)第一个树形结构没有画出startIndex的作用,**这里这里纠正一下,准确的树形结构如图所示:**
|
||||
|
||||
|
||||
|
||||
|
||||
## 周二
|
||||
|
||||
|
||||
@ -116,8 +116,8 @@ void backtracking(参数) {
|
||||
**注意以上我只是说求组合的情况,如果是排列问题,又是另一套分析的套路**。
|
||||
|
||||
树形结构如下:
|
||||

|
||||
|
||||

|
||||
|
||||
最后还给出了本题的剪枝优化,如下:
|
||||
|
||||
|
||||
@ -8,6 +8,9 @@
|
||||
|
||||
# 动态规划:01背包理论基础
|
||||
|
||||
|
||||
本题力扣上没有原题,大家可以去[卡码网第46题](https://kamacoder.com/problem.php?id=1046)去练习,题意是一样的。
|
||||
|
||||
## 算法公开课
|
||||
|
||||
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[带你学透0-1背包问题!](https://www.bilibili.com/video/BV1cg411g7Y6/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
@ -261,6 +264,55 @@ int main() {
|
||||
|
||||
```
|
||||
|
||||
本题力扣上没有原题,大家可以去[卡码网第46题](https://kamacoder.com/problem.php?id=1046)去练习,题意是一样的,代码如下:
|
||||
|
||||
```CPP
|
||||
|
||||
//二维dp数组实现
|
||||
#include <bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
int n, bagweight;// bagweight代表行李箱空间
|
||||
void solve() {
|
||||
vector<int> weight(n, 0); // 存储每件物品所占空间
|
||||
vector<int> value(n, 0); // 存储每件物品价值
|
||||
for(int i = 0; i < n; ++i) {
|
||||
cin >> weight[i];
|
||||
}
|
||||
for(int j = 0; j < n; ++j) {
|
||||
cin >> value[j];
|
||||
}
|
||||
// dp数组, dp[i][j]代表行李箱空间为j的情况下,从下标为[0, i]的物品里面任意取,能达到的最大价值
|
||||
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
|
||||
|
||||
// 初始化, 因为需要用到dp[i - 1]的值
|
||||
// j < weight[0]已在上方被初始化为0
|
||||
// j >= weight[0]的值就初始化为value[0]
|
||||
for (int j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
for(int i = 1; i < weight.size(); i++) { // 遍历科研物品
|
||||
for(int j = 0; j <= bagweight; j++) { // 遍历行李箱容量
|
||||
// 如果装不下这个物品,那么就继承dp[i - 1][j]的值
|
||||
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
|
||||
// 如果能装下,就将值更新为 不装这个物品的最大值 和 装这个物品的最大值 中的 最大值
|
||||
// 装这个物品的最大值由容量为j - weight[i]的包任意放入序号为[0, i - 1]的最大值 + 该物品的价值构成
|
||||
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
cout << dp[weight.size() - 1][bagweight] << endl;
|
||||
}
|
||||
|
||||
int main() {
|
||||
while(cin >> n >> bagweight) {
|
||||
solve();
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
|
||||
@ -6,6 +6,7 @@
|
||||
|
||||
# 动态规划:01背包理论基础(滚动数组)
|
||||
|
||||
本题力扣上没有原题,大家可以去[卡码网第46题](https://kamacoder.com/problem.php?id=1046)去练习
|
||||
|
||||
## 算法公开课
|
||||
|
||||
@ -13,7 +14,6 @@
|
||||
|
||||
## 思路
|
||||
|
||||
|
||||
昨天[动态规划:关于01背包问题,你该了解这些!](https://programmercarl.com/背包理论基础01背包-1.html)中是用二维dp数组来讲解01背包。
|
||||
|
||||
今天我们就来说一说滚动数组,其实在前面的题目中我们已经用到过滚动数组了,就是把二维dp降为一维dp,一些录友当时还表示比较困惑。
|
||||
@ -159,6 +159,8 @@ dp[1] = dp[1 - weight[0]] + value[0] = 15
|
||||
|
||||
|
||||
|
||||
C++代码如下:
|
||||
|
||||
```CPP
|
||||
void test_1_wei_bag_problem() {
|
||||
vector<int> weight = {1, 3, 4};
|
||||
@ -181,6 +183,49 @@ int main() {
|
||||
|
||||
```
|
||||
|
||||
本题力扣上没有原题,大家可以去[卡码网第46题](https://kamacoder.com/problem.php?id=1046)去练习,题意是一样的,代码如下:
|
||||
|
||||
```CPP
|
||||
// 一维dp数组实现
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
// 读取 M 和 N
|
||||
int M, N;
|
||||
cin >> M >> N;
|
||||
|
||||
vector<int> costs(M);
|
||||
vector<int> values(M);
|
||||
|
||||
for (int i = 0; i < M; i++) {
|
||||
cin >> costs[i];
|
||||
}
|
||||
for (int j = 0; j < M; j++) {
|
||||
cin >> values[j];
|
||||
}
|
||||
|
||||
// 创建一个动态规划数组dp,初始值为0
|
||||
vector<int> dp(N + 1, 0);
|
||||
|
||||
// 外层循环遍历每个类型的研究材料
|
||||
for (int i = 0; i < M; ++i) {
|
||||
// 内层循环从 N 空间逐渐减少到当前研究材料所占空间
|
||||
for (int j = N; j >= costs[i]; --j) {
|
||||
// 考虑当前研究材料选择和不选择的情况,选择最大值
|
||||
dp[j] = max(dp[j], dp[j - costs[i]] + values[i]);
|
||||
}
|
||||
}
|
||||
|
||||
// 输出dp[N],即在给定 N 行李空间可以携带的研究材料最大价值
|
||||
cout << dp[N] << endl;
|
||||
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
可以看出,一维dp 的01背包,要比二维简洁的多! 初始化 和 遍历顺序相对简单了。
|
||||
|
||||
**所以我倾向于使用一维dp数组的写法,比较直观简洁,而且空间复杂度还降了一个数量级!**
|
||||
|
||||
@ -7,6 +7,8 @@
|
||||
|
||||
# 动态规划:完全背包理论基础
|
||||
|
||||
本题力扣上没有原题,大家可以去[卡码网第52题](https://kamacoder.com/problem.php?id=1046)去练习,题意是一样的。
|
||||
|
||||
## 算法公开课
|
||||
|
||||
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[带你学透完全背包问题! ](https://www.bilibili.com/video/BV1uK411o7c9/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
@ -162,6 +164,43 @@ int main() {
|
||||
|
||||
```
|
||||
|
||||
本题力扣上没有原题,大家可以去[卡码网第46题](https://kamacoder.com/problem.php?id=1046)去练习,题意是一样的,C++代码如下:
|
||||
|
||||
```cpp
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
|
||||
// 先遍历背包,再遍历物品
|
||||
void test_CompletePack(vector<int> weight, vector<int> value, int bagWeight) {
|
||||
|
||||
vector<int> dp(bagWeight + 1, 0);
|
||||
|
||||
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
|
||||
for(int i = 0; i < weight.size(); i++) { // 遍历物品
|
||||
if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
cout << dp[bagWeight] << endl;
|
||||
}
|
||||
int main() {
|
||||
int N, V;
|
||||
cin >> N >> V;
|
||||
vector<int> weight;
|
||||
vector<int> value;
|
||||
for (int i = 0; i < N; i++) {
|
||||
int w;
|
||||
int v;
|
||||
cin >> w >> v;
|
||||
weight.push_back(w);
|
||||
value.push_back(v);
|
||||
}
|
||||
test_CompletePack(weight, value, V);
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
|
||||
Reference in New Issue
Block a user