mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-10 12:15:58 +08:00
Merge branch 'master' of github.com:youngyangyang04/leetcode-master
This commit is contained in:
56
107寻找存在的路径Java代码
Normal file
56
107寻找存在的路径Java代码
Normal file
@ -0,0 +1,56 @@
|
||||
JAVA:
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.*;
|
||||
|
||||
public class Main{
|
||||
public static void main(String[] args) {
|
||||
int N, M;
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
N = scanner.nextInt();
|
||||
M = scanner.nextInt();
|
||||
DisJoint disJoint = new DisJoint(N + 1);
|
||||
for (int i = 0; i < M; ++i) {
|
||||
disJoint.join(scanner.nextInt(), scanner.nextInt());
|
||||
}
|
||||
if(disJoint.isSame(scanner.nextInt(), scanner.nextInt())) {
|
||||
System.out.println("1");
|
||||
} else {
|
||||
System.out.println("0");
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
//并查集模板
|
||||
class DisJoint{
|
||||
private int[] father;
|
||||
|
||||
public DisJoint(int N) {
|
||||
father = new int[N];
|
||||
for (int i = 0; i < N; ++i){
|
||||
father[i] = i;
|
||||
}
|
||||
}
|
||||
|
||||
public int find(int n) {
|
||||
return n == father[n] ? n : (father[n] = find(father[n]));
|
||||
}
|
||||
|
||||
public void join (int n, int m) {
|
||||
n = find(n);
|
||||
m = find(m);
|
||||
if (n == m) return;
|
||||
father[m] = n;
|
||||
}
|
||||
|
||||
public boolean isSame(int n, int m){
|
||||
n = find(n);
|
||||
m = find(m);
|
||||
return n == m;
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
@ -249,6 +249,29 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
```
|
||||
// 解法3
|
||||
class Solution {
|
||||
public int canCompleteCircuit(int[] gas, int[] cost) {
|
||||
int tank = 0; // 当前油量
|
||||
int totalGas = 0; // 总加油量
|
||||
int totalCost = 0; // 总油耗
|
||||
int start = 0; // 起点
|
||||
for (int i = 0; i < gas.length; i++) {
|
||||
totalGas += gas[i];
|
||||
totalCost += cost[i];
|
||||
|
||||
tank += gas[i] - cost[i];
|
||||
if (tank < 0) { // tank 变为负数 意味着 从0到i之间出发都不能顺利环路一周,因为在此i点必会没油
|
||||
tank = 0; // reset tank,类似于题目53.最大子树和reset sum
|
||||
start = i + 1; // 起点变为i点往后一位
|
||||
}
|
||||
}
|
||||
if (totalCost > totalGas) return -1;
|
||||
return start;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Python
|
||||
暴力法
|
||||
|
||||
@ -474,6 +474,7 @@ class Solution:
|
||||
words = s.split() #type(words) --- list
|
||||
words = words[::-1] # 反转单词
|
||||
return ' '.join(words) #列表转换成字符串
|
||||
```
|
||||
|
||||
### Go:
|
||||
|
||||
|
||||
@ -128,6 +128,36 @@ class Solution {
|
||||
|
||||
}
|
||||
}
|
||||
|
||||
// 版本二:排序数组并贪心地尽可能将负数翻转为正数,再根据剩余的k值调整最小元素的符号,从而最大化数组的总和。
|
||||
class Solution {
|
||||
public int largestSumAfterKNegations(int[] nums, int k) {
|
||||
if (nums.length == 1) return nums[0];
|
||||
|
||||
// 排序:先把负数处理了
|
||||
Arrays.sort(nums);
|
||||
|
||||
for (int i = 0; i < nums.length && k > 0; i++) { // 贪心点, 通过负转正, 消耗尽可能多的k
|
||||
if (nums[i] < 0) {
|
||||
nums[i] = -nums[i];
|
||||
k--;
|
||||
}
|
||||
}
|
||||
|
||||
// 退出循环, k > 0 || k < 0 (k消耗完了不用讨论)
|
||||
if (k % 2 == 1) { // k > 0 && k is odd:对于负数:负-正-负-正
|
||||
Arrays.sort(nums); // 再次排序得到剩余的负数,或者最小的正数
|
||||
nums[0] = -nums[0];
|
||||
}
|
||||
// k > 0 && k is even,flip数字不会产生影响: 对于负数: 负-正-负;对于正数:正-负-正
|
||||
|
||||
int sum = 0;
|
||||
for (int num : nums) { // 计算最大和
|
||||
sum += num;
|
||||
}
|
||||
return sum;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
@ -38,7 +38,7 @@
|
||||
5 6 2
|
||||
5 7 1
|
||||
6 7 1
|
||||
```
|
||||
```
|
||||
|
||||
输出示例:
|
||||
|
||||
@ -79,7 +79,7 @@ kruscal的思路:
|
||||
|
||||
|
||||
|
||||
--------
|
||||
--------
|
||||
|
||||
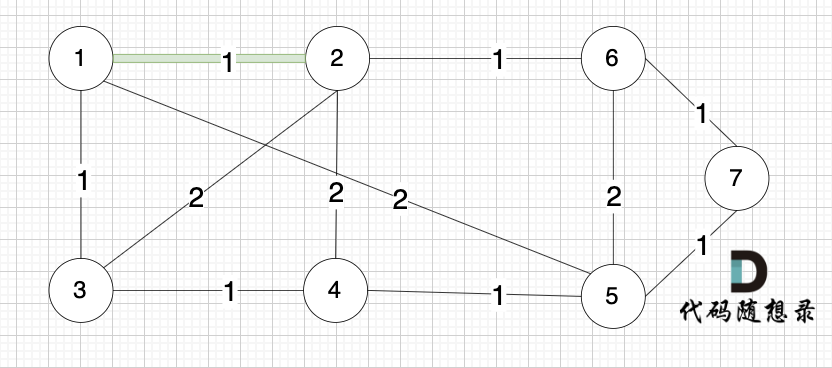
选边(4,5),节点4 和 节点 5 不在同一个集合,生成树可以添加边(4,5) ,并将节点4,节点5 放到同一个集合。
|
||||
|
||||
@ -87,7 +87,7 @@ kruscal的思路:
|
||||
|
||||
**大家判断两个节点是否在同一个集合,就看图中两个节点是否有绿色的粗线连着就行**
|
||||
|
||||
------
|
||||
------
|
||||
|
||||
(这里在强调一下,以下选边是按照上面排序好的边的数组来选择的)
|
||||
|
||||
@ -95,13 +95,13 @@ kruscal的思路:
|
||||
|
||||
|
||||
|
||||
---------
|
||||
---------
|
||||
|
||||
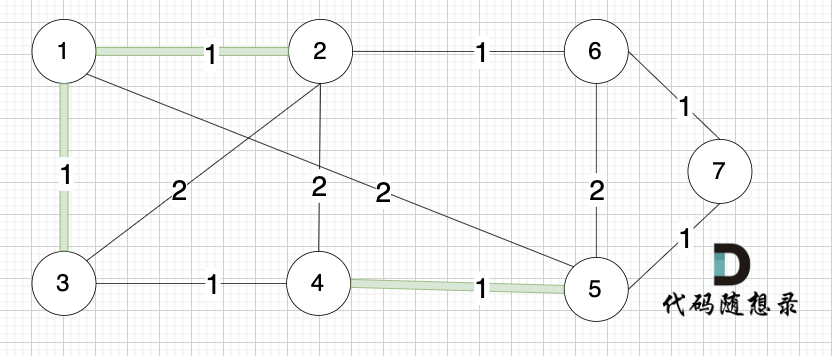
选边(2,6),节点2 和 节点6 不在同一个集合,生成树添加边(2,6),并将节点2,节点6 放到同一个集合。
|
||||
|
||||
|
||||
|
||||
--------
|
||||
--------
|
||||
|
||||
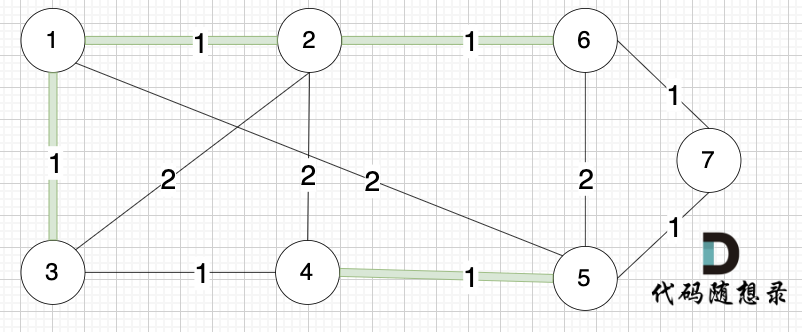
选边(3,4),节点3 和 节点4 不在同一个集合,生成树添加边(3,4),并将节点3,节点4 放到同一个集合。
|
||||
|
||||
@ -113,7 +113,7 @@ kruscal的思路:
|
||||
|
||||
|
||||
|
||||
-----------
|
||||
-----------
|
||||
|
||||
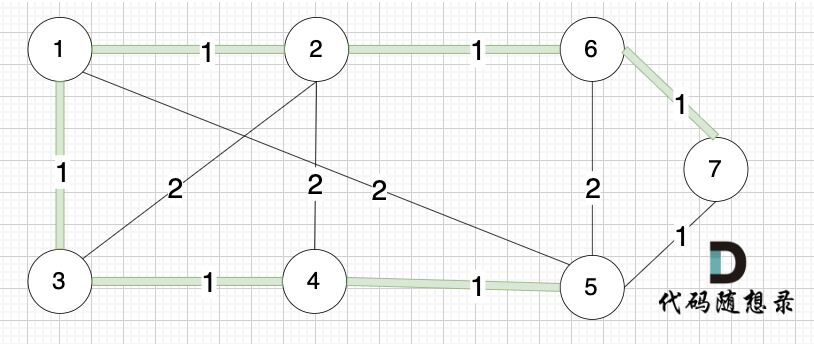
选边(5,7),节点5 和 节点7 在同一个集合,不做计算。
|
||||
|
||||
@ -122,7 +122,7 @@ kruscal的思路:
|
||||
后面遍历 边(3,2),(2,4),(5,6) 同理,都因两个节点已经在同一集合,不做计算。
|
||||
|
||||
|
||||
-------
|
||||
-------
|
||||
|
||||
此时 我们就已经生成了一个最小生成树,即:
|
||||
|
||||
@ -230,7 +230,7 @@ int main() {
|
||||
|
||||
如果题目要求将最小生成树的边输出的话,应该怎么办呢?
|
||||
|
||||
Kruskal 算法 输出边的话,相对prim 要容易很多,因为 Kruskal 本来就是直接操作边,边的结构自然清晰,不用像 prim一样 需要再节点练成线输出边 (因为prim是对节点操作,而 Kruskal是对边操作,这是本质区别)
|
||||
Kruskal 算法 输出边的话,相对prim 要容易很多,因为 Kruskal 本来就是直接操作边,边的结构自然清晰,不用像 prim一样 需要再将节点连成线输出边 (因为prim是对节点操作,而 Kruskal是对边操作,这是本质区别)
|
||||
|
||||
本题中,边的结构为:
|
||||
|
||||
|
||||
@ -605,6 +605,125 @@ if __name__ == "__main__":
|
||||
```
|
||||
### Go
|
||||
|
||||
#### 邻接矩阵写法
|
||||
```go
|
||||
package main
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
)
|
||||
|
||||
var result [][]int // 收集符合条件的路径
|
||||
var path []int // 1节点到终点的路径
|
||||
|
||||
func dfs(graph [][]int, x, n int) {
|
||||
// 当前遍历的节点x 到达节点n
|
||||
if x == n { // 找到符合条件的一条路径
|
||||
temp := make([]int, len(path))
|
||||
copy(temp, path)
|
||||
result = append(result, temp)
|
||||
return
|
||||
}
|
||||
for i := 1; i <= n; i++ { // 遍历节点x链接的所有节点
|
||||
if graph[x][i] == 1 { // 找到 x链接的节点
|
||||
path = append(path, i) // 遍历到的节点加入到路径中来
|
||||
dfs(graph, i, n) // 进入下一层递归
|
||||
path = path[:len(path)-1] // 回溯,撤销本节点
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
func main() {
|
||||
var n, m int
|
||||
fmt.Scanf("%d %d", &n, &m)
|
||||
|
||||
// 节点编号从1到n,所以申请 n+1 这么大的数组
|
||||
graph := make([][]int, n+1)
|
||||
for i := range graph {
|
||||
graph[i] = make([]int, n+1)
|
||||
}
|
||||
|
||||
for i := 0; i < m; i++ {
|
||||
var s, t int
|
||||
fmt.Scanf("%d %d", &s, &t)
|
||||
// 使用邻接矩阵表示无向图,1 表示 s 与 t 是相连的
|
||||
graph[s][t] = 1
|
||||
}
|
||||
|
||||
path = append(path, 1) // 无论什么路径已经是从1节点出发
|
||||
dfs(graph, 1, n) // 开始遍历
|
||||
|
||||
// 输出结果
|
||||
if len(result) == 0 {
|
||||
fmt.Println(-1)
|
||||
} else {
|
||||
for _, pa := range result {
|
||||
for i := 0; i < len(pa)-1; i++ {
|
||||
fmt.Print(pa[i], " ")
|
||||
}
|
||||
fmt.Println(pa[len(pa)-1])
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
#### 邻接表写法
|
||||
```go
|
||||
package main
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
)
|
||||
|
||||
var result [][]int
|
||||
var path []int
|
||||
|
||||
func dfs(graph [][]int, x, n int) {
|
||||
if x == n {
|
||||
temp := make([]int, len(path))
|
||||
copy(temp, path)
|
||||
result = append(result, temp)
|
||||
return
|
||||
}
|
||||
for _, i := range graph[x] {
|
||||
path = append(path, i)
|
||||
dfs(graph, i, n)
|
||||
path = path[:len(path)-1]
|
||||
}
|
||||
}
|
||||
|
||||
func main() {
|
||||
var n, m int
|
||||
fmt.Scanf("%d %d", &n, &m)
|
||||
|
||||
graph := make([][]int, n+1)
|
||||
for i := 0; i <= n; i++ {
|
||||
graph[i] = make([]int, 0)
|
||||
}
|
||||
|
||||
for m > 0 {
|
||||
var s, t int
|
||||
fmt.Scanf("%d %d", &s, &t)
|
||||
graph[s] = append(graph[s], t)
|
||||
m--
|
||||
}
|
||||
|
||||
path = append(path, 1)
|
||||
dfs(graph, 1, n)
|
||||
|
||||
if len(result) == 0 {
|
||||
fmt.Println(-1)
|
||||
} else {
|
||||
for _, pa := range result {
|
||||
for i := 0; i < len(pa)-1; i++ {
|
||||
fmt.Print(pa[i], " ")
|
||||
}
|
||||
fmt.Println(pa[len(pa)-1])
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
@ -322,6 +322,72 @@ print(result)
|
||||
|
||||
### Go
|
||||
|
||||
``` go
|
||||
|
||||
package main
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
)
|
||||
|
||||
var count int
|
||||
var dir = [][]int{{0, 1}, {1, 0}, {-1, 0}, {0, -1}} // 四个方向
|
||||
|
||||
func dfs(grid [][]int, visited [][]bool, x, y int) {
|
||||
for i := 0; i < 4; i++ {
|
||||
nextx := x + dir[i][0]
|
||||
nexty := y + dir[i][1]
|
||||
if nextx < 0 || nextx >= len(grid) || nexty < 0 || nexty >= len(grid[0]) {
|
||||
continue // 越界了,直接跳过
|
||||
}
|
||||
if !visited[nextx][nexty] && grid[nextx][nexty] == 1 { // 没有访问过的 同时 是陆地的
|
||||
visited[nextx][nexty] = true
|
||||
count++
|
||||
dfs(grid, visited, nextx, nexty)
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
func main() {
|
||||
var n, m int
|
||||
fmt.Scan(&n, &m)
|
||||
|
||||
grid := make([][]int, n)
|
||||
for i := 0; i < n; i++ {
|
||||
grid[i] = make([]int, m)
|
||||
for j := 0; j < m; j++ {
|
||||
fmt.Scan(&grid[i][j])
|
||||
}
|
||||
}
|
||||
|
||||
visited := make([][]bool, n)
|
||||
for i := 0; i < n; i++ {
|
||||
visited[i] = make([]bool, m)
|
||||
}
|
||||
|
||||
result := 0
|
||||
for i := 0; i < n; i++ {
|
||||
for j := 0; j < m; j++ {
|
||||
if !visited[i][j] && grid[i][j] == 1 {
|
||||
count = 1 // 因为dfs处理下一个节点,所以这里遇到陆地了就先计数,dfs处理接下来的相邻陆地
|
||||
visited[i][j] = true
|
||||
dfs(grid, visited, i, j)
|
||||
if count > result {
|
||||
result = count
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
fmt.Println(result)
|
||||
}
|
||||
|
||||
|
||||
|
||||
```
|
||||
|
||||
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
@ -420,6 +486,65 @@ const bfs = (graph, visited, x, y) => {
|
||||
|
||||
### PhP
|
||||
|
||||
``` php
|
||||
|
||||
<?php
|
||||
|
||||
function dfs(&$grid, &$visited, $x, $y, &$count, &$dir) {
|
||||
for ($i = 0; $i < 4; $i++) {
|
||||
$nextx = $x + $dir[$i][0];
|
||||
$nexty = $y + $dir[$i][1];
|
||||
if ($nextx < 0 || $nextx >= count($grid) || $nexty < 0 || $nexty >= count($grid[0])) continue; // 越界了,直接跳过
|
||||
if (!$visited[$nextx][$nexty] && $grid[$nextx][$nexty] == 1) { // 没有访问过的 同时 是陆地的
|
||||
$visited[$nextx][$nexty] = true;
|
||||
$count++;
|
||||
dfs($grid, $visited, $nextx, $nexty, $count, $dir);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// Main function
|
||||
function main() {
|
||||
$input = trim(fgets(STDIN));
|
||||
list($n, $m) = explode(' ', $input);
|
||||
|
||||
$grid = [];
|
||||
for ($i = 0; $i < $n; $i++) {
|
||||
$input = trim(fgets(STDIN));
|
||||
$grid[] = array_map('intval', explode(' ', $input));
|
||||
}
|
||||
|
||||
$visited = [];
|
||||
for ($i = 0; $i < $n; $i++) {
|
||||
$visited[] = array_fill(0, $m, false);
|
||||
}
|
||||
|
||||
$result = 0;
|
||||
$count = 0;
|
||||
$dir = [[0, 1], [1, 0], [-1, 0], [0, -1]]; // 四个方向
|
||||
|
||||
for ($i = 0; $i < $n; $i++) {
|
||||
for ($j = 0; $j < $m; $j++) {
|
||||
if (!$visited[$i][$j] && $grid[$i][$j] == 1) {
|
||||
$count = 1; // 因为dfs处理下一个节点,所以这里遇到陆地了就先计数,dfs处理接下来的相邻陆地
|
||||
$visited[$i][$j] = true;
|
||||
dfs($grid, $visited, $i, $j, $count, $dir); // 将与其链接的陆地都标记上 true
|
||||
$result = max($result, $count);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
echo $result . "\n";
|
||||
}
|
||||
|
||||
main();
|
||||
|
||||
?>
|
||||
|
||||
|
||||
```
|
||||
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
@ -185,6 +185,77 @@ int main() {
|
||||
|
||||
### Java
|
||||
|
||||
``` java
|
||||
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
private static int count = 0;
|
||||
private static final int[][] dir = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}}; // 四个方向
|
||||
|
||||
private static void bfs(int[][] grid, int x, int y) {
|
||||
Queue<int[]> que = new LinkedList<>();
|
||||
que.add(new int[]{x, y});
|
||||
grid[x][y] = 0; // 只要加入队列,立刻标记
|
||||
count++;
|
||||
while (!que.isEmpty()) {
|
||||
int[] cur = que.poll();
|
||||
int curx = cur[0];
|
||||
int cury = cur[1];
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = curx + dir[i][0];
|
||||
int nexty = cury + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length) continue; // 越界了,直接跳过
|
||||
if (grid[nextx][nexty] == 1) {
|
||||
que.add(new int[]{nextx, nexty});
|
||||
count++;
|
||||
grid[nextx][nexty] = 0; // 只要加入队列立刻标记
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int m = scanner.nextInt();
|
||||
int[][] grid = new int[n][m];
|
||||
|
||||
// 读取网格
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
grid[i][j] = scanner.nextInt();
|
||||
}
|
||||
}
|
||||
|
||||
// 从左侧边,和右侧边向中间遍历
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (grid[i][0] == 1) bfs(grid, i, 0);
|
||||
if (grid[i][m - 1] == 1) bfs(grid, i, m - 1);
|
||||
}
|
||||
|
||||
// 从上边和下边向中间遍历
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[0][j] == 1) bfs(grid, 0, j);
|
||||
if (grid[n - 1][j] == 1) bfs(grid, n - 1, j);
|
||||
}
|
||||
|
||||
count = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == 1) bfs(grid, i, j);
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println(count);
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
|
||||
```
|
||||
|
||||
|
||||
### Python
|
||||
```python
|
||||
from collections import deque
|
||||
@ -238,6 +309,97 @@ print(count)
|
||||
```
|
||||
### Go
|
||||
|
||||
``` go
|
||||
|
||||
package main
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
)
|
||||
|
||||
var count int
|
||||
var dir = [4][2]int{{0, 1}, {1, 0}, {-1, 0}, {0, -1}} // 四个方向
|
||||
|
||||
func bfs(grid [][]int, x, y int) {
|
||||
queue := [][2]int{{x, y}}
|
||||
grid[x][y] = 0 // 只要加入队列,立刻标记
|
||||
count++
|
||||
|
||||
for len(queue) > 0 {
|
||||
cur := queue[0]
|
||||
queue = queue[1:]
|
||||
curx, cury := cur[0], cur[1]
|
||||
|
||||
for i := 0; i < 4; i++ {
|
||||
nextx := curx + dir[i][0]
|
||||
nexty := cury + dir[i][1]
|
||||
|
||||
if nextx < 0 || nextx >= len(grid) || nexty < 0 || nexty >= len(grid[0]) {
|
||||
continue // 越界了,直接跳过
|
||||
}
|
||||
|
||||
if grid[nextx][nexty] == 1 {
|
||||
queue = append(queue, [2]int{nextx, nexty})
|
||||
count++
|
||||
grid[nextx][nexty] = 0 // 只要加入队列立刻标记
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
func main() {
|
||||
var n, m int
|
||||
fmt.Scan(&n, &m)
|
||||
|
||||
grid := make([][]int, n)
|
||||
for i := range grid {
|
||||
grid[i] = make([]int, m)
|
||||
}
|
||||
|
||||
for i := 0; i < n; i++ {
|
||||
for j := 0; j < m; j++ {
|
||||
fmt.Scan(&grid[i][j])
|
||||
}
|
||||
}
|
||||
|
||||
// 从左侧边,和右侧边向中间遍历
|
||||
for i := 0; i < n; i++ {
|
||||
if grid[i][0] == 1 {
|
||||
bfs(grid, i, 0)
|
||||
}
|
||||
if grid[i][m-1] == 1 {
|
||||
bfs(grid, i, m-1)
|
||||
}
|
||||
}
|
||||
|
||||
// 从上边和下边向中间遍历
|
||||
for j := 0; j < m; j++ {
|
||||
if grid[0][j] == 1 {
|
||||
bfs(grid, 0, j)
|
||||
}
|
||||
if grid[n-1][j] == 1 {
|
||||
bfs(grid, n-1, j)
|
||||
}
|
||||
}
|
||||
|
||||
// 清空之前的计数
|
||||
count = 0
|
||||
|
||||
// 遍历所有位置
|
||||
for i := 0; i < n; i++ {
|
||||
for j := 0; j < m; j++ {
|
||||
if grid[i][j] == 1 {
|
||||
bfs(grid, i, j)
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
fmt.Println(count)
|
||||
}
|
||||
|
||||
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
@ -362,6 +362,350 @@ public class Main {
|
||||
|
||||
### Javascript
|
||||
|
||||
#### 深搜
|
||||
|
||||
```javascript
|
||||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||||
// 创建readline接口
|
||||
let iter = r1[Symbol.asyncIterator]();
|
||||
// 创建异步迭代器
|
||||
const readline = async () => (await iter.next()).value;
|
||||
|
||||
let graph // 地图
|
||||
let N, M // 地图大小
|
||||
const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
|
||||
|
||||
|
||||
// 读取输入,初始化地图
|
||||
const initGraph = async () => {
|
||||
let line = await readline();
|
||||
[N, M] = line.split(' ').map(Number);
|
||||
graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
|
||||
|
||||
for (let i = 0; i < N; i++) {
|
||||
line = await readline()
|
||||
line = line.split(' ').map(Number)
|
||||
for (let j = 0; j < M; j++) {
|
||||
graph[i][j] = line[j]
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/**
|
||||
* @description: 从(x,y)开始深度优先遍历地图
|
||||
* @param {*} graph 地图
|
||||
* @param {*} visited 可访问节点
|
||||
* @param {*} x 开始搜索节点的下标
|
||||
* @param {*} y 开始搜索节点的下标
|
||||
* @return {*}
|
||||
*/
|
||||
const dfs = (graph, visited, x, y) => {
|
||||
if (visited[x][y]) return
|
||||
visited[x][y] = true // 标记为可访问
|
||||
|
||||
for (let i = 0; i < 4; i++) {
|
||||
let nextx = x + dir[i][0]
|
||||
let nexty = y + dir[i][1]
|
||||
if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界,跳过
|
||||
if (graph[x][y] < graph[nextx][nexty]) continue //不能流过.跳过
|
||||
dfs(graph, visited, nextx, nexty)
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/**
|
||||
* @description: 判断地图上的(x, y)是否可以到达第一组边界和第二组边界
|
||||
* @param {*} x 坐标
|
||||
* @param {*} y 坐标
|
||||
* @return {*} true可以到达,false不可以到达
|
||||
*/
|
||||
const isResult = (x, y) => {
|
||||
let visited = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||||
|
||||
let isFirst = false //是否可到达第一边界
|
||||
let isSecond = false //是否可到达第二边界
|
||||
|
||||
// 深搜,将(x, y)可到达的所有节点做标记
|
||||
dfs(graph, visited, x, y)
|
||||
|
||||
// 判断能否到第一边界左边
|
||||
for (let i = 0; i < N; i++) {
|
||||
if (visited[i][0]) {
|
||||
isFirst = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
// 判断能否到第一边界上边
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (visited[0][j]) {
|
||||
isFirst = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
// 判断能否到第二边界右边
|
||||
for (let i = 0; i < N; i++) {
|
||||
if (visited[i][M - 1]) {
|
||||
isSecond = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
// 判断能否到第二边界下边
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (visited[N - 1][j]) {
|
||||
isSecond = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
return isFirst && isSecond
|
||||
}
|
||||
|
||||
(async function () {
|
||||
|
||||
// 读取输入,初始化地图
|
||||
await initGraph()
|
||||
|
||||
// 遍历地图,判断是否能到达第一组边界和第二组边界
|
||||
for (let i = 0; i < N; i++) {
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (isResult(i, j)) console.log(i + ' ' + j);
|
||||
}
|
||||
}
|
||||
})()
|
||||
```
|
||||
|
||||
|
||||
|
||||
#### 广搜-解法一
|
||||
|
||||
```java
|
||||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||||
// 创建readline接口
|
||||
let iter = r1[Symbol.asyncIterator]();
|
||||
// 创建异步迭代器
|
||||
const readline = async () => (await iter.next()).value;
|
||||
|
||||
let graph // 地图
|
||||
let N, M // 地图大小
|
||||
const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
|
||||
|
||||
|
||||
// 读取输入,初始化地图
|
||||
const initGraph = async () => {
|
||||
let line = await readline();
|
||||
[N, M] = line.split(' ').map(Number);
|
||||
graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
|
||||
|
||||
for (let i = 0; i < N; i++) {
|
||||
line = await readline()
|
||||
line = line.split(' ').map(Number)
|
||||
for (let j = 0; j < M; j++) {
|
||||
graph[i][j] = line[j]
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/**
|
||||
* @description: 从(x,y)开始广度优先遍历地图
|
||||
* @param {*} graph 地图
|
||||
* @param {*} visited 可访问节点
|
||||
* @param {*} x 开始搜索节点的下标
|
||||
* @param {*} y 开始搜索节点的下标
|
||||
* @return {*}
|
||||
*/
|
||||
const bfs = (graph, visited, x, y) => {
|
||||
let queue = []
|
||||
queue.push([x, y])
|
||||
visited[x][y] = true
|
||||
|
||||
while (queue.length) {
|
||||
const [xx, yy] = queue.shift()
|
||||
for (let i = 0; i < 4; i++) {
|
||||
let nextx = xx + dir[i][0]
|
||||
let nexty = yy + dir[i][1]
|
||||
if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界, 跳过
|
||||
|
||||
// 可访问或者不能流过, 跳过 (注意这里是graph[xx][yy] < graph[nextx][nexty], 不是graph[x][y] < graph[nextx][nexty])
|
||||
if (visited[nextx][nexty] || graph[xx][yy] < graph[nextx][nexty]) continue
|
||||
|
||||
queue.push([nextx, nexty])
|
||||
visited[nextx][nexty] = true
|
||||
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/**
|
||||
* @description: 判断地图上的(x, y)是否可以到达第一组边界和第二组边界
|
||||
* @param {*} x 坐标
|
||||
* @param {*} y 坐标
|
||||
* @return {*} true可以到达,false不可以到达
|
||||
*/
|
||||
const isResult = (x, y) => {
|
||||
let visited = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||||
|
||||
let isFirst = false //是否可到达第一边界
|
||||
let isSecond = false //是否可到达第二边界
|
||||
|
||||
// 深搜,将(x, y)可到达的所有节点做标记
|
||||
bfs(graph, visited, x, y)
|
||||
|
||||
// console.log(visited);
|
||||
|
||||
// 判断能否到第一边界左边
|
||||
for (let i = 0; i < N; i++) {
|
||||
if (visited[i][0]) {
|
||||
isFirst = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
// 判断能否到第一边界上边
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (visited[0][j]) {
|
||||
isFirst = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
// 判断能否到第二边界右边
|
||||
for (let i = 0; i < N; i++) {
|
||||
if (visited[i][M - 1]) {
|
||||
isSecond = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
// 判断能否到第二边界下边
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (visited[N - 1][j]) {
|
||||
isSecond = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
return isFirst && isSecond
|
||||
}
|
||||
|
||||
(async function () {
|
||||
|
||||
// 读取输入,初始化地图
|
||||
await initGraph()
|
||||
|
||||
// 遍历地图,判断是否能到达第一组边界和第二组边界
|
||||
for (let i = 0; i < N; i++) {
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (isResult(i, j)) console.log(i + ' ' + j);
|
||||
}
|
||||
}
|
||||
})()
|
||||
```
|
||||
|
||||
|
||||
|
||||
#### 广搜-解法二
|
||||
|
||||
从第一边界和第二边界开始向高处流, 标记可以流到的位置, 两个边界都能到达的位置就是所求结果
|
||||
|
||||
```javascript
|
||||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||||
// 创建readline接口
|
||||
let iter = r1[Symbol.asyncIterator]();
|
||||
// 创建异步迭代器
|
||||
const readline = async () => (await iter.next()).value;
|
||||
|
||||
let graph // 地图
|
||||
let N, M // 地图大小
|
||||
const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
|
||||
|
||||
|
||||
// 读取输入,初始化地图
|
||||
const initGraph = async () => {
|
||||
let line = await readline();
|
||||
[N, M] = line.split(' ').map(Number);
|
||||
graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
|
||||
|
||||
for (let i = 0; i < N; i++) {
|
||||
line = await readline()
|
||||
line = line.split(' ').map(Number)
|
||||
for (let j = 0; j < M; j++) {
|
||||
graph[i][j] = line[j]
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/**
|
||||
* @description: 从(x,y)开始广度优先遍历地图
|
||||
* @param {*} graph 地图
|
||||
* @param {*} visited 可访问节点
|
||||
* @param {*} x 开始搜索节点的下标
|
||||
* @param {*} y 开始搜索节点的下标
|
||||
* @return {*}
|
||||
*/
|
||||
const bfs = (graph, visited, x, y) => {
|
||||
if(visited[x][y]) return
|
||||
|
||||
let queue = []
|
||||
queue.push([x, y])
|
||||
visited[x][y] = true
|
||||
|
||||
while (queue.length) {
|
||||
const [xx, yy] = queue.shift()
|
||||
for (let i = 0; i < 4; i++) {
|
||||
let nextx = xx + dir[i][0]
|
||||
let nexty = yy + dir[i][1]
|
||||
if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界, 跳过
|
||||
|
||||
// 可访问或者不能流过, 跳过 (注意因为是从边界往高处流, 所以这里是graph[xx][yy] >= graph[nextx][nexty], 还要注意不是graph[xx][yy] >= graph[nextx][nexty])
|
||||
if (visited[nextx][nexty] || graph[xx][yy] >= graph[nextx][nexty]) continue
|
||||
|
||||
queue.push([nextx, nexty])
|
||||
visited[nextx][nexty] = true
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
(async function () {
|
||||
|
||||
// 读取输入,初始化地图
|
||||
await initGraph()
|
||||
|
||||
// 记录第一边界可到达的节点
|
||||
let firstBorder = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||||
|
||||
// 记录第二边界可到达的节点
|
||||
let secondBorder = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||||
|
||||
// 第一边界左边和第二边界右边
|
||||
for (let i = 0; i < N; i++) {
|
||||
bfs(graph, firstBorder, i, 0)
|
||||
bfs(graph, secondBorder, i, M - 1)
|
||||
}
|
||||
|
||||
// 第一边界上边和第二边界下边
|
||||
for (let j = 0; j < M; j++) {
|
||||
bfs(graph, firstBorder, 0, j)
|
||||
bfs(graph, secondBorder, N - 1, j)
|
||||
}
|
||||
|
||||
// 遍历地图,判断是否能到达第一组边界和第二组边界
|
||||
for (let i = 0; i < N; i++) {
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (firstBorder[i][j] && secondBorder[i][j]) console.log(i + ' ' + j);
|
||||
}
|
||||
}
|
||||
})()
|
||||
```
|
||||
|
||||
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
@ -78,7 +78,7 @@
|
||||
|
||||
|
||||
|
||||
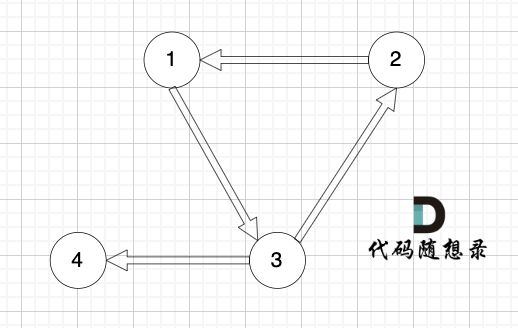
对于情况二,删掉构成环的边就可以了。
|
||||
对于情况三,删掉构成环的边就可以了。
|
||||
|
||||
|
||||
## 写代码
|
||||
|
||||
@ -69,7 +69,7 @@ for (int i = 0; i < array.size(); i++) {
|
||||
|
||||
其实使用双指针也可以解决1.两数之和的问题,只不过1.两数之和求的是两个元素的下标,没法用双指针,如果改成求具体两个元素的数值就可以了,大家可以尝试用双指针做一个leetcode上两数之和的题目,就可以体会到我说的意思了。
|
||||
|
||||
使用了哈希法解决了两数之和,但是哈希法并不使用于三数之和!
|
||||
使用了哈希法解决了两数之和,但是哈希法并不适用于三数之和!
|
||||
|
||||
使用哈希法的过程中要把符合条件的三元组放进vector中,然后在去去重,这样是非常费时的,很容易超时,也是三数之和通过率如此之低的根源所在。
|
||||
|
||||
|
||||
Reference in New Issue
Block a user