LeetCode-Go/website/content/ChapterThree/Segment_Tree.md

title	type	weight
3.1 Segment Tree	docs	1

线段树 Segment Tree

线段树 Segment tree 是一种二叉树形数据结构，1977年由Jon Louis Bentley发明，用以存储区间或线段，并且允许快速查询结构内包含某一点的所有区间。

一个包含 {{< katex >}}n {{< /katex >}}个区间的线段树，空间复杂度为 {{< katex >}}O(n) {{< /katex >}}，查询的时间复杂度则为{{< katex >}}O(log n+k) {{< /katex >}}，其中 {{< katex >}} k {{< /katex >}} 是符合条件的区间数量。线段树的数据结构也可推广到高维度。

一. 什么是线段树

以一维的线段树为例。

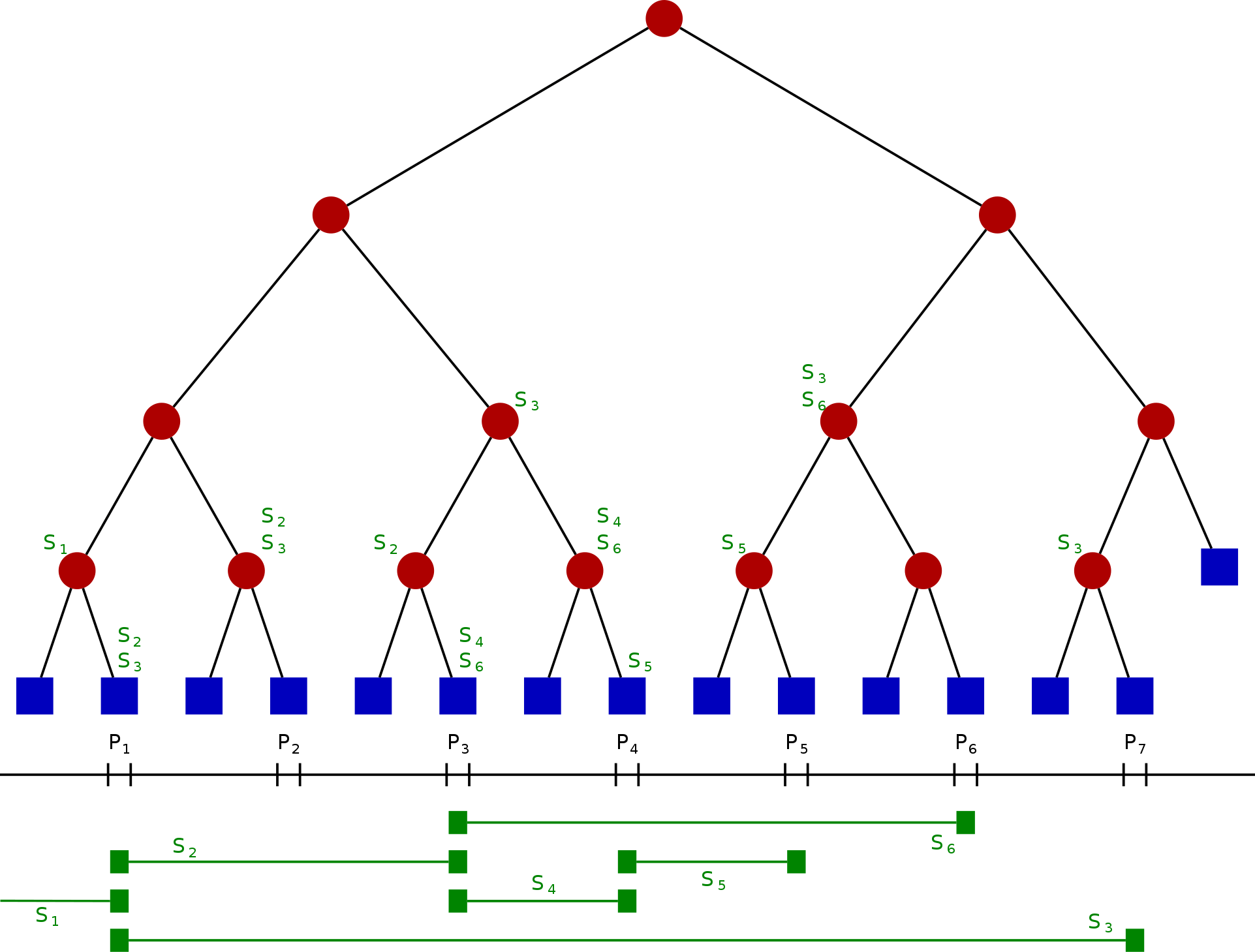
令 S 是一维线段的集合。将这些线段的端点坐标由小到大排序，令其为{{< katex >}}x_{1},x_{2},\cdots ,x_{m} {{< /katex >}}。我们将被这些端点切分的每一个区间称为“单位区间”（每个端点所在的位置会单独成为一个单位区间），从左到右包含：

{{< katex >}} (-\infty ,x_{1}),[x_{1},x_{1}],(x_{1},x_{2}),[x_{2},x_{2}],...,(x_{m-1},x_{m}),[x_{m},x_{m}],(x_{m},+\infty ){{< /katex >}}

线段树的结构为一个二叉树，每个节点都代表一个坐标区间，节点 N 所代表的区间记为 Int(N)，则其需符合以下条件：

• 其每一个叶节点，从左到右代表每个单位区间。
• 其内部节点代表的区间是其两个儿子代表的区间之联集。
• 每个节点（包含叶子）中有一个存储线段的数据结构。若一个线段 S 的坐标区间包含 Int(N) 但不包含 Int(parent(N))，则节点 N 中会存储线段 S。

二. 为什么需要这种数据结构

三. 构造线段树

四. 线段树的查询

五. 线段树的更新

1. 直接更新

2. 懒更新

package template

// SegmentTree define
type SegmentTree struct {
	data, tree, lazy []int
	left, right      int
	merge            func(i, j int) int
}

// Init define
func (st *SegmentTree) Init(nums []int, oper func(i, j int) int) {
	st.merge = oper
	data, tree, lazy := make([]int, len(nums)), make([]int, 4*len(nums)), make([]int, 4*len(nums))
	for i := 0; i < len(nums); i++ {
		data[i] = nums[i]
	}
	st.data, st.tree, st.lazy = data, tree, lazy
	if len(nums) > 0 {
		st.buildSegmentTree(0, 0, len(nums)-1)
	}
}

// 在 treeIndex 的位置创建 [left....right] 区间的线段树
func (st *SegmentTree) buildSegmentTree(treeIndex, left, right int) {
	if left == right {
		st.tree[treeIndex] = st.data[left]
		return
	}
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	st.buildSegmentTree(leftTreeIndex, left, midTreeIndex)
	st.buildSegmentTree(rightTreeIndex, midTreeIndex+1, right)
	st.tree[treeIndex] = st.merge(st.tree[leftTreeIndex], st.tree[rightTreeIndex])
}

func (st *SegmentTree) leftChild(index int) int {
	return 2*index + 1
}

func (st *SegmentTree) rightChild(index int) int {
	return 2*index + 2
}

// 查询 [left....right] 区间内的值

// Query define
func (st *SegmentTree) Query(left, right int) int {
	if len(st.data) > 0 {
		return st.queryInTree(0, 0, len(st.data)-1, left, right)
	}
	return 0
}

// 在以 treeIndex 为根的线段树中 [left...right] 的范围里，搜索区间 [queryLeft...queryRight] 的值
func (st *SegmentTree) queryInTree(treeIndex, left, right, queryLeft, queryRight int) int {
	if left == queryLeft && right == queryRight {
		return st.tree[treeIndex]
	}
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	if queryLeft > midTreeIndex {
		return st.queryInTree(rightTreeIndex, midTreeIndex+1, right, queryLeft, queryRight)
	} else if queryRight <= midTreeIndex {
		return st.queryInTree(leftTreeIndex, left, midTreeIndex, queryLeft, queryRight)
	}
	return st.merge(st.queryInTree(leftTreeIndex, left, midTreeIndex, queryLeft, midTreeIndex),
		st.queryInTree(rightTreeIndex, midTreeIndex+1, right, midTreeIndex+1, queryRight))
}

// 查询 [left....right] 区间内的值

// QueryLazy define
func (st *SegmentTree) QueryLazy(left, right int) int {
	if len(st.data) > 0 {
		return st.queryLazyInTree(0, 0, len(st.data)-1, left, right)
	}
	return 0
}

func (st *SegmentTree) queryLazyInTree(treeIndex, left, right, queryLeft, queryRight int) int {
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	if left > queryRight || right < queryLeft { // segment completely outside range
		return 0 // represents a null node
	}
	if st.lazy[treeIndex] != 0 { // this node is lazy
		for i := 0; i < right-left+1; i++ {
			st.tree[treeIndex] = st.merge(st.tree[treeIndex], st.lazy[treeIndex])
			// st.tree[treeIndex] += (right - left + 1) * st.lazy[treeIndex] // normalize current node by removing lazinesss
		}
		if left != right { // update lazy[] for children nodes
			st.lazy[leftTreeIndex] = st.merge(st.lazy[leftTreeIndex], st.lazy[treeIndex])
			st.lazy[rightTreeIndex] = st.merge(st.lazy[rightTreeIndex], st.lazy[treeIndex])
			// st.lazy[leftTreeIndex] += st.lazy[treeIndex]
			// st.lazy[rightTreeIndex] += st.lazy[treeIndex]
		}
		st.lazy[treeIndex] = 0 // current node processed. No longer lazy
	}
	if queryLeft <= left && queryRight >= right { // segment completely inside range
		return st.tree[treeIndex]
	}
	if queryLeft > midTreeIndex {
		return st.queryLazyInTree(rightTreeIndex, midTreeIndex+1, right, queryLeft, queryRight)
	} else if queryRight <= midTreeIndex {
		return st.queryLazyInTree(leftTreeIndex, left, midTreeIndex, queryLeft, queryRight)
	}
	// merge query results
	return st.merge(st.queryLazyInTree(leftTreeIndex, left, midTreeIndex, queryLeft, midTreeIndex),
		st.queryLazyInTree(rightTreeIndex, midTreeIndex+1, right, midTreeIndex+1, queryRight))
}

// 更新 index 位置的值

// Update define
func (st *SegmentTree) Update(index, val int) {
	if len(st.data) > 0 {
		st.updateInTree(0, 0, len(st.data)-1, index, val)
	}
}

// 以 treeIndex 为根，更新 index 位置上的值为 val
func (st *SegmentTree) updateInTree(treeIndex, left, right, index, val int) {
	if left == right {
		st.tree[treeIndex] = val
		return
	}
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	if index > midTreeIndex {
		st.updateInTree(rightTreeIndex, midTreeIndex+1, right, index, val)
	} else {
		st.updateInTree(leftTreeIndex, left, midTreeIndex, index, val)
	}
	st.tree[treeIndex] = st.merge(st.tree[leftTreeIndex], st.tree[rightTreeIndex])
}

// 更新 [updateLeft....updateRight] 位置的值
// 注意这里的更新值是在原来值的基础上增加或者减少，而不是把这个区间内的值都赋值为 x，区间更新和单点更新不同
// 这里的区间更新关注的是变化，单点更新关注的是定值
// 当然区间更新也可以都更新成定值，如果只区间更新成定值，那么 lazy 更新策略需要变化，merge 策略也需要变化，这里暂不详细讨论

// UpdateLazy define
func (st *SegmentTree) UpdateLazy(updateLeft, updateRight, val int) {
	if len(st.data) > 0 {
		st.updateLazyInTree(0, 0, len(st.data)-1, updateLeft, updateRight, val)
	}
}

func (st *SegmentTree) updateLazyInTree(treeIndex, left, right, updateLeft, updateRight, val int) {
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	if st.lazy[treeIndex] != 0 { // this node is lazy
		for i := 0; i < right-left+1; i++ {
			st.tree[treeIndex] = st.merge(st.tree[treeIndex], st.lazy[treeIndex])
			//st.tree[treeIndex] += (right - left + 1) * st.lazy[treeIndex] // normalize current node by removing laziness
		}
		if left != right { // update lazy[] for children nodes
			st.lazy[leftTreeIndex] = st.merge(st.lazy[leftTreeIndex], st.lazy[treeIndex])
			st.lazy[rightTreeIndex] = st.merge(st.lazy[rightTreeIndex], st.lazy[treeIndex])
			// st.lazy[leftTreeIndex] += st.lazy[treeIndex]
			// st.lazy[rightTreeIndex] += st.lazy[treeIndex]
		}
		st.lazy[treeIndex] = 0 // current node processed. No longer lazy
	}

	if left > right || left > updateRight || right < updateLeft {
		return // out of range. escape.
	}

	if updateLeft <= left && right <= updateRight { // segment is fully within update range
		for i := 0; i < right-left+1; i++ {
			st.tree[treeIndex] = st.merge(st.tree[treeIndex], val)
			//st.tree[treeIndex] += (right - left + 1) * val // update segment
		}
		if left != right { // update lazy[] for children
			st.lazy[leftTreeIndex] = st.merge(st.lazy[leftTreeIndex], val)
			st.lazy[rightTreeIndex] = st.merge(st.lazy[rightTreeIndex], val)
			// st.lazy[leftTreeIndex] += val
			// st.lazy[rightTreeIndex] += val
		}
		return
	}
	st.updateLazyInTree(leftTreeIndex, left, midTreeIndex, updateLeft, updateRight, val)
	st.updateLazyInTree(rightTreeIndex, midTreeIndex+1, right, updateLeft, updateRight, val)
	// merge updates
	st.tree[treeIndex] = st.merge(st.tree[leftTreeIndex], st.tree[rightTreeIndex])
}

// SegmentCountTree define
type SegmentCountTree struct {
	data, tree  []int
	left, right int
	merge       func(i, j int) int
}

// Init define
func (st *SegmentCountTree) Init(nums []int, oper func(i, j int) int) {
	st.merge = oper

	data, tree := make([]int, len(nums)), make([]int, 4*len(nums))
	for i := 0; i < len(nums); i++ {
		data[i] = nums[i]
	}
	st.data, st.tree = data, tree
}

// 在 treeIndex 的位置创建 [left....right] 区间的线段树
func (st *SegmentCountTree) buildSegmentTree(treeIndex, left, right int) {
	if left == right {
		st.tree[treeIndex] = st.data[left]
		return
	}
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	st.buildSegmentTree(leftTreeIndex, left, midTreeIndex)
	st.buildSegmentTree(rightTreeIndex, midTreeIndex+1, right)
	st.tree[treeIndex] = st.merge(st.tree[leftTreeIndex], st.tree[rightTreeIndex])
}

func (st *SegmentCountTree) leftChild(index int) int {
	return 2*index + 1
}

func (st *SegmentCountTree) rightChild(index int) int {
	return 2*index + 2
}

// 查询 [left....right] 区间内的值

// Query define
func (st *SegmentCountTree) Query(left, right int) int {
	if len(st.data) > 0 {
		return st.queryInTree(0, 0, len(st.data)-1, left, right)
	}
	return 0
}

// 在以 treeIndex 为根的线段树中 [left...right] 的范围里，搜索区间 [queryLeft...queryRight] 的值，值是计数值
func (st *SegmentCountTree) queryInTree(treeIndex, left, right, queryLeft, queryRight int) int {
	if queryRight < st.data[left] || queryLeft > st.data[right] {
		return 0
	}
	if queryLeft <= st.data[left] && queryRight >= st.data[right] || left == right {
		return st.tree[treeIndex]
	}
	midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
	return st.queryInTree(rightTreeIndex, midTreeIndex+1, right, queryLeft, queryRight) +
		st.queryInTree(leftTreeIndex, left, midTreeIndex, queryLeft, queryRight)
}

// 更新计数

// UpdateCount define
func (st *SegmentCountTree) UpdateCount(val int) {
	if len(st.data) > 0 {
		st.updateCountInTree(0, 0, len(st.data)-1, val)
	}
}

// 以 treeIndex 为根，更新 [left...right] 区间内的计数
func (st *SegmentCountTree) updateCountInTree(treeIndex, left, right, val int) {
	if val >= st.data[left] && val <= st.data[right] {
		st.tree[treeIndex]++
		if left == right {
			return
		}
		midTreeIndex, leftTreeIndex, rightTreeIndex := left+(right-left)>>1, st.leftChild(treeIndex), st.rightChild(treeIndex)
		st.updateCountInTree(rightTreeIndex, midTreeIndex+1, right, val)
		st.updateCountInTree(leftTreeIndex, left, midTreeIndex, val)
	}
}

---

⬅️上一页

下一页➡️