Update Segment Tree

website/content/ChapterThree/Segment_Tree.md

@@ -6,6 +6,47 @@ weight: 1
 
 # 线段树 Segment Tree
 
+线段树 Segment tree 是一种二叉树形数据结构，1977年由Jon Louis Bentley发明，用以存储区间或线段，并且允许快速查询结构内包含某一点的所有区间。
+
+一个包含 {{< katex >}}n {{< /katex >}}个区间的线段树，空间复杂度为 {{< katex >}}O(n) {{< /katex >}}，查询的时间复杂度则为{{< katex >}}O(log n+k) {{< /katex >}}，其中 {{< katex >}} k {{< /katex >}} 是符合条件的区间数量。线段树的数据结构也可推广到高维度。
+
+## 一. 什么是线段树
+
+以一维的线段树为例。
+
+![](https://img.halfrost.com/Blog/ArticleImage/153_1.png)
+
+
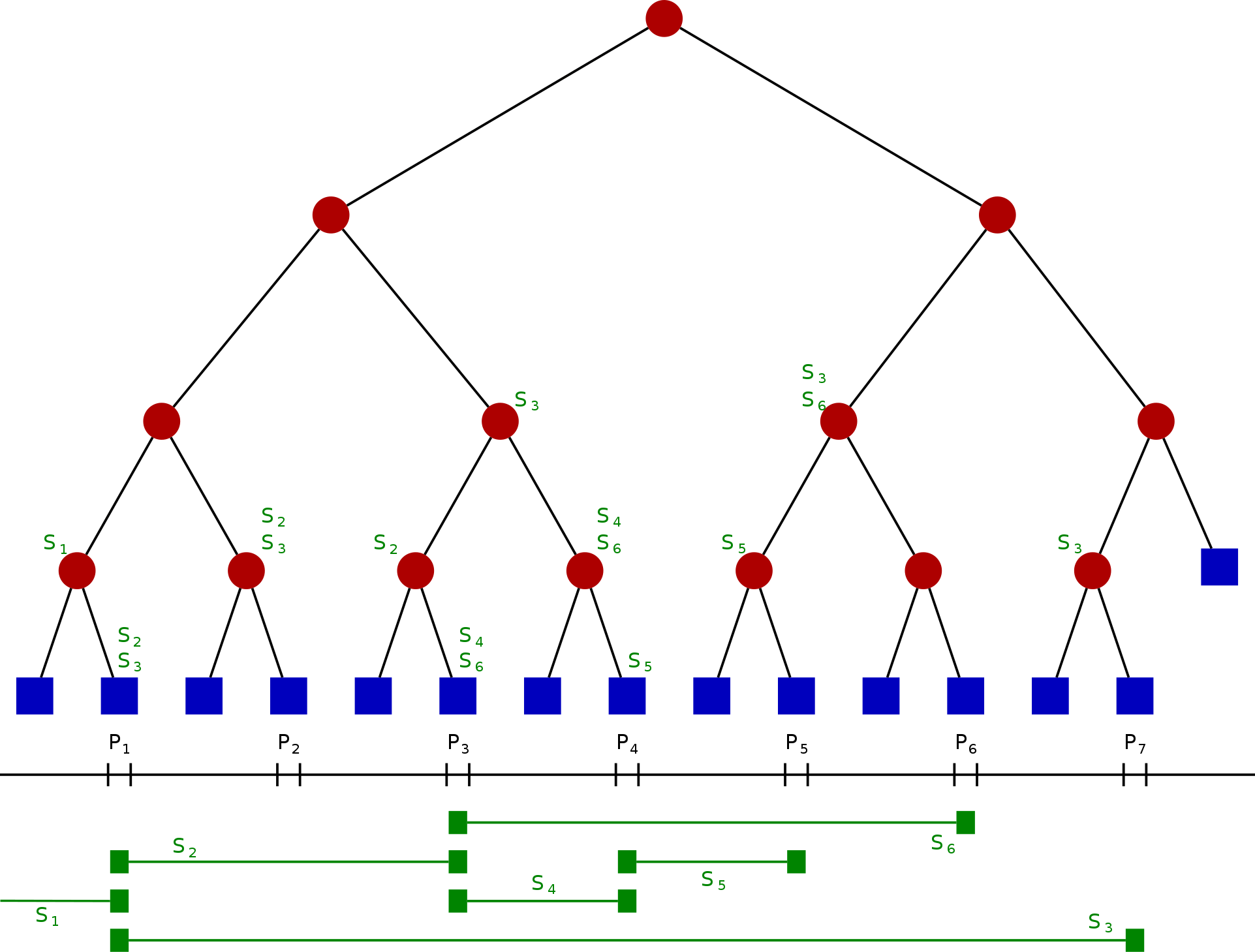
+令 S 是一维线段的集合。将这些线段的端点坐标由小到大排序，令其为{{< katex >}}x_{1},x_{2},\cdots ,x_{m} {{< /katex >}}。我们将被这些端点切分的每一个区间称为“单位区间”（每个端点所在的位置会单独成为一个单位区间），从左到右包含：
+
+{{< katex >}} (-\infty ,x_{1}),[x_{1},x_{1}],(x_{1},x_{2}),[x_{2},x_{2}],...,(x_{m-1},x_{m}),[x_{m},x_{m}],(x_{m},+\infty ){{< /katex >}}
+
+线段树的结构为一个二叉树，每个节点都代表一个坐标区间，节点 N 所代表的区间记为 Int(N)，则其需符合以下条件：
+
+- 其每一个叶节点，从左到右代表每个单位区间。
+- 其内部节点代表的区间是其两个儿子代表的区间之联集。
+- 每个节点（包含叶子）中有一个存储线段的数据结构。若一个线段 S 的坐标区间包含 Int(N) 但不包含 Int(parent(N))，则节点 N 中会存储线段 S。
+
+
+
+## 二. 为什么需要这种数据结构
+
+
+## 三. 构造线段树
+
+## 四. 线段树的查询
+
+
+
+## 五. 线段树的更新
+
+### 1. 直接更新
+
+
+### 2. 懒更新
+
+
+
 ```go
 package template