mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-05 16:36:41 +08:00
148 lines
5.6 KiB
Markdown
148 lines
5.6 KiB
Markdown
# [1463. Cherry Pickup II](https://leetcode.com/problems/cherry-pickup-ii/)
|
||
|
||
## 题目
|
||
|
||
Given a `rows x cols` matrix `grid` representing a field of cherries. Each cell in `grid` represents the number of cherries that you can collect.
|
||
|
||
You have two robots that can collect cherries for you, Robot #1 is located at the top-left corner (0,0) , and Robot #2 is located at the top-right corner (0, cols-1) of the grid.
|
||
|
||
Return the maximum number of cherries collection using both robots by following the rules below:
|
||
|
||
- From a cell (i,j), robots can move to cell (i+1, j-1) , (i+1, j) or (i+1, j+1).
|
||
- When any robot is passing through a cell, It picks it up all cherries, and the cell becomes an empty cell (0).
|
||
- When both robots stay on the same cell, only one of them takes the cherries.
|
||
- Both robots cannot move outside of the grid at any moment.
|
||
- Both robots should reach the bottom row in the `grid`.
|
||
|
||
**Example 1:**
|
||
|
||
|
||
|
||
```
|
||
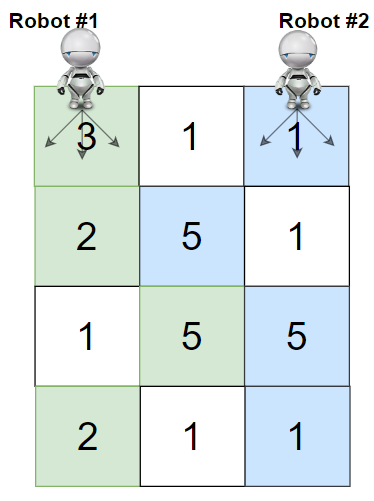
Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
|
||
Output: 24
|
||
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
|
||
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
|
||
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
|
||
Total of cherries: 12 + 12 = 24.
|
||
```
|
||
|
||
**Example 2:**
|
||
|
||
|
||
|
||
```
|
||
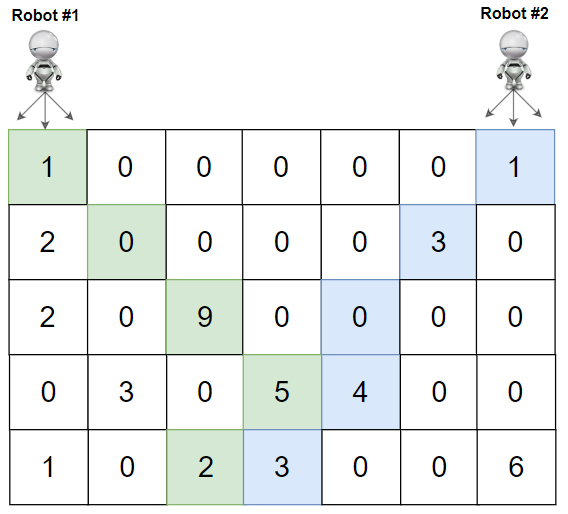
Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
|
||
Output: 28
|
||
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
|
||
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
|
||
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
|
||
Total of cherries: 17 + 11 = 28.
|
||
```
|
||
|
||
**Example 3:**
|
||
|
||
```
|
||
Input: grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]]
|
||
Output: 22
|
||
```
|
||
|
||
**Example 4:**
|
||
|
||
```
|
||
Input: grid = [[1,1],[1,1]]
|
||
Output: 4
|
||
```
|
||
|
||
**Constraints:**
|
||
|
||
- `rows == grid.length`
|
||
- `cols == grid[i].length`
|
||
- `2 <= rows, cols <= 70`
|
||
- `0 <= grid[i][j] <= 100`
|
||
|
||
## 题目大意
|
||
|
||
给你一个 rows x cols 的矩阵 grid 来表示一块樱桃地。 grid 中每个格子的数字表示你能获得的樱桃数目。你有两个机器人帮你收集樱桃,机器人 1 从左上角格子 (0,0) 出发,机器人 2 从右上角格子 (0, cols-1) 出发。请你按照如下规则,返回两个机器人能收集的最多樱桃数目:
|
||
|
||
- 从格子 (i,j) 出发,机器人可以移动到格子 (i+1, j-1),(i+1, j) 或者 (i+1, j+1) 。
|
||
- 当一个机器人经过某个格子时,它会把该格子内所有的樱桃都摘走,然后这个位置会变成空格子,即没有樱桃的格子。
|
||
- 当两个机器人同时到达同一个格子时,它们中只有一个可以摘到樱桃。
|
||
- 两个机器人在任意时刻都不能移动到 grid 外面。
|
||
- 两个机器人最后都要到达 grid 最底下一行。
|
||
|
||
## 解题思路
|
||
|
||
- 如果没有思路可以先用暴力解法 DFS 尝试。读完题可以分析出求最多樱桃数目,里面包含了很多重叠子问题,于是乎自然而然思路是用动态规划。数据规模上看,100 的数据规模最多能保证 O(n^3) 时间复杂度的算法不超时。
|
||
- 这一题的变量有 2 个,一个是行号,另外一个是机器人所在的列。具体来说,机器人每走一步的移动范围只能往下走,不能往上走,所以 2 个机器人所在行号一定相同。两个机器人的列号不同。综上,变量有 3 个,1 个行号和2 个列号。定义 `dp[i][j][k]` 代表第一个机器人从 (0,0) 走到 (i,k) 坐标,第二个机器人从 (0,n-1) 走到 (i,k) 坐标,两者最多能收集樱桃的数目。状态转移方程为 :
|
||
|
||
{{< katex display >}}
|
||
dp[i][j][k] = max \begin{pmatrix}\begin{array}{lr} dp[i-1][f(j_1))][f(j_2)] + grid[i][j_1] + grid[i][j_2], j_1\neq j_2 \\ dp[i-1][f(j_1))][f(j_2)] + grid[i][j_1], j_1 = j_2 \end{array} \end{pmatrix}
|
||
{{< /katex>}}
|
||
|
||
其中:
|
||
|
||
{{< katex display >}}
|
||
\left\{\begin{matrix}f(j_1) \in [0,n), f(j_1) - j_1 \in [-1,0,1]\\ f(j_2) \in [0,n), f(j_2) - j_2 \in [-1,0,1]\end{matrix}\right.
|
||
{{< /katex>}}
|
||
|
||
即状态转移过程中需要在 `[j1 - 1, j1, j1 + 1]` 中枚举 `j1`,同理,在 在 `[j2 - 1, j2, j2 + 1]` 中枚举 `j2`,每个状态转移需要枚举这 3*3 = 9 种状态。
|
||
|
||
- 边界条件 `dp[i][0][n-1] = grid[0][0] + grid[0][n-1]`,最终答案存储在 `dp[m-1]` 行中,循环找出 `dp[m-1][j1][j2]` 中的最大值,到此该题得解。
|
||
|
||
## 代码
|
||
|
||
```go
|
||
package leetcode
|
||
|
||
func cherryPickup(grid [][]int) int {
|
||
rows, cols := len(grid), len(grid[0])
|
||
dp := make([][][]int, rows)
|
||
for i := 0; i < rows; i++ {
|
||
dp[i] = make([][]int, cols)
|
||
for j := 0; j < cols; j++ {
|
||
dp[i][j] = make([]int, cols)
|
||
}
|
||
}
|
||
for i := 0; i < rows; i++ {
|
||
for j := 0; j <= i && j < cols; j++ {
|
||
for k := cols - 1; k >= cols-1-i && k >= 0; k-- {
|
||
max := 0
|
||
for a := j - 1; a <= j+1; a++ {
|
||
for b := k - 1; b <= k+1; b++ {
|
||
sum := isInBoard(dp, i-1, a, b)
|
||
if a == b && i > 0 && a >= 0 && a < cols {
|
||
sum -= grid[i-1][a]
|
||
}
|
||
if sum > max {
|
||
max = sum
|
||
}
|
||
}
|
||
}
|
||
if j == k {
|
||
max += grid[i][j]
|
||
} else {
|
||
max += grid[i][j] + grid[i][k]
|
||
}
|
||
dp[i][j][k] = max
|
||
}
|
||
}
|
||
}
|
||
count := 0
|
||
for j := 0; j < cols && j < rows; j++ {
|
||
for k := cols - 1; k >= 0 && k >= cols-rows; k-- {
|
||
if dp[rows-1][j][k] > count {
|
||
count = dp[rows-1][j][k]
|
||
}
|
||
}
|
||
}
|
||
return count
|
||
}
|
||
|
||
func isInBoard(dp [][][]int, i, j, k int) int {
|
||
if i < 0 || j < 0 || j >= len(dp[0]) || k < 0 || k >= len(dp[0]) {
|
||
return 0
|
||
}
|
||
return dp[i][j][k]
|
||
}
|
||
``` |