LeetCode-Go/leetcode/1203.Sort-Items-by-Groups-Respecting-Dependencies/README.md

# [1203. Sort Items by Groups Respecting Dependencies](https://leetcode.com/problems/sort-items-by-groups-respecting-dependencies/)


## 题目

There are `n` items each belonging to zero or one of `m` groups where `group[i]` is the group that the `i`-th item belongs to and it's equal to `-1` if the `i`-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.

Return a sorted list of the items such that:

- The items that belong to the same group are next to each other in the sorted list.
- There are some relations between these items where `beforeItems[i]` is a list containing all the items that should come before the `i`th item in the sorted array (to the left of the `i`th item).

Return any solution if there is more than one solution and return an **empty list** if there is no solution.

**Example 1:**

![](https://assets.leetcode.com/uploads/2019/09/11/1359_ex1.png)

```
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
Output: [6,3,4,1,5,2,0,7]

```

**Example 2:**

```
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
Output: []
Explanation: This is the same as example 1 except that 4 needs to be before 6 in the sorted list.

```

**Constraints:**

- `1 <= m <= n <= 3 * 104`
- `group.length == beforeItems.length == n`
- `1 <= group[i] <= m - 1`
- `0 <= beforeItems[i].length <= n - 1`
- `0 <= beforeItems[i][j] <= n - 1`
- `i != beforeItems[i][j]`
- `beforeItems[i]` does not contain duplicates elements.

## 题目大意

有 n 个项目，每个项目或者不属于任何小组，或者属于 m 个小组之一。group[i] 表示第 i 个小组所属的小组，如果第 i 个项目不属于任何小组，则 group[i] 等于 -1。项目和小组都是从零开始编号的。可能存在小组不负责任何项目，即没有任何项目属于这个小组。

请你帮忙按要求安排这些项目的进度，并返回排序后的项目列表：

- 同一小组的项目，排序后在列表中彼此相邻。
- 项目之间存在一定的依赖关系，我们用一个列表 beforeItems 来表示，其中 beforeItems[i] 表示在进行第 i 个项目前（位于第 i 个项目左侧）应该完成的所有项目。

如果存在多个解决方案，只需要返回其中任意一个即可。如果没有合适的解决方案，就请返回一个 空列表 。

## 解题思路

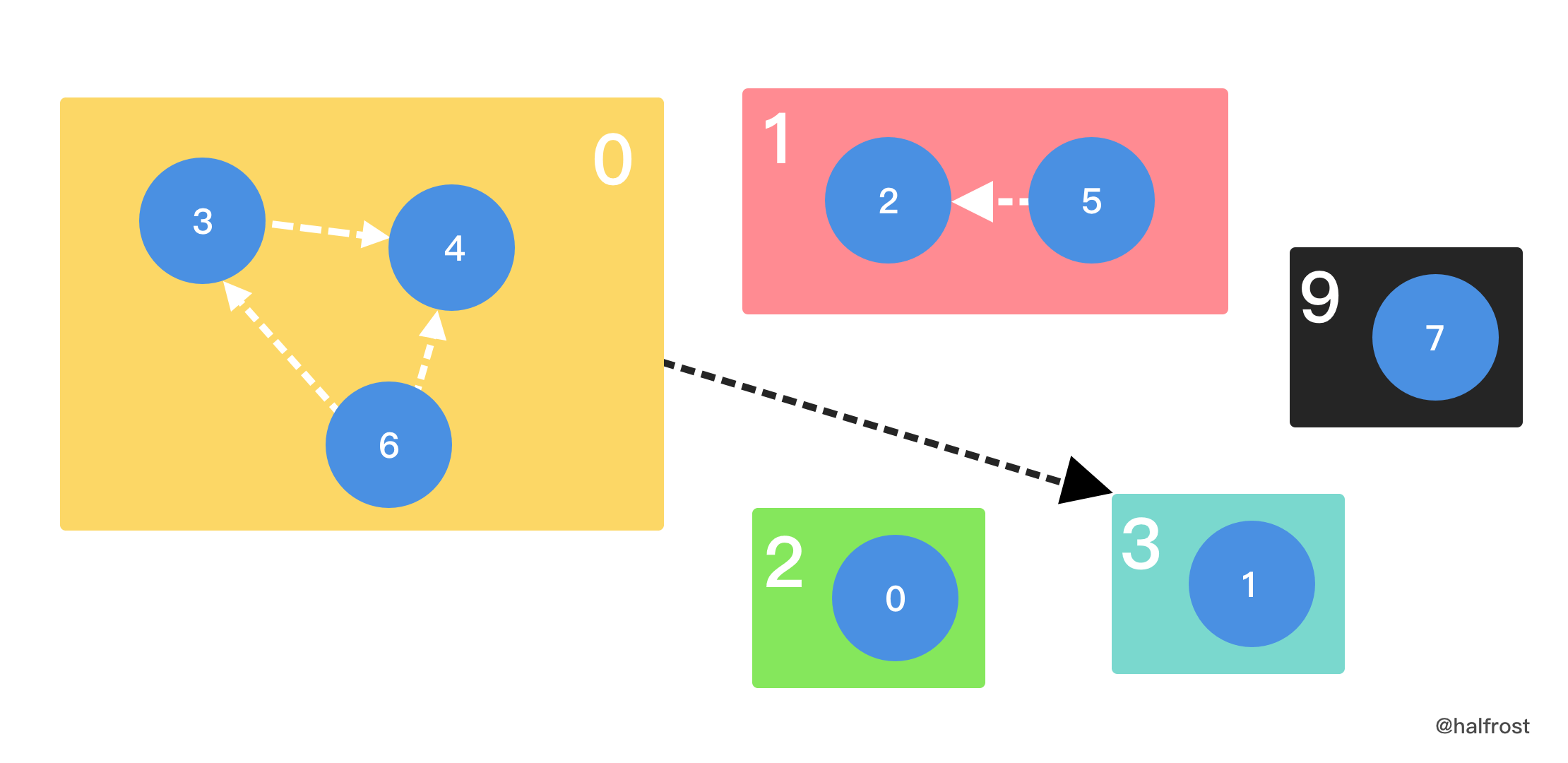
- 读完题能确定这一题是拓扑排序。但是和单纯的拓扑排序有区别的是，同一小组内的项目需要彼此相邻。用 2 次拓扑排序即可解决。第一次拓扑排序排出组间的顺序，第二次拓扑排序排出组内的顺序。为了实现方便，用 map 给虚拟分组标记编号。如下图，将 3，4，6 三个任务打包到 0 号分组里面，将 2，5 两个任务打包到 1 号分组里面，其他任务单独各自为一组。组间的依赖是 6 号任务依赖 1 号任务。由于 6 号任务封装在 0 号分组里，所以 3 号分组依赖 0 号分组。先组间排序，确定分组顺序，再组内拓扑排序，排出最终顺序。

    ![](https://img.halfrost.com/Leetcode/leetcode_1203_1.png)

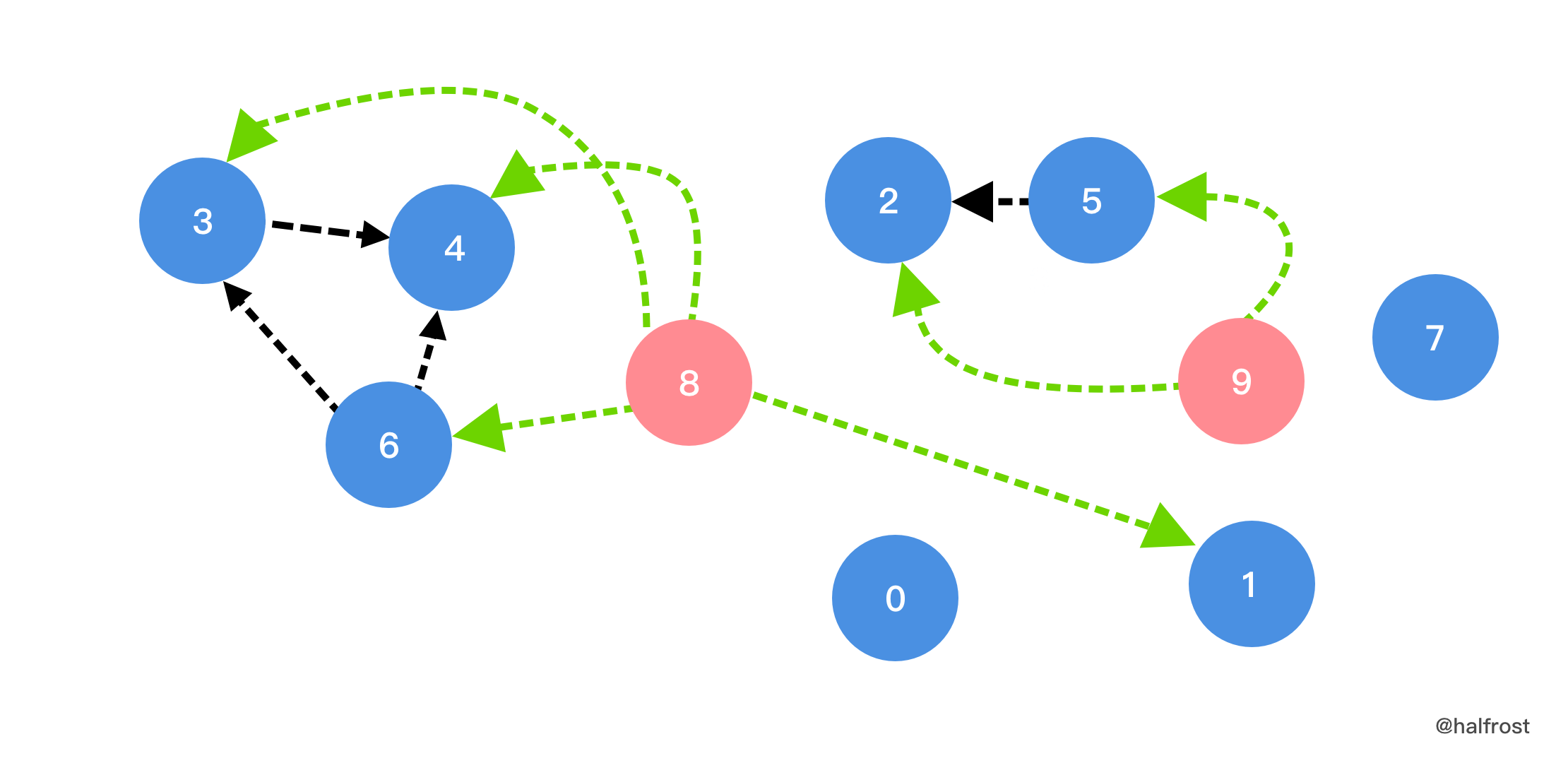
- 上面的解法可以 AC，但是时间太慢了。因为做了一些不必要的操作。有没有可能只用一次拓扑排序呢？将必须要在一起的结点统一依赖一个虚拟结点，例如下图中的虚拟结点 8 和 9 。3，4，6 都依赖 8 号任务，2 和 5 都依赖 9 号任务。1 号任务本来依赖 6 号任务，由于 6 由依赖 8 ，所以添加 1 依赖 8 的边。通过增加虚拟结点，增加了需要打包在一起结点的入度。构建出以上关系以后，按照入度为 0 的原则，依次进行 DFS。8 号和 9 号两个虚拟结点的入度都为 0 ，对它们进行 DFS，必定会使得与它关联的节点都被安排在一起，这样就满足了题意：同一小组的项目，排序后在列表中彼此相邻。一遍扫完，满足题意的顺序就排出来了。这个解法 beat 100%！

    ![](https://img.halfrost.com/Leetcode/leetcode_1203_2.png)

## 代码

```go
package leetcode

// 解法一 拓扑排序版的 DFS
func sortItems(n int, m int, group []int, beforeItems [][]int) []int {
	groups, inDegrees := make([][]int, n+m), make([]int, n+m)
	for i, g := range group {
		if g > -1 {
			g += n
			groups[g] = append(groups[g], i)
			inDegrees[i]++
		}
	}
	for i, ancestors := range beforeItems {
		gi := group[i]
		if gi == -1 {
			gi = i
		} else {
			gi += n
		}
		for _, ancestor := range ancestors {
			ga := group[ancestor]
			if ga == -1 {
				ga = ancestor
			} else {
				ga += n
			}
			if gi == ga {
				groups[ancestor] = append(groups[ancestor], i)
				inDegrees[i]++
			} else {
				groups[ga] = append(groups[ga], gi)
				inDegrees[gi]++
			}
		}
	}
	res := []int{}
	for i, d := range inDegrees {
		if d == 0 {
			sortItemsDFS(i, n, &res, &inDegrees, &groups)
		}
	}
	if len(res) != n {
		return nil
	}
	return res
}

func sortItemsDFS(i, n int, res, inDegrees *[]int, groups *[][]int) {
	if i < n {
		*res = append(*res, i)
	}
	(*inDegrees)[i] = -1
	for _, ch := range (*groups)[i] {
		if (*inDegrees)[ch]--; (*inDegrees)[ch] == 0 {
			sortItemsDFS(ch, n, res, inDegrees, groups)
		}
	}
}

// 解法二 二维拓扑排序 时间复杂度 O(m+n)，空间复杂度 O(m+n)
func sortItems1(n int, m int, group []int, beforeItems [][]int) []int {
	groupItems, res := map[int][]int{}, []int{}
	for i := 0; i < len(group); i++ {
		if group[i] == -1 {
			group[i] = m + i
		}
		groupItems[group[i]] = append(groupItems[group[i]], i)
	}
	groupGraph, groupDegree, itemGraph, itemDegree := make([][]int, m+n), make([]int, m+n), make([][]int, n), make([]int, n)
	for i := 0; i < len(beforeItems); i++ {
		for j := 0; j < len(beforeItems[i]); j++ {
			if group[beforeItems[i][j]] != group[i] {
				// 不同组项目，确定组间依赖关系
				groupGraph[group[beforeItems[i][j]]] = append(groupGraph[group[beforeItems[i][j]]], group[i])
				groupDegree[group[i]]++
			} else {
				// 同组项目，确定组内依赖关系
				itemGraph[beforeItems[i][j]] = append(itemGraph[beforeItems[i][j]], i)
				itemDegree[i]++
			}
		}
	}
	items := []int{}
	for i := 0; i < m+n; i++ {
		items = append(items, i)
	}
	// 组间拓扑
	groupOrders := topSort(groupGraph, groupDegree, items)
	if len(groupOrders) < len(items) {
		return nil
	}
	for i := 0; i < len(groupOrders); i++ {
		items := groupItems[groupOrders[i]]
		// 组内拓扑
		orders := topSort(itemGraph, itemDegree, items)
		if len(orders) < len(items) {
			return nil
		}
		res = append(res, orders...)
	}
	return res
}

func topSort(graph [][]int, deg, items []int) (orders []int) {
	q := []int{}
	for _, i := range items {
		if deg[i] == 0 {
			q = append(q, i)
		}
	}
	for len(q) > 0 {
		from := q[0]
		q = q[1:]
		orders = append(orders, from)
		for _, to := range graph[from] {
			deg[to]--
			if deg[to] == 0 {
				q = append(q, to)
			}
		}
	}
	return
}
```