mirror of
https://github.com/halfrost/LeetCode-Go.git
synced 2025-07-05 08:27:30 +08:00
Use Katex in solution markdown
This commit is contained in:
@ -5,9 +5,7 @@ import (
|
||||
)
|
||||
|
||||
func isPalindrome(s string) bool {
|
||||
|
||||
s = strings.ToLower(s)
|
||||
|
||||
i, j := 0, len(s)-1
|
||||
for i < j {
|
||||
for i < j && !isChar(s[i]) {
|
||||
@ -22,7 +20,6 @@ func isPalindrome(s string) bool {
|
||||
i++
|
||||
j--
|
||||
}
|
||||
|
||||
return true
|
||||
}
|
||||
|
||||
|
||||
@ -14,7 +14,7 @@ Return any solution if there is more than one solution and return an **empty li
|
||||
|
||||
**Example 1:**
|
||||
|
||||

|
||||

|
||||
|
||||
```
|
||||
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
|
||||
@ -56,11 +56,11 @@ Explanation: This is the same as example 1 except that 4 needs to be before 6 i
|
||||
|
||||
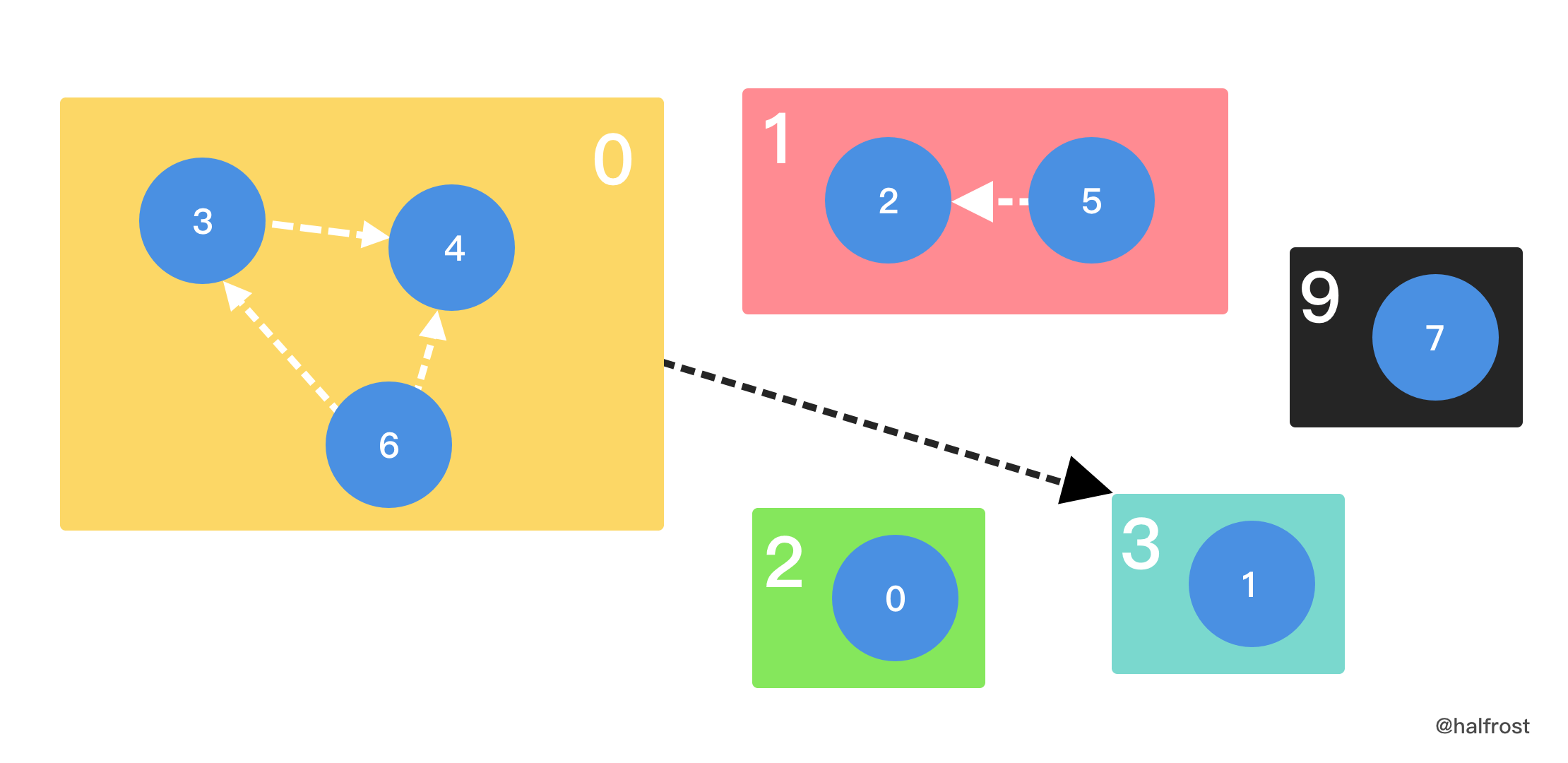
- 读完题能确定这一题是拓扑排序。但是和单纯的拓扑排序有区别的是,同一小组内的项目需要彼此相邻。用 2 次拓扑排序即可解决。第一次拓扑排序排出组间的顺序,第二次拓扑排序排出组内的顺序。为了实现方便,用 map 给虚拟分组标记编号。如下图,将 3,4,6 三个任务打包到 0 号分组里面,将 2,5 两个任务打包到 1 号分组里面,其他任务单独各自为一组。组间的依赖是 6 号任务依赖 1 号任务。由于 6 号任务封装在 0 号分组里,所以 3 号分组依赖 0 号分组。先组间排序,确定分组顺序,再组内拓扑排序,排出最终顺序。
|
||||
|
||||
|
||||

|
||||
|
||||
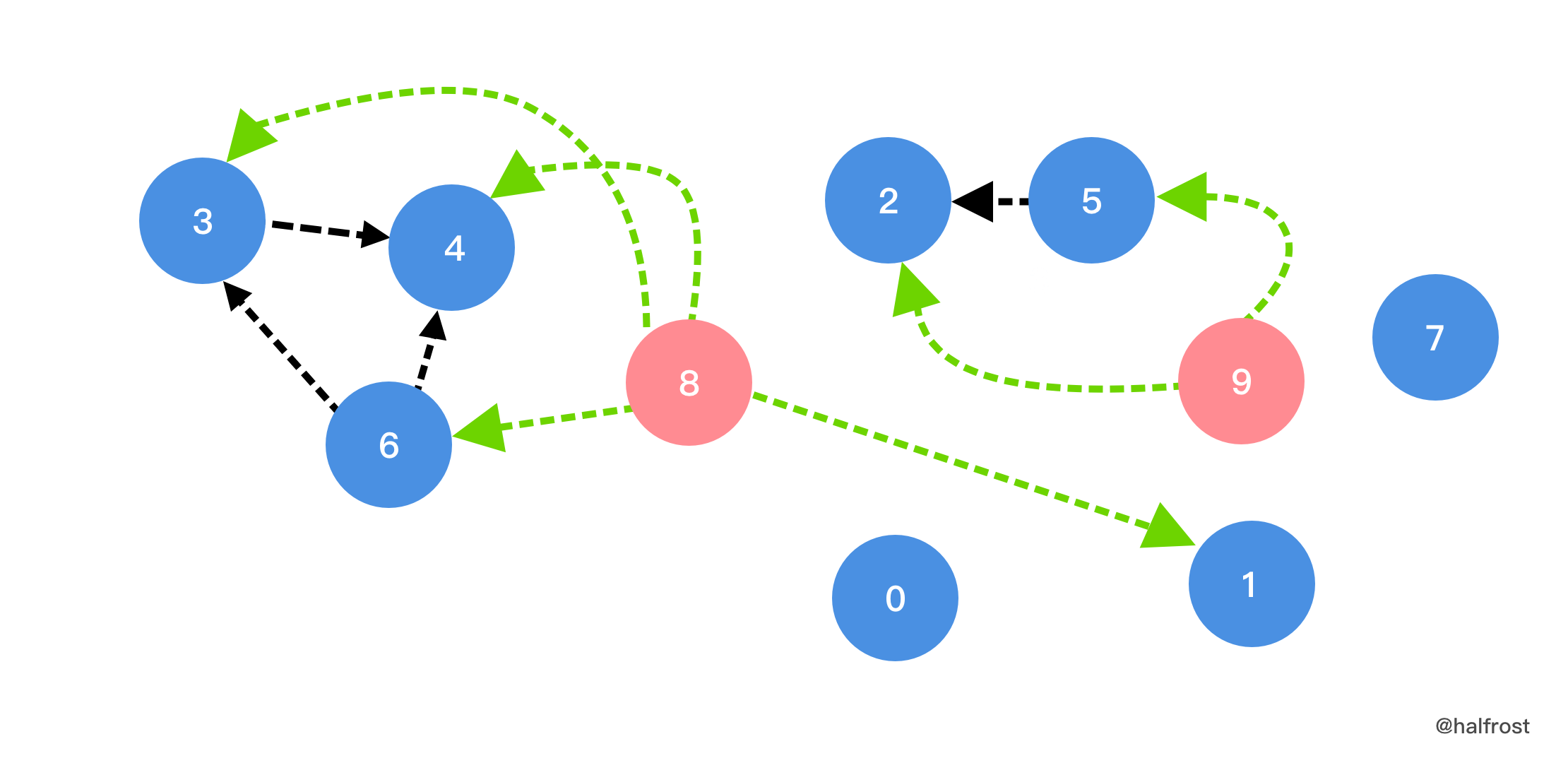
- 上面的解法可以 AC,但是时间太慢了。因为做了一些不必要的操作。有没有可能只用一次拓扑排序呢?将必须要在一起的结点统一依赖一个虚拟结点,例如下图中的虚拟结点 8 和 9 。3,4,6 都依赖 8 号任务,2 和 5 都依赖 9 号任务。1 号任务本来依赖 6 号任务,由于 6 由依赖 8 ,所以添加 1 依赖 8 的边。通过增加虚拟结点,增加了需要打包在一起结点的入度。构建出以上关系以后,按照入度为 0 的原则,依次进行 DFS。8 号和 9 号两个虚拟结点的入度都为 0 ,对它们进行 DFS,必定会使得与它关联的节点都被安排在一起,这样就满足了题意:同一小组的项目,排序后在列表中彼此相邻。一遍扫完,满足题意的顺序就排出来了。这个解法 beat 100%!
|
||||
|
||||
|
||||

|
||||
|
||||
## 代码
|
||||
|
||||
|
||||
@ -34,13 +34,11 @@ For the purpose of this problem, we define empty string as valid palindrome.
|
||||
package leetcode
|
||||
|
||||
import (
|
||||
"strings"
|
||||
"strings"
|
||||
)
|
||||
|
||||
func isPalindrome(s string) bool {
|
||||
|
||||
s = strings.ToLower(s)
|
||||
|
||||
s = strings.ToLower(s)
|
||||
i, j := 0, len(s)-1
|
||||
for i < j {
|
||||
for i < j && !isChar(s[i]) {
|
||||
@ -55,7 +53,6 @@ func isPalindrome(s string) bool {
|
||||
i++
|
||||
j--
|
||||
}
|
||||
|
||||
return true
|
||||
}
|
||||
|
||||
|
||||
@ -41,11 +41,20 @@ For example, given the dungeon below, the initial health of the knight must be a
|
||||
## 解题思路
|
||||
|
||||
- 在二维地图上给出每个格子扣血数,负数代表扣血,正数代表补血。左上角第一个格子是起点,右下角最后一个格子是终点。问骑士初始最少多少血才能走完迷宫,顺利营救位于终点的公主。需要注意的是,起点和终点都会对血量进行影响。每到一个格子,骑士的血都不能少于 1,一旦少于 1 点血,骑士就会死去。
|
||||
- 这一题首先想到的解题思路是动态规划。从终点逆推回起点。`dp[i][j]` 代表骑士进入坐标为 `(i,j)` 的格子之前最少的血量值。 那么 `dp[m-1][n-1]` 应该同时满足两个条件,`dp[m-1][n-1] + dungeon[m-1][n-1] ≥ 1` 并且 `dp[m-1][n-1] ≥ 1`,由于这两个不等式的方向是相同的,取交集以后,起决定作用的是数轴最右边的数,即 `max(1-dungeon[m-1][n-1] , 1)`。算出 `dp[m-1][n-1]` 以后,接着可以推出 `dp[m-1][i]` 这一行和 `dp[i][n-1]` 这一列的值。因为骑士只能往右走和往下走。往回推,即只能往上走和往左走。到这里,DP 的初始条件都准备好了。那么状态转移方程是什么呢?分析一般的情况,`dp[i][j]` 这个值应该是和 `dp[i+1][j]` 和 `dp[i][j+1]` 这两者有关系。即 `dp[i][j]` 经过自己本格子的扣血以后,要能至少满足下一行和右一列格子血量的最少要求。并且自己的血量也应该 `≥1`。即需要满足下面这两组不等式。
|
||||
\begin{matrix} \left\{ \begin{array}{lr} dp[i][j] + dungeon[i][j] \geqslant dp[i+1][j] \\ dp[i][j] \geqslant 1 \end{array} \right. \end{matrix}
|
||||
\begin{matrix} \left\{ \begin{array}{lr} dp[i][j] + dungeon[i][j] \geqslant dp[i][j+1] \\ dp[i][j] \geqslant 1 \end{array} \right. \end{matrix}
|
||||
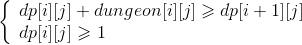
|
||||
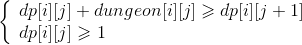
|
||||
- 这一题首先想到的解题思路是动态规划。从终点逆推回起点。`dp[i][j]` 代表骑士进入坐标为 `(i,j)` 的格子之前最少的血量值。 那么 `dp[m-1][n-1]` 应该同时满足两个条件,`dp[m-1][n-1] + dungeon[m-1][n-1] ≥ 1` 并且 `dp[m-1][n-1] ≥ 1`,由于这两个不等式的方向是相同的,取交集以后,起决定作用的是数轴最右边的数,即 `max(1-dungeon[m-1][n-1] , 1)`。算出 `dp[m-1][n-1]` 以后,接着可以推出 `dp[m-1][i]` 这一行和 `dp[i][n-1]` 这一列的值。因为骑士只能往右走和往下走。往回推,即只能往上走和往左走。到这里,DP 的初始条件都准备好了。那么状态转移方程是什么呢?分析一般的情况,`dp[i][j]` 这个值应该是和 `dp[i+1][j]` 和 `dp[i][j+1]` 这两者有关系。即 `dp[i][j]` 经过自己本格子的扣血以后,要能至少满足下一行和右一列格子血量的最少要求。并且自己的血量也应该 `≥1`。即需要满足下面这两组不等式。
|
||||
|
||||
{{< katex display >}}
|
||||
\begin{matrix} \left\{
|
||||
\begin{array}{lr}
|
||||
dp[i][j] + dungeon[i][j] \geqslant dp[i+1][j] \\
|
||||
dp[i][j] \geqslant 1
|
||||
\end{array} \right.
|
||||
\end{matrix}
|
||||
{{< /katex >}}
|
||||
|
||||
{{< katex display >}}
|
||||
\begin{matrix} \left\{ \begin{array}{lr} dp[i][j] + dungeon[i][j] \geqslant dp[i][j+1] \\ dp[i][j] \geqslant 1 \end{array} \right. \end{matrix}
|
||||
{{< /katex >}}
|
||||
上面不等式中第一组不等式是满足下一行格子的最低血量要求,第二组不等式是满足右一列格子的最低血量要求。第一个式子化简即 `dp[i][j] = max(1, dp[i+1][j]-dungeon[i][j])`,第二个式子化简即 `dp[i][j] = max(1, dp[i][j+1]-dungeon[i][j])`。求得了这两种走法的最低血量值,从这两个值里面取最小,即是当前格子所需的最低血量,所以状态转移方程为 `dp[i][j] = min(max(1, dp[i][j+1]-dungeon[i][j]), max(1, dp[i+1][j]-dungeon[i][j]))`。DP 完成以后,`dp[0][0]` 中记录的就是骑士初始最低血量值。时间复杂度 O(m\*n),空间复杂度 O(m\*n)。
|
||||
|
||||
- 这一题还可以用二分搜索来求解。骑士的血量取值范围一定是在 `[1,+∞)` 这个区间内。那么二分这个区间,每次二分的中间值,再用 dp 在地图中去判断是否能到达终点,如果能,就缩小搜索空间至 `[1,mid]`,否则搜索空间为 `[mid + 1,+∞)` 。时间复杂度 O(m\*n\* log math.MaxInt64),空间复杂度 O(m\*n)。
|
||||
|
||||
@ -51,46 +51,47 @@ Now given a string representing n, you should return the smallest good base of n
|
||||
- 给出一个数 n,要求找一个进制 k,使得数字 n 在 k 进制下每一位都是 1 。求最小的进制 k。
|
||||
- 这一题等价于求最小的正整数 k,满足存在一个正整数 m 使得
|
||||
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_483_1.png'>
|
||||
</p>
|
||||
{{< katex display >}}
|
||||
\sum_{i=0}^{m} k^{i} = \frac{1-k^{m+1}}{1-k} = n
|
||||
{{< /katex >}}
|
||||
|
||||
|
||||
- 这一题需要确定 k 和 m 两个数的值。m 和 k 是有关系的,确定了一个值,另外一个值也确定了。由
|
||||
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_483_2.png'>
|
||||
</p>
|
||||
{{< katex display >}}
|
||||
\frac{1-k^{m+1}}{1-k} = n \\
|
||||
{{< /katex >}}
|
||||
|
||||
|
||||
可得:
|
||||
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_483_3.png'>
|
||||
</p>
|
||||
{{< katex display >}}
|
||||
m = log_{k}(kn-n+1) - 1 < log_{k}(kn) = 1 + log_{k}n
|
||||
{{< /katex >}}
|
||||
|
||||
|
||||
根据题意,可以知道 k ≥2,m ≥1 ,所以有:
|
||||
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_483_4.png'>
|
||||
</p>
|
||||
{{< katex display >}}
|
||||
1 \leqslant m \leqslant log_{2}n
|
||||
{{< /katex >}}
|
||||
|
||||
|
||||
所以 m 的取值范围确定了。那么外层循环从 1 到 log n 遍历。找到一个最小的 k ,能满足:
|
||||
|
||||
可以用二分搜索来逼近找到最小的 k。先找到 k 的取值范围。由
|
||||
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_483_5.png'>
|
||||
</p>
|
||||
{{< katex display >}}
|
||||
\frac{1-k^{m+1}}{1-k} = n \\
|
||||
{{< /katex >}}
|
||||
|
||||
|
||||
可得,
|
||||
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_483_6.png'>
|
||||
</p>
|
||||
{{< katex display >}}
|
||||
k^{m+1} = nk-n+1 < nk\\ \Rightarrow k < \sqrt[m]{n}
|
||||
{{< /katex >}}
|
||||
|
||||
|
||||
所以 k 的取值范围是 [2, n*(1/m) ]。再利用二分搜索逼近找到最小的 k 即为答案。
|
||||
|
||||
|
||||
@ -41,27 +41,22 @@ f(x) 是 x! 末尾是0的数量。(回想一下 x! = 1 * 2 * 3 * ... * x
|
||||
- 给出一个数 K,要求有多少个 n 能使得 n!末尾 0 的个数等于 K。
|
||||
- 这一题是基于第 172 题的逆过程加强版。第 172 题是给出 `n`,求得末尾 0 的个数。由第 172 题可以知道,`n!`末尾 0 的个数取决于因子 5 的个数。末尾可能有 `K` 个 0,那么 `n` 最多可以等于 `5 * K`,在 `[0, 5* K]` 区间内二分搜索,判断 `mid` 末尾 0 的个数,如果能找到 `K`,那么就范围 5,如果找不到这个 `K`,返回 0 。为什么答案取值只有 0 和 5 呢?因为当 `n` 增加 5 以后,因子 5 的个数又加一了,末尾又可以多 1 个或者多个 0(如果加 5 以后,有多个 5 的因子,例如 25,125,就有可能末尾增加多个 0)。所以有效的 `K` 值对应的 `n` 的范围区间就是 5 。反过来,无效的 `K` 值对应的 `n` 是 0。`K` 在 `5^n` 的分界线处会发生跳变,所有有些值取不到。例如,`n` 在 `[0,5)` 内取值,`K = 0`;`n` 在 `[5,10)` 内取值,`K = 1`;`n` 在 `[10,15)` 内取值,`K = 2`;`n` 在 `[15,20)` 内取值,`K = 3`;`n` 在 `[20,25)` 内取值,`K = 4`;`n` 在 `[25,30)` 内取值,`K = 6`,因为 25 提供了 2 个 5,也就提供了 2 个 0,所以 `K` 永远无法取值等于 5,即当 `K = 5` 时,找不到任何的 `n` 与之对应。
|
||||
- 这一题也可以用数学的方法解题。见解法二。这个解法的灵感来自于:n!末尾 0 的个数等于 [1,n] 所有数的因子 5 的个数总和。其次此题的结果一定只有 0 和 5 (分析见上一种解法)。有了这两个结论以后,就可以用数学的方法推导了。首先 n 可以表示为 5 进制的形式
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_793_1.png'>
|
||||
</p>
|
||||
上面式子中,所有有因子 5 的个数为:
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_793_2.png'>
|
||||
</p>
|
||||
|
||||
这个总数就即是 K。针对不同的 n,an 的通项公式不同,所以表示的 K 的系数也不同。cn 的通项公式呢?
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_793_2.png'>
|
||||
</p>
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_793_3.png'>
|
||||
</p>
|
||||
|
||||
由上面这个递推还能推出通项公式(不过这题不适用通项公式,是用递推公式更方便):
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_793_4.png'>
|
||||
</p>
|
||||
判断 K 是否能表示成两个数列的表示形式,等价于判断 K 是否能转化为以 Cn 为基的变进制数。到此,转化成类似第 483 题了。代码实现不难,见解法二。
|
||||
{{< katex display >}}
|
||||
n = 5^{0} * a_{0} + 5^{1} * a_{1} + 5^{2} * a_{2} + ... + 5^{n} * a_{n}, (a_{n} < 5)
|
||||
{{< /katex >}}
|
||||
上面式子中,所有有因子 5 的个数为:
|
||||
{{< katex display >}}
|
||||
K = \sum_{n=0}^{n} a_{n} * c_{n}
|
||||
{{< /katex >}}
|
||||
这个总数就即是 K。针对不同的 n,an 的通项公式不同,所以表示的 K 的系数也不同。cn 的通项公式呢?
|
||||
{{< katex display >}}
|
||||
c_{n} = 5 * c_{n-1} + 1,c_{0} = 0
|
||||
{{< /katex >}}
|
||||
由上面这个递推还能推出通项公式(不过这题不适用通项公式,是用递推公式更方便):
|
||||
{{< katex display >}}
|
||||
c_{n} = \frac{5^{n} - 1 }{4}
|
||||
{{< /katex >}}
|
||||
判断 K 是否能表示成两个数列的表示形式,等价于判断 K 是否能转化为以 Cn 为基的变进制数。到此,转化成类似第 483 题了。代码实现不难,见解法二。
|
||||
|
||||
|
||||
## 代码
|
||||
|
||||
@ -56,11 +56,10 @@ What is the minimum number of moves that you need to know with certainty what
|
||||
|
||||
- 给出 `K` 个鸡蛋,`N` 层楼,要求确定安全楼层 `F` 需要最小步数 `t`。
|
||||
- 这一题是微软的经典面试题。拿到题最容易想到的是二分搜索。但是仔细分析以后会发现单纯的二分是不对的。不断的二分确实能找到最终安全的楼层,但是这里没有考虑到 `K` 个鸡蛋。鸡蛋数的限制会导致二分搜索无法找到最终楼层。题目要求要在保证能找到最终安全楼层的情况下,找到最小步数。所以单纯的二分搜索并不能解答这道题。
|
||||
- 这一题如果按照题意正向考虑,动态规划的状态转移方程是 `searchTime(K, N) = max( searchTime(K-1, X-1), searchTime(K, N-X) )`。其中 `X` 是丢鸡蛋的楼层。随着 `X` 从 `[1,N]`,都能计算出一个 `searchTime` 的值,在所有这 `N` 个值之中,取最小值就是本题的答案了。这个解法可以 AC 这道题。不过这个解法不细展开了。时间复杂度 `O(k*N^2)`。
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_887_8.png'>
|
||||
</p>
|
||||
|
||||
- 这一题如果按照题意正向考虑,动态规划的状态转移方程是 `searchTime(K, N) = max( searchTime(K-1, X-1), searchTime(K, N-X) )`。其中 `X` 是丢鸡蛋的楼层。随着 `X` 从 `[1,N]`,都能计算出一个 `searchTime` 的值,在所有这 `N` 个值之中,取最小值就是本题的答案了。这个解法可以 AC 这道题。不过这个解法不细展开了。时间复杂度 `O(k*N^2)`。
|
||||
{{< katex display >}}
|
||||
dp(K,N) = MIN \begin{bmatrix} \, \, MAX(dp(K-1,X-1),dp(K,N-X))\, \, \end{bmatrix} ,1\leqslant x \leqslant N \\
|
||||
{{< /katex >}}
|
||||
- 换个角度来看这个问题,定义 `dp[k][m]` 代表 `K` 个鸡蛋,`M` 次移动能检查的最大楼层。考虑某一步 `t` 应该在哪一层丢鸡蛋呢?一个正确的选择是在 `dp[k-1][t-1] + 1` 层丢鸡蛋,结果分两种情况:
|
||||
1. 如果鸡蛋碎了,我们首先排除了该层以上的所有楼层(不管这个楼有多高),而对于剩下的 `dp[k-1][t-1]` 层楼,我们一定能用 `k-1` 个鸡蛋在 `t-1` 步内求解。因此这种情况下,我们总共可以求解无限高的楼层。可见,这是一种非常好的情况,但并不总是发生。
|
||||
2. 如果鸡蛋没碎,我们首先排除了该层以下的 `dp[k-1][t-1]` 层楼,此时我们还有 `k` 个蛋和 `t-1` 步,那么我们去该层以上的楼层继续测得 `dp[k][t-1]` 层楼。因此这种情况下,我们总共可以求解 `dp[k-1][t-1] + 1 + dp[k][t-1]` 层楼。
|
||||
@ -70,43 +69,34 @@ What is the minimum number of moves that you need to know with certainty what
|
||||
2. 如果在更高的楼层丢鸡蛋,假设是第 `dp[k-1][t-1] + 2` 层丢鸡蛋,如果这次鸡蛋碎了,剩下 `k-1` 个鸡蛋和 `t-1` 步只能保证验证 `dp[k-1][t-1]` 的楼层,这里还剩**第** `dp[k-1][t-1]+ 1` 的楼层,不能保证最终一定能找到安全楼层了。
|
||||
- 用反证法就能得出每一步都应该在第 `dp[k-1][t-1] + 1` 层丢鸡蛋。
|
||||
- 这道题还可以用二分搜索来解答。回到上面分析的状态转移方程:`dp[k][m] = dp[k-1][m-1] + dp[k][m-1] + 1` 。用数学方法来解析这个递推关系。令 `f(t,k)` 为 `t` 和 `k` 的函数,题目所要求能测到最大楼层是 `N` 的最小步数,即要求出 `f(t,k) ≥ N` 时候的最小 `t`。由状态转移方程可以知道:`f(t,k) = f(t-1,k) + f(t-1,k-1) + 1`,当 `k = 1` 的时候,对应一个鸡蛋的情况,`f(t,1) = t`,当 `t = 1` 的时候,对应一步的情况,`f(1,k) = 1`。有状态转移方程得:
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_887_1.png'>
|
||||
</p>
|
||||
|
||||
- 令 `g(t,k) = f(t,k) - f(t,k-1)`,可以得到:
|
||||
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_887_2.png'>
|
||||
</p>
|
||||
|
||||
- 可以知道 `g(t,k)` 是一个杨辉三角,即二项式系数:
|
||||
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_887_3.png'>
|
||||
</p>
|
||||
|
||||
- 利用裂项相消的方法:
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_887_4.png'>
|
||||
</p>
|
||||
|
||||
- 于是可以得到:
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_887_5.png'>
|
||||
</p>
|
||||
|
||||
- 其中:
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_887_6.png'>
|
||||
</p>
|
||||
|
||||
- 于是针对每一项的二项式常数,都可以由前一项乘以一个分数得到下一项。
|
||||
<p align='center'>
|
||||
<img src='https://img.halfrost.com/Leetcode/leetcode_887_7.png'>
|
||||
</p>
|
||||
|
||||
- 利用二分搜索,不断的二分 `t`,直到逼近找到 `f(t,k) ≥ N` 时候最小的 `t`。时间复杂度 `O(K * log N)`,空间复杂度 `O(1)`。
|
||||
{{< katex display >}}
|
||||
\begin{aligned} f(t,k) &= 1 + f(t-1,k-1) + f(t-1,k) \\ f(t,k-1) &= 1 + f(t-1,k-2) + f(t-1,k-1) \\ \end{aligned}
|
||||
{{< /katex >}}
|
||||
令 `g(t,k) = f(t,k) - f(t,k-1)`,可以得到:
|
||||
{{< katex display >}}
|
||||
g(t,k) = g(t-1,k) + g(t-1,k-1)
|
||||
{{< /katex >}}
|
||||
可以知道 `g(t,k)` 是一个杨辉三角,即二项式系数:
|
||||
{{< katex display >}}
|
||||
g(t,k) = \binom{t}{k+1} = C_{t}^{k+1}
|
||||
{{< /katex >}}
|
||||
利用裂项相消的方法:
|
||||
{{< katex display >}}
|
||||
\begin{aligned} g(t,x) &= f(t,x) - f(t,x-1) \\ g(t,x-1) &= f(t,x-1) - f(t,x-2) \\ g(t,x-2) &= f(t,x-2) - f(t,x-3) \\ \begin{matrix} .\\ .\\ .\\ \end{matrix}\\ g(t,2) &= f(t,2) - f(t,1) \\ g(t,1) &= f(t,1) - f(t,0) \\ \end{aligned}
|
||||
{{< /katex >}}
|
||||
于是可以得到:
|
||||
{{< katex display >}}
|
||||
\begin{aligned} f(t,k) &= \sum_{1}^{k}g(t,x) = \sum_{0}^{k} \binom{t}{x} \\ &= C_{t}^{0} + C_{t}^{1} + C_{t}^{2} + ... + C_{t}^{k} \\ \end{aligned}
|
||||
{{< /katex >}}
|
||||
其中:
|
||||
{{< katex display >}}
|
||||
\begin{aligned} C_{t}^{k} \cdot \frac{n-k}{k+1} &= C_{t}^{k+1} \\ C_{t}^{k} &= C_{t}^{k-1} \cdot \frac{t-k+1}{k} \\ \end{aligned}
|
||||
{{< /katex >}}
|
||||
于是针对每一项的二项式常数,都可以由前一项乘以一个分数得到下一项。
|
||||
{{< katex display >}}
|
||||
\begin{aligned} C_{t}^{0} &= 1 \\ C_{t}^{1} &= C_{t}^{0} \cdot \frac{t-1+1}{1} \\ C_{t}^{2} &= C_{t}^{1} \cdot \frac{t-2+1}{2} \\ C_{t}^{3} &= C_{t}^{2} \cdot \frac{t-3+1}{3} \\ \begin{matrix} .\\ .\\ .\\ \end{matrix}\\ C_{t}^{k} &= C_{t}^{k-1} \cdot \frac{t-k+1}{k} \\ \end{aligned}
|
||||
{{< /katex >}}
|
||||
利用二分搜索,不断的二分 `t`,直到逼近找到 `f(t,k) ≥ N` 时候最小的 `t`。时间复杂度 `O(K * log N)`,空间复杂度 `O(1)`。
|
||||
|
||||
|
||||
|
||||
|
||||
@ -53,9 +53,9 @@ Return the number of possible playlists. **As the answer can be very large, ret
|
||||
- 简化抽象一下题意,给 N 个数,要求从这 N 个数里面组成一个长度为 L 的序列,并且相同元素的间隔不能小于 K 个数。问总共有多少组组成方法。
|
||||
- 一拿到题,会觉得这一题是三维 DP,因为存在 3 个变量,但是实际考虑一下,可以降一维。我们先不考虑 K 的限制,只考虑 N 和 L。定义 `dp[i][j]` 代表播放列表里面有 `i` 首歌,其中包含 `j` 首不同的歌曲,那么题目要求的最终解存在 `dp[L][N]` 中。考虑 `dp[i][j]` 的递归公式,音乐列表当前需要组成 `i` 首歌,有 2 种方式可以得到,由 `i - 1` 首歌的列表中添加一首列表中**不存在**的新歌曲,或者由 `i - 1` 首歌的列表中添加一首列表中**已经存在**的歌曲。即,`dp[i][j]` 可以由 `dp[i - 1][j - 1]` 得到,也可以由 `dp[i - 1][j]` 得到。如果是第一种情况,添加一首新歌,那么新歌有 N - ( j - 1 ) 首,如果是第二种情况,添加一首已经存在的歌,歌有 j 首,所以状态转移方程是 `dp[i][j] = dp[i - 1][j - 1] * ( N - ( j - 1 ) ) + dp[i - 1][j] * j` 。但是这个方程是在不考虑 K 的限制条件下得到的,距离满足题意还差一步。接下来需要考虑加入 K 这个限制条件以后,状态转移方程该如何推导。
|
||||
- 如果是添加一首新歌,是不受 K 限制的,所以 `dp[i - 1][j - 1] * ( N - ( j - 1 ) )` 这里不需要变化。如果是添加一首存在的歌曲,这个时候就会受到 K 的限制了。如果当前播放列表里面的歌曲有 `j` 首,并且 `j > K`,那么选择歌曲只能从 `j - K` 里面选,因为不能选择 `j - 1` 到 `j - k` 的这些歌,选择了就不满足重复的歌之间间隔不能小于 `K` 的限制条件了。那 j ≤ K 呢?这个时候一首歌都不能选,因为歌曲数都没有超过 K,当然不能再选择重复的歌曲。(选择了就再次不满足重复的歌之间间隔不能小于 `K` 的限制条件了)。经过上述分析,可以得到最终的状态转移方程:
|
||||
|
||||
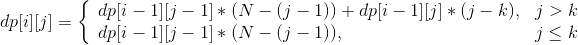
|
||||
|
||||
{{< katex display >}}
|
||||
dp[i][j]= \begin{matrix} \left\{ \begin{array}{lr} dp[i - 1][j - 1] * ( N - ( j - 1 ) ) + dp[i - 1][j] * ( j - k ) , & {j > k}\\ dp[i - 1][j - 1] * ( N - ( j - 1 ) ), & {j \leq k} \end{array} \right. \end{matrix}
|
||||
{{< /katex >}}
|
||||
- 上面的式子可以合并简化成下面这个式子:`dp[i][j] = dp[i - 1][j - 1]*(N - (j - 1)) + dp[i-1][j]*max(j-K, 0)`,递归初始值 `dp[0][0] = 1`。
|
||||
|
||||
|
||||
|
||||
@ -53,8 +53,9 @@ Two submatrices `(x1, y1, x2, y2)` and `(x1', y1', x2', y2')` are different
|
||||
- 给出一个矩阵,要求在这个矩阵中找出子矩阵的和等于 target 的矩阵个数。
|
||||
- 这一题读完题感觉是滑动窗口的二维版本。如果把它拍扁,在一维数组中,求连续的子数组和为 target,这样就很好做。如果这题不降维,纯暴力解是 O(n^6)。如何优化降低时间复杂度呢?
|
||||
- 联想到第 1 题 Two Sum 问题,可以把 2 个数求和的问题优化到 O(n)。这里也用类似的思想,用一个 map 来保存行方向上曾经出现过的累加和,相减就可以得到本行的和。这里可能读者会有疑惑,为什么不能每一行都单独保存呢?为什么一定要用累加和相减的方式来获取每一行的和呢?因为这一题要求子矩阵所有解,如果只单独保存每一行的和,只能求得小的子矩阵,子矩阵和子矩阵组成的大矩阵的情况会漏掉(当然再循环一遍,把子矩阵累加起来也可以,但是这样就多了一层循环了),例如子矩阵是 1*4 的,但是 2 个这样的子矩阵摞在一起形成 2 * 4 也能满足条件,如果不用累加和的办法,只单独存每一行的和,最终还要有组合的步骤。经过这样的优化,可以从 O(n^6) 优化到 O(n^4),能 AC 这道题,但是时间复杂度太高了。如何优化?
|
||||
- 首先,子矩阵需要上下左右 4 个边界,4 个变量控制循环就需要 O(n^4),行和列的区间累加还需要 O(n^2)。行和列的区间累加可以通过 preSum 来解决。例如 `sum[i,j] = sum[j] - sum[i - 1]`,其中 sum[k] 中存的是从 0 到 K 的累加和: 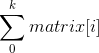
|
||||
|
||||
- 首先,子矩阵需要上下左右 4 个边界,4 个变量控制循环就需要 O(n^4),行和列的区间累加还需要 O(n^2)。行和列的区间累加可以通过 preSum 来解决。例如 `sum[i,j] = sum[j] - sum[i - 1]`,其中 sum[k] 中存的是从 0 到 K 的累加和: {{< katex display >}}
|
||||
\sum_{0}^{k} matrix[i]
|
||||
{{< /katex >}}
|
||||
那么一个区间内的累加和可以由这个区间的右边界减去区间左边界左边的那个累加和得到(由于是闭区间,所需要取左边界左边的和)。经过这样的处理,列方向的维度就被我们拍扁了。
|
||||
|
||||
- 再来看看行方向的和,现在每一列的和都可以通过区间相减的方法得到。那么这道题就变成了第 1 题 Two Sum 的问题了。Two Sum 问题只需要 O(n) 的时间复杂度求解,这一题由于是二维的,所以两个列的边界还需要循环,所以最终优化下来的时间复杂度是 O(n^3)。计算 presum 可以直接用原数组,所以空间复杂度只有一个 O(n) 的字典。
|
||||
|
||||
@ -14,7 +14,7 @@ Return any solution if there is more than one solution and return an **empty li
|
||||
|
||||
**Example 1:**
|
||||
|
||||

|
||||

|
||||
|
||||
```
|
||||
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
|
||||
@ -56,11 +56,11 @@ Explanation: This is the same as example 1 except that 4 needs to be before 6 i
|
||||
|
||||
- 读完题能确定这一题是拓扑排序。但是和单纯的拓扑排序有区别的是,同一小组内的项目需要彼此相邻。用 2 次拓扑排序即可解决。第一次拓扑排序排出组间的顺序,第二次拓扑排序排出组内的顺序。为了实现方便,用 map 给虚拟分组标记编号。如下图,将 3,4,6 三个任务打包到 0 号分组里面,将 2,5 两个任务打包到 1 号分组里面,其他任务单独各自为一组。组间的依赖是 6 号任务依赖 1 号任务。由于 6 号任务封装在 0 号分组里,所以 3 号分组依赖 0 号分组。先组间排序,确定分组顺序,再组内拓扑排序,排出最终顺序。
|
||||
|
||||

|
||||

|
||||
|
||||
- 上面的解法可以 AC,但是时间太慢了。因为做了一些不必要的操作。有没有可能只用一次拓扑排序呢?将必须要在一起的结点统一依赖一个虚拟结点,例如下图中的虚拟结点 8 和 9 。3,4,6 都依赖 8 号任务,2 和 5 都依赖 9 号任务。1 号任务本来依赖 6 号任务,由于 6 由依赖 8 ,所以添加 1 依赖 8 的边。通过增加虚拟结点,增加了需要打包在一起结点的入度。构建出以上关系以后,按照入度为 0 的原则,依次进行 DFS。8 号和 9 号两个虚拟结点的入度都为 0 ,对它们进行 DFS,必定会使得与它关联的节点都被安排在一起,这样就满足了题意:同一小组的项目,排序后在列表中彼此相邻。一遍扫完,满足题意的顺序就排出来了。这个解法 beat 100%!
|
||||
|
||||

|
||||

|
||||
|
||||
## 代码
|
||||
|
||||
|
||||
@ -76,7 +76,7 @@ Explanation: Sell the 1st color 1000000000 times for a total value of 5000000005
|
||||
|
||||
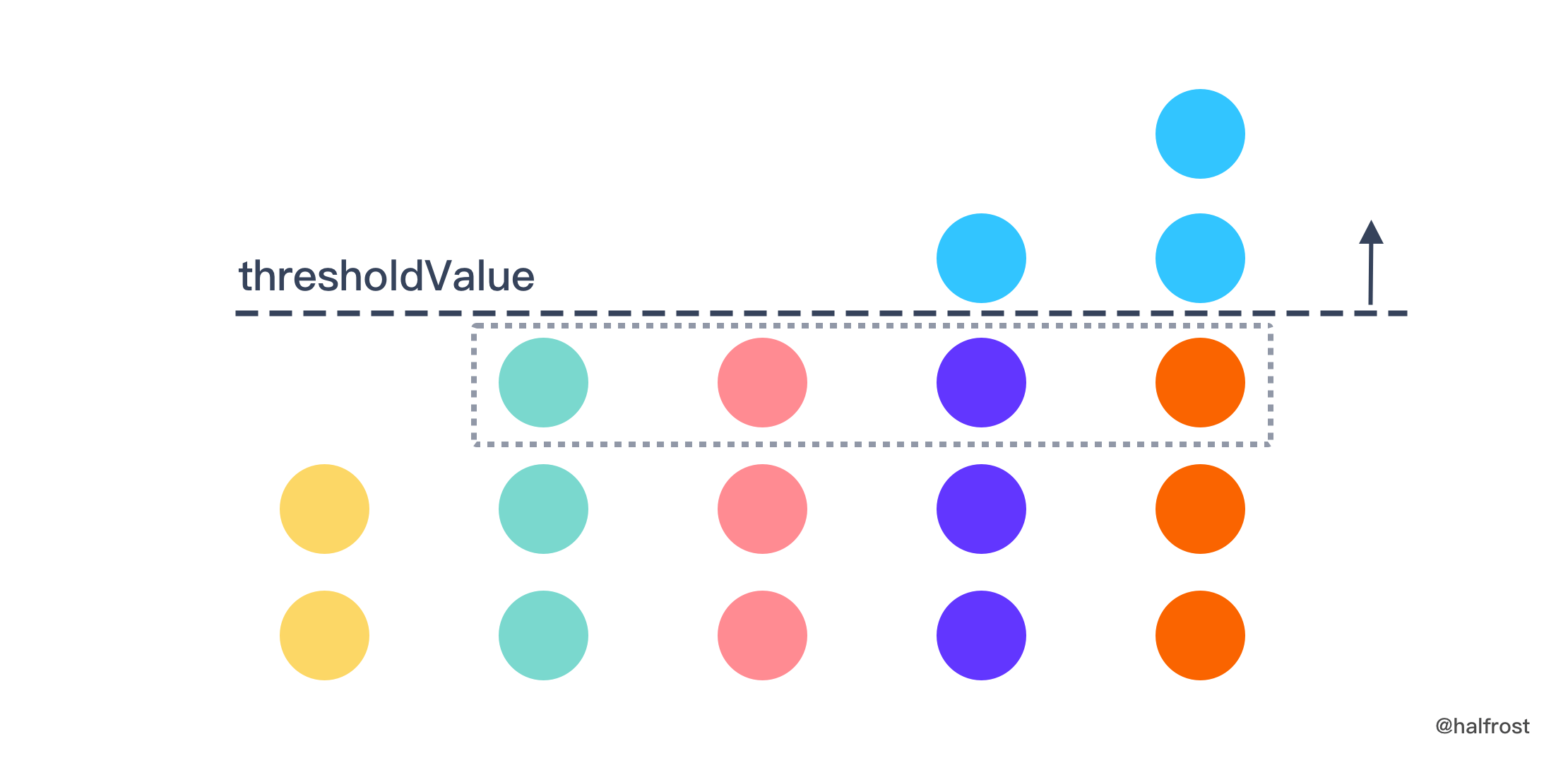
`thresholdValue` 越小,不等式左边的值越大,随着 `thresholdValue` 的增大,不等式左边的值越来越小,直到刚刚能小于等于 `orders`。求出了 `thresholdValue` 值以后,还需要再判断有多少值等于 `thresholdValue - 1` 值了。
|
||||
|
||||
|
||||

|
||||
|
||||
- 还是举上面的例子,原始数组是 [2,3,3,4,5],`orders` = 4,我们可以求得 `thresholdValue` = 3 。`inventory[i]` > `thresholdValue` 的那部分 100% 的要取走,`thresholdValue` 就像一个水平面,突出水平面的那些都要拿走,每列的值按照等差数列求和公式计算即可。但是 `orders` - `thresholdValue` = 1,说明水平面以下还要拿走一个,即 `thresholdValue` 线下的虚线框里面的那 4 个球,还需要任意取走一个。最后总的结果是这 2 部分的总和,( ( 5 + 4 ) + 4 ) + 3 = 16 。
|
||||
|
||||
|
||||
Reference in New Issue
Block a user