mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-24 00:57:05 +08:00
529 lines
16 KiB
Markdown
529 lines
16 KiB
Markdown
|
||
<p align="center">
|
||
<a href="https://programmercarl.com/other/xunlianying.html" target="_blank">
|
||
<img src="../pics/训练营.png" width="1000"/>
|
||
</a>
|
||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||
|
||
|
||
|
||
# 47.全排列 II
|
||
|
||
[力扣题目链接](https://leetcode.cn/problems/permutations-ii/)
|
||
|
||
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
|
||
|
||
示例 1:
|
||
|
||
* 输入:nums = [1,1,2]
|
||
* 输出:
|
||
[[1,1,2],
|
||
[1,2,1],
|
||
[2,1,1]]
|
||
|
||
示例 2:
|
||
|
||
* 输入:nums = [1,2,3]
|
||
* 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
|
||
|
||
提示:
|
||
|
||
* 1 <= nums.length <= 8
|
||
* -10 <= nums[i] <= 10
|
||
|
||
# 算法公开课
|
||
|
||
**《代码随想录》算法视频公开课:[回溯算法求解全排列,如何去重?| LeetCode:47.全排列 II](https://www.bilibili.com/video/BV1R84y1i7Tm/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||
|
||
|
||
## 思路
|
||
|
||
这道题目和[46.全排列](https://programmercarl.com/0046.全排列.html)的区别在与**给定一个可包含重复数字的序列**,要返回**所有不重复的全排列**。
|
||
|
||
这里又涉及到去重了。
|
||
|
||
在[40.组合总和II](https://programmercarl.com/0040.组合总和II.html) 、[90.子集II](https://programmercarl.com/0090.子集II.html)我们分别详细讲解了组合问题和子集问题如何去重。
|
||
|
||
那么排列问题其实也是一样的套路。
|
||
|
||
**还要强调的是去重一定要对元素进行排序,这样我们才方便通过相邻的节点来判断是否重复使用了**。
|
||
|
||
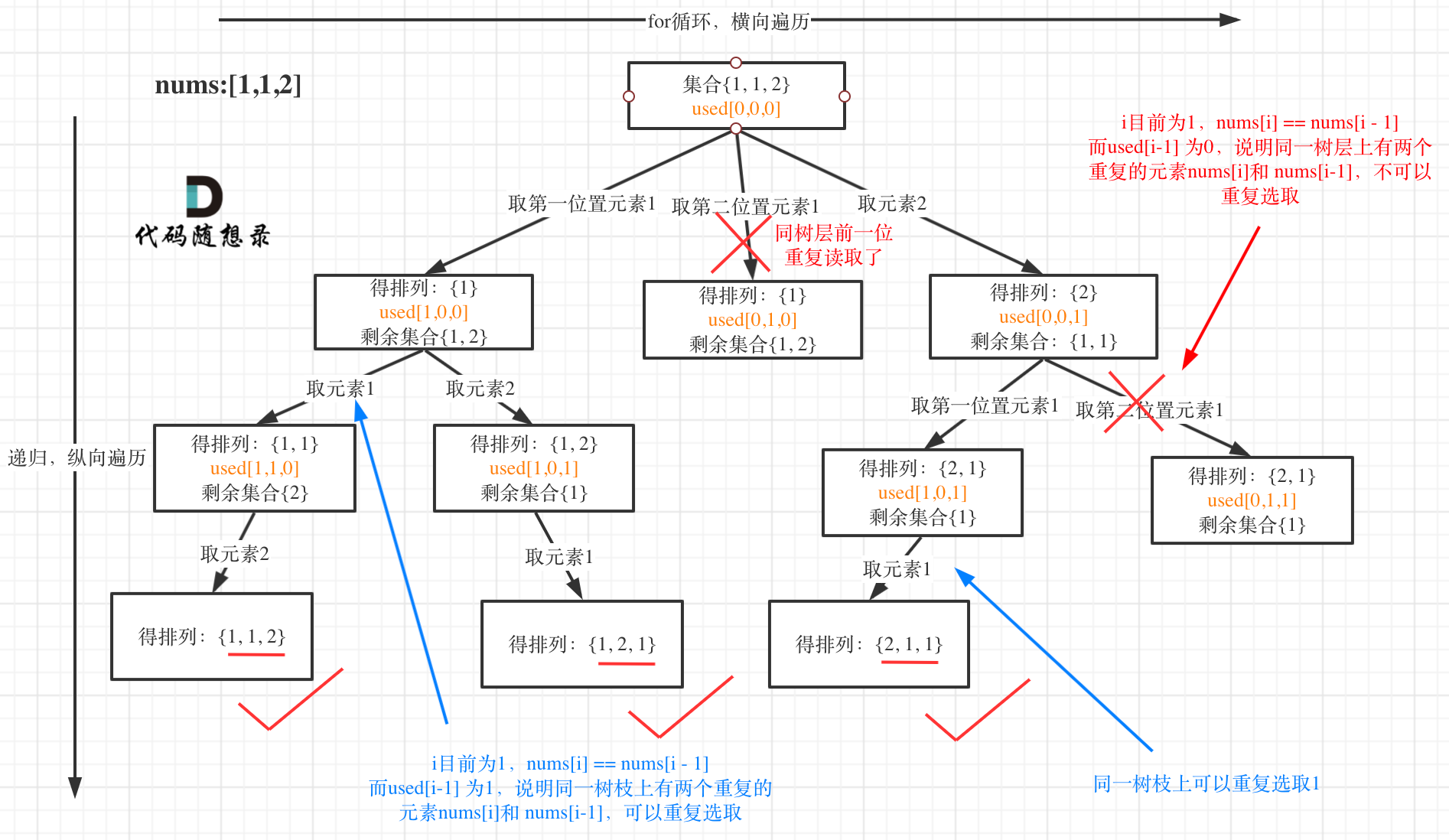
我以示例中的 [1,1,2]为例 (为了方便举例,已经排序)抽象为一棵树,去重过程如图:
|
||
|
||
|
||
|
||
图中我们对同一树层,前一位(也就是nums[i-1])如果使用过,那么就进行去重。
|
||
|
||
**一般来说:组合问题和排列问题是在树形结构的叶子节点上收集结果,而子集问题就是取树上所有节点的结果**。
|
||
|
||
在[46.全排列](https://programmercarl.com/0046.全排列.html)中已经详细讲解了排列问题的写法,在[40.组合总和II](https://programmercarl.com/0040.组合总和II.html) 、[90.子集II](https://programmercarl.com/0090.子集II.html)中详细讲解了去重的写法,所以这次我就不用回溯三部曲分析了,直接给出代码,如下:
|
||
|
||
## C++代码
|
||
|
||
```CPP
|
||
class Solution {
|
||
private:
|
||
vector<vector<int>> result;
|
||
vector<int> path;
|
||
void backtracking (vector<int>& nums, vector<bool>& used) {
|
||
// 此时说明找到了一组
|
||
if (path.size() == nums.size()) {
|
||
result.push_back(path);
|
||
return;
|
||
}
|
||
for (int i = 0; i < nums.size(); i++) {
|
||
// used[i - 1] == true,说明同一树枝nums[i - 1]使用过
|
||
// used[i - 1] == false,说明同一树层nums[i - 1]使用过
|
||
// 如果同一树层nums[i - 1]使用过则直接跳过
|
||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
|
||
continue;
|
||
}
|
||
if (used[i] == false) {
|
||
used[i] = true;
|
||
path.push_back(nums[i]);
|
||
backtracking(nums, used);
|
||
path.pop_back();
|
||
used[i] = false;
|
||
}
|
||
}
|
||
}
|
||
public:
|
||
vector<vector<int>> permuteUnique(vector<int>& nums) {
|
||
result.clear();
|
||
path.clear();
|
||
sort(nums.begin(), nums.end()); // 排序
|
||
vector<bool> used(nums.size(), false);
|
||
backtracking(nums, used);
|
||
return result;
|
||
}
|
||
};
|
||
|
||
// 时间复杂度: 最差情况所有元素都是唯一的。复杂度和全排列1都是 O(n! * n) 对于 n 个元素一共有 n! 中排列方案。而对于每一个答案,我们需要 O(n) 去复制最终放到 result 数组
|
||
// 空间复杂度: O(n) 回溯树的深度取决于我们有多少个元素
|
||
```
|
||
* 时间复杂度: O(n! * n)
|
||
* 空间复杂度: O(n)
|
||
|
||
## 拓展
|
||
|
||
大家发现,去重最为关键的代码为:
|
||
|
||
```cpp
|
||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
|
||
continue;
|
||
}
|
||
```
|
||
|
||
**如果改成 `used[i - 1] == true`, 也是正确的!**,去重代码如下:
|
||
|
||
```cpp
|
||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
|
||
continue;
|
||
}
|
||
```
|
||
|
||
这是为什么呢,就是上面我刚说的,如果要对树层中前一位去重,就用`used[i - 1] == false`,如果要对树枝前一位去重用`used[i - 1] == true`。
|
||
|
||
**对于排列问题,树层上去重和树枝上去重,都是可以的,但是树层上去重效率更高!**
|
||
|
||
这么说是不是有点抽象?
|
||
|
||
来来来,我就用输入: [1,1,1] 来举一个例子。
|
||
|
||
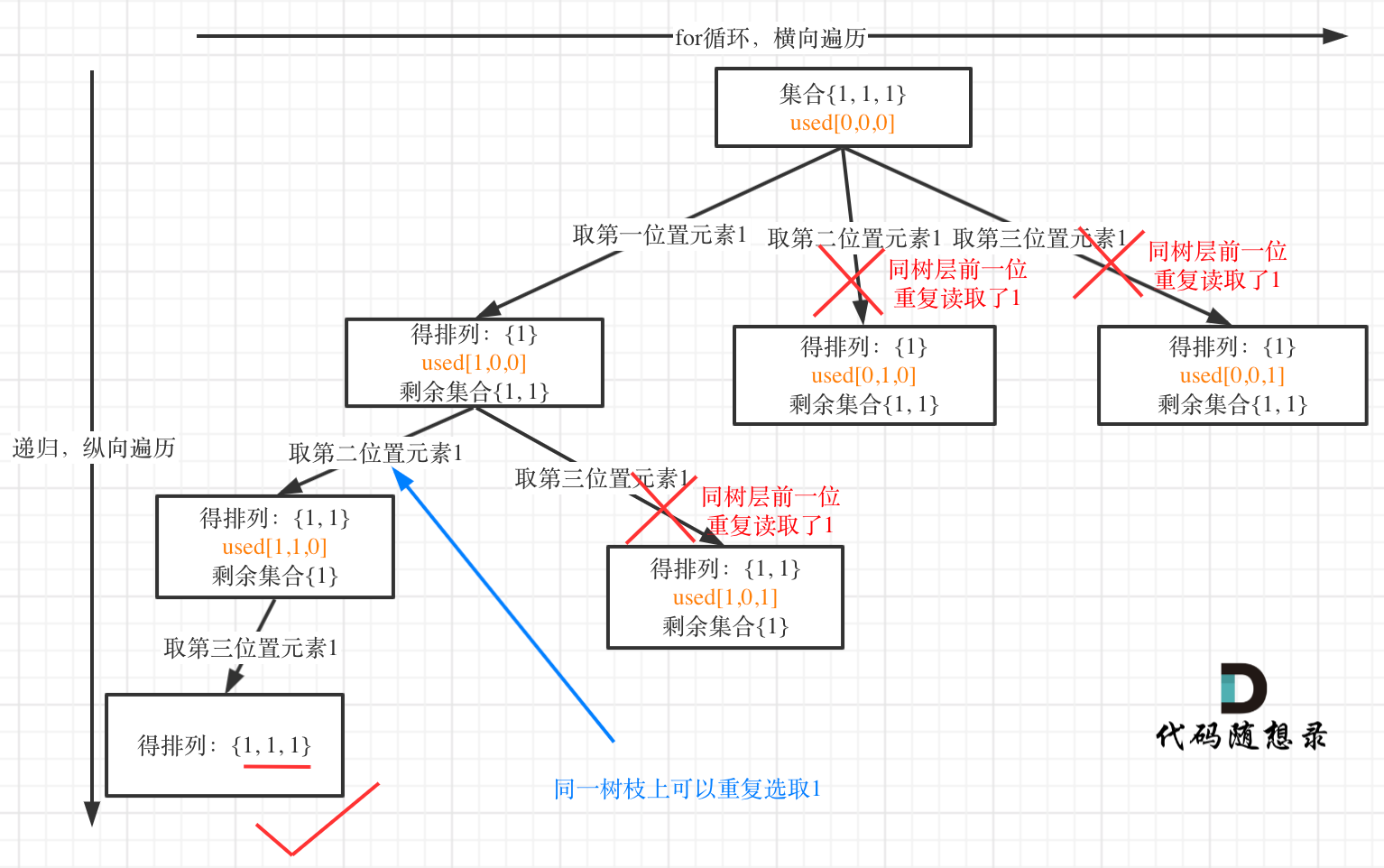
树层上去重(used[i - 1] == false),的树形结构如下:
|
||
|
||
|
||
|
||
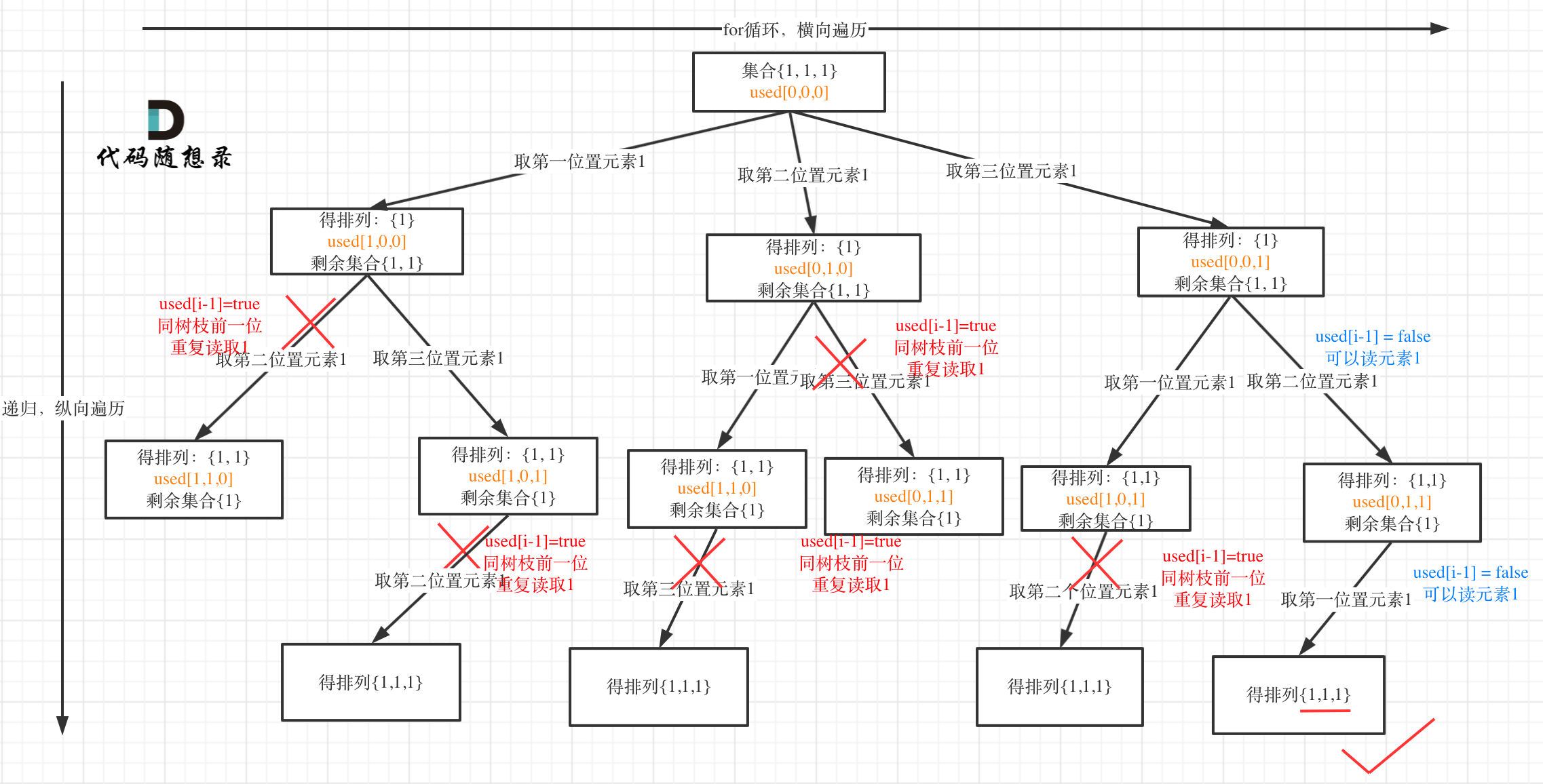
树枝上去重(used[i - 1] == true)的树型结构如下:
|
||
|
||
|
||
|
||
大家应该很清晰的看到,树层上对前一位去重非常彻底,效率很高,树枝上对前一位去重虽然最后可以得到答案,但是做了很多无用搜索。
|
||
|
||
## 总结
|
||
|
||
这道题其实还是用了我们之前讲过的去重思路,但有意思的是,去重的代码中,这么写:
|
||
|
||
```cpp
|
||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
|
||
continue;
|
||
}
|
||
```
|
||
|
||
和这么写:
|
||
|
||
```cpp
|
||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
|
||
continue;
|
||
}
|
||
```
|
||
|
||
都是可以的,这也是很多同学做这道题目困惑的地方,知道`used[i - 1] == false`也行而`used[i - 1] == true`也行,但是就想不明白为啥。
|
||
|
||
所以我通过举[1,1,1]的例子,把这两个去重的逻辑分别抽象成树形结构,大家可以一目了然:为什么两种写法都可以以及哪一种效率更高!
|
||
|
||
这里可能大家又有疑惑,既然 `used[i - 1] == false`也行而`used[i - 1] == true`也行,那为什么还要写这个条件呢?
|
||
|
||
直接这样写 不就完事了?
|
||
|
||
```cpp
|
||
if (i > 0 && nums[i] == nums[i - 1]) {
|
||
continue;
|
||
}
|
||
```
|
||
|
||
其实并不行,一定要加上 `used[i - 1] == false`或者`used[i - 1] == true`,因为 used[i - 1] 要一直是 true 或者一直是false 才可以,而不是 一会是true 一会又是false。 所以这个条件要写上。
|
||
|
||
|
||
是不是豁然开朗了!!
|
||
|
||
## 其他语言版本
|
||
|
||
### java
|
||
|
||
```java
|
||
class Solution {
|
||
//存放结果
|
||
List<List<Integer>> result = new ArrayList<>();
|
||
//暂存结果
|
||
List<Integer> path = new ArrayList<>();
|
||
|
||
public List<List<Integer>> permuteUnique(int[] nums) {
|
||
boolean[] used = new boolean[nums.length];
|
||
Arrays.fill(used, false);
|
||
Arrays.sort(nums);
|
||
backTrack(nums, used);
|
||
return result;
|
||
}
|
||
|
||
private void backTrack(int[] nums, boolean[] used) {
|
||
if (path.size() == nums.length) {
|
||
result.add(new ArrayList<>(path));
|
||
return;
|
||
}
|
||
for (int i = 0; i < nums.length; i++) {
|
||
// used[i - 1] == true,说明同⼀树⽀nums[i - 1]使⽤过
|
||
// used[i - 1] == false,说明同⼀树层nums[i - 1]使⽤过
|
||
// 如果同⼀树层nums[i - 1]使⽤过则直接跳过
|
||
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
|
||
continue;
|
||
}
|
||
//如果同⼀树⽀nums[i]没使⽤过开始处理
|
||
if (used[i] == false) {
|
||
used[i] = true;//标记同⼀树⽀nums[i]使⽤过,防止同一树枝重复使用
|
||
path.add(nums[i]);
|
||
backTrack(nums, used);
|
||
path.remove(path.size() - 1);//回溯,说明同⼀树层nums[i]使⽤过,防止下一树层重复
|
||
used[i] = false;//回溯
|
||
}
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
### python
|
||
|
||
```python
|
||
class Solution:
|
||
def permuteUnique(self, nums):
|
||
nums.sort() # 排序
|
||
result = []
|
||
self.backtracking(nums, [], [False] * len(nums), result)
|
||
return result
|
||
|
||
def backtracking(self, nums, path, used, result):
|
||
if len(path) == len(nums):
|
||
result.append(path[:])
|
||
return
|
||
for i in range(len(nums)):
|
||
if (i > 0 and nums[i] == nums[i - 1] and not used[i - 1]) or used[i]:
|
||
continue
|
||
used[i] = True
|
||
path.append(nums[i])
|
||
self.backtracking(nums, path, used, result)
|
||
path.pop()
|
||
used[i] = False
|
||
|
||
```
|
||
|
||
### Go
|
||
|
||
```go
|
||
var (
|
||
res [][]int
|
||
path []int
|
||
st []bool // state的缩写
|
||
)
|
||
func permuteUnique(nums []int) [][]int {
|
||
res, path = make([][]int, 0), make([]int, 0, len(nums))
|
||
st = make([]bool, len(nums))
|
||
sort.Ints(nums)
|
||
dfs(nums, 0)
|
||
return res
|
||
}
|
||
|
||
func dfs(nums []int, cur int) {
|
||
if cur == len(nums) {
|
||
tmp := make([]int, len(path))
|
||
copy(tmp, path)
|
||
res = append(res, tmp)
|
||
}
|
||
for i := 0; i < len(nums); i++ {
|
||
if i != 0 && nums[i] == nums[i-1] && !st[i-1] { // 去重,用st来判别是深度还是广度
|
||
continue
|
||
}
|
||
if !st[i] {
|
||
path = append(path, nums[i])
|
||
st[i] = true
|
||
dfs(nums, cur + 1)
|
||
st[i] = false
|
||
path = path[:len(path)-1]
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
### Javascript
|
||
|
||
```javascript
|
||
var permuteUnique = function (nums) {
|
||
nums.sort((a, b) => {
|
||
return a - b
|
||
})
|
||
let result = []
|
||
let path = []
|
||
|
||
function backtracing( used) {
|
||
if (path.length === nums.length) {
|
||
result.push([...path])
|
||
return
|
||
}
|
||
for (let i = 0; i < nums.length; i++) {
|
||
if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) {
|
||
continue
|
||
}
|
||
if (!used[i]) {
|
||
used[i] = true
|
||
path.push(nums[i])
|
||
backtracing(used)
|
||
path.pop()
|
||
used[i] = false
|
||
}
|
||
|
||
|
||
}
|
||
}
|
||
backtracing([])
|
||
return result
|
||
};
|
||
|
||
```
|
||
|
||
### TypeScript
|
||
|
||
```typescript
|
||
function permuteUnique(nums: number[]): number[][] {
|
||
nums.sort((a, b) => a - b);
|
||
const resArr: number[][] = [];
|
||
const usedArr: boolean[] = new Array(nums.length).fill(false);
|
||
backTracking(nums, []);
|
||
return resArr;
|
||
function backTracking(nums: number[], route: number[]): void {
|
||
if (route.length === nums.length) {
|
||
resArr.push([...route]);
|
||
return;
|
||
}
|
||
for (let i = 0, length = nums.length; i < length; i++) {
|
||
if (i > 0 && nums[i] === nums[i - 1] && usedArr[i - 1] === false) continue;
|
||
if (usedArr[i] === false) {
|
||
route.push(nums[i]);
|
||
usedArr[i] = true;
|
||
backTracking(nums, route);
|
||
usedArr[i] = false;
|
||
route.pop();
|
||
}
|
||
}
|
||
}
|
||
};
|
||
```
|
||
|
||
### Swift
|
||
|
||
```swift
|
||
func permuteUnique(_ nums: [Int]) -> [[Int]] {
|
||
let nums = nums.sorted() // 先排序,以方便相邻元素去重
|
||
var result = [[Int]]()
|
||
var path = [Int]()
|
||
var used = [Bool](repeating: false, count: nums.count)
|
||
func backtracking() {
|
||
if path.count == nums.count {
|
||
result.append(path)
|
||
return
|
||
}
|
||
|
||
for i in 0 ..< nums.count {
|
||
// !used[i - 1]表示同一树层nums[i - 1]使用过,直接跳过,这一步很关键!
|
||
if i > 0, nums[i] == nums[i - 1], !used[i - 1] { continue }
|
||
if used[i] { continue }
|
||
used[i] = true
|
||
path.append(nums[i])
|
||
backtracking()
|
||
// 回溯
|
||
path.removeLast()
|
||
used[i] = false
|
||
}
|
||
}
|
||
backtracking()
|
||
return result
|
||
}
|
||
```
|
||
|
||
### Rust
|
||
|
||
```Rust
|
||
impl Solution {
|
||
fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, nums: &Vec<i32>, used: &mut Vec<bool>) {
|
||
let len = nums.len();
|
||
if path.len() == len {
|
||
result.push(path.clone());
|
||
return;
|
||
}
|
||
for i in 0..len {
|
||
if i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false { continue; }
|
||
if used[i] == false {
|
||
used[i] = true;
|
||
path.push(nums[i]);
|
||
Self::backtracking(result, path, nums, used);
|
||
path.pop();
|
||
used[i] = false;
|
||
}
|
||
}
|
||
}
|
||
|
||
pub fn permute_unique(nums: Vec<i32>) -> Vec<Vec<i32>> {
|
||
let mut result: Vec<Vec<i32>> = Vec::new();
|
||
let mut path: Vec<i32> = Vec::new();
|
||
let mut used = vec![false; nums.len()];
|
||
let mut nums= nums;
|
||
nums.sort();
|
||
Self::backtracking(&mut result, &mut path, &nums, &mut used);
|
||
result
|
||
}
|
||
}
|
||
```
|
||
|
||
### C
|
||
|
||
```c
|
||
//临时数组
|
||
int *path;
|
||
//返回数组
|
||
int **ans;
|
||
int *used;
|
||
int pathTop, ansTop;
|
||
|
||
//拷贝path到ans中
|
||
void copyPath() {
|
||
int *tempPath = (int*)malloc(sizeof(int) * pathTop);
|
||
int i;
|
||
for(i = 0; i < pathTop; ++i) {
|
||
tempPath[i] = path[i];
|
||
}
|
||
ans[ansTop++] = tempPath;
|
||
}
|
||
|
||
void backTracking(int* used, int *nums, int numsSize) {
|
||
//若path中元素个数等于numsSize,将path拷贝入ans数组中
|
||
if(pathTop == numsSize)
|
||
copyPath();
|
||
int i;
|
||
for(i = 0; i < numsSize; i++) {
|
||
//若当前元素已被使用
|
||
//或前一位元素与当前元素值相同但并未被使用
|
||
//则跳过此分支
|
||
if(used[i] || (i != 0 && nums[i] == nums[i-1] && used[i-1] == 0))
|
||
continue;
|
||
|
||
//将当前元素的使用情况设为True
|
||
used[i] = 1;
|
||
path[pathTop++] = nums[i];
|
||
backTracking(used, nums, numsSize);
|
||
used[i] = 0;
|
||
--pathTop;
|
||
}
|
||
}
|
||
|
||
int cmp(void* elem1, void* elem2) {
|
||
return *((int*)elem1) - *((int*)elem2);
|
||
}
|
||
|
||
int** permuteUnique(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
|
||
//排序数组
|
||
qsort(nums, numsSize, sizeof(int), cmp);
|
||
//初始化辅助变量
|
||
pathTop = ansTop = 0;
|
||
path = (int*)malloc(sizeof(int) * numsSize);
|
||
ans = (int**)malloc(sizeof(int*) * 1000);
|
||
//初始化used辅助数组
|
||
used = (int*)malloc(sizeof(int) * numsSize);
|
||
int i;
|
||
for(i = 0; i < numsSize; i++) {
|
||
used[i] = 0;
|
||
}
|
||
|
||
backTracking(used, nums, numsSize);
|
||
|
||
//设置返回的数组的长度
|
||
*returnSize = ansTop;
|
||
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
|
||
int z;
|
||
for(z = 0; z < ansTop; z++) {
|
||
(*returnColumnSizes)[z] = numsSize;
|
||
}
|
||
return ans;
|
||
}
|
||
```
|
||
|
||
### Scala
|
||
|
||
```scala
|
||
object Solution {
|
||
import scala.collection.mutable
|
||
def permuteUnique(nums: Array[Int]): List[List[Int]] = {
|
||
var result = mutable.ListBuffer[List[Int]]()
|
||
var path = mutable.ListBuffer[Int]()
|
||
var num = nums.sorted // 首先对数据进行排序
|
||
|
||
def backtracking(used: Array[Boolean]): Unit = {
|
||
if (path.size == num.size) {
|
||
// 如果path的size等于num了,那么可以添加到结果集
|
||
result.append(path.toList)
|
||
return
|
||
}
|
||
// 循环守卫,当前元素没被使用过就进入循环体
|
||
for (i <- num.indices if used(i) == false) {
|
||
// 当前索引为0,不存在和前一个数字相等可以进入回溯
|
||
// 当前索引值和上一个索引不相等,可以回溯
|
||
// 前一个索引对应的值没有被选,可以回溯
|
||
// 因为Scala没有continue,只能将逻辑反过来写
|
||
if (i == 0 || (i > 0 && num(i) != num(i - 1)) || used(i-1) == false) {
|
||
used(i) = true
|
||
path.append(num(i))
|
||
backtracking(used)
|
||
path.remove(path.size - 1)
|
||
used(i) = false
|
||
}
|
||
}
|
||
}
|
||
|
||
backtracking(new Array[Boolean](nums.length))
|
||
result.toList
|
||
}
|
||
}
|
||
```
|
||
|
||
<p align="center">
|
||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||
</a>
|