leetcode-master/problems/0827.最大人工岛.md

827. 最大人工岛

给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。

返回执行此操作后，grid 中最大的岛屿面积是多少？

岛屿 由一组上、下、左、右四个方向相连的 1 形成。

示例 1:

• 输入: grid = 1, 0], [0, 1
• 输出: 3
• 解释: 将一格0变成1，最终连通两个小岛得到面积为 3 的岛屿。

示例 2:

• 输入: grid = 1, 1], [1, 0
• 输出: 4
• 解释: 将一格0变成1，岛屿的面积扩大为 4。

示例 3:

• 输入: grid = 1, 1], [1, 1
• 输出: 4
• 解释: 没有0可以让我们变成1，面积依然为 4。

思路

本题的一个暴力想法，应该是遍历地图尝试 将每一个 0 改成1，然后去搜索地图中的最大的岛屿面积。

计算地图的最大面积：遍历地图 + 深搜岛屿，时间复杂度为 n * n

每改变一个0的方格，都需要重新计算一个地图的最大面积，所以 整体时间复杂度为：n^4。

如果对深度优先搜索不了解的录友，可以看这里：深度优先搜索精讲

优化思路

其实每次深搜遍历计算最大岛屿面积，我们都做了很多重复的工作。

只要把深搜就可以并每个岛屿的面积记录下来就好。

第一步：一次遍历地图，得出各个岛屿的面积，并做编号记录。可以使用map记录，key为岛屿编号，value为岛屿面积 第二步：在遍历地图，遍历0的方格（因为要将0变成1），并统计该1（由0变成的1）周边岛屿面积，将其相邻面积相加在一起，遍历所有 0 之后，就可以得出 选一个0变成1 之后的最大面积。

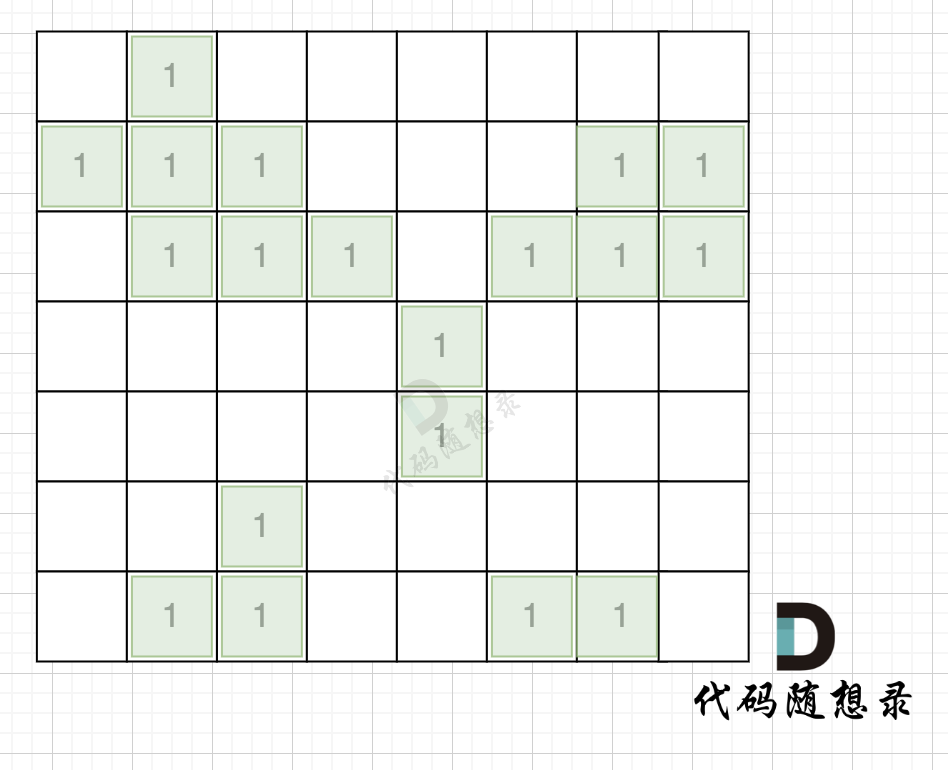
拿如下地图的岛屿情况来举例： （1为陆地）

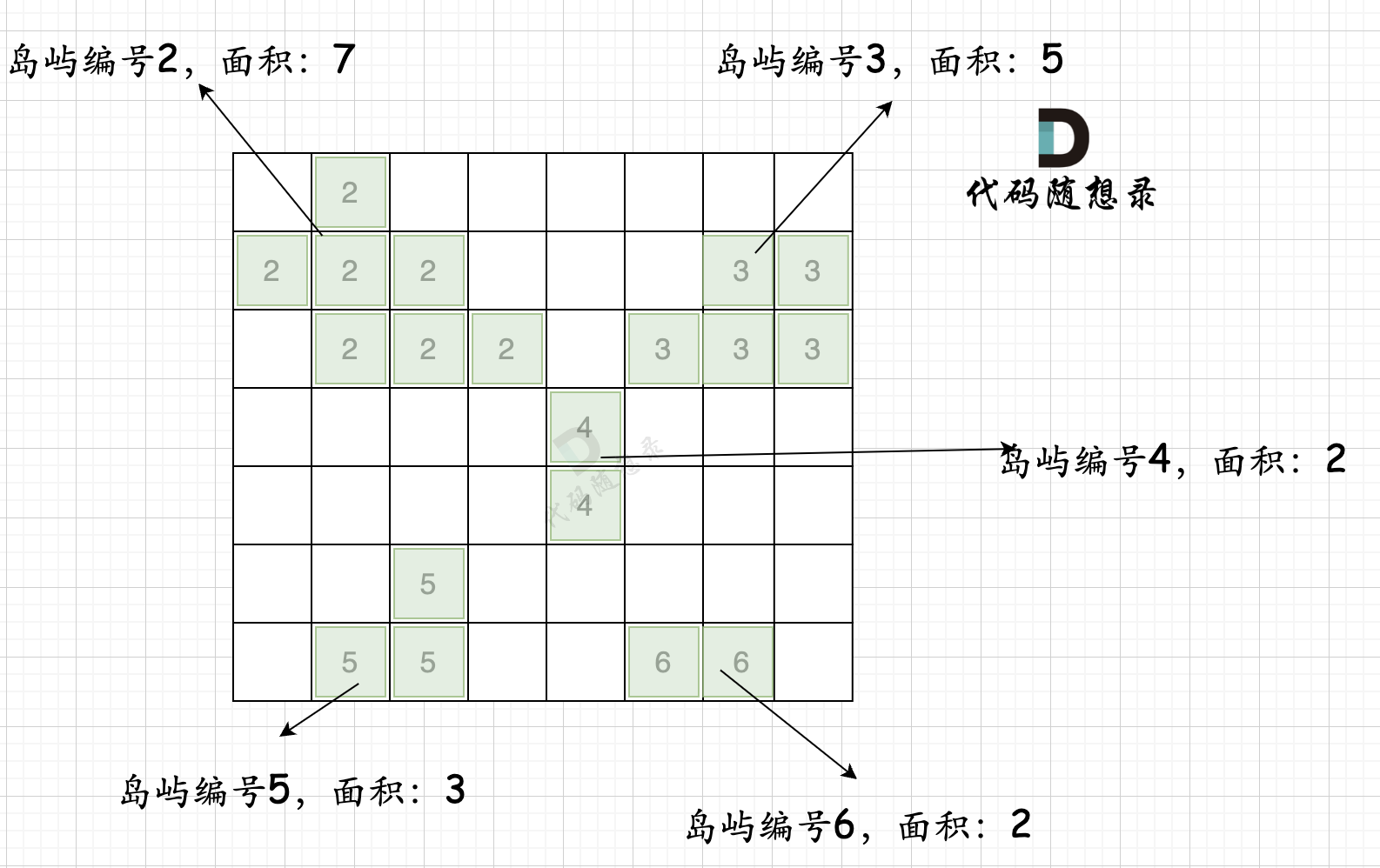
第一步，则遍历题目，并将岛屿到编号和面积上的统计，过程如图所示：

本过程代码如下：

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
    if (visited[x][y] || grid[x][y] == 0) return; // 终止条件：访问过的节点 或者 遇到海水
    visited[x][y] = true; // 标记访问过
    grid[x][y] = mark; // 给陆地标记新标签
    count++;
    for (int i = 0; i < 4; i++) {
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
        if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 越界了，直接跳过
        dfs(grid, visited, nextx, nexty, mark);
    }
}

int largestIsland(vector<vector<int>>& grid) {
    int n = grid.size(), m = grid[0].size();
    vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
    unordered_map<int ,int> gridNum;
    int mark = 2; // 记录每个岛屿的编号
    bool isAllGrid = true; // 标记是否整个地图都是陆地
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grid[i][j] == 0) isAllGrid = false;
            if (!visited[i][j] && grid[i][j] == 1) {
                count = 0;
                dfs(grid, visited, i, j, mark); // 将与其链接的陆地都标记上 true
                gridNum[mark] = count; // 记录每一个岛屿的面积
                mark++; // 记录下一个岛屿编号
            }
        }
    }
}

这个过程时间复杂度 n * n 。可能有录友想：分明是两个for循环下面套这一个dfs，时间复杂度怎么回事 n * n呢？

其实大家可以自己看代码的时候，n * n这个方格地图中，每个节点我们就遍历一次，并不会重复遍历。

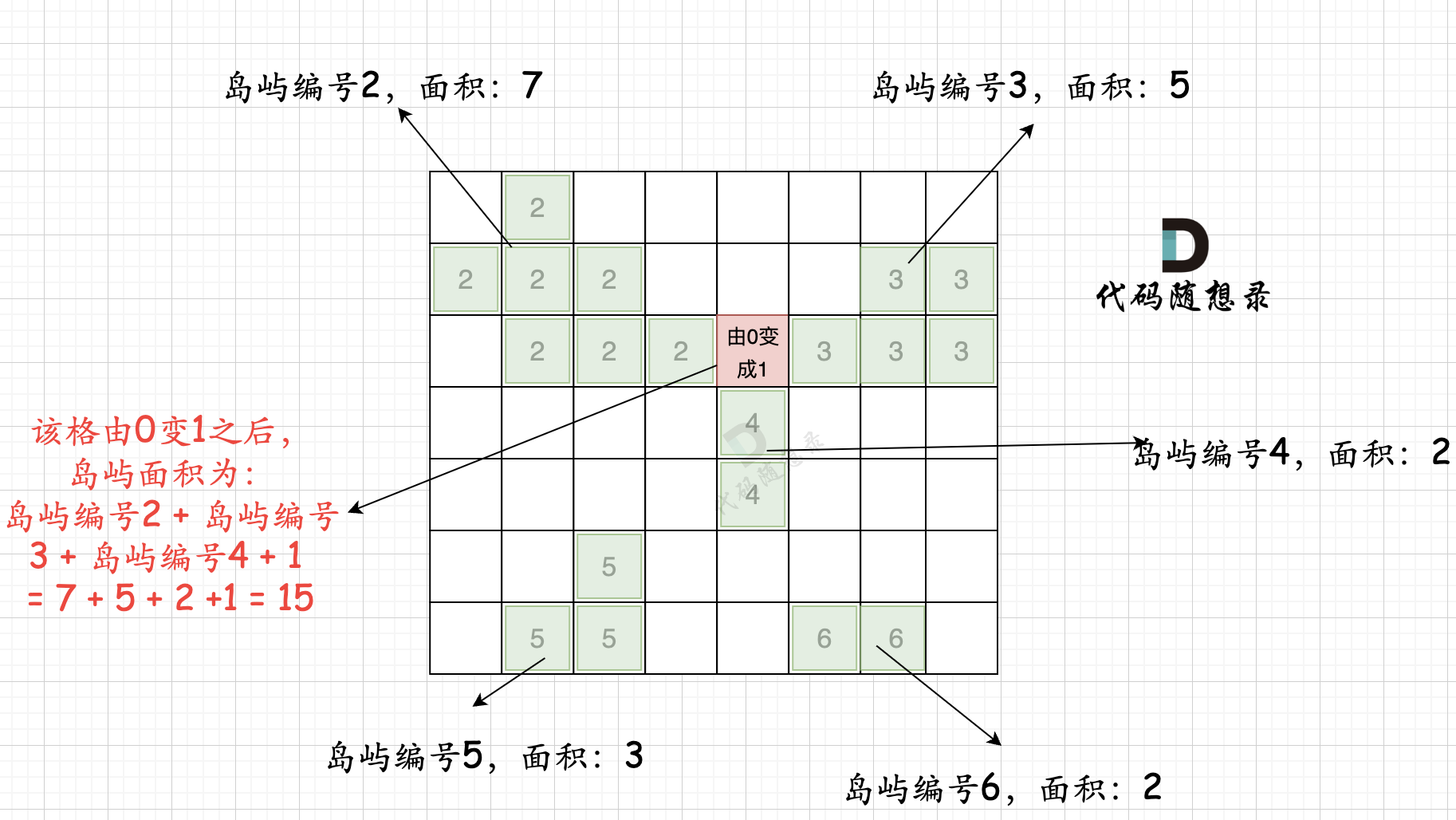
第二步过程如图所示：

也就是遍历每一个0的方格，并统计其相邻岛屿面积，最后取一个最大值。

这个过程的时间复杂度也为 n * n。

所以整个解法的时间复杂度，为 n * n + n * n 也就是 n^2。

最后，整体代码如下：

class Solution {
private:
    int count;
    int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
    void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
        if (visited[x][y] || grid[x][y] == 0) return; // 终止条件：访问过的节点 或者 遇到海水
        visited[x][y] = true; // 标记访问过
        grid[x][y] = mark; // 给陆地标记新标签
        count++;
        for (int i = 0; i < 4; i++) {
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 越界了，直接跳过
            dfs(grid, visited, nextx, nexty, mark);
        }
    }

public:
    int largestIsland(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
        unordered_map<int ,int> gridNum;
        int mark = 2; // 记录每个岛屿的编号
        bool isAllGrid = true; // 标记是否整个地图都是陆地
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (grid[i][j] == 0) isAllGrid = false;
                if (!visited[i][j] && grid[i][j] == 1) {
                    count = 0;
                    dfs(grid, visited, i, j, mark); // 将与其链接的陆地都标记上 true
                    gridNum[mark] = count; // 记录每一个岛屿的面积
                    mark++; // 记录下一个岛屿编号
                }
            }
        }
        if (isAllGrid) return n * m; // 如果都是陆地，返回全面积

        // 以下逻辑是根据添加陆地的位置，计算周边岛屿面积之和
        int result = 0; // 记录最后结果
        unordered_set<int> visitedGrid; // 标记访问过的岛屿
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                int count = 1; // 记录连接之后的岛屿数量
                visitedGrid.clear(); // 每次使用时，清空
                if (grid[i][j] == 0) {
                    for (int k = 0; k < 4; k++) {
                        int neari = i + dir[k][1]; // 计算相邻坐标
                        int nearj = j + dir[k][0];
                        if (neari < 0 || neari >= grid.size() || nearj < 0 || nearj >= grid[0].size()) continue;
                        if (visitedGrid.count(grid[neari][nearj])) continue; // 添加过的岛屿不要重复添加
                        // 把相邻四面的岛屿数量加起来
                        count += gridNum[grid[neari][nearj]];
                        visitedGrid.insert(grid[neari][nearj]); // 标记该岛屿已经添加过
                    }
                }
                result = max(result, count);
            }
        }
        return result;
    }
};