leetcode-master/problems/1971.寻找图中是否存在路径.md

1971. 寻找图中是否存在路径

题目链接

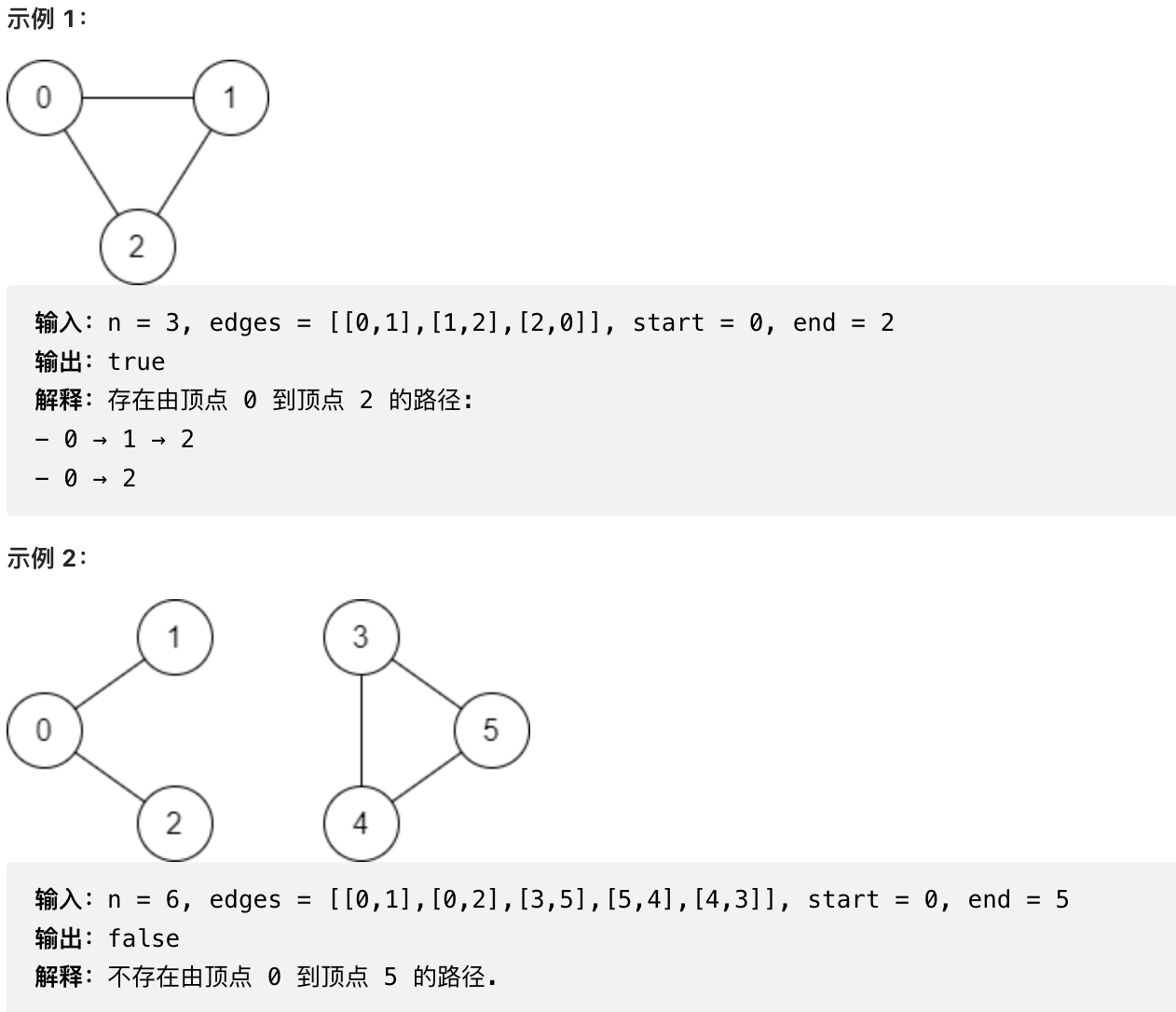
有一个具有 n个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 start 开始，到顶点 end 结束的 有效路径 。

给你数组 edges 和整数 n、start和end，如果从 start 到 end 存在 有效路径 ，则返回 true，否则返回 false 。

提示:

• 1 <= n <= 2 * 10^5
• 0 <= edges.length <= 2 * 10^5
• edges[i].length == 2
• 0 <= ui, vi <= n - 1
• ui != vi
• 0 <= start, end <= n - 1
• 不存在双向边
• 不存在指向顶点自身的边

思路

这道题目也是并查集基础题目。

首先要知道并查集可以解决什么问题呢？

主要就是集合问题，两个节点在不在一个集合，也可以将两个节点添加到一个集合中。

这里整理出我的并查集模板如下：

int n = 1005; // 节点数量3 到 1000
int father[1005];

// 并查集初始化
void init() {
    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }
}
// 并查集里寻根的过程
int find(int u) {
    return u == father[u] ? u : father[u] = find(father[u]);
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
    u = find(u);
    v = find(v);
    if (u == v) return ;
    father[v] = u;
}
// 判断 u 和 v是否找到同一个根
bool same(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

以上模板汇总，只要修改 n 和father数组的大小就可以了。

并查集主要有三个功能。

1. 寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个
2. 将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
3. 判断两个节点是否在同一个集合，函数：same(int u, int v)，就是判断两个节点是不是同一个根节点

简单介绍并查集之后，我们再来看一下这道题目。

为什么说这道题目是并查集基础题目，因为 可以直接套用模板。

使用join(int u, int v)将每条边加入到并查集。

最后 same(int u, int v) 判断是否是同一个根 就可以里。

代码如下：

class Solution {

private:
    int n = 200005; // 节点数量 20000 
    int father[200005];

    // 并查集初始化
    void init() {
        for (int i = 0; i < n; ++i) {
            father[i] = i;
        }
    }
    // 并查集里寻根的过程
    int find(int u) {
        return u == father[u] ? u : father[u] = find(father[u]);
    }
    // 将v->u 这条边加入并查集
    void join(int u, int v) {
        u = find(u);
        v = find(v);
        if (u == v) return ;
        father[v] = u;
    }
    // 判断 u 和 v是否找到同一个根，本题用不上
    bool same(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }

public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        init(); 
        for (int i = 0; i < edges.size(); i++) {
            join(edges[i][0], edges[i][1]); 
        }
        return same(source, destination);
    }
};