leetcode-master/problems/0104.二叉树的最大深度.md

题目地址

https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/

思路

递归法

按照递归三部曲，来看看如何来写。

1. 确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。

代码如下：

int getDepth(TreeNode* node)

2. 确定终止条件：如果为空节点的话，就返回0，表示高度为0。

代码如下：

if (node == NULL) return 0;

3. 确定单层递归的逻辑：先求它的左子树的深度，再求的右子树的深度，最后去左右深度最大的数值+1 就是目前节点为根节点的树的深度。

代码如下：

int leftDepth = getDepth(node->left);
int rightDepth = getDepth(node->right);
int depth = 1 + max(leftDepth, rightDepth);
return depth;

所以整体代码如下：

class Solution {
public:
    int getDepth(TreeNode* node) {
        if (node == NULL) return 0;
        return 1 + max(getDepth(node->left), getDepth(node->right));
    }
    int maxDepth(TreeNode* root) {
        return getDepth(root);
    }
};

迭代法

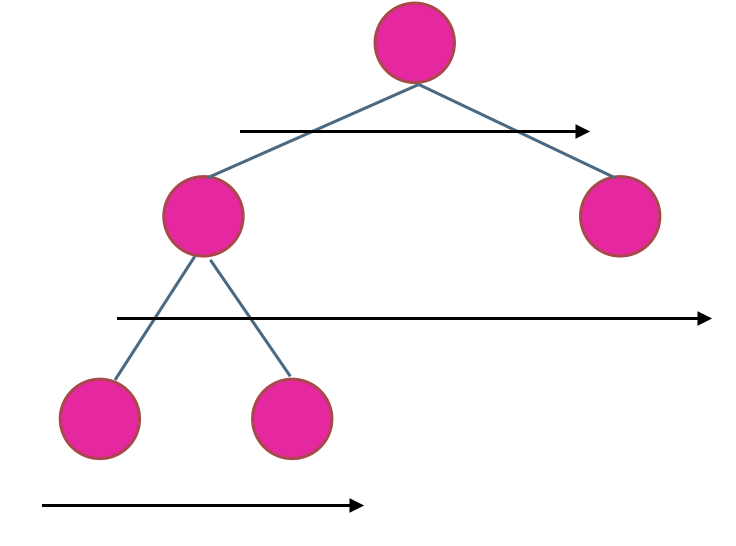
在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，如图所示：

所以这道题依然是一道模板题，依然可以使用二叉树层序遍历的模板来解决的。

我总结的算法模板会放到这里leetcode刷题攻略，大家可以去看一下。

代码如下：

C++代码

递归

class Solution {
public:
    int getDepth(TreeNode* node) {
        if (node == NULL) return 0;
        return 1 + max(getDepth(node->left), getDepth(node->right));
    }
    int maxDepth(TreeNode* root) {
        return getDepth(root);
    }
};

迭代法

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == NULL) return 0;
        int depth = 0;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()) {
            int size = que.size(); // 必须要这么写，要固定size大小
            depth++;    // 记录深度
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return depth;
    }
};

更多算法干货文章持续更新，可以微信搜索「代码随想录」第一时间围观，关注后，回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等，就可以获得我多年整理的学习资料。