mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-05 14:46:51 +08:00
Update
This commit is contained in:
@ -3,8 +3,8 @@
|
||||
👉 推荐 [Gitee同步](https://gitee.com/programmercarl/leetcode-master)
|
||||
|
||||
> 1. **介绍** :本项目是一套完整的刷题计划,旨在帮助大家少走弯路,循序渐进学算法,[关注作者](#关于作者)
|
||||
> 2. **正式出版** :[《代码随想录》](https://programmercarl.com/other/publish.html) 。
|
||||
> 3. **PDF版本** :[「代码随想录」算法精讲 PDF 版本](https://programmercarl.com/other/algo_pdf.html) 。
|
||||
> 2. **正式出版** :[《代码随想录》](https://programmercarl.com/qita/publish.html) 。
|
||||
> 3. **PDF版本** :[「代码随想录」算法精讲 PDF 版本](https://programmercarl.com/qita/algo_pdf.html) 。
|
||||
> 4. **算法公开课** :[《代码随想录》算法视频公开课](https://www.bilibili.com/video/BV1fA4y1o715) 。
|
||||
> 5. **最强八股文** :[代码随想录知识星球精华PDF](https://www.programmercarl.com/other/kstar_baguwen.html) 。
|
||||
> 6. **刷题顺序** :README已经将刷题顺序排好了,按照顺序一道一道刷就可以。
|
||||
|
||||
@ -52,7 +52,7 @@ graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节
|
||||
|
||||
至于 单一路径,和路径集合可以放在全局变量,那么代码是这样的:
|
||||
|
||||
```c++
|
||||
```CPP
|
||||
vector<vector<int>> result; // 收集符合条件的路径
|
||||
vector<int> path; // 0节点到终点的路径
|
||||
// x:目前遍历的节点
|
||||
@ -71,7 +71,7 @@ void dfs (vector<vector<int>>& graph, int x)
|
||||
所以 但 x 等于 graph.size() - 1 的时候就找到一条有效路径。 代码如下:
|
||||
|
||||
|
||||
```c++
|
||||
```CPP
|
||||
// 要求从节点 0 到节点 n-1 的路径并输出,所以是 graph.size() - 1
|
||||
if (x == graph.size() - 1) { // 找到符合条件的一条路径
|
||||
result.push_back(path); // 收集有效路径
|
||||
@ -104,13 +104,13 @@ path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
|
||||
|
||||
进入下一层递归
|
||||
|
||||
```C++
|
||||
```CPP
|
||||
dfs(graph, graph[x][i]); // 进入下一层递归
|
||||
```
|
||||
|
||||
最后就是回溯的过程,撤销本次添加节点的操作。 该过程整体代码:
|
||||
|
||||
```C++
|
||||
```CPP
|
||||
for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点
|
||||
path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
|
||||
dfs(graph, graph[x][i]); // 进入下一层递归
|
||||
@ -120,7 +120,7 @@ for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节
|
||||
|
||||
本题整体代码如下:
|
||||
|
||||
```c++
|
||||
```CPP
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result; // 收集符合条件的路径
|
||||
|
||||
@ -16,16 +16,7 @@
|
||||
|
||||
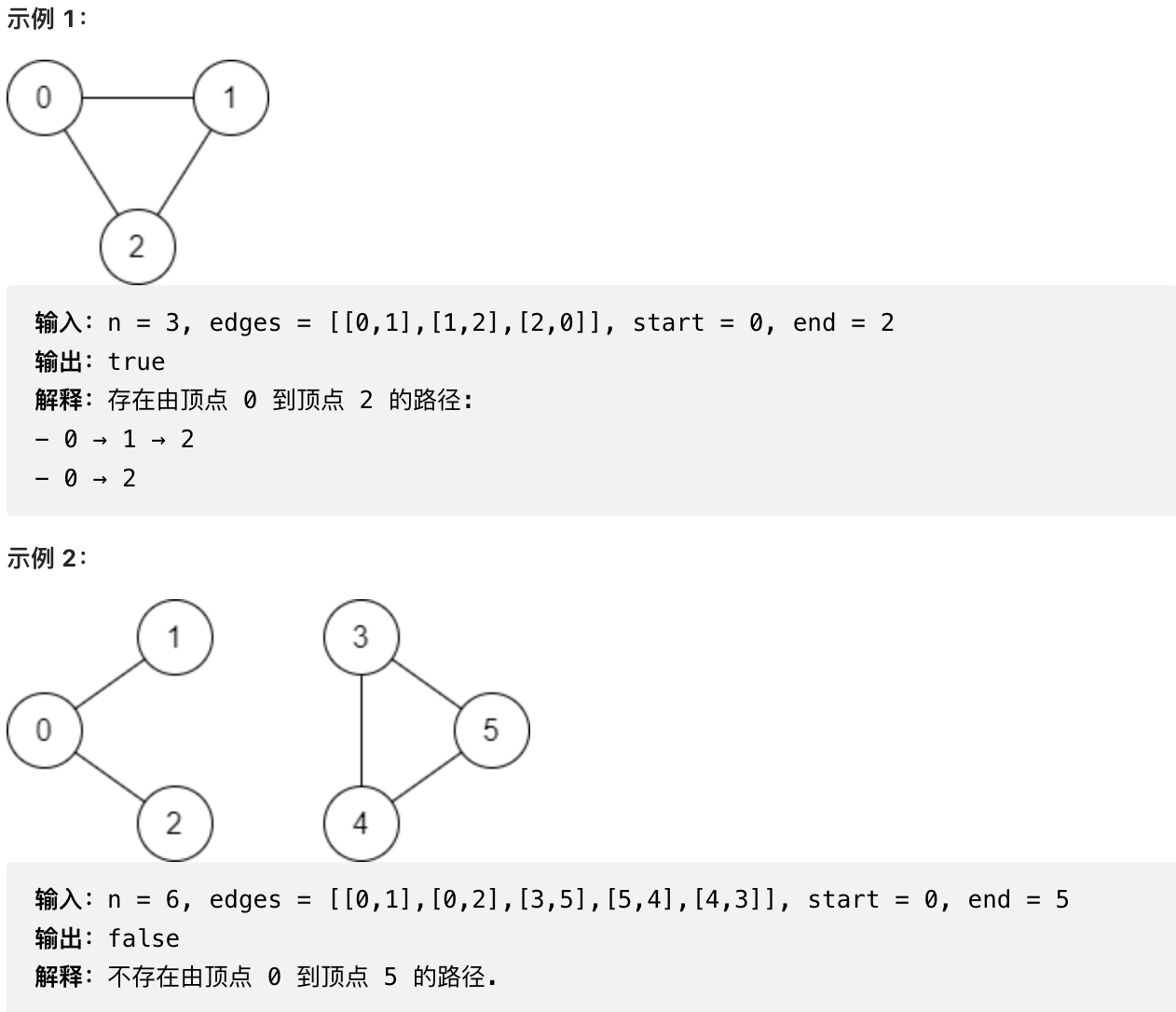
|
||||
|
||||
提示:
|
||||
|
||||
- 1 <= n <= 2 \* 10^5
|
||||
- 0 <= edges.length <= 2 \* 10^5
|
||||
- edges[i].length == 2
|
||||
- 0 <= ui, vi <= n - 1
|
||||
- ui != vi
|
||||
- 0 <= start, end <= n - 1
|
||||
- 不存在双向边
|
||||
- 不存在指向顶点自身的边
|
||||
|
||||
## 思路
|
||||
|
||||
|
||||
@ -1,5 +1,5 @@
|
||||
|
||||
# 寻宝
|
||||
# kruskal算法精讲
|
||||
|
||||
[卡码网:53. 寻宝](https://kamacoder.com/problempage.php?pid=1053)
|
||||
|
||||
@ -1,5 +1,5 @@
|
||||
|
||||
# 寻宝
|
||||
# prim算法精讲
|
||||
|
||||
[卡码网:53. 寻宝](https://kamacoder.com/problempage.php?pid=1053)
|
||||
|
||||
286
problems/kama0094.城市间货物运输I-SPFA.md
Normal file
286
problems/kama0094.城市间货物运输I-SPFA.md
Normal file
@ -0,0 +1,286 @@
|
||||
|
||||
# Bellman_ford 队列优化算法(又名SPFA)
|
||||
|
||||
[卡码网: 94. 城市间货物运输 I](https://kamacoder.com/problempage.php?pid=1152)
|
||||
|
||||
题目描述
|
||||
|
||||
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
|
||||
|
||||
|
||||
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
|
||||
|
||||
|
||||
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。如果最低运输成本是一个负数,它表示在遵循最优路径的情况下,运输过程中反而能够实现盈利。
|
||||
|
||||
|
||||
城市 1 到城市 n 之间可能会出现没有路径的情况,同时保证道路网络中不存在任何负权回路。
|
||||
|
||||
输入描述
|
||||
|
||||
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
|
||||
|
||||
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v(单向图)。
|
||||
|
||||
输出描述
|
||||
|
||||
如果能够从城市 1 到连通到城市 n, 请输出一个整数,表示运输成本。如果该整数是负数,则表示实现了盈利。如果从城市 1 没有路径可达城市 n,请输出 "unconnected"。
|
||||
|
||||
输入示例:
|
||||
|
||||
```
|
||||
6 7
|
||||
5 6 -2
|
||||
1 2 1
|
||||
5 3 1
|
||||
2 5 2
|
||||
2 4 -3
|
||||
4 6 4
|
||||
1 3 5
|
||||
```
|
||||
|
||||
## 思路
|
||||
|
||||
本题我们来系统讲解 Bellman_ford 队列优化算法 ,也叫SPFA算法(Shortest Path Faster Algorithm)。
|
||||
|
||||
> SPFA的称呼来自 1994年西南交通大学段凡丁的论文,其实Bellman_ford 提出后不久 (20世纪50年代末期) 就有队列优化的版本,国际上不承认这个算法是是国内提出的。 所以国际上一般称呼 算法为 Bellman_ford 队列优化算法(Queue improved Bellman-Ford)
|
||||
|
||||
大家知道以上来历,知道 SPFA 和 Bellman_ford 队列优化算法 指的都是一个算法就好。
|
||||
|
||||
如果大家还不够了解 Bellman_ford 算法,强烈建议按照《代码随想录》的顺序学习,否则可能看不懂下面的讲解。
|
||||
|
||||
大家可以发现 Bellman_ford 算法每次松弛 都是对所有边进行松弛。
|
||||
|
||||
但真正有效的松弛,是基于已经计算过的节点在做的松弛。
|
||||
|
||||
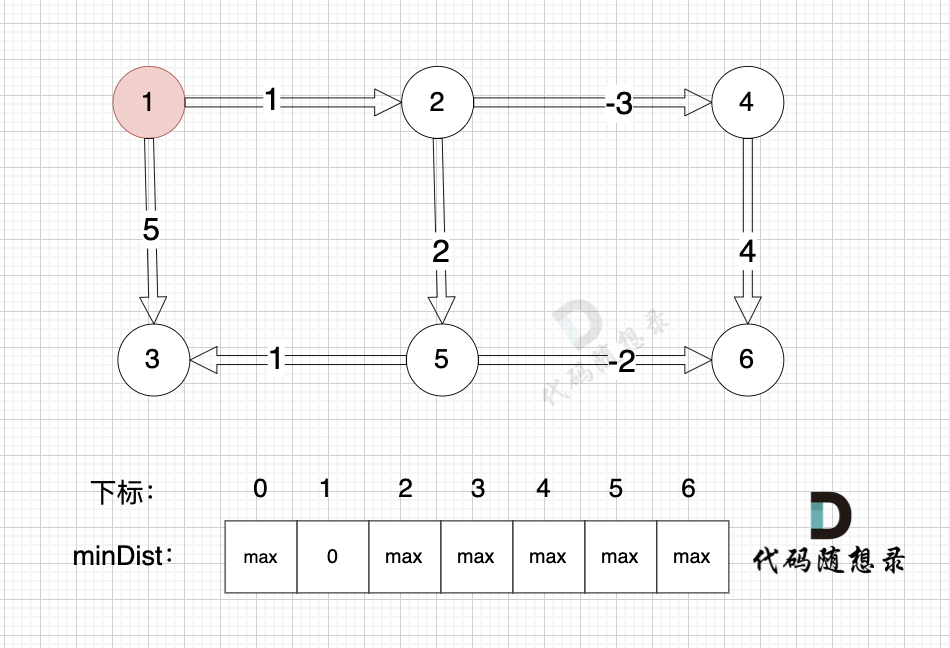
给大家举一个例子:
|
||||
|
||||
|
||||
|
||||
本图中,对所有边进行松弛,真正有效的松弛,只有松弛 边(节点1->节点2) 和 边(节点1->节点5) 。
|
||||
|
||||
而松弛 边(节点4->节点6) ,边(节点5->节点3)等等 都是无效的操作,因为 节点4 和 节点 5 都是没有被计算过的节点。
|
||||
|
||||
|
||||
所以 Bellman_ford 算法 每次都是对所有边进行松弛,其实是多做了一些无用功。
|
||||
|
||||
**只需要对 上一次松弛的时候更新过的节点作为出发节点所连接的边 进行松弛就够了**。
|
||||
|
||||
基于以上思路,如何记录 上次松弛的时候更新过的节点呢?
|
||||
|
||||
用队列来记录。
|
||||
|
||||
接下来来举例这个队列是如何工作的。
|
||||
|
||||
以示例给出的所有边为例:
|
||||
|
||||
```
|
||||
5 6 -2
|
||||
1 2 1
|
||||
5 3 1
|
||||
2 5 2
|
||||
2 4 -3
|
||||
4 6 4
|
||||
1 3 5
|
||||
```
|
||||
|
||||
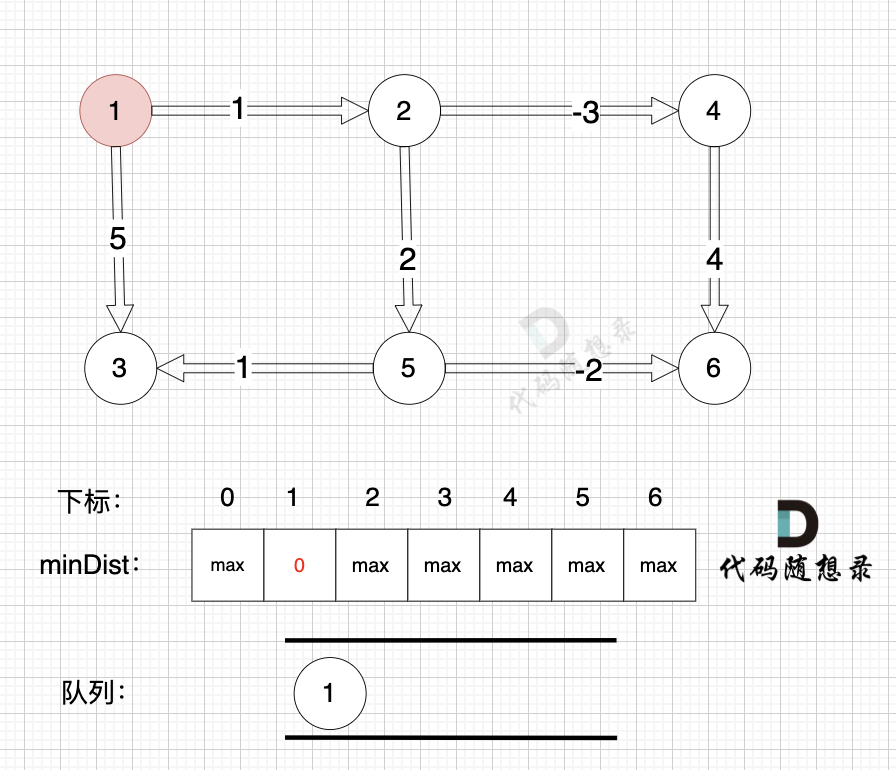
我们依然使用**minDist数组来表达 起点到各个节点的最短距离**,例如minDist[3] = 5 表示起点到达节点3 的最小距离为5
|
||||
|
||||
初始化,起点为节点1, 起点到起点的最短距离为0,所以minDist[1] 为 0。 将节点1 加入队列 (下次松弛送节点1开始)
|
||||
|
||||
|
||||
|
||||
------------
|
||||
|
||||
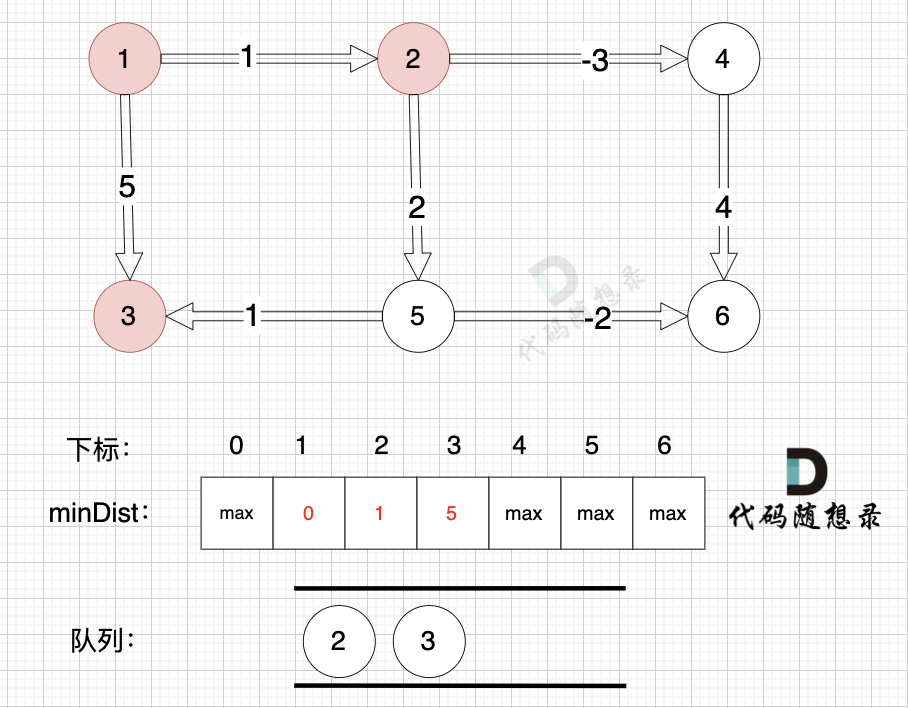
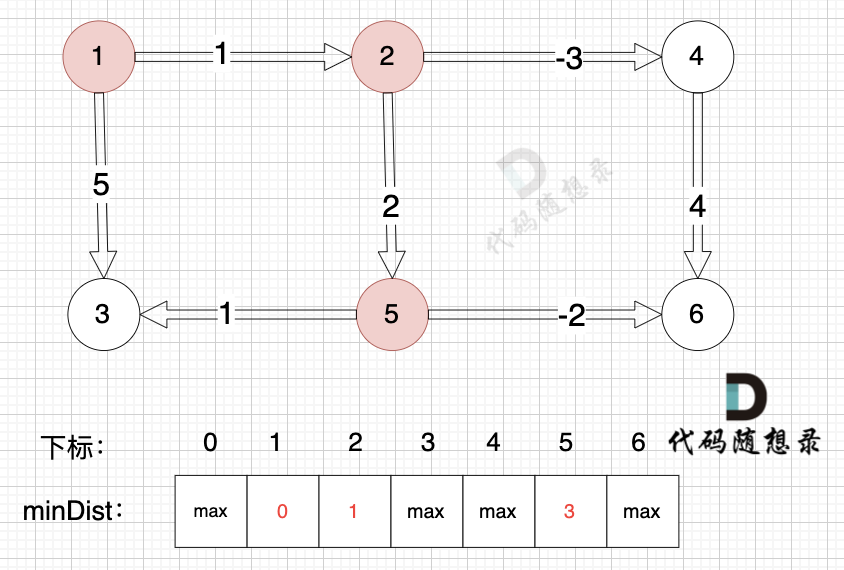
从队列里取出节点1,松弛节点1 作为出发点链接的边(节点1 -> 节点2)和边(节点1 -> 节点3)
|
||||
|
||||
边:节点1 -> 节点2,权值为1 ,minDist[2] > minDist[1] + 1 ,更新 minDist[2] = minDist[1] + 1 = 0 + 1 = 1 。
|
||||
|
||||
边:节点1 -> 节点3,权值为5 ,minDist[3] > minDist[1] + 5,更新 minDist[3] = minDist[1] + 5 = 0 + 5 = 5。
|
||||
|
||||
将节点2,节点3 加入队列,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
-----------------
|
||||
|
||||
|
||||
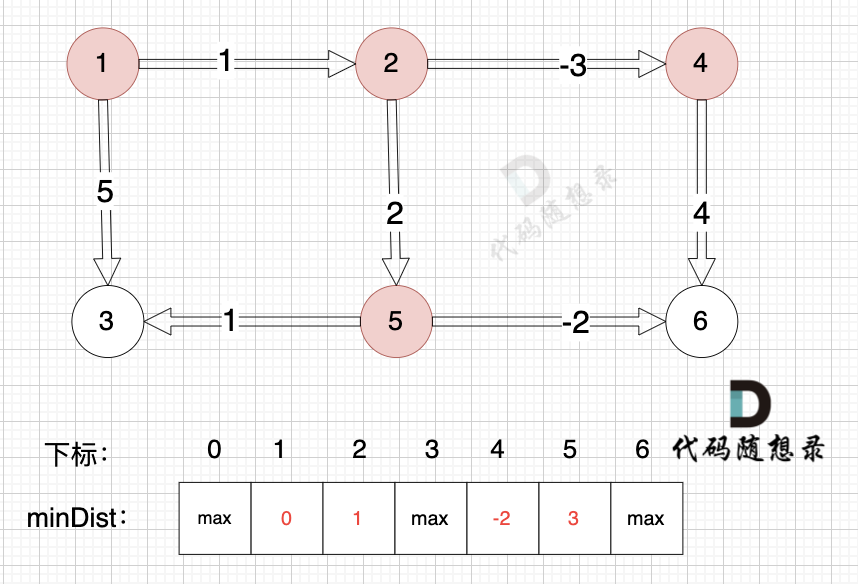
从队列里取出节点2,松弛节点2 作为出发点链接的边(节点2 -> 节点4)和边(节点2 -> 节点5)
|
||||
|
||||
边:节点2 -> 节点4,权值为1 ,minDist[4] > minDist[2] + (-3) ,更新 minDist[4] = minDist[2] + (-3) = 1 + (-3) = -2 。
|
||||
|
||||
边:节点2 -> 节点5,权值为2 ,minDist[5] > minDist[2] + 2 ,更新 minDist[5] = minDist[2] + 2 = 1 + 2 = 3 。
|
||||
|
||||
|
||||
将节点4,节点5 加入队列,如图:
|
||||
|
||||

|
||||
|
||||
|
||||
--------------------
|
||||
|
||||
|
||||
从队列里出去节点3,松弛节点3 作为出发点链接的边。
|
||||
|
||||
因为没有从节点3作为出发点的边,所以这里就从队列里取出节点3就好,不用做其他操作,如图:
|
||||
|
||||

|
||||
|
||||
|
||||
------------
|
||||
|
||||
从队列中取出节点4,松弛节点4作为出发点链接的边(节点4 -> 节点6)
|
||||
|
||||
边:节点4 -> 节点6,权值为4 ,minDist[6] > minDist[4] + 4,更新 minDist[6] = minDist[4] + 4 = -2 + 4 = 2 。
|
||||
|
||||
讲节点6加入队列
|
||||
|
||||
如图:
|
||||
|
||||

|
||||
|
||||
|
||||
---------------
|
||||
|
||||
从队列中取出节点5,松弛节点5作为出发点链接的边(节点5 -> 节点3),边(节点5 -> 节点6)
|
||||
|
||||
边:节点5 -> 节点3,权值为1 ,minDist[3] > minDist[5] + 1 ,更新 minDist[3] = minDist[5] + 1 = 3 + 1 = 4
|
||||
|
||||
边:节点5 -> 节点6,权值为-2 ,minDist[6] > minDist[5] + (-2) ,更新 minDist[6] = minDist[5] + (-2) = 3 - 2 = 1
|
||||
|
||||
如图:
|
||||
|
||||

|
||||
|
||||
|
||||
因为节点3,和 节点6 都曾经加入过队列,不用重复加入,避免重复计算。
|
||||
|
||||
|
||||
--------------
|
||||
|
||||
从队列中取出节点6,松弛节点6 作为出发点链接的边。
|
||||
|
||||
节点6作为终点,没有可以出发的边。
|
||||
|
||||
所以直接从队列中取出,如图:
|
||||
|
||||
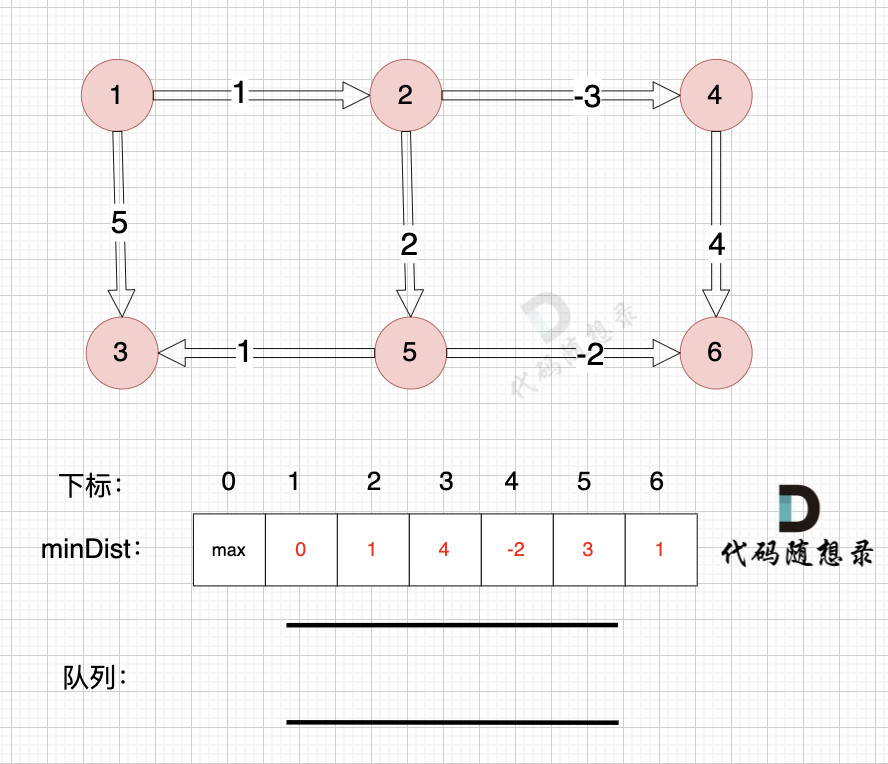
|
||||
|
||||
|
||||
----------
|
||||
|
||||
这样我们就完成了基于队列优化的bellman_ford的算法模拟过程。
|
||||
|
||||
大家可以发现 基于队列优化的算法,要比bellman_ford 算法 减少很多无用的松弛情况,特别是对于边树众多的大图 优化效果明显。
|
||||
|
||||
了解了大体流程,我们再看代码应该怎么写。
|
||||
|
||||
在上面模拟过程中,我们每次都要知道 一个节点作为出发点 链接了哪些节点。
|
||||
|
||||
如果想方便这道这些数据,就需要使用邻接表来存储这个图,如果对于邻接表不了解的话,可以看 [kama0047.参会dijkstra堆](./kama0047.参会dijkstra堆.md) 中 图的存储 部分。
|
||||
|
||||
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <queue>
|
||||
#include <list>
|
||||
#include <climits>
|
||||
using namespace std;
|
||||
|
||||
struct Edge { //邻接表
|
||||
int to; // 链接的节点
|
||||
int val; // 边的权重
|
||||
|
||||
Edge(int t, int w): to(t), val(w) {} // 构造函数
|
||||
};
|
||||
|
||||
|
||||
int main() {
|
||||
int n, m, p1, p2, val;
|
||||
cin >> n >> m;
|
||||
|
||||
vector<list<Edge>> grid(n + 1); // 邻接表
|
||||
|
||||
// 将所有边保存起来
|
||||
for(int i = 0; i < m; i++){
|
||||
cin >> p1 >> p2 >> val;
|
||||
// p1 指向 p2,权值为 val
|
||||
grid[p1].push_back(Edge(p2, val));
|
||||
}
|
||||
int start = 1; // 起点
|
||||
int end = n; // 终点
|
||||
|
||||
vector<int> minDist(n + 1 , INT_MAX);
|
||||
minDist[start] = 0;
|
||||
|
||||
queue<int> que;
|
||||
que.push(start);
|
||||
int que_size;
|
||||
while (!que.empty()) {
|
||||
// 注意这个数组放的位置
|
||||
vector<bool> visited(n + 1, false); // 可加,可不加,加了效率高一些,防止队列里重复访问,其数值已经算过了
|
||||
que_size = que.size();
|
||||
|
||||
int node = que.front(); que.pop();
|
||||
|
||||
for (Edge edge : grid[node]) {
|
||||
int from = node;
|
||||
int to = edge.to;
|
||||
int price = edge.val;
|
||||
if (minDist[to] > minDist[from] + price) { // 开始松弛
|
||||
minDist[to] = minDist[from] + price;
|
||||
if(visited[to]) continue; // 节点不用重复放入队列,但节点需要重复计算,所以放在这里位置
|
||||
visited[to] = true;
|
||||
que.push(to);
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
|
||||
else cout << minDist[end] << endl; // 到达终点最短路径
|
||||
}
|
||||
```
|
||||
|
||||
代码中有一点需要注意,即 `if(visited[to]) continue;` 这段代码放的位置。
|
||||
|
||||
|
||||
一些录友可能写成这样:
|
||||
|
||||
```CPP
|
||||
if (minDist[to] > minDist[from] + price) { // 开始松弛
|
||||
if(visited[to]) continue;
|
||||
minDist[to] = minDist[from] + price;
|
||||
visited[to] = true;
|
||||
que.push(to);
|
||||
}
|
||||
```
|
||||
|
||||
这是不对了,我们仅仅是控制节点不用重复加入队列,但对于边的松弛,节点数值的更新,是要重复计算的,要不然如何 不断更新最短路径呢?
|
||||
|
||||
所以 `if(visited[to]) continue;` 应该放在这里:
|
||||
|
||||
```CPP
|
||||
if (minDist[to] > minDist[from] + price) { // 开始松弛
|
||||
minDist[to] = minDist[from] + price;
|
||||
if(visited[to]) continue; // 仅仅控制节点不要重复加入队列
|
||||
visited[to] = true;
|
||||
que.push(to);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
## 拓展
|
||||
|
||||
关于 加visited 方式节点重复方便,可能也有录友认为,加上 visited 也是防止 如果图中出现了环的话,会导致的 队列里一直不为空。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@ -1,7 +1,7 @@
|
||||
|
||||
# 94. 城市间货物运输 I
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1152)
|
||||
[卡码网: 94. 城市间货物运输 I](https://kamacoder.com/problempage.php?pid=1152)
|
||||
|
||||
题目描述
|
||||
|
||||
@ -159,7 +159,7 @@ if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
|
||||
|
||||
|
||||
|
||||
边:节点2 -> 节点4,权值为-3 ,minDist[4] > minDist[2] + 2,更新 minDist[4] = minDist[2] + (-3) = 1 + (-3) = -2 ,如图:
|
||||
边:节点2 -> 节点4,权值为-3 ,minDist[4] > minDist[2] + (-3),更新 minDist[4] = minDist[2] + (-3) = 1 + (-3) = -2 ,如图:
|
||||
|
||||
|
||||
|
||||
@ -261,6 +261,16 @@ int main() {
|
||||
}
|
||||
```
|
||||
|
||||
* 时间复杂度: O(N * E) , N为节点数量,E为图中边的数量
|
||||
* 空间复杂度: O(N) ,即 minDist 数组所开辟的空间
|
||||
|
||||
关于空间复杂度,可能有录友疑惑,代码中数组grid不也开辟空间了吗? 为什么只算minDist数组的空间呢?
|
||||
|
||||
grid数组是用来存图的,这是题目描述中必须要使用的空间,而不是我们算法所使用的空间。
|
||||
|
||||
我们在讲空间复杂度的时候,一般都是说,我们这个算法的空间复杂度。
|
||||
|
||||
|
||||
### 拓展
|
||||
|
||||
有录友可能会想,那我 松弛 n 次,松弛 n + 1次,松弛 2 * n 次会怎么样?
|
||||
@ -148,3 +148,6 @@ int main() {
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
* 时间复杂度: O(N * E) , N为节点数量,E为图中边的数量
|
||||
* 空间复杂度: O(N) ,即 minDist 数组所开辟的空间
|
||||
392
problems/kama0096.城市间货物运输III.md
Normal file
392
problems/kama0096.城市间货物运输III.md
Normal file
@ -0,0 +1,392 @@
|
||||
|
||||
# 96. 城市间货物运输 III
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1154)
|
||||
|
||||
【题目描述】
|
||||
|
||||
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
|
||||
|
||||
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。
|
||||
|
||||
权值为正表示扣除了政府补贴后运输货物仍需支付的费用;
|
||||
|
||||
权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
|
||||
|
||||
请计算在最多经过 k 个城市的条件下,从城市 src 到城市 dst 的最低运输成本。
|
||||
|
||||
【输入描述】
|
||||
|
||||
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
|
||||
|
||||
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
|
||||
|
||||
最后一行包含三个正整数,src、dst、和 k,src 和 dst 为城市编号,从 src 到 dst 经过的城市数量限制。
|
||||
|
||||
【输出描述】
|
||||
|
||||
输出一个整数,表示从城市 src 到城市 dst 的最低运输成本,如果无法在给定经过城市数量限制下找到从 src 到 dst 的路径,则输出 "unreachable",表示不存在符合条件的运输方案。
|
||||
|
||||
输入示例:
|
||||
|
||||
```
|
||||
6 7
|
||||
1 2 1
|
||||
2 4 -3
|
||||
2 5 2
|
||||
1 3 5
|
||||
3 5 1
|
||||
4 6 4
|
||||
5 6 -2
|
||||
2 6 1
|
||||
```
|
||||
|
||||
输出示例:
|
||||
|
||||
```
|
||||
0
|
||||
```
|
||||
|
||||
## 思路
|
||||
|
||||
本题为单源有限最短路问题,同样是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 延伸题目。
|
||||
|
||||
注意题目中描述是 **最多经过 k 个城市的条件下,而不是一定经过k个城市,也可以经过的城市数量比k小,但要最短的路径**。
|
||||
|
||||
在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 中我们讲了:**对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离**。
|
||||
|
||||
节点数量为n,起点到终点,最多是 n-1 条边相连。 那么对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。
|
||||
|
||||
(如果对以上讲解看不懂,建议详看 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) )
|
||||
|
||||
本题是最多经过 k 个城市, 那么是 k + 1条边相连的节点。 这里可能有录友想不懂为什么是k + 1,来看这个图:
|
||||
|
||||
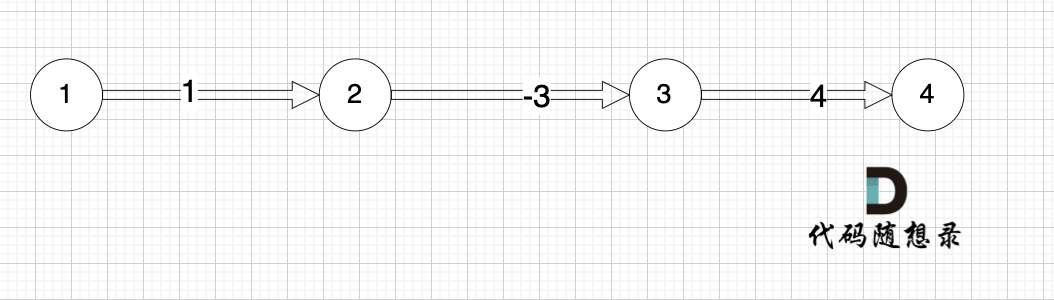
|
||||
|
||||
图中,节点2 最多已经经过2个节点 到达节点4,那么中间是有多少条边呢,是 3 条边对吧。
|
||||
|
||||
所以本题就是求,起点最多经过k + 1 条边到达终点的最短距离。
|
||||
|
||||
对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离,那么对所有边松弛 k + 1次,就是求 起点到达 与起点k + 1条边相连的节点的 最短距离。
|
||||
|
||||
**注意**: 本题是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 的拓展题,如果对 bellman_ford 没有深入了解,强烈建议先看 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 再做本题。
|
||||
|
||||
理解以上内容,其实本题代码就很容易了,bellman_ford 标准写法是松弛 n-1 次,本题就松弛 k + 1次就好。
|
||||
|
||||
此时我们可以写出如下代码:
|
||||
|
||||
```CPP
|
||||
// 版本一
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <list>
|
||||
#include <climits>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int src, dst,k ,p1, p2, val ,m , n;
|
||||
|
||||
cin >> n >> m;
|
||||
|
||||
vector<vector<int>> grid;
|
||||
|
||||
for(int i = 0; i < m; i++){
|
||||
cin >> p1 >> p2 >> val;
|
||||
// p1 指向 p2,权值为 val
|
||||
grid.push_back({p1, p2, val});
|
||||
}
|
||||
|
||||
cin >> src >> dst >> k;
|
||||
|
||||
vector<int> minDist(n + 1 , INT_MAX);
|
||||
minDist[src] = 0;
|
||||
for (int i = 1; i <= k + 1; i++) { // 对所有边松弛 k + 1次
|
||||
for (vector<int> &side : grid) {
|
||||
int from = side[0];
|
||||
int to = side[1];
|
||||
int price = side[2];
|
||||
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) minDist[to] = minDist[from] + price;
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
if (minDist[dst] == INT_MAX) cout << "unreachable" << endl; // 不能到达终点
|
||||
else cout << minDist[dst] << endl; // 到达终点最短路径
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
以上代码 标准 bellman_ford 写法,松弛 k + 1次,看上去没什么问题。
|
||||
|
||||
但大家提交后,居然没通过!
|
||||
|
||||
这是为什么呢?
|
||||
|
||||
接下来我们拿这组数据来举例:
|
||||
|
||||
```
|
||||
4 4
|
||||
1 2 -1
|
||||
2 3 1
|
||||
3 1 -1
|
||||
3 4 1
|
||||
1 4 3
|
||||
```
|
||||
|
||||
(**注意上面的示例是有负权回路的,只有带负权回路的图才能说明问题**)
|
||||
|
||||
> 负权回路是指一条道路的总权值为负,这样的回路使得通过反复经过回路中的道路,理论上可以无限地减少总成本或无限地增加总收益。
|
||||
|
||||
正常来说,这组数据输出应该是 1,但以上代码输出的是 -2。
|
||||
|
||||
|
||||
在讲解原因的时候,强烈建议大家,先把 minDist数组打印出来,看看minDist数组是不是按照自己的想法变化的,这样更容易理解我接下来的讲解内容。 (**一定要动手,实践出真实,脑洞模拟不靠谱**)
|
||||
|
||||
打印的代码可以是这样:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <list>
|
||||
#include <climits>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int src, dst,k ,p1, p2, val ,m , n;
|
||||
|
||||
cin >> n >> m;
|
||||
|
||||
vector<vector<int>> grid;
|
||||
|
||||
for(int i = 0; i < m; i++){
|
||||
cin >> p1 >> p2 >> val;
|
||||
// p1 指向 p2,权值为 val
|
||||
grid.push_back({p1, p2, val});
|
||||
}
|
||||
|
||||
cin >> src >> dst >> k;
|
||||
|
||||
vector<int> minDist(n + 1 , INT_MAX);
|
||||
minDist[src] = 0;
|
||||
for (int i = 1; i <= k + 1; i++) { // 对所有边松弛 k + 1次
|
||||
for (vector<int> &side : grid) {
|
||||
int from = side[0];
|
||||
int to = side[1];
|
||||
int price = side[2];
|
||||
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) minDist[to] = minDist[from] + price;
|
||||
}
|
||||
// 打印 minDist 数组
|
||||
for (int j = 1; j <= n; j++) cout << minDist[j] << " ";
|
||||
cout << endl;
|
||||
|
||||
}
|
||||
|
||||
if (minDist[dst] == INT_MAX) cout << "unreachable" << endl; // 不能到达终点
|
||||
else cout << minDist[dst] << endl; // 到达终点最短路径
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
接下来,我按照上面的示例带大家 画图举例 对所有边松弛一次 的效果图。
|
||||
|
||||
起点为节点1, 起点到起点的距离为0,所以 minDist[1] 初始化为0 ,如图:
|
||||
|
||||
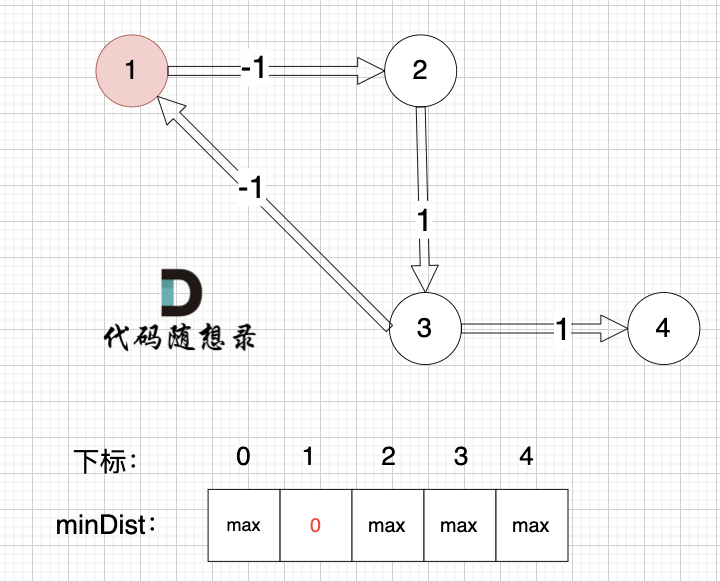
|
||||
|
||||
其他节点对应的minDist初始化为max,因为我们要求最小距离,那么还没有计算过的节点 默认是一个最大数,这样才能更新最小距离。
|
||||
|
||||
当我们开始对所有边开始第一次松弛:
|
||||
|
||||
边:节点1 -> 节点2,权值为-1 ,minDist[2] > minDist[1] + (-1),更新 minDist[2] = minDist[1] + (-1) = 0 - 1 = -1 ,如图:
|
||||
|
||||
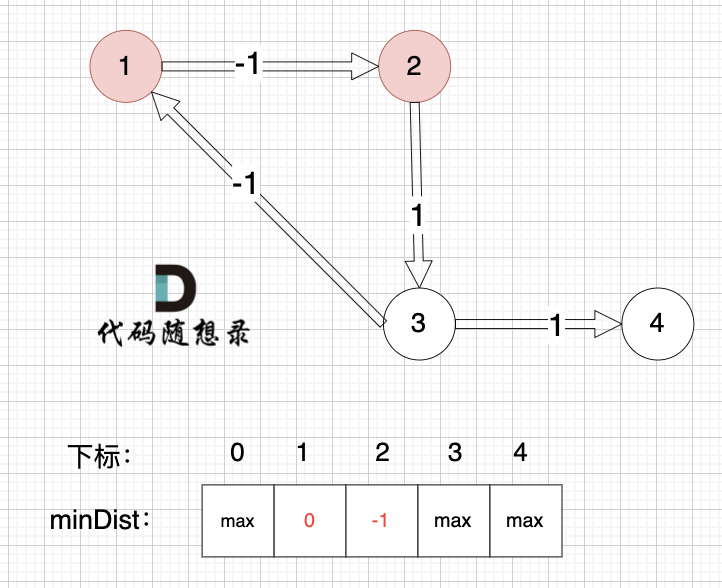
|
||||
|
||||
|
||||
边:节点2 -> 节点3,权值为1 ,minDist[3] > minDist[2] + 1 ,更新 minDist[3] = minDist[2] + 1 = -1 + 1 = 0 ,如图:
|
||||
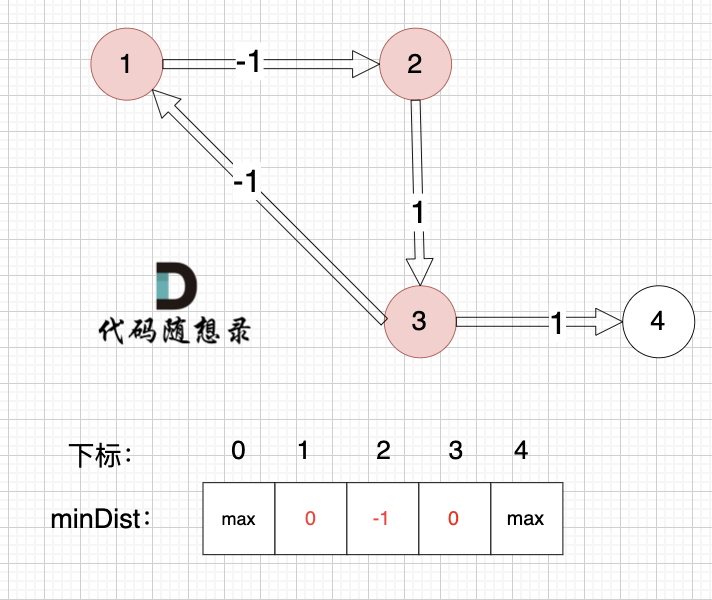
|
||||
|
||||
|
||||
边:节点3 -> 节点1,权值为-1 ,minDist[1] > minDist[3] + (-1),更新 minDist[1] = 0 + (-1) = -1 ,如图:
|
||||
|
||||

|
||||
|
||||
|
||||
边:节点3 -> 节点4,权值为1 ,minDist[4] > minDist[3] + 1,更新 minDist[4] = 0 + (-1) = -1 ,如图:
|
||||
|
||||
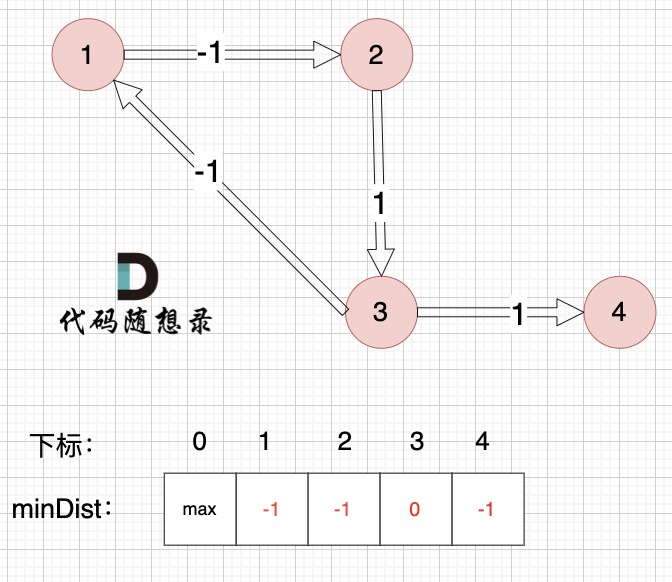
|
||||
|
||||
|
||||
以上是对所有边进行的第一次松弛,最后 minDist数组为 :-1 -1 0 1 ,(从下标1算起)
|
||||
|
||||
后面几次松弛我就不挨个画图了,过程大同小异,我直接给出minDist数组的变化:
|
||||
|
||||
所有边进行的第二次松弛,minDist数组为 : -2 -2 -1 0
|
||||
所有边进行的第三次松弛,minDist数组为 : -3 -3 -2 -1
|
||||
所有边进行的第四次松弛,minDist数组为 : -4 -4 -3 -2 (本示例中k为3,所以松弛4次)
|
||||
|
||||
最后计算的结果minDist[4] = -2,即 起点到 节点4,最多经过 3 个节点的最短距离是 -2,但 正确的结果应该是 1,即路径:节点1 -> 节点2 -> 节点3 -> 节点4。
|
||||
|
||||
理论上来说,**对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离**。
|
||||
|
||||
对所有边松弛两次,相当于计算 起点到达 与起点两条边相连的节点的最短距离。
|
||||
|
||||
对所有边松弛三次,以此类推。
|
||||
|
||||
但在对所有边松弛第一次的过程中,大家会发现,不仅仅 与起点一条边相连的节点更新了,所有节点都更新了。
|
||||
|
||||
而且对所有边的后面几次松弛,同样是更新了所有的节点,说明 至多经过k 个节点 这个限制 根本没有限制住,每个节点的数值都被更新了。
|
||||
|
||||
这是为什么?
|
||||
|
||||
在上面画图距离中,对所有边进行第一次松弛,在计算 边(节点2 -> 节点3) 的时候,更新了 节点3。
|
||||
|
||||

|
||||
|
||||
理论上来说节点3 应该在对所有边第二次松弛的时候才更新。 这因为当时是基于已经计算好的 节点2(minDist[2])来做计算了。
|
||||
|
||||
minDist[2]在计算边:(节点1 -> 节点2)的时候刚刚被赋值为 -1。
|
||||
|
||||
这样就造成了一个情况,即:计算minDist数组的时候,基于了本次松弛的 minDist数值,而不是上一次 松弛时候minDist的数值。
|
||||
所以在每次计算 minDist 时候,要基于 对所有边上一次松弛的 minDist 数值才行,所以我们要记录上一次松弛的minDist。
|
||||
|
||||
代码修改如下: (关键地方已经注释)
|
||||
|
||||
```CPP
|
||||
// 版本二
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <list>
|
||||
#include <climits>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int src, dst,k ,p1, p2, val ,m , n;
|
||||
|
||||
cin >> n >> m;
|
||||
|
||||
vector<vector<int>> grid;
|
||||
|
||||
for(int i = 0; i < m; i++){
|
||||
cin >> p1 >> p2 >> val;
|
||||
grid.push_back({p1, p2, val});
|
||||
}
|
||||
|
||||
cin >> src >> dst >> k;
|
||||
|
||||
vector<int> minDist(n + 1 , INT_MAX);
|
||||
minDist[src] = 0;
|
||||
vector<int> minDist_copy(n + 1); // 用来记录上一次遍历的结果
|
||||
for (int i = 1; i <= k + 1; i++) {
|
||||
minDist_copy = minDist; // 获取上一次计算的结果
|
||||
for (vector<int> &side : grid) {
|
||||
int from = side[0];
|
||||
int to = side[1];
|
||||
int price = side[2];
|
||||
// 注意使用 minDist_copy 来计算 minDist
|
||||
if (minDist_copy[from] != INT_MAX && minDist[to] > minDist_copy[from] + price) {
|
||||
minDist[to] = minDist_copy[from] + price;
|
||||
}
|
||||
}
|
||||
}
|
||||
if (minDist[dst] == INT_MAX) cout << "unreachable" << endl; // 不能到达终点
|
||||
else cout << minDist[dst] << endl; // 到达终点最短路径
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
* 时间复杂度: O(K * E) , K为至多经过K个节点,E为图中边的数量
|
||||
* 空间复杂度: O(N) ,即 minDist 数组所开辟的空间
|
||||
|
||||
## 拓展一(边的顺序的影响)
|
||||
|
||||
其实边的顺序会影响我们每一次拓展的结果。
|
||||
|
||||
我来给大家举个例子。
|
||||
|
||||
我上面讲解中,给出的示例是这样的:
|
||||
```
|
||||
4 4
|
||||
1 2 -1
|
||||
2 3 1
|
||||
3 1 -1
|
||||
3 4 1
|
||||
1 4 3
|
||||
```
|
||||
|
||||
我将示例中边的顺序改一下,给成:
|
||||
|
||||
```
|
||||
4 4
|
||||
3 1 -1
|
||||
3 4 1
|
||||
2 3 1
|
||||
1 2 -1
|
||||
1 4 3
|
||||
```
|
||||
|
||||
所构成是图是一样的,都是如下的这个图,但给出的边的顺序是不一样的。
|
||||
|
||||
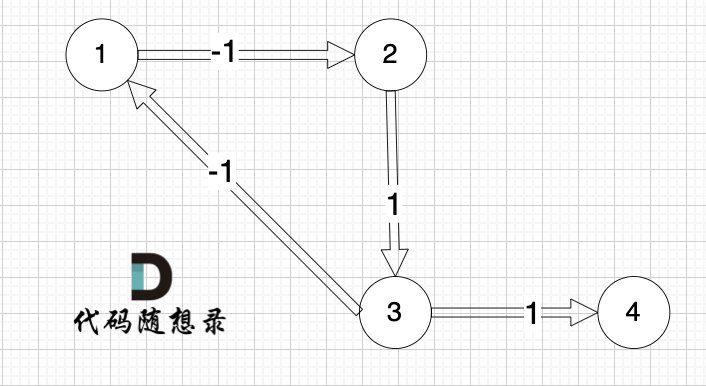
|
||||
|
||||
再用版本一的代码是运行一下,发现结果输出是 1, 是对的。
|
||||
|
||||

|
||||
|
||||
分明刚刚输出的结果是 -2,是错误的,怎么 一样的图,这次输出的结果就对了呢?
|
||||
|
||||
其实这是和示例中给出的边的顺序是有关的,
|
||||
|
||||
我们按照我修改后的示例再来模拟 对所有边的第一次拓展情况。
|
||||
|
||||
初始化:
|
||||
|
||||
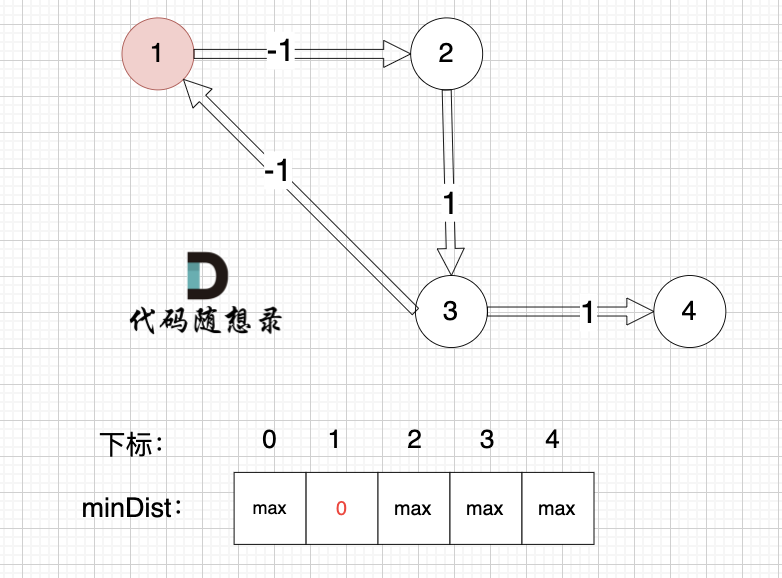
|
||||
|
||||
边:节点3 -> 节点1,权值为-1 ,节点3还没有被计算过,节点1 不更新。
|
||||
|
||||
边:节点3 -> 节点4,权值为1 ,节点3还没有被计算过,节点4 不更新。
|
||||
|
||||
边:节点2 -> 节点3,权值为 1 ,节点2还没有被计算过,节点3 不更新。
|
||||
|
||||
边:节点1 -> 节点2,权值为 -1 ,minDist[2] > minDist[1] + (-1),更新 minDist[2] = 0 + (-1) = -1 ,如图:
|
||||
|
||||
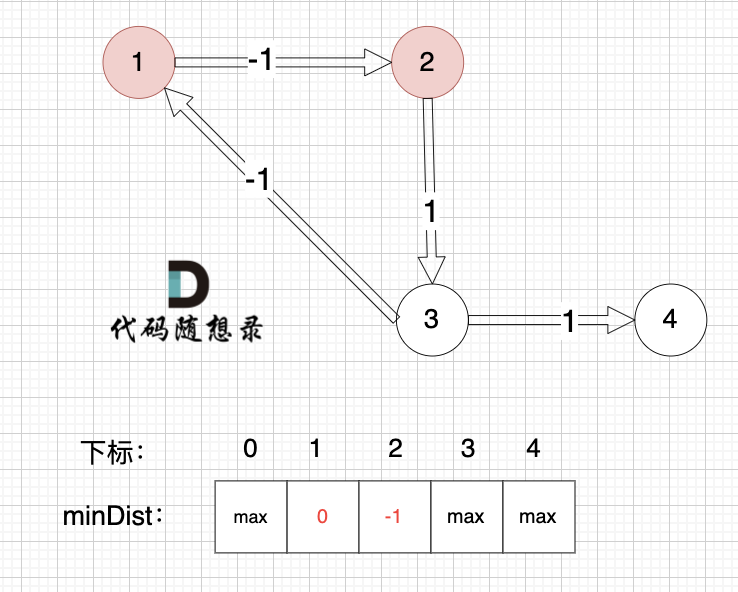
|
||||
|
||||
以上是对所有边 松弛一次的状态。
|
||||
|
||||
可以发现 同样的图,边的顺序不一样,使用版本一的代码 每次松弛更新的节点也是不一样的。
|
||||
|
||||
而边的顺序是随机的,是题目给我们的,所以本题我们才需要 记录上一次松弛的minDist,来保障 每一次对所有边松弛的结果。
|
||||
|
||||
|
||||
## 拓展二(本题本质)
|
||||
|
||||
那么前面讲解过的 [94.城市间货物运输I](./kama94.城市间货物运输I.md) 和 [95.城市间货物运输II](./kama95.城市间货物运输II.md) 也是bellman_ford经典算法,也没使用 minDist_copy,怎么就没问题呢?
|
||||
|
||||
> 如果没看过我上面这两篇讲解的话,建议详细学习上面两篇,在看我下面讲的区别,否则容易看不懂。
|
||||
|
||||
[94.城市间货物运输I](./kama94.城市间货物运输I.md), 是没有 负权回路的,那么 多松弛多少次,对结果都没有影响。
|
||||
|
||||
求 节点1 到 节点n 的最短路径,松弛n-1 次就够了,松弛 大于 n-1次,结果也不会变。
|
||||
|
||||
那么在对所有边进行第一次松弛的时候,如果基于 最近计算的 minDist 来计算 minDist (相当于多做松弛了),也是对最终结果没影响。
|
||||
|
||||
[95.城市间货物运输II](./kama95.城市间货物运输II.md) 是判断是否有 负权回路,一旦有负权回路, 对所有边松弛 n -1 次以后,在做松弛 minDist 数值一定会变,根据这一点是判断是否有负权回路。
|
||||
|
||||
所以 在对所有边进行第一次松弛的时候,如果基于 最近计算的 minDist 来计算 minDist (相当于多做松弛了),对最后判断是否有负权回路同样没有影响。
|
||||
|
||||
你可以理解 minDist的数组其实是不准确了,但它只要变化了就可以让我们来判断 是否有 负权回路。
|
||||
|
||||
|
||||
那么本题 为什么计算minDist 一定要基于上次 的 minDist 数值。
|
||||
|
||||
其关键在于本题的两个因素:
|
||||
|
||||
* 本题可以有负权回路,说明只要多做松弛,结果是会变的。
|
||||
* 本题要求最多经过k个节点,对松弛次数是有限制的。
|
||||
|
||||
如果本题中 没有负权回路的测试用例, 那版本一的代码就可以过了,也就不用我费这么大口舌去讲解的这个坑了。
|
||||
|
||||
57
problems/kama0097.小明逛公园.md
Normal file
57
problems/kama0097.小明逛公园.md
Normal file
@ -0,0 +1,57 @@
|
||||
|
||||
# Floyd 算法精讲
|
||||
|
||||
[卡码网:97. 小明逛公园](https://kamacoder.com/problempage.php?pid=1155)
|
||||
|
||||
【题目描述】
|
||||
|
||||
小明喜欢去公园散步,公园内布置了许多的景点,相互之间通过小路连接,小明希望在观看景点的同时,能够节省体力,走最短的路径。
|
||||
|
||||
|
||||
给定一个公园景点图,图中有 N 个景点(编号为 1 到 N),以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。
|
||||
|
||||
|
||||
小明有 Q 个观景计划,每个计划都有一个起点 start 和一个终点 end,表示他想从景点 start 前往景点 end。由于小明希望节省体力,他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。
|
||||
|
||||
【输入描述】
|
||||
|
||||
第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。
|
||||
|
||||
接下来的 M 行,每行包含三个整数 u, v, w,表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。
|
||||
|
||||
接下里的一行包含一个整数 Q,表示观景计划的数量。
|
||||
|
||||
接下来的 Q 行,每行包含两个整数 start, end,表示一个观景计划的起点和终点。
|
||||
|
||||
【输出描述】
|
||||
|
||||
对于每个观景计划,输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径,则输出 -1。
|
||||
|
||||
【输入示例】
|
||||
|
||||
7 3
|
||||
1 2 4
|
||||
2 5 6
|
||||
3 6 8
|
||||
2
|
||||
1 2
|
||||
2 3
|
||||
|
||||
【输出示例】
|
||||
|
||||
4
|
||||
-1
|
||||
|
||||
【提示信息】
|
||||
|
||||
从 1 到 2 的路径长度为 4,2 到 3 之间并没有道路。
|
||||
|
||||
1 <= N, M, Q <= 1000.
|
||||
|
||||
## 思路
|
||||
|
||||
本题是经典的多源最短路问题。
|
||||
|
||||
我们之前讲解过的算法,dijkstra,
|
||||
|
||||
|
||||
@ -1,125 +0,0 @@
|
||||
|
||||
# 96. 城市间货物运输 III
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1154)
|
||||
|
||||
【题目描述】
|
||||
|
||||
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
|
||||
|
||||
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。
|
||||
|
||||
权值为正表示扣除了政府补贴后运输货物仍需支付的费用;
|
||||
|
||||
权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
|
||||
|
||||
请计算在最多经过 k 个城市的条件下,从城市 src 到城市 dst 的最低运输成本。
|
||||
|
||||
【输入描述】
|
||||
|
||||
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
|
||||
|
||||
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
|
||||
|
||||
最后一行包含三个正整数,src、dst、和 k,src 和 dst 为城市编号,从 src 到 dst 经过的城市数量限制。
|
||||
|
||||
【输出描述】
|
||||
|
||||
输出一个整数,表示从城市 src 到城市 dst 的最低运输成本,如果无法在给定经过城市数量限制下找到从 src 到 dst 的路径,则输出 "unreachable",表示不存在符合条件的运输方案。
|
||||
|
||||
输入示例:
|
||||
|
||||
```
|
||||
6 7
|
||||
1 2 1
|
||||
2 4 -3
|
||||
2 5 2
|
||||
1 3 5
|
||||
3 5 1
|
||||
4 6 4
|
||||
5 6 -2
|
||||
2 6 1
|
||||
```
|
||||
|
||||
输出示例:
|
||||
|
||||
```
|
||||
0
|
||||
```
|
||||
|
||||
## 思路
|
||||
|
||||
本题为单源有限最短路问题,同样是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 延伸题目。
|
||||
|
||||
在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 中我们讲了:**对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离**。
|
||||
|
||||
节点数量为n,那么起点到终点,最多是 n-1 条边相连。 那么对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。
|
||||
|
||||
(如果对以上讲解看不懂,建议详看 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) )
|
||||
|
||||
本题是最多经过 k 个城市, 那么是 k + 1条边相连的节点。 这里可能有录友想不懂为什么是k + 1,来看这个图:
|
||||
|
||||

|
||||
|
||||
图中,节点2 最多已经经过2个节点 到达节点4,那么中间是有多少条边呢,是 3 条边对吧。
|
||||
|
||||
所以本题就是求,起点最多经过k + 1 条边到达终点的最短距离。
|
||||
|
||||
|
||||
对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离,那么对所有边松弛 k + 1次,就是求 起点到达 与起点k + 1条边相连的节点的 最短距离。
|
||||
|
||||
如果 终点数值没有被计算覆盖,那就是无法到达。
|
||||
|
||||
**注意**: 本题是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 的拓展题,如果对 bellman_ford 没有深入了解,强烈建议先看 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 再做本题。
|
||||
|
||||
理解以上内容,其实本题代码就很容易了,bellman_ford 标准写法是松弛 n-1 次,本题就松弛 k + 1次就好。
|
||||
|
||||
如果大家理解后,建议先自己写写代码,提交一下看看,因为 这里还有一个坑,如果不自己去试试,体会就不够深刻了。
|
||||
|
||||
|
||||
|
||||
代码如下: (关键地方详细注释)
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <list>
|
||||
#include <climits>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int src, dst,k ,p1, p2, val ,m , n;
|
||||
|
||||
cin >> n >> m;
|
||||
|
||||
vector<vector<int>> grid;
|
||||
|
||||
for(int i = 0; i < m; i++){
|
||||
cin >> p1 >> p2 >> val;
|
||||
// p1 指向 p2,权值为 val
|
||||
grid.push_back({p1, p2, val});
|
||||
}
|
||||
|
||||
cin >> src >> dst >> k;
|
||||
|
||||
vector<int> minDist(n + 1 , INT_MAX);
|
||||
minDist[src] = 0;
|
||||
vector<int> minDist_copy(n + 1); // 用来记录每一次遍历的结果
|
||||
for (int i = 1; i <= k + 1; i++) {
|
||||
minDist_copy = minDist; // 获取上一次计算的结果
|
||||
for (vector<int> &side : grid) {
|
||||
int from = side[0];
|
||||
int to = side[1];
|
||||
int price = side[2];
|
||||
//cout << f[0] << " " << f[1] << " " << f[2] << endl;
|
||||
if (minDist_copy[from] != INT_MAX && minDist[to] > minDist_copy[from] + price) minDist[to] = minDist_copy[from] + price;
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
if (minDist[dst] == INT_MAX) cout << "unreachable" << endl; // 不能到达终点
|
||||
else cout << minDist[dst] << endl; // 到达终点最短路径
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
@ -1,7 +1,9 @@
|
||||
|
||||
# 代码随想录算法训练营
|
||||
|
||||
> 训练营17期将在6月28日开营,目前可以报名,提前拉群,在群里等着开营就好!
|
||||
::: tip 通知
|
||||
训练营35期,将于 4月3日开营,目前可以报名,报名后提前拉群,在群里等着开营就好。
|
||||
:::
|
||||
|
||||
大家可以百度搜索:代码随想录算法训练营, 看看往期录友们在训练营里打卡总结的博客。
|
||||
|
||||
@ -9,14 +11,39 @@
|
||||
|
||||
这是训练营里录友坚持到最后一天的打卡,大家可以看看他们的博客是每天都有记录的:
|
||||
|
||||
* [训练营结束,深感坚持是最难的(Java-犯困-东南研二)](https://blog.csdn.net/weixin_57956443/article/details/128995318)
|
||||
* [这种方式,有效逼我坚持下来(C++-小飞-嘉院大三)(精华)](https://blog.csdn.net/weixin_60353640/article/details/133797799)
|
||||
* [完成比完美重要(Java-小姜-已工作/南京)(精华)](https://xie.infoq.cn/article/3d07b4040ceab0f546d66e3e1)
|
||||
* [已经刷了500题的基础,参加训练营依然收获满满(Java-怪懒懒-求职)(精华)](https://blog.csdn.net/2301_78266314/article/details/132144046)
|
||||
|
||||
* [算法超级弱,最后坚持下来了(Java-信任呢-上大研二)(精华)](https://blog.csdn.net/xinrenne/article/details/133267089)
|
||||
* [第一次比较完整的刷题训练经历,群里氛围超级好(JAVA-雷贯三十三重天-北航研二)(精华)](https://blog.csdn.net/qq_44120129/article/details/133230372)
|
||||
* [我全程坚持下来,还是很有成就感的(python-wj-待业)(精华)](https://blog.csdn.net/u013441272/article/details/133229421)
|
||||
|
||||
* [一点基础都没有,坚持下来了(C++ 润 大二)(精华)](https://blog.csdn.net/m0_74583479/article/details/132776719)
|
||||
* [这个钱花的很值得(C++-GMZ-研一)(精华)](https://blog.csdn.net/weixin_43303286/article/details/132796571)
|
||||
* [看着名单里录友都在坚持,自己也要坚持(C++-凯-湖工大研三)(精华)](https://blog.csdn.net/weixin_62453859/article/details/132788830)
|
||||
|
||||
* [一刷心得(Java-小何同学-广财大二)(精华)](https://juejin.cn/post/7272250890597531684)
|
||||
* [花钱买服务、买环境、买时间(Java-古今-大工研二)(精华)](https://blog.csdn.net/dannky_Z/article/details/132532049)
|
||||
* [一刷心得(java-唔哩凹-大三)(精华)](https://blog.csdn.net/iwtup/article/details/132545456)
|
||||
|
||||
* [训练营结束有点不舍,坚持最久的一件事(C++-徐一-中科院研二)(精华)](https://blog.csdn.net/weixin_46108098/article/details/132158352)
|
||||
* [同学推荐,报名训练营,坚持下来了(c++-刘浩-沈自所-研二)(精华)](https://blog.csdn.net/qq1156148707/article/details/132155446)
|
||||
|
||||
* [每日的刷题训练真的艰难,但坚持下来了(C++-五-已工作福建)(精华)](https://blog.csdn.net/weixin_44952586/article/details/131909720)
|
||||
* [加入训练营,就是因为这个气氛,只靠自己很难坚持(cpp-Lord HouSton-cqu研二)(精华)](https://blog.csdn.net/HSL13594379250/article/details/131889934)
|
||||
* [很幸运,我坚持下来了,感觉收货满满(java-李-UCAS研0)(精华)](https://blog.csdn.net/ResNet156/article/details/131920163)
|
||||
* [谈谈自己的收获,养成了写博客的习惯(java-翌-研二)(精华)](https://blog.csdn.net/weixin_47460244/article/details/131912316)
|
||||
|
||||
* [养成了刷题的习惯(C++-热心市民C先生-南理工研一)(精华)](https://blog.csdn.net/qqq1521902442/article/details/131614999)
|
||||
* [工作也坚持下来(Python-Hongying-已工作杭州)(精华)](https://blog.csdn.net/weixin_42286468/article/details/131628069)
|
||||
* [入营不亏(C++-小叶子-云财研二)(精华)](https://blog.csdn.net/dream_aleaf/article/details/131613667)
|
||||
|
||||
* [训练营一刷总结(Java-HQH-研二)](https://blog.csdn.net/weixin_43821876/article/details/128991822)
|
||||
* [训练营总结,一群人才能走的更远(Java-Lixy-已工作南京)](https://blog.csdn.net/weixin_45368277/article/details/128997823)
|
||||
* [训练营总结,中途🐑了,也坚持下来(C++-Jane-科大研二)](https://blog.csdn.net/Jane_10358/article/details/128977424)
|
||||
* [这两个月有很多不可控因素,但依然坚持下来(java-hha-南工大二)](https://blog.csdn.net/qerwtrt4t/article/details/128975401)
|
||||
* [训练营总结,最后坚持下来(C++ - 阿舟 - 已工作武汉)](https://blog.csdn.net/m0_74360161/article/details/129000723)
|
||||
* [训练营总结,一刷知识点回顾(Java-魏-待就业)](https://blog.csdn.net/weixin_48111139/article/details/128973746)
|
||||
* [在训练营中,零基础刷一遍的感受(C++-东风-东北大学研二)](https://blog.csdn.net/nightcood/article/details/128947111)
|
||||
|
||||
|
||||
博客链接:[https://blog.csdn.net/m0_61724447/article/details/128443084](https://blog.csdn.net/m0_61724447/article/details/128443084)
|
||||
@ -69,7 +96,7 @@
|
||||
-----------
|
||||
|
||||
|
||||
### 训练营的目的是什么?
|
||||
## 训练营的目的是什么?
|
||||
|
||||
对于刷题,学算法,[《代码随想录》](https://programmercarl.com/other/publish.html)(programmercarl.com)已经把刷题顺序给大家列好了,大家跟着刷就行。
|
||||
|
||||
@ -97,7 +124,7 @@
|
||||
|
||||
我亲自给大家规划节奏,大家一起按照我的节奏来,规定时间内,一刷一定能把代码随想录所有内容吃透,然后大家自己去二刷,三刷就好了,师傅领进门修行在个人。
|
||||
|
||||
### 训练营提供一些什么呢?
|
||||
## 训练营提供一些什么呢?
|
||||
|
||||
1.具体内容
|
||||
|
||||
@ -180,7 +207,7 @@
|
||||
|
||||
毕竟内容是开源的,质量如何 大家自己去看就好。
|
||||
|
||||
### 训练营的学习方式
|
||||
## 训练营的学习方式
|
||||
|
||||
组织方式:一个学习微信群(180人左右),大家进群之后,等群公告就好,我会通知开始时间和每日刷题计划。
|
||||
|
||||
@ -194,11 +221,11 @@
|
||||
|
||||
所需语言:**所有语种都可以**,毕竟代码随想录几乎支持所有主流语言,**也会针对大家所用的语言做针对性答疑**。
|
||||
|
||||
### 开营时间
|
||||
## 开营时间
|
||||
|
||||
**训练营开始常态化报名,即一直可以报名,当人满180人的时候,就开始新的一期**。 最新的一期可以看文章评论区。
|
||||
**训练营开始常态化报名,即一直可以报名,当人满180人的时候,就开始新的一期**。 最新的一期可以看文章评论区,或者文章开头。
|
||||
|
||||
### 训练营的价格
|
||||
## 训练营的价格
|
||||
|
||||
大家应该最关心的是价格了,**定价依然是268元**,注意这是两个月训练营的费用,而且是全程规划,指导,监督和答疑。
|
||||
|
||||
@ -208,7 +235,7 @@
|
||||
|
||||
后面一定会涨价的,**如果你确实需要有人带,有监督,给规划,有答疑,能花两个月时间更下来的话,还是早报早学习**。
|
||||
|
||||
### 我适合报名吗?
|
||||
## 我适合报名吗?
|
||||
|
||||
符合一下特点的录友可以报名:
|
||||
|
||||
@ -233,7 +260,7 @@
|
||||
**训练营不限编程语言**,任何语言都可以报名,都会答疑。
|
||||
|
||||
|
||||
### 常见疑问
|
||||
## 常见疑问
|
||||
|
||||
**海外录友有时差可以报名吗**?
|
||||
|
||||
@ -265,22 +292,29 @@
|
||||
|
||||
至于三个月的训练营,是可以考虑的,不过安排时间还要待定。
|
||||
|
||||
### 报名方式
|
||||
## 报名方式
|
||||
|
||||
扫码支付268元。 (如果是[代码随想录知识星球](https://programmercarl.com/other/kstar.html)成员录友,只需要支付238元,提交客服的时候需提供知识星球截图,**注意一定要是代码随想录知识星球**)
|
||||
* 正常支付,价格:268 (支付成功后,支付记录发给客服
|
||||
* 知识星球录友支付,价格:238 (支付成功后,[代码随想录知识星球](https://programmercarl.com/other/kstar.html)截图 和 支付记录发给客服
|
||||
* 往期算法训练营录友再次报名,价格:130 (支付成功后,往期训练营群或者支付记录 和 本次支付记录发给客服
|
||||
|
||||
(**注意一定要是[代码随想录知识星球](https://programmercarl.com/other/kstar.html)成员才会有优惠**)
|
||||
|
||||
支付宝支付如下:
|
||||
|
||||
<div align="center"><img src='https://code-thinking-1253855093.file.myqcloud.com/pics/20230603175016.png' width=500 alt=''> </img></div>
|
||||
|
||||
[微信支付点击这里](https://www.programmercarl.com/other/weixinzhifu.html)
|
||||
|
||||
付款后,将付款截图发给客服,客服会在24h内统一回复,**所以大家发给客服信息不要急,当天一定会回复的**。
|
||||
|
||||

|
||||
|
||||
客服的联系方式就在大家的微信聊天窗口,不用担心突出聊天窗口错过消息,客服回复之后 会有微信提示的。
|
||||
<div align="center"><img src='https://code-thinking-1253855093.file.myqcloud.com/pics/20231012125112.png' width=500 alt=''> </img></div>
|
||||
|
||||
关于训练营的任何问题,可以在客服这里咨询!
|
||||
|
||||
|
||||
### 最后
|
||||
|
||||
## 最后
|
||||
|
||||
训练营其实算是代码随想录的一个补充,其内容都是免费开放的,有学习能力的录友自己学习就好。
|
||||
|
||||
@ -294,5 +328,10 @@
|
||||
|
||||
关于训练营的任何疑问都可以扫码联系客服
|
||||
|
||||

|
||||
<div align="center"><img src='https://code-thinking-1253855093.file.myqcloud.com/pics/20231012125112.png' width=500 alt=''> </img></div>
|
||||
|
||||
|
||||
|
||||
<Valine></Valine>
|
||||
|
||||
|
||||
|
||||
@ -1,165 +0,0 @@
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/xunlianying.html" target="_blank">
|
||||
<img src="../pics/训练营.png" width="1000"/>
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
# 时间复杂度
|
||||
|
||||
## 究竟什么是时间复杂度
|
||||
|
||||
**时间复杂度是一个函数,它定性描述该算法的运行时间**。
|
||||
|
||||
我们在软件开发中,时间复杂度就是用来方便开发者估算出程序运行的大体时间。
|
||||
|
||||
那么该如何估计程序运行时间呢,通常会估算算法的操作单元数量来代表程序消耗的时间,这里默认CPU的每个单元运行消耗的时间都是相同的。
|
||||
|
||||
假设算法的问题规模为n,那么操作单元数量便用函数f(n)来表示,随着数据规模n的增大,算法执行时间的增长率和f(n)的增长率相同,这称作为算法的渐近时间复杂度,简称时间复杂度,记为 O(f(n))。
|
||||
|
||||
## 什么是大O
|
||||
|
||||
这里的大O是指什么呢,说到时间复杂度,**大家都知道O(n),O(n^2),却说不清什么是大O**。
|
||||
|
||||
算法导论给出的解释:**大O用来表示上界的**,当用它作为算法的最坏情况运行时间的上界,就是对任意数据输入的运行时间的上界。
|
||||
|
||||
同样算法导论给出了例子:拿插入排序来说,插入排序的时间复杂度我们都说是O(n^2) 。
|
||||
|
||||
输入数据的形式对程序运算时间是有很大影响的,在数据本来有序的情况下时间复杂度是O(n),但如果数据是逆序的话,插入排序的时间复杂度就是O(n^2),也就对于所有输入情况来说,最坏是O(n^2) 的时间复杂度,所以称插入排序的时间复杂度为O(n^2)。
|
||||
|
||||
同样的同理再看一下快速排序,都知道快速排序是O(nlog n),但是当数据已经有序情况下,快速排序的时间复杂度是O(n^2) 的,**所以严格从大O的定义来讲,快速排序的时间复杂度应该是O(n^2)**。
|
||||
|
||||
**但是我们依然说快速排序是O(nlog n)的时间复杂度,这个就是业内的一个默认规定,这里说的O代表的就是一般情况,而不是严格的上界**。如图所示:
|
||||

|
||||
|
||||
我们主要关心的还是一般情况下的数据形式。
|
||||
|
||||
**面试中说道算法的时间复杂度是多少指的都是一般情况**。但是如果面试官和我们深入探讨一个算法的实现以及性能的时候,就要时刻想着数据用例的不一样,时间复杂度也是不同的,这一点是一定要注意的。
|
||||
|
||||
|
||||
## 不同数据规模的差异
|
||||
|
||||
如下图中可以看出不同算法的时间复杂度在不同数据输入规模下的差异。
|
||||
|
||||
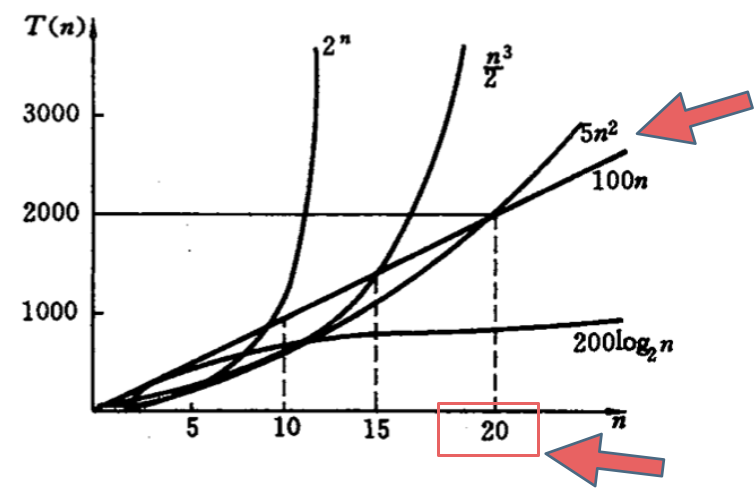
|
||||
|
||||
在决定使用哪些算法的时候,不是时间复杂越低的越好(因为简化后的时间复杂度忽略了常数项等等),要考虑数据规模,如果数据规模很小甚至可以用O(n^2)的算法比O(n)的更合适(在有常数项的时候)。
|
||||
|
||||
就像上图中 O(5n^2) 和 O(100n) 在n为20之前 很明显 O(5n^2)是更优的,所花费的时间也是最少的。
|
||||
|
||||
那为什么在计算时间复杂度的时候要忽略常数项系数呢,也就说O(100n) 就是O(n)的时间复杂度,O(5n^2) 就是O(n^2)的时间复杂度,而且要默认O(n) 优于O(n^2) 呢 ?
|
||||
|
||||
这里就又涉及到大O的定义,**因为大O就是数据量级突破一个点且数据量级非常大的情况下所表现出的时间复杂度,这个数据量也就是常数项系数已经不起决定性作用的数据量**。
|
||||
|
||||
例如上图中20就是那个点,n只要大于20 常数项系数已经不起决定性作用了。
|
||||
|
||||
**所以我们说的时间复杂度都是省略常数项系数的,是因为一般情况下都是默认数据规模足够的大,基于这样的事实,给出的算法时间复杂的的一个排行如下所示**:
|
||||
|
||||
O(1) 常数阶 < O(\log n) 对数阶 < O(n) 线性阶 < O(n^2) 平方阶 < O(n^3) 立方阶 < O(2^n)指数阶
|
||||
|
||||
但是也要注意大常数,如果这个常数非常大,例如10^7 ,10^9 ,那么常数就是不得不考虑的因素了。
|
||||
|
||||
## 复杂表达式的化简
|
||||
|
||||
有时候我们去计算时间复杂度的时候发现不是一个简单的O(n) 或者O(n^2), 而是一个复杂的表达式,例如:
|
||||
|
||||
```
|
||||
O(2*n^2 + 10*n + 1000)
|
||||
```
|
||||
|
||||
那这里如何描述这个算法的时间复杂度呢,一种方法就是简化法。
|
||||
|
||||
去掉运行时间中的加法常数项 (因为常数项并不会因为n的增大而增加计算机的操作次数)。
|
||||
|
||||
```
|
||||
O(2*n^2 + 10*n)
|
||||
```
|
||||
|
||||
去掉常数系数(上文中已经详细讲过为什么可以去掉常数项的原因)。
|
||||
|
||||
```
|
||||
O(n^2 + n)
|
||||
```
|
||||
|
||||
只保留最高项,去掉数量级小一级的n (因为n^2 的数据规模远大于n),最终简化为:
|
||||
|
||||
```
|
||||
O(n^2)
|
||||
```
|
||||
|
||||
如果这一步理解有困难,那也可以做提取n的操作,变成O(n(n+1)),省略加法常数项后也就变成了:
|
||||
|
||||
```
|
||||
O(n^2)
|
||||
```
|
||||
|
||||
所以最后我们说:这个算法的算法时间复杂度是O(n^2) 。
|
||||
|
||||
|
||||
也可以用另一种简化的思路,其实当n大于40的时候, 这个复杂度会恒小于O(3 × n^2),
|
||||
O(2 × n^2 + 10 × n + 1000) < O(3 × n^2),3 × n^2省略掉常数项系数,最终时间复杂度也是O(n^2)。
|
||||
|
||||
## O(log n)中的log是以什么为底?
|
||||
|
||||
平时说这个算法的时间复杂度是logn的,那么一定是log 以2为底n的对数么?
|
||||
|
||||
其实不然,也可以是以10为底n的对数,也可以是以20为底n的对数,**但我们统一说 logn,也就是忽略底数的描述**。
|
||||
|
||||
为什么可以这么做呢?如下图所示:
|
||||
|
||||

|
||||
|
||||
|
||||
假如有两个算法的时间复杂度,分别是log以2为底n的对数和log以10为底n的对数,那么这里如果还记得高中数学的话,应该不能理解`以2为底n的对数 = 以2为底10的对数 * 以10为底n的对数`。
|
||||
|
||||
而以2为底10的对数是一个常数,在上文已经讲述了我们计算时间复杂度是忽略常数项系数的。
|
||||
|
||||
抽象一下就是在时间复杂度的计算过程中,log以i为底n的对数等于log 以j为底n的对数,所以忽略了i,直接说是logn。
|
||||
|
||||
这样就应该不难理解为什么忽略底数了。
|
||||
|
||||
## 举一个例子
|
||||
|
||||
通过这道面试题目,来分析一下时间复杂度。题目描述:找出n个字符串中相同的两个字符串(假设这里只有两个相同的字符串)。
|
||||
|
||||
如果是暴力枚举的话,时间复杂度是多少呢,是O(n^2)么?
|
||||
|
||||
这里一些同学会忽略了字符串比较的时间消耗,这里并不像int 型数字做比较那么简单,除了n^2次的遍历次数外,字符串比较依然要消耗m次操作(m也就是字母串的长度),所以时间复杂度是O(m × n × n)。
|
||||
|
||||
接下来再想一下其他解题思路。
|
||||
|
||||
先对n个字符串按字典序来排序,排序后n个字符串就是有序的,意味着两个相同的字符串就是挨在一起,然后再遍历一遍n个字符串,这样就找到两个相同的字符串了。
|
||||
|
||||
那看看这种算法的时间复杂度,快速排序时间复杂度为O(nlog n),依然要考虑字符串的长度是m,那么快速排序每次的比较都要有m次的字符比较的操作,就是O(m × n × log n)。
|
||||
|
||||
之后还要遍历一遍这n个字符串找出两个相同的字符串,别忘了遍历的时候依然要比较字符串,所以总共的时间复杂度是 O(m × n × log n + n × m)。
|
||||
|
||||
我们对O(m × n × log n + n × m)进行简化操作,把m × n提取出来变成O(m × n × (log n + 1)),再省略常数项最后的时间复杂度是O(m × n × log n)。
|
||||
|
||||
最后很明显O(m × n × log n) 要优于O(m × n × n)!
|
||||
|
||||
所以先把字符串集合排序再遍历一遍找到两个相同字符串的方法要比直接暴力枚举的方式更快。
|
||||
|
||||
这就是我们通过分析两种算法的时间复杂度得来的结论。
|
||||
|
||||
**当然这不是这道题目的最优解,我仅仅是用这道题目来讲解一下时间复杂度**。
|
||||
|
||||
## 总结
|
||||
|
||||
本篇讲解了什么是时间复杂度,复杂度是用来干什么的,以及数据规模对时间复杂度的影响。
|
||||
|
||||
还讲解了被大多数同学忽略的大O的定义以及log究竟是以谁为底的问题。
|
||||
|
||||
再分析了如何简化复杂的时间复杂度,最后举一个具体的例子,把本篇的内容串起来。
|
||||
|
||||
相信看完本篇,大家对时间复杂度的认识会深刻很多!
|
||||
|
||||
如果感觉「代码随想录」很不错,赶快推荐给身边的朋友同学们吧,他们发现和「代码随想录」相见恨晚!
|
||||
|
||||
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
Reference in New Issue
Block a user