Update

problems/0121.买卖股票的最佳时机.md

@@ -0,0 +1,71 @@
+
+# 思路
+
+## 暴力 
+
+这道题目最直观的想法，就是暴力，找优间距了。
+
+```
+class Solution {
+public:
+    int maxProfit(vector<int>& prices) {
+        int result = 0;
+        for (int i = 0; i < prices.size(); i++) {
+            for (int j = i + 1; j < prices.size(); j++){
+                result = max(result, prices[j] - prices[i]);
+            }
+        }
+        return result;
+    }
+};
+```
+
+* 时间复杂度：O(n^2) 
+* 空间复杂度：O(1)
+
+当然该方法超时了。
+
+
+## 贪心 
+
+因为股票就买卖一次，那么贪心的想法很自然就是取最左最小值，取最右最大值，那么得到的差值就是最大利润。
+
+C++代码如下：
+
+```C++
+class Solution {
+public:
+    int maxProfit(vector<int>& prices) {
+        int low = INT_MAX;
+        int result = 0;
+        for (int i = 0; i < prices.size(); i++) {
+            low = min(low, prices[i]);  // 取最左最小价格
+            result = max(result, prices[i] - low); // 直接取最大区间利润
+        }
+        return result;
+    }
+};
+```
+
+## 动态规划 
+
+dp[i][0] 表示第i天持有股票所得现金
+dp[i][1] 表示第i天不持有股票所得现金
+
+```
+class Solution {
+public:
+    int maxProfit(vector<int>& prices) {
+        int n = prices.size();
+        if (n == 0) return 0;
+        vector<vector<int>> dp(n, vector<int>(2, 0));
+        dp[0][0] -= prices[0]; // 持股票
+        for (int i = 1; i < n; i++) {
+            dp[i][0] = max(dp[i - 1][0], -prices[i]); // 买入
+            dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]); // 卖出
+        }
+        return dp[n - 1][1];
+    }
+};
+```
+

problems/0123.买卖股票的最佳时机III.md

@@ -0,0 +1,140 @@
+# 思路 
+
+这道题目相对 121.买卖股票的最佳时机 和 122.买卖股票的最佳时机II 难了不少。
+
+关键在于至多买卖两次，这意味着可以买卖一次，可以买卖两次，也可以不买卖。
+
+接来下我用动态规划五部曲详细分析一下：
+
+### 确定dp数组以及下标的含义
+
+一天一共就有五个状态，
+0. 没有操作 
+1. 第一次买入
+2. 第一次卖出 
+3. 第二次买入
+4. 第二次卖出 
+
+dp[i][j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金。
+
+### 确定递推公式
+
+dp[i][0] = dp[i - 1][0];
+
+需要注意：dp[i][1]，**表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票，这是很多同学容易陷入的误区**。
+
+达到dp[i][1]状态，有两个具体操作：
+
+* 操作一：第i天买入股票了，那么dp[i][1] = dp[i-1][0] - prices[i] 
+* 操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][0] 
+
+那么dp[i][1]究竟选 dp[i-1][0] - prices[i]，还是dp[i - 1][0]呢？ 
+
+一定是选最大的，所以 dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][0]);
+
+同理dp[i][2]也有两个操作：
+
+* 操作一：第i天卖出股票了，那么dp[i][2] = dp[i - 1][i] + prices[i]
+* 操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]
+
+所以dp[i][2] = max(dp[i - 1][i] + prices[i], dp[i][2])
+
+同理可推出剩下状态部分：
+
+dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
+dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]); 
+
+
+### dp数组如何初始化
+
+
+第0天没有操作，这个最容易想到，就是0，即：dp[0][0] = 0; 
+
+第0天做第一次买入的操作，dp[0][1] = -prices[0]; 
+
+第0天做第一次卖出的操作，这个初始值应该是多少呢？
+
+首先卖出的操作一定是收获利润，整个股票买卖最差情况也就是没有盈利即全程无操作现金为0，
+
+从递推公式中可以看出每次是取最大值，那么既然是收获利润如果比0还小了就没有必要收获这个利润了。
+
+所以dp[0][2] = 0;
+
+第0天第二次买入操作，初始值应该是多少呢？
+
+不用管第几次，现在手头上没有现金，只要买入，现金就做相应的减少。
+
+所以第二次买入操作，初始化为：dp[0][3] = -prices[0];
+
+同理第二次卖出初始化dp[0][4] = 0;
+
+### 确定遍历顺序
+
+从递归公式其实已经可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。
+
+
+### 举例推导dp数组
+
+以输入[1,2,3,4,5]为例
+
+
+![123.买卖股票的最佳时机III](https://img-blog.csdnimg.cn/20201228181724295.png)
+
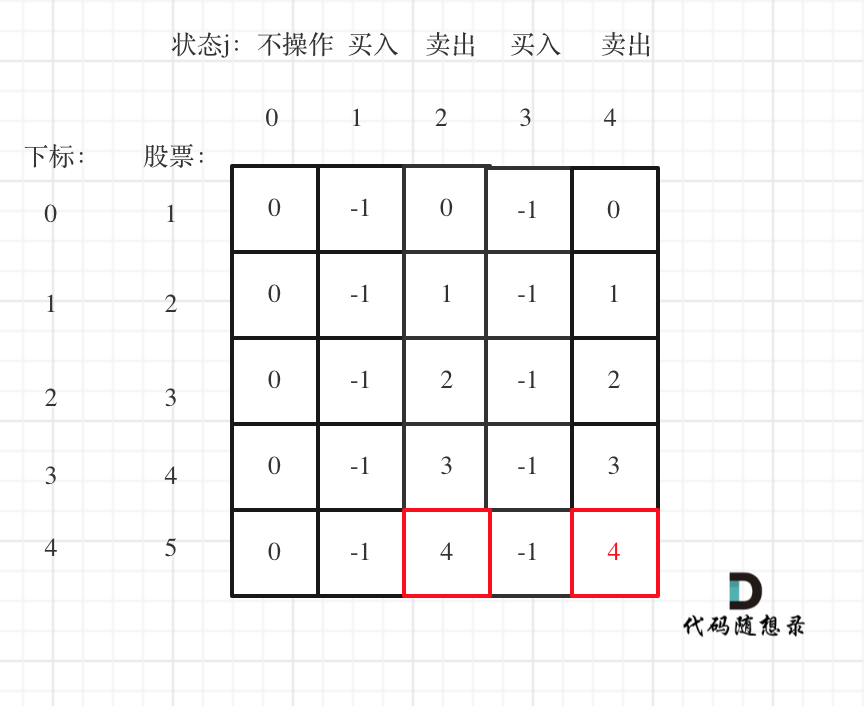
+红色为最终求解。
+
+因为利润最大一定是卖出的状态，所以最终最大利润是max(dp[4][2], dp[4][4]);
+
+### C++代码 
+
+以上五步都分析完了，不难写出如下代码：
+
+```
+class Solution {
+public:
+    int maxProfit(vector<int>& prices) {
+        if (prices.size() == 0) return 0;
+        vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
+        dp[0][0] = 0;
+        dp[0][1] = -prices[0];
+        dp[0][3] = -prices[0];
+        for (int i = 1; i < prices.size(); i++) {
+            dp[i][0] = dp[i - 1][0];
+            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
+            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
+            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
+            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
+        }
+        return max(dp[prices.size() - 1][2], dp[prices.size() - 1][4]);
+
+    }
+};
+```
+
+* 时间复杂度：O(n)
+* 空间复杂度：O(n * 5)
+
+
+
+当然，大家在网上看到的题解还有一种优化空间写法，如下：
+
+```
+class Solution {
+public:
+    int maxProfit(vector<int>& prices) {
+        if (prices.size() == 0) return 0;
+        vector<int> dp(5, 0);
+        dp[0] = 0;
+        dp[1] = -prices[0];
+        dp[3] = -prices[0];
+        for (int i = 1; i < prices.size(); i++) {
+            dp[1] = max(dp[1], dp[0] - prices[i]);
+            dp[2] = max(dp[2], dp[1] + prices[i]);
+            dp[3] = max(dp[3], dp[2] - prices[i]);
+            dp[4] = max(dp[4], dp[3] + prices[i]);
+        }
+        return max(dp[2], dp[4]);
+
+    }
+};
+```
+但这种写法，dp[2] 利用的是当天的dp[1]，我还没有理解为什么这种写法也可以通过，网上的题解也没有做出解释，可能这就是神代码吧，欢迎大家来讨论一波！

problems/0188.买卖股票的最佳时机IV.md

@@ -0,0 +1,127 @@
+
+# 思路 
+
+这道题目可以说是123.买卖股票的最佳时机III的进阶版， 这里要求至多有k次交易。
+
+在123.买卖股票的最佳时机III中，我是定义了一个二维dp数组，本题其实依然可以用一个二维dp数组。
+
+动规五部曲，分析如下：
+
+### 确定dp数组以及下标的含义
+
+使用二维数组 dp[i][j] ：第i天的状态为j，所剩下的最大现金是dp[i][j]
+
+j的状态表示为： 
+
+* 0 表示不操作
+* 1 第一次买入 
+* 2 第一次卖出
+* 3 第一次买入 
+* 4 第一次卖出
+.....
+
+大家应该发现规律了吧 ，除了0以外，偶数就是卖出，奇数就是买入。
+
+题目要求是至多有K笔交易，那么j的范围就定义为 2 * k + 1 就可以了。
+
+所以二维dp数组的C++定义为：
+
+```
+vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
+```
+
+### 确定递推公式
+
+在123.买卖股票的最佳时机III中 
+
+需要注意：dp[i][1]，**表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票，这是很多同学容易陷入的误区**。
+
+达到dp[i][1]状态，有两个具体操作：
+
+* 操作一：第i天买入股票了，那么dp[i][1] = dp[i-1][0] - prices[i] 
+* 操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][0] 
+
+那么dp[i][1]究竟选 dp[i-1][0] - prices[i]，还是dp[i - 1][0]呢？ 
+
+一定是选最大的，所以 dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][0]);
+
+同理dp[i][2]也有两个操作：
+
+* 操作一：第i天卖出股票了，那么dp[i][2] = dp[i - 1][i] + prices[i]
+* 操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]
+
+所以dp[i][2] = max(dp[i - 1][i] + prices[i], dp[i][2])
+
+同理可推出剩下状态部分：
+
+dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
+dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]); 
+
+* dp数组如何初始化
+* 确定遍历顺序
+* 举例推导dp数组
+
+```
+class Solution {
+public:
+    int maxProfit(int k, vector<int>& prices) {
+
+        if (prices.size() == 0) return 0;
+        vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
+        for (int j = 1; j < 2 * k; j += 2) {
+            dp[0][j] = -prices[0];
+        }
+        for (int i = 1;i < prices.size(); i++) {
+            for (int j = 0; j < 2 * k - 1; j += 2) { // 注意这里是等于
+                dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
+                dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
+            }
+        }
+        int result = 0;
+        for (int j = 2; j <= 2 * k; j += 2) {
+            result = max(result, dp[prices.size() - 1][j]);
+        }
+        return result;
+    }
+};
+```
+
+```
+class Solution {
+public:
+    int maxProfit(int k, vector<int>& prices) {
+        const int n = prices.size();
+        if (n == 0) return 0;
+        vector<int> dp(2 * k + 1, 0);
+        for (int i = 1;i < 2 * k;i += 2)
+            dp[i] = -prices[0];
+        for (int i = 1;i < n;++i) {
+            for (int j = 0;j < 2 * k;j += 2) {
+                dp[j] = max(dp[j], dp[j + 1] + prices[i]);
+                dp[j + 1] = max(dp[j + 1], dp[j + 2] - prices[i]);
+            }
+        }
+        return dp[0];
+    }
+};
+
+
+class Solution {
+public:
+    int maxProfit(vector<int>& prices) {
+        if (prices.size() == 0) return 0;
+        vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
+        dp[0][0] = 0;
+        dp[0][1] = -prices[0];
+        dp[0][3] = -prices[0];
+        for (int i = 1; i < prices.size(); i++) {
+            dp[i][0] = dp[i - 1][0];
+            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
+            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
+            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
+            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
+        }
+        return max(dp[prices.size() - 1][2], dp[prices.size() - 1][4]);
+
+    }
+};

problems/0205.同构字符串.md

@@ -4,6 +4,8 @@ https://leetcode-cn.com/problems/isomorphic-strings/
 
 ## 思路 
 
+字符串没有说都是小写字母之类的，所以用数组不合适了，用map来做映射。
+
 使用两个map 保存 s[i] 到 t[j] 和 t[j] 到 s[i] 的映射关系，如果发现对应不上，立刻返回 false 
 
 ## C++代码

problems/0714.买卖股票的最佳时机含手续费.md

@@ -1,24 +1,55 @@
+> 
+
+# 714. 买卖股票的最佳时机含手续费 
+
+题目链接：https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/
+
+给定一个整数数组 prices，其中第 i 个元素代表了第 i 天的股票价格 ；非负整数 fee 代表了交易股票的手续费用。
+
+你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。
+
+返回获得利润的最大值。
+
+注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。
+
+示例 1:
+输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
+输出: 8
+
+解释: 能够达到的最大利润:      
+在此处买入 prices[0] = 1       
+在此处卖出 prices[3] = 8       
+在此处买入 prices[4] = 4     
+在此处卖出 prices[5] = 9   
+总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.      
+
+注意:
+* 0 < prices.length <= 50000.
+* 0 < prices[i] < 50000.
+* 0 <= fee < 50000.
 
 # 思路
+
 本题相对于[贪心算法：122.买卖股票的最佳时机II](https://mp.weixin.qq.com/s/VsTFA6U96l18Wntjcg3fcg)，多添加了一个条件就是手续费。
 
 ## 贪心算法 
 
-在[贪心算法：122.买卖股票的最佳时机II](https://mp.weixin.qq.com/s/VsTFA6U96l18Wntjcg3fcg)中使用贪心策略不用关系具体什么时候买卖，只要收集每天的正利润，最后稳稳的就是最大利润了。
+在[贪心算法：122.买卖股票的最佳时机II](https://mp.weixin.qq.com/s/VsTFA6U96l18Wntjcg3fcg)中使用贪心策略不用关心具体什么时候买卖，只要收集每天的正利润，最后稳稳的就是最大利润了。
 
-而本题有了手续费，就要关系什么时候买卖了，因为只计算所获得利润，可能不足以手续费。
+而本题有了手续费，就要关系什么时候买卖了，因为计算所获得利润，需要考虑买卖利润可能不足以手续费的情况。
 
 如果使用贪心策略，就是最低值买，最高值（如果算上手续费还盈利）就卖。
 
 此时无非就是要找到两个点，买入日期，和卖出日期。
 
 * 买入日期：其实很好想，遇到更低点就记录一下。
-* 卖出日期：这个就不好算了，但也没有必要算出准确的卖出日期，只要当前价格大于（最低价格+费用），就可以收获利润，至于准确的卖出日期，就是连续收获利润区间里的最后一天。
+* 卖出日期：这个就不好算了，但也没有必要算出准确的卖出日期，只要当前价格大于（最低价格+手续费），就可以收获利润，至于准确的卖出日期，就是连续收获利润区间里的最后一天（并不需要计算是具体哪一天）。
 
-所以我们在做收获利润操作的时候其实有两种情况：
+所以我们在做收获利润操作的时候其实有三种情况：
 
 * 情况一：收获利润的这一天并不是收获利润区间里的最后一天（不是真正的卖出，相当于持有股票），所以后面要继续收获利润。
-* 情况二：收获利润的这一天是收获利润区间里的最后一天（相当于真正的卖出了），后面要重新记录最小价格了。
+* 情况二：前一天是收获利润区间里的最后一天（相当于真正的卖出了），今天要重新记录最小价格了。
+* 情况三：不作操作，保持原有状态（买入，卖出，不买不卖）
 
 贪心算法C++代码如下：
 
@@ -29,12 +60,17 @@ public:
         int result = 0;
         int minPrice = prices[0]; // 记录最低价格
         for (int i = 1; i < prices.size(); i++) {
-            // 买入
-            if (prices[i] < minPrice) minPrice = prices[i]; // 情况二
+            // 情况二：相当于买入
+            if (prices[i] < minPrice) minPrice = prices[i]; 
+
+            // 情况三：保持原有状态（因为此时买则不便宜，卖则亏本）
+            if (prices[i] >= minPrice && prices[i] <= minPrice + fee) {
+                continue;
+            }
 
             // 计算利润，可能有多次计算利润，最后一次计算利润才是真正意义的卖出
             if (prices[i] > minPrice + fee) {
-                result += prices[i] - minPrice - fee;
+                result += prices[i] - minPrice - fee; 
                 minPrice = prices[i] - fee; // 情况一，这一步很关键
             }
         }
@@ -43,14 +79,16 @@ public:
 };
 ```
 
-从代码中可以看出对情况一的操作，因为如果还在收获利润的区间里，表示并不是真正的卖出，而计算利润每次都要减去手续费，
-**所以要让minPrice = prices[i] - fee;，这样在明天收获利润的时候，才不会多减一次手续费！**
+* 时间复杂度：O(n)
+* 空间复杂度：O(1)
 
-理解这里很关键，其实也是核心所在，很多题解关于这块都没有说清楚。
+从代码中可以看出对情况一的操作，因为如果还在收获利润的区间里，表示并不是真正的卖出，而计算利润每次都要减去手续费，**所以要让minPrice = prices[i] - fee;，这样在明天收获利润的时候，才不会多减一次手续费！**
+
+大家也可以发现，情况三，那块代码是可以删掉的，我是为了让代码表达清晰，所以没有精简。
 
 ## 动态规划 
 
-我在「代码随想录」公众号里正在讲解贪心算法，将在下一个系列详细讲解动态规划，所以本题解先给出我的C++代码（带详细注释），感兴趣的同学可以自己先学习一下。
+我在公众号「代码随想录」里将在下一个系列详细讲解动态规划，所以本题解先给出我的C++代码（带详细注释），感兴趣的同学可以自己先学习一下。
 
 相对于[贪心算法：122.买卖股票的最佳时机II](https://mp.weixin.qq.com/s/VsTFA6U96l18Wntjcg3fcg)的动态规划解法中，只需要在计算卖出操作的时候减去手续费就可以了，代码几乎是一样的。
 
@@ -66,9 +104,7 @@ public:
         vector<vector<int>> dp(n, vector<int>(2, 0));
         dp[0][0] -= prices[0]; // 持股票
         for (int i = 1; i < n; i++) {
-            // 第i天持股票所剩最多现金 = max(第i-1天持股票所剩现金, 第i-1天持现金-买第i天的股票)
             dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
-            // 第i天持有最多现金 = max(第i-1天持有的最多现金，第i-1天持有股票所剩的最多现金+第i天卖出股票-手续费)
             dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
         }
         return max(dp[n - 1][0], dp[n - 1][1]);
@@ -76,6 +112,9 @@ public:
 };
 ```
 
+* 时间复杂度：O(n)
+* 空间复杂度：O(n)
+
 当然可以对空间经行优化，因为当前状态只是依赖前一个状态。
 
 C++ 代码如下：
@@ -96,7 +135,16 @@ public:
     }
 };
 ```
+* 时间复杂度：O(n)
+* 空间复杂度：O(1)
+
+# 总结 
+
+本题贪心的思路其实是比较难的，动态规划才是常规做法，但也算是给大家拓展一下思路，感受一下贪心的魅力。
+
+后期我们在讲解 股票问题系列的时候，会用动规的方式把股票问题穿个线。
+
+就酱，学算法，认准「代码随想录」，值得推荐给身边的朋友同学们！
 
-细心的同学可能发现，在计算saleStock的时候 使用的已经是最新的holdStock了，理论上应该使用上一个状态的holdStock即（i-1时候的holdstock），但是
 
 

problems/0738.单调递增的数字.md

@@ -1,10 +1,33 @@
 
+> 
+
+# 738.单调递增的数字 
+
+给定一个非负整数 N，找出小于或等于 N 的最大的整数，同时这个整数需要满足其各个位数上的数字是单调递增。
+
+（当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。）
+
+示例 1:     
+输入: N = 10  
+输出: 9     
+
+示例 2:     
+输入: N = 1234    
+输出: 1234   
+
+示例 3:     
+输入: N = 332   
+输出: 299      
+
+说明: N 是在 [0, 10^9] 范围内的一个整数。
+
 # 思路 
 
 ## 暴力解法
 
-暴力一波 果然超时了
+题意很简单，那么首先想的就是暴力解法了，来我提大家暴力一波，结果自然是超时！
 
+代码如下：
 ```C++
 class Solution {
 private:
@@ -27,6 +50,9 @@ public:
     }
 };
 ```
+* 时间复杂度：O(n * m) m为n的数字长度 
+* 空间复杂度：O(1)
+
 ## 贪心算法 
 
 题目要求小于等于N的最大单调递增的整数，那么拿一个两位的数字来举例。 
@@ -43,12 +69,13 @@ public:
 
 此时是从前向后遍历还是从后向前遍历呢？ 
 
-这里其实还有一个贪心选择，对于“遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]--，然后strNum[i]给为9”的情况，这个strNum[i - 1]--的操作应该是越靠后越好。 
+从前向后遍历的话，遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]减一，但此时如果strNum[i - 1]减一了，可能又小于strNum[i - 2]。
 
-因为这样才能让这个单调递增整数尽可能的大。例如：对于5486，第一位的5能不减一尽量不减一，因为这个减一对整体损失最大。
+这么说有点抽象，举个例子，数字：332，从前向后遍历的话，那么就把变成了329，此时2又小于了第一位的3了，真正的结果应该是299。
 
-所以要从后向前遍历，遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]--，然后strNum[i]给为9，这样保证这个减一的操作尽可能在后面进行（即整数的尽可能小的位数上进行）。
+**所以从前后向遍历会改变已经遍历过的结果！**
 
+那么从后向前遍历，就可以重复利用上次比较得出的结果了，从后向前遍历332的数值变化为：332 -> 329 -> 299
 
 确定了遍历顺序之后，那么此时局部最优就可以推出全局，找不出反例，试试贪心。
 
@@ -76,6 +103,20 @@ public:
 };
 
 ```
+
+* 时间复杂度：O(n) n 为数字长度 
+* 空间复杂度：O(n) 需要一个字符串，转化为字符串操作更方便
+
+# 总结 
+
+本题只要想清楚个例，例如98，一旦出现strNum[i - 1] > strNum[i]的情况（非单调递增），首先想让strNum[i - 1]减一，strNum[i]赋值9，这样这个整数就是89。就可以很自然想到对应的贪心解法了。
+
+想到了贪心，还要考虑遍历顺序，只有从后向前遍历才能重复利用上次比较的结果。
+
+最后代码实现的时候，也需要一些技巧，例如用一个flag来标记从哪里开始赋值9。
+
+就酱，循序渐进学算法，认准「代码随想录」！
+
 > **我是[程序员Carl](https://github.com/youngyangyang04)，可以找我[组队刷题](https://img-blog.csdnimg.cn/20201115103410182.png)，也可以在[B站上找到我](https://space.bilibili.com/525438321)，本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录，更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在公众号：[代码随想录](https://img-blog.csdnimg.cn/20201124161234338.png)，关注后就会发现和「代码随想录」相见恨晚！**
 
 **如果感觉题解对你有帮助，不要吝啬给一个👍吧！**