Merge branch 'master' of github.com:youngyangyang04/leetcode-master

problems/0024.两两交换链表中的节点.md

@@ -81,7 +81,7 @@ public:
 
 上面的代码我第一次提交执行用时8ms，打败6.5%的用户，差点吓到我了。
 
-心想应该没有更好的方法了吧，也就$O(n)$的时间复杂度，重复提交几次，这样了：
+心想应该没有更好的方法了吧，也就 $O(n)$ 的时间复杂度，重复提交几次，这样了：
 
 ![24.两两交换链表中的节点](https://code-thinking.cdn.bcebos.com/pics/24.%E4%B8%A4%E4%B8%A4%E4%BA%A4%E6%8D%A2%E9%93%BE%E8%A1%A8%E4%B8%AD%E7%9A%84%E8%8A%82%E7%82%B9.png)
 
@@ -181,6 +181,23 @@ class Solution {
 }
 ```
 
+```java
+// 将步骤 2,3 交换顺序，这样不用定义 temp 节点
+public ListNode swapPairs(ListNode head) {
+    ListNode dummy = new ListNode(0, head);
+    ListNode cur = dummy;
+    while (cur.next != null && cur.next.next != null) {
+        ListNode node1 = cur.next;// 第 1 个节点
+        ListNode node2 = cur.next.next;// 第 2 个节点
+        cur.next = node2; // 步骤 1
+        node1.next = node2.next;// 步骤 3
+        node2.next = node1;// 步骤 2
+        cur = cur.next.next;
+    }
+    return dummy.next;
+}
+```
+
 ### Python：
 
 ```python
@@ -285,6 +302,21 @@ var swapPairs = function (head) {
 };
 ```
 
+```javascript
+// 递归版本
+var swapPairs = function (head) {
+  if (head == null || head.next == null) {
+    return head;
+  }
+
+  let after = head.next;
+  head.next = swapPairs(after.next);
+  after.next = head;
+
+  return after;
+};
+```
+
 ### TypeScript：
 
 ```typescript

problems/0028.实现strStr.md

@@ -564,6 +564,38 @@ public:
 ## 其他语言版本
 
 ### Java：
+```Java
+class Solution {
+    /**
+	牺牲空间，换取最直白的暴力法
+        时间复杂度 O(n * m)
+        空间 O(n + m)
+     */
+    public int strStr(String haystack, String needle) {
+        // 获取 haystack 和 needle 的长度
+        int n = haystack.length(), m = needle.length();
+        // 将字符串转换为字符数组，方便索引操作
+        char[] s = haystack.toCharArray(), p = needle.toCharArray();
+
+        // 遍历 haystack 字符串
+        for (int i = 0; i < n - m + 1; i++) {
+            // 初始化匹配的指针
+            int a = i, b = 0;
+            // 循环检查 needle 是否在当前位置开始匹配
+            while (b < m && s[a] == p[b]) {
+                // 如果当前字符匹配，则移动指针
+                a++;
+                b++;
+            }
+            // 如果 b 等于 m，说明 needle 已经完全匹配，返回当前位置 i
+            if (b == m) return i;
+        }
+
+        // 如果遍历完毕仍未找到匹配的子串，则返回 -1
+        return -1;
+    }
+}
+```
 
 ```Java
 class Solution {

problems/0035.搜索插入位置.md

@@ -332,6 +332,7 @@ impl Solution {
 ### Python
 
 ```python
+# 第一种二分法: [left, right]左闭右闭区间
 class Solution:
     def searchInsert(self, nums: List[int], target: int) -> int:
         left, right = 0, len(nums) - 1
@@ -348,6 +349,26 @@ class Solution:
         return right + 1
 ```
 
+```python
+# 第二种二分法: [left, right)左闭右开区间
+class Solution:
+    def searchInsert(self, nums: List[int], target: int) -> int:
+        left = 0
+        right = len(nums)
+
+        while (left < right):
+            middle = (left + right) // 2
+
+            if nums[middle] > target:
+                right = middle
+            elif nums[middle] < target:
+                left = middle + 1
+            else:
+                return middle
+
+        return right
+```
+
 ### JavaScript
 
 ```js

problems/0104.二叉树的最大深度.md

@@ -77,7 +77,7 @@ return depth;
 所以整体c++代码如下：
 
 ```CPP
-class solution {
+class Solution {
 public:
     int getdepth(TreeNode* node) {
         if (node == NULL) return 0;
@@ -94,7 +94,7 @@ public:
 
 代码精简之后c++代码如下：
 ```CPP
-class solution {
+class Solution {
 public:
     int maxDepth(TreeNode* root) {
         if (root == null) return 0;
@@ -110,7 +110,7 @@ public:
 本题当然也可以使用前序，代码如下：(**充分表现出求深度回溯的过程**)
 
 ```CPP
-class solution {
+class Solution {
 public:
     int result;
     void getdepth(TreeNode* node, int depth) {
@@ -144,7 +144,7 @@ public:
 注意以上代码是为了把细节体现出来，简化一下代码如下：
 
 ```CPP
-class solution {
+class Solution {
 public:
     int result;
     void getdepth(TreeNode* node, int depth) {
@@ -183,7 +183,7 @@ public:
 c++代码如下：
 
 ```CPP
-class solution {
+class Solution {
 public:
     int maxDepth(TreeNode* root) {
         if (root == NULL) return 0;
@@ -232,7 +232,7 @@ public:
 c++代码：
 
 ```CPP
-class solution {
+class Solution {
 public:
     int maxDepth(Node* root) {
         if (root == 0) return 0;
@@ -249,7 +249,7 @@ public:
 依然是层序遍历，代码如下：
 
 ```CPP
-class solution {
+class Solution {
 public:
     int maxDepth(Node* root) {
         queue<Node*> que;
@@ -278,7 +278,7 @@ public:
 104.二叉树的最大深度
 
 ```java
-class solution {
+class Solution {
     /**
      * 递归法
      */
@@ -319,7 +319,7 @@ class Solution {
 ```
 
 ```java
-class solution {
+class Solution {
     /**
      * 迭代法，使用层序遍历
      */
@@ -369,7 +369,7 @@ class Solution {
 ```
 
 ```java
-class solution {
+class Solution {
     /**
      * 迭代法，使用层序遍历
      */
@@ -402,7 +402,7 @@ class solution {
 
 递归法：
 ```python
-class solution:
+class Solution:
     def maxdepth(self, root: treenode) -> int:
         return self.getdepth(root)
         
@@ -417,7 +417,7 @@ class solution:
 
 递归法：精简代码
 ```python
-class solution:
+class Solution:
     def maxdepth(self, root: treenode) -> int:
         if not root:
             return 0

problems/0108.将有序数组转换为二叉搜索树.md

@@ -334,6 +334,18 @@ class Solution:
         return root
 
 ```
+递归 精简(自身调用)
+```python
+class Solution:
+    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
+        if not nums:
+            return
+        mid = len(nums) // 2
+        root = TreeNode(nums[mid])
+        root.left = self.sortedArrayToBST(nums[:mid])
+        root.right = self.sortedArrayToBST(nums[mid + 1 :])
+        return root
+```
 
 迭代法
 ```python

problems/0203.移除链表元素.md

@@ -497,27 +497,67 @@ func removeElements(_ head: ListNode?, _ val: Int) -> ListNode? {
 
 ```php
 /**
- * Definition for singly-linked list.
- * type ListNode struct {
- *     Val int
- *     Next *ListNode
+ * Definition for a singly-linked list.
+ * class ListNode {
+ *     public $val = 0;
+ *     public $next = null;
+ *     function __construct($val = 0, $next = null) {
+ *         $this->val = $val;
+ *         $this->next = $next;
+ *     }
  * }
  */
- // 虚拟头+双指针
-func removeElements(head *ListNode, val int) *ListNode {
-    dummyHead := &ListNode{}
-    dummyHead.Next = head
-    pred := dummyHead
-    cur := head
-    for cur != nil {
-        if cur.Val == val {
-            pred.Next = cur.Next
-        } else {
-            pred = cur
+
+//版本一（在原链表上直接删除）：
+class Solution {
+
+    /**
+     * @param ListNode $head
+     * @param Integer $val
+     * @return ListNode
+     */
+    function removeElements($head, $val)
+    {
+  	if ($head == null) {
+            return null;
         }
-        cur = cur.Next
+
+        $now = $head;
+        while ($now->next != null) {
+            if ($now->next->val == $val) {
+                $now->next = $now->next->next;
+            } else {
+                $now = $now->next;
+            }
+        }
+        if ($head->val == $val) {
+            return $head->next;
+        }
+        return $head;
+    }
+}
+
+//版本二（虚拟头结点方式）：
+class Solution {
+
+    /**
+     * @param ListNode $head
+     * @param Integer $val
+     * @return ListNode
+     */
+    function removeElements($head, $val)
+    {
+        $dummyHead = new ListNode(0, $head);
+        $now = $dummyHead;
+        while ($now->next != null){
+            if ($now->next->val == $val) {
+                $now->next = $now->next->next;
+            } else {
+                $now = $now->next;
+            }
+        }
+        return $dummyHead->next;
     }
-    return dummyHead.Next
 }
 ```
 

problems/前序/On的算法居然超时了，此时的n究竟是多大？.md

@@ -14,9 +14,9 @@
 
 也就是说程序运行的时间超过了规定的时间，一般OJ（online judge）的超时时间就是1s，也就是用例数据输入后最多要1s内得到结果，暂时还不清楚leetcode的判题规则，下文为了方便讲解，暂定超时时间就是1s。
 
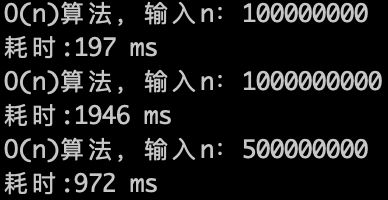
-如果写出了一个$O(n)$的算法 ，其实可以估算出来n是多大的时候算法的执行时间就会超过1s了。
+如果写出了一个 $O(n)$ 的算法 ，其实可以估算出来n是多大的时候算法的执行时间就会超过1s了。
 
-如果n的规模已经足够让$O(n)$的算法运行时间超过了1s，就应该考虑log(n)的解法了。
+如果n的规模已经足够让 $O(n)$ 的算法运行时间超过了1s，就应该考虑log(n)的解法了。
 
 ## 从硬件配置看计算机的性能
 
@@ -60,7 +60,7 @@
 
 测试硬件：2015年MacPro，CPU配置：2.7 GHz Dual-Core Intel Core i5
 
-实现三个函数，时间复杂度分别是 $O(n)$ , $O(n^2)$, $O(n\log n)$，使用加法运算来统一测试。
+实现三个函数，时间复杂度分别是 $O(n)$ , $O(n^2)$ , $O(n\log n)$ ，使用加法运算来统一测试。
 
 ```CPP
 // O(n)
@@ -126,19 +126,19 @@ int main() {
 
 ![程序超时2](https://code-thinking-1253855093.file.myqcloud.com/pics/20200729200018460-20230310124315093.png)
 
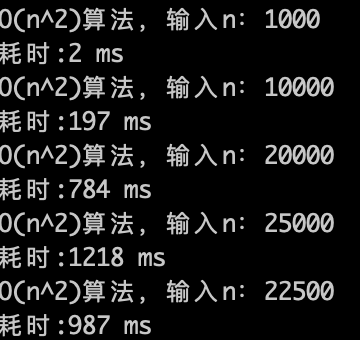
-O(n)的算法，1s内大概计算机可以运行 5 * (10^8)次计算，可以推测一下$O(n^2)$ 的算法应该1s可以处理的数量级的规模是 5 * (10^8)开根号，实验数据如下。
+O(n)的算法，1s内大概计算机可以运行 5 * (10^8)次计算，可以推测一下 $O(n^2)$ 的算法应该1s可以处理的数量级的规模是 5 * (10^8)开根号，实验数据如下。
 
 ![程序超时3](https://code-thinking-1253855093.file.myqcloud.com/pics/2020072919590970-20230310124318532.png)
 
 O(n^2)的算法，1s内大概计算机可以运行 22500次计算，验证了刚刚的推测。
 
-在推测一下$O(n\log n)$的话， 1s可以处理的数据规模是什么呢？
+在推测一下 $O(n\log n)$ 的话， 1s可以处理的数据规模是什么呢？
 
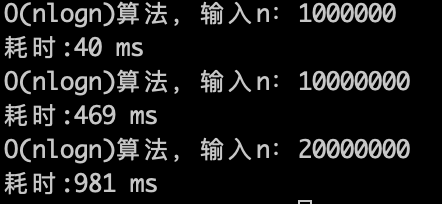
-理论上应该是比 $O(n)$少一个数量级，因为$\log n$的复杂度 其实是很快，看一下实验数据。
+理论上应该是比 $O(n)$ 少一个数量级，因为 $\log n$ 的复杂度 其实是很快，看一下实验数据。
 
 ![程序超时4](https://code-thinking-1253855093.file.myqcloud.com/pics/20200729195729407-20230310124322232.png)
 
-$O(n\log n)$的算法，1s内大概计算机可以运行 2 * (10^7)次计算，符合预期。
+$O(n\log n)$ 的算法，1s内大概计算机可以运行 2 * (10^7)次计算，符合预期。
 
 这是在我个人PC上测出来的数据，不能说是十分精确，但数量级是差不多的，大家也可以在自己的计算机上测一下。
 
@@ -263,7 +263,7 @@ public class TimeComplexity {
 
 ## 总结
 
-本文详细分析了在leetcode上做题程序为什么会有超时，以及从硬件配置上大体知道CPU的执行速度，然后亲自做一个实验来看看$O(n)$的算法，跑一秒钟，这个n究竟是做大，最后给出不同时间复杂度，一秒内可以运算出来的n的大小。
+本文详细分析了在leetcode上做题程序为什么会有超时，以及从硬件配置上大体知道CPU的执行速度，然后亲自做一个实验来看看 $O(n)$ 的算法，跑一秒钟，这个n究竟是做大，最后给出不同时间复杂度，一秒内可以运算出来的n的大小。
 
 建议录友们也都自己做一做实验，测一测，看看是不是和我的测出来的结果差不多。
 

problems/前序/关于空间复杂度，可能有几个疑问？.md

@@ -32,7 +32,7 @@
 
 同样在工程实践中，计算机的内存空间也不是无限的，需要工程师对软件运行时所使用的内存有一个大体评估，这都需要用到算法空间复杂度的分析。
 
-来看一下例子，什么时候的空间复杂度是$O(1)$呢，C++代码如下：
+来看一下例子，什么时候的空间复杂度是 $O(1)$ 呢，C++代码如下：
 
 ```CPP
 int j = 0;

problems/前序/递归算法的时间与空间复杂度分析.md

@@ -191,7 +191,7 @@ int main()
 
 因为每次递归所需的空间都被压到调用栈里（这是内存管理里面的数据结构，和算法里的栈原理是一样的），一次递归结束，这个栈就是就是把本次递归的数据弹出去。所以这个栈最大的长度就是递归的深度。
 
-此时可以分析这段递归的空间复杂度，从代码中可以看出每次递归所需要的空间大小都是一样的，所以每次递归中需要的空间是一个常量，并不会随着n的变化而变化，每次递归的空间复杂度就是$O(1)$。
+此时可以分析这段递归的空间复杂度，从代码中可以看出每次递归所需要的空间大小都是一样的，所以每次递归中需要的空间是一个常量，并不会随着n的变化而变化，每次递归的空间复杂度就是 $O(1)$ 。
 
 在看递归的深度是多少呢？如图所示：
 

problems/双指针总结.md

@@ -90,7 +90,7 @@ for (int i = 0; i < array.size(); i++) {
 
 ## 总结 
 
-本文中一共介绍了leetcode上九道使用双指针解决问题的经典题目，除了链表一些题目一定要使用双指针，其他题目都是使用双指针来提高效率，一般是将O(n^2)的时间复杂度，降为$O(n)$。
+本文中一共介绍了leetcode上九道使用双指针解决问题的经典题目，除了链表一些题目一定要使用双指针，其他题目都是使用双指针来提高效率，一般是将O(n^2)的时间复杂度，降为 $O(n)$ 。
 
 建议大家可以把文中涉及到的题目在好好做一做，琢磨琢磨，基本对双指针法就不在话下了。
 

problems/周总结/20201003二叉树周末总结.md

@@ -13,9 +13,9 @@
 
 而本题的迭代法中我们使用了队列，需要注意的是这不是层序遍历，而且仅仅通过一个容器来成对的存放我们要比较的元素，认识到这一点之后就发现：用队列，用栈，甚至用数组，都是可以的。
 
-那么做完本题之后，在看如下两个题目。
-* 100.相同的树
-* 572.另一个树的子树
+那么做完本题之后，再看如下两个题目。
+* [100.相同的树](https://leetcode.cn/problems/same-tree/description/)
+* [572.另一个树的子树](https://leetcode.cn/problems/subtree-of-another-tree/)
 
 **[二叉树：我对称么？](https://programmercarl.com/0101.对称二叉树.html)中的递归法和迭代法只需要稍作修改其中一个树的遍历顺序，便可刷了100.相同的树。**
 

problems/周总结/20201210复杂度分析周末总结.md

@@ -54,10 +54,10 @@
 文中涉及如下问题：
 
 * 究竟什么是大O？大O表示什么意思？严格按照大O的定义来说，快排应该是$O(n^2)$的算法！
-* $O(n^2)$的算法为什么有时候比$O(n)$的算法更优？
+* $O(n^2)$ 的算法为什么有时候比 $O(n)$ 的算法更优？
 * 什么时间复杂度为什么可以忽略常数项？
 * 如何简化复杂的时间复杂度表达式，原理是什么？
-* $O(\log n)$中的log究竟是以谁为底？
+* $O(\log n)$ 中的log究竟是以谁为底？
 
 这些问题大家可能懵懵懂懂的了解一些，但一细问又答不上来。
 
@@ -96,7 +96,7 @@
 
 文中给出了四个版本的代码实现，并逐一分析了其时间复杂度。
 
-此时大家就会发现，同一道题目，同样使用递归算法，有的同学会写出了O(n)的代码，有的同学就写出了$O(\log n)$的代码。
+此时大家就会发现，同一道题目，同样使用递归算法，有的同学会写出了O(n)的代码，有的同学就写出了 $O(\log n)$ 的代码。
 
 其本质是要对递归的时间复杂度有清晰的认识，才能运用递归来有效的解决问题！
 

problems/栈与队列总结.md

@@ -142,7 +142,7 @@ cd a/b/c/../../
 
 本题就要**使用优先级队列来对部分频率进行排序。**  注意这里是对部分数据进行排序而不需要对所有数据排序！
 
-所以排序的过程的时间复杂度是$O(\log k)$，整个算法的时间复杂度是$O(n\log k)$。
+所以排序的过程的时间复杂度是 $O(\log k)$ ，整个算法的时间复杂度是 $O(n\log k)$ 。
 
 ## 总结