algorithm/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2025-07-08 00:43:04 +08:00
Code Issues Packages Projects Releases Wiki Activity

Merge pull request #1814 from juguagua/leetcode-modify-the-code-of-the-backtracking

Browse Source 
更新回溯部分：从“子集II” 到 “全排列II”
This commit is contained in:
程序员Carl
2022-12-11 10:09:39 +08:00
committed by GitHub
parent 5af63a5ab5 787dbbc840
commit e4166ff5e7
4 changed files with 103 additions and 87 deletions
Download Patch File Download Diff File Expand all files Collapse all files

45
problems/0046.全排列.md
View File

@ -275,29 +275,34 @@ class Solution:
### Go
```Go
var res [][]int
var (
res [][]int
path []int
st []bool // state的缩写
)
func permute(nums []int) [][]int {
res = [][]int{}
backTrack(nums,len(nums),[]int{})
return res
}
func backTrack(nums []int,numsLen int,path []int) {
if len(nums)==0{
p:=make([]int,len(path))
copy(p,path)
res = append(res,p)
}
for i:=0;i<numsLen;i++{
cur:=nums[i]
path = append(path,cur)
nums = append(nums[:i],nums[i+1:]...)//直接使用切片
backTrack(nums,len(nums),path)
nums = append(nums[:i],append([]int{cur},nums[i:]...)...)//回溯的时候切片也要复原，元素位置不能变
path = path[:len(path)-1]
}
res, path = make([][]int, 0), make([]int, 0, len(nums))
st = make([]bool, len(nums))
dfs(nums, 0)
return res
}
func dfs(nums []int, cur int) {
if cur == len(nums) {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
}
for i := 0; i < len(nums); i++ {
if !st[i] {
path = append(path, nums[i])
st[i] = true
dfs(nums, cur + 1)
st[i] = false
path = path[:len(path)-1]
}
}
}
```
### Javascript

56
problems/0047.全排列II.md
View File

@ -49,7 +49,7 @@
**一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果**。
在[46.全排列](https://programmercarl.com/0046.全排列.html)中已经详解讲解了排列问题的写法，在[40.组合总和II](https://programmercarl.com/0040.组合总和II.html) 、[90.子集II](https://programmercarl.com/0090.子集II.html)中详细讲解的去重的写法，所以这次我就不用回溯三部曲分析了，直接给出代码，如下：
在[46.全排列](https://programmercarl.com/0046.全排列.html)中已经详细讲解了排列问题的写法，在[40.组合总和II](https://programmercarl.com/0040.组合总和II.html) 、[90.子集II](https://programmercarl.com/0090.子集II.html)中详细讲解了去重的写法，所以这次我就不用回溯三部曲分析了，直接给出代码，如下：
## C++代码
@ -225,33 +225,37 @@ class Solution:
### Go
```go
var res [][]int
func permute(nums []int) [][]int {
res = [][]int{}
backTrack(nums,len(nums),[]int{})
return res
var (
res [][]int
path []int
st []bool // state的缩写
)
func permuteUnique(nums []int) [][]int {
res, path = make([][]int, 0), make([]int, 0, len(nums))
st = make([]bool, len(nums))
sort.Ints(nums)
dfs(nums, 0)
return res
}
func backTrack(nums []int,numsLen int,path []int) {
if len(nums)==0{
p:=make([]int,len(path))
copy(p,path)
res = append(res,p)
}
used := [21]int{}//跟前一题唯一的区别，同一层不使用重复的数。关于used的思想carl在递增子序列那一题中提到过
for i:=0;i<numsLen;i++{
if used[nums[i]+10]==1{
continue
}
cur:=nums[i]
path = append(path,cur)
used[nums[i]+10]=1
nums = append(nums[:i],nums[i+1:]...)
backTrack(nums,len(nums),path)
nums = append(nums[:i],append([]int{cur},nums[i:]...)...)
path = path[:len(path)-1]
}
func dfs(nums []int, cur int) {
if cur == len(nums) {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
}
for i := 0; i < len(nums); i++ {
if i != 0 && nums[i] == nums[i-1] && !st[i-1] { // 去重，用st来判别是深度还是广度
continue
}
if !st[i] {
path = append(path, nums[i])
st[i] = true
dfs(nums, cur + 1)
st[i] = false
path = path[:len(path)-1]
}
}
}
```

46
problems/0090.子集II.md
View File

@ -261,10 +261,10 @@ class Solution:
self.path.pop()
```
### Python3
#### Python3
不使用used数组
```python3
```python
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
res = []
@ -291,7 +291,7 @@ class Solution:
```
使用used数组
```python3
```python
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
result = []
@ -315,26 +315,30 @@ class Solution:
### Go
```Go
var res[][]int
func subsetsWithDup(nums []int)[][]int {
res=make([][]int,0)
sort.Ints(nums)
dfs([]int{},nums,0)
return res
var (
path []int
res [][]int
)
func subsetsWithDup(nums []int) [][]int {
path, res = make([]int, 0, len(nums)), make([][]int, 0)
sort.Ints(nums)
dfs(nums, 0)
return res
}
func dfs(temp, num []int, start int) {
tmp:=make([]int,len(temp))
copy(tmp,temp)
res=append(res,tmp)
for i:=start;i<len(num);i++{
if i>start&&num[i]==num[i-1]{
continue
}
temp=append(temp,num[i])
dfs(temp,num,i+1)
temp=temp[:len(temp)-1]
}
func dfs(nums []int, start int) {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
for i := start; i < len(nums); i++ {
if i != start && nums[i] == nums[i-1] {
continue
}
path = append(path, nums[i])
dfs(nums, i+1)
path = path[:len(path)-1]
}
}
```

43
problems/0491.递增子序列.md
View File

@ -37,7 +37,7 @@
在[90.子集II](https://programmercarl.com/0090.子集II.html)中我们是通过排序，再加一个标记数组来达到去重的目的。
而本题求自增子序列，是不能对原数组经行排序的，排完序的数组都是自增子序列了。
而本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。
**所以不能使用之前的去重逻辑！**
@ -78,7 +78,7 @@ if (path.size() > 1) {
* 单层搜索逻辑
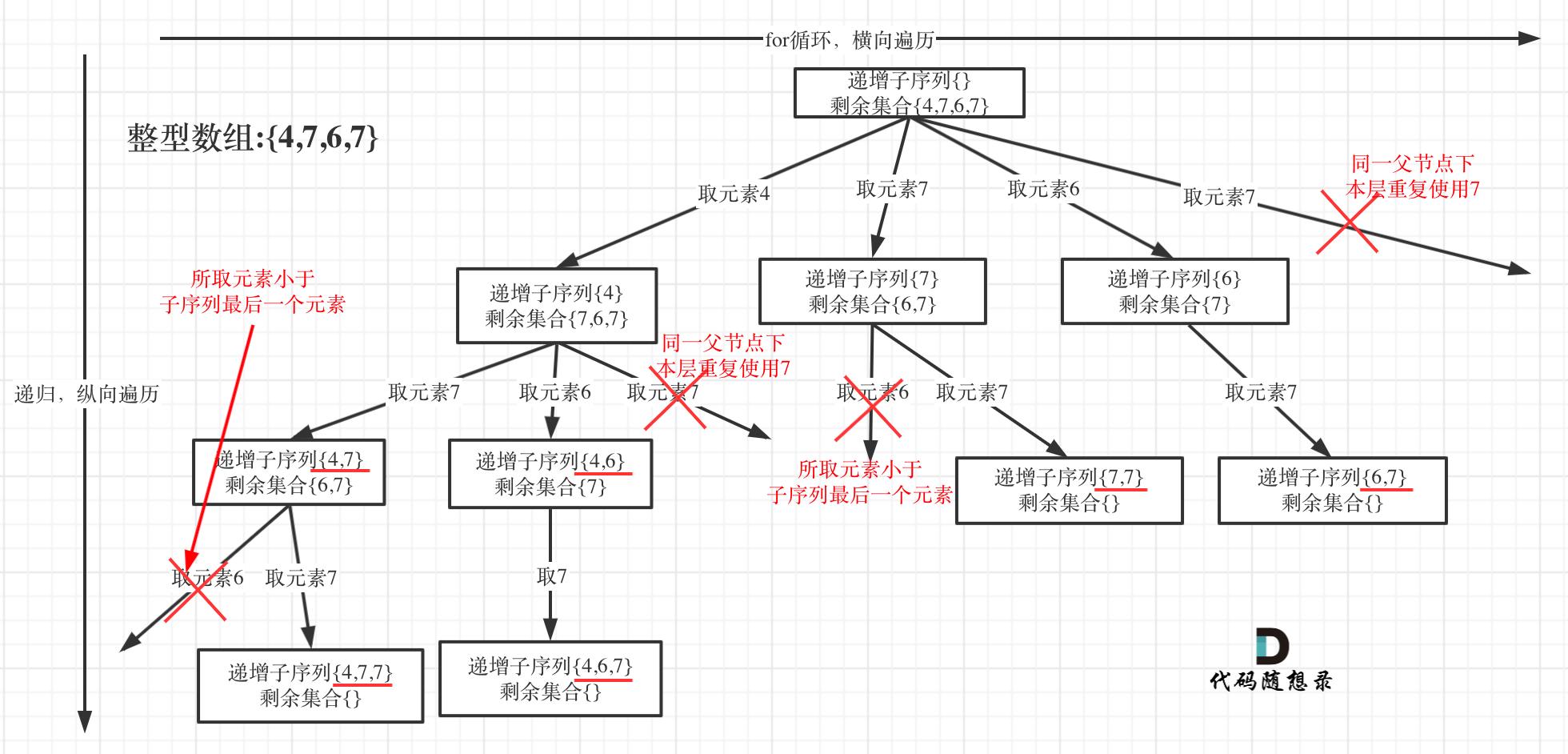
![491. 递增子序列1](https://img-blog.csdnimg.cn/20201124200229824.png)
在图中可以看出，**同一父节点下的同层上使用过的元素就不能在使用了**
在图中可以看出，**同一父节点下的同层上使用过的元素就不能再使用了**
那么单层搜索代码如下：
@ -340,30 +340,33 @@ class Solution:
```
### Go
```golang
```go
var (
res [][]int
path []int
)
func findSubsequences(nums []int) [][]int {
var subRes []int
var res [][]int
backTring(0,nums,subRes,&res)
res, path = make([][]int, 0), make([]int, 0, len(nums))
dfs(nums, 0)
return res
}
func backTring(startIndex int,nums,subRes []int,res *[][]int){
if len(subRes)>1{
tmp:=make([]int,len(subRes))
copy(tmp,subRes)
*res=append(*res,tmp)
func dfs(nums []int, start int) {
if len(path) >= 2 {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
}
history:=[201]int{}//记录本层元素使用记录
for i:=startIndex;i<len(nums);i++{
//分两种情况判断：一，当前取的元素小于子集的最后一个元素，则继续寻找下一个适合的元素
// 或者二，当前取的元素在本层已经出现过了，所以跳过该元素，继续寻找
if len(subRes)>0&&nums[i]<subRes[len(subRes)-1]||history[nums[i] + 100]==1{
used := make(map[int]bool, len(nums)) // 初始化used字典，用以对同层元素去重
for i := start; i < len(nums); i++ {
if used[nums[i]] { // 去重
continue
}
history[nums[i] + 100]=1//表示本层该元素使用过了
subRes=append(subRes,nums[i])
backTring(i+1,nums,subRes,res)
subRes=subRes[:len(subRes)-1]
if len(path) == 0 || nums[i] >= path[len(path)-1] {
path = append(path, nums[i])
used[nums[i]] = true
dfs(nums, i+1)
path = path[:len(path)-1]
}
}
}
```