Update

README.md

@@ -148,6 +148,8 @@
     * [回溯算法：排列问题！](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)
     * [回溯算法：排列问题（二）](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)
     * [本周小结！（回溯算法系列三）](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA)
+    * [本周小结！（回溯算法系列三）续集](https://mp.weixin.qq.com/s/kSMGHc_YpsqL2j-jb_E_Ag)
+    * [视频来了！！带你学透回溯算法（理论篇）](https://mp.weixin.qq.com/s/wDd5azGIYWjbU0fdua_qBg)
 
 
 （持续更新中....）
@@ -388,6 +390,7 @@
 |[0350.两个数组的交集II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0350.两个数组的交集II.md) |哈希表 |简单|**哈希**|
 |[0383.赎金信](https://github.com/youngyangyang04/leetcode/blob/master/problems/0383.赎金信.md) |数组 |简单|**暴力** **字典计数** **哈希**|
 |[0404.左叶子之和](https://github.com/youngyangyang04/leetcode/blob/master/problems/0404.左叶子之和.md) |树/二叉树 |简单|**递归** **迭代**|
+|[0406.根据身高重建队列](https://github.com/youngyangyang04/leetcode/blob/master/problems/0406.根据身高重建队列.md) |树/二叉树 |简单|**递归** **迭代**|
 |[0416.分割等和子集](https://github.com/youngyangyang04/leetcode/blob/master/problems/0416.分割等和子集.md) |动态规划 |中等|**背包问题/01背包**|
 |[0429.N叉树的层序遍历](https://github.com/youngyangyang04/leetcode/blob/master/problems/0429.N叉树的层序遍历.md) |树 |简单|**队列/广度优先搜索**|
 |[0434.字符串中的单词数](https://github.com/youngyangyang04/leetcode/blob/master/problems/0434.字符串中的单词数.md) |字符串 |简单|**模拟**|

problems/0028.实现strStr().md

@@ -320,7 +320,7 @@ void getNext(int* next, const string& s){
 
 在文本串s里 找是否出现过模式串t。
 
-定义两个下表j 指向模式串起始位置，i指向文本串其实位置。
+定义两个下表j 指向模式串起始位置，i指向文本串起始位置。
 
 那么j初始值依然为-1，为什么呢？ **依然因为next数组里记录的起始位置为-1。**
 

problems/0051.N皇后.md

@@ -1,9 +1,12 @@
+> 开始棋盘问题，如果对回溯法还不了解的同学可以看这个视频
 
-# 题目链接 
+如果对回溯法理论还不清楚的同学，可以先看这个视频[视频来了！！带你学透回溯算法（理论篇）](https://mp.weixin.qq.com/s/wDd5azGIYWjbU0fdua_qBg)
 
-https://leetcode-cn.com/problems/n-queens/ 
 
 # 第51题. N皇后
+
+题目链接： https://leetcode-cn.com/problems/n-queens/ 
+
 n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。 
 
 上图为 8 皇后问题的一种解法。
@@ -14,29 +17,27 @@ n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并
 每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。
 
 示例:
-
-输入: 4
-输出: [
- [".Q..",  // 解法 1
-  "...Q",
-  "Q...",
-  "..Q."],
-
- ["..Q.",  // 解法 2
-  "Q...",
-  "...Q",
-  ".Q.."]
-]
-解释: 4 皇后问题存在两个不同的解法。
-
-提示：
-
+输入: 4    
+输出: [   
+ [".Q..",  // 解法 1   
+  "...Q",    
+  "Q...",   
+  "..Q."],   
+     
+ ["..Q.",  // 解法 2    
+  "Q...",    
+  "...Q",   
+  ".Q.."]   
+]   
+解释: 4 皇后问题存在两个不同的解法。    
+    
+提示：    
 > 皇后，是国际象棋中的棋子，意味着国王的妻子。皇后只做一件事，那就是“吃子”。当她遇见可以吃的棋子时，就迅速冲上去吃掉棋子。当然，她横、竖、斜都可走一到七步，可进可退。（引用自 百度百科 - 皇后 ）
 
 
 # 思路
 
-都知道n皇后问题是回溯算法解决的经典问题，但是用回溯解决多了 排列，组合，子集问题之后，遇到这种二位矩阵还会有点不知所措。
+都知道n皇后问题是回溯算法解决的经典问题，但是用回溯解决多了组合、切割、子集、排列问题之后，遇到这种二位矩阵还会有点不知所措。
 
 首先来看一下皇后们的约束条件：
 
@@ -44,56 +45,140 @@ n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并
 2. 不能同列 
 3. 不能同斜线
 
-
 确定完约束条件，来看看究竟要怎么去搜索皇后们的位置，其实搜索皇后的位置，可以抽象为一棵树。
 
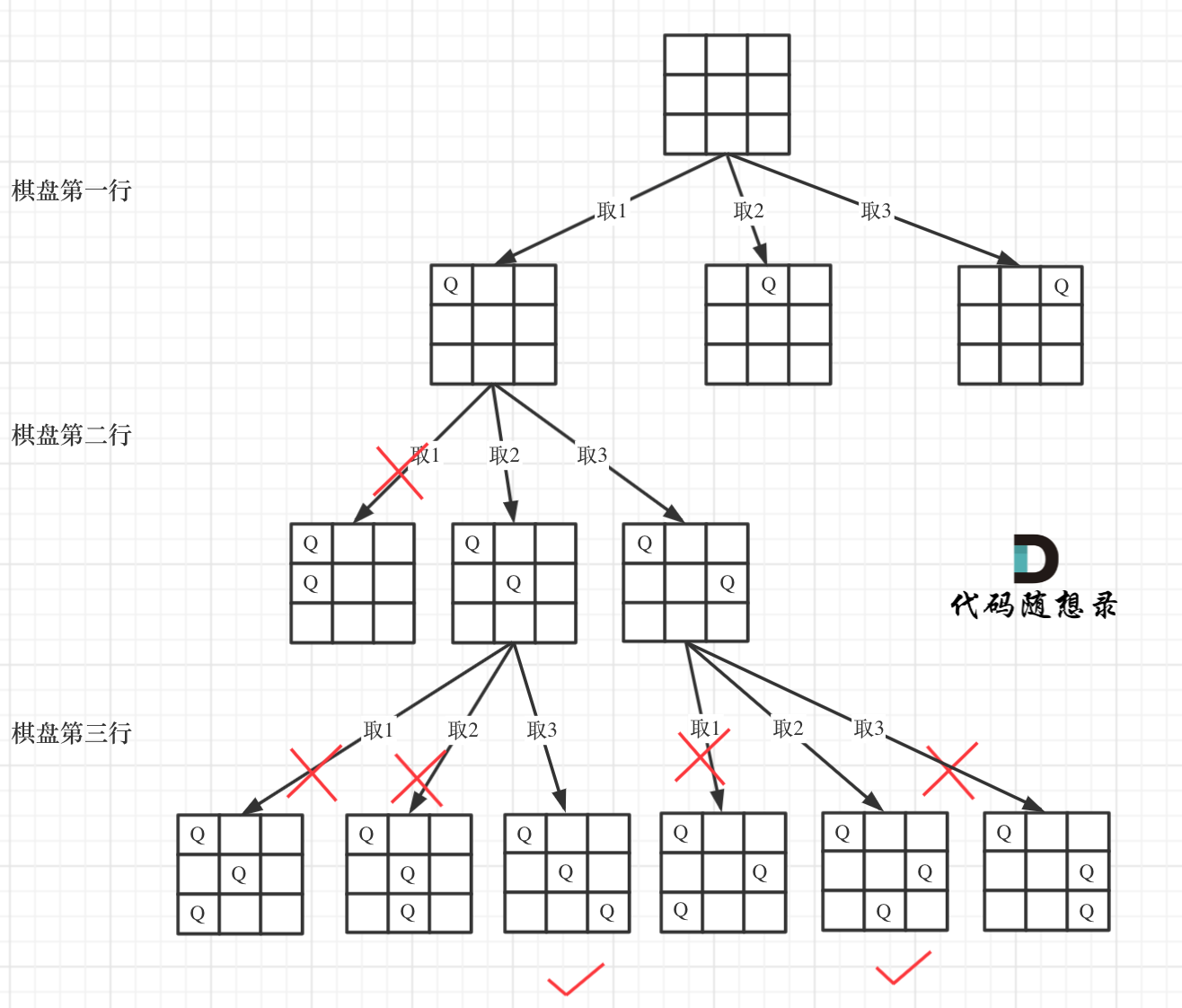
-下面我用一个3 * 3 的棋牌，如图：
+下面我用一个3 * 3 的棋牌，将搜索过程抽象为一颗树，如图：
 
-<img src='../pics/51.N皇后1.png' width=600> </img></div>
+![51.N皇后](https://img-blog.csdnimg.cn/20201116173551789.png)
 
-将搜索过程抽象为一颗树，如图：
+从图中，可以看出，二维矩阵中矩阵的高就是这颗树的高度，矩阵的宽就是树形结构中每一个节点的宽度。
 
+那么我们用皇后们的约束条件，来回溯搜索这颗树，**只要搜索到了树的叶子节点，说明就找到了皇后们的合理位置了**。 
 
-<img src='../pics/51.N皇后.png' width=600> </img></div>
+## 回溯三部曲 
 
-从图中，可以看出，二维矩阵，其实矩阵的行，就是 这颗树的高度，矩阵的宽就是二叉树没一个节点孩子的宽度。
-
-
-那么我们用皇后们的约束条件，来回溯搜索这颗二叉树，**只要搜索到了树的叶子节点，说明就找到了皇后们的合理位置了。** 
-
-我总结的回溯模板如下：
+按照我总结的如下回溯模板，我们来依次分析：
 
 ```
-backtracking() {
+void backtracking(参数) {
     if (终止条件) {
         存放结果;
+        return;
     }
-
-    for (枚举同一个位置的所有可能性，可以想成节点孩子的数量) {
-        递归，处理节点;
-        backtracking();
+    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
+        处理节点;
+        backtracking(路径，选择列表); // 递归
         回溯，撤销处理结果
     }
 }
 ```
 
-那么按照这个模板不能写出如下代码：
+* 递归函数参数 
 
-# C++代码
+我依然是定义全局变量二维数组result来记录最终结果。
+
+参数n是棋牌的大小，然后用row来记录当前遍历到棋盘的第几层了。 
+
+代码如下：
+
+```
+vector<vector<string>> result;
+void backtracking(int n, int row, vector<string>& chessboard) {
+```
+
+* 递归终止条件 
+
+在如下树形结构中：
+![51.N皇后](https://img-blog.csdnimg.cn/20201116173551789.png)
+
+可以看出，当递归到棋盘最底层（也就是叶子节点）的时候，就可以收集结果并返回了。
+
+代码如下：
+
+```
+if (row == n) {
+    result.push_back(chessboard);
+    return;
+}
+```
+
+* 单层搜索的逻辑 
+
+递归深度就是row控制棋盘的行，每一层里for循环的col控制棋盘的列，一行一列，确定了放置皇后的位置。 
+
+每次都是要从新的一行的起始位置开始搜，所以都是从0开始。
+
+代码如下：
+
+```
+for (int col = 0; col < n; col++) {
+    if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
+        chessboard[row][col] = 'Q'; // 放置皇后
+        backtracking(n, row + 1, chessboard);
+        chessboard[row][col] = '.'; // 回溯，撤销皇后
+    }
+}
+```
+
+* 验证棋牌是否合法
+
+按照如下标准去重：
+
+1. 不能同行
+2. 不能同列 
+3. 不能同斜线 （45度和135度角）
+
+代码如下： 
+
+```
+bool isValid(int row, int col, vector<string>& chessboard, int n) {
+    int count = 0;
+    // 检查列
+    for (int i = 0; i < row; i++) { // 这是一个剪枝
+        if (chessboard[i][col] == 'Q') {
+            return false;
+        }
+    }
+    // 检查 45度角是否有皇后
+    for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
+        if (chessboard[i][j] == 'Q') {
+            return false;
+        }
+    }
+    // 检查 135度角是否有皇后
+    for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
+        if (chessboard[i][j] == 'Q') {
+            return false;
+        }
+    }
+    return true;
+}
+```
+
+在这份代码中，细心的同学可以发现为什么没有在同行进行检查呢？ 
+
+因为在单层搜索的过程中，每一层递归，只会选for循环（也就是同一行）里的一个元素，所以不用去重了。
+
+那么按照这个模板不难写出如下代码：
+
+## C++代码
 
 ```
 class Solution {
 private:
-void backtracking(int n, int row, vector<string>& chessboard, vector<vector<string>>& result) {
+vector<vector<string>> result;
+// n 为输入的棋盘大小
+// row 是当前递归到棋牌的第几行了
+void backtracking(int n, int row, vector<string>& chessboard) {
     if (row == n) {
         result.push_back(chessboard);
         return;
     }
     for (int col = 0; col < n; col++) {
-        if (isValid(row, col, chessboard, n)) {
-            chessboard[row][col] = 'Q';
-            backtracking(n, row + 1, chessboard, result);
-            chessboard[row][col] = '.';
+        if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
+            chessboard[row][col] = 'Q'; // 放置皇后
+            backtracking(n, row + 1, chessboard);
+            chessboard[row][col] = '.'; // 回溯，撤销皇后
         }
     }
 }
@@ -121,11 +206,25 @@ bool isValid(int row, int col, vector<string>& chessboard, int n) {
 }
 public:
     vector<vector<string>> solveNQueens(int n) {
+        result.clear();
         std::vector<std::string> chessboard(n, std::string(n, '.'));
-        vector<vector<string>> result;
-
-        backtracking(n, 0, chessboard, result);
+        backtracking(n, 0, chessboard);
         return result;
     }
 };
 ```
+
+可以看出，除了验证棋盘合法性的代码，省下来部分就是按照回溯法模板来的。
+
+# 总结 
+
+本题是我们解决棋盘问题的第一道题目。
+
+如果从来没有接触过N皇后问题的同学看着这样的题会感觉无从下手，可能知道要用回溯法，但也不知道该怎么去搜。
+
+**这里我明确给出了棋盘的宽度就是for循环的长度，递归的深度就是棋盘的高度，这样就可以套进回溯法的模板里了**。
+
+大家可以在仔细体会体会！
+
+就酱，如果感觉「代码随想录」干货满满，就分享给身边的朋友同学吧，他们可能也需要！
+

problems/0053.最大子序和.md

@@ -49,7 +49,7 @@ public:
 
 <img src='../video/53.最大子序和.gif' width=600> </img></div>
 
-红色的其实位置就是贪心每次取count为正数的时候，开始一个区间的统计。
+红色的起始位置就是贪心每次取count为正数的时候，开始一个区间的统计。
 
 不难写出如下C++代码（关键地方已经注释）
 

problems/0135.分发糖果.md

@@ -1,27 +1,85 @@
 
+## 思路 
+
+这道题目一定是要确定一边之后，再确定另一边，例如比较每一个孩子的左边，然后再比较右边，如果两边一起考虑就会顾此失彼。
+
+本题贪心贪在哪里呢？ 
+
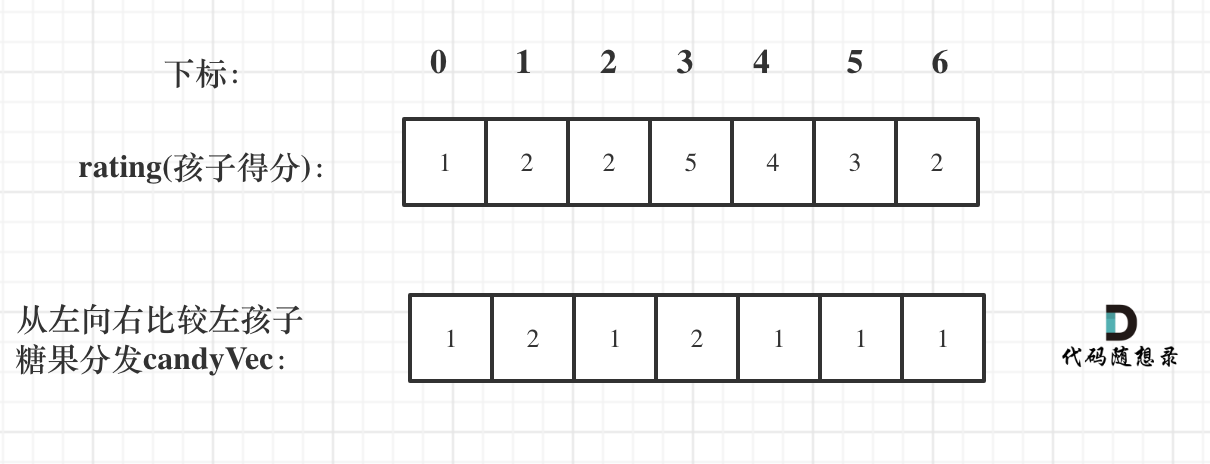
+先确定每个孩子左边的情况（也就是从前向后遍历）
+
+如果ratings[i] > ratings[i - 1] 那么[i]的糖 一定要比[i - 1]的糖多一个，所以贪心：candyVec[i] = candyVec[i - 1] + 1 
+
+代码如下：
+
+```
+// 从前向后 
+for (int i = 1; i < ratings.size(); i++) {
+    if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
+}
+```
+
+如图：
+
+![135.分发糖果](https://img-blog.csdnimg.cn/20201117114916878.png)
+
+再确定每个孩子右边的情况（从后向前遍历） 
+
+遍历顺序这里有同学可能会有疑问，为什么不能从前向后遍历呢？ 
+
+因为如果从前向后遍历，根据 ratings[i + 1] 来确定 ratings[i] 对应的糖果，那么每次都不能利用上前一次的比较结果了。 
+**所以确定每个孩子右边的情况一定要从后向前遍历！** 
+
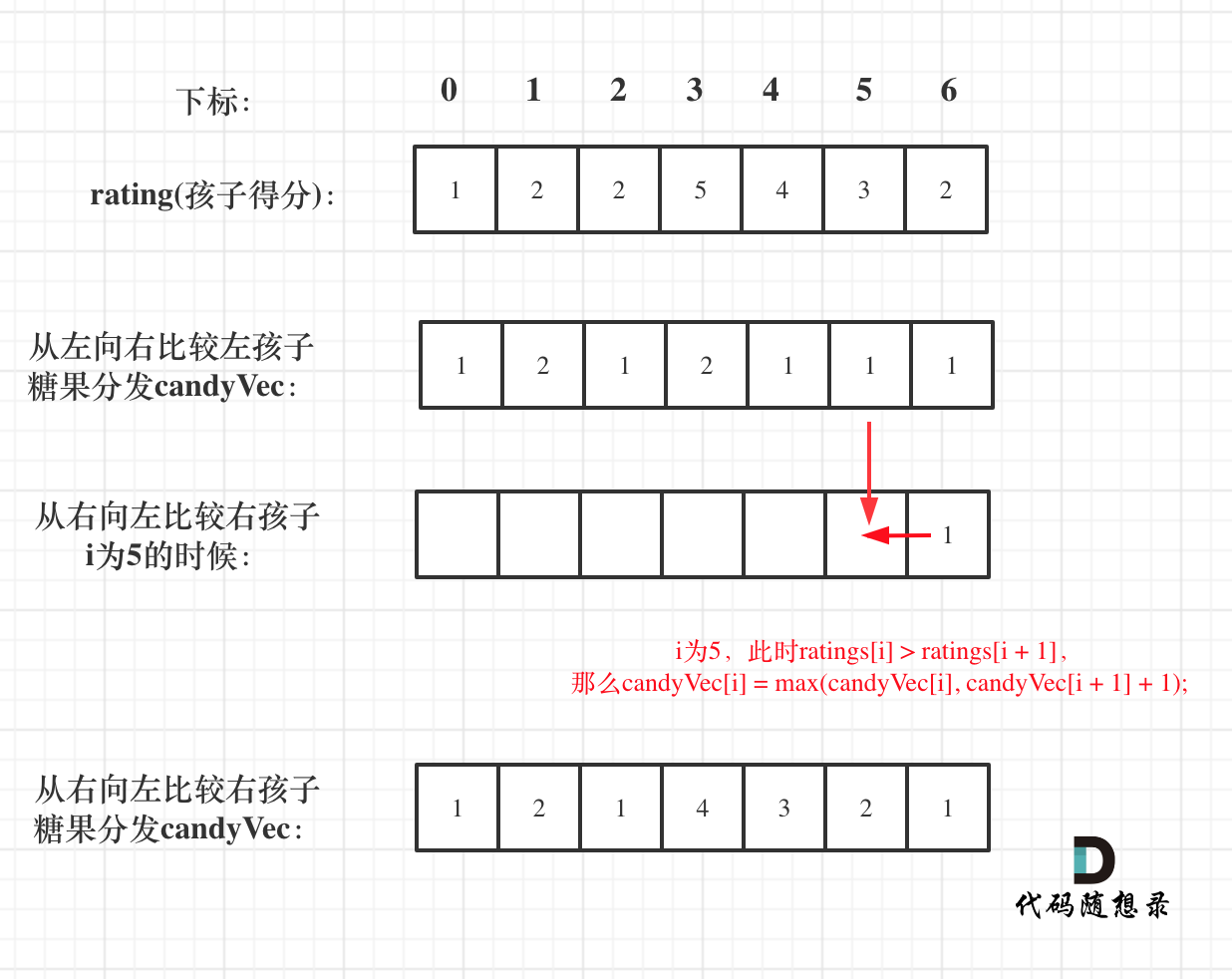
+此时又要开始贪心，如果 ratings[i] > ratings[i + 1]，就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，**因为candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多，也比右边candyVec[i + 1]的糖果多**。
+
+如图：
+
+![135.分发糖果1](https://img-blog.csdnimg.cn/20201117115658791.png)
+
+所以代码如下：
+
+```
+// 从后向前
+for (int i = ratings.size() - 2; i >= 0; i--) {
+    if (ratings[i] > ratings[i + 1] ) {
+        candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
+    }
+}
+```
+
+* 将问题分解为若干个子问题
+* 找出适合的贪心策略
+* 求解每一个子问题的最优解
+* 将局部最优解堆叠成全局最优解
+
+* 分解为子问题 
+
+
+
 这道题目上来也是没什么思路啊
 
 
 这道题目不好想啊，贪心很巧妙
+
 ```
 class Solution {
 public:
     int candy(vector<int>& ratings) {
         vector<int> candyVec(ratings.size(), 1);
-        // 从前向后 
+        // 从前向后
         for (int i = 1; i < ratings.size(); i++) {
             if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
         }
         // 从后向前
         for (int i = ratings.size() - 2; i >= 0; i--) {
-            if (ratings[i] > ratings[i + 1] && candyVec[i] < candyVec[i + 1] + 1) {
-                candyVec[i] = candyVec[i + 1] + 1;
+            if (ratings[i] > ratings[i + 1] ) {
+                candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
             }
         }
-        // 统计结果 
+        // 统计结果
         int result = 0;
         for (int i = 0; i < candyVec.size(); i++) result += candyVec[i];
         return result;
     }
 };
+
 ```

problems/0332.重新安排行程.md

@@ -172,7 +172,7 @@ if (result.size() == ticketNum + 1) {
         if (target.second > 0 ) { // 记录到达机场是否飞过了
             result.push_back(target.first);
             target.second--;
-            if (backtracking(ticketNum, index + 1, result)) return true;
+            if (backtracking(ticketNum, result)) return true;
             result.pop_back();
             target.second++;
         }

problems/0406.根据身高重建队列.md

@@ -0,0 +1,62 @@
+
+## 思路
+
+本题有两个维度，h和k，看到这种题目一定要想如何确定一个维度，然后在按照另一个维度重新排列。
+
+**如果两个维度一起考虑一定会顾此失彼**。
+
+相信大家困惑的点是先确实k还是先确定h呢，也就是 究竟先按h排序呢，还先按照k排序呢？
+
+如果按照k来从小到大排序，排完之后，会发现k的排列并不符合条件，身高也不符合条件，两个维度哪一个都没确定下来。
+
+那么按照身高h来排序呢，身高一定是从大到小排（身高相同k小的站前面），让高个子在前面。
+
+**此时我们可以确定一个维度了，就是身高，前面的节点一定都比本节点高！**
+
+此时只需要按照k为下表重新插入队列，就可以了呢，为什么呢？ 
+
+以图中{5,2} 为例：
+
+<img src='../pics/406.根据身高重建队列.png' width=600> </img></div>
+
+**都说用贪心算法，是贪心究竟贪在哪里呢？** 
+
+贪心在优先按照身高高的people的k来插入，后序插入节点也不会影响前面已经插入的节点，最终按照k的规则完成了队列。
+
+整个插入过程如下：
+
+排序完：
+[[7,0], [7,1], [6,1], [5,0], [5,2]，[4,4]]
+插入的过程：
+插入[7,0]：[[7,0]]
+插入[7,1]：[[7,0],[7,1]]
+插入[6,1]：[[7,0],[6,1],[7,1]]
+插入[5,0]：[[5,0],[7,0],[6,1],[7,1]]
+插入[5,2]：[[5,0],[7,0],[5,2],[6,1],[7,1]]
+插入[4,4]：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
+
+
+C++代码如下：
+```
+class Solution {
+public:
+    // 身高从大到小排（身高相同k小的站前面）
+    static bool cmp(const vector<int> a, const vector<int> b) {
+        if (a[0] == b[0]) return a[1] < b[1];
+        return a[0] > b[0];
+    }
+    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
+        sort (people.begin(), people.end(), cmp);
+        list<vector<int>> que; // 使用list底层是链表实现，插入效率比vector高的多
+        for (int i = 0; i < people.size(); i++) {
+            int position = people[i][1]; // 插入到下标为position的位置
+            std::list<vector<int>>::iterator it = que.begin();
+            while (position--) { 
+                it++;
+            }
+            que.insert(it, people[i]);
+        }
+        return vector<vector<int>>(que.begin(), que.end());
+    }
+};
+```

problems/0977.有序数组的平方.md

@@ -26,7 +26,7 @@ public:
 
 那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。
 
-此时可以考虑双指针法了，i指向其实位置，j指向终止位置。
+此时可以考虑双指针法了，i指向起始位置，j指向终止位置。
 
 定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。
 

problems/贪心算法理论基础.md

@@ -1,5 +1,7 @@
 
-贪心的本质是选择每一阶段的局部最优，从而达到全局最优。 
+## 什么是贪心 
+
+**贪心的本质是选择每一阶段的局部最优，从而达到全局最优**。 
 
 这么说有点抽象，来举一个例子：
 
@@ -9,66 +11,72 @@
 
 每次拿最大的就是局部最优，最后拿走最大数额的钱就是推出全局最优。
 
-在举一个例子如果是 有一堆盒子，你有一个背包体积为n，如何把背包尽可能装满，如果还每次选最大的盒子，一定不行。这时候就需要动态规划。动态规划的问题在下一个系列会详细讲解。
+再举一个例子如果是 有一堆盒子，你有一个背包体积为n，如何把背包尽可能装满，如果还每次选最大的盒子，一定不行。这时候就需要动态规划。动态规划的问题在下一个系列会详细讲解。
 
+## 贪心的套路（什么时候用贪心）
 
-很多同学做贪心的题目的时候，想不出来是贪心，想知道有没有什么套路可以一看看出来是贪心，说实话贪心算法并没有固定的套路。
+很多同学做贪心的题目的时候，想不出来是贪心，想知道有没有什么套路可以一看就看出来是贪心。
+
+**说实话贪心算法并没有固定的套路**。
 
 所以唯一的难点就是如何通过局部最优，推出整体最优。 
 
-那么如何能看出局部最优是否能退出整体最优呢？有没有什么固定策略或者套路呢？
+那么如何能看出局部最优是否能推出整体最优呢？有没有什么固定策略或者套路呢？
 
-**不好意思，没有！** 靠自己手动模拟，如果模拟可行，就可以试一试贪心策略，如果不可行，可能需要动态规划。
+**不好意思，也没有！** 靠自己手动模拟，如果模拟可行，就可以试一试贪心策略，如果不可行，可能需要动态规划。
 
-验证可不可以用贪心最好用的策略就是举反例，如果想不到反例，那么就试一试贪心吧。
+有同学问了如何验证可不可以用贪心算法呢？
 
-那又有同学认为手动模拟，举例子得出的结论不靠谱，想要严格的数学证明。 
+**最好用的策略就是举反例，如果想不到反例，那么就试一试贪心吧**。
 
-数学证明一般可以是：
+可有有同学认为手动模拟，举例子得出的结论不靠谱，想要严格的数学证明。 
+
+一般数学证明有如下两种方法：
 
 * 数学归纳法
 * 反证法
 
-看教课书上讲解贪心真的是一堆公式，估计连看都不想看。
+看教课书上讲解贪心可以是一堆公式，估计大家连看都不想看，所以数学证明就不在我要讲解的范围内了，大家感兴趣可以自行查找资料。
 
-所以做了贪心题目的时候大家就会发现，如果啥都要数学证明一下，就是把简单问题搞复杂了。
-
-**面试中基本不会让面试者现场证明贪心的合理性，代码写出来跑过测试用例即可，或者自己能自圆其说就行**。
+**面试中基本不会让面试者现场证明贪心的合理性，代码写出来跑过测试用例即可，或者自己能自圆其说理由就行了**。
 
 举一个不太恰当的例子：我要用一下1+1 = 2，但我要先证明1+1 为什么等于2。严谨是严谨了，但没必要。
 
-虽然这个例子有点极端，但可以表达这么个意思：就是手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。
+虽然这个例子很极端，但可以表达这么个意思：**刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心**。
 
-**例如刚刚举的拿钞票的例子，就是模拟一下每次那做大的，最后就能拿到最多的钱，这还要数学证明的话，其实就不在算法面试的范围内了，可以看看专业的数学书籍！**
+**例如刚刚举的拿钞票的例子，就是模拟一下每次拿做大的，最后就能拿到最多的钱，这还要数学证明的话，其实就不在算法面试的范围内了，可以看看专业的数学书籍！**
 
-所以这也是为什么有的通过AC（accept）了一些贪心的题目，但都不知道自己用了贪心算法，因为贪心有时候就是常识性的推导，所以会认为本就应该这么做！
+所以这也是为什么很多同学通过（accept）了贪心的题目，但都不知道自己用了贪心算法，因为贪心有时候就是常识性的推导，所以会认为本应该就这么做！
 
-那么刷题的时候什么时候真的需要数学推导呢？ 
+**那么刷题的时候什么时候真的需要数学推导呢？** 
 
 例如环形链表2，这道题目不用数学推导一下，就找不出环的起始位置，想试一下就不知道怎么试，这种题目确实需要数学简单推导一下。
 
-**但贪心问题就不必了，模拟一下感觉是这么回事，就迅速试一试**。
+## 贪心一般解题步骤
 
-
-贪心算法求解步骤：
+贪心算法一般分为如下四步：
 
 * 将问题分解为若干个子问题
 * 找出适合的贪心策略
 * 求解每一个子问题的最优解
 * 将局部最优解堆叠成全局最优解
 
+一个子问题的最优解会是下一个子问题最优解的一部分，重复这个操作直到推出整个问题的最优解！ 
 
-当前子问题的最优解
+# 总结 
+
+理论篇给出了什么是贪心以及大家关心的贪心算法固定套路。
+
+不好意思了，贪心没有套路，平时刷题或者面试的时候就是常识性推导加上举反例。
+
+最后给出一个贪心的一般解题步骤，大家可以发现这个解题步骤也是毕竟抽象的，不像是 二叉树，回溯算法，给出了那么具体的解题套路和模板。
 
-一个子问题的最优解会是下一个子问题最优解的一部分，重复这个操作直到堆叠出该问题的最优解 
 
-贪心算法最关键的部分在于贪心策略的选择，贪心选择的意思是对于所求问题的整体最优解可以通过一系列的局部最优选择求得。
 
-而必须注意的是，贪心选择必须具备无后效性，也就是某个状态不会影响之前求得的局部最优解。
 
 
 贪心算法的应用
 对数据压缩编码的霍夫曼编码（Huffman Coding）
-求最小生成树的 Prim 算法和 Kruskal 算法
+求最小生成树的 Prim 算法 
 求单源最短路径的Dijkstra算法