Merge pull request #955 from bqlin/master

回溯算法补充Swift版本

problems/0037.解数独.md

@@ -61,7 +61,7 @@
 
 代码如下：
 
-```
+```cpp
 bool backtracking(vector<vector<char>>& board)
 ```
 
@@ -504,5 +504,54 @@ void solveSudoku(char** board, int boardSize, int* boardColSize) {
 }
 ```
 
+### Swift
+
+```swift
+func solveSudoku(_ board: inout [[Character]]) {
+    // 判断对应格子的值是否合法
+    func isValid(row: Int, col: Int, val: Character) -> Bool {
+        // 行中是否重复
+        for i in 0 ..< 9 {
+            if board[row][i] == val { return false }
+        }
+
+        // 列中是否重复
+        for j in 0 ..< 9 {
+            if board[j][col] == val { return false }
+        }
+
+        // 9方格内是否重复
+        let startRow = row / 3 * 3
+        let startCol = col / 3 * 3
+        for i in startRow ..< startRow + 3 {
+            for j in startCol ..< startCol + 3 {
+                if board[i][j] == val { return false }
+            }
+        }
+        return true
+    }
+
+    @discardableResult
+    func backtracking() -> Bool {
+        for i in 0 ..< board.count { // i：行坐标
+            for j in 0 ..< board[0].count { // j：列坐标
+                guard board[i][j] == "." else { continue } // 跳过已填写格子
+                // 填写格子
+                for val in 1 ... 9 {
+                    let charVal = Character("\(val)")
+                    guard isValid(row: i, col: j, val: charVal) else { continue } // 跳过不合法的
+                    board[i][j] = charVal // 填写
+                    if backtracking() { return true }
+                    board[i][j] = "." // 回溯：擦除
+                }
+                return false // 遍历完数字都不行
+            }
+        }
+        return true // 没有不合法的，填写正确
+    }
+    backtracking()
+}
+```
+
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/0051.N皇后.md

@@ -33,7 +33,7 @@ n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，
 **如果对回溯算法基础还不了解的话，我还特意录制了一期视频：[带你学透回溯算法（理论篇）](https://www.bilibili.com/video/BV1cy4y167mM/)**  可以结合题解和视频一起看，希望对大家理解回溯算法有所帮助。
 
 
-都知道n皇后问题是回溯算法解决的经典问题，但是用回溯解决多了组合、切割、子集、排列问题之后，遇到这种二位矩阵还会有点不知所措。
+都知道n皇后问题是回溯算法解决的经典问题，但是用回溯解决多了组合、切割、子集、排列问题之后，遇到这种二维矩阵还会有点不知所措。
 
 首先来看一下皇后们的约束条件：
 
@@ -43,7 +43,7 @@ n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，
 
 确定完约束条件，来看看究竟要怎么去搜索皇后们的位置，其实搜索皇后的位置，可以抽象为一棵树。
 
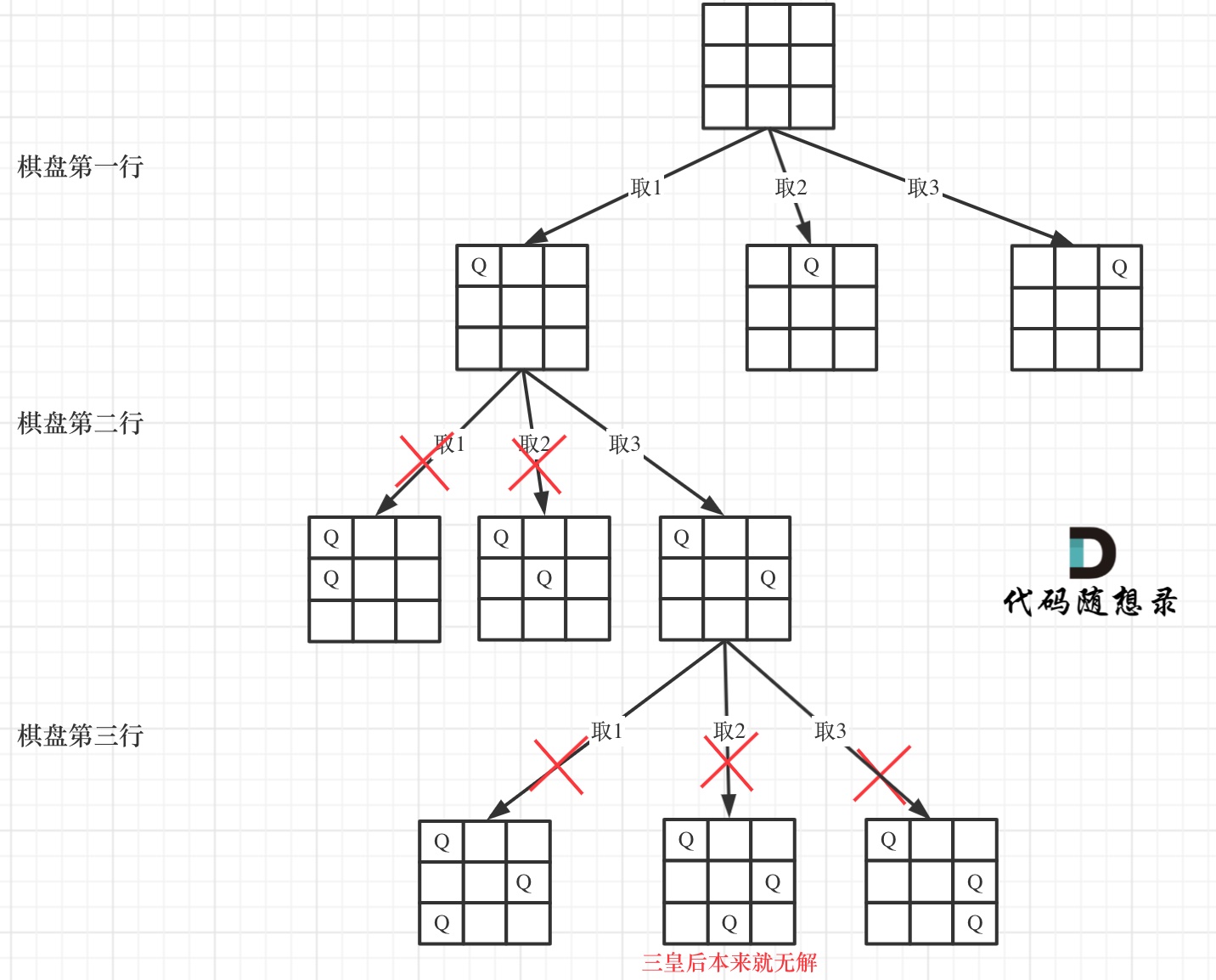
-下面我用一个3 * 3 的棋牌，将搜索过程抽象为一颗树，如图：
+下面我用一个 3 * 3 的棋盘，将搜索过程抽象为一颗树，如图：
 
 ![51.N皇后](https://img-blog.csdnimg.cn/20210130182532303.jpg)
 
@@ -73,11 +73,11 @@ void backtracking(参数) {
 
 我依然是定义全局变量二维数组result来记录最终结果。
 
-参数n是棋牌的大小，然后用row来记录当前遍历到棋盘的第几层了。
+参数n是棋盘的大小，然后用row来记录当前遍历到棋盘的第几层了。
 
 代码如下：
 
-```
+```cpp
 vector<vector<string>> result;
 void backtracking(int n, int row, vector<string>& chessboard) {
 ```
@@ -92,7 +92,7 @@ void backtracking(int n, int row, vector<string>& chessboard) {
 
 代码如下：
 
-```
+```cpp
 if (row == n) {
     result.push_back(chessboard);
     return;
@@ -107,7 +107,7 @@ if (row == n) {
 
 代码如下：
 
-```
+```cpp
 for (int col = 0; col < n; col++) {
     if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
         chessboard[row][col] = 'Q'; // 放置皇后
@@ -117,7 +117,7 @@ for (int col = 0; col < n; col++) {
 }
 ```
 
-* 验证棋牌是否合法
+* 验证棋盘是否合法
 
 按照如下标准去重：
 
@@ -163,7 +163,7 @@ class Solution {
 private:
 vector<vector<string>> result;
 // n 为输入的棋盘大小
-// row 是当前递归到棋牌的第几行了
+// row 是当前递归到棋盘的第几行了
 void backtracking(int n, int row, vector<string>& chessboard) {
     if (row == n) {
         result.push_back(chessboard);
@@ -470,7 +470,56 @@ var solveNQueens = function(n) {
 };
 ```
 
+### Swift
 
+```swift
+func solveNQueens(_ n: Int) -> [[String]] {
+    var result = [[String]]()
+    // 棋盘，使用Character的二维数组，以便于更新元素
+    var chessboard = [[Character]](repeating: [Character](repeating: ".", count: n), count: n)
+    // 检查棋盘是否符合N皇后
+    func isVaild(row: Int, col: Int) -> Bool {
+        // 检查列
+        for i in 0 ..< row {
+            if chessboard[i][col] == "Q" { return false }
+        }
+
+        var i, j: Int
+        // 检查45度
+        i = row - 1
+        j = col - 1
+        while i >= 0, j >= 0 {
+            if chessboard[i][j] == "Q" { return false }
+            i -= 1
+            j -= 1
+        }
+        // 检查135度
+        i = row - 1
+        j = col + 1
+        while i >= 0, j < n {
+            if chessboard[i][j] == "Q" { return false }
+            i -= 1
+            j += 1
+        }
+
+        return true
+    }
+    func backtracking(row: Int) {
+        if row == n {
+            result.append(chessboard.map { String($0) })
+        }
+
+        for col in 0 ..< n {
+            guard isVaild(row: row, col: col) else { continue }
+            chessboard[row][col] = "Q" // 放置皇后
+            backtracking(row: row + 1)
+            chessboard[row][col] = "." // 回溯
+        }
+    }
+    backtracking(row: 0)
+    return result
+}
+```
 
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/0332.重新安排行程.md

@@ -125,7 +125,7 @@ void backtracking(参数) {
 
 代码如下：
 
-```
+```cpp
 // unordered_map<出发机场, map<到达机场, 航班次数>> targets
 unordered_map<string, map<string, int>> targets;
 bool backtracking(int ticketNum, vector<string>& result) {
@@ -142,7 +142,8 @@ bool backtracking(int ticketNum, vector<string>& result) {
 所以找到了这个叶子节点了直接返回，这个递归函数的返回值问题我们在讲解二叉树的系列的时候，在这篇[二叉树：递归函数究竟什么时候需要返回值，什么时候不要返回值？](https://programmercarl.com/0112.路径总和.html)详细介绍过。
 
 当然本题的targets和result都需要初始化，代码如下：
-```
+
+```cpp
 for (const vector<string>& vec : tickets) {
     targets[vec[0]][vec[1]]++; // 记录映射关系
 }
@@ -157,7 +158,7 @@ result.push_back("JFK"); // 起始机场
 
 代码如下：
 
-```
+```cpp
 if (result.size() == ticketNum + 1) {
     return true;
 }
@@ -230,13 +231,15 @@ public:
 一波分析之后，可以看出我就是按照回溯算法的模板来的。
 
 代码中
-```
+
+```cpp
 for (pair<const string, int>& target : targets[result[result.size() - 1]])
 ```
 pair里要有const，因为map中的key是不可修改的，所以是`pair<const string, int>`。
 
 如果不加const，也可以复制一份pair，例如这么写：
-```
+
+```cpp
 for (pair<string, int>target : targets[result[result.size() - 1]])
 ```
 
@@ -445,5 +448,125 @@ var findItinerary = function(tickets) {
 
 ```
 
+### Swift
+
+直接迭代tickets数组：
+
+```swift
+func findItinerary(_ tickets: [[String]]) -> [String] {
+    // 先对路线进行排序
+    let tickets = tickets.sorted { (arr1, arr2) -> Bool in
+        if arr1[0] < arr2[0] {
+            return true
+        } else if arr1[0] > arr2[0] {
+            return false
+        }
+        if arr1[1] < arr2[1] {
+            return true
+        } else if arr1[1] > arr2[1] {
+            return false
+        }
+        return true
+    }
+    var path = ["JFK"]
+    var used = [Bool](repeating: false, count: tickets.count)
+
+    @discardableResult
+    func backtracking() -> Bool {
+        // 结束条件：满足一条路径的数量
+        if path.count == tickets.count + 1 { return true }
+
+        for i in 0 ..< tickets.count {
+            // 巧妙之处！跳过处理过或出发站不是path末尾站的线路，即筛选出未处理的又可以衔接path的线路
+            guard !used[i], tickets[i][0] == path.last! else { continue }
+            // 处理
+            used[i] = true
+            path.append(tickets[i][1])
+            // 递归
+            if backtracking() { return true }
+            // 回溯
+            path.removeLast()
+            used[i] = false
+        }
+        return false
+    }
+    backtracking()
+    return path
+}
+```
+
+使用字典优化迭代遍历：
+
+```swift
+func findItinerary(_ tickets: [[String]]) -> [String] {
+    // 建立出发站和目的站的一对多关系，要对目的地进行排序
+    typealias Destination = (name: String, used: Bool)
+    var targets = [String: [Destination]]()
+    for line in tickets {
+        let src = line[0], des = line[1]
+        var value = targets[src] ?? []
+        value.append((des, false))
+        targets[src] = value
+    }
+    for (k, v) in targets {
+        targets[k] = v.sorted { $0.name < $1.name }
+    }
+
+    var path = ["JFK"]
+    let pathCount = tickets.count + 1
+    @discardableResult
+    func backtracking() -> Bool {
+        if path.count == pathCount { return true }
+
+        let startPoint = path.last!
+        guard let end = targets[startPoint]?.count, end > 0 else { return false }
+        for i in 0 ..< end {
+            // 排除处理过的线路
+            guard !targets[startPoint]![i].used else { continue }
+            // 处理
+            targets[startPoint]![i].used = true
+            path.append(targets[startPoint]![i].name)
+            // 递归
+            if backtracking() { return true }
+            // 回溯
+            path.removeLast()
+            targets[startPoint]![i].used = false
+        }
+        return false
+    }
+    backtracking()
+    return path
+}
+```
+
+使用插入时排序优化targets字典的构造：
+
+```swift
+// 建立出发站和目的站的一对多关系，在构建的时候进行插入排序
+typealias Destination = (name: String, used: Bool)
+var targets = [String: [Destination]]()
+func sortedInsert(_ element: Destination, to array: inout [Destination]) {
+    var left = 0, right = array.count - 1
+    while left <= right {
+        let mid = left + (right - left) / 2
+        if array[mid].name < element.name {
+            left = mid + 1
+        } else if array[mid].name > element.name {
+            right = mid - 1
+        } else {
+            left = mid
+            break
+        }
+    }
+    array.insert(element, at: left)
+}
+for line in tickets {
+    let src = line[0], des = line[1]
+    var value = targets[src] ?? []
+    sortedInsert((des, false), to: &value)
+    targets[src] = value
+}
+```
+
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/周总结/20201112回溯周末总结.md

@@ -72,8 +72,8 @@
 **所以这块就说一说我个人理解，对内容持开放态度，集思广益，欢迎大家来讨论！**
 
 子集问题分析：
-* 时间复杂度：$O(n × 2^n)$，因为每一个元素的状态无外乎取与不取，所以时间复杂度为$O(2^n)$，构造每一组子集都需要填进数组，又有需要$O(n)$，最终时间复杂度：$O(n × 2^n)$
+* 时间复杂度：$O(n × 2^n)$，因为每一个元素的状态无外乎取与不取，所以时间复杂度为$O(2^n)$，构造每一组子集都需要填进数组，又有需要$O(n)$，最终时间复杂度：$O(n × 2^n)$。
-* 空间复杂度：$O(n)$，递归深度为n，所以系统栈所用空间为$O(n)$，每一层递归所用的空间都是常数级别，注意代码里的result和path都是全局变量，就算是放在参数里，传的也是引用，并不会新申请内存空间，最终空间复杂度为$O(n)$
+* 空间复杂度：$O(n)$，递归深度为n，所以系统栈所用空间为$O(n)$，每一层递归所用的空间都是常数级别，注意代码里的result和path都是全局变量，就算是放在参数里，传的也是引用，并不会新申请内存空间，最终空间复杂度为$O(n)$。
 
 排列问题分析：
 * 时间复杂度：$O(n!)$，这个可以从排列的树形图中很明显发现，每一层节点为n，第二层每一个分支都延伸了n-1个分支，再往下又是n-2个分支，所以一直到叶子节点一共就是 n * n-1 * n-2 * ..... 1 = n!。