Update

problems/0045.跳跃游戏II.md

@@ -73,11 +73,11 @@ public:
         for (int i = 0; i < nums.size(); i++) {
             nextDistance = max(nums[i] + i, nextDistance);  // 更新下一步覆盖最远距离下标
             if (i == curDistance) {                         // 遇到当前覆盖最远距离下标
-                if (curDistance != nums.size() - 1) {       // 如果当前覆盖最远距离下标不是终点
+                if (curDistance < nums.size() - 1) {       // 如果当前覆盖最远距离下标不是终点
                     ans++;                                  // 需要走下一步
                     curDistance = nextDistance;             // 更新当前覆盖最远距离下标（相当于加油了）
                     if (nextDistance >= nums.size() - 1) break; // 下一步的覆盖范围已经可以达到终点，结束循环
-                } else break;                               // 当前覆盖最远距离下标是集合终点，不用做ans++操作了，直接结束
+                } else break;                               // 当前覆盖最远距到达集合终点，不用做ans++操作了，直接结束
             }
         }
         return ans;
@@ -126,7 +126,7 @@ public:
 
 可以看出版本二的代码相对于版本一简化了不少！
 
-其精髓在于控制移动下标i只移动到nums.size() - 2的位置，所以移动下标只要遇到当前覆盖最远距离的下标，直接步数加一，不用考虑别的了。
+**其精髓在于控制移动下标i只移动到nums.size() - 2的位置**，所以移动下标只要遇到当前覆盖最远距离的下标，直接步数加一，不用考虑别的了。
 
 ## 总结
 

problems/0053.最大子序和.md

@@ -12,9 +12,9 @@
 给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
 
 示例:
-输入: [-2,1,-3,4,-1,2,1,-5,4]
+* 输入: [-2,1,-3,4,-1,2,1,-5,4]
-输出: 6
+* 输出: 6
-解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
+* 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
 
 
 ## 暴力解法
@@ -103,8 +103,28 @@ public:
 
 当然题目没有说如果数组为空，应该返回什么，所以数组为空的话返回啥都可以了。
 
+
+## 常见误区 
+
+误区一： 
+
 不少同学认为 如果输入用例都是-1，或者 都是负数，这个贪心算法跑出来的结果是0， 这是**又一次证明脑洞模拟不靠谱的经典案例**，建议大家把代码运行一下试一试，就知道了，也会理解 为什么 result 要初始化为最小负数了。
 
+
+误区二：
+
+大家在使用贪心算法求解本题，经常陷入的误区，就是分不清，是遇到 负数就选择起始位置，还是连续和为负选择起始位置。 
+
+在动画演示用，大家可以发现， 4，遇到 -1 的时候，我们依然累加了，为什么呢？ 
+
+因为和为3，只要连续和还是正数就会 对后面的元素 起到增大总和的作用。 所以只要连续和为正数我们就保留。 
+
+这里也会有录友疑惑，那 4 +  -1 之后 不就变小了吗？ 会不会错过 4 成为最大连续和的可能性？ 
+
+其实并不会，因为还有一个变量result 一直在更新 最大的连续和，只要有更大的连续和出现，result就更新了，那么result已经把4更新了，后面 连续和变成3，也不会对最后结果有影响。 
+
+
+
 ## 动态规划
 
 当然本题还可以用动态规划来做，当前[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png)主要讲解贪心系列，后续到动态规划系列的时候会详细讲解本题的dp方法。
@@ -135,7 +155,7 @@ public:
 
 本题的贪心思路其实并不好想，这也进一步验证了，别看贪心理论很直白，有时候看似是常识，但贪心的题目一点都不简单！
 
-后续将介绍的贪心题目都挺难的，哈哈，所以贪心很有意思，别小看贪心！
+后续将介绍的贪心题目都挺难的，所以贪心很有意思，别小看贪心！
 
 ## 其他语言版本
 

problems/0055.跳跃游戏.md

@@ -78,7 +78,7 @@ public:
 
 一些同学可能感觉，我在讲贪心系列的时候，题目和题目之间貌似没有什么联系？
 
-**是真的就是没什么联系，因为贪心无套路！**没有个整体的贪心框架解决一系列问题，只能是接触各种类型的题目锻炼自己的贪心思维！
+**是真的就是没什么联系，因为贪心无套路**！没有个整体的贪心框架解决一系列问题，只能是接触各种类型的题目锻炼自己的贪心思维！
 
 ## 其他语言版本
 

problems/0130.被围绕的区域.md

@@ -83,6 +83,7 @@ public:
 ```
 
 ## 其他语言版本 
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>

problems/0455.分发饼干.md

@@ -52,6 +52,7 @@
 C++代码整体如下：
 
 ```CPP
+// 版本一 
 // 时间复杂度：O(nlogn)
 // 空间复杂度：O(1)
 class Solution {
@@ -61,8 +62,8 @@ public:
         sort(s.begin(), s.end());
         int index = s.size() - 1; // 饼干数组的下标
         int result = 0;
-        for (int i = g.size() - 1; i >= 0; i--) {
+        for (int i = g.size() - 1; i >= 0; i--) { // 遍历胃口 
-            if (index >= 0 && s[index] >= g[i]) {
+            if (index >= 0 && s[index] >= g[i]) { // 遍历饼干 
                 result++;
                 index--;
             }
@@ -76,6 +77,26 @@ public:
 
 有的同学看到要遍历两个数组，就想到用两个for循环，那样逻辑其实就复杂了。
 
+
+### 注意事项 
+
+注意版本一的代码中，可以看出来，是先遍历的胃口，在遍历的饼干，那么可不可以 先遍历 饼干，在遍历胃口呢？ 
+
+其实是不可以的。 
+
+外面的for 是里的下标i 是固定移动的，而if里面的下标 index 是符合条件才移动的。 
+
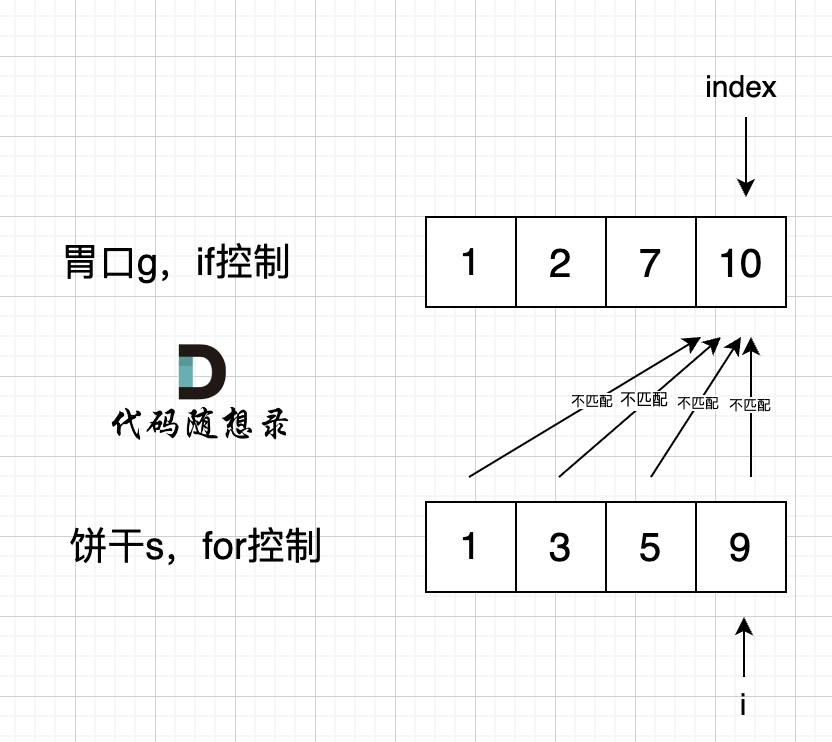
+如果 for 控制的是饼干， if 控制胃口，就是出现如下情况 ： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20230112102848.png)
+
+if 里的 index 指向 胃口 10， for里的i指向饼干9，因为 饼干9 满足不了 胃口10，所以 i 持续向前移动，而index 走不到` s[index] >= g[i]` 的逻辑，所以index不会移动，那么当i 持续向前移动，最后所有的饼干都匹配不上。  
+
+所以 一定要for 控制 胃口，里面的if控制饼干。 
+
+
+### 其他思路
+
 **也可以换一个思路，小饼干先喂饱小胃口**
 
 代码如下：
@@ -87,15 +108,19 @@ public:
         sort(g.begin(),g.end());
         sort(s.begin(),s.end());
         int index = 0;
-        for(int i = 0;i < s.size();++i){
+        for(int i = 0; i < s.size(); i++) { // 饼干
-            if(index < g.size() && g[index] <= s[i]){
+            if(index < g.size() && g[index] <= s[i]){ // 胃口
                 index++;
             }
         }
         return index;
     }
 };
-```
+``` 
+
+细心的录友可以发现，这种写法，两个循环的顺序改变了，先遍历的饼干，在遍历的胃口，这是因为遍历顺序变了，我们是从小到大遍历。 
+
+理由在上面 “注意事项”中 已经讲过。 
 
 ## 总结
 

problems/1005.K次取反后最大化的数组和.md

@@ -44,7 +44,7 @@
 
 那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让 数组和 达到最大。
 
-那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大。
+那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值和可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大。
 
 虽然这道题目大家做的时候，可能都不会去想什么贪心算法，一鼓作气，就AC了。
 

problems/1020.飞地的数量.md

@@ -144,6 +144,11 @@ public:
     }
 };
 ```
+## 类似题目 
+
+* 1254. 统计封闭岛屿的数目  
+
+
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">
   <img src="../pics/网站星球宣传海报.jpg" width="1000"/>