mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-06 07:06:42 +08:00
Update
This commit is contained in:
@ -147,6 +147,7 @@
|
||||
* [回溯算法:递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)
|
||||
* [回溯算法:排列问题!](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)
|
||||
* [回溯算法:排列问题(二)](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)
|
||||
* [本周小结!(回溯算法系列三)](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA)
|
||||
|
||||
(持续更新中....)
|
||||
|
||||
|
||||
BIN
pics/90.子集II1.png
Normal file
BIN
pics/90.子集II1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 118 KiB |
BIN
pics/90.子集II2.png
Normal file
BIN
pics/90.子集II2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 120 KiB |
@ -77,6 +77,39 @@ public:
|
||||
|
||||
```
|
||||
|
||||
使用set去重的版本。
|
||||
```
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
|
||||
result.push_back(path);
|
||||
unordered_set<int> uset;
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
if (uset.find(nums[i]) != uset.end()) {
|
||||
continue;
|
||||
}
|
||||
uset.insert(nums[i]);
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1, used);
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
|
||||
public:
|
||||
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
vector<bool> used(nums.size(), false);
|
||||
sort(nums.begin(), nums.end()); // 去重需要排序
|
||||
backtracking(nums, 0, used);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
# 总结
|
||||
|
||||
其实这道题目的知识点,我们之前都讲过了,如果之前讲过的子集问题和去重问题都掌握的好,这道题目应该分分钟AC。
|
||||
|
||||
240
problems/回溯算法去重问题的另一种写法.md
Normal file
240
problems/回溯算法去重问题的另一种写法.md
Normal file
@ -0,0 +1,240 @@
|
||||
|
||||
|
||||
> 在 [本周小结!(回溯算法系列三)](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA) 中一位录友对 整颗树的本层和同一节点的本层有疑问,也让我重新思考了一下,发现这里确实有问题,所以专门写一篇来纠正,感谢录友们的积极交流哈!
|
||||
|
||||
接下来我再把这块再讲一下。
|
||||
|
||||
在[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中的去重和 [回溯算法:递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)中的去重 都是 同一父节点下本层的去重。
|
||||
|
||||
[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)也可以使用set针对同一父节点本层去重,但子集问题一定要排序,为什么呢?
|
||||
|
||||
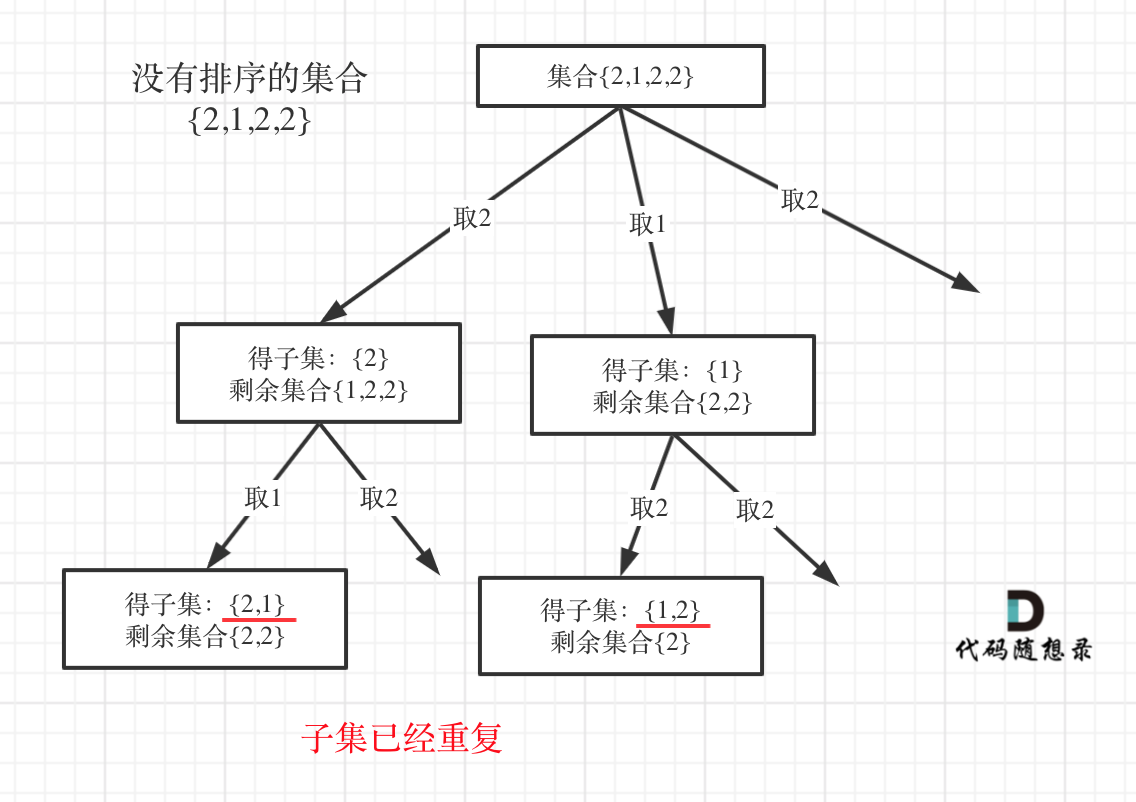
我用没有排序的集合{2,1,2,2}来举例子画一个图,如图:
|
||||
|
||||
|
||||
|
||||
图中,大家就很明显的看到,子集重复了。
|
||||
|
||||
那么下面我针对[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ) 给出使用set来对本层去重的代码实现。
|
||||
|
||||
# 90.子集II
|
||||
|
||||
used数组去重版本: [回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)
|
||||
|
||||
使用set去重的版本如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
|
||||
result.push_back(path);
|
||||
unordered_set<int> uset; // 定义set对同一节点下的本层去重
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
if (uset.find(nums[i]) != uset.end()) { // 如果发现出现过就pass
|
||||
continue;
|
||||
}
|
||||
uset.insert(nums[i]); // set跟新元素
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1, used);
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
|
||||
public:
|
||||
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
vector<bool> used(nums.size(), false);
|
||||
sort(nums.begin(), nums.end()); // 去重需要排序
|
||||
backtracking(nums, 0, used);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
针对留言区录友们的疑问,我再补充一些常见的错误写法,
|
||||
|
||||
|
||||
## 错误写法一
|
||||
|
||||
把uset定义放到类成员位置,然后模拟回溯的样子 insert一次,erase一次。
|
||||
|
||||
例如:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
unordered_set<int> uset; // 把uset定义放到类成员位置
|
||||
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
|
||||
result.push_back(path);
|
||||
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
if (uset.find(nums[i]) != uset.end()) {
|
||||
continue;
|
||||
}
|
||||
uset.insert(nums[i]); // 递归之前insert
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1, used);
|
||||
path.pop_back();
|
||||
uset.erase(nums[i]); // 回溯再erase
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
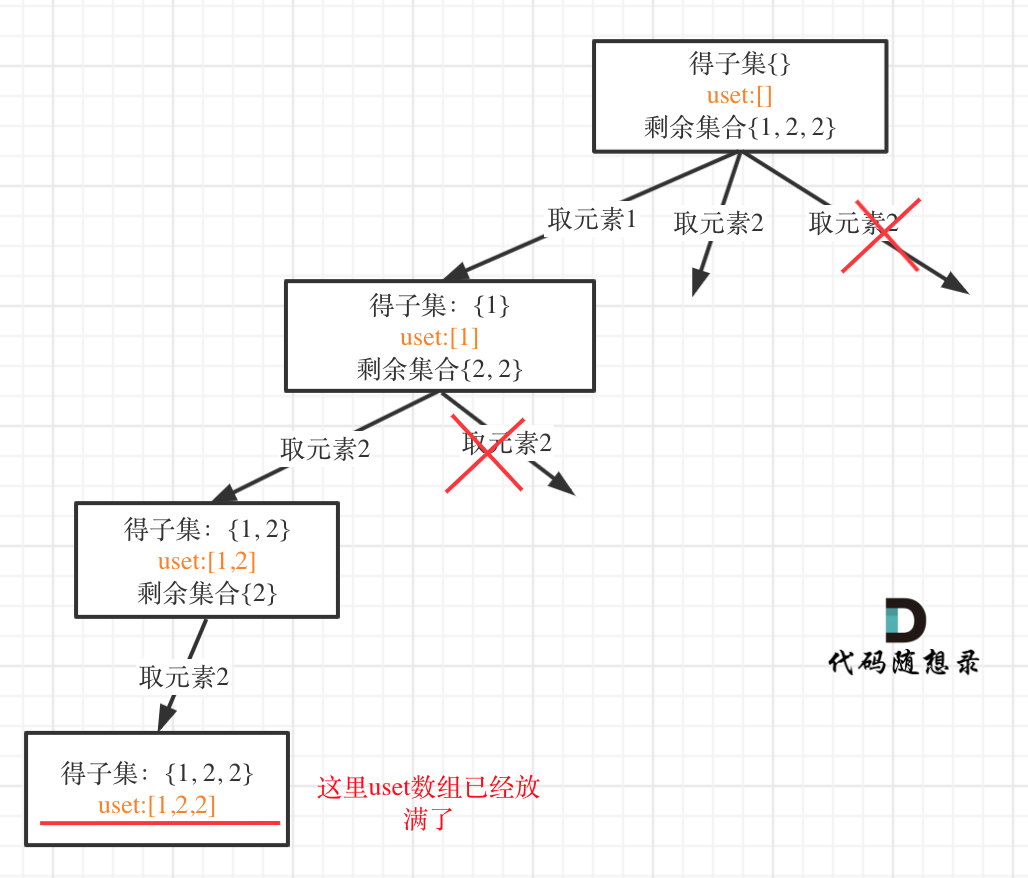
在树形结构中,**如果把unordered_set<int> uset放在类成员的位置(相当于全局变量),就把树枝的情况都记录了,不是单纯的控制某一节点下的同一层了**。
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
可以看出一旦把unordered_set<int> uset放在类成员位置,它控制的就是整棵树,包括树枝。
|
||||
|
||||
**所以这么写不行!**
|
||||
|
||||
## 错误写法二
|
||||
|
||||
有同学把 unordered_set<int> uset; 放到类成员位置,然后每次进入单层的时候用uset.clear()。
|
||||
|
||||
代码如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
unordered_set<int> uset; // 把uset定义放到类成员位置
|
||||
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
|
||||
result.push_back(path);
|
||||
uset.clear(); // 到每一层的时候,清空uset
|
||||
for (int i = startIndex; i < nums.size(); i++) {
|
||||
if (uset.find(nums[i]) != uset.end()) {
|
||||
continue;
|
||||
}
|
||||
uset.insert(nums[i]); // set记录元素
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, i + 1, used);
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
```
|
||||
uset已经是全局变量,本层的uset记录了一个元素,然后进入下一层之后这个uset(和上一层是同一个uset)就被清空了,也就是说,层与层之间的uset是同一个,那么就会相互影响。
|
||||
|
||||
**所以这么写依然不行!**
|
||||
|
||||
**组合问题和排列问题,其实也可以使用set来对同一节点下本层去重,下面我都分别给出实现代码**。
|
||||
|
||||
# 40. 组合总和 II
|
||||
|
||||
使用used数组去重版本:[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)
|
||||
|
||||
使用set去重的版本如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
|
||||
if (sum == target) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
unordered_set<int> uset; // 控制某一节点下的同一层元素不能重复
|
||||
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
|
||||
if (uset.find(candidates[i]) != uset.end()) {
|
||||
continue;
|
||||
}
|
||||
uset.insert(candidates[i]); // 记录元素
|
||||
sum += candidates[i];
|
||||
path.push_back(candidates[i]);
|
||||
backtracking(candidates, target, sum, i + 1);
|
||||
sum -= candidates[i];
|
||||
path.pop_back();
|
||||
}
|
||||
}
|
||||
|
||||
public:
|
||||
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
|
||||
path.clear();
|
||||
result.clear();
|
||||
sort(candidates.begin(), candidates.end());
|
||||
backtracking(candidates, target, 0, 0);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
# 47. 全排列 II
|
||||
|
||||
使用used数组去重版本:[回溯算法:排列问题(二)](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)
|
||||
|
||||
使用set去重的版本如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
void backtracking (vector<int>& nums, vector<bool>& used) {
|
||||
if (path.size() == nums.size()) {
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
unordered_set<int> uset; // 控制某一节点下的同一层元素不能重复
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
if (uset.find(nums[i]) != uset.end()) {
|
||||
continue;
|
||||
}
|
||||
if (used[i] == false) {
|
||||
uset.insert(nums[i]); // 记录元素
|
||||
used[i] = true;
|
||||
path.push_back(nums[i]);
|
||||
backtracking(nums, used);
|
||||
path.pop_back();
|
||||
used[i] = false;
|
||||
}
|
||||
}
|
||||
}
|
||||
public:
|
||||
vector<vector<int>> permuteUnique(vector<int>& nums) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
sort(nums.begin(), nums.end()); // 排序
|
||||
vector<bool> used(nums.size(), false);
|
||||
backtracking(nums, used);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
# 两种写法的性能分析
|
||||
|
||||
需要注意的是:**使用set去重的版本相对于used数组的版本效率都要低很多**,大家在leetcode上提交,能明显发现。
|
||||
|
||||
原因在[回溯算法:递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)中也分析过,主要是因为程序运行的时候对unordered_set 频繁的insert,unordered_set需要做哈希映射(也就是把key通过hash function映射为唯一的哈希值)相对费时间,而且insert的时候其底层的符号表也要做相应的扩充,也是费时的。
|
||||
|
||||
**而使用used数组在时间复杂度上几乎没有额外负担!**
|
||||
|
||||
**使用set去重,不仅时间复杂度高了,空间复杂度也高了**,在[本周小结!(回溯算法系列三)](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA)中分析过,组合,子集,排列问题的空间复杂度都是O(n),但如果使用set去重,空间复杂度就变成了O(n^2),因为每一层递归都有一个set集合,系统栈空间是n,每一个空间都有set集合。
|
||||
|
||||
那有同学可能疑惑 用used数组也是占用O(n)的空间啊?
|
||||
|
||||
used数组可是全局变量,每层与每层之间公用一个used数组,所以空间复杂度是O(n + n),最终空间复杂度还是O(n)。
|
||||
|
||||
# 总结
|
||||
|
||||
本篇本打算是对[本周小结!(回溯算法系列三)](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA)的一个点做一下纠正,没想到又写出来这么多!
|
||||
|
||||
**这个点都源于一位录友的疑问,然后我思考总结了一下,就写着这一篇,所以还是得多交流啊!**
|
||||
|
||||
如果大家对「代码随想录」文章有什么疑问,尽管打卡留言的时候提出来哈,或者在交流群里提问。
|
||||
|
||||
**其实这就是相互学习的过程,交流一波之后都对题目理解的更深刻了,我如果发现文中有问题,都会在评论区或者下一篇文章中即时修正,保证不会给大家带跑偏!**
|
||||
|
||||
就酱,「代码随想录」一直都是干货满满,公众号里的一抹清流,值得推荐给身边的每一位同学朋友!
|
||||
|
||||
@ -12,20 +12,19 @@
|
||||
在举一个例子如果是 有一堆盒子,你有一个背包体积为n,如何把背包尽可能装满,如果还每次选最大的盒子,一定不行。这时候就需要动态规划。动态规划的问题在下一个系列会详细讲解。
|
||||
|
||||
|
||||
|
||||
很多同学做贪心的题目的时候,想不出来是贪心,想知道有没有什么套路可以一看看出来是贪心,说实话贪心算法并没有固定的套路。
|
||||
|
||||
所以唯一的难点就是如何通过局部最优,推出整体最优。
|
||||
|
||||
那么如何能看出局部最优是否能退出整体最优呢?有没有什么固定策略呢?
|
||||
那么如何能看出局部最优是否能退出整体最优呢?有没有什么固定策略或者套路呢?
|
||||
|
||||
不好意思,也没有,靠自己手动模拟,如果模拟可行,就可以试一试贪心策略,如果不可行,可能需要动态规划。
|
||||
**不好意思,没有!** 靠自己手动模拟,如果模拟可行,就可以试一试贪心策略,如果不可行,可能需要动态规划。
|
||||
|
||||
验证可不可以用贪心最好用的策略就是举反例,如果想不到反例,那么就试一试贪心吧。
|
||||
|
||||
那又有同学认为手动模拟,举例子得出的结论不靠谱,想要严格的数学证明。
|
||||
|
||||
数学证明一般可以是
|
||||
数学证明一般可以是:
|
||||
|
||||
* 数学归纳法
|
||||
* 反证法
|
||||
@ -34,13 +33,13 @@
|
||||
|
||||
所以做了贪心题目的时候大家就会发现,如果啥都要数学证明一下,就是把简单问题搞复杂了。
|
||||
|
||||
面试中基本不会让面试者现场证明贪心的合理性,代码写出来跑过测试用例即可,或者自己能自圆其说就行。
|
||||
**面试中基本不会让面试者现场证明贪心的合理性,代码写出来跑过测试用例即可,或者自己能自圆其说就行**。
|
||||
|
||||
举一个不太恰当的例子:我要用一下1+1 = 2,但我要先证明1+1 为什么等于2。严谨是严谨了,但没必要。
|
||||
|
||||
虽然这个例子有点极端,但可以表达这么个意思,就是手动模拟一下感觉可以局部最优推出整体最优,那么就试一试贪心。
|
||||
虽然这个例子有点极端,但可以表达这么个意思:就是手动模拟一下感觉可以局部最优推出整体最优,而且想不到反例,那么就试一试贪心。
|
||||
|
||||
例如刚刚举的拿钞票的例子,就是模拟一下每次那做大的,最后就能拿到最多的钱,这还要数学证明的话,是不是感觉有点怪怪的。
|
||||
**例如刚刚举的拿钞票的例子,就是模拟一下每次那做大的,最后就能拿到最多的钱,这还要数学证明的话,其实就不在算法面试的范围内了,可以看看专业的数学书籍!**
|
||||
|
||||
所以这也是为什么有的通过AC(accept)了一些贪心的题目,但都不知道自己用了贪心算法,因为贪心有时候就是常识性的推导,所以会认为本就应该这么做!
|
||||
|
||||
|
||||
Reference in New Issue
Block a user