mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-12 13:45:39 +08:00
Merge branch 'youngyangyang04:master' into master
This commit is contained in:
@ -107,7 +107,9 @@
|
||||
5. [数组:209.长度最小的子数组](./problems/0209.长度最小的子数组.md)
|
||||
6. [数组:区间和](./problems/kamacoder/0058.区间和.md)
|
||||
6. [数组:59.螺旋矩阵II](./problems/0059.螺旋矩阵II.md)
|
||||
7. [数组:总结篇](./problems/数组总结篇.md)
|
||||
7. [数组:区间和](./problems/kamacoder/0058.区间和.md)
|
||||
8. [数组:开发商购买土地](./problems/kamacoder/0044.开发商购买土地.md)
|
||||
9. [数组:总结篇](./problems/数组总结篇.md)
|
||||
|
||||
## 链表
|
||||
|
||||
|
||||
@ -264,7 +264,7 @@ class Solution {
|
||||
|
||||
// nums[i]+nums[j] > target 直接返回, 剪枝操作
|
||||
if (nums[i]+nums[j] > 0 && nums[i]+nums[j] > target) {
|
||||
return result;
|
||||
break;
|
||||
}
|
||||
|
||||
if (j > i + 1 && nums[j - 1] == nums[j]) { // 对nums[j]去重
|
||||
|
||||
@ -42,7 +42,8 @@
|
||||
|
||||
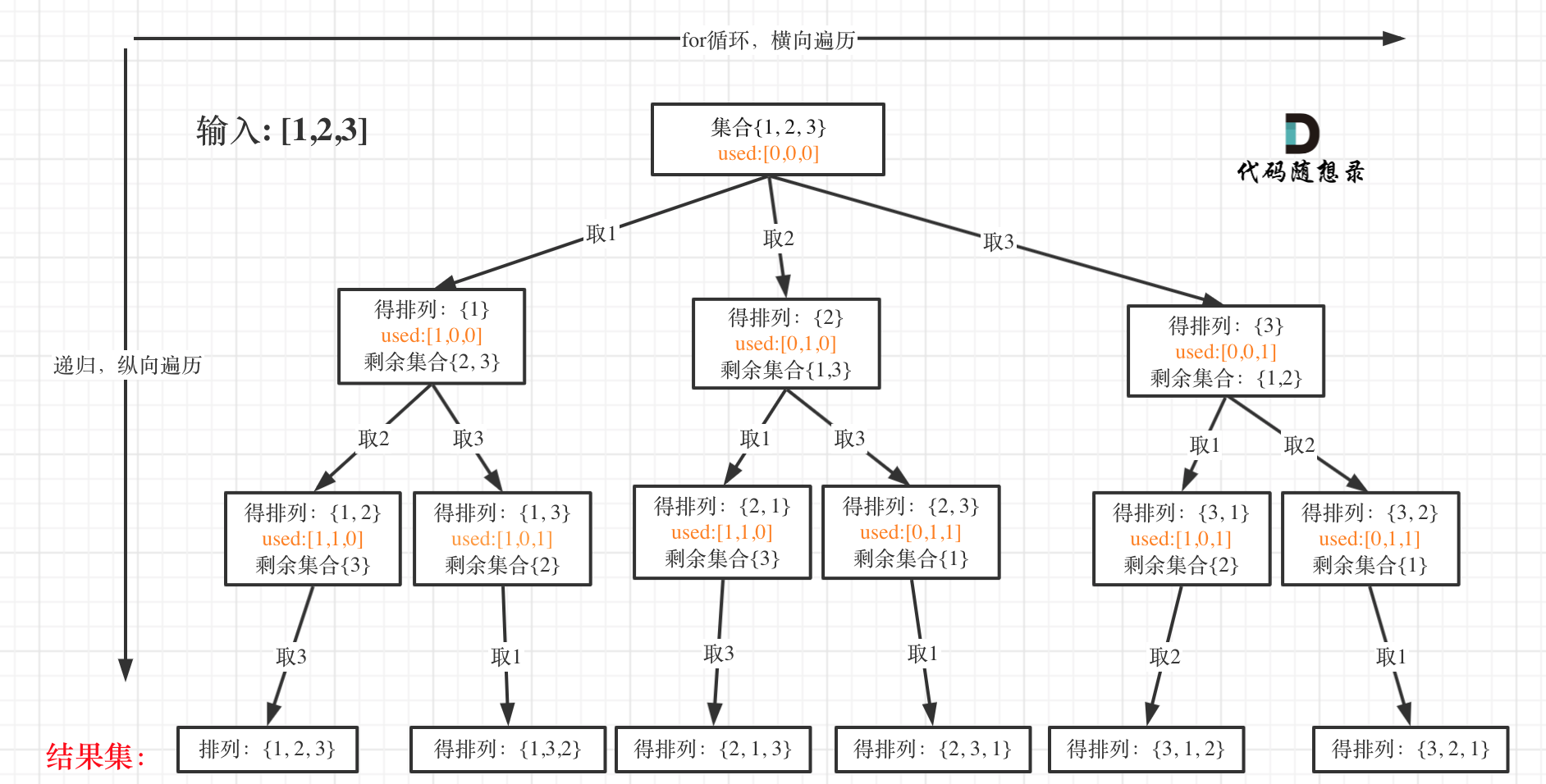
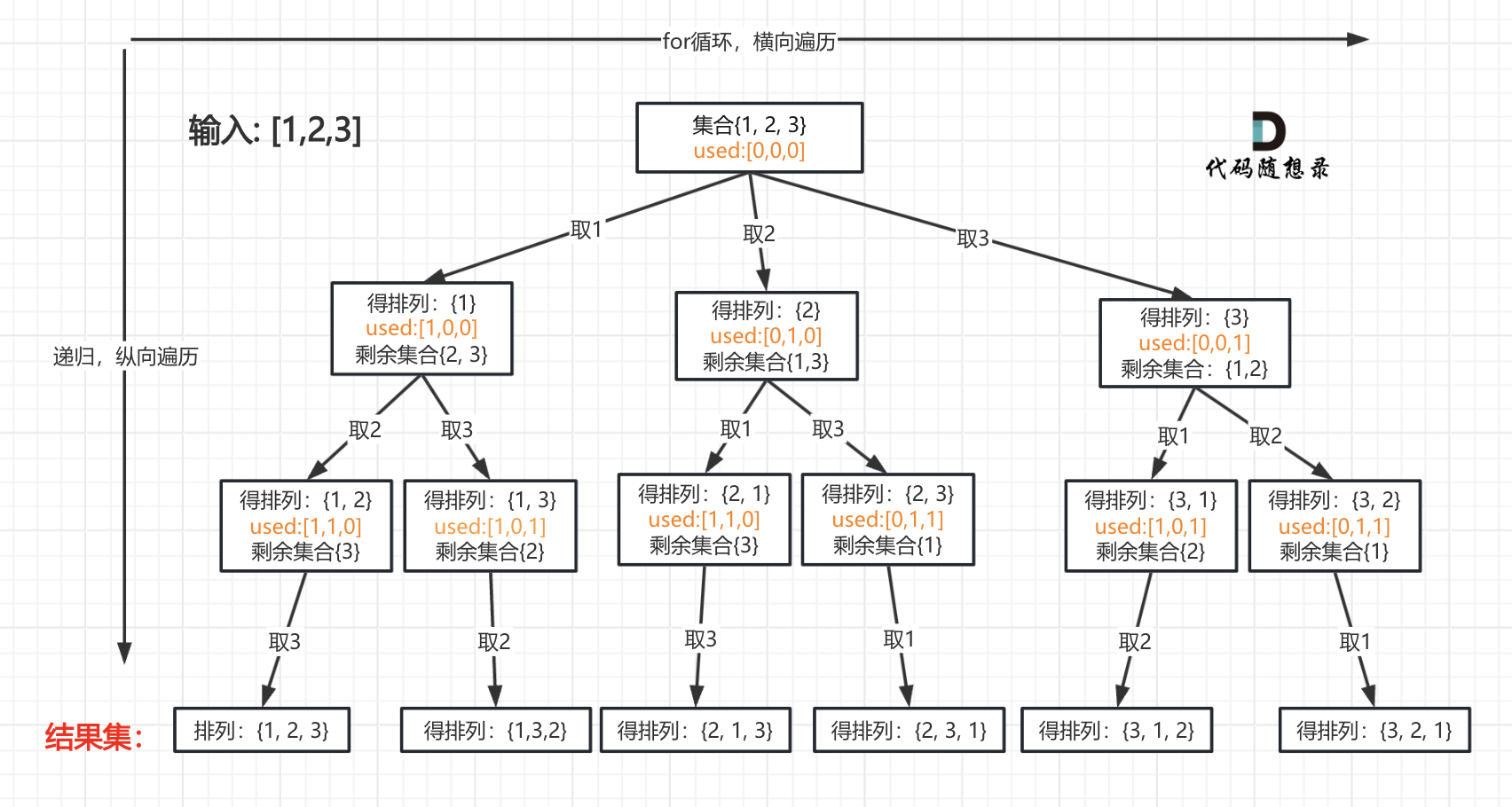
我以[1,2,3]为例,抽象成树形结构如下:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### 回溯三部曲
|
||||
|
||||
@ -54,7 +55,7 @@
|
||||
|
||||
但排列问题需要一个used数组,标记已经选择的元素,如图橘黄色部分所示:
|
||||
|
||||

|
||||

|
||||
|
||||
代码如下:
|
||||
|
||||
@ -66,7 +67,7 @@ void backtracking (vector<int>& nums, vector<bool>& used)
|
||||
|
||||
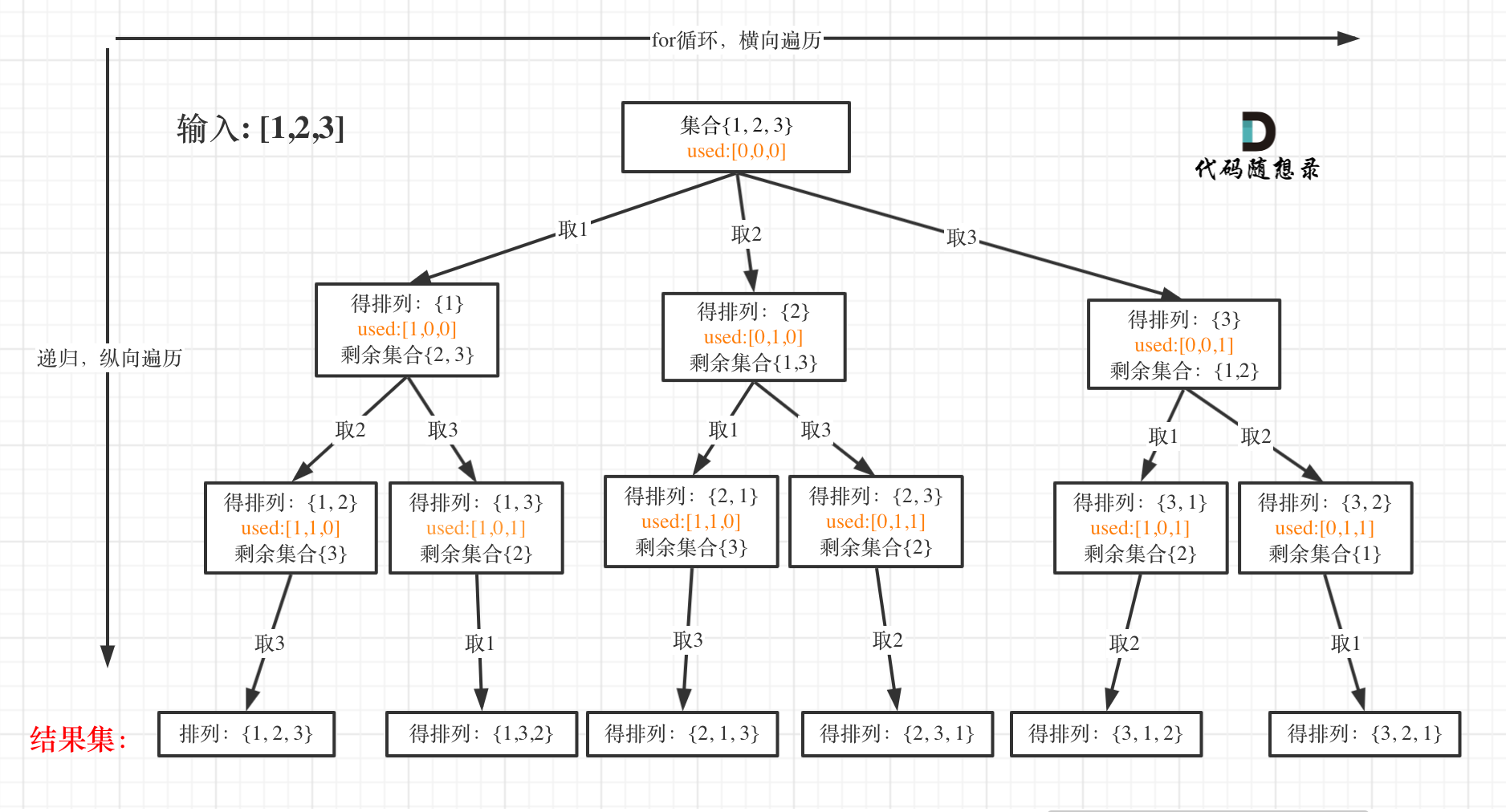
* 递归终止条件
|
||||
|
||||
|
||||

|
||||
|
||||
可以看出叶子节点,就是收割结果的地方。
|
||||
|
||||
|
||||
@ -371,6 +371,7 @@ class Solution:
|
||||
```
|
||||
### Go
|
||||
|
||||
动态规划
|
||||
```Go
|
||||
func uniquePaths(m int, n int) int {
|
||||
dp := make([][]int, m)
|
||||
@ -390,6 +391,26 @@ func uniquePaths(m int, n int) int {
|
||||
}
|
||||
```
|
||||
|
||||
数论方法
|
||||
```Go
|
||||
func uniquePaths(m int, n int) int {
|
||||
numerator := 1
|
||||
denominator := m - 1
|
||||
count := m - 1
|
||||
t := m + n - 2
|
||||
for count > 0 {
|
||||
numerator *= t
|
||||
t--
|
||||
for denominator != 0 && numerator % denominator == 0 {
|
||||
numerator /= denominator
|
||||
denominator--
|
||||
}
|
||||
count--
|
||||
}
|
||||
return numerator
|
||||
}
|
||||
```
|
||||
|
||||
### Javascript
|
||||
|
||||
```Javascript
|
||||
|
||||
@ -310,6 +310,43 @@ class Solution:
|
||||
```
|
||||
### Go
|
||||
|
||||
使用used数组
|
||||
```Go
|
||||
var (
|
||||
result [][]int
|
||||
path []int
|
||||
)
|
||||
|
||||
func subsetsWithDup(nums []int) [][]int {
|
||||
result = make([][]int, 0)
|
||||
path = make([]int, 0)
|
||||
used := make([]bool, len(nums))
|
||||
sort.Ints(nums) // 去重需要排序
|
||||
backtracing(nums, 0, used)
|
||||
return result
|
||||
}
|
||||
|
||||
func backtracing(nums []int, startIndex int, used []bool) {
|
||||
tmp := make([]int, len(path))
|
||||
copy(tmp, path)
|
||||
result = append(result, tmp)
|
||||
for i := startIndex; i < len(nums); i++ {
|
||||
// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
|
||||
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
|
||||
// 而我们要对同一树层使用过的元素进行跳过
|
||||
if i > 0 && nums[i] == nums[i-1] && used[i-1] == false {
|
||||
continue
|
||||
}
|
||||
path = append(path, nums[i])
|
||||
used[i] = true
|
||||
backtracing(nums, i + 1, used)
|
||||
path = path[:len(path)-1]
|
||||
used[i] = false
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
不使用used数组
|
||||
```Go
|
||||
var (
|
||||
path []int
|
||||
|
||||
@ -143,7 +143,7 @@ for (int i = startIndex; i < s.size(); i++) {
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
|
||||
// 判断字符串s在左闭右闭区间[start, end]所组成的数字是否合法
|
||||
bool isValid(const string& s, int start, int end) {
|
||||
if (start > end) {
|
||||
return false;
|
||||
@ -208,7 +208,7 @@ private:
|
||||
} else break; // 不合法,直接结束本层循环
|
||||
}
|
||||
}
|
||||
// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
|
||||
// 判断字符串s在左闭右闭区间[start, end]所组成的数字是否合法
|
||||
bool isValid(const string& s, int start, int end) {
|
||||
if (start > end) {
|
||||
return false;
|
||||
|
||||
@ -623,6 +623,8 @@ class Solution:
|
||||
```
|
||||
### Go:
|
||||
|
||||
递归法
|
||||
|
||||
```Go
|
||||
func isBalanced(root *TreeNode) bool {
|
||||
h := getHeight(root)
|
||||
@ -653,6 +655,64 @@ func max(a, b int) int {
|
||||
}
|
||||
```
|
||||
|
||||
迭代法
|
||||
|
||||
```Go
|
||||
func isBalanced(root *TreeNode) bool {
|
||||
st := make([]*TreeNode, 0)
|
||||
if root == nil {
|
||||
return true
|
||||
}
|
||||
st = append(st, root)
|
||||
for len(st) > 0 {
|
||||
node := st[len(st)-1]
|
||||
st = st[:len(st)-1]
|
||||
if math.Abs(float64(getDepth(node.Left)) - float64(getDepth(node.Right))) > 1 {
|
||||
return false
|
||||
}
|
||||
if node.Right != nil {
|
||||
st = append(st, node.Right)
|
||||
}
|
||||
if node.Left != nil {
|
||||
st = append(st, node.Left)
|
||||
}
|
||||
}
|
||||
return true
|
||||
}
|
||||
|
||||
func getDepth(cur *TreeNode) int {
|
||||
st := make([]*TreeNode, 0)
|
||||
if cur != nil {
|
||||
st = append(st, cur)
|
||||
}
|
||||
depth := 0
|
||||
result := 0
|
||||
for len(st) > 0 {
|
||||
node := st[len(st)-1]
|
||||
if node != nil {
|
||||
st = st[:len(st)-1]
|
||||
st = append(st, node, nil)
|
||||
depth++
|
||||
if node.Right != nil {
|
||||
st = append(st, node.Right)
|
||||
}
|
||||
if node.Left != nil {
|
||||
st = append(st, node.Left)
|
||||
}
|
||||
} else {
|
||||
st = st[:len(st)-1]
|
||||
node = st[len(st)-1]
|
||||
st = st[:len(st)-1]
|
||||
depth--
|
||||
}
|
||||
if result < depth {
|
||||
result = depth
|
||||
}
|
||||
}
|
||||
return result
|
||||
}
|
||||
```
|
||||
|
||||
### JavaScript:
|
||||
|
||||
递归法:
|
||||
|
||||
@ -727,6 +727,48 @@ class Solution:
|
||||
|
||||
```go
|
||||
//递归法
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func hasPathSum(root *TreeNode, targetSum int) bool {
|
||||
if root == nil {
|
||||
return false
|
||||
}
|
||||
return traversal(root, targetSum - root.Val)
|
||||
}
|
||||
|
||||
func traversal(cur *TreeNode, count int) bool {
|
||||
if cur.Left == nil && cur.Right == nil && count == 0 {
|
||||
return true
|
||||
}
|
||||
if cur.Left == nil && cur.Right == nil {
|
||||
return false
|
||||
}
|
||||
if cur.Left != nil {
|
||||
count -= cur.Left.Val
|
||||
if traversal(cur.Left, count) {
|
||||
return true
|
||||
}
|
||||
count += cur.Left.Val
|
||||
}
|
||||
if cur.Right != nil {
|
||||
count -= cur.Right.Val
|
||||
if traversal(cur.Right, count) {
|
||||
return true
|
||||
}
|
||||
count += cur.Right.Val
|
||||
}
|
||||
return false
|
||||
}
|
||||
```
|
||||
|
||||
```go
|
||||
//递归法精简
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
|
||||
@ -308,7 +308,7 @@ class Solution:
|
||||
class Solution:
|
||||
def maxProfit(self, prices: List[int]) -> int:
|
||||
length = len(prices)
|
||||
if len == 0:
|
||||
if length == 0:
|
||||
return 0
|
||||
dp = [[0] * 2 for _ in range(length)]
|
||||
dp[0][0] = -prices[0]
|
||||
|
||||
@ -527,6 +527,7 @@ class Solution:
|
||||
|
||||
```
|
||||
### Go
|
||||
回溯 基本版
|
||||
```go
|
||||
var (
|
||||
path []string // 放已经回文的子串
|
||||
@ -565,6 +566,63 @@ func isPalindrome(s string) bool {
|
||||
}
|
||||
```
|
||||
|
||||
回溯+动态规划优化回文串判断
|
||||
```go
|
||||
var (
|
||||
result [][]string
|
||||
path []string // 放已经回文的子串
|
||||
isPalindrome [][]bool // 放事先计算好的是否回文子串的结果
|
||||
)
|
||||
|
||||
func partition(s string) [][]string {
|
||||
result = make([][]string, 0)
|
||||
path = make([]string, 0)
|
||||
computePalindrome(s)
|
||||
backtracing(s, 0)
|
||||
return result
|
||||
}
|
||||
|
||||
func backtracing(s string, startIndex int) {
|
||||
// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了
|
||||
if startIndex >= len(s) {
|
||||
tmp := make([]string, len(path))
|
||||
copy(tmp, path)
|
||||
result = append(result, tmp)
|
||||
return
|
||||
}
|
||||
for i := startIndex; i < len(s); i++ {
|
||||
if isPalindrome[startIndex][i] { // 是回文子串
|
||||
// 获取[startIndex,i]在s中的子串
|
||||
path = append(path, s[startIndex:i+1])
|
||||
} else { // 不是回文,跳过
|
||||
continue
|
||||
}
|
||||
backtracing(s, i + 1) // 寻找i+1为起始位置的子串
|
||||
path = path[:len(path)-1] // 回溯过程,弹出本次已经添加的子串
|
||||
}
|
||||
}
|
||||
|
||||
func computePalindrome(s string) {
|
||||
// isPalindrome[i][j] 代表 s[i:j](双边包括)是否是回文字串
|
||||
isPalindrome = make([][]bool, len(s))
|
||||
for i := 0; i < len(isPalindrome); i++ {
|
||||
isPalindrome[i] = make([]bool, len(s))
|
||||
}
|
||||
for i := len(s)-1; i >= 0; i-- {
|
||||
// 需要倒序计算, 保证在i行时, i+1行已经计算好了
|
||||
for j := i; j < len(s); j++ {
|
||||
if j == i {
|
||||
isPalindrome[i][j] = true
|
||||
} else if j - i == 1 {
|
||||
isPalindrome[i][j] = s[i] == s[j]
|
||||
} else {
|
||||
isPalindrome[i][j] = s[i] == s[j] && isPalindrome[i+1][j-1]
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### JavaScript
|
||||
|
||||
```js
|
||||
|
||||
@ -249,6 +249,29 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
```
|
||||
// 解法3
|
||||
class Solution {
|
||||
public int canCompleteCircuit(int[] gas, int[] cost) {
|
||||
int tank = 0; // 当前油量
|
||||
int totalGas = 0; // 总加油量
|
||||
int totalCost = 0; // 总油耗
|
||||
int start = 0; // 起点
|
||||
for (int i = 0; i < gas.length; i++) {
|
||||
totalGas += gas[i];
|
||||
totalCost += cost[i];
|
||||
|
||||
tank += gas[i] - cost[i];
|
||||
if (tank < 0) { // tank 变为负数 意味着 从0到i之间出发都不能顺利环路一周,因为在此i点必会没油
|
||||
tank = 0; // reset tank,类似于题目53.最大子树和reset sum
|
||||
start = i + 1; // 起点变为i点往后一位
|
||||
}
|
||||
}
|
||||
if (totalCost > totalGas) return -1;
|
||||
return start;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Python
|
||||
暴力法
|
||||
@ -322,6 +345,37 @@ class Solution:
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
贪心算法(方法一)
|
||||
```go
|
||||
func canCompleteCircuit(gas []int, cost []int) int {
|
||||
curSum := 0
|
||||
min := math.MaxInt64
|
||||
for i := 0; i < len(gas); i++ {
|
||||
rest := gas[i] - cost[i]
|
||||
curSum += rest
|
||||
if curSum < min {
|
||||
min = curSum
|
||||
}
|
||||
}
|
||||
if curSum < 0 {
|
||||
return -1
|
||||
}
|
||||
if min >= 0 {
|
||||
return 0
|
||||
}
|
||||
for i := len(gas) - 1; i > 0; i-- {
|
||||
rest := gas[i] - cost[i]
|
||||
min += rest
|
||||
if min >= 0 {
|
||||
return i
|
||||
}
|
||||
}
|
||||
return -1
|
||||
}
|
||||
```
|
||||
|
||||
贪心算法(方法二)
|
||||
```go
|
||||
func canCompleteCircuit(gas []int, cost []int) int {
|
||||
curSum := 0
|
||||
|
||||
@ -474,6 +474,7 @@ class Solution:
|
||||
words = s.split() #type(words) --- list
|
||||
words = words[::-1] # 反转单词
|
||||
return ' '.join(words) #列表转换成字符串
|
||||
```
|
||||
|
||||
### Go:
|
||||
|
||||
|
||||
@ -149,7 +149,35 @@ public:
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
|
||||
**也可以通过递归的思路解决本题:**
|
||||
|
||||
基础情况:对于空链表,不需要移除元素。
|
||||
|
||||
递归情况:首先检查头节点的值是否为 val,如果是则移除头节点,答案即为在头节点的后续节点上递归的结果;如果头节点的值不为 val,则答案为头节点与在头节点的后续节点上递归得到的新链表拼接的结果。
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
ListNode* removeElements(ListNode* head, int val) {
|
||||
// 基础情况:空链表
|
||||
if (head == nullptr) {
|
||||
return nullptr;
|
||||
}
|
||||
|
||||
// 递归处理
|
||||
if (head->val == val) {
|
||||
ListNode* newHead = removeElements(head->next, val);
|
||||
delete head;
|
||||
return newHead;
|
||||
} else {
|
||||
head->next = removeElements(head->next, val);
|
||||
return head;
|
||||
}
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(n)
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
@ -14,7 +14,7 @@
|
||||
|
||||
|
||||
|
||||
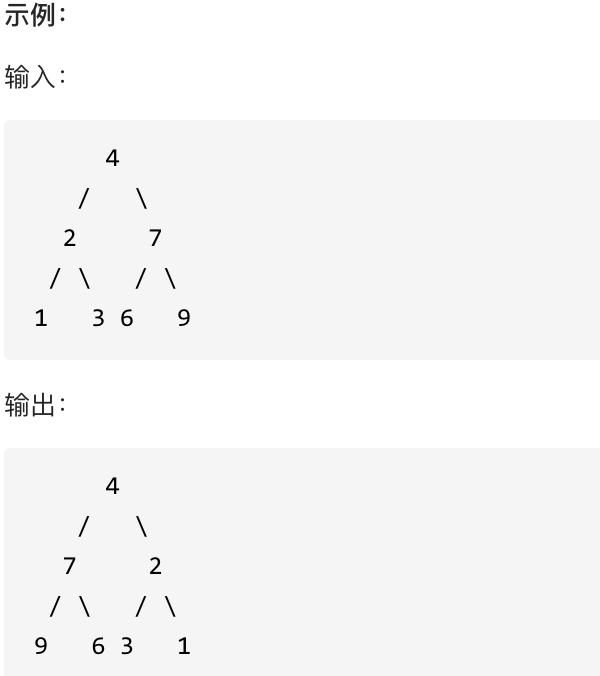
这道题目背后有一个让程序员心酸的故事,听说 Homebrew的作者Max Howell,就是因为没在白板上写出翻转二叉树,最后被Google拒绝了。(真假不做判断,权当一个乐子哈)
|
||||
这道题目背后有一个让程序员心酸的故事,听说 Homebrew的作者Max Howell,就是因为没在白板上写出翻转二叉树,最后被Google拒绝了。(真假不做判断,全当一个乐子哈)
|
||||
|
||||
## 算法公开课
|
||||
|
||||
@ -1033,3 +1033,4 @@ public TreeNode InvertTree(TreeNode root) {
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
@ -337,6 +337,21 @@ func sumOfLeftLeaves(root *TreeNode) int {
|
||||
}
|
||||
```
|
||||
|
||||
**递归精简版**
|
||||
|
||||
```go
|
||||
func sumOfLeftLeaves(root *TreeNode) int {
|
||||
if root == nil {
|
||||
return 0
|
||||
}
|
||||
leftValue := 0
|
||||
if root.Left != nil && root.Left.Left == nil && root.Left.Right == nil {
|
||||
leftValue = root.Left.Val
|
||||
}
|
||||
return leftValue + sumOfLeftLeaves(root.Left) + sumOfLeftLeaves(root.Right)
|
||||
}
|
||||
```
|
||||
|
||||
**迭代法(前序遍历)**
|
||||
|
||||
```go
|
||||
|
||||
@ -226,21 +226,36 @@ class Solution:
|
||||
```
|
||||
|
||||
### Go
|
||||
```golang
|
||||
//排序后,局部最优
|
||||
|
||||
版本一 大饼干优先
|
||||
```Go
|
||||
func findContentChildren(g []int, s []int) int {
|
||||
sort.Ints(g)
|
||||
sort.Ints(s)
|
||||
|
||||
// 从小到大
|
||||
child := 0
|
||||
for sIdx := 0; child < len(g) && sIdx < len(s); sIdx++ {
|
||||
if s[sIdx] >= g[child] {//如果饼干的大小大于或等于孩子的为空则给与,否则不给予,继续寻找选一个饼干是否符合
|
||||
child++
|
||||
sort.Ints(g)
|
||||
sort.Ints(s)
|
||||
index := len(s) - 1
|
||||
result := 0
|
||||
for i := len(g) - 1; i >= 0; i-- {
|
||||
if index >= 0 && s[index] >= g[i] {
|
||||
result++
|
||||
index--
|
||||
}
|
||||
}
|
||||
}
|
||||
return result
|
||||
}
|
||||
```
|
||||
|
||||
return child
|
||||
版本二 小饼干优先
|
||||
```Go
|
||||
func findContentChildren(g []int, s []int) int {
|
||||
sort.Ints(g)
|
||||
sort.Ints(s)
|
||||
index := 0
|
||||
for i := 0; i < len(s); i++ {
|
||||
if index < len(g) && g[index] <= s[i] {
|
||||
index++
|
||||
}
|
||||
}
|
||||
return index
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
@ -615,7 +615,7 @@ impl Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
## C
|
||||
### C
|
||||
|
||||
```c
|
||||
#define max(a, b) ((a) > (b) ? (a) : (b))
|
||||
|
||||
@ -134,17 +134,17 @@ x = (target + sum) / 2
|
||||
|
||||
大家看到(target + sum) / 2 应该担心计算的过程中向下取整有没有影响。
|
||||
|
||||
这么担心就对了,例如sum 是5,S是2的话其实就是无解的,所以:
|
||||
这么担心就对了,例如sum是5,target是2 的话其实就是无解的,所以:
|
||||
|
||||
```CPP
|
||||
(C++代码中,输入的S 就是题目描述的 target)
|
||||
if ((S + sum) % 2 == 1) return 0; // 此时没有方案
|
||||
if ((target + sum) % 2 == 1) return 0; // 此时没有方案
|
||||
```
|
||||
|
||||
同时如果 S的绝对值已经大于sum,那么也是没有方案的。
|
||||
同时如果target 的绝对值已经大于sum,那么也是没有方案的。
|
||||
|
||||
```CPP
|
||||
(C++代码中,输入的S 就是题目描述的 target)
|
||||
if (abs(S) > sum) return 0; // 此时没有方案
|
||||
if (abs(target) > sum) return 0; // 此时没有方案
|
||||
```
|
||||
|
||||
再回归到01背包问题,为什么是01背包呢?
|
||||
@ -213,9 +213,9 @@ dp[j]其他下标对应的数值也应该初始化为0,从递推公式也可
|
||||
|
||||
5. 举例推导dp数组
|
||||
|
||||
输入:nums: [1, 1, 1, 1, 1], S: 3
|
||||
输入:nums: [1, 1, 1, 1, 1], target: 3
|
||||
|
||||
bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4
|
||||
bagSize = (target + sum) / 2 = (3 + 5) / 2 = 4
|
||||
|
||||
dp数组状态变化如下:
|
||||
|
||||
@ -226,12 +226,12 @@ C++代码如下:
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
int findTargetSumWays(vector<int>& nums, int S) {
|
||||
int findTargetSumWays(vector<int>& nums, int target) {
|
||||
int sum = 0;
|
||||
for (int i = 0; i < nums.size(); i++) sum += nums[i];
|
||||
if (abs(S) > sum) return 0; // 此时没有方案
|
||||
if ((S + sum) % 2 == 1) return 0; // 此时没有方案
|
||||
int bagSize = (S + sum) / 2;
|
||||
if (abs(target) > sum) return 0; // 此时没有方案
|
||||
if ((target + sum) % 2 == 1) return 0; // 此时没有方案
|
||||
int bagSize = (target + sum) / 2;
|
||||
vector<int> dp(bagSize + 1, 0);
|
||||
dp[0] = 1;
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
@ -585,7 +585,7 @@ impl Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
## C
|
||||
### C
|
||||
|
||||
```c
|
||||
int getSum(int * nums, int numsSize){
|
||||
@ -655,3 +655,52 @@ public class Solution
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
class Solution {
|
||||
public:
|
||||
int findTargetSumWays(vector<int>& nums, int target) {
|
||||
int sum = 0;
|
||||
for (int i = 0; i < nums.size(); i++) sum += nums[i];
|
||||
if (abs(target) > sum) return 0; // 此时没有方案
|
||||
if ((target + sum) % 2 == 1) return 0; // 此时没有方案
|
||||
int bagSize = (target + sum) / 2;
|
||||
|
||||
vector<vector<int>> dp(nums.size(), vector<int>(bagSize + 1, 0));
|
||||
|
||||
if (nums[0] <= bagSize) dp[0][nums[0]] = 1;
|
||||
|
||||
dp[0][0] = 1;
|
||||
|
||||
int numZero = 0;
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
if (nums[i] == 0) numZero++;
|
||||
dp[i][0] = (int) pow(2.0, numZero);
|
||||
}
|
||||
|
||||
for (int i = 1; i < nums.size(); i++) {
|
||||
for (int j = 0; j <= bagSize; j++) {
|
||||
if (nums[i] > j) dp[i][j] = dp[i - 1][j];
|
||||
else dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
|
||||
}
|
||||
}
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
for (int j = 0; j <= bagSize; j++) {
|
||||
cout << dp[i][j] << " ";
|
||||
}
|
||||
cout << endl;
|
||||
}
|
||||
return dp[nums.size() - 1][bagSize];
|
||||
}
|
||||
};
|
||||
|
||||
1 1 0 0 0
|
||||
1 2 1 0 0
|
||||
1 3 3 1 0
|
||||
1 4 6 4 1
|
||||
1 5 10 10 5
|
||||
|
||||
初始化 如果没有0, dp[i][0] = 1; 即所有元素都不取。
|
||||
|
||||
用元素 取与不取来举例
|
||||
|
||||
|
||||
@ -165,6 +165,140 @@ private:
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
### C++双链表法:
|
||||
|
||||
```CPP
|
||||
//采用循环虚拟结点的双链表实现
|
||||
class MyLinkedList {
|
||||
public:
|
||||
// 定义双向链表节点结构体
|
||||
struct DList {
|
||||
int elem; // 节点存储的元素
|
||||
DList *next; // 指向下一个节点的指针
|
||||
DList *prev; // 指向上一个节点的指针
|
||||
// 构造函数,创建一个值为elem的新节点
|
||||
DList(int elem) : elem(elem), next(nullptr), prev(nullptr) {};
|
||||
};
|
||||
|
||||
// 构造函数,初始化链表
|
||||
MyLinkedList() {
|
||||
sentinelNode = new DList(0); // 创建哨兵节点,不存储有效数据
|
||||
sentinelNode->next = sentinelNode; // 哨兵节点的下一个节点指向自身,形成循环
|
||||
sentinelNode->prev = sentinelNode; // 哨兵节点的上一个节点指向自身,形成循环
|
||||
size = 0; // 初始化链表大小为0
|
||||
}
|
||||
|
||||
// 获取链表中第index个节点的值
|
||||
int get(int index) {
|
||||
if (index > (size - 1) || index < 0) { // 检查索引是否超出范围
|
||||
return -1; // 如果超出范围,返回-1
|
||||
}
|
||||
int num;
|
||||
int mid = size >> 1; // 计算链表中部位置
|
||||
DList *curNode = sentinelNode; // 从哨兵节点开始
|
||||
if (index < mid) { // 如果索引小于中部位置,从前往后遍历
|
||||
for (int i = 0; i < index + 1; i++) {
|
||||
curNode = curNode->next; // 移动到目标节点
|
||||
}
|
||||
} else { // 如果索引大于等于中部位置,从后往前遍历
|
||||
for (int i = 0; i < size - index; i++) {
|
||||
curNode = curNode->prev; // 移动到目标节点
|
||||
}
|
||||
}
|
||||
num = curNode->elem; // 获取目标节点的值
|
||||
return num; // 返回节点的值
|
||||
}
|
||||
|
||||
// 在链表头部添加节点
|
||||
void addAtHead(int val) {
|
||||
DList *newNode = new DList(val); // 创建新节点
|
||||
DList *next = sentinelNode->next; // 获取当前头节点的下一个节点
|
||||
newNode->prev = sentinelNode; // 新节点的上一个节点指向哨兵节点
|
||||
newNode->next = next; // 新节点的下一个节点指向原来的头节点
|
||||
size++; // 链表大小加1
|
||||
sentinelNode->next = newNode; // 哨兵节点的下一个节点指向新节点
|
||||
next->prev = newNode; // 原来的头节点的上一个节点指向新节点
|
||||
}
|
||||
|
||||
// 在链表尾部添加节点
|
||||
void addAtTail(int val) {
|
||||
DList *newNode = new DList(val); // 创建新节点
|
||||
DList *prev = sentinelNode->prev; // 获取当前尾节点的上一个节点
|
||||
newNode->next = sentinelNode; // 新节点的下一个节点指向哨兵节点
|
||||
newNode->prev = prev; // 新节点的上一个节点指向原来的尾节点
|
||||
size++; // 链表大小加1
|
||||
sentinelNode->prev = newNode; // 哨兵节点的上一个节点指向新节点
|
||||
prev->next = newNode; // 原来的尾节点的下一个节点指向新节点
|
||||
}
|
||||
|
||||
// 在链表中的第index个节点之前添加值为val的节点
|
||||
void addAtIndex(int index, int val) {
|
||||
if (index > size) { // 检查索引是否超出范围
|
||||
return; // 如果超出范围,直接返回
|
||||
}
|
||||
if (index <= 0) { // 如果索引为0或负数,在头部添加节点
|
||||
addAtHead(val);
|
||||
return;
|
||||
}
|
||||
int num;
|
||||
int mid = size >> 1; // 计算链表中部位置
|
||||
DList *curNode = sentinelNode; // 从哨兵节点开始
|
||||
if (index < mid) { // 如果索引小于中部位置,从前往后遍历
|
||||
for (int i = 0; i < index; i++) {
|
||||
curNode = curNode->next; // 移动到目标位置的前一个节点
|
||||
}
|
||||
DList *temp = curNode->next; // 获取目标位置的节点
|
||||
DList *newNode = new DList(val); // 创建新节点
|
||||
curNode->next = newNode; // 在目标位置前添加新节点
|
||||
temp->prev = newNode; // 目标位置的节点的前一个节点指向新节点
|
||||
newNode->next = temp; // 新节点的下一个节点指向目标位置的结点
|
||||
newNode->prev = curNode; // 新节点的上一个节点指向当前节点
|
||||
} else { // 如果索引大于等于中部位置,从后往前遍历
|
||||
for (int i = 0; i < size - index; i++) {
|
||||
curNode = curNode->prev; // 移动到目标位置的后一个节点
|
||||
}
|
||||
DList *temp = curNode->prev; // 获取目标位置的节点
|
||||
DList *newNode = new DList(val); // 创建新节点
|
||||
curNode->prev = newNode; // 在目标位置后添加新节点
|
||||
temp->next = newNode; // 目标位置的节点的下一个节点指向新节点
|
||||
newNode->prev = temp; // 新节点的上一个节点指向目标位置的节点
|
||||
newNode->next = curNode; // 新节点的下一个节点指向当前节点
|
||||
}
|
||||
size++; // 链表大小加1
|
||||
}
|
||||
|
||||
// 删除链表中的第index个节点
|
||||
void deleteAtIndex(int index) {
|
||||
if (index > (size - 1) || index < 0) { // 检查索引是否超出范围
|
||||
return; // 如果超出范围,直接返回
|
||||
}
|
||||
int num;
|
||||
int mid = size >> 1; // 计算链表中部位置
|
||||
DList *curNode = sentinelNode; // 从哨兵节点开始
|
||||
if (index < mid) { // 如果索引小于中部位置,从前往后遍历
|
||||
for (int i = 0; i < index; i++) {
|
||||
curNode = curNode->next; // 移动到目标位置的前一个节点
|
||||
}
|
||||
DList *next = curNode->next->next; // 获取目标位置的下一个节点
|
||||
curNode->next = next; // 删除目标位置的节点
|
||||
next->prev = curNode; // 目标位置的下一个节点的前一个节点指向当前节点
|
||||
} else { // 如果索引大于等于中部位置,从后往前遍历
|
||||
for (int i = 0; i < size - index - 1; i++) {
|
||||
curNode = curNode->prev; // 移动到目标位置的后一个节点
|
||||
}
|
||||
DList *prev = curNode->prev->prev; // 获取目标位置的下一个节点
|
||||
curNode->prev = prev; // 删除目标位置的节点
|
||||
prev->next = curNode; // 目标位置的下一个节点的下一个节点指向当前节点
|
||||
}
|
||||
size--; // 链表大小减1
|
||||
}
|
||||
|
||||
private:
|
||||
int size; // 链表的大小
|
||||
DList *sentinelNode; // 哨兵节点的指针
|
||||
};
|
||||
```
|
||||
|
||||
### C:
|
||||
|
||||
```C
|
||||
|
||||
@ -100,6 +100,18 @@ public:
|
||||
## 其他语言版本
|
||||
|
||||
### Java:
|
||||
排序法
|
||||
```Java
|
||||
class Solution {
|
||||
public int[] sortedSquares(int[] nums) {
|
||||
for (int i = 0; i < nums.length; i++) {
|
||||
nums[i] = nums[i] * nums[i];
|
||||
}
|
||||
Arrays.sort(nums);
|
||||
return nums;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```Java
|
||||
class Solution {
|
||||
|
||||
@ -128,6 +128,36 @@ class Solution {
|
||||
|
||||
}
|
||||
}
|
||||
|
||||
// 版本二:排序数组并贪心地尽可能将负数翻转为正数,再根据剩余的k值调整最小元素的符号,从而最大化数组的总和。
|
||||
class Solution {
|
||||
public int largestSumAfterKNegations(int[] nums, int k) {
|
||||
if (nums.length == 1) return nums[0];
|
||||
|
||||
// 排序:先把负数处理了
|
||||
Arrays.sort(nums);
|
||||
|
||||
for (int i = 0; i < nums.length && k > 0; i++) { // 贪心点, 通过负转正, 消耗尽可能多的k
|
||||
if (nums[i] < 0) {
|
||||
nums[i] = -nums[i];
|
||||
k--;
|
||||
}
|
||||
}
|
||||
|
||||
// 退出循环, k > 0 || k < 0 (k消耗完了不用讨论)
|
||||
if (k % 2 == 1) { // k > 0 && k is odd:对于负数:负-正-负-正
|
||||
Arrays.sort(nums); // 再次排序得到剩余的负数,或者最小的正数
|
||||
nums[0] = -nums[0];
|
||||
}
|
||||
// k > 0 && k is even,flip数字不会产生影响: 对于负数: 负-正-负;对于正数:正-负-正
|
||||
|
||||
int sum = 0;
|
||||
for (int num : nums) { // 计算最大和
|
||||
sum += num;
|
||||
}
|
||||
return sum;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
@ -1,6 +1,10 @@
|
||||
|
||||
# 44. 开发商购买土地
|
||||
|
||||
> 本题为代码随想录后续扩充题目,还没有视频讲解,顺便让大家练习一下ACM输入输出模式(笔试面试必备)
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1044)
|
||||
|
||||
【题目描述】
|
||||
|
||||
在一个城市区域内,被划分成了n * m个连续的区块,每个区块都拥有不同的权值,代表着其土地价值。目前,有两家开发公司,A 公司和 B 公司,希望购买这个城市区域的土地。
|
||||
@ -57,7 +61,7 @@
|
||||
|
||||
如果本题要求 任何两个行(或者列)之间的数值总和,大家在[0058.区间和](./0058.区间和.md) 的基础上 应该知道怎么求。
|
||||
|
||||
就是前缀和的思路,先统计好,前n行的和 q[n],如果要求矩阵 a 行到 b行 之间的总和,那么就 q[b] - q[a - 1]就好。
|
||||
就是前缀和的思路,先统计好,前n行的和 q[n],如果要求矩阵 a行 到 b行 之间的总和,那么就 q[b] - q[a - 1]就好。
|
||||
|
||||
至于为什么是 a - 1,大家去看 [0058.区间和](./0058.区间和.md) 的分析,使用 前缀和 要注意 区间左右边的开闭情况。
|
||||
|
||||
|
||||
@ -38,7 +38,7 @@
|
||||
5 6 2
|
||||
5 7 1
|
||||
6 7 1
|
||||
```
|
||||
```
|
||||
|
||||
输出示例:
|
||||
|
||||
@ -79,7 +79,7 @@ kruscal的思路:
|
||||
|
||||
|
||||
|
||||
--------
|
||||
--------
|
||||
|
||||
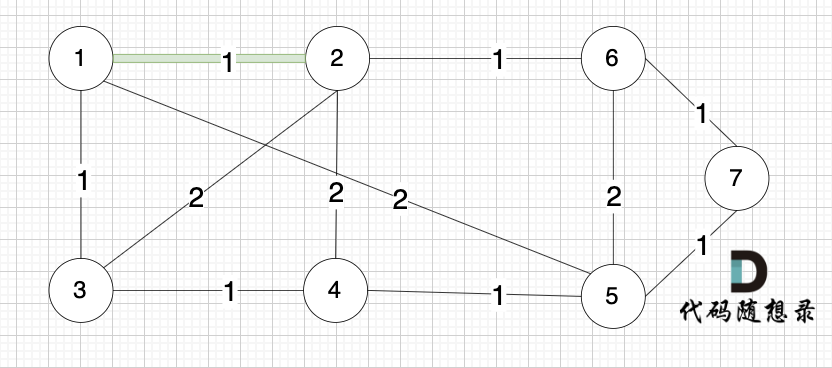
选边(4,5),节点4 和 节点 5 不在同一个集合,生成树可以添加边(4,5) ,并将节点4,节点5 放到同一个集合。
|
||||
|
||||
@ -87,7 +87,7 @@ kruscal的思路:
|
||||
|
||||
**大家判断两个节点是否在同一个集合,就看图中两个节点是否有绿色的粗线连着就行**
|
||||
|
||||
------
|
||||
------
|
||||
|
||||
(这里在强调一下,以下选边是按照上面排序好的边的数组来选择的)
|
||||
|
||||
@ -95,13 +95,13 @@ kruscal的思路:
|
||||
|
||||
|
||||
|
||||
---------
|
||||
---------
|
||||
|
||||
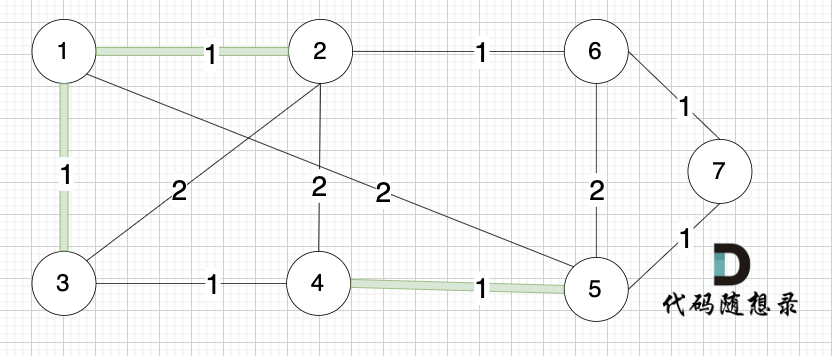
选边(2,6),节点2 和 节点6 不在同一个集合,生成树添加边(2,6),并将节点2,节点6 放到同一个集合。
|
||||
|
||||
|
||||
|
||||
--------
|
||||
--------
|
||||
|
||||
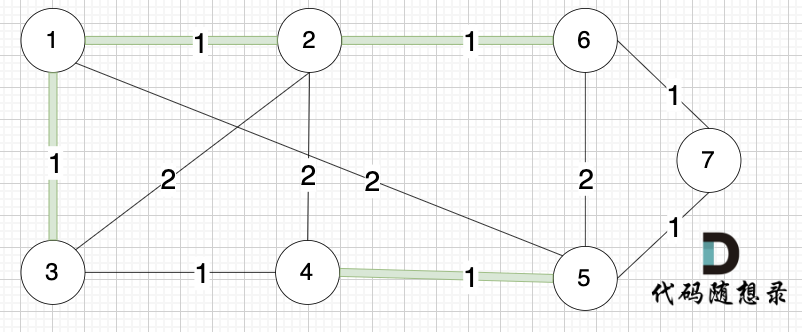
选边(3,4),节点3 和 节点4 不在同一个集合,生成树添加边(3,4),并将节点3,节点4 放到同一个集合。
|
||||
|
||||
@ -113,7 +113,7 @@ kruscal的思路:
|
||||
|
||||
|
||||
|
||||
-----------
|
||||
-----------
|
||||
|
||||
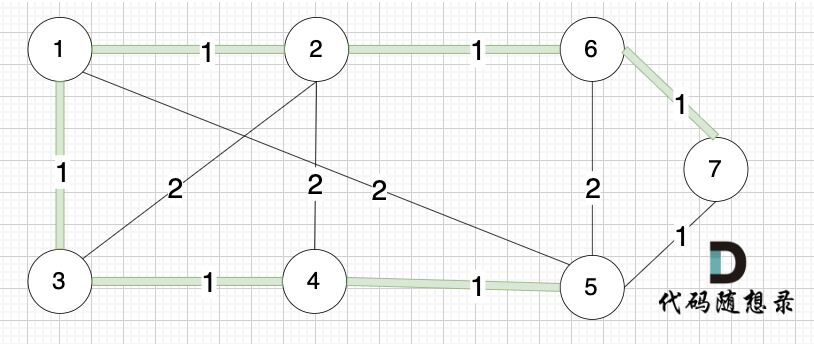
选边(5,7),节点5 和 节点7 在同一个集合,不做计算。
|
||||
|
||||
@ -122,7 +122,7 @@ kruscal的思路:
|
||||
后面遍历 边(3,2),(2,4),(5,6) 同理,都因两个节点已经在同一集合,不做计算。
|
||||
|
||||
|
||||
-------
|
||||
-------
|
||||
|
||||
此时 我们就已经生成了一个最小生成树,即:
|
||||
|
||||
@ -230,7 +230,7 @@ int main() {
|
||||
|
||||
如果题目要求将最小生成树的边输出的话,应该怎么办呢?
|
||||
|
||||
Kruskal 算法 输出边的话,相对prim 要容易很多,因为 Kruskal 本来就是直接操作边,边的结构自然清晰,不用像 prim一样 需要再节点练成线输出边 (因为prim是对节点操作,而 Kruskal是对边操作,这是本质区别)
|
||||
Kruskal 算法 输出边的话,相对prim 要容易很多,因为 Kruskal 本来就是直接操作边,边的结构自然清晰,不用像 prim一样 需要再将节点连成线输出边 (因为prim是对节点操作,而 Kruskal是对边操作,这是本质区别)
|
||||
|
||||
本题中,边的结构为:
|
||||
|
||||
|
||||
@ -1,6 +1,8 @@
|
||||
|
||||
# 58. 区间和
|
||||
|
||||
> 本题为代码随想录后续扩充题目,还没有视频讲解,顺便让大家练习一下ACM输入输出模式(笔试面试必备)
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1070)
|
||||
|
||||
题目描述
|
||||
@ -97,11 +99,11 @@ int main() {
|
||||
|
||||
为什么呢?
|
||||
|
||||
p[1] = vec[0] + vec[1];
|
||||
`p[1] = vec[0] + vec[1];`
|
||||
|
||||
p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];
|
||||
`p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];`
|
||||
|
||||
p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];
|
||||
`p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];`
|
||||
|
||||
这不就是我们要求的 下标 2 到下标 5 之间的累加和吗。
|
||||
|
||||
@ -109,15 +111,17 @@ p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];
|
||||
|
||||

|
||||
|
||||
p[5] - p[1] 就是 红色部分的区间和。
|
||||
`p[5] - p[1]` 就是 红色部分的区间和。
|
||||
|
||||
而 p 数组是我们之前就计算好的累加和,所以后面每次求区间和的之后 我们只需要 O(1)的操作。
|
||||
而 p 数组是我们之前就计算好的累加和,所以后面每次求区间和的之后 我们只需要 O(1) 的操作。
|
||||
|
||||
**特别注意**: 在使用前缀和求解的时候,要特别注意 求解区间。
|
||||
|
||||
如上图,如果我们要求 区间下标 [2, 5] 的区间和,那么应该是 p[5] - p[1],而不是 p[5] - p[2]。
|
||||
|
||||
很多录友在使用前缀和的时候,分不清前缀和的区间,建议画一画图,模拟一下 思路会更清晰。
|
||||
**很多录友在使用前缀和的时候,分不清前缀和的区间,建议画一画图,模拟一下 思路会更清晰**。
|
||||
|
||||
本题C++代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
|
||||
@ -64,7 +64,7 @@
|
||||
|
||||
|
||||
|
||||
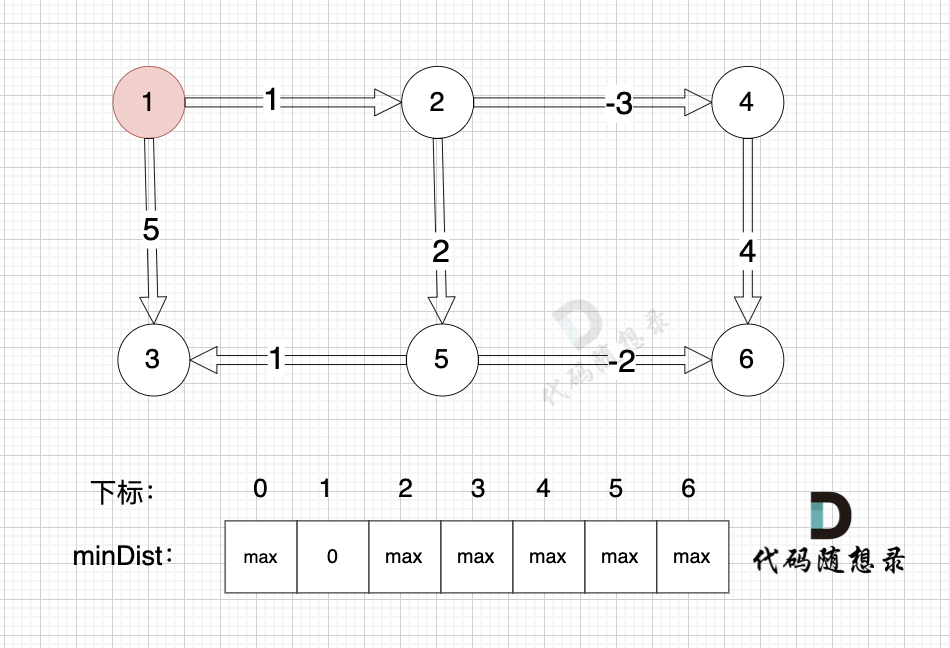
本图中,对所有边进行松弛,真正有效的松弛,只有松弛 边(节点1->节点2) 和 边(节点1->节点5) 。
|
||||
本图中,对所有边进行松弛,真正有效的松弛,只有松弛 边(节点1->节点2) 和 边(节点1->节点3) 。
|
||||
|
||||
而松弛 边(节点4->节点6) ,边(节点5->节点3)等等 都是无效的操作,因为 节点4 和 节点 5 都是没有被计算过的节点。
|
||||
|
||||
@ -158,16 +158,11 @@
|
||||
|
||||
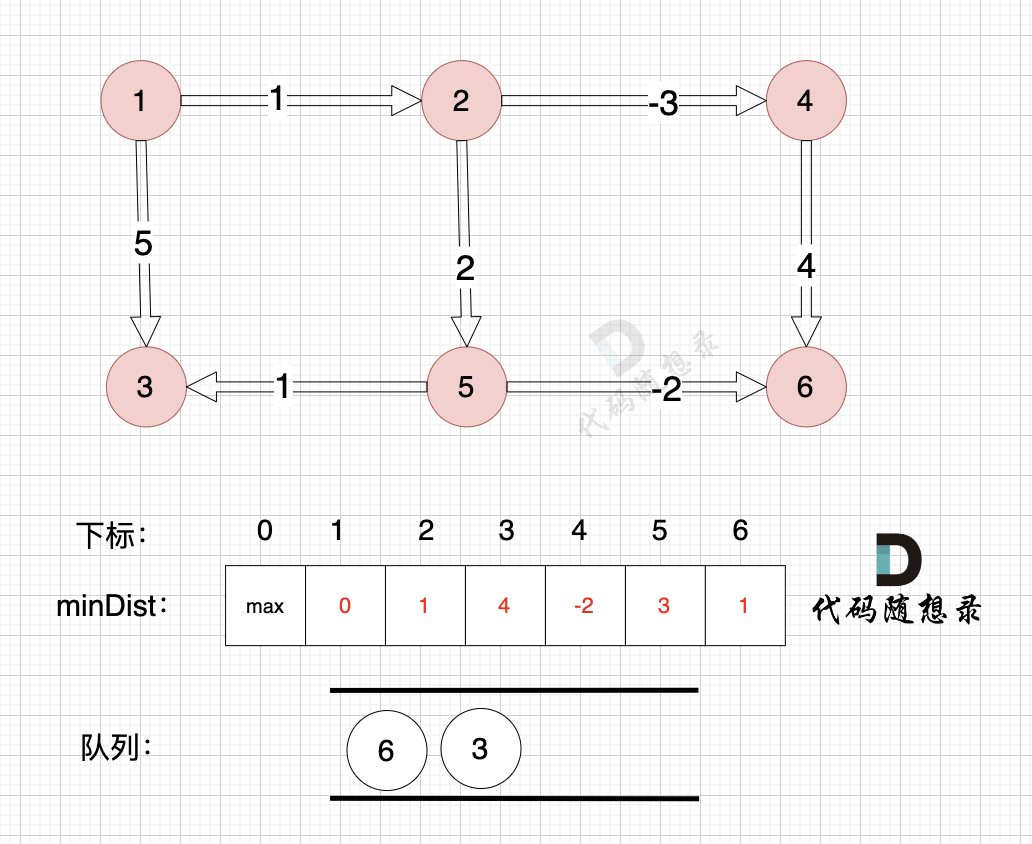
边:节点5 -> 节点6,权值为-2 ,minDist[6] > minDist[5] + (-2) ,更新 minDist[6] = minDist[5] + (-2) = 3 - 2 = 1
|
||||
|
||||
如图:
|
||||
如图,将节点3加入队列,因为节点6已经在队列里,所以不用重复添加
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
因为节点3 和 节点6 都曾经加入过队列,不用重复加入,避免重复计算。
|
||||
|
||||
在代码中我们可以用一个数组 visited 来记录入过队列的元素,加入过队列的元素,不再重复入队列。
|
||||
|
||||
|
||||
所以我们在加入队列的过程可以有一个优化,**用visited数组记录已经在队列里的元素,已经在队列的元素不用重复加入**
|
||||
|
||||
--------------
|
||||
|
||||
@ -175,11 +170,12 @@
|
||||
|
||||
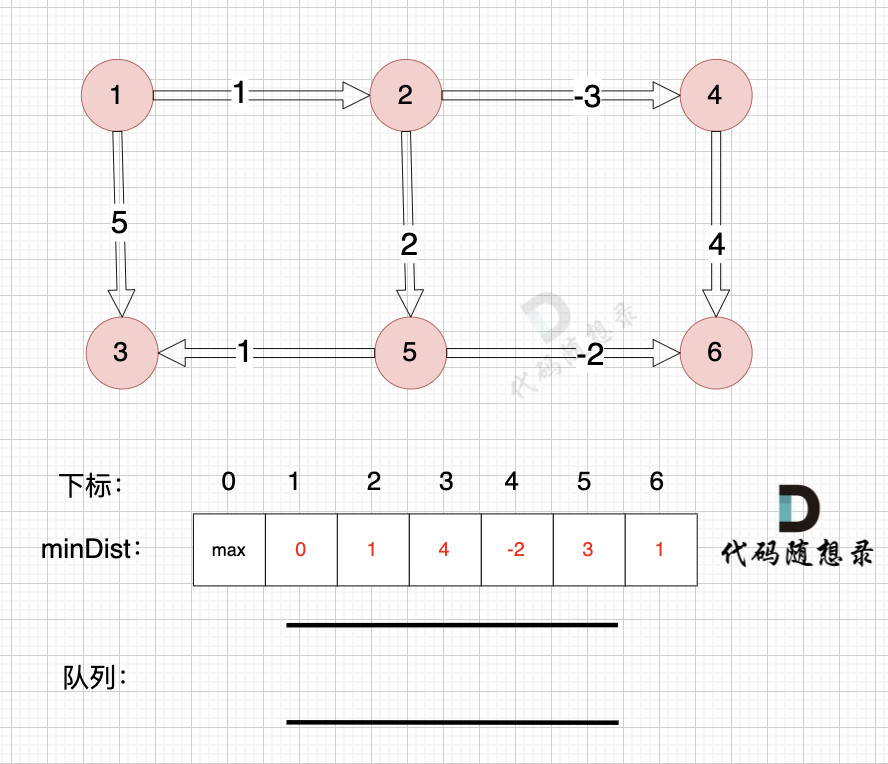
节点6作为终点,没有可以出发的边。
|
||||
|
||||
同理从队列中取出节点3,也没有可以出发的边
|
||||
|
||||
所以直接从队列中取出,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
----------
|
||||
|
||||
这样我们就完成了基于队列优化的bellman_ford的算法模拟过程。
|
||||
@ -190,12 +186,12 @@
|
||||
|
||||
在上面模拟过程中,我们每次都要知道 一个节点作为出发点连接了哪些节点。
|
||||
|
||||
如果想方便知道这些数据,就需要使用邻接表来存储这个图,如果对于邻接表不了解的话,可以看 [kama0047.参会dijkstra堆](./kama0047.参会dijkstra堆.md) 中 图的存储 部分。
|
||||
如果想方便知道这些数据,就需要使用邻接表来存储这个图,如果对于邻接表不了解的话,可以看 [kama0047.参会dijkstra堆](./0047.参会dijkstra堆.md) 中 图的存储 部分。
|
||||
|
||||
|
||||
整体代码如下:
|
||||
|
||||
```CPP
|
||||
```
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <queue>
|
||||
@ -215,7 +211,9 @@ int main() {
|
||||
int n, m, p1, p2, val;
|
||||
cin >> n >> m;
|
||||
|
||||
vector<list<Edge>> grid(n + 1); // 邻接表
|
||||
vector<list<Edge>> grid(n + 1);
|
||||
|
||||
vector<bool> isInQueue(n + 1); // 加入优化,已经在队里里的元素不用重复添加
|
||||
|
||||
// 将所有边保存起来
|
||||
for(int i = 0; i < m; i++){
|
||||
@ -230,24 +228,26 @@ int main() {
|
||||
minDist[start] = 0;
|
||||
|
||||
queue<int> que;
|
||||
que.push(start); // 队列里放入起点
|
||||
que.push(start);
|
||||
|
||||
while (!que.empty()) {
|
||||
|
||||
int node = que.front(); que.pop();
|
||||
|
||||
isInQueue[node] = false; // 从队列里取出的时候,要取消标记,我们只保证已经在队列里的元素不用重复加入
|
||||
for (Edge edge : grid[node]) {
|
||||
int from = node;
|
||||
int to = edge.to;
|
||||
int value = edge.val;
|
||||
if (minDist[to] > minDist[from] + value) { // 开始松弛
|
||||
minDist[to] = minDist[from] + value;
|
||||
que.push(to);
|
||||
minDist[to] = minDist[from] + value;
|
||||
if (isInQueue[to] == false) { // 已经在队列里的元素不用重复添加
|
||||
que.push(to);
|
||||
isInQueue[to] = true;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
|
||||
else cout << minDist[end] << endl; // 到达终点最短路径
|
||||
}
|
||||
|
||||
@ -422,7 +422,8 @@ int main() {
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
#### 邻接矩阵写法
|
||||
|
||||
邻接矩阵写法
|
||||
```java
|
||||
import java.util.ArrayList;
|
||||
import java.util.List;
|
||||
@ -477,7 +478,7 @@ public class Main {
|
||||
}
|
||||
```
|
||||
|
||||
#### 邻接表写法
|
||||
邻接表写法
|
||||
```java
|
||||
import java.util.ArrayList;
|
||||
import java.util.LinkedList;
|
||||
@ -533,7 +534,7 @@ public class Main {
|
||||
}
|
||||
```
|
||||
### Python
|
||||
#### 邻接矩阵写法
|
||||
邻接矩阵写法
|
||||
``` python
|
||||
def dfs(graph, x, n, path, result):
|
||||
if x == n:
|
||||
@ -566,7 +567,7 @@ if __name__ == "__main__":
|
||||
main()
|
||||
```
|
||||
|
||||
#### 邻接表写法
|
||||
邻接表写法
|
||||
``` python
|
||||
from collections import defaultdict
|
||||
|
||||
@ -604,6 +605,125 @@ if __name__ == "__main__":
|
||||
```
|
||||
### Go
|
||||
|
||||
#### 邻接矩阵写法
|
||||
```go
|
||||
package main
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
)
|
||||
|
||||
var result [][]int // 收集符合条件的路径
|
||||
var path []int // 1节点到终点的路径
|
||||
|
||||
func dfs(graph [][]int, x, n int) {
|
||||
// 当前遍历的节点x 到达节点n
|
||||
if x == n { // 找到符合条件的一条路径
|
||||
temp := make([]int, len(path))
|
||||
copy(temp, path)
|
||||
result = append(result, temp)
|
||||
return
|
||||
}
|
||||
for i := 1; i <= n; i++ { // 遍历节点x链接的所有节点
|
||||
if graph[x][i] == 1 { // 找到 x链接的节点
|
||||
path = append(path, i) // 遍历到的节点加入到路径中来
|
||||
dfs(graph, i, n) // 进入下一层递归
|
||||
path = path[:len(path)-1] // 回溯,撤销本节点
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
func main() {
|
||||
var n, m int
|
||||
fmt.Scanf("%d %d", &n, &m)
|
||||
|
||||
// 节点编号从1到n,所以申请 n+1 这么大的数组
|
||||
graph := make([][]int, n+1)
|
||||
for i := range graph {
|
||||
graph[i] = make([]int, n+1)
|
||||
}
|
||||
|
||||
for i := 0; i < m; i++ {
|
||||
var s, t int
|
||||
fmt.Scanf("%d %d", &s, &t)
|
||||
// 使用邻接矩阵表示无向图,1 表示 s 与 t 是相连的
|
||||
graph[s][t] = 1
|
||||
}
|
||||
|
||||
path = append(path, 1) // 无论什么路径已经是从1节点出发
|
||||
dfs(graph, 1, n) // 开始遍历
|
||||
|
||||
// 输出结果
|
||||
if len(result) == 0 {
|
||||
fmt.Println(-1)
|
||||
} else {
|
||||
for _, pa := range result {
|
||||
for i := 0; i < len(pa)-1; i++ {
|
||||
fmt.Print(pa[i], " ")
|
||||
}
|
||||
fmt.Println(pa[len(pa)-1])
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
#### 邻接表写法
|
||||
```go
|
||||
package main
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
)
|
||||
|
||||
var result [][]int
|
||||
var path []int
|
||||
|
||||
func dfs(graph [][]int, x, n int) {
|
||||
if x == n {
|
||||
temp := make([]int, len(path))
|
||||
copy(temp, path)
|
||||
result = append(result, temp)
|
||||
return
|
||||
}
|
||||
for _, i := range graph[x] {
|
||||
path = append(path, i)
|
||||
dfs(graph, i, n)
|
||||
path = path[:len(path)-1]
|
||||
}
|
||||
}
|
||||
|
||||
func main() {
|
||||
var n, m int
|
||||
fmt.Scanf("%d %d", &n, &m)
|
||||
|
||||
graph := make([][]int, n+1)
|
||||
for i := 0; i <= n; i++ {
|
||||
graph[i] = make([]int, 0)
|
||||
}
|
||||
|
||||
for m > 0 {
|
||||
var s, t int
|
||||
fmt.Scanf("%d %d", &s, &t)
|
||||
graph[s] = append(graph[s], t)
|
||||
m--
|
||||
}
|
||||
|
||||
path = append(path, 1)
|
||||
dfs(graph, 1, n)
|
||||
|
||||
if len(result) == 0 {
|
||||
fmt.Println(-1)
|
||||
} else {
|
||||
for _, pa := range result {
|
||||
for i := 0; i < len(pa)-1; i++ {
|
||||
fmt.Print(pa[i], " ")
|
||||
}
|
||||
fmt.Println(pa[len(pa)-1])
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
@ -322,6 +322,72 @@ print(result)
|
||||
|
||||
### Go
|
||||
|
||||
``` go
|
||||
|
||||
package main
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
)
|
||||
|
||||
var count int
|
||||
var dir = [][]int{{0, 1}, {1, 0}, {-1, 0}, {0, -1}} // 四个方向
|
||||
|
||||
func dfs(grid [][]int, visited [][]bool, x, y int) {
|
||||
for i := 0; i < 4; i++ {
|
||||
nextx := x + dir[i][0]
|
||||
nexty := y + dir[i][1]
|
||||
if nextx < 0 || nextx >= len(grid) || nexty < 0 || nexty >= len(grid[0]) {
|
||||
continue // 越界了,直接跳过
|
||||
}
|
||||
if !visited[nextx][nexty] && grid[nextx][nexty] == 1 { // 没有访问过的 同时 是陆地的
|
||||
visited[nextx][nexty] = true
|
||||
count++
|
||||
dfs(grid, visited, nextx, nexty)
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
func main() {
|
||||
var n, m int
|
||||
fmt.Scan(&n, &m)
|
||||
|
||||
grid := make([][]int, n)
|
||||
for i := 0; i < n; i++ {
|
||||
grid[i] = make([]int, m)
|
||||
for j := 0; j < m; j++ {
|
||||
fmt.Scan(&grid[i][j])
|
||||
}
|
||||
}
|
||||
|
||||
visited := make([][]bool, n)
|
||||
for i := 0; i < n; i++ {
|
||||
visited[i] = make([]bool, m)
|
||||
}
|
||||
|
||||
result := 0
|
||||
for i := 0; i < n; i++ {
|
||||
for j := 0; j < m; j++ {
|
||||
if !visited[i][j] && grid[i][j] == 1 {
|
||||
count = 1 // 因为dfs处理下一个节点,所以这里遇到陆地了就先计数,dfs处理接下来的相邻陆地
|
||||
visited[i][j] = true
|
||||
dfs(grid, visited, i, j)
|
||||
if count > result {
|
||||
result = count
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
fmt.Println(result)
|
||||
}
|
||||
|
||||
|
||||
|
||||
```
|
||||
|
||||
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
@ -420,6 +486,65 @@ const bfs = (graph, visited, x, y) => {
|
||||
|
||||
### PhP
|
||||
|
||||
``` php
|
||||
|
||||
<?php
|
||||
|
||||
function dfs(&$grid, &$visited, $x, $y, &$count, &$dir) {
|
||||
for ($i = 0; $i < 4; $i++) {
|
||||
$nextx = $x + $dir[$i][0];
|
||||
$nexty = $y + $dir[$i][1];
|
||||
if ($nextx < 0 || $nextx >= count($grid) || $nexty < 0 || $nexty >= count($grid[0])) continue; // 越界了,直接跳过
|
||||
if (!$visited[$nextx][$nexty] && $grid[$nextx][$nexty] == 1) { // 没有访问过的 同时 是陆地的
|
||||
$visited[$nextx][$nexty] = true;
|
||||
$count++;
|
||||
dfs($grid, $visited, $nextx, $nexty, $count, $dir);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// Main function
|
||||
function main() {
|
||||
$input = trim(fgets(STDIN));
|
||||
list($n, $m) = explode(' ', $input);
|
||||
|
||||
$grid = [];
|
||||
for ($i = 0; $i < $n; $i++) {
|
||||
$input = trim(fgets(STDIN));
|
||||
$grid[] = array_map('intval', explode(' ', $input));
|
||||
}
|
||||
|
||||
$visited = [];
|
||||
for ($i = 0; $i < $n; $i++) {
|
||||
$visited[] = array_fill(0, $m, false);
|
||||
}
|
||||
|
||||
$result = 0;
|
||||
$count = 0;
|
||||
$dir = [[0, 1], [1, 0], [-1, 0], [0, -1]]; // 四个方向
|
||||
|
||||
for ($i = 0; $i < $n; $i++) {
|
||||
for ($j = 0; $j < $m; $j++) {
|
||||
if (!$visited[$i][$j] && $grid[$i][$j] == 1) {
|
||||
$count = 1; // 因为dfs处理下一个节点,所以这里遇到陆地了就先计数,dfs处理接下来的相邻陆地
|
||||
$visited[$i][$j] = true;
|
||||
dfs($grid, $visited, $i, $j, $count, $dir); // 将与其链接的陆地都标记上 true
|
||||
$result = max($result, $count);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
echo $result . "\n";
|
||||
}
|
||||
|
||||
main();
|
||||
|
||||
?>
|
||||
|
||||
|
||||
```
|
||||
|
||||
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
|
||||
@ -185,6 +185,77 @@ int main() {
|
||||
|
||||
### Java
|
||||
|
||||
``` java
|
||||
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
private static int count = 0;
|
||||
private static final int[][] dir = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}}; // 四个方向
|
||||
|
||||
private static void bfs(int[][] grid, int x, int y) {
|
||||
Queue<int[]> que = new LinkedList<>();
|
||||
que.add(new int[]{x, y});
|
||||
grid[x][y] = 0; // 只要加入队列,立刻标记
|
||||
count++;
|
||||
while (!que.isEmpty()) {
|
||||
int[] cur = que.poll();
|
||||
int curx = cur[0];
|
||||
int cury = cur[1];
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = curx + dir[i][0];
|
||||
int nexty = cury + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length) continue; // 越界了,直接跳过
|
||||
if (grid[nextx][nexty] == 1) {
|
||||
que.add(new int[]{nextx, nexty});
|
||||
count++;
|
||||
grid[nextx][nexty] = 0; // 只要加入队列立刻标记
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int m = scanner.nextInt();
|
||||
int[][] grid = new int[n][m];
|
||||
|
||||
// 读取网格
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
grid[i][j] = scanner.nextInt();
|
||||
}
|
||||
}
|
||||
|
||||
// 从左侧边,和右侧边向中间遍历
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (grid[i][0] == 1) bfs(grid, i, 0);
|
||||
if (grid[i][m - 1] == 1) bfs(grid, i, m - 1);
|
||||
}
|
||||
|
||||
// 从上边和下边向中间遍历
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[0][j] == 1) bfs(grid, 0, j);
|
||||
if (grid[n - 1][j] == 1) bfs(grid, n - 1, j);
|
||||
}
|
||||
|
||||
count = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == 1) bfs(grid, i, j);
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println(count);
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
|
||||
```
|
||||
|
||||
|
||||
### Python
|
||||
```python
|
||||
from collections import deque
|
||||
@ -238,6 +309,97 @@ print(count)
|
||||
```
|
||||
### Go
|
||||
|
||||
``` go
|
||||
|
||||
package main
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
)
|
||||
|
||||
var count int
|
||||
var dir = [4][2]int{{0, 1}, {1, 0}, {-1, 0}, {0, -1}} // 四个方向
|
||||
|
||||
func bfs(grid [][]int, x, y int) {
|
||||
queue := [][2]int{{x, y}}
|
||||
grid[x][y] = 0 // 只要加入队列,立刻标记
|
||||
count++
|
||||
|
||||
for len(queue) > 0 {
|
||||
cur := queue[0]
|
||||
queue = queue[1:]
|
||||
curx, cury := cur[0], cur[1]
|
||||
|
||||
for i := 0; i < 4; i++ {
|
||||
nextx := curx + dir[i][0]
|
||||
nexty := cury + dir[i][1]
|
||||
|
||||
if nextx < 0 || nextx >= len(grid) || nexty < 0 || nexty >= len(grid[0]) {
|
||||
continue // 越界了,直接跳过
|
||||
}
|
||||
|
||||
if grid[nextx][nexty] == 1 {
|
||||
queue = append(queue, [2]int{nextx, nexty})
|
||||
count++
|
||||
grid[nextx][nexty] = 0 // 只要加入队列立刻标记
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
func main() {
|
||||
var n, m int
|
||||
fmt.Scan(&n, &m)
|
||||
|
||||
grid := make([][]int, n)
|
||||
for i := range grid {
|
||||
grid[i] = make([]int, m)
|
||||
}
|
||||
|
||||
for i := 0; i < n; i++ {
|
||||
for j := 0; j < m; j++ {
|
||||
fmt.Scan(&grid[i][j])
|
||||
}
|
||||
}
|
||||
|
||||
// 从左侧边,和右侧边向中间遍历
|
||||
for i := 0; i < n; i++ {
|
||||
if grid[i][0] == 1 {
|
||||
bfs(grid, i, 0)
|
||||
}
|
||||
if grid[i][m-1] == 1 {
|
||||
bfs(grid, i, m-1)
|
||||
}
|
||||
}
|
||||
|
||||
// 从上边和下边向中间遍历
|
||||
for j := 0; j < m; j++ {
|
||||
if grid[0][j] == 1 {
|
||||
bfs(grid, 0, j)
|
||||
}
|
||||
if grid[n-1][j] == 1 {
|
||||
bfs(grid, n-1, j)
|
||||
}
|
||||
}
|
||||
|
||||
// 清空之前的计数
|
||||
count = 0
|
||||
|
||||
// 遍历所有位置
|
||||
for i := 0; i < n; i++ {
|
||||
for j := 0; j < m; j++ {
|
||||
if grid[i][j] == 1 {
|
||||
bfs(grid, i, j)
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
fmt.Println(count)
|
||||
}
|
||||
|
||||
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
@ -355,6 +355,62 @@ public class Main {
|
||||
```
|
||||
|
||||
### Python
|
||||
```Python
|
||||
first = set()
|
||||
second = set()
|
||||
directions = [[-1, 0], [0, 1], [1, 0], [0, -1]]
|
||||
|
||||
def dfs(i, j, graph, visited, side):
|
||||
if visited[i][j]:
|
||||
return
|
||||
|
||||
visited[i][j] = True
|
||||
side.add((i, j))
|
||||
|
||||
for x, y in directions:
|
||||
new_x = i + x
|
||||
new_y = j + y
|
||||
if (
|
||||
0 <= new_x < len(graph)
|
||||
and 0 <= new_y < len(graph[0])
|
||||
and int(graph[new_x][new_y]) >= int(graph[i][j])
|
||||
):
|
||||
dfs(new_x, new_y, graph, visited, side)
|
||||
|
||||
def main():
|
||||
global first
|
||||
global second
|
||||
|
||||
N, M = map(int, input().strip().split())
|
||||
graph = []
|
||||
for _ in range(N):
|
||||
row = input().strip().split()
|
||||
graph.append(row)
|
||||
|
||||
# 是否可到达第一边界
|
||||
visited = [[False] * M for _ in range(N)]
|
||||
for i in range(M):
|
||||
dfs(0, i, graph, visited, first)
|
||||
for i in range(N):
|
||||
dfs(i, 0, graph, visited, first)
|
||||
|
||||
# 是否可到达第二边界
|
||||
visited = [[False] * M for _ in range(N)]
|
||||
for i in range(M):
|
||||
dfs(N - 1, i, graph, visited, second)
|
||||
for i in range(N):
|
||||
dfs(i, M - 1, graph, visited, second)
|
||||
|
||||
# 可到达第一边界和第二边界
|
||||
res = first & second
|
||||
|
||||
for x, y in res:
|
||||
print(f"{x} {y}")
|
||||
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
@ -362,6 +418,350 @@ public class Main {
|
||||
|
||||
### Javascript
|
||||
|
||||
#### 深搜
|
||||
|
||||
```javascript
|
||||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||||
// 创建readline接口
|
||||
let iter = r1[Symbol.asyncIterator]();
|
||||
// 创建异步迭代器
|
||||
const readline = async () => (await iter.next()).value;
|
||||
|
||||
let graph // 地图
|
||||
let N, M // 地图大小
|
||||
const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
|
||||
|
||||
|
||||
// 读取输入,初始化地图
|
||||
const initGraph = async () => {
|
||||
let line = await readline();
|
||||
[N, M] = line.split(' ').map(Number);
|
||||
graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
|
||||
|
||||
for (let i = 0; i < N; i++) {
|
||||
line = await readline()
|
||||
line = line.split(' ').map(Number)
|
||||
for (let j = 0; j < M; j++) {
|
||||
graph[i][j] = line[j]
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/**
|
||||
* @description: 从(x,y)开始深度优先遍历地图
|
||||
* @param {*} graph 地图
|
||||
* @param {*} visited 可访问节点
|
||||
* @param {*} x 开始搜索节点的下标
|
||||
* @param {*} y 开始搜索节点的下标
|
||||
* @return {*}
|
||||
*/
|
||||
const dfs = (graph, visited, x, y) => {
|
||||
if (visited[x][y]) return
|
||||
visited[x][y] = true // 标记为可访问
|
||||
|
||||
for (let i = 0; i < 4; i++) {
|
||||
let nextx = x + dir[i][0]
|
||||
let nexty = y + dir[i][1]
|
||||
if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界,跳过
|
||||
if (graph[x][y] < graph[nextx][nexty]) continue //不能流过.跳过
|
||||
dfs(graph, visited, nextx, nexty)
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/**
|
||||
* @description: 判断地图上的(x, y)是否可以到达第一组边界和第二组边界
|
||||
* @param {*} x 坐标
|
||||
* @param {*} y 坐标
|
||||
* @return {*} true可以到达,false不可以到达
|
||||
*/
|
||||
const isResult = (x, y) => {
|
||||
let visited = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||||
|
||||
let isFirst = false //是否可到达第一边界
|
||||
let isSecond = false //是否可到达第二边界
|
||||
|
||||
// 深搜,将(x, y)可到达的所有节点做标记
|
||||
dfs(graph, visited, x, y)
|
||||
|
||||
// 判断能否到第一边界左边
|
||||
for (let i = 0; i < N; i++) {
|
||||
if (visited[i][0]) {
|
||||
isFirst = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
// 判断能否到第一边界上边
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (visited[0][j]) {
|
||||
isFirst = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
// 判断能否到第二边界右边
|
||||
for (let i = 0; i < N; i++) {
|
||||
if (visited[i][M - 1]) {
|
||||
isSecond = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
// 判断能否到第二边界下边
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (visited[N - 1][j]) {
|
||||
isSecond = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
return isFirst && isSecond
|
||||
}
|
||||
|
||||
(async function () {
|
||||
|
||||
// 读取输入,初始化地图
|
||||
await initGraph()
|
||||
|
||||
// 遍历地图,判断是否能到达第一组边界和第二组边界
|
||||
for (let i = 0; i < N; i++) {
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (isResult(i, j)) console.log(i + ' ' + j);
|
||||
}
|
||||
}
|
||||
})()
|
||||
```
|
||||
|
||||
|
||||
|
||||
#### 广搜-解法一
|
||||
|
||||
```java
|
||||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||||
// 创建readline接口
|
||||
let iter = r1[Symbol.asyncIterator]();
|
||||
// 创建异步迭代器
|
||||
const readline = async () => (await iter.next()).value;
|
||||
|
||||
let graph // 地图
|
||||
let N, M // 地图大小
|
||||
const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
|
||||
|
||||
|
||||
// 读取输入,初始化地图
|
||||
const initGraph = async () => {
|
||||
let line = await readline();
|
||||
[N, M] = line.split(' ').map(Number);
|
||||
graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
|
||||
|
||||
for (let i = 0; i < N; i++) {
|
||||
line = await readline()
|
||||
line = line.split(' ').map(Number)
|
||||
for (let j = 0; j < M; j++) {
|
||||
graph[i][j] = line[j]
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/**
|
||||
* @description: 从(x,y)开始广度优先遍历地图
|
||||
* @param {*} graph 地图
|
||||
* @param {*} visited 可访问节点
|
||||
* @param {*} x 开始搜索节点的下标
|
||||
* @param {*} y 开始搜索节点的下标
|
||||
* @return {*}
|
||||
*/
|
||||
const bfs = (graph, visited, x, y) => {
|
||||
let queue = []
|
||||
queue.push([x, y])
|
||||
visited[x][y] = true
|
||||
|
||||
while (queue.length) {
|
||||
const [xx, yy] = queue.shift()
|
||||
for (let i = 0; i < 4; i++) {
|
||||
let nextx = xx + dir[i][0]
|
||||
let nexty = yy + dir[i][1]
|
||||
if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界, 跳过
|
||||
|
||||
// 可访问或者不能流过, 跳过 (注意这里是graph[xx][yy] < graph[nextx][nexty], 不是graph[x][y] < graph[nextx][nexty])
|
||||
if (visited[nextx][nexty] || graph[xx][yy] < graph[nextx][nexty]) continue
|
||||
|
||||
queue.push([nextx, nexty])
|
||||
visited[nextx][nexty] = true
|
||||
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/**
|
||||
* @description: 判断地图上的(x, y)是否可以到达第一组边界和第二组边界
|
||||
* @param {*} x 坐标
|
||||
* @param {*} y 坐标
|
||||
* @return {*} true可以到达,false不可以到达
|
||||
*/
|
||||
const isResult = (x, y) => {
|
||||
let visited = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||||
|
||||
let isFirst = false //是否可到达第一边界
|
||||
let isSecond = false //是否可到达第二边界
|
||||
|
||||
// 深搜,将(x, y)可到达的所有节点做标记
|
||||
bfs(graph, visited, x, y)
|
||||
|
||||
// console.log(visited);
|
||||
|
||||
// 判断能否到第一边界左边
|
||||
for (let i = 0; i < N; i++) {
|
||||
if (visited[i][0]) {
|
||||
isFirst = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
// 判断能否到第一边界上边
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (visited[0][j]) {
|
||||
isFirst = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
// 判断能否到第二边界右边
|
||||
for (let i = 0; i < N; i++) {
|
||||
if (visited[i][M - 1]) {
|
||||
isSecond = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
// 判断能否到第二边界下边
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (visited[N - 1][j]) {
|
||||
isSecond = true
|
||||
break
|
||||
}
|
||||
}
|
||||
|
||||
return isFirst && isSecond
|
||||
}
|
||||
|
||||
(async function () {
|
||||
|
||||
// 读取输入,初始化地图
|
||||
await initGraph()
|
||||
|
||||
// 遍历地图,判断是否能到达第一组边界和第二组边界
|
||||
for (let i = 0; i < N; i++) {
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (isResult(i, j)) console.log(i + ' ' + j);
|
||||
}
|
||||
}
|
||||
})()
|
||||
```
|
||||
|
||||
|
||||
|
||||
#### 广搜-解法二
|
||||
|
||||
从第一边界和第二边界开始向高处流, 标记可以流到的位置, 两个边界都能到达的位置就是所求结果
|
||||
|
||||
```javascript
|
||||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||||
// 创建readline接口
|
||||
let iter = r1[Symbol.asyncIterator]();
|
||||
// 创建异步迭代器
|
||||
const readline = async () => (await iter.next()).value;
|
||||
|
||||
let graph // 地图
|
||||
let N, M // 地图大小
|
||||
const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
|
||||
|
||||
|
||||
// 读取输入,初始化地图
|
||||
const initGraph = async () => {
|
||||
let line = await readline();
|
||||
[N, M] = line.split(' ').map(Number);
|
||||
graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
|
||||
|
||||
for (let i = 0; i < N; i++) {
|
||||
line = await readline()
|
||||
line = line.split(' ').map(Number)
|
||||
for (let j = 0; j < M; j++) {
|
||||
graph[i][j] = line[j]
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/**
|
||||
* @description: 从(x,y)开始广度优先遍历地图
|
||||
* @param {*} graph 地图
|
||||
* @param {*} visited 可访问节点
|
||||
* @param {*} x 开始搜索节点的下标
|
||||
* @param {*} y 开始搜索节点的下标
|
||||
* @return {*}
|
||||
*/
|
||||
const bfs = (graph, visited, x, y) => {
|
||||
if(visited[x][y]) return
|
||||
|
||||
let queue = []
|
||||
queue.push([x, y])
|
||||
visited[x][y] = true
|
||||
|
||||
while (queue.length) {
|
||||
const [xx, yy] = queue.shift()
|
||||
for (let i = 0; i < 4; i++) {
|
||||
let nextx = xx + dir[i][0]
|
||||
let nexty = yy + dir[i][1]
|
||||
if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界, 跳过
|
||||
|
||||
// 可访问或者不能流过, 跳过 (注意因为是从边界往高处流, 所以这里是graph[xx][yy] >= graph[nextx][nexty], 还要注意不是graph[xx][yy] >= graph[nextx][nexty])
|
||||
if (visited[nextx][nexty] || graph[xx][yy] >= graph[nextx][nexty]) continue
|
||||
|
||||
queue.push([nextx, nexty])
|
||||
visited[nextx][nexty] = true
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
(async function () {
|
||||
|
||||
// 读取输入,初始化地图
|
||||
await initGraph()
|
||||
|
||||
// 记录第一边界可到达的节点
|
||||
let firstBorder = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||||
|
||||
// 记录第二边界可到达的节点
|
||||
let secondBorder = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||||
|
||||
// 第一边界左边和第二边界右边
|
||||
for (let i = 0; i < N; i++) {
|
||||
bfs(graph, firstBorder, i, 0)
|
||||
bfs(graph, secondBorder, i, M - 1)
|
||||
}
|
||||
|
||||
// 第一边界上边和第二边界下边
|
||||
for (let j = 0; j < M; j++) {
|
||||
bfs(graph, firstBorder, 0, j)
|
||||
bfs(graph, secondBorder, N - 1, j)
|
||||
}
|
||||
|
||||
// 遍历地图,判断是否能到达第一组边界和第二组边界
|
||||
for (let i = 0; i < N; i++) {
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (firstBorder[i][j] && secondBorder[i][j]) console.log(i + ' ' + j);
|
||||
}
|
||||
}
|
||||
})()
|
||||
```
|
||||
|
||||
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
@ -366,6 +366,79 @@ public class Main {
|
||||
|
||||
### Python
|
||||
|
||||
```Python
|
||||
import collections
|
||||
|
||||
directions = [[-1, 0], [0, 1], [0, -1], [1, 0]]
|
||||
area = 0
|
||||
|
||||
def dfs(i, j, grid, visited, num):
|
||||
global area
|
||||
|
||||
if visited[i][j]:
|
||||
return
|
||||
|
||||
visited[i][j] = True
|
||||
grid[i][j] = num # 标记岛屿号码
|
||||
area += 1
|
||||
|
||||
for x, y in directions:
|
||||
new_x = i + x
|
||||
new_y = j + y
|
||||
if (
|
||||
0 <= new_x < len(grid)
|
||||
and 0 <= new_y < len(grid[0])
|
||||
and grid[new_x][new_y] == "1"
|
||||
):
|
||||
dfs(new_x, new_y, grid, visited, num)
|
||||
|
||||
|
||||
def main():
|
||||
global area
|
||||
|
||||
N, M = map(int, input().strip().split())
|
||||
grid = []
|
||||
for i in range(N):
|
||||
grid.append(input().strip().split())
|
||||
visited = [[False] * M for _ in range(N)]
|
||||
rec = collections.defaultdict(int)
|
||||
|
||||
cnt = 2
|
||||
for i in range(N):
|
||||
for j in range(M):
|
||||
if grid[i][j] == "1":
|
||||
area = 0
|
||||
dfs(i, j, grid, visited, cnt)
|
||||
rec[cnt] = area # 纪录岛屿面积
|
||||
cnt += 1
|
||||
|
||||
res = 0
|
||||
for i in range(N):
|
||||
for j in range(M):
|
||||
if grid[i][j] == "0":
|
||||
max_island = 1 # 将水变为陆地,故从1开始计数
|
||||
v = set()
|
||||
for x, y in directions:
|
||||
new_x = i + x
|
||||
new_y = j + y
|
||||
if (
|
||||
0 <= new_x < len(grid)
|
||||
and 0 <= new_y < len(grid[0])
|
||||
and grid[new_x][new_y] != "0"
|
||||
and grid[new_x][new_y] not in v # 岛屿不可重复
|
||||
):
|
||||
max_island += rec[grid[new_x][new_y]]
|
||||
v.add(grid[new_x][new_y])
|
||||
res = max(res, max_island)
|
||||
|
||||
if res == 0:
|
||||
return max(rec.values()) # 无水的情况
|
||||
return res
|
||||
|
||||
if __name__ == "__main__":
|
||||
print(main())
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
@ -158,7 +158,62 @@ int main() {
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
### Java
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.*;
|
||||
|
||||
public class Main{
|
||||
public static void main(String[] args) {
|
||||
int N, M;
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
N = scanner.nextInt();
|
||||
M = scanner.nextInt();
|
||||
DisJoint disJoint = new DisJoint(N + 1);
|
||||
for (int i = 0; i < M; ++i) {
|
||||
disJoint.join(scanner.nextInt(), scanner.nextInt());
|
||||
}
|
||||
if(disJoint.isSame(scanner.nextInt(), scanner.nextInt())) {
|
||||
System.out.println("1");
|
||||
} else {
|
||||
System.out.println("0");
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
//并查集模板
|
||||
class DisJoint{
|
||||
private int[] father;
|
||||
|
||||
public DisJoint(int N) {
|
||||
father = new int[N];
|
||||
for (int i = 0; i < N; ++i){
|
||||
father[i] = i;
|
||||
}
|
||||
}
|
||||
|
||||
public int find(int n) {
|
||||
return n == father[n] ? n : (father[n] = find(father[n]));
|
||||
}
|
||||
|
||||
public void join (int n, int m) {
|
||||
n = find(n);
|
||||
m = find(m);
|
||||
if (n == m) return;
|
||||
father[m] = n;
|
||||
}
|
||||
|
||||
public boolean isSame(int n, int m){
|
||||
n = find(n);
|
||||
m = find(m);
|
||||
return n == m;
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
|
||||
@ -141,6 +141,70 @@ int main() {
|
||||
|
||||
### Javascript
|
||||
|
||||
```javascript
|
||||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||||
// 创建readline接口
|
||||
let iter = r1[Symbol.asyncIterator]();
|
||||
// 创建异步迭代器
|
||||
const readline = async () => (await iter.next()).value;
|
||||
|
||||
|
||||
let N // 节点数和边数
|
||||
let father = [] // 并查集
|
||||
|
||||
|
||||
// 并查集初始化
|
||||
const init = () => {
|
||||
for (let i = 1; i <= N; i++) father[i] = i;
|
||||
}
|
||||
|
||||
// 并查集里寻根的过程
|
||||
const find = (u) => {
|
||||
return u == father[u] ? u : father[u] = find(father[u])
|
||||
}
|
||||
|
||||
// 将v->u 这条边加入并查集
|
||||
const join = (u, v) => {
|
||||
u = find(u)
|
||||
v = find(v)
|
||||
if (u == v) return // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
|
||||
father[v] = u
|
||||
}
|
||||
|
||||
// 判断 u 和 v是否找到同一个根
|
||||
const isSame = (u, v) => {
|
||||
u = find(u)
|
||||
v = find(v)
|
||||
return u == v
|
||||
}
|
||||
|
||||
|
||||
(async function () {
|
||||
// 读取第一行输入
|
||||
let line = await readline();
|
||||
N = Number(line);
|
||||
|
||||
// 初始化并查集
|
||||
father = new Array(N)
|
||||
init()
|
||||
|
||||
// 读取边信息, 加入并查集
|
||||
for (let i = 0; i < N; i++) {
|
||||
line = await readline()
|
||||
line = line.split(' ').map(Number)
|
||||
|
||||
if (!isSame(line[0], line[1])) {
|
||||
join(line[0], line[1])
|
||||
}else{
|
||||
console.log(line[0], line[1]);
|
||||
break
|
||||
}
|
||||
}
|
||||
})()
|
||||
```
|
||||
|
||||
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
@ -78,7 +78,7 @@
|
||||
|
||||
|
||||
|
||||
对于情况二,删掉构成环的边就可以了。
|
||||
对于情况三,删掉构成环的边就可以了。
|
||||
|
||||
|
||||
## 写代码
|
||||
@ -225,6 +225,7 @@ int main() {
|
||||
vec.push_back(i);
|
||||
}
|
||||
}
|
||||
// 情况一、情况二
|
||||
if (vec.size() > 0) {
|
||||
// 放在vec里的边已经按照倒叙放的,所以这里就优先删vec[0]这条边
|
||||
if (isTreeAfterRemoveEdge(edges, vec[0])) {
|
||||
|
||||
@ -217,6 +217,38 @@ public class Main {
|
||||
```
|
||||
|
||||
### Python
|
||||
```Python
|
||||
def judge(s1,s2):
|
||||
count=0
|
||||
for i in range(len(s1)):
|
||||
if s1[i]!=s2[i]:
|
||||
count+=1
|
||||
return count==1
|
||||
|
||||
if __name__=='__main__':
|
||||
n=int(input())
|
||||
beginstr,endstr=map(str,input().split())
|
||||
if beginstr==endstr:
|
||||
print(0)
|
||||
exit()
|
||||
strlist=[]
|
||||
for i in range(n):
|
||||
strlist.append(input())
|
||||
|
||||
# use bfs
|
||||
visit=[False for i in range(n)]
|
||||
queue=[[beginstr,1]]
|
||||
while queue:
|
||||
str,step=queue.pop(0)
|
||||
if judge(str,endstr):
|
||||
print(step+1)
|
||||
exit()
|
||||
for i in range(n):
|
||||
if visit[i]==False and judge(strlist[i],str):
|
||||
visit[i]=True
|
||||
queue.append([strlist[i],step+1])
|
||||
print(0)
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
|
||||
59
problems/kamacoder/0113.国际象棋.md
Normal file
59
problems/kamacoder/0113.国际象棋.md
Normal file
@ -0,0 +1,59 @@
|
||||
|
||||
# 113.国际象棋
|
||||
|
||||
广搜,但本题如果广搜枚举马和象的话会超时。
|
||||
|
||||
广搜要只枚举马的走位,同时判断是否在对角巷直接走象
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
using namespace std;
|
||||
const int N = 100005, mod = 1000000007;
|
||||
using ll = long long;
|
||||
int n, ans;
|
||||
int dir[][2] = {{1, 2}, {1, -2}, {-1, 2}, {-1, -2}, {2, 1}, {2, -1}, {-2, -1}, {-2, 1}};
|
||||
int main() {
|
||||
int x1, y1, x2, y2;
|
||||
cin >> n;
|
||||
while (n--) {
|
||||
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
|
||||
if (x1 == x2 && y1 == y2) {
|
||||
cout << 0 << endl;
|
||||
continue;
|
||||
}
|
||||
// 判断象走一步到达
|
||||
int d = abs(x1 - x2) - abs(y1 - y2);
|
||||
if (!d) {cout << 1 << endl; continue;}
|
||||
// 判断马走一步到达
|
||||
bool one = 0;
|
||||
for (int i = 0; i < 8; ++i) {
|
||||
int dx = x1 + dir[i][0], dy = y1 + dir[i][1];
|
||||
if (dx == x2 && dy == y2) {
|
||||
cout << 1 << endl;
|
||||
one = true;
|
||||
break;
|
||||
}
|
||||
}
|
||||
if (one) continue;
|
||||
// 接下来为两步的逻辑, 象走两步或者马走一步,象走一步
|
||||
// 象直接两步可以到达,这个计算是不是同颜色的格子,象可以在两步到达所有同颜色的格子
|
||||
int d2 = abs(x1 - x2) + abs(y1 - y2);
|
||||
if (d2 % 2 == 0) {
|
||||
cout << 2 << endl;
|
||||
continue;
|
||||
}
|
||||
// 接下来判断马 + 象的组合
|
||||
bool two = 0;
|
||||
for (int i = 0; i < 8; ++i) {
|
||||
int dx = x1 + dir[i][0], dy = y1 + dir[i][1];
|
||||
int d = abs(dx - x2) - abs(dy - y2);
|
||||
if (!d) {cout << 2 << endl; two = true; break;}
|
||||
}
|
||||
if (two) continue;
|
||||
// 剩下的格子全都是三步到达的
|
||||
cout << 3 << endl;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
@ -193,7 +193,7 @@
|
||||
|
||||
理解思想后,确实不难,但代码写起来也不容易。
|
||||
|
||||
为了每次可以找到所有节点的入度信息,我们要在初始话的时候,就把每个节点的入度 和 每个节点的依赖关系做统计。
|
||||
为了每次可以找到所有节点的入度信息,我们要在初始化的时候,就把每个节点的入度 和 每个节点的依赖关系做统计。
|
||||
|
||||
代码如下:
|
||||
|
||||
@ -451,6 +451,80 @@ if __name__ == "__main__":
|
||||
|
||||
### Javascript
|
||||
|
||||
```javascript
|
||||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||||
// 创建readline接口
|
||||
let iter = r1[Symbol.asyncIterator]();
|
||||
// 创建异步迭代器
|
||||
const readline = async () => (await iter.next()).value;
|
||||
|
||||
|
||||
let N, M // 节点数和边数
|
||||
let inDegrees = [] // 入度
|
||||
let umap = new Map() // 记录文件依赖关系
|
||||
let result = [] // 结果
|
||||
|
||||
|
||||
// 根据输入, 初始化数据
|
||||
const init = async () => {
|
||||
// 读取第一行输入
|
||||
let line = await readline();
|
||||
[N, M] = line.split(' ').map(Number)
|
||||
|
||||
inDegrees = new Array(N).fill(0)
|
||||
|
||||
// 读取边集
|
||||
while (M--) {
|
||||
line = await readline();
|
||||
let [x, y] = line.split(' ').map(Number)
|
||||
|
||||
// 记录入度
|
||||
inDegrees[y]++
|
||||
|
||||
// 记录x指向哪些文件
|
||||
if (!umap.has(x)) {
|
||||
umap.set(x, [y])
|
||||
} else {
|
||||
umap.get(x).push(y)
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
(async function () {
|
||||
// 根据输入, 初始化数据
|
||||
await init()
|
||||
|
||||
let queue = [] // 入度为0的节点
|
||||
for (let i = 0; i < N; i++) {
|
||||
if (inDegrees[i] == 0) {
|
||||
queue.push(i)
|
||||
}
|
||||
}
|
||||
|
||||
while (queue.length) {
|
||||
let cur = queue.shift() //当前文件
|
||||
|
||||
result.push(cur)
|
||||
|
||||
let files = umap.get(cur) // 当前文件指向的文件
|
||||
|
||||
// 当前文件指向的文件入度减1
|
||||
if (files && files.length) {
|
||||
for (let i = 0; i < files.length; i++) {
|
||||
inDegrees[files[i]]--
|
||||
if (inDegrees[files[i]] == 0) queue.push(files[i])
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 这里result.length == N 一定要判断, 因为可能存在环
|
||||
if (result.length == N) return console.log(result.join(' '))
|
||||
console.log(-1)
|
||||
})()
|
||||
```
|
||||
|
||||
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
132
problems/kamacoder/0121.小红的区间翻转.md
Normal file
132
problems/kamacoder/0121.小红的区间翻转.md
Normal file
@ -0,0 +1,132 @@
|
||||
|
||||
# 121. 小红的区间翻转
|
||||
|
||||
比较暴力的方式,就是直接模拟, 枚举所有 区间,然后检查其翻转的情况。
|
||||
|
||||
在检查翻转的时候,需要一些代码优化,否则容易超时。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
|
||||
bool canTransform(const vector<int>& a, const vector<int>& b, int left, int right) {
|
||||
// 提前检查翻转区间的值是否可以匹配
|
||||
for (int i = left, j = right; i <= right; i++, j--) {
|
||||
if (a[i] != b[j]) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
// 检查翻转区间外的值是否匹配
|
||||
for (int i = 0; i < left; i++) {
|
||||
if (a[i] != b[i]) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
for (int i = right + 1; i < a.size(); i++) {
|
||||
if (a[i] != b[i]) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
|
||||
vector<int> a(n);
|
||||
vector<int> b(n);
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> a[i];
|
||||
}
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> b[i];
|
||||
}
|
||||
|
||||
int count = 0;
|
||||
|
||||
// 遍历所有可能的区间
|
||||
for (int left = 0; left < n; left++) {
|
||||
for (int right = left; right < n; right++) {
|
||||
// 检查翻转区间 [left, right] 后,a 是否可以变成 b
|
||||
if (canTransform(a, b, left, right)) {
|
||||
count++;
|
||||
}
|
||||
}
|
||||
}
|
||||
cout << count << endl;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
也可以事先计算好,最长公共前缀,和最长公共后缀。
|
||||
|
||||
在公共前缀和公共后缀之间的部分进行翻转操作,这样我们可以减少很多不必要的翻转尝试。
|
||||
|
||||
通过在公共前缀和后缀之间的部分,找到可以通过翻转使得 a 和 b 相等的区间。
|
||||
|
||||
以下 为评论区 卡码网用户:码鬼的C++代码
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
vector<int> a(n), b(n);
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> a[i];
|
||||
}
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> b[i];
|
||||
}
|
||||
|
||||
vector<int> prefix(n, 0), suffix(n, 0);
|
||||
|
||||
// 计算前缀相等的位置
|
||||
int p = 0;
|
||||
while (p < n && a[p] == b[p]) {
|
||||
prefix[p] = 1;
|
||||
p++;
|
||||
}
|
||||
|
||||
// 计算后缀相等的位置
|
||||
int s = n - 1;
|
||||
while (s >= 0 && a[s] == b[s]) {
|
||||
suffix[s] = 1;
|
||||
s--;
|
||||
}
|
||||
|
||||
int count = 0;
|
||||
|
||||
// 遍历所有可能的区间
|
||||
for (int i = 0; i < n - 1; i++) {
|
||||
for (int j = i + 1; j < n; j++) {
|
||||
// 判断前缀和后缀是否相等
|
||||
if ((i == 0 || prefix[i - 1] == 1) && (j == n - 1 || suffix[j + 1] == 1)) {
|
||||
// 判断翻转后的子数组是否和目标数组相同
|
||||
bool is_palindrome = true;
|
||||
for (int k = 0; k <= (j - i) / 2; k++) {
|
||||
if (a[i + k] != b[j - k]) {
|
||||
is_palindrome = false;
|
||||
break;
|
||||
}
|
||||
}
|
||||
if (is_palindrome) {
|
||||
count++;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
cout << count << endl;
|
||||
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
108
problems/kamacoder/0142.两个字符串的最小ASCII删除总和.md
Normal file
108
problems/kamacoder/0142.两个字符串的最小ASCII删除总和.md
Normal file
@ -0,0 +1,108 @@
|
||||
|
||||
# 142. 两个字符串的最小 ASCII 删除总和
|
||||
|
||||
本题和[代码随想录:两个字符串的删除操作](https://www.programmercarl.com/0583.%E4%B8%A4%E4%B8%AA%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%88%A0%E9%99%A4%E6%93%8D%E4%BD%9C.html) 思路基本是一样的。
|
||||
|
||||
属于编辑距离问题,如果想彻底了解,建议看看「代码随想录」的编辑距离总结篇。
|
||||
|
||||
本题dp数组含义:
|
||||
|
||||
dp[i][j] 表示 以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最小ASCII 删除总和。
|
||||
|
||||
如果 s1[i - 1] 与 s2[j - 1] 相同,则不用删:`dp[i][j] = dp[i - 1][j - 1]`
|
||||
|
||||
如果 s1[i - 1] 与 s2[j - 1] 不相同,删word1 的 最小删除和: `dp[i - 1][j] + s1[i - 1]` ,删word2的最小删除和: `dp[i][j - 1] + s2[j - 1]`
|
||||
|
||||
取最小值: `dp[i][j] = min(dp[i - 1][j] + s1[i - 1], dp[i][j - 1] + s2[j - 1])`
|
||||
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
string s1, s2;
|
||||
cin >> s1 >> s2;
|
||||
vector<vector<int>> dp(s1.size() + 1, vector<int>(s2.size() + 1, 0));
|
||||
|
||||
// s1 如果变成空串的最小删除ASCLL值综合
|
||||
for (int i = 1; i <= s1.size(); i++) dp[i][0] = dp[i - 1][0] + s1[i - 1];
|
||||
// s2 如果变成空串的最小删除ASCLL值综合
|
||||
for (int j = 1; j <= s2.size(); j++) dp[0][j] = dp[0][j - 1] + s2[j - 1];
|
||||
|
||||
for (int i = 1; i <= s1.size(); i++) {
|
||||
for (int j = 1; j <= s2.size(); j++) {
|
||||
if (s1[i - 1] == s2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
|
||||
else dp[i][j] = min(dp[i - 1][j] + s1[i - 1], dp[i][j - 1] + s2[j - 1]);
|
||||
}
|
||||
}
|
||||
cout << dp[s1.size()][s2.size()] << endl;
|
||||
}
|
||||
```
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
String s1 = scanner.nextLine();
|
||||
String s2 = scanner.nextLine();
|
||||
int[][] dp = new int[s1.length() + 1][s2.length() + 1];
|
||||
|
||||
// s1 如果变成空串的最小删除ASCII值综合
|
||||
for (int i = 1; i <= s1.length(); i++) {
|
||||
dp[i][0] = dp[i - 1][0] + s1.charAt(i - 1);
|
||||
}
|
||||
// s2 如果变成空串的最小删除ASCII值综合
|
||||
for (int j = 1; j <= s2.length(); j++) {
|
||||
dp[0][j] = dp[0][j - 1] + s2.charAt(j - 1);
|
||||
}
|
||||
|
||||
for (int i = 1; i <= s1.length(); i++) {
|
||||
for (int j = 1; j <= s2.length(); j++) {
|
||||
if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
|
||||
dp[i][j] = dp[i - 1][j - 1];
|
||||
} else {
|
||||
dp[i][j] = Math.min(dp[i - 1][j] + s1.charAt(i - 1), dp[i][j - 1] + s2.charAt(j - 1));
|
||||
}
|
||||
}
|
||||
}
|
||||
System.out.println(dp[s1.length()][s2.length()]);
|
||||
scanner.close();
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
```
|
||||
|
||||
### python
|
||||
|
||||
```python
|
||||
def min_delete_sum(s1: str, s2: str) -> int:
|
||||
dp = [[0] * (len(s2) + 1) for _ in range(len(s1) + 1)]
|
||||
|
||||
# s1 如果变成空串的最小删除ASCII值综合
|
||||
for i in range(1, len(s1) + 1):
|
||||
dp[i][0] = dp[i - 1][0] + ord(s1[i - 1])
|
||||
# s2 如果变成空串的最小删除ASCII值综合
|
||||
for j in range(1, len(s2) + 1):
|
||||
dp[0][j] = dp[0][j - 1] + ord(s2[j - 1])
|
||||
|
||||
for i in range(1, len(s1) + 1):
|
||||
for j in range(1, len(s2) + 1):
|
||||
if s1[i - 1] == s2[j - 1]:
|
||||
dp[i][j] = dp[i - 1][j - 1]
|
||||
else:
|
||||
dp[i][j] = min(dp[i - 1][j] + ord(s1[i - 1]), dp[i][j - 1] + ord(s2[j - 1]))
|
||||
|
||||
return dp[len(s1)][len(s2)]
|
||||
|
||||
if __name__ == "__main__":
|
||||
s1 = input().strip()
|
||||
s2 = input().strip()
|
||||
print(min_delete_sum(s1, s2))
|
||||
```
|
||||
237
problems/kamacoder/0143.最长同值路径.md
Normal file
237
problems/kamacoder/0143.最长同值路径.md
Normal file
@ -0,0 +1,237 @@
|
||||
|
||||
|
||||
# 143. 最长同值路径
|
||||
|
||||
|
||||
本题两个考点:
|
||||
|
||||
1. 层序遍历构造二叉树
|
||||
2. 树形dp,找出最长路径
|
||||
|
||||
对于写代码不多,或者动手能力比较差的录友,第一个 构造二叉树 基本就被卡主了。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <queue>
|
||||
#include <vector>
|
||||
|
||||
using namespace std;
|
||||
|
||||
// 定义二叉树节点结构
|
||||
struct TreeNode {
|
||||
int val;
|
||||
TreeNode* left;
|
||||
TreeNode* right;
|
||||
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
|
||||
};
|
||||
|
||||
// 根据层序遍历数组构建二叉树
|
||||
TreeNode* constructBinaryTree(const vector<string>& levelOrder) {
|
||||
if (levelOrder.empty()) return NULL;
|
||||
|
||||
TreeNode* root = new TreeNode(stoi(levelOrder[0]));
|
||||
queue<TreeNode*> q;
|
||||
q.push(root);
|
||||
int i = 1;
|
||||
|
||||
while (!q.empty() && i < levelOrder.size()) {
|
||||
TreeNode* current = q.front();
|
||||
q.pop();
|
||||
|
||||
if (i < levelOrder.size() && levelOrder[i] != "null") {
|
||||
current->left = new TreeNode(stoi(levelOrder[i]));
|
||||
q.push(current->left);
|
||||
}
|
||||
i++;
|
||||
|
||||
if (i < levelOrder.size() && levelOrder[i] != "null") {
|
||||
current->right = new TreeNode(stoi(levelOrder[i]));
|
||||
q.push(current->right);
|
||||
}
|
||||
i++;
|
||||
}
|
||||
|
||||
return root;
|
||||
}
|
||||
|
||||
int result = 0;
|
||||
|
||||
// 树形DP
|
||||
int dfs(TreeNode* node) {
|
||||
if (node == NULL) return 0;
|
||||
int leftPath = dfs(node->left);
|
||||
int rightPath = dfs(node->right);
|
||||
|
||||
int leftNum = 0, rightNum = 0;
|
||||
if (node->left != NULL && node->left->val == node->val) {
|
||||
leftNum = leftPath + 1;
|
||||
}
|
||||
if (node->right != NULL && node->right->val == node->val) {
|
||||
rightNum = rightPath + 1;
|
||||
}
|
||||
result = max(result, leftNum + rightNum);
|
||||
return max(leftNum, rightNum);
|
||||
|
||||
}
|
||||
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
vector<string> levelOrder(n);
|
||||
for (int i = 0; i < n ; i++) cin >> levelOrder[i];
|
||||
|
||||
TreeNode* root = constructBinaryTree(levelOrder);
|
||||
dfs(root);
|
||||
cout << result << endl;
|
||||
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
import java.util.*;
|
||||
|
||||
class TreeNode {
|
||||
int val;
|
||||
TreeNode left, right;
|
||||
TreeNode(int x) {
|
||||
val = x;
|
||||
left = null;
|
||||
right = null;
|
||||
}
|
||||
}
|
||||
|
||||
public class Main {
|
||||
public static int result = 0;
|
||||
|
||||
public static TreeNode constructBinaryTree(List<String> levelOrder) {
|
||||
if (levelOrder.isEmpty()) return null;
|
||||
|
||||
TreeNode root = new TreeNode(Integer.parseInt(levelOrder.get(0)));
|
||||
Queue<TreeNode> queue = new LinkedList<>();
|
||||
queue.add(root);
|
||||
int i = 1;
|
||||
|
||||
while (!queue.isEmpty() && i < levelOrder.size()) {
|
||||
TreeNode current = queue.poll();
|
||||
|
||||
if (i < levelOrder.size() && !levelOrder.get(i).equals("null")) {
|
||||
current.left = new TreeNode(Integer.parseInt(levelOrder.get(i)));
|
||||
queue.add(current.left);
|
||||
}
|
||||
i++;
|
||||
|
||||
if (i < levelOrder.size() && !levelOrder.get(i).equals("null")) {
|
||||
current.right = new TreeNode(Integer.parseInt(levelOrder.get(i)));
|
||||
queue.add(current.right);
|
||||
}
|
||||
i++;
|
||||
}
|
||||
|
||||
return root;
|
||||
}
|
||||
|
||||
public static int dfs(TreeNode node) {
|
||||
if (node == null) return 0;
|
||||
int leftPath = dfs(node.left);
|
||||
int rightPath = dfs(node.right);
|
||||
|
||||
int leftNum = 0, rightNum = 0;
|
||||
if (node.left != null && node.left.val == node.val) {
|
||||
leftNum = leftPath + 1;
|
||||
}
|
||||
if (node.right != null && node.right.val == node.val) {
|
||||
rightNum = rightPath + 1;
|
||||
}
|
||||
result = Math.max(result, leftNum + rightNum);
|
||||
return Math.max(leftNum, rightNum);
|
||||
}
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int n = sc.nextInt();
|
||||
sc.nextLine(); // consume the newline character
|
||||
List<String> levelOrder = new ArrayList<>();
|
||||
for (int i = 0; i < n; i++) {
|
||||
levelOrder.add(sc.next());
|
||||
}
|
||||
TreeNode root = constructBinaryTree(levelOrder);
|
||||
dfs(root);
|
||||
System.out.println(result);
|
||||
sc.close();
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
### python
|
||||
|
||||
```python
|
||||
from typing import List, Optional
|
||||
from collections import deque
|
||||
import sys
|
||||
|
||||
class TreeNode:
|
||||
def __init__(self, val: int = 0, left: 'TreeNode' = None, right: 'TreeNode' = None):
|
||||
self.val = val
|
||||
self.left = left
|
||||
self.right = right
|
||||
|
||||
def construct_binary_tree(level_order: List[str]) -> Optional[TreeNode]:
|
||||
if not level_order:
|
||||
return None
|
||||
|
||||
root = TreeNode(int(level_order[0]))
|
||||
queue = deque([root])
|
||||
i = 1
|
||||
|
||||
while queue and i < len(level_order):
|
||||
current = queue.popleft()
|
||||
|
||||
if i < len(level_order) and level_order[i] != "null":
|
||||
current.left = TreeNode(int(level_order[i]))
|
||||
queue.append(current.left)
|
||||
i += 1
|
||||
|
||||
if i < len(level_order) and level_order[i] != "null":
|
||||
current.right = TreeNode(int(level_order[i]))
|
||||
queue.append(current.right)
|
||||
i += 1
|
||||
|
||||
return root
|
||||
|
||||
result = 0
|
||||
|
||||
def dfs(node: Optional[TreeNode]) -> int:
|
||||
global result
|
||||
if node is None:
|
||||
return 0
|
||||
|
||||
left_path = dfs(node.left)
|
||||
right_path = dfs(node.right)
|
||||
|
||||
left_num = right_num = 0
|
||||
if node.left is not None and node.left.val == node.val:
|
||||
left_num = left_path + 1
|
||||
if node.right is not None and node.right.val == node.val:
|
||||
right_num = right_path + 1
|
||||
|
||||
result = max(result, left_num + right_num)
|
||||
return max(left_num, right_num)
|
||||
|
||||
if __name__ == "__main__":
|
||||
input = sys.stdin.read
|
||||
data = input().strip().split()
|
||||
|
||||
n = int(data[0])
|
||||
level_order = data[1:]
|
||||
|
||||
root = construct_binary_tree(level_order)
|
||||
dfs(root)
|
||||
print(result)
|
||||
|
||||
|
||||
```
|
||||
66
problems/kamacoder/0144.字典序最小的01字符串.md
Normal file
66
problems/kamacoder/0144.字典序最小的01字符串.md
Normal file
@ -0,0 +1,66 @@
|
||||
|
||||
# 0144.字典序最小的01字符串
|
||||
|
||||
贪心思路:移动尽可能 移动前面的1 ,这样可以是 字典序最小
|
||||
|
||||
从前到后遍历,遇到 0 ,就用前面的 1 来交换
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <string>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n,k;
|
||||
cin >> n >> k;
|
||||
string s;
|
||||
cin >> s;
|
||||
for(int i = 0; i < n && k > 0; i++) {
|
||||
if(s[i] == '0') {
|
||||
// 开始用前面的 1 来交换
|
||||
int j = i;
|
||||
while(j > 0 && s[j - 1] == '1' && k > 0) {
|
||||
swap(s[j], s[j - 1]);
|
||||
--j;
|
||||
--k;
|
||||
}
|
||||
}
|
||||
}
|
||||
cout << s << endl;
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
Java:
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int k = scanner.nextInt();
|
||||
scanner.nextLine(); // 消耗掉换行符
|
||||
String s = scanner.nextLine();
|
||||
char[] ch = s.toCharArray();
|
||||
|
||||
for (int i = 0; i < n && k > 0; i++) {
|
||||
if (ch[i] == '0') {
|
||||
// 开始用前面的 1 来交换
|
||||
int j = i;
|
||||
while (j > 0 && ch[j - 1] == '1' && k > 0) {
|
||||
char tmp = ch[j];
|
||||
ch[j] = ch[j - 1];
|
||||
ch[j - 1] = tmp;
|
||||
j--;
|
||||
k--;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println(new String(ch));
|
||||
}
|
||||
}
|
||||
```
|
||||
98
problems/kamacoder/0145.数组子序列的排列.md
Normal file
98
problems/kamacoder/0145.数组子序列的排列.md
Normal file
@ -0,0 +1,98 @@
|
||||
|
||||
# 145. 数组子序列的排列
|
||||
|
||||
每个元素出现的次数相乘就可以了。
|
||||
|
||||
注意 “长度为 m 的数组,1 到 m 每个元素都出现过,且恰好出现 1 次。” ,题目中有n个元素,所以我们要统计的就是 1 到 n 元素出现的个数。
|
||||
|
||||
因为如果有一个元素x 大于n了, 那不可能出现 长度为x的数组 且 1 到 x 每个元素都出现过。
|
||||
|
||||
```CPP
|
||||
#include "bits/stdc++.h"
|
||||
using namespace std;
|
||||
int main(){
|
||||
int n;
|
||||
int x;
|
||||
cin >> n;
|
||||
unordered_map<int, int> umap;
|
||||
for(int i = 0; i < n; ++i){
|
||||
cin >> x;
|
||||
if(umap.find(x) != umap.end()) umap[x]++;
|
||||
else umap[x] = 1;
|
||||
}
|
||||
long long res = 0;
|
||||
long long num = 1;
|
||||
for (int i = 1; i <= n; i++) {
|
||||
if (umap.find(i) == umap.end()) break; // 如果i都没出现,后面得数也不能 1 到 m 每个元素都出现过
|
||||
num = (num * umap[i]) % 1000000007;
|
||||
res += num;
|
||||
res %= 1000000007;
|
||||
}
|
||||
cout << res << endl;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.HashMap;
|
||||
import java.util.Map;
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int n = sc.nextInt();
|
||||
Map<Integer, Integer> map = new HashMap<>();
|
||||
for (int i = 0; i < n; i++) {
|
||||
int x = sc.nextInt();
|
||||
map.put(x, map.getOrDefault(x, 0) + 1);
|
||||
}
|
||||
long res = 0;
|
||||
long num = 1;
|
||||
for (int i = 1; i <= n; i++) {
|
||||
if (!map.containsKey(i)) break; // 如果i都没出现,后面得数也不能1到m每个元素都出现过
|
||||
num = (num * map.get(i)) % 1000000007;
|
||||
res += num;
|
||||
res %= 1000000007;
|
||||
}
|
||||
System.out.println(res);
|
||||
sc.close();
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
|
||||
```python
|
||||
def main():
|
||||
import sys
|
||||
input = sys.stdin.read
|
||||
data = input().split()
|
||||
|
||||
n = int(data[0])
|
||||
umap = {}
|
||||
|
||||
for i in range(1, n + 1):
|
||||
x = int(data[i])
|
||||
if x in umap:
|
||||
umap[x] += 1
|
||||
else:
|
||||
umap[x] = 1
|
||||
|
||||
res = 0
|
||||
num = 1
|
||||
MOD = 1000000007
|
||||
|
||||
for i in range(1, n + 1):
|
||||
if i not in umap:
|
||||
break # 如果i都没出现,后面得数也不能1到m每个元素都出现过
|
||||
num = (num * umap[i]) % MOD
|
||||
res = (res + num) % MOD
|
||||
|
||||
print(res)
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
|
||||
```
|
||||
65
problems/kamacoder/0146.传送树.md
Normal file
65
problems/kamacoder/0146.传送树.md
Normal file
@ -0,0 +1,65 @@
|
||||
|
||||
|
||||
|
||||
|
||||
# 146. 传送树
|
||||
|
||||
本题题意是比较绕的,我后面给补上了 【提示信息】对 题目输出样例讲解一下,相对会容易理解的多。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <algorithm>
|
||||
using namespace std;
|
||||
|
||||
vector<vector<int>> edge; // 邻接表来存图
|
||||
vector<int> nxt;
|
||||
int n;
|
||||
|
||||
/*
|
||||
* 递归函数,用于找到每个节点的下一个传送门节点,并记录在nxt数组中。
|
||||
* 遍历当前节点的所有子节点,递归调用findNext以确保子节点的nxt值已经计算出来。
|
||||
* 更新当前节点的nxt值为其子节点中编号最小的节点。
|
||||
* 如果当前节点是叶子节点(即没有子节点),则将其nxt值设置为自身。
|
||||
*/
|
||||
void findNext(int node) {
|
||||
for (int v : edge[node]) {
|
||||
findNext(v);
|
||||
if (nxt[node] == -1 || nxt[node] > min(v, nxt[v])) {
|
||||
nxt[node] = min(v, nxt[v]);
|
||||
}
|
||||
}
|
||||
|
||||
// 叶子节点
|
||||
if (nxt[node] == -1) {
|
||||
nxt[node] = node;
|
||||
}
|
||||
}
|
||||
|
||||
// 计算从节点u出发经过若干次传送门到达叶子节点所需的步数。
|
||||
// 通过不断访问nxt节点,直到到达叶子节点,记录访问的节点数。
|
||||
int get(int u) {
|
||||
int cnt = 1;
|
||||
while (nxt[u] != u) {
|
||||
cnt++;
|
||||
u = nxt[u];
|
||||
}
|
||||
return cnt;
|
||||
}
|
||||
|
||||
int main() {
|
||||
cin >> n;
|
||||
edge.resize(n + 1);
|
||||
nxt.resize(n + 1, -1);
|
||||
for (int i = 1; i <= n; ++i) {
|
||||
int a, b;
|
||||
cin >> a >> b;
|
||||
edge[a].push_back(b);
|
||||
}
|
||||
findNext(1);
|
||||
for (int i = 1; i <= n; ++i) {
|
||||
cout << get(i) << ' ';
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
78
problems/kamacoder/0147.三珠互斥.md
Normal file
78
problems/kamacoder/0147.三珠互斥.md
Normal file
@ -0,0 +1,78 @@
|
||||
|
||||
# 三珠互斥
|
||||
|
||||
1. 如果k * 3 大于 n 了,那说明一定没结果,如果没想明白,大家举个例子试试看
|
||||
2. 分别求出三个红珠子之间的距离
|
||||
3. 对这三段距离从小到大排序 y1, y2, y3
|
||||
4. 如果第一段距离y1 小于k,说明需要交换 k - y 次, 同理 第二段距离y2 小于k,说明需要交换 k - y2 次
|
||||
5. y1 y2 都调整好了,不用计算y3,因为 y3是距离最大
|
||||
|
||||
```CPP
|
||||
#include<bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
int main(){
|
||||
int t;
|
||||
cin >> t;
|
||||
int n, k, a1, a2, a3;
|
||||
vector<int> dis(3);
|
||||
|
||||
while (t--) {
|
||||
cin >> n >> k >> a1 >> a2 >> a3;
|
||||
if(k * 3 > n){
|
||||
cout << -1 << endl;
|
||||
continue;
|
||||
}
|
||||
dis[0] = min(abs(a1 - a2), n - abs(a1 - a2));
|
||||
dis[1] = min(abs(a1 - a3), n - abs(a1 - a3));
|
||||
dis[2] = min(abs(a3 - a2), n - abs(a3 - a2));
|
||||
|
||||
sort(dis.begin(), dis.end());
|
||||
|
||||
int result = 0;
|
||||
if (dis[0] < k) result += (k - dis[0]);
|
||||
if (dis[1] < k) result += (k - dis[1]);
|
||||
|
||||
cout << result << endl;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Java代码:
|
||||
|
||||
```Java
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int t = scanner.nextInt();
|
||||
|
||||
while (t-- > 0) {
|
||||
int n = scanner.nextInt();
|
||||
int k = scanner.nextInt();
|
||||
int a1 = scanner.nextInt();
|
||||
int a2 = scanner.nextInt();
|
||||
int a3 = scanner.nextInt();
|
||||
if (k * 3 > n) {
|
||||
System.out.println(-1);
|
||||
continue;
|
||||
}
|
||||
|
||||
List<Integer> dis = new ArrayList<>(3);
|
||||
dis.add(Math.min(Math.abs(a1 - a2), n - Math.abs(a1 - a2)));
|
||||
dis.add(Math.min(Math.abs(a1 - a3), n - Math.abs(a1 - a3)));
|
||||
dis.add(Math.min(Math.abs(a3 - a2), n - Math.abs(a3 - a2)));
|
||||
|
||||
Collections.sort(dis);
|
||||
|
||||
int result = 0;
|
||||
if (dis.get(0) < k) result += (k - dis.get(0));
|
||||
if (dis.get(1) < k) result += (k - dis.get(1));
|
||||
|
||||
System.out.println(result);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
122
problems/kamacoder/0148.扑克牌同花顺.md
Normal file
122
problems/kamacoder/0148.扑克牌同花顺.md
Normal file
@ -0,0 +1,122 @@
|
||||
|
||||
# 扑克牌同花顺
|
||||
|
||||
首先我们要定义一个结构体,来存放我们的数据
|
||||
|
||||
`map<花色,{同一花色牌集合,同一花色的牌对应的牌数量}>`
|
||||
|
||||
再遍历 每一个花色下,每一个牌 的数量
|
||||
|
||||
代码如下详细注释:
|
||||
|
||||
|
||||
```CPP
|
||||
#include<bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
string cards[] = {"H","S","D","C"};
|
||||
typedef long long ll;
|
||||
struct color
|
||||
{
|
||||
set<int> st; // 同一花色 牌的集合
|
||||
map<int, ll> cnt; // 同一花色 牌对应的数量
|
||||
};
|
||||
unordered_map<string, color> umap;
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
for (int i = 0; i < n; i++) {
|
||||
int x, y;
|
||||
string card;
|
||||
cin >> x >> y >> card;
|
||||
umap[card].st.insert(x);
|
||||
umap[card].cnt[x] += y;
|
||||
}
|
||||
ll sum = 0;
|
||||
// 遍历每一个花色
|
||||
for (string cardOne : cards) {
|
||||
color colorOne = umap[cardOne];
|
||||
// 遍历 同花色 每一个牌
|
||||
for (int number : colorOne.st) {
|
||||
ll numberCount = colorOne.cnt[number]; // 获取牌为number的数量是 numberCount
|
||||
|
||||
// 统计 number 到 number + 4 都是否有牌,用cal 把 number 到number+4 的数量记下来
|
||||
ll cal = numberCount;
|
||||
for (int j = number + 1; j <= number + 4; j++) cal = min(cal, colorOne.cnt[j]);
|
||||
// 统计结果
|
||||
sum += cal;
|
||||
// 把统计过的同花顺数量减下去
|
||||
for (int j = number + 1; j <= number + 4; j++) colorOne.cnt[j] -= cal;
|
||||
}
|
||||
}
|
||||
cout << sum << endl;
|
||||
}
|
||||
```
|
||||
|
||||
Java代码如下:
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
static String[] cards = {"H", "S", "D", "C"}; // 花色数组
|
||||
|
||||
static class Color {
|
||||
Set<Integer> st; // 同一花色牌的集合
|
||||
Map<Integer, Long> cnt; // 同一花色牌对应的数量
|
||||
|
||||
Color() {
|
||||
st = new HashSet<>(); // 初始化集合
|
||||
cnt = new HashMap<>(); // 初始化映射
|
||||
}
|
||||
}
|
||||
|
||||
static Map<String, Color> umap = new HashMap<>(); // 用于存储每种花色对应的Color对象
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt(); // 读取牌的数量
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
int x = scanner.nextInt(); // 读取牌的值
|
||||
int y = scanner.nextInt(); // 读取牌的数量
|
||||
String card = scanner.next(); // 读取牌的花色
|
||||
|
||||
umap.putIfAbsent(card, new Color()); // 如果不存在该花色,则创建一个新的Color对象
|
||||
umap.get(card).st.add(x); // 将牌的值加入集合
|
||||
umap.get(card).cnt.put(x, umap.get(card).cnt.getOrDefault(x, 0L) + y); // 更新牌的数量
|
||||
}
|
||||
|
||||
long sum = 0; // 结果累加器
|
||||
|
||||
// 遍历每一种花色
|
||||
for (String cardOne : cards) {
|
||||
Color colorOne = umap.getOrDefault(cardOne, new Color()); // 获取对应花色的Color对象
|
||||
|
||||
// 遍历同花色的每一张牌
|
||||
for (int number : colorOne.st) {
|
||||
long numberCount = colorOne.cnt.get(number); // 获取当前牌的数量
|
||||
|
||||
// 计算从当前牌到number+4的最小数量
|
||||
long cal = numberCount;
|
||||
for (int j = number + 1; j <= number + 4; j++) {
|
||||
cal = Math.min(cal, colorOne.cnt.getOrDefault(j, 0L)); // 更新cal为最小值
|
||||
}
|
||||
|
||||
// 将结果累加到sum
|
||||
sum += cal;
|
||||
|
||||
// 将统计过的同花顺数量减去
|
||||
for (int j = number + 1; j <= number + 4; j++) {
|
||||
colorOne.cnt.put(j, colorOne.cnt.getOrDefault(j, 0L) - cal);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println(sum); // 输出结果
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
102
problems/kamacoder/0149.好数组.md
Normal file
102
problems/kamacoder/0149.好数组.md
Normal file
@ -0,0 +1,102 @@
|
||||
|
||||
# 149. 好数组
|
||||
|
||||
贪心思路:
|
||||
|
||||
整体思路是移动到中间位置(中位数),一定是 移动次数最小的。
|
||||
|
||||
有一个数可以不改变,对数组排序之后, 最小数 和 最大数 一定是移动次数最多的,所以分别保留最小 和 最大的不变。
|
||||
|
||||
中间可能有两个位置,所以要计算中间偏前 和 中间偏后的
|
||||
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
#include<bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
vector<long> arr(n);
|
||||
for (int i = 0; i < n; ++i) {
|
||||
cin >> arr[i];
|
||||
}
|
||||
sort(arr.begin(), arr.end());
|
||||
|
||||
if (arr[0] == arr[n - 1]) {
|
||||
cout << 1 << endl;
|
||||
return 0;
|
||||
}
|
||||
long cnt = 0L;
|
||||
long cnt1 = 0L;
|
||||
|
||||
// 如果要保留一个不改变,要不不改最小的,要不不改最大的。
|
||||
|
||||
// 取中间偏前的位置
|
||||
long mid = arr[(n - 2) / 2];
|
||||
|
||||
// 不改最大的
|
||||
for (int i = 0; i < n - 1; i++) {
|
||||
cnt += abs(arr[i] - mid);
|
||||
}
|
||||
|
||||
// 取中间偏后的位置
|
||||
mid = arr[n / 2];
|
||||
|
||||
// 不改最小的
|
||||
for (int i = 1; i < n; i++) {
|
||||
cnt1 += abs(arr[i] - mid);
|
||||
}
|
||||
|
||||
cout << min(cnt, cnt1) << endl;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Java代码如下:
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
long[] arr = new long[n];
|
||||
for (int i = 0; i < n; ++i) {
|
||||
arr[i] = scanner.nextLong();
|
||||
}
|
||||
Arrays.sort(arr);
|
||||
|
||||
if (arr[0] == arr[n - 1]) {
|
||||
System.out.println(1);
|
||||
return;
|
||||
}
|
||||
long cnt = 0L;
|
||||
long cnt1 = 0L;
|
||||
|
||||
// 如果要保留一个不改变,要不不改最小的,要不不改最大的。
|
||||
|
||||
// 取中间偏前的位置
|
||||
long mid = arr[(n - 2) / 2];
|
||||
|
||||
// 不改最大的
|
||||
for (int i = 0; i < n - 1; i++) {
|
||||
cnt += Math.abs(arr[i] - mid);
|
||||
}
|
||||
|
||||
// 取中间偏后的位置
|
||||
mid = arr[n / 2];
|
||||
|
||||
// 不改最小的
|
||||
for (int i = 1; i < n; i++) {
|
||||
cnt1 += Math.abs(arr[i] - mid);
|
||||
}
|
||||
|
||||
System.out.println(Math.min(cnt, cnt1));
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
66
problems/kamacoder/0150.极长连续段的权值.md
Normal file
66
problems/kamacoder/0150.极长连续段的权值.md
Normal file
@ -0,0 +1,66 @@
|
||||
|
||||
# 150. 极长连续段的权值
|
||||
|
||||
动态规划,枚举最后边节点的情况:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <string>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
string s;
|
||||
cin >> s;
|
||||
|
||||
long long result = 1;
|
||||
long long a = 1;
|
||||
|
||||
for (int i = 1; i < n; ++i) {
|
||||
// 加上本身长度为1的子串
|
||||
if (s[i] == s[i - 1]) {
|
||||
a += 1;
|
||||
result += a;
|
||||
// 以最右节点为终点,每个子串的级长连续段都+1,再加本身长度为1的子串
|
||||
} else {
|
||||
a = a + i + 1;
|
||||
result += a;
|
||||
}
|
||||
}
|
||||
cout << result << endl;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Java代码如下:
|
||||
|
||||
```Java
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
String s = scanner.next();
|
||||
|
||||
long result = 1;
|
||||
long a = 1;
|
||||
|
||||
for (int i = 1; i < n; ++i) {
|
||||
// 加上本身长度为1的子串
|
||||
if (s.charAt(i) == s.charAt(i - 1)) {
|
||||
a += 1;
|
||||
result += a;
|
||||
// 以最右节点为终点,每个子串的级长连续段都+1,再加本身长度为1的子串
|
||||
} else {
|
||||
a = a + i + 1;
|
||||
result += a;
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println(result);
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
127
problems/kamacoder/0151.手机流畅运行的秘密.md
Normal file
127
problems/kamacoder/0151.手机流畅运行的秘密.md
Normal file
@ -0,0 +1,127 @@
|
||||
# 151. 手机流畅运行的秘密
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1229)
|
||||
|
||||
先运行 能留下电量多的 任务,才能有余电运行其他任务。
|
||||
|
||||
任务1,1:10 ,运行完 能留下 9个电
|
||||
|
||||
任务2,2:12,运行完 能留下 10个电
|
||||
|
||||
任务3,3:10,运行完 能留下 7个电。
|
||||
|
||||
运行顺序: 任务2 -> 任务1 -> 任务3
|
||||
|
||||
按照 最低初始电量 - 耗电量,从大到小排序。
|
||||
|
||||
计算总电量,需要 从小到大 遍历, 不断取 总电量 + 任务耗电量 与 任务最低初始电量 的最大值。
|
||||
|
||||
```CPP
|
||||
#include<bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
bool cmp(const pair<int,int>& taskA, const pair<int,int>& taskB) {
|
||||
return (taskA.second - taskA.first) < (taskB.second - taskB.first);
|
||||
}
|
||||
int main() {
|
||||
string str, tmp;
|
||||
vector<pair<int,int>> tasks;
|
||||
|
||||
//处理输入
|
||||
getline(cin, str);
|
||||
stringstream ss(str);
|
||||
while (getline(ss, tmp, ',')) {
|
||||
int p = tmp.find(":");
|
||||
string a = tmp.substr(0, p);
|
||||
string b = tmp.substr(p + 1);
|
||||
tasks.push_back({stoi(a), stoi(b)});
|
||||
}
|
||||
|
||||
// 按照差值从小到大排序
|
||||
sort(tasks.begin(), tasks.end(), cmp);
|
||||
|
||||
// 收集结果
|
||||
int result = 0;
|
||||
for (int i = 0 ; i < tasks.size(); i++) {
|
||||
result = max(result + tasks[i].first, tasks[i].second);
|
||||
}
|
||||
|
||||
result = result <= 4800 ? result : -1;
|
||||
cout << result << endl;
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
Java版本:
|
||||
|
||||
```Java
|
||||
import java.util.*;
|
||||
import java.util.stream.Collectors;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
String str = sc.nextLine();
|
||||
String[] tasksArray = str.split(",");
|
||||
List<Pair> tasks = Arrays.stream(tasksArray)
|
||||
.map(task -> {
|
||||
String[] parts = task.split(":");
|
||||
return new Pair(Integer.parseInt(parts[0]), Integer.parseInt(parts[1]));
|
||||
})
|
||||
.collect(Collectors.toList());
|
||||
|
||||
// 按照差值从小到大排序
|
||||
Collections.sort(tasks, (taskA, taskB) ->
|
||||
(taskA.second - taskA.first) - (taskB.second - taskB.first)
|
||||
);
|
||||
|
||||
// 收集结果
|
||||
int result = 0;
|
||||
for (Pair task : tasks) {
|
||||
result = Math.max(result + task.first, task.second);
|
||||
}
|
||||
|
||||
result = result <= 4800 ? result : -1;
|
||||
System.out.println(result);
|
||||
}
|
||||
}
|
||||
|
||||
class Pair {
|
||||
int first;
|
||||
int second;
|
||||
|
||||
Pair(int first, int second) {
|
||||
this.first = first;
|
||||
this.second = second;
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
Python版本:
|
||||
|
||||
```python
|
||||
def main():
|
||||
import sys
|
||||
input = sys.stdin.read
|
||||
|
||||
str = input().strip()
|
||||
tasks = []
|
||||
for tmp in str.split(','):
|
||||
a, b = map(int, tmp.split(':'))
|
||||
tasks.append((a, b))
|
||||
|
||||
# 按照差值从小到大排序
|
||||
tasks.sort(key=lambda task: task[1] - task[0])
|
||||
|
||||
# 收集结果
|
||||
result = 0
|
||||
for task in tasks:
|
||||
result = max(result + task[0], task[1])
|
||||
|
||||
result = result if result <= 4800 else -1
|
||||
print(result)
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
```
|
||||
121
problems/kamacoder/0152.小米手机通信校准.md
Normal file
121
problems/kamacoder/0152.小米手机通信校准.md
Normal file
@ -0,0 +1,121 @@
|
||||
|
||||
|
||||
# 152. 小米手机通信校准
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1230)
|
||||
|
||||
一道模拟题,但比较考察 代码能力。
|
||||
|
||||
遍历去找 里 freq 最近的 freg就好, 需要记录刚遍历过的的freg和 loss,因为可能有 相邻一样的 freg。
|
||||
|
||||
```CPP
|
||||
#include <bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int freq;
|
||||
cin >> freq;
|
||||
string data;
|
||||
double result = 0;
|
||||
int last_freg = 0; // 记录上一个 freg
|
||||
int last_loss = 0; // 记录上一个loss
|
||||
while(cin >> data) {
|
||||
int index = data.find(':');
|
||||
int freg = stoi(data.substr(0, index)); // 获取 freg 和 loss
|
||||
int loss = stoi(data.substr(index + 1));
|
||||
// 两遍一样
|
||||
if(abs(freg - freq) == abs(last_freg - freq)) {
|
||||
result = (double)(last_loss + loss)/2.0;
|
||||
} // 否则更新最新的result
|
||||
else if(abs(freg - freq) < abs(last_freg - freq)){
|
||||
result = (double)loss;
|
||||
}
|
||||
last_freg = freg;
|
||||
last_loss = loss;
|
||||
}
|
||||
printf("%.1lf\n", result);
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
Java 版本:
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int freq = sc.nextInt();
|
||||
sc.nextLine(); // 读取换行符
|
||||
|
||||
String inputLine = sc.nextLine(); // 读取包含所有后续输入的行
|
||||
String[] data = inputLine.split(" "); // 根据空格分割输入
|
||||
|
||||
double result = 0;
|
||||
int lastFreq = 0; // 记录上一个 freg
|
||||
int lastLoss = 0; // 记录上一个 loss
|
||||
|
||||
for (String entry : data) {
|
||||
int index = entry.indexOf(':');
|
||||
int freg = Integer.parseInt(entry.substring(0, index)); // 获取 freg 和 loss
|
||||
int loss = Integer.parseInt(entry.substring(index + 1));
|
||||
|
||||
// 两遍一样
|
||||
if (Math.abs(freg - freq) == Math.abs(lastFreq - freq)) {
|
||||
result = (double) (lastLoss + loss) / 2.0;
|
||||
}
|
||||
// 否则更新最新的 result
|
||||
else if (Math.abs(freg - freq) < Math.abs(lastFreq - freq)) {
|
||||
result = (double) loss;
|
||||
}
|
||||
|
||||
lastFreq = freg;
|
||||
lastLoss = loss;
|
||||
}
|
||||
|
||||
System.out.printf("%.1f\n", result);
|
||||
sc.close();
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
Python版本:
|
||||
|
||||
```python
|
||||
def main():
|
||||
import sys
|
||||
input = sys.stdin.read
|
||||
data = input().split()
|
||||
|
||||
freq = int(data[0])
|
||||
result = 0
|
||||
last_freg = 0 # 记录上一个 freg
|
||||
last_loss = 0 # 记录上一个 loss
|
||||
|
||||
for i in range(1, len(data)):
|
||||
item = data[i]
|
||||
index = item.find(':')
|
||||
freg = int(item[:index]) # 获取 freg 和 loss
|
||||
loss = int(item[index + 1:])
|
||||
|
||||
# 两遍一样
|
||||
if abs(freg - freq) == abs(last_freg - freq):
|
||||
result = (last_loss + loss) / 2.0
|
||||
# 否则更新最新的 result
|
||||
elif abs(freg - freq) < abs(last_freg - freq):
|
||||
result = loss
|
||||
|
||||
last_freg = freg
|
||||
last_loss = loss
|
||||
|
||||
print(f"{result:.1f}")
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
|
||||
|
||||
```
|
||||
@ -1,30 +0,0 @@
|
||||
|
||||
|
||||
本题和[代码随想录:两个字符串的删除操作](https://www.programmercarl.com/0583.%E4%B8%A4%E4%B8%AA%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%88%A0%E9%99%A4%E6%93%8D%E4%BD%9C.html) 思路基本是一样的。
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
string s1, s2;
|
||||
cin >> s1 >> s2;
|
||||
vector<vector<int>> dp(s1.size() + 1, vector<int>(s2.size() + 1, 0));
|
||||
|
||||
// s1 如果变成空串的最小删除ASCLL值综合
|
||||
for (int i = 1; i <= s1.size(); i++) dp[i][0] = dp[i - 1][0] + s1[i - 1];
|
||||
// s2 如果变成空串的最小删除ASCLL值综合
|
||||
for (int j = 1; j <= s2.size(); j++) dp[0][j] = dp[0][j - 1] + s2[j - 1];
|
||||
|
||||
for (int i = 1; i <= s1.size(); i++) {
|
||||
for (int j = 1; j <= s2.size(); j++) {
|
||||
if (s1[i - 1] == s2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
|
||||
else dp[i][j] = min(dp[i - 1][j] + s1[i - 1], dp[i][j - 1] + s2[j - 1]);
|
||||
}
|
||||
}
|
||||
cout << dp[s1.size()][s2.size()] << endl;
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
@ -1,109 +0,0 @@
|
||||
|
||||
|
||||
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int n = sc.nextInt();
|
||||
int[] a = new int[n];
|
||||
int[] b = new int[n];
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
a[i] = sc.nextInt();
|
||||
}
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
b[i] = sc.nextInt();
|
||||
}
|
||||
|
||||
int p = -1, s = -1;
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (a[i] == b[i]) p = i;
|
||||
else break;
|
||||
}
|
||||
|
||||
for (int j = n - 1 ; j >= 0 ; j--) {
|
||||
if (a[j] == b[j]) s = j;
|
||||
else break;
|
||||
}
|
||||
|
||||
|
||||
boolean[][] dp = new boolean[n][n];
|
||||
int res = 0;
|
||||
|
||||
for (int j = 0; j < n; j++) {
|
||||
for (int i = j ; i >= 0 ; i--) {
|
||||
if (i == j) dp[i][j] = a[i] == b[i];
|
||||
else if (i + 1 == j) dp[i][j] = (a[i] == b[j] && a[j] == b[i]);
|
||||
else {
|
||||
dp[i][j] = dp[i+1][j-1] && (a[i] == b[j] && a[j] == b[i]);
|
||||
}
|
||||
if (dp[i][j] && (i == 0 || p >= i-1) && (j == n - 1 || j+1 >= s)) res++;
|
||||
}
|
||||
}
|
||||
System.out.println(res);
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int n = sc.nextInt();
|
||||
|
||||
int[] a = new int[n];
|
||||
int[] b = new int[n];
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
a[i] = sc.nextInt();
|
||||
}
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
b[i] = sc.nextInt();
|
||||
}
|
||||
|
||||
int count = 0;
|
||||
|
||||
// 遍历所有可能的区间
|
||||
for (int left = 0; left < n; left++) {
|
||||
for (int right = left; right < n; right++) {
|
||||
// 检查翻转区间 [left, right] 后,a 是否可以变成 b
|
||||
if (canTransform(a, b, left, right)) {
|
||||
count++;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println(count);
|
||||
}
|
||||
|
||||
private static boolean canTransform(int[] a, int[] b, int left, int right) {
|
||||
// 提前检查翻转区间的值是否可以匹配
|
||||
for (int i = left, j = right; i <= right; i++, j--) {
|
||||
if (a[i] != b[j]) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
|
||||
// 检查翻转区间外的值是否匹配
|
||||
for (int i = 0; i < left; i++) {
|
||||
if (a[i] != b[i]) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
|
||||
for (int i = right + 1; i < a.length; i++) {
|
||||
if (a[i] != b[i]) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
|
||||
return true;
|
||||
}
|
||||
}
|
||||
@ -1,81 +0,0 @@
|
||||
|
||||
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <queue>
|
||||
#include <vector>
|
||||
|
||||
using namespace std;
|
||||
|
||||
// 定义二叉树节点结构
|
||||
struct TreeNode {
|
||||
int val;
|
||||
TreeNode* left;
|
||||
TreeNode* right;
|
||||
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
|
||||
};
|
||||
|
||||
// 根据层序遍历数组构建二叉树
|
||||
TreeNode* constructBinaryTree(const vector<string>& levelOrder) {
|
||||
if (levelOrder.empty()) return NULL;
|
||||
|
||||
TreeNode* root = new TreeNode(stoi(levelOrder[0]));
|
||||
queue<TreeNode*> q;
|
||||
q.push(root);
|
||||
int i = 1;
|
||||
|
||||
while (!q.empty() && i < levelOrder.size()) {
|
||||
TreeNode* current = q.front();
|
||||
q.pop();
|
||||
|
||||
if (i < levelOrder.size() && levelOrder[i] != "null") {
|
||||
current->left = new TreeNode(stoi(levelOrder[i]));
|
||||
q.push(current->left);
|
||||
}
|
||||
i++;
|
||||
|
||||
if (i < levelOrder.size() && levelOrder[i] != "null") {
|
||||
current->right = new TreeNode(stoi(levelOrder[i]));
|
||||
q.push(current->right);
|
||||
}
|
||||
i++;
|
||||
}
|
||||
|
||||
return root;
|
||||
}
|
||||
|
||||
int result = 0;
|
||||
int dfs(TreeNode* node) {
|
||||
if (node == NULL) return 0;
|
||||
int leftPath = dfs(node->left);
|
||||
int rightPath = dfs(node->right);
|
||||
|
||||
int leftNum = 0, rightNum = 0;
|
||||
if (node->left != NULL && node->left->val == node->val) {
|
||||
leftNum = leftPath + 1;
|
||||
}
|
||||
if (node->right != NULL && node->right->val == node->val) {
|
||||
rightNum = rightPath + 1;
|
||||
}
|
||||
result = max(result, leftNum + rightNum);
|
||||
return max(leftNum, rightNum);
|
||||
|
||||
}
|
||||
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
vector<string> levelOrder(n);
|
||||
for (int i = 0; i < n ; i++) cin >> levelOrder[i];
|
||||
|
||||
TreeNode* root = constructBinaryTree(levelOrder);
|
||||
dfs(root);
|
||||
cout << result << endl;
|
||||
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
@ -69,7 +69,7 @@ for (int i = 0; i < array.size(); i++) {
|
||||
|
||||
其实使用双指针也可以解决1.两数之和的问题,只不过1.两数之和求的是两个元素的下标,没法用双指针,如果改成求具体两个元素的数值就可以了,大家可以尝试用双指针做一个leetcode上两数之和的题目,就可以体会到我说的意思了。
|
||||
|
||||
使用了哈希法解决了两数之和,但是哈希法并不使用于三数之和!
|
||||
使用了哈希法解决了两数之和,但是哈希法并不适用于三数之和!
|
||||
|
||||
使用哈希法的过程中要把符合条件的三元组放进vector中,然后在去去重,这样是非常费时的,很容易超时,也是三数之和通过率如此之低的根源所在。
|
||||
|
||||
|
||||
@ -40,7 +40,7 @@
|
||||
|
||||
* 陷阱二
|
||||
|
||||
在一个有序序列求最值的时候,不要定义一个全局遍历,然后遍历序列更新全局变量求最值。因为最值可能就是int 或者 longlong的最小值。
|
||||
在一个有序序列求最值的时候,不要定义一个全局变量,然后遍历序列更新全局变量求最值。因为最值可能就是int 或者 longlong的最小值。
|
||||
|
||||
推荐要通过前一个数值(pre)和后一个数值比较(cur),得出最值。
|
||||
|
||||
|
||||
@ -117,6 +117,13 @@
|
||||
|
||||
相信大家有遇到过这种情况: 感觉题目的边界调节超多,一波接着一波的判断,找边界,拆了东墙补西墙,好不容易运行通过了,代码写的十分冗余,毫无章法,其实**真正解决题目的代码都是简洁的,或者有原则性的**,大家可以在这道题目中体会到这一点。
|
||||
|
||||
### 前缀和
|
||||
|
||||
> 代码随想录后续补充题目
|
||||
|
||||
* [数组:求取区间和](https://programmercarl.com/kamacoder/0058.区间和.html)
|
||||
|
||||
前缀和的思路其实很简单,但非常实用,如果没接触过的录友,也很难想到这个解法维度,所以 这是开阔思路 而难度又不高的好题。
|
||||
|
||||
## 总结
|
||||
|
||||
|
||||
@ -17,21 +17,15 @@
|
||||
|
||||
## 思路
|
||||
|
||||
正式开始讲解背包问题!
|
||||
|
||||
这周我们正式开始讲解背包问题!
|
||||
|
||||
背包问题的经典资料当然是:背包九讲。在公众号「代码随想录」后台回复:背包九讲,就可以获得背包九讲的pdf。
|
||||
|
||||
但说实话,背包九讲对于小白来说确实不太友好,看起来还是有点费劲的,而且都是伪代码理解起来也吃力。
|
||||
|
||||
对于面试的话,其实掌握01背包,和完全背包,就够用了,最多可以再来一个多重背包。
|
||||
对于面试的话,其实掌握01背包和完全背包,就够用了,最多可以再来一个多重背包。
|
||||
|
||||
如果这几种背包,分不清,我这里画了一个图,如下:
|
||||
|
||||
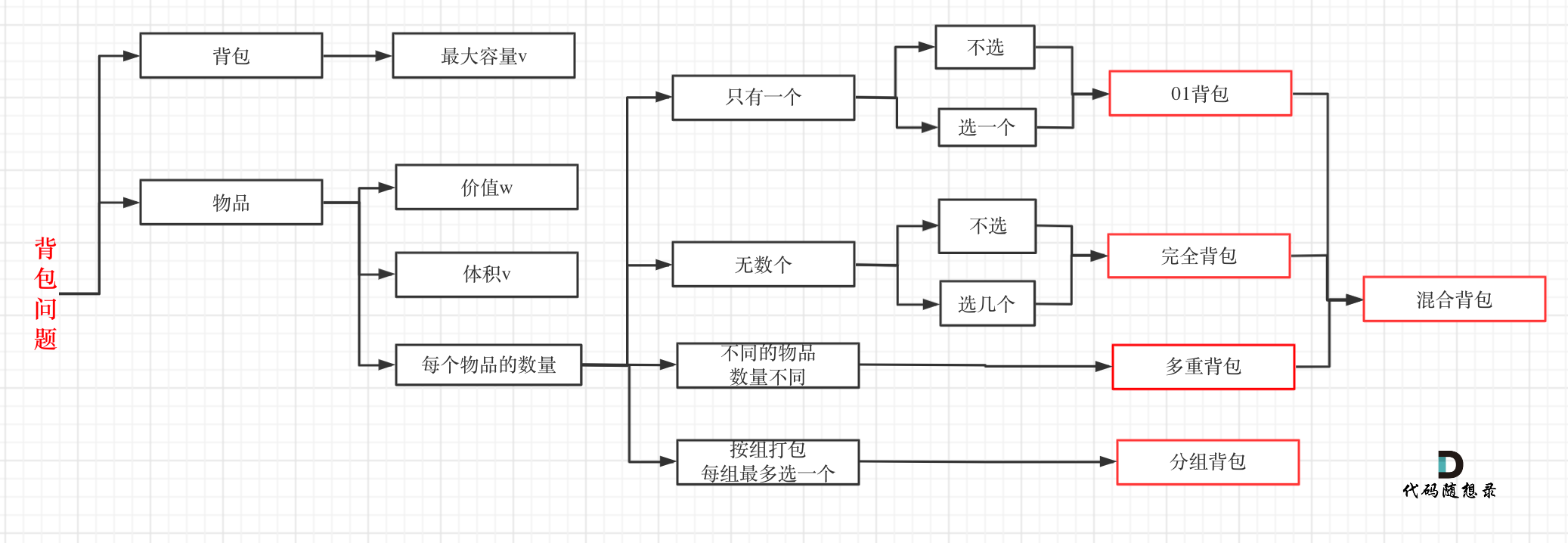
|
||||
|
||||
|
||||
至于背包九讲其他背包,面试几乎不会问,都是竞赛级别的了,leetcode上连多重背包的题目都没有,所以题库也告诉我们,01背包和完全背包就够用了。
|
||||
除此以外其他类型的背包,面试几乎不会问,都是竞赛级别的了,leetcode上连多重背包的题目都没有,所以题库也告诉我们,01背包和完全背包就够用了。
|
||||
|
||||
而完全背包又是也是01背包稍作变化而来,即:完全背包的物品数量是无限的。
|
||||
|
||||
@ -53,7 +47,7 @@ leetcode上没有纯01背包的问题,都是01背包应用方面的题目,
|
||||
|
||||
这样其实是没有从底向上去思考,而是习惯性想到了背包,那么暴力的解法应该是怎么样的呢?
|
||||
|
||||
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是$o(2^n)$,这里的n表示物品数量。
|
||||
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是O(2^n),这里的n表示物品数量。
|
||||
|
||||
**所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化!**
|
||||
|
||||
@ -73,30 +67,111 @@ leetcode上没有纯01背包的问题,都是01背包应用方面的题目,
|
||||
|
||||
以下讲解和图示中出现的数字都是以这个例子为例。
|
||||
|
||||
|
||||
### 二维dp数组01背包
|
||||
|
||||
依然动规五部曲分析一波。
|
||||
|
||||
1. 确定dp数组以及下标的含义
|
||||
|
||||
对于背包问题,有一种写法, 是使用二维数组,即**dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少**。
|
||||
我们需要使用二维数组,为什么呢?
|
||||
|
||||
只看这个二维数组的定义,大家一定会有点懵,看下面这个图:
|
||||
因为有两个维度需要表示,分别是:物品 和 背包容量
|
||||
|
||||
如图,二维数组为 dp[i][j]。
|
||||
|
||||
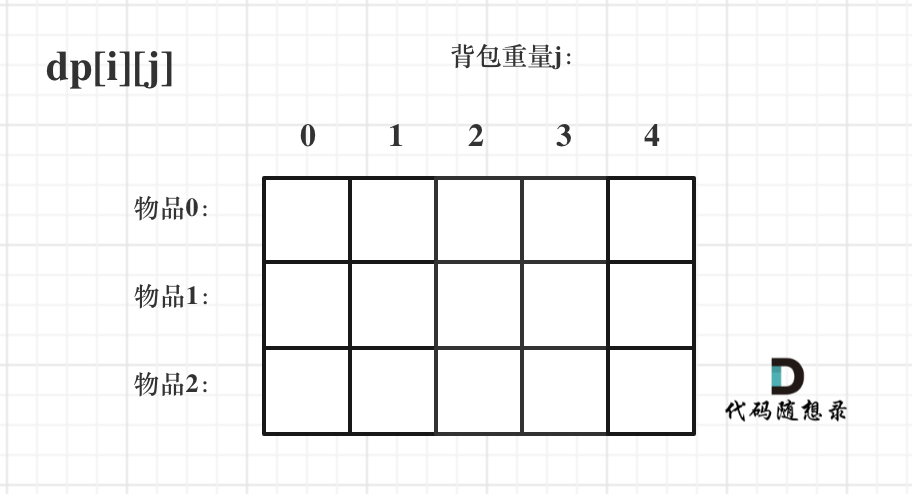
|
||||
|
||||
那么这里 i 、j、dp[i][j] 分别表示什么呢?
|
||||
|
||||
i 来表示物品、j表示背包容量。
|
||||
|
||||
(如果想用j 表示物品,j表示背包容量 行不行? 都可以的,个人习惯而已)
|
||||
|
||||
我们来尝试把上面的 二维表格填写一下。
|
||||
|
||||
动态规划的思路是根据子问题的求解推导出整体的最优解。
|
||||
|
||||
我们先看把物品0 放入背包的情况:
|
||||
|
||||

|
||||
|
||||
背包容量为0,放不下物品0,此时背包里的价值为0。
|
||||
|
||||
背包容量为1,可以放下物品0,此时背包里的价值为15.
|
||||
|
||||
背包容量为2,依然可以放下物品0 (注意 01背包里物品只有一个),此时背包里的价值为15。
|
||||
|
||||
以此类推。
|
||||
|
||||
再看把物品1 放入背包:
|
||||
|
||||

|
||||
|
||||
背包容量为 0,放不下物品0 或者物品1,此时背包里的价值为0。
|
||||
|
||||
背包容量为 1,只能放下物品1,背包里的价值为15。
|
||||
|
||||
背包容量为 2,只能放下物品1,背包里的价值为15。
|
||||
|
||||
背包容量为 3,上一行同一状态,背包只能放物品0,这次也可以选择物品1了,背包可以放物品2 或者 物品1,物品2价值更大,背包里的价值为20。
|
||||
|
||||
背包容量为 4,上一行同一状态,背包只能放物品0,这次也可以选择物品1了,背包都可都放下,背包价值为35。
|
||||
|
||||
以上举例,是比较容易看懂,我主要是通过这个例子,来帮助大家明确dp数组的含义。
|
||||
|
||||
上图中,我们看 dp[1][4] 表示什么意思呢。
|
||||
|
||||
任取 物品0,物品1 放进容量为4的背包里,最大价值是 dp[1][4]。
|
||||
|
||||
通过这个举例,我们来进一步明确dp数组的含义。
|
||||
|
||||
即**dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少**。
|
||||
|
||||
**要时刻记着这个dp数组的含义,下面的一些步骤都围绕这dp数组的含义进行的**,如果哪里看懵了,就来回顾一下i代表什么,j又代表什么。
|
||||
|
||||
2. 确定递推公式
|
||||
|
||||
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
|
||||
这里在把基本信息给出来:
|
||||
|
||||
那么可以有两个方向推出来dp[i][j],
|
||||
| | 重量 | 价值 |
|
||||
| ----- | ---- | ---- |
|
||||
| 物品0 | 1 | 15 |
|
||||
| 物品1 | 3 | 20 |
|
||||
| 物品2 | 4 | 30 |
|
||||
|
||||
对于递推公式,首先我们要明确有哪些方向可以推导出 dp[i][j]。
|
||||
|
||||
这里我们dp[1][4]的状态来举例:
|
||||
|
||||
绝对 dp[1][4],就是放物品1 ,还是不放物品1。
|
||||
|
||||
如果不放物品1, 那么背包的价值应该是 dp[0][4] 即 容量为4的背包,只放物品0的情况。
|
||||
|
||||
推导方向如图:
|
||||
|
||||
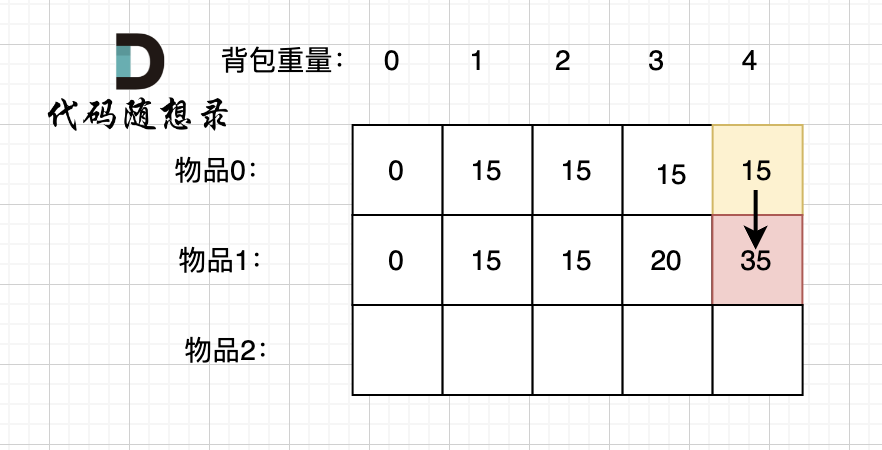
|
||||
|
||||
|
||||
如果放物品1, **那么背包要先留出物品1的容量**,目前容量是4,物品1 需要重量为3,此时背包剩下容量为1。
|
||||
|
||||
容量为1,只考虑放物品0 的最大价值是 dp[0][1],这个值我们之前就计算过。
|
||||
|
||||
所以 放物品1 的情况 = dp[0][1] + 物品1 的重量,推导方向如图:
|
||||
|
||||

|
||||
|
||||
两种情况,分别是放物品1 和 不放物品1,我们要取最大值(毕竟求的是最大价值)
|
||||
|
||||
`dp[1][4] = max(dp[0][4], dp[0][1] + 物品1 的重量) `
|
||||
|
||||
以上过程,抽象化如下:
|
||||
|
||||
* **不放物品i**:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。
|
||||
|
||||
* **不放物品i**:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
|
||||
* **放物品i**:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
|
||||
|
||||
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
递归公式: `dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);`
|
||||
|
||||
3. dp数组如何初始化
|
||||
|
||||
@ -108,17 +183,17 @@ leetcode上没有纯01背包的问题,都是01背包应用方面的题目,
|
||||
|
||||
在看其他情况。
|
||||
|
||||
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
|
||||
状态转移方程 `dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);` 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
|
||||
|
||||
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
|
||||
|
||||
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
|
||||
那么很明显当 `j < weight[0]`的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
|
||||
|
||||
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
|
||||
当`j >= weight[0]`时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
|
||||
|
||||
代码初始化如下:
|
||||
|
||||
```
|
||||
```CPP
|
||||
for (int j = 0 ; j < weight[0]; j++) { // 当然这一步,如果把dp数组预先初始化为0了,这一步就可以省略,但很多同学应该没有想清楚这一点。
|
||||
dp[0][j] = 0;
|
||||
}
|
||||
@ -147,7 +222,7 @@ dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化
|
||||
|
||||
最后初始化代码如下:
|
||||
|
||||
```
|
||||
```CPP
|
||||
// 初始化 dp
|
||||
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
|
||||
for (int j = weight[0]; j <= bagweight; j++) {
|
||||
@ -171,7 +246,7 @@ for (int j = weight[0]; j <= bagweight; j++) {
|
||||
|
||||
那么我先给出先遍历物品,然后遍历背包重量的代码。
|
||||
|
||||
```
|
||||
```CPP
|
||||
// weight数组的大小 就是物品个数
|
||||
for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
|
||||
@ -186,7 +261,7 @@ for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
|
||||
例如这样:
|
||||
|
||||
```
|
||||
```CPP
|
||||
// weight数组的大小 就是物品个数
|
||||
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
|
||||
for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
@ -200,7 +275,7 @@ for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
|
||||
|
||||
**要理解递归的本质和递推的方向**。
|
||||
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
|
||||
`dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);` 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
|
||||
|
||||
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程如图所示:
|
||||
|
||||
@ -232,50 +307,20 @@ dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括
|
||||
|
||||
主要就是自己没有动手推导一下dp数组的演变过程,如果推导明白了,代码写出来就算有问题,只要把dp数组打印出来,对比一下和自己推导的有什么差异,很快就可以发现问题了。
|
||||
|
||||
```cpp
|
||||
void test_2_wei_bag_problem1() {
|
||||
vector<int> weight = {1, 3, 4};
|
||||
vector<int> value = {15, 20, 30};
|
||||
int bagweight = 4;
|
||||
|
||||
// 二维数组
|
||||
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
|
||||
|
||||
// 初始化
|
||||
for (int j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
// weight数组的大小 就是物品个数
|
||||
for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
|
||||
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
|
||||
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
|
||||
}
|
||||
}
|
||||
|
||||
cout << dp[weight.size() - 1][bagweight] << endl;
|
||||
}
|
||||
|
||||
int main() {
|
||||
test_2_wei_bag_problem1();
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
本题力扣上没有原题,大家可以去[卡码网第46题](https://kamacoder.com/problempage.php?pid=1046)去练习,题意是一样的,代码如下:
|
||||
|
||||
```CPP
|
||||
|
||||
//二维dp数组实现
|
||||
#include <bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
int n, bagweight;// bagweight代表行李箱空间
|
||||
void solve() {
|
||||
int main() {
|
||||
int n, bagweight;// bagweight代表行李箱空间
|
||||
|
||||
cin >> n >> bagweight;
|
||||
|
||||
vector<int> weight(n, 0); // 存储每件物品所占空间
|
||||
vector<int> value(n, 0); // 存储每件物品价值
|
||||
|
||||
for(int i = 0; i < n; ++i) {
|
||||
cin >> weight[i];
|
||||
}
|
||||
@ -294,33 +339,28 @@ void solve() {
|
||||
|
||||
for(int i = 1; i < weight.size(); i++) { // 遍历科研物品
|
||||
for(int j = 0; j <= bagweight; j++) { // 遍历行李箱容量
|
||||
// 如果装不下这个物品,那么就继承dp[i - 1][j]的值
|
||||
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
|
||||
// 如果能装下,就将值更新为 不装这个物品的最大值 和 装这个物品的最大值 中的 最大值
|
||||
// 装这个物品的最大值由容量为j - weight[i]的包任意放入序号为[0, i - 1]的最大值 + 该物品的价值构成
|
||||
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 如果装不下这个物品,那么就继承dp[i - 1][j]的值
|
||||
else {
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
cout << dp[weight.size() - 1][bagweight] << endl;
|
||||
}
|
||||
cout << dp[n - 1][bagweight] << endl;
|
||||
|
||||
int main() {
|
||||
while(cin >> n >> bagweight) {
|
||||
solve();
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
|
||||
|
||||
```
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
讲了这么多才刚刚把二维dp的01背包讲完,**这里大家其实可以发现最简单的是推导公式了,推导公式估计看一遍就记下来了,但难就难在如何初始化和遍历顺序上**。
|
||||
背包问题 是动态规划里的经典类型题目,大家要细细品味。
|
||||
|
||||
可能有的同学并没有注意到初始化 和 遍历顺序的重要性,我们后面做力扣上背包面试题目的时候,大家就会感受出来了。
|
||||
|
||||
下一篇 还是理论基础,我们再来讲一维dp数组实现的01背包(滚动数组),分析一下和二维有什么区别,在初始化和遍历顺序上又有什么差异,敬请期待!
|
||||
下一篇 还是理论基础,我们再来讲一维dp数组实现的01背包(滚动数组),分析一下和二维有什么区别,在初始化和遍历顺序上又有什么差异。
|
||||
|
||||
|
||||
|
||||
@ -329,120 +369,42 @@ int main() {
|
||||
|
||||
### Java
|
||||
|
||||
```java
|
||||
public class BagProblem {
|
||||
```Java
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
int[] weight = {1,3,4};
|
||||
int[] value = {15,20,30};
|
||||
int bagSize = 4;
|
||||
testWeightBagProblem(weight,value,bagSize);
|
||||
}
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int bagweight = scanner.nextInt();
|
||||
|
||||
/**
|
||||
* 动态规划获得结果
|
||||
* @param weight 物品的重量
|
||||
* @param value 物品的价值
|
||||
* @param bagSize 背包的容量
|
||||
*/
|
||||
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
|
||||
int[] weight = new int[n];
|
||||
int[] value = new int[n];
|
||||
|
||||
// 创建dp数组
|
||||
int goods = weight.length; // 获取物品的数量
|
||||
int[][] dp = new int[goods][bagSize + 1];
|
||||
for (int i = 0; i < n; ++i) {
|
||||
weight[i] = scanner.nextInt();
|
||||
}
|
||||
for (int j = 0; j < n; ++j) {
|
||||
value[j] = scanner.nextInt();
|
||||
}
|
||||
|
||||
// 初始化dp数组
|
||||
// 创建数组后,其中默认的值就是0
|
||||
for (int j = weight[0]; j <= bagSize; j++) {
|
||||
int[][] dp = new int[n][bagweight + 1];
|
||||
|
||||
for (int j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
// 填充dp数组
|
||||
for (int i = 1; i < weight.length; i++) {
|
||||
for (int j = 1; j <= bagSize; j++) {
|
||||
for (int i = 1; i < n; i++) {
|
||||
for (int j = 0; j <= bagweight; j++) {
|
||||
if (j < weight[i]) {
|
||||
/**
|
||||
* 当前背包的容量都没有当前物品i大的时候,是不放物品i的
|
||||
* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
|
||||
*/
|
||||
dp[i][j] = dp[i-1][j];
|
||||
} else {
|
||||
/**
|
||||
* 当前背包的容量可以放下物品i
|
||||
* 那么此时分两种情况:
|
||||
* 1、不放物品i
|
||||
* 2、放物品i
|
||||
* 比较这两种情况下,哪种背包中物品的最大价值最大
|
||||
*/
|
||||
dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 打印dp数组
|
||||
for (int i = 0; i < goods; i++) {
|
||||
for (int j = 0; j <= bagSize; j++) {
|
||||
System.out.print(dp[i][j] + "\t");
|
||||
}
|
||||
System.out.println("\n");
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
```java
|
||||
import java.util.Arrays;
|
||||
|
||||
public class BagProblem {
|
||||
public static void main(String[] args) {
|
||||
int[] weight = {1,3,4};
|
||||
int[] value = {15,20,30};
|
||||
int bagSize = 4;
|
||||
testWeightBagProblem(weight,value,bagSize);
|
||||
}
|
||||
|
||||
/**
|
||||
* 初始化 dp 数组做了简化(给物品增加冗余维)。这样初始化dp数组,默认全为0即可。
|
||||
* dp[i][j] 表示从下标为[0 - i-1]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
|
||||
* 其实是模仿背包重量从 0 开始,背包容量 j 为 0 的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为 0。
|
||||
* 可选物品也可以从无开始,也就是没有物品可选,即dp[0][j],这样无论背包容量为多少,背包价值总和一定为 0。
|
||||
* @param weight 物品的重量
|
||||
* @param value 物品的价值
|
||||
* @param bagSize 背包的容量
|
||||
*/
|
||||
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
|
||||
|
||||
// 创建dp数组
|
||||
int goods = weight.length; // 获取物品的数量
|
||||
int[][] dp = new int[goods + 1][bagSize + 1]; // 给物品增加冗余维,i = 0 表示没有物品可选
|
||||
|
||||
// 初始化dp数组,默认全为0即可
|
||||
// 填充dp数组
|
||||
for (int i = 1; i <= goods; i++) {
|
||||
for (int j = 1; j <= bagSize; j++) {
|
||||
if (j < weight[i - 1]) { // i - 1 对应物品 i
|
||||
/**
|
||||
* 当前背包的容量都没有当前物品i大的时候,是不放物品i的
|
||||
* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
|
||||
*/
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
/**
|
||||
* 当前背包的容量可以放下物品i
|
||||
* 那么此时分两种情况:
|
||||
* 1、不放物品i
|
||||
* 2、放物品i
|
||||
* 比较这两种情况下,哪种背包中物品的最大价值最大
|
||||
*/
|
||||
dp[i][j] = Math.max(dp[i - 1][j] , dp[i - 1][j - weight[i - 1]] + value[i - 1]); // i - 1 对应物品 i
|
||||
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 打印dp数组
|
||||
for(int[] arr : dp){
|
||||
System.out.println(Arrays.toString(arr));
|
||||
}
|
||||
System.out.println(dp[n - 1][bagweight]);
|
||||
}
|
||||
}
|
||||
|
||||
@ -450,137 +412,71 @@ public class BagProblem {
|
||||
|
||||
### Python
|
||||
|
||||
无参数版
|
||||
```python
|
||||
def test_2_wei_bag_problem1():
|
||||
weight = [1, 3, 4]
|
||||
value = [15, 20, 30]
|
||||
bagweight = 4
|
||||
n, bagweight = map(int, input().split())
|
||||
|
||||
# 二维数组
|
||||
dp = [[0] * (bagweight + 1) for _ in range(len(weight))]
|
||||
weight = list(map(int, input().split()))
|
||||
value = list(map(int, input().split()))
|
||||
|
||||
# 初始化
|
||||
for j in range(weight[0], bagweight + 1):
|
||||
dp[0][j] = value[0]
|
||||
dp = [[0] * (bagweight + 1) for _ in range(n)]
|
||||
|
||||
# weight数组的大小就是物品个数
|
||||
for i in range(1, len(weight)): # 遍历物品
|
||||
for j in range(bagweight + 1): # 遍历背包容量
|
||||
if j < weight[i]:
|
||||
dp[i][j] = dp[i - 1][j]
|
||||
else:
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
|
||||
for j in range(weight[0], bagweight + 1):
|
||||
dp[0][j] = value[0]
|
||||
|
||||
print(dp[len(weight) - 1][bagweight])
|
||||
|
||||
test_2_wei_bag_problem1()
|
||||
|
||||
```
|
||||
有参数版
|
||||
```python
|
||||
def test_2_wei_bag_problem1(weight, value, bagweight):
|
||||
# 二维数组
|
||||
dp = [[0] * (bagweight + 1) for _ in range(len(weight))]
|
||||
|
||||
# 初始化
|
||||
for j in range(weight[0], bagweight + 1):
|
||||
dp[0][j] = value[0]
|
||||
|
||||
# weight数组的大小就是物品个数
|
||||
for i in range(1, len(weight)): # 遍历物品
|
||||
for j in range(bagweight + 1): # 遍历背包容量
|
||||
if j < weight[i]:
|
||||
dp[i][j] = dp[i - 1][j]
|
||||
else:
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
|
||||
|
||||
return dp[len(weight) - 1][bagweight]
|
||||
|
||||
if __name__ == "__main__":
|
||||
|
||||
weight = [1, 3, 4]
|
||||
value = [15, 20, 30]
|
||||
bagweight = 4
|
||||
|
||||
result = test_2_wei_bag_problem1(weight, value, bagweight)
|
||||
print(result)
|
||||
for i in range(1, n):
|
||||
for j in range(bagweight + 1):
|
||||
if j < weight[i]:
|
||||
dp[i][j] = dp[i - 1][j]
|
||||
else:
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
|
||||
|
||||
print(dp[n - 1][bagweight])
|
||||
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
```go
|
||||
func test_2_wei_bag_problem1(weight, value []int, bagweight int) int {
|
||||
// 定义dp数组
|
||||
dp := make([][]int, len(weight))
|
||||
for i, _ := range dp {
|
||||
dp[i] = make([]int, bagweight+1)
|
||||
}
|
||||
// 初始化
|
||||
for j := bagweight; j >= weight[0]; j-- {
|
||||
dp[0][j] = dp[0][j-weight[0]] + value[0]
|
||||
}
|
||||
// 递推公式
|
||||
for i := 1; i < len(weight); i++ {
|
||||
//正序,也可以倒序
|
||||
for j := 0; j <= bagweight; j++ {
|
||||
if j < weight[i] {
|
||||
dp[i][j] = dp[i-1][j]
|
||||
} else {
|
||||
dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[len(weight)-1][bagweight]
|
||||
}
|
||||
|
||||
func max(a,b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
|
||||
func main() {
|
||||
weight := []int{1,3,4}
|
||||
value := []int{15,20,30}
|
||||
test_2_wei_bag_problem1(weight,value,4)
|
||||
}
|
||||
```
|
||||
|
||||
### Javascript
|
||||
|
||||
```js
|
||||
function testWeightBagProblem (weight, value, size) {
|
||||
// 定义 dp 数组
|
||||
const len = weight.length,
|
||||
dp = Array(len).fill().map(() => Array(size + 1).fill(0));
|
||||
const readline = require('readline').createInterface({
|
||||
input: process.stdin,
|
||||
output: process.stdout
|
||||
});
|
||||
|
||||
// 初始化
|
||||
for(let j = weight[0]; j <= size; j++) {
|
||||
let input = [];
|
||||
|
||||
readline.on('line', (line) => {
|
||||
input.push(line);
|
||||
});
|
||||
|
||||
readline.on('close', () => {
|
||||
let [n, bagweight] = input[0].split(' ').map(Number);
|
||||
let weight = input[1].split(' ').map(Number);
|
||||
let value = input[2].split(' ').map(Number);
|
||||
|
||||
let dp = Array.from({ length: n }, () => Array(bagweight + 1).fill(0));
|
||||
|
||||
for (let j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
// weight 数组的长度len 就是物品个数
|
||||
for(let i = 1; i < len; i++) { // 遍历物品
|
||||
for(let j = 0; j <= size; j++) { // 遍历背包容量
|
||||
if(j < weight[i]) dp[i][j] = dp[i - 1][j];
|
||||
else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
for (let i = 1; i < n; i++) {
|
||||
for (let j = 0; j <= bagweight; j++) {
|
||||
if (j < weight[i]) {
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
console.table(dp)
|
||||
console.log(dp[n - 1][bagweight]);
|
||||
});
|
||||
|
||||
return dp[len - 1][size];
|
||||
}
|
||||
|
||||
function test () {
|
||||
console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
|
||||
}
|
||||
|
||||
test();
|
||||
```
|
||||
|
||||
|
||||
@ -589,158 +485,63 @@ test();
|
||||
```c
|
||||
#include <stdio.h>
|
||||
#include <stdlib.h>
|
||||
#include <string.h>
|
||||
|
||||
#define MAX(a, b) (((a) > (b)) ? (a) : (b))
|
||||
#define ARR_SIZE(a) (sizeof((a)) / sizeof((a)[0]))
|
||||
#define BAG_WEIGHT 4
|
||||
int max(int a, int b) {
|
||||
return a > b ? a : b;
|
||||
}
|
||||
|
||||
void backPack(int* weights, int weightSize, int* costs, int costSize, int bagWeight) {
|
||||
// 开辟dp数组
|
||||
int dp[weightSize][bagWeight + 1];
|
||||
memset(dp, 0, sizeof(int) * weightSize * (bagWeight + 1));
|
||||
int main() {
|
||||
int n, bagweight;
|
||||
scanf("%d %d", &n, &bagweight);
|
||||
|
||||
int i, j;
|
||||
// 当背包容量大于物品0的重量时,将物品0放入到背包中
|
||||
for(j = weights[0]; j <= bagWeight; ++j) {
|
||||
dp[0][j] = costs[0];
|
||||
int *weight = (int *)malloc(n * sizeof(int));
|
||||
int *value = (int *)malloc(n * sizeof(int));
|
||||
|
||||
for (int i = 0; i < n; ++i) {
|
||||
scanf("%d", &weight[i]);
|
||||
}
|
||||
for (int j = 0; j < n; ++j) {
|
||||
scanf("%d", &value[j]);
|
||||
}
|
||||
|
||||
// 先遍历物品,再遍历重量
|
||||
for(j = 1; j <= bagWeight; ++j) {
|
||||
for(i = 1; i < weightSize; ++i) {
|
||||
// 如果当前背包容量小于物品重量
|
||||
if(j < weights[i])
|
||||
// 背包物品的价值等于背包不放置当前物品时的价值
|
||||
dp[i][j] = dp[i-1][j];
|
||||
// 若背包当前重量可以放置物品
|
||||
else
|
||||
// 背包的价值等于放置该物品或不放置该物品的最大值
|
||||
dp[i][j] = MAX(dp[i - 1][j], dp[i - 1][j - weights[i]] + costs[i]);
|
||||
int **dp = (int **)malloc(n * sizeof(int *));
|
||||
for (int i = 0; i < n; ++i) {
|
||||
dp[i] = (int *)malloc((bagweight + 1) * sizeof(int));
|
||||
for (int j = 0; j <= bagweight; ++j) {
|
||||
dp[i][j] = 0;
|
||||
}
|
||||
}
|
||||
|
||||
printf("%d\n", dp[weightSize - 1][bagWeight]);
|
||||
}
|
||||
|
||||
int main(int argc, char* argv[]) {
|
||||
int weights[] = {1, 3, 4};
|
||||
int costs[] = {15, 20, 30};
|
||||
backPack(weights, ARR_SIZE(weights), costs, ARR_SIZE(costs), BAG_WEIGHT);
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
### TypeScript
|
||||
|
||||
```typescript
|
||||
function testWeightBagProblem(
|
||||
weight: number[],
|
||||
value: number[],
|
||||
size: number
|
||||
): number {
|
||||
/**
|
||||
* dp[i][j]: 前i个物品,背包容量为j,能获得的最大价值
|
||||
* dp[0][*]: u=weight[0],u之前为0,u之后(含u)为value[0]
|
||||
* dp[*][0]: 0
|
||||
* ...
|
||||
* dp[i][j]: max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);
|
||||
*/
|
||||
const goodsNum: number = weight.length;
|
||||
const dp: number[][] = new Array(goodsNum)
|
||||
.fill(0)
|
||||
.map((_) => new Array(size + 1).fill(0));
|
||||
for (let i = weight[0]; i <= size; i++) {
|
||||
dp[0][i] = value[0];
|
||||
}
|
||||
for (let i = 1; i < goodsNum; i++) {
|
||||
for (let j = 1; j <= size; j++) {
|
||||
if (j < weight[i]) {
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[goodsNum - 1][size];
|
||||
}
|
||||
// test
|
||||
const weight = [1, 3, 4];
|
||||
const value = [15, 20, 30];
|
||||
const size = 4;
|
||||
console.log(testWeightBagProblem(weight, value, size));
|
||||
```
|
||||
|
||||
### Scala
|
||||
|
||||
```scala
|
||||
object Solution {
|
||||
// 01背包
|
||||
def test_2_wei_bag_problem1(): Unit = {
|
||||
var weight = Array[Int](1, 3, 4)
|
||||
var value = Array[Int](15, 20, 30)
|
||||
var baseweight = 4
|
||||
|
||||
// 二维数组
|
||||
var dp = Array.ofDim[Int](weight.length, baseweight + 1)
|
||||
|
||||
// 初始化
|
||||
for (j <- weight(0) to baseweight) {
|
||||
dp(0)(j) = value(0)
|
||||
for (int j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
// 遍历
|
||||
for (i <- 1 until weight.length; j <- 1 to baseweight) {
|
||||
if (j - weight(i) >= 0) dp(i)(j) = dp(i - 1)(j - weight(i)) + value(i)
|
||||
dp(i)(j) = math.max(dp(i)(j), dp(i - 1)(j))
|
||||
}
|
||||
|
||||
// 打印数组
|
||||
dp.foreach(x => println("[" + x.mkString(",") + "]"))
|
||||
|
||||
dp(weight.length - 1)(baseweight) // 最终返回
|
||||
}
|
||||
|
||||
def main(args: Array[String]): Unit = {
|
||||
test_2_wei_bag_problem1()
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
```rust
|
||||
pub struct Solution;
|
||||
|
||||
impl Solution {
|
||||
pub fn wei_bag_problem1(weight: Vec<usize>, value: Vec<usize>, bag_size: usize) -> usize {
|
||||
let mut dp = vec![vec![0; bag_size + 1]; weight.len()];
|
||||
for j in weight[0]..=weight.len() {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
for i in 1..weight.len() {
|
||||
for j in 0..=bag_size {
|
||||
match j < weight[i] {
|
||||
true => dp[i][j] = dp[i - 1][j],
|
||||
false => dp[i][j] = dp[i - 1][j].max(dp[i - 1][j - weight[i]] + value[i]),
|
||||
}
|
||||
for (int i = 1; i < n; i++) {
|
||||
for (int j = 0; j <= bagweight; j++) {
|
||||
if (j < weight[i]) {
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
dp[weight.len() - 1][bag_size]
|
||||
}
|
||||
|
||||
printf("%d\n", dp[n - 1][bagweight]);
|
||||
|
||||
for (int i = 0; i < n; ++i) {
|
||||
free(dp[i]);
|
||||
}
|
||||
free(dp);
|
||||
free(weight);
|
||||
free(value);
|
||||
|
||||
return 0;
|
||||
}
|
||||
|
||||
#[test]
|
||||
fn test_wei_bag_problem1() {
|
||||
println!(
|
||||
"{}",
|
||||
Solution::wei_bag_problem1(vec![1, 3, 4], vec![15, 20, 30], 4)
|
||||
);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
|
||||
@ -56,17 +56,31 @@
|
||||
|
||||
1. 确定dp数组的定义
|
||||
|
||||
关于dp数组的定义,我在 [01背包理论基础](https://programmercarl.com/背包理论基础01背包-1.html) 有详细讲解
|
||||
|
||||
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
|
||||
|
||||
2. 一维dp数组的递推公式
|
||||
|
||||
dp[j]为 容量为j的背包所背的最大价值,那么如何推导dp[j]呢?
|
||||
二维dp数组的递推公式为: `dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);`
|
||||
|
||||
公式是怎么来的 在这里 [01背包理论基础](https://programmercarl.com/背包理论基础01背包-1.html) 有详细讲解。
|
||||
|
||||
一维dp数组,其实就上上一层 dp[i-1] 这一层 拷贝的 dp[i]来。
|
||||
|
||||
所以在 上面递推公式的基础上,去掉i这个维度就好。
|
||||
|
||||
递推公式为:`dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);`
|
||||
|
||||
以下为分析:
|
||||
|
||||
dp[j]为 容量为j的背包所背的最大价值。
|
||||
|
||||
dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
|
||||
|
||||
dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
|
||||
`dp[j - weight[i]] + value[i]` 表示 容量为 [j - 物品i重量] 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
|
||||
|
||||
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,
|
||||
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取`dp[j - weight[i]] + value[i]`,即放物品i,指定是取最大的,毕竟是求最大价值,
|
||||
|
||||
所以递归公式为:
|
||||
|
||||
@ -145,10 +159,6 @@ dp[1] = dp[1 - weight[0]] + value[0] = 15
|
||||
|
||||
因为一维dp的写法,背包容量一定是要倒序遍历(原因上面已经讲了),如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品。
|
||||
|
||||
倒序遍历的原因是,本质上还是一个对二维数组的遍历,并且右下角的值依赖上一层左上角的值,因此需要保证左边的值仍然是上一层的,从右向左覆盖。
|
||||
|
||||
(这里如果读不懂,就再回想一下dp[j]的定义,或者就把两个for循环顺序颠倒一下试试!)
|
||||
|
||||
**所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的!**,这一点大家一定要注意。
|
||||
|
||||
5. 举例推导dp数组
|
||||
@ -158,31 +168,6 @@ dp[1] = dp[1 - weight[0]] + value[0] = 15
|
||||
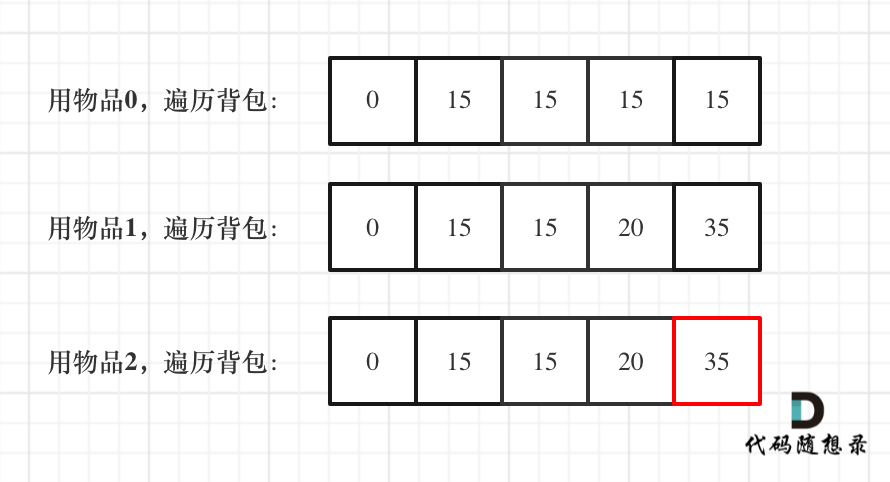
|
||||
|
||||
|
||||
|
||||
C++代码如下:
|
||||
|
||||
```CPP
|
||||
void test_1_wei_bag_problem() {
|
||||
vector<int> weight = {1, 3, 4};
|
||||
vector<int> value = {15, 20, 30};
|
||||
int bagWeight = 4;
|
||||
|
||||
// 初始化
|
||||
vector<int> dp(bagWeight + 1, 0);
|
||||
for(int i = 0; i < weight.size(); i++) { // 遍历物品
|
||||
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
|
||||
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
cout << dp[bagWeight] << endl;
|
||||
}
|
||||
|
||||
int main() {
|
||||
test_1_wei_bag_problem();
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
本题力扣上没有原题,大家可以去[卡码网第46题](https://kamacoder.com/problempage.php?pid=1046)去练习,题意是一样的,代码如下:
|
||||
|
||||
```CPP
|
||||
@ -256,251 +241,229 @@ int main() {
|
||||
|
||||
即使代码没有通过,也会有自己的逻辑去debug,这样就思维清晰了。
|
||||
|
||||
接下来就要开始用这两天的理论基础去做力扣上的背包面试题目了,录友们握紧扶手,我们要上高速啦!
|
||||
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
```java
|
||||
public static void main(String[] args) {
|
||||
int[] weight = {1, 3, 4};
|
||||
int[] value = {15, 20, 30};
|
||||
int bagWight = 4;
|
||||
testWeightBagProblem(weight, value, bagWight);
|
||||
}
|
||||
import java.util.Scanner;
|
||||
|
||||
public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
|
||||
int wLen = weight.length;
|
||||
//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值
|
||||
int[] dp = new int[bagWeight + 1];
|
||||
//遍历顺序:先遍历物品,再遍历背包容量
|
||||
for (int i = 0; i < wLen; i++){
|
||||
for (int j = bagWeight; j >= weight[i]; j--){
|
||||
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int bagweight = scanner.nextInt();
|
||||
|
||||
int[] weight = new int[n];
|
||||
int[] value = new int[n];
|
||||
|
||||
for (int i = 0; i < n; ++i) {
|
||||
weight[i] = scanner.nextInt();
|
||||
}
|
||||
for (int j = 0; j < n; ++j) {
|
||||
value[j] = scanner.nextInt();
|
||||
}
|
||||
|
||||
int[][] dp = new int[n][bagweight + 1];
|
||||
|
||||
for (int j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
for (int i = 1; i < n; i++) {
|
||||
for (int j = 0; j <= bagweight; j++) {
|
||||
if (j < weight[i]) {
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
//打印dp数组
|
||||
for (int j = 0; j <= bagWeight; j++){
|
||||
System.out.print(dp[j] + " ");
|
||||
}
|
||||
|
||||
System.out.println(dp[n - 1][bagweight]);
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
### Python
|
||||
无参版
|
||||
|
||||
```python
|
||||
def test_1_wei_bag_problem():
|
||||
weight = [1, 3, 4]
|
||||
value = [15, 20, 30]
|
||||
bagWeight = 4
|
||||
n, bagweight = map(int, input().split())
|
||||
|
||||
# 初始化
|
||||
dp = [0] * (bagWeight + 1)
|
||||
for i in range(len(weight)): # 遍历物品
|
||||
for j in range(bagWeight, weight[i] - 1, -1): # 遍历背包容量
|
||||
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
|
||||
weight = list(map(int, input().split()))
|
||||
value = list(map(int, input().split()))
|
||||
|
||||
print(dp[bagWeight])
|
||||
dp = [[0] * (bagweight + 1) for _ in range(n)]
|
||||
|
||||
for j in range(weight[0], bagweight + 1):
|
||||
dp[0][j] = value[0]
|
||||
|
||||
test_1_wei_bag_problem()
|
||||
```
|
||||
有参版
|
||||
```python
|
||||
def test_1_wei_bag_problem(weight, value, bagWeight):
|
||||
# 初始化
|
||||
dp = [0] * (bagWeight + 1)
|
||||
for i in range(len(weight)): # 遍历物品
|
||||
for j in range(bagWeight, weight[i] - 1, -1): # 遍历背包容量
|
||||
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
|
||||
for i in range(1, n):
|
||||
for j in range(bagweight + 1):
|
||||
if j < weight[i]:
|
||||
dp[i][j] = dp[i - 1][j]
|
||||
else:
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
|
||||
|
||||
return dp[bagWeight]
|
||||
|
||||
|
||||
if __name__ == "__main__":
|
||||
|
||||
weight = [1, 3, 4]
|
||||
value = [15, 20, 30]
|
||||
bagweight = 4
|
||||
|
||||
result = test_1_wei_bag_problem(weight, value, bagweight)
|
||||
print(result)
|
||||
print(dp[n - 1][bagweight])
|
||||
|
||||
```
|
||||
### Go
|
||||
```go
|
||||
func test_1_wei_bag_problem(weight, value []int, bagWeight int) int {
|
||||
// 定义 and 初始化
|
||||
dp := make([]int,bagWeight+1)
|
||||
// 递推顺序
|
||||
for i := 0 ;i < len(weight) ; i++ {
|
||||
// 这里必须倒序,区别二维,因为二维dp保存了i的状态
|
||||
for j:= bagWeight; j >= weight[i] ; j-- {
|
||||
// 递推公式
|
||||
dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
|
||||
}
|
||||
}
|
||||
//fmt.Println(dp)
|
||||
return dp[bagWeight]
|
||||
}
|
||||
|
||||
func max(a,b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
package main
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
)
|
||||
|
||||
func main() {
|
||||
weight := []int{1,3,4}
|
||||
value := []int{15,20,30}
|
||||
test_1_wei_bag_problem(weight,value,4)
|
||||
var n, bagweight int
|
||||
fmt.Scan(&n, &bagweight)
|
||||
|
||||
weight := make([]int, n)
|
||||
value := make([]int, n)
|
||||
|
||||
for i := 0; i < n; i++ {
|
||||
fmt.Scan(&weight[i])
|
||||
}
|
||||
for j := 0; j < n; j++ {
|
||||
fmt.Scan(&value[j])
|
||||
}
|
||||
|
||||
dp := make([][]int, n)
|
||||
for i := range dp {
|
||||
dp[i] = make([]int, bagweight+1)
|
||||
}
|
||||
|
||||
for j := weight[0]; j <= bagweight; j++ {
|
||||
dp[0][j] = value[0]
|
||||
}
|
||||
|
||||
for i := 1; i < n; i++ {
|
||||
for j := 0; j <= bagweight; j++ {
|
||||
if j < weight[i] {
|
||||
dp[i][j] = dp[i-1][j]
|
||||
} else {
|
||||
dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
fmt.Println(dp[n-1][bagweight])
|
||||
}
|
||||
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
### JavaScript
|
||||
|
||||
```js
|
||||
const readline = require('readline').createInterface({
|
||||
input: process.stdin,
|
||||
output: process.stdout
|
||||
});
|
||||
|
||||
function testWeightBagProblem(wight, value, size) {
|
||||
const len = wight.length,
|
||||
dp = Array(size + 1).fill(0);
|
||||
for(let i = 1; i <= len; i++) {
|
||||
for(let j = size; j >= wight[i - 1]; j--) {
|
||||
dp[j] = Math.max(dp[j], value[i - 1] + dp[j - wight[i - 1]]);
|
||||
let input = [];
|
||||
|
||||
readline.on('line', (line) => {
|
||||
input.push(line);
|
||||
});
|
||||
|
||||
readline.on('close', () => {
|
||||
let [n, bagweight] = input[0].split(' ').map(Number);
|
||||
let weight = input[1].split(' ').map(Number);
|
||||
let value = input[2].split(' ').map(Number);
|
||||
|
||||
let dp = Array.from({ length: n }, () => Array(bagweight + 1).fill(0));
|
||||
|
||||
for (let j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
}
|
||||
return dp[size];
|
||||
}
|
||||
|
||||
for (let i = 1; i < n; i++) {
|
||||
for (let j = 0; j <= bagweight; j++) {
|
||||
if (j < weight[i]) {
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
console.log(dp[n - 1][bagweight]);
|
||||
});
|
||||
|
||||
|
||||
function test () {
|
||||
console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
|
||||
}
|
||||
|
||||
test();
|
||||
```
|
||||
|
||||
### C
|
||||
```c
|
||||
#include <stdio.h>
|
||||
#include <string.h>
|
||||
#include <stdlib.h>
|
||||
|
||||
#define MAX(a, b) (((a) > (b)) ? (a) : (b))
|
||||
#define ARR_SIZE(arr) ((sizeof((arr))) / sizeof((arr)[0]))
|
||||
#define BAG_WEIGHT 4
|
||||
int max(int a, int b) {
|
||||
return a > b ? a : b;
|
||||
}
|
||||
|
||||
void test_back_pack(int* weights, int weightSize, int* values, int valueSize, int bagWeight) {
|
||||
int dp[bagWeight + 1];
|
||||
memset(dp, 0, sizeof(int) * (bagWeight + 1));
|
||||
int main() {
|
||||
int n, bagweight;
|
||||
scanf("%d %d", &n, &bagweight);
|
||||
|
||||
int i, j;
|
||||
// 先遍历物品
|
||||
for(i = 0; i < weightSize; ++i) {
|
||||
// 后遍历重量。从后向前遍历
|
||||
for(j = bagWeight; j >= weights[i]; --j) {
|
||||
dp[j] = MAX(dp[j], dp[j - weights[i]] + values[i]);
|
||||
int *weight = (int *)malloc(n * sizeof(int));
|
||||
int *value = (int *)malloc(n * sizeof(int));
|
||||
|
||||
for (int i = 0; i < n; ++i) {
|
||||
scanf("%d", &weight[i]);
|
||||
}
|
||||
for (int j = 0; j < n; ++j) {
|
||||
scanf("%d", &value[j]);
|
||||
}
|
||||
|
||||
int **dp = (int **)malloc(n * sizeof(int *));
|
||||
for (int i = 0; i < n; ++i) {
|
||||
dp[i] = (int *)malloc((bagweight + 1) * sizeof(int));
|
||||
for (int j = 0; j <= bagweight; ++j) {
|
||||
dp[i][j] = 0;
|
||||
}
|
||||
}
|
||||
|
||||
// 打印最优结果
|
||||
printf("%d\n", dp[bagWeight]);
|
||||
}
|
||||
|
||||
int main(int argc, char** argv) {
|
||||
int weights[] = {1, 3, 4};
|
||||
int values[] = {15, 20, 30};
|
||||
test_back_pack(weights, ARR_SIZE(weights), values, ARR_SIZE(values), BAG_WEIGHT);
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
```typescript
|
||||
function testWeightBagProblem(
|
||||
weight: number[],
|
||||
value: number[],
|
||||
size: number
|
||||
): number {
|
||||
const goodsNum: number = weight.length;
|
||||
const dp: number[] = new Array(size + 1).fill(0);
|
||||
for (let i = 0; i < goodsNum; i++) {
|
||||
for (let j = size; j >= weight[i]; j--) {
|
||||
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
return dp[size];
|
||||
}
|
||||
const weight = [1, 3, 4];
|
||||
const value = [15, 20, 30];
|
||||
const size = 4;
|
||||
console.log(testWeightBagProblem(weight, value, size));
|
||||
|
||||
```
|
||||
|
||||
### Scala
|
||||
|
||||
```scala
|
||||
object Solution {
|
||||
// 滚动数组
|
||||
def test_1_wei_bag_problem(): Unit = {
|
||||
var weight = Array[Int](1, 3, 4)
|
||||
var value = Array[Int](15, 20, 30)
|
||||
var baseweight = 4
|
||||
|
||||
// dp数组
|
||||
var dp = new Array[Int](baseweight + 1)
|
||||
|
||||
// 遍历
|
||||
for (i <- 0 until weight.length; j <- baseweight to weight(i) by -1) {
|
||||
dp(j) = math.max(dp(j), dp(j - weight(i)) + value(i))
|
||||
for (int j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
// 打印数组
|
||||
println("[" + dp.mkString(",") + "]")
|
||||
}
|
||||
|
||||
def main(args: Array[String]): Unit = {
|
||||
test_1_wei_bag_problem()
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
```rust
|
||||
pub struct Solution;
|
||||
|
||||
impl Solution {
|
||||
pub fn wei_bag_problem2(weight: Vec<usize>, value: Vec<usize>, bag_size: usize) -> usize {
|
||||
let mut dp = vec![0; bag_size + 1];
|
||||
for i in 0..weight.len() {
|
||||
for j in (weight[i]..=bag_size).rev() {
|
||||
if j >= weight[i] {
|
||||
dp[j] = dp[j].max(dp[j - weight[i]] + value[i]);
|
||||
}
|
||||
for (int i = 1; i < n; i++) {
|
||||
for (int j = 0; j <= bagweight; j++) {
|
||||
if (j < weight[i]) {
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
dp[dp.len() - 1]
|
||||
}
|
||||
|
||||
printf("%d\n", dp[n - 1][bagweight]);
|
||||
|
||||
for (int i = 0; i < n; ++i) {
|
||||
free(dp[i]);
|
||||
}
|
||||
free(dp);
|
||||
free(weight);
|
||||
free(value);
|
||||
|
||||
return 0;
|
||||
}
|
||||
|
||||
#[test]
|
||||
fn test_wei_bag_problem2() {
|
||||
println!(
|
||||
"{}",
|
||||
Solution::wei_bag_problem2(vec![1, 3, 4], vec![15, 20, 30], 4)
|
||||
);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
Reference in New Issue
Block a user