algorithm/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2025-07-08 00:43:04 +08:00
Code Issues Packages Projects Releases Wiki Activity

Update

Browse Source
This commit is contained in:
youngyangyang04
2020-09-29 10:08:39 +08:00
parent 1a0da92dcc
commit c0be90a277
9 changed files with 235 additions and 41 deletions
Download Patch File Download Diff File Expand all files Collapse all files

3
README.md
View File

@ -87,6 +87,8 @@
* [二叉树：前中后序迭代方式的写法就不能统一一下么？](https://mp.weixin.qq.com/s/WKg0Ty1_3SZkztpHubZPRg)
* [二叉树：层序遍历登场！](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)
* [二叉树：你真的会翻转二叉树么？](https://mp.weixin.qq.com/s/6gY1MiXrnm-khAAJiIb5Bg)
* [本周小结！（二叉树）](https://mp.weixin.qq.com/s/JWmTeC7aKbBfGx4TY6uwuQ)
* [二叉树：我对称么？](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)
（持续更新中....）
@ -282,6 +284,7 @@
|[0515.在每个树行中找最大值](https://github.com/youngyangyang04/leetcode/blob/master/problems/0515.在每个树行中找最大值.md) |二叉树 |简单|**广度优先搜索/队列**|
|[0538.把二叉搜索树转换为累加树](https://github.com/youngyangyang04/leetcode/blob/master/problems/0538.把二叉搜索树转换为累加树.md) |二叉树 |简单|**递归** **迭代**|
|[0541.反转字符串II](https://github.com/youngyangyang04/leetcode/blob/master/problems/0541.反转字符串II.md) |字符串 |简单| **模拟**|
|[0559.N叉树的最大深度](https://github.com/youngyangyang04/leetcode/blob/master/problems/0559.N叉树的最大深度.md) |N叉树 |简单| **递归**|
|[0575.分糖果](https://github.com/youngyangyang04/leetcode/blob/master/problems/0575.分糖果.md) |哈希表 |简单|**哈希**|
|[0589.N叉树的前序遍历](https://github.com/youngyangyang04/leetcode/blob/master/problems/0589.N叉树的前序遍历.md) |树 |简单|**递归** **栈/迭代**|
|[0590.N叉树的后序遍历](https://github.com/youngyangyang04/leetcode/blob/master/problems/0590.N叉树的后序遍历.md) |树 |简单|**递归** **栈/迭代**|

BIN
pics/104. 二叉树的最大深度.png Normal file
View File

Binary file not shown.
Side by Side

After

Width:  |  Height:  |  Size: 8.7 KiB

BIN
pics/559.N叉树的最大深度.png Normal file
View File

Binary file not shown.
Side by Side

After

Width:  |  Height:  |  Size: 30 KiB

38
problems/0100.相同的树.md
View File

@ -5,7 +5,7 @@ https://leetcode-cn.com/problems/same-tree/
这道题目和101 基本是一样的
## C++代码
## 递归
```
class Solution {
@ -23,4 +23,40 @@ public:
}
};
```
## 迭代法
```
lass Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (p == NULL && q == NULL) return true;
if (p == NULL || q == NULL) return false;
queue<TreeNode*> que;
que.push(p); //
que.push(q); //
while (!que.empty()) { //
TreeNode* leftNode = que.front(); que.pop();
TreeNode* rightNode = que.front(); que.pop();
if (!leftNode && !rightNode) { //
continue;
}
//
if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
return false;
}
que.push(leftNode->left); //
que.push(rightNode->left); //
que.push(leftNode->right); //
que.push(rightNode->right); //
}
return true;
}
};
```
> 更多算法干货文章持续更新，可以微信搜索「代码随想录」第一时间围观，关注后，回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等，就可以获得我多年整理的学习资料。

152
problems/0104.二叉树的最大深度.md
View File

@ -1,9 +1,33 @@
## 题目地址
https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
## 思路
> “简单题”系列
看完本篇可以一起做了如下两道题目：
* 104.二叉树的最大深度
* 559.N叉树的最大深度
# 104.二叉树的最大深度
给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例：
给定二叉树 [3,9,20,null,null,15,7]，
<img src='../pics/104. 二叉树的最大深度.png' width=600> </img></div>
返回它的最大深度 3 。
# 思路
## 递归法
本题其实也要后序遍历（左右中），依然是因为要通过递归函数的返回值做计算树的高度。
### 递归法
按照递归三部曲，来看看如何来写。
1. 确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。
@ -12,6 +36,7 @@ https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
```
int getDepth(TreeNode* node)
```
2. 确定终止条件：如果为空节点的话，就返回0，表示高度为0。
代码如下：
@ -19,25 +44,28 @@ int getDepth(TreeNode* node)
if (node == NULL) return 0;
```
3. 确定单层递归的逻辑：先求它的左子树的深度，再求的右子树的深度，最后去左右深度最大的数值+1 就是目前节点为根节点的树的深度。
3. 确定单层递归的逻辑：先求它的左子树的深度，再求的右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。
代码如下：
```
int leftDepth = getDepth(node->left);
int rightDepth = getDepth(node->right);
int depth = 1 + max(leftDepth, rightDepth);
int leftDepth = getDepth(node->left); // 左
int rightDepth = getDepth(node->right); // 右
int depth = 1 + max(leftDepth, rightDepth); // 中
return depth;
```
所以整体代码如下：
所以整体C++代码如下：
```
class Solution {
public:
int getDepth(TreeNode* node) {
if (node == NULL) return 0;
return 1 + max(getDepth(node->left), getDepth(node->right));
int leftDepth = getDepth(node->left); // 左
int rightDepth = getDepth(node->right); // 右
int depth = 1 + max(leftDepth, rightDepth); // 中
return depth;
}
int maxDepth(TreeNode* root) {
return getDepth(root);
@ -45,36 +73,34 @@ public:
};
```
### 迭代法
代码精简之后C++代码如下：
```
class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == NULL) return 0;
return 1 + max(maxDepth(root->left), maxDepth(root->right));
}
};
```
**精简之后的代码根本看不出是哪种遍历方式，也看不出递归三部曲的步骤，所以如果对二叉树的操作还不熟练，尽量不要直接照着精简代码来学。**
## 迭代法
使用迭代法的话，使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。
在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，如图所示：
![层序遍历](https://img-blog.csdnimg.cn/20200810193056585.png)
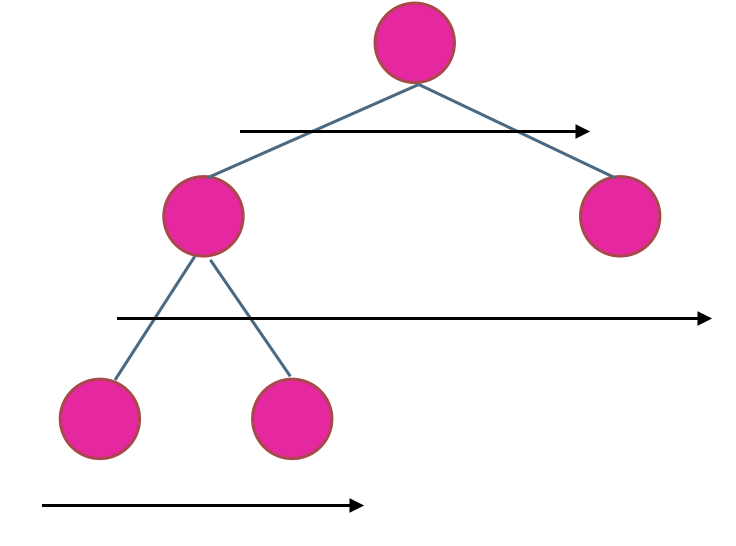
所以这道题依然是一道模板题，依然可以使用二叉树层序遍历的模板来解决的。
所以这道题的迭代法就是一道模板题，可以使用二叉树层序遍历的模板来解决的。
我总结的算法模板会放到这里[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)，大家可以去看一下。
如果对层序遍历还不清楚的话，可以看这篇：[二叉树：层序遍历登场！](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)
代码如下：
## C++代码
### 递归
```
class Solution {
public:
int getDepth(TreeNode* node) {
if (node == NULL) return 0;
return 1 + max(getDepth(node->left), getDepth(node->right));
}
int maxDepth(TreeNode* root) {
return getDepth(root);
}
};
```
### 迭代法
C++代码如下：
```
class Solution {
@ -85,7 +111,7 @@ public:
queue<TreeNode*> que;
que.push(root);
while(!que.empty()) {
int size = que.size(); // 必须要这么写，要固定size大小
int size = que.size();
depth++; // 记录深度
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
@ -99,4 +125,66 @@ public:
};
```
那么我们可以顺便解决一下N叉树的最大深度问题
# 559.N叉树的最大深度
https://leetcode-cn.com/problems/maximum-depth-of-n-ary-tree/
给定一个 N 叉树，找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
例如，给定一个 3叉树 :
<img src='../pics/559.N叉树的最大深度.png' width=600> </img></div>
我们应返回其最大深度，3。
# 思路
依然可以提供递归法和迭代法，来解决这个问题，思路是和二叉树思路一样的，直接给出代码如下：
## 递归法
C++代码：
```
class Solution {
public:
int maxDepth(Node* root) {
if (root == 0) return 0;
int depth = 0;
for (int i = 0; i < root->children.size(); i++) {
depth = max (depth, maxDepth(root->children[i]));
}
return depth + 1;
}
};
```
## 迭代法
依然是层序遍历，代码如下：
```
class Solution {
public:
int maxDepth(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
int depth = 0;
while (!que.empty()) {
int size = que.size();
depth++; // 记录深度
for (int i = 0; i < size; i++) {
Node* node = que.front();
que.pop();
for (int i = 0; i < node->children.size(); i++) {
if (node->children[i]) que.push(node->children[i]);
}
}
}
return depth;
}
};
```
> 更多算法干货文章持续更新，可以微信搜索「代码随想录」第一时间围观，关注后，回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等，就可以获得我多年整理的学习资料。

24
problems/0111.二叉树的最小深度.md
View File

@ -4,15 +4,12 @@ https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/
## 思路
这道题目建议和[0104.二叉树的最大深度](https://github.com/youngyangyang04/leetcode/blob/master/problems/0104.二叉树的最大深度.md)一起来做。
看完了这篇[二叉树：看看这些树的最大深度]()，再来看看如何求最小深度。
直觉上好像和求最大深度差不多，其实还是差挺多的，一起来看一下。
来来来，一起递归三部曲：
* 确定递归函数的参数和返回值
* 确定终止条件
* 确定单层递归的逻辑
1. 确定递归函数的参数和返回值
参数为要传入的二叉树根节点，返回的是int类型的深度。
@ -33,8 +30,21 @@ int getDepth(TreeNode* node)
if (node == NULL) return 0;
```
3. 确定单层递归的逻辑
2. 确定单层递归的逻辑
这块和求最大深度可就不一样了，一些同学可能会写如下代码
```
int leftDepth = getDepth(node->left);
int rightDepth = getDepth(node->right);
if (node->left == NULL && node->right != NULL) { 
    return 1 + rightDepth;
}   
if (node->left != NULL && node->right == NULL) { 
    return 1 + leftDepth;
}
return 1 + min(leftDepth, rightDepth);
```
首先取左右子树的深度，如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。

9
problems/0144.二叉树的前序遍历.md
View File

@ -4,6 +4,15 @@ https://leetcode-cn.com/problems/binary-tree-preorder-traversal/
# 思路
这篇文章，**彻底讲清楚应该如何写递归，并给出了前中后序三种不同的迭代法，然后分析迭代法的代码风格为什么没有统一，最后给出统一的前中后序迭代法的代码，帮大家彻底吃透二叉树的深度优先遍历。**
对二叉树基础理论还不清楚的话，可以看看这个[关于二叉树，你该了解这些！](https://mp.weixin.qq.com/s/_ymfWYvTNd2GvWvC5HOE4A)。
[二叉树：一入递归深似海，从此offer是路人](https://mp.weixin.qq.com/s/PwVIfxDlT3kRgMASWAMGhA)介绍了二叉树的前后中序的递归遍历方式。
[二叉树：听说递归能做的，栈也能做！](https://mp.weixin.qq.com/s/c_zCrGHIVlBjUH_hJtghCg)介绍了二叉树的前后中序迭代写法。
[二叉树：前中后序迭代方式的写法就不能统一一下么？](https://mp.weixin.qq.com/s/WKg0Ty1_3SZkztpHubZPRg) 介绍了二叉树前中后迭代方式的统一写法。
以下开始开始正文：
* 二叉树深度优先遍历
* 前序遍历： [0144.二叉树的前序遍历](https://github.com/youngyangyang04/leetcode/blob/master/problems/0144.二叉树的前序遍历.md)

2
problems/0429.N叉树的层序遍历.md
View File

@ -8,6 +8,8 @@ https://leetcode-cn.com/problems/sum-of-left-leaves/
## C++代码
### 递归法
```
class Solution {
public:

46
problems/0559.N叉树的最大深度.md Normal file
View File

@ -0,0 +1,46 @@
## 地址
## 思路
## C++代码
### 递归法
```
class Solution {
public:
int maxDepth(Node* root) {
if (root == 0) return 0;
int depth = 0;
for (int i = 0; i < root->children.size(); i++) {
depth = max (depth, maxDepth(root->children[i]));
}
return depth + 1;
}
};
```
### 迭代法
```
class Solution {
public:
int maxDepth(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
int depth = 0;
while (!que.empty()) {
int size = que.size();
vector<int> vec;
depth++;
for (int i = 0; i < size; i++) {
Node* node = que.front();
que.pop();
for (int i = 0; i < node->children.size(); i++) {
if (node->children[i]) que.push(node->children[i]);
}
}
}
return depth;
}
};
```