Merge branch 'youngyangyang04:master' into master

problems/0017.电话号码的字母组合.md

@@ -37,7 +37,7 @@
 
 ## 数字和字母如何映射
 
-可以使用map或者定义一个二位数组，例如：string letterMap[10]，来做映射，我这里定义一个二维数组，代码如下：
+可以使用map或者定义一个二维数组，例如：string letterMap[10]，来做映射，我这里定义一个二维数组，代码如下：
 
 ```cpp
 const string letterMap[10] = {

problems/0039.组合总和.md

@@ -455,7 +455,6 @@ func combinationSum(_ candidates: [Int], _ target: Int) -> [[Int]] {
     var path = [Int]()
     func backtracking(sum: Int, startIndex: Int) {
         // 终止条件
-        if sum > target { return }
         if sum == target {
             result.append(path)
             return
@@ -464,8 +463,11 @@ func combinationSum(_ candidates: [Int], _ target: Int) -> [[Int]] {
         let end = candidates.count
         guard startIndex < end else { return }
         for i in startIndex ..< end {
+            let sum = sum + candidates[i] // 使用局部变量隐藏回溯
+            if sum > target { continue } // 剪枝
+
             path.append(candidates[i]) // 处理
-            backtracking(sum: sum + candidates[i], startIndex: i) // sum这里用新变量完成回溯，i不用+1以重复访问
+            backtracking(sum: sum, startIndex: i) // i不用+1以重复访问
             path.removeLast() // 回溯
         }
     }

problems/0077.组合.md

@@ -627,7 +627,7 @@ int** combine(int n, int k, int* returnSize, int** returnColumnSizes){
 func combine(_ n: Int, _ k: Int) -> [[Int]] {
     var path = [Int]()
     var result = [[Int]]()
-    func backtracking(_ n: Int, _ k: Int, _ startIndex: Int) {
+    func backtracking(start: Int) {
         // 结束条件，并收集结果
         if path.count == k {
             result.append(path)
@@ -638,15 +638,15 @@ func combine(_ n: Int, _ k: Int) -> [[Int]] {
         // let end = n
         // 剪枝优化
         let end = n - (k - path.count) + 1
-        guard startIndex <= end else { return }
-        for i in startIndex ... end {
+        guard start <= end else { return }
+        for i in start ... end {
             path.append(i) // 处理结点
-            backtracking(n, k, i + 1) // 递归
+            backtracking(start: i + 1) // 递归
             path.removeLast() // 回溯
         }
     }
 
-    backtracking(n, k, 1)
+    backtracking(start: 1)
     return result
 }
 ```

problems/0077.组合优化.md

@@ -300,7 +300,7 @@ Swift：
 func combine(_ n: Int, _ k: Int) -> [[Int]] {
     var path = [Int]()
     var result = [[Int]]()
-    func backtracking(_ n: Int, _ k: Int, _ startIndex: Int) {
+    func backtracking(start: Int) {
         // 结束条件，并收集结果
         if path.count == k {
             result.append(path)
@@ -311,15 +311,15 @@ func combine(_ n: Int, _ k: Int) -> [[Int]] {
         // let end = n
         // 剪枝优化
         let end = n - (k - path.count) + 1
-        guard startIndex <= end else { return }
-        for i in startIndex ... end {
+        guard start <= end else { return }
+        for i in start ... end {
             path.append(i) // 处理结点
-            backtracking(n, k, i + 1) // 递归
+            backtracking(start: i + 1) // 递归
             path.removeLast() // 回溯
         }
     }
 
-    backtracking(n, k, 1)
+    backtracking(start: 1)
     return result
 }
 ```

problems/0131.分割回文串.md

@@ -575,12 +575,9 @@ func partition(_ s: String) -> [[String]] {
 
         for i in startIndex ..< s.count {
             // 回文则收集，否则跳过
-            if isPalindrome(start: startIndex, end: i) {
-                let substring = String(s[startIndex ... i])
-                path.append(substring)
-            } else {
-                continue
-            }
+            guard isPalindrome(start: startIndex, end: i) else { continue }
+            let substring = String(s[startIndex ... i])
+            path.append(substring) // 处理
             backtracking(startIndex: i + 1) // 寻找下一个起始位置的子串
             if !path.isEmpty { path.removeLast() } // 回溯
         }

problems/0139.单词拆分.md

@@ -220,7 +220,7 @@ public:
 
 但因为分割子串的特殊性，遍历背包放在外循环，将遍历物品放在内循环更方便一些。
 
-本题其实递推公式都不是重点，遍历顺序才是重点，如果我直接把代码贴出来，估计同学们也会想两个for循环的顺序理所当然就是这样，甚至都不会想为什么遍历背包的for循环为什么在外层。
+本题其实递推公式都不是重点，遍历顺序才是重点，如果我直接把代码贴出来，估计同学们也会想两个for循环的顺序理所当然就是这样，甚至都不会想为什么遍历背包的for循环在外层。
 
 不分析透彻不是Carl的风格啊，哈哈
 

problems/0216.组合总和III.md

@@ -462,7 +462,7 @@ int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes){
 func combinationSum3(_ count: Int, _ targetSum: Int) -> [[Int]] {
     var result = [[Int]]()
     var path = [Int]()
-    func backtracking(sum: Int, startIndex: Int) {
+    func backtracking(sum: Int, start: Int) {
         // 剪枝
         if sum > targetSum { return }
         // 终止条件
@@ -474,16 +474,16 @@ func combinationSum3(_ count: Int, _ targetSum: Int) -> [[Int]] {
         }
 
         // 单层逻辑
-        let endIndex = 9
-        guard startIndex <= endIndex else { return }
-        for i in startIndex ... endIndex {
+        let end = 9
+        guard start <= end else { return }
+        for i in start ... end {
             path.append(i) // 处理
-            backtracking(sum: sum + i, startIndex: i + 1)
+            backtracking(sum: sum + i, start: i + 1)
             path.removeLast() // 回溯
         }
     }
 
-    backtracking(sum: 0, startIndex: 1)
+    backtracking(sum: 0, start: 1)
     return result
 }
 ```

problems/0279.完全平方数.md

@@ -40,7 +40,7 @@
 
 1. 确定dp数组（dp table）以及下标的含义
 
-**dp[i]：和为i的完全平方数的最少数量为dp[i]**
+**dp[j]：和为j的完全平方数的最少数量为dp[j]**
 
 2. 确定递推公式
 
@@ -58,7 +58,7 @@ dp[0]表示 和为0的完全平方数的最小数量，那么dp[0]一定是0。
 
 非0下标的dp[j]应该是多少呢？
 
-从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的，**所以非0下标的dp[i]一定要初始为最大值，这样dp[j]在递推的时候才不会被初始值覆盖**。
+从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的，**所以非0下标的dp[j]一定要初始为最大值，这样dp[j]在递推的时候才不会被初始值覆盖**。
 
 4. 确定遍历顺序
 
@@ -70,9 +70,9 @@ dp[0]表示 和为0的完全平方数的最小数量，那么dp[0]一定是0。
 
 在[动态规划：322. 零钱兑换](https://programmercarl.com/0322.零钱兑换.html)中我们就深入探讨了这个问题，本题也是一样的，是求最小数！
 
-**所以本题外层for遍历背包，里层for遍历物品，还是外层for遍历物品，内层for遍历背包，都是可以的！**
+**所以本题外层for遍历背包，内层for遍历物品，还是外层for遍历物品，内层for遍历背包，都是可以的！**
 
-我这里先给出外层遍历背包，里层遍历物品的代码：
+我这里先给出外层遍历背包，内层遍历物品的代码：
 
 ```CPP
 vector<int> dp(n + 1, INT_MAX);

problems/0322.零钱兑换.md

@@ -81,7 +81,7 @@ dp[0] = 0;
 
 4. 确定遍历顺序
 
-本题求钱币最小个数，**那么钱币有顺序和没有顺序都可以，都不影响钱币的最小个数。**。
+本题求钱币最小个数，**那么钱币有顺序和没有顺序都可以，都不影响钱币的最小个数**。
 
 所以本题并不强调集合是组合还是排列。
 
@@ -170,7 +170,7 @@ public:
 
 这也是我为什么要先讲518.零钱兑换II 然后再讲本题即：322.零钱兑换，这是Carl的良苦用心那。
 
-相信大家看完之后，对背包问题中的遍历顺序又了更深的理解了。
+相信大家看完之后，对背包问题中的遍历顺序有更深的理解了。
 
 
 

problems/0376.摆动序列.md

@@ -261,6 +261,7 @@ func wiggleMaxLength(nums []int) int {
 ```
 
 ### Javascript 
+**贪心**
 ```Javascript
 var wiggleMaxLength = function(nums) {
     if(nums.length <= 1) return nums.length
@@ -277,6 +278,25 @@ var wiggleMaxLength = function(nums) {
     return result
 };
 ```
+**动态规划**
+```Javascript
+var wiggleMaxLength = function(nums) {
+    if (nums.length === 1) return 1; 
+    // 考虑前i个数，当第i个值作为峰谷时的情况（则第i-1是峰顶）
+    let down = 1;
+    // 考虑前i个数，当第i个值作为峰顶时的情况（则第i-1是峰谷）
+    let up = 1;
+    for (let i = 1; i < nums.length; i++) {
+        if (nums[i] < nums[i - 1]) {
+            down = Math.max(up + 1, down);
+        }
+        if (nums[i] > nums[i - 1]) {
+            up = Math.max(down + 1, up)
+        }
+    }
+    return Math.max(down, up);
+};
+```
 
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/0739.每日温度.md

@@ -152,8 +152,7 @@ public:
     vector<int> dailyTemperatures(vector<int>& T) {
         stack<int> st; // 递减栈
         vector<int> result(T.size(), 0);
-        st.push(0);
-        for (int i = 1; i < T.size(); i++) {
+        for (int i = 0; i < T.size(); i++) {
             while (!st.empty() && T[i] > T[st.top()]) { // 注意栈不能为空
                 result[st.top()] = i - st.top();
                 st.pop();

problems/周总结/20210204动规周末总结.md

@@ -85,7 +85,7 @@ public:
 
 关键看遍历顺序。
 
-本题求钱币最小个数，**那么钱币有顺序和没有顺序都可以，都不影响钱币的最小个数。**。
+本题求钱币最小个数，**那么钱币有顺序和没有顺序都可以，都不影响钱币的最小个数**。
 
 所以本题并不强调集合是组合还是排列。
 

problems/周总结/20210225动规周末总结.md

@@ -3,7 +3,7 @@
 
 ## 周一
 
-[动态规划：开始打家劫舍！](https://programmercarl.com/0198.打家劫舍.html)中就是给一个数组相邻之间不能连着偷，如果偷才能得到最大金钱。
+[动态规划：开始打家劫舍！](https://programmercarl.com/0198.打家劫舍.html)中就是给一个数组相邻之间不能连着偷，如何偷才能得到最大金钱。
 
 1. 确定dp数组含义
 
@@ -65,7 +65,7 @@ dp[1] = max(nums[0], nums[1]);
 
 ## 周三
 
-[动态规划：还要打家劫舍！](https://programmercarl.com/0337.打家劫舍III.html)这次是在一颗二叉树上打家劫舍了，条件还是一样的，相临的不能偷。
+[动态规划：还要打家劫舍！](https://programmercarl.com/0337.打家劫舍III.html)这次是在一棵二叉树上打家劫舍了，条件还是一样的，相临的不能偷。
 
 这道题目是树形DP的入门题目，其实树形DP其实就是在树上进行递推公式的推导，没有什么神秘的。
 
@@ -191,12 +191,12 @@ return {val2, val1};
 
 ## 周四
 
-[动态规划：买卖股票的最佳时机](https://programmercarl.com/0121.买卖股票的最佳时机.html) 一段时间，只能买买一次，问最大收益。
+[动态规划：买卖股票的最佳时机](https://programmercarl.com/0121.买卖股票的最佳时机.html) 一段时间，只能买卖一次，问最大收益。
 
-这里我给出了三中解法：
+这里我给出了三种解法：
 
 暴力解法代码：
-```
+```CPP
 class Solution {
 public:
     int maxProfit(vector<int>& prices) {

problems/回溯总结.md

@@ -331,7 +331,7 @@ used数组可是全局变量，每层与每层之间公用一个used数组，所
 
 在[回溯算法：N皇后问题](https://programmercarl.com/0051.N皇后.html)中终于迎来了传说中的N皇后。
 
-下面我用一个3 * 3 的棋牌，将搜索过程抽象为一颗树，如图：
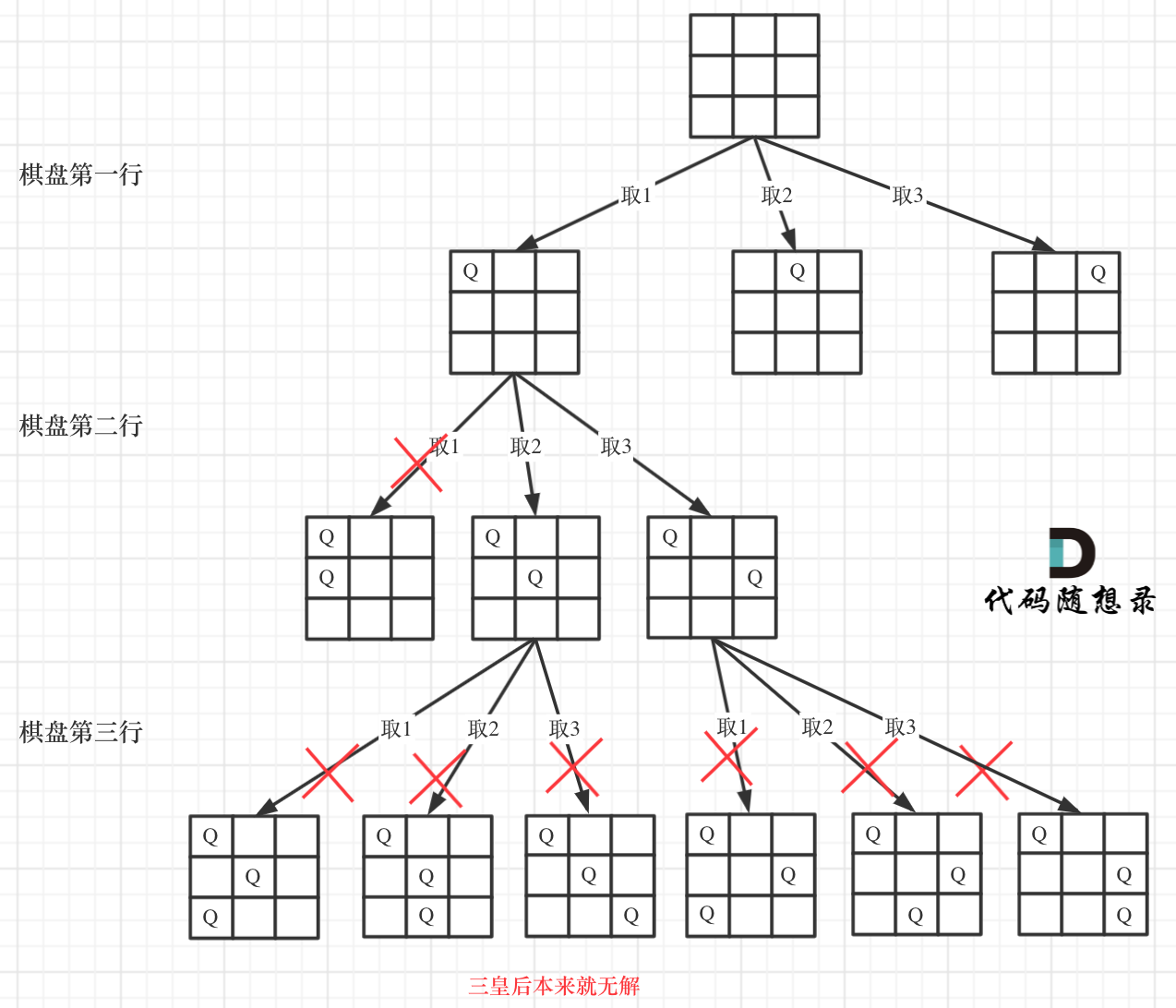
+下面我用一个3 * 3 的棋盘，将搜索过程抽象为一颗树，如图：
 
 ![51.N皇后](https://img-blog.csdnimg.cn/20201118225433127.png)
 
@@ -437,20 +437,5 @@ N皇后问题分析：
 **回溯算法系列正式结束，新的系列终将开始，录友们准备开启新的征程！**
 
 
-
-## 其他语言版本
-
-
-Java：
-
-
-Python：
-
-
-Go：
-
-
-
-
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/背包问题理论基础多重背包.md

@@ -7,7 +7,7 @@
 
 # 动态规划：关于多重背包，你该了解这些！
 
-之前我们已经体统的讲解了01背包和完全背包，如果没有看过的录友，建议先把如下三篇文章仔细阅读一波。
+之前我们已经系统的讲解了01背包和完全背包，如果没有看过的录友，建议先把如下三篇文章仔细阅读一波。
 
 * [动态规划：关于01背包问题，你该了解这些！](https://programmercarl.com/背包理论基础01背包-1.html)
 * [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)

problems/背包问题理论基础完全背包.md

@@ -177,41 +177,41 @@ int main() {
 Java：
 
 ```java
-		//先遍历物品，再遍历背包
-    private static void testCompletePack(){
-        int[] weight = {1, 3, 4};
-        int[] value = {15, 20, 30};
-        int bagWeight = 4;
-        int[] dp = new int[bagWeight + 1];
-        for (int i = 0; i < weight.length; i++){
-            for (int j = 1; j <= bagWeight; j++){
-                if (j - weight[i] >= 0){
-                    dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
-                }
+//先遍历物品，再遍历背包
+private static void testCompletePack(){
+    int[] weight = {1, 3, 4};
+    int[] value = {15, 20, 30};
+    int bagWeight = 4;
+    int[] dp = new int[bagWeight + 1];
+    for (int i = 0; i < weight.length; i++){
+        for (int j = 1; j <= bagWeight; j++){
+            if (j - weight[i] >= 0){
+                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
             }
         }
-        for (int maxValue : dp){
-            System.out.println(maxValue + "   ");
-        }
     }
+    for (int maxValue : dp){
+        System.out.println(maxValue + "   ");
+    }
+}
 
-    //先遍历背包，再遍历物品
-    private static void testCompletePackAnotherWay(){
-        int[] weight = {1, 3, 4};
-        int[] value = {15, 20, 30};
-        int bagWeight = 4;
-        int[] dp = new int[bagWeight + 1];
-        for (int i = 1; i <= bagWeight; i++){
-            for (int j = 0; j < weight.length; j++){
-                if (i - weight[j] >= 0){
-                    dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
-                }
+//先遍历背包，再遍历物品
+private static void testCompletePackAnotherWay(){
+    int[] weight = {1, 3, 4};
+    int[] value = {15, 20, 30};
+    int bagWeight = 4;
+    int[] dp = new int[bagWeight + 1];
+    for (int i = 1; i <= bagWeight; i++){
+        for (int j = 0; j < weight.length; j++){
+            if (i - weight[j] >= 0){
+                dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
             }
         }
-        for (int maxValue : dp){
-            System.out.println(maxValue + "   ");
-        }
     }
+    for (int maxValue : dp){
+        System.out.println(maxValue + "   ");
+    }
+}
 ```