mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-09 03:34:02 +08:00
Merge branch 'youngyangyang04:master' into master
This commit is contained in:
@ -639,7 +639,46 @@ func reverse(b []byte) {
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```go
|
||||
//双指针解法。指针逆序遍历,将遍历后得到的单词(间隔为空格,用以区分)顺序放置在额外空间
|
||||
//时间复杂度O(n),空间复杂度O(n)
|
||||
func reverseWords(s string) string {
|
||||
strBytes := []byte(s)
|
||||
n := len(strBytes)
|
||||
// 记录有效字符范围的起始和结束位置
|
||||
start, end := 0, n-1
|
||||
// 去除开头空格
|
||||
for start < n && strBytes[start] == 32 {
|
||||
start++
|
||||
}
|
||||
// 处理全是空格或空字符串情况
|
||||
if start == n {
|
||||
return ""
|
||||
}
|
||||
// 去除结尾空格
|
||||
for end >= 0 && strBytes[end] == 32 {
|
||||
end--
|
||||
}
|
||||
// 结果切片,预分配容量
|
||||
res := make([]byte, 0, end-start+1)//这里挺重要的,本人之前没有预分配容量,每次循环都添加单词,导致内存超限(也可能就是我之前的思路有问题)
|
||||
// 从后往前遍历有效字符范围
|
||||
for i := end; i >= start; {
|
||||
// 找单词起始位置,直接通过循环条件判断定位
|
||||
for ; i >= start && strBytes[i] == 32; i-- {
|
||||
}
|
||||
j := i
|
||||
for ; j >= start && strBytes[j]!= 32; j-- {
|
||||
}
|
||||
res = append(res, strBytes[j+1:i+1]...)
|
||||
// 只在不是最后一个单词时添加空格
|
||||
if j > start {
|
||||
res = append(res, 32)
|
||||
}
|
||||
i = j
|
||||
}
|
||||
return string(res)
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
### JavaScript:
|
||||
|
||||
@ -60,7 +60,7 @@
|
||||
* [动态规划:关于01背包问题,你该了解这些!](https://programmercarl.com/背包理论基础01背包-1.html)
|
||||
* [动态规划:关于01背包问题,你该了解这些!(滚动数组)](https://programmercarl.com/背包理论基础01背包-2.html)
|
||||
|
||||
### 01背包问题
|
||||
## 01背包问题
|
||||
|
||||
01背包问题,大家都知道,有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
|
||||
|
||||
@ -92,7 +92,7 @@
|
||||
|
||||
动规五部曲分析如下:
|
||||
|
||||
1. 确定dp数组以及下标的含义
|
||||
### 1. 确定dp数组以及下标的含义
|
||||
|
||||
01背包中,dp[j] 表示: 容量(所能装的重量)为j的背包,所背的物品价值最大可以为dp[j]。
|
||||
|
||||
@ -104,7 +104,7 @@
|
||||
|
||||
而dp[6] 就可以等于6了,放进1 和 5,那么dp[6] == 6,说明背包装满了。
|
||||
|
||||
2. 确定递推公式
|
||||
### 2. 确定递推公式
|
||||
|
||||
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
|
||||
|
||||
@ -113,7 +113,7 @@
|
||||
所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
|
||||
|
||||
|
||||
3. dp数组如何初始化
|
||||
### 3. dp数组如何初始化
|
||||
|
||||
在01背包,一维dp如何初始化,已经讲过,
|
||||
|
||||
@ -133,7 +133,7 @@
|
||||
vector<int> dp(10001, 0);
|
||||
```
|
||||
|
||||
4. 确定遍历顺序
|
||||
### 4. 确定遍历顺序
|
||||
|
||||
在[动态规划:关于01背包问题,你该了解这些!(滚动数组)](https://programmercarl.com/背包理论基础01背包-2.html)中就已经说明:如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
|
||||
|
||||
@ -148,7 +148,7 @@ for(int i = 0; i < nums.size(); i++) {
|
||||
}
|
||||
```
|
||||
|
||||
5. 举例推导dp数组
|
||||
### 5. 举例推导dp数组
|
||||
|
||||
dp[j]的数值一定是小于等于j的。
|
||||
|
||||
|
||||
@ -689,6 +689,29 @@ var repeatedSubstringPattern = function (s) {
|
||||
};
|
||||
```
|
||||
|
||||
> 正则匹配
|
||||
```javascript
|
||||
/**
|
||||
* @param {string} s
|
||||
* @return {boolean}
|
||||
*/
|
||||
var repeatedSubstringPattern = function(s) {
|
||||
let reg = /^(\w+)\1+$/
|
||||
return reg.test(s)
|
||||
};
|
||||
```
|
||||
> 移动匹配
|
||||
```javascript
|
||||
/**
|
||||
* @param {string} s
|
||||
* @return {boolean}
|
||||
*/
|
||||
var repeatedSubstringPattern = function (s) {
|
||||
let ss = s + s;
|
||||
return ss.substring(1, ss.length - 1).includes(s);
|
||||
};
|
||||
```
|
||||
|
||||
### TypeScript:
|
||||
|
||||
> 前缀表统一减一
|
||||
@ -894,8 +917,10 @@ impl Solution {
|
||||
}
|
||||
```
|
||||
### C#
|
||||
|
||||
> 前缀表不减一
|
||||
|
||||
```csharp
|
||||
// 前缀表不减一
|
||||
public bool RepeatedSubstringPattern(string s)
|
||||
{
|
||||
if (s.Length == 0)
|
||||
@ -920,6 +945,13 @@ public int[] GetNext(string s)
|
||||
}
|
||||
```
|
||||
|
||||
> 移动匹配
|
||||
```csharp
|
||||
public bool RepeatedSubstringPattern(string s) {
|
||||
string ss = (s + s).Substring(1, (s + s).Length - 2);
|
||||
return ss.Contains(s);
|
||||
}
|
||||
```
|
||||
### C
|
||||
|
||||
```c
|
||||
|
||||
@ -44,7 +44,7 @@
|
||||
|
||||
这里其实涉及到dfs的两种写法。
|
||||
|
||||
写法一,dfs只处理下一个节点,即在主函数遇到岛屿就计数为1,dfs处理接下来的相邻陆地
|
||||
写法一,dfs处理当前节点的相邻节点,即在主函数遇到岛屿就计数为1,dfs处理接下来的相邻陆地
|
||||
|
||||
```CPP
|
||||
// 版本一
|
||||
@ -87,7 +87,7 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
写法二,dfs处理当前节点,即即在主函数遇到岛屿就计数为0,dfs处理接下来的全部陆地
|
||||
写法二,dfs处理当前节点,即在主函数遇到岛屿就计数为0,dfs处理接下来的全部陆地
|
||||
|
||||
dfs
|
||||
```CPP
|
||||
|
||||
@ -1191,6 +1191,160 @@ MyLinkedList.prototype.deleteAtIndex = function(index) {
|
||||
*/
|
||||
```
|
||||
|
||||
```js
|
||||
/**
|
||||
定义双头节点的结构:同时包含前指针`prev`和后指针next`
|
||||
*/
|
||||
class Node {
|
||||
constructor(val, prev, next) {
|
||||
this.val = val
|
||||
this.prev = prev
|
||||
this.next = next
|
||||
}
|
||||
}
|
||||
|
||||
/**
|
||||
双链表:维护 `head` 和 `tail` 两个哨兵节点,这样可以简化对于中间节点的操作
|
||||
并且维护 `size`,使得能够以O(1)时间判断操作是否合法
|
||||
*/
|
||||
var MyLinkedList = function () {
|
||||
this.tail = new Node(-1)
|
||||
this.head = new Node(-1)
|
||||
this.tail.prev = this.head
|
||||
this.head.next = this.tail
|
||||
this.size = 0
|
||||
};
|
||||
|
||||
/**
|
||||
* 获取在index处节点的值
|
||||
*
|
||||
* @param {number} index
|
||||
* @return {number}
|
||||
*
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
*/
|
||||
MyLinkedList.prototype.get = function (index) {
|
||||
// 当索引超出范围时,返回-1
|
||||
if (index > this.size) {
|
||||
return -1
|
||||
}
|
||||
|
||||
let cur = this.head
|
||||
for (let i = 0; i <= index; i++) {
|
||||
cur = cur.next
|
||||
}
|
||||
|
||||
return cur.val
|
||||
};
|
||||
|
||||
/**
|
||||
* 在链表头部添加一个新节点
|
||||
*
|
||||
* @param {number} val
|
||||
* @return {void}
|
||||
*
|
||||
* 时间复杂度: O(1)
|
||||
* 空间复杂度: O(1)
|
||||
*/
|
||||
MyLinkedList.prototype.addAtHead = function (val) {
|
||||
/**
|
||||
head <-> [newNode] <-> originNode
|
||||
*/
|
||||
this.size++
|
||||
const originNode = this.head.next
|
||||
// 创建新节点,并建立连接
|
||||
const newNode = new Node(val, this.head, originNode)
|
||||
|
||||
// 取消原前后结点的连接
|
||||
this.head.next = newNode
|
||||
originNode.prev = newNode
|
||||
};
|
||||
|
||||
/**
|
||||
* 在链表尾部添加一个新节点
|
||||
*
|
||||
* @param {number} val
|
||||
* @return {void}
|
||||
*
|
||||
* 时间复杂度: O(1)
|
||||
* 空间复杂度: O(1)
|
||||
*/
|
||||
MyLinkedList.prototype.addAtTail = function (val) {
|
||||
/**
|
||||
originNode <-> [newNode] <-> tail
|
||||
*/
|
||||
this.size++
|
||||
const originNode = this.tail.prev
|
||||
|
||||
// 创建新节点,并建立连接
|
||||
const newNode = new Node(val, originNode, this.tail)
|
||||
|
||||
// 取消原前后结点的连接
|
||||
this.tail.prev = newNode
|
||||
originNode.next = newNode
|
||||
};
|
||||
|
||||
/**
|
||||
* 在指定索引位置前添加一个新节点
|
||||
*
|
||||
* @param {number} index
|
||||
* @param {number} val
|
||||
* @return {void}
|
||||
*
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
*/
|
||||
MyLinkedList.prototype.addAtIndex = function (index, val) {
|
||||
// 当索引超出范围时,直接返回
|
||||
if (index > this.size) {
|
||||
return
|
||||
}
|
||||
this.size++
|
||||
|
||||
let cur = this.head
|
||||
for (let i = 0; i < index; i++) {
|
||||
cur = cur.next
|
||||
}
|
||||
|
||||
const new_next = cur.next
|
||||
|
||||
// 创建新节点,并建立连接
|
||||
const node = new Node(val, cur, new_next)
|
||||
|
||||
// 取消原前后结点的连接
|
||||
cur.next = node
|
||||
new_next.prev = node
|
||||
};
|
||||
|
||||
/**
|
||||
* 删除指定索引位置的节点
|
||||
*
|
||||
* @param {number} index
|
||||
* @return {void}
|
||||
*
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
*/
|
||||
MyLinkedList.prototype.deleteAtIndex = function (index) {
|
||||
// 当索引超出范围时,直接返回
|
||||
if (index >= this.size) {
|
||||
return
|
||||
}
|
||||
|
||||
this.size--
|
||||
let cur = this.head
|
||||
for (let i = 0; i < index; i++) {
|
||||
cur = cur.next
|
||||
}
|
||||
|
||||
const new_next = cur.next.next
|
||||
// 取消原前后结点的连接
|
||||
new_next.prev = cur
|
||||
cur.next = new_next
|
||||
};
|
||||
```
|
||||
|
||||
### TypeScript:
|
||||
|
||||
```TypeScript
|
||||
|
||||
@ -273,22 +273,20 @@ class Solution:
|
||||
### Go
|
||||
```go
|
||||
func monotoneIncreasingDigits(n int) int {
|
||||
s := strconv.Itoa(N)//将数字转为字符串,方便使用下标
|
||||
ss := []byte(s)//将字符串转为byte数组,方便更改。
|
||||
n := len(ss)
|
||||
if n <= 1 {
|
||||
return n
|
||||
}
|
||||
for i := n-1; i > 0; i-- {
|
||||
if ss[i-1] > ss[i] { //前一个大于后一位,前一位减1,后面的全部置为9
|
||||
ss[i-1] -= 1
|
||||
for j := i; j < n; j++ { //后面的全部置为9
|
||||
ss[j] = '9'
|
||||
}
|
||||
}
|
||||
}
|
||||
res, _ := strconv.Atoi(string(ss))
|
||||
return res
|
||||
s := strconv.Itoa(n)
|
||||
// 从左到右遍历字符串,找到第一个不满足单调递增的位置
|
||||
for i := len(s) - 2; i >= 0; i-- {
|
||||
if s[i] > s[i+1] {
|
||||
// 将该位置的数字减1
|
||||
s = s[:i] + string(s[i]-1) + s[i+1:]
|
||||
// 将该位置之后的所有数字置为9
|
||||
for j := i + 1; j < len(s); j++ {
|
||||
s = s[:j] + "9" + s[j+1:]
|
||||
}
|
||||
}
|
||||
}
|
||||
result, _ := strconv.Atoi(s)
|
||||
return result
|
||||
}
|
||||
```
|
||||
|
||||
@ -447,3 +445,4 @@ public class Solution
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
@ -527,3 +527,89 @@ int main()
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
前缀和
|
||||
|
||||
```go
|
||||
package main
|
||||
|
||||
import (
|
||||
"fmt"
|
||||
"os"
|
||||
"bufio"
|
||||
"strings"
|
||||
"strconv"
|
||||
"math"
|
||||
)
|
||||
|
||||
func main() {
|
||||
var n, m int
|
||||
|
||||
reader := bufio.NewReader(os.Stdin)
|
||||
|
||||
line, _ := reader.ReadString('\n')
|
||||
line = strings.TrimSpace(line)
|
||||
params := strings.Split(line, " ")
|
||||
|
||||
n, _ = strconv.Atoi(params[0])
|
||||
m, _ = strconv.Atoi(params[1])//n和m读取完成
|
||||
|
||||
land := make([][]int, n)//土地矩阵初始化
|
||||
|
||||
for i := 0; i < n; i++ {
|
||||
line, _ := reader.ReadString('\n')
|
||||
line = strings.TrimSpace(line)
|
||||
values := strings.Split(line, " ")
|
||||
land[i] = make([]int, m)
|
||||
for j := 0; j < m; j++ {
|
||||
value, _ := strconv.Atoi(values[j])
|
||||
land[i][j] = value
|
||||
}
|
||||
}//所有读取完成
|
||||
|
||||
//初始化前缀和矩阵
|
||||
preMatrix := make([][]int, n+1)
|
||||
for i := 0; i <= n; i++ {
|
||||
preMatrix[i] = make([]int, m+1)
|
||||
}
|
||||
|
||||
for a := 1; a < n+1; a++ {
|
||||
for b := 1; b < m+1; b++ {
|
||||
preMatrix[a][b] = land[a-1][b-1] + preMatrix[a-1][b] + preMatrix[a][b-1] - preMatrix[a-1][b-1]
|
||||
}
|
||||
}
|
||||
|
||||
totalSum := preMatrix[n][m]
|
||||
|
||||
minDiff := math.MaxInt32//初始化极大数,用于比较
|
||||
|
||||
//按行分割
|
||||
for i := 1; i < n; i++ {
|
||||
topSum := preMatrix[i][m]
|
||||
|
||||
bottomSum := totalSum - topSum
|
||||
|
||||
diff := int(math.Abs(float64(topSum - bottomSum)))
|
||||
if diff < minDiff {
|
||||
minDiff = diff
|
||||
}
|
||||
}
|
||||
|
||||
//按列分割
|
||||
for j := 1; j < m; j++ {
|
||||
topSum := preMatrix[n][j]
|
||||
|
||||
bottomSum := totalSum - topSum
|
||||
|
||||
diff := int(math.Abs(float64(topSum - bottomSum)))
|
||||
if diff < minDiff {
|
||||
minDiff = diff
|
||||
}
|
||||
}
|
||||
|
||||
fmt.Println(minDiff)
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
@ -7,7 +7,7 @@
|
||||
|
||||
【题目描述】
|
||||
|
||||
给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个函数,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
|
||||
给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个程序,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
|
||||
|
||||
【输入描述】
|
||||
|
||||
|
||||
@ -72,7 +72,7 @@
|
||||
|
||||
如果从队列拿出节点,再去标记这个节点走过,就会发生下图所示的结果,会导致很多节点重复加入队列。
|
||||
|
||||
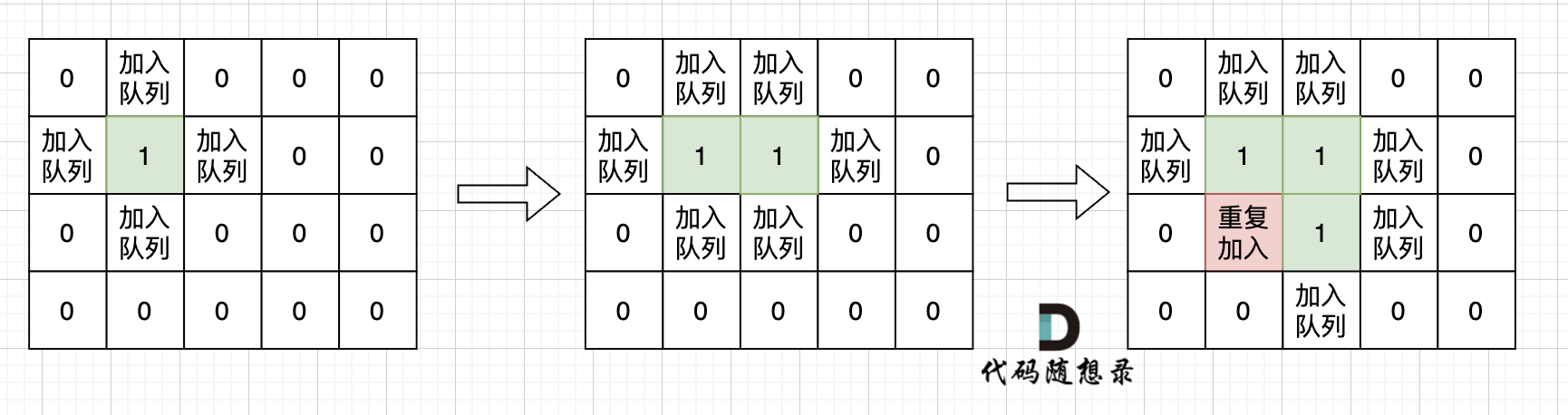
|
||||

|
||||
|
||||
超时写法 (从队列中取出节点再标记,注意代码注释的地方)
|
||||
|
||||
|
||||
@ -63,7 +63,7 @@
|
||||
|
||||
这里其实涉及到dfs的两种写法。
|
||||
|
||||
写法一,dfs只处理下一个节点,即在主函数遇到岛屿就计数为1,dfs处理接下来的相邻陆地
|
||||
写法一,dfs处理当前节点的相邻节点,即在主函数遇到岛屿就计数为1,dfs处理接下来的相邻陆地
|
||||
|
||||
```CPP
|
||||
// 版本一
|
||||
|
||||
@ -72,10 +72,8 @@
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
|
||||
int count; // 统计符合题目要求的陆地空格数量
|
||||
void dfs(vector<vector<int>>& grid, int x, int y) {
|
||||
grid[x][y] = 0;
|
||||
count++;
|
||||
for (int i = 0; i < 4; i++) { // 向四个方向遍历
|
||||
int nextx = x + dir[i][0];
|
||||
int nexty = y + dir[i][1];
|
||||
@ -109,16 +107,17 @@ int main() {
|
||||
if (grid[0][j] == 1) dfs(grid, 0, j);
|
||||
if (grid[n - 1][j] == 1) dfs(grid, n - 1, j);
|
||||
}
|
||||
count = 0;
|
||||
int count = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == 1) dfs(grid, i, j);
|
||||
if (grid[i][j] == 1) count++;
|
||||
}
|
||||
}
|
||||
cout << count << endl;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
采用广度优先搜索的代码如下:
|
||||
|
||||
```CPP
|
||||
@ -126,13 +125,11 @@ int main() {
|
||||
#include <vector>
|
||||
#include <queue>
|
||||
using namespace std;
|
||||
int count = 0;
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void bfs(vector<vector<int>>& grid, int x, int y) {
|
||||
queue<pair<int, int>> que;
|
||||
que.push({x, y});
|
||||
grid[x][y] = 0; // 只要加入队列,立刻标记
|
||||
count++;
|
||||
while(!que.empty()) {
|
||||
pair<int ,int> cur = que.front(); que.pop();
|
||||
int curx = cur.first;
|
||||
@ -143,7 +140,6 @@ void bfs(vector<vector<int>>& grid, int x, int y) {
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
|
||||
if (grid[nextx][nexty] == 1) {
|
||||
que.push({nextx, nexty});
|
||||
count++;
|
||||
grid[nextx][nexty] = 0; // 只要加入队列立刻标记
|
||||
}
|
||||
}
|
||||
@ -169,15 +165,16 @@ int main() {
|
||||
if (grid[0][j] == 1) bfs(grid, 0, j);
|
||||
if (grid[n - 1][j] == 1) bfs(grid, n - 1, j);
|
||||
}
|
||||
count = 0;
|
||||
int count = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == 1) bfs(grid, i, j);
|
||||
if (grid[i][j] == 1) count++;
|
||||
}
|
||||
}
|
||||
|
||||
cout << count << endl;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
|
||||
|
||||
@ -162,7 +162,7 @@ if (终止条件) {
|
||||
|
||||
终止添加不仅是结束本层递归,同时也是我们收获结果的时候。
|
||||
|
||||
另外,其实很多dfs写法,没有写终止条件,其实终止条件写在了, 下面dfs递归的逻辑里了,也就是不符合条件,直接不会向下递归。这里如果大家不理解的话,没关系,后面会有具体题目来讲解。
|
||||
另外,其实很多dfs写法,没有写终止条件,其实终止条件写在了, 隐藏在下面dfs递归的逻辑里了,也就是不符合条件,直接不会向下递归。这里如果大家不理解的话,没关系,后面会有具体题目来讲解。
|
||||
|
||||
3. 处理目前搜索节点出发的路径
|
||||
|
||||
|
||||
@ -128,6 +128,29 @@
|
||||
|
||||
主要是 朴素存储、邻接表和邻接矩阵。
|
||||
|
||||
关于朴素存储,这是我自创的名字,因为这种存储方式,就是将所有边存下来。
|
||||
|
||||
例如图:
|
||||
|
||||

|
||||
|
||||
图中有8条边,我们就定义 8 * 2的数组,即有n条边就申请n * 2,这么大的数组:
|
||||
|
||||

|
||||
|
||||
数组第一行:6 7,就表示节点6 指向 节点7,以此类推。
|
||||
|
||||
当然可以不用数组,用map,或者用 类 到可以表示出 这种边的关系。
|
||||
|
||||
这种表示方式的好处就是直观,把节点与节点之间关系很容易展现出来。
|
||||
|
||||
但如果我们想知道 节点1 和 节点6 是否相连,我们就需要把存储空间都枚举一遍才行。
|
||||
|
||||
这是明显的缺点,同时,我们在深搜和广搜的时候,都不会使用这种存储方式。
|
||||
|
||||
因为 搜索中,需要知道 节点与其他节点的链接情况,而这种朴素存储,都需要全部枚举才知道链接情况。
|
||||
|
||||
在图论章节的后面文章讲解中,我会举例说明的。大家先有个印象。
|
||||
|
||||
### 邻接矩阵
|
||||
|
||||
|
||||
@ -316,7 +316,51 @@ print(knapsack(n, bag_weight, weight, value))
|
||||
|
||||
### JavaScript
|
||||
|
||||
```js
|
||||
const readline = require('readline').createInterface({
|
||||
input: process.stdin,
|
||||
output: process.stdout
|
||||
});
|
||||
|
||||
let input = [];
|
||||
readline.on('line', (line) => {
|
||||
input.push(line.trim());
|
||||
});
|
||||
|
||||
readline.on('close', () => {
|
||||
// 第一行解析 n 和 v
|
||||
const [n, bagweight] = input[0].split(' ').map(Number);
|
||||
|
||||
/// 剩余 n 行解析重量和价值
|
||||
const weight = [];
|
||||
const value = [];
|
||||
for (let i = 1; i <= n; i++) {
|
||||
const [wi, vi] = input[i].split(' ').map(Number);
|
||||
weight.push(wi);
|
||||
value.push(vi);
|
||||
}
|
||||
|
||||
|
||||
let dp = Array.from({ length: n }, () => Array(bagweight + 1).fill(0));
|
||||
|
||||
for (let j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = dp[0][j-weight[0]] + value[0];
|
||||
}
|
||||
|
||||
for (let i = 1; i < n; i++) {
|
||||
for (let j = 0; j <= bagweight; j++) {
|
||||
if (j < weight[i]) {
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
console.log(dp[n - 1][bagweight]);
|
||||
});
|
||||
|
||||
```
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
|
||||
Reference in New Issue
Block a user