Merge branch 'youngyangyang04:master' into master

problems/0017.电话号码的字母组合.md

@@ -420,6 +420,40 @@ var letterCombinations = function(digits) {
 };
 ```
 
+## TypeScript
+
+```typescript
+function letterCombinations(digits: string): string[] {
+    if (digits === '') return [];
+    const strMap: { [index: string]: string[] } = {
+        1: [],
+        2: ['a', 'b', 'c'],
+        3: ['d', 'e', 'f'],
+        4: ['g', 'h', 'i'],
+        5: ['j', 'k', 'l'],
+        6: ['m', 'n', 'o'],
+        7: ['p', 'q', 'r', 's'],
+        8: ['t', 'u', 'v'],
+        9: ['w', 'x', 'y', 'z'],
+    }
+    const resArr: string[] = [];
+    function backTracking(digits: string, curIndex: number, route: string[]): void {
+        if (curIndex === digits.length) {
+            resArr.push(route.join(''));
+            return;
+        }
+        let tempArr: string[] = strMap[digits[curIndex]];
+        for (let i = 0, length = tempArr.length; i < length; i++) {
+            route.push(tempArr[i]);
+            backTracking(digits, curIndex + 1, route);
+            route.pop();
+        }
+    }
+    backTracking(digits, 0, []);
+    return resArr;
+};
+```
+
 ## C
 
 ```c

problems/0039.组合总和.md

@@ -392,7 +392,34 @@ var combinationSum = function(candidates, target) {
 };
 ```
 
+## TypeScript
+
+```typescript
+function combinationSum(candidates: number[], target: number): number[][] {
+    const resArr: number[][] = [];
+    function backTracking(
+        candidates: number[], target: number,
+        startIndex: number, route: number[], curSum: number
+    ): void {
+        if (curSum > target) return;
+        if (curSum === target) {
+            resArr.push(route.slice());
+            return
+        }
+        for (let i = startIndex, length = candidates.length; i < length; i++) {
+            let tempVal: number = candidates[i];
+            route.push(tempVal);
+            backTracking(candidates, target, i, route, curSum + tempVal);
+            route.pop();
+        }
+    }
+    backTracking(candidates, target, 0, [], 0);
+    return resArr;
+};
+```
+
 ## C 
+
 ```c
 int* path;
 int pathTop;

problems/0040.组合总和II.md

@@ -532,6 +532,7 @@ var combinationSum2 = function(candidates, target) {
 };
 ```
 **使用used去重**
+
 ```js
 var combinationSum2 = function(candidates, target) {
     let res = [];
@@ -562,6 +563,37 @@ var combinationSum2 = function(candidates, target) {
 };
 ```
 
+## TypeScript
+
+```typescript
+function combinationSum2(candidates: number[], target: number): number[][] {
+    candidates.sort((a, b) => a - b);
+    const resArr: number[][] = [];
+    function backTracking(
+        candidates: number[], target: number,
+        curSum: number, startIndex: number, route: number[]
+    ) {
+        if (curSum > target) return;
+        if (curSum === target) {
+            resArr.push(route.slice());
+            return;
+        }
+        for (let i = startIndex, length = candidates.length; i < length; i++) {
+            if (i > startIndex && candidates[i] === candidates[i - 1]) {
+                continue;
+            }
+            let tempVal: number = candidates[i];
+            route.push(tempVal);
+            backTracking(candidates, target, curSum + tempVal, i + 1, route);
+            route.pop();
+
+        }
+    }
+    backTracking(candidates, target, 0, 0, []);
+    return resArr;
+};
+```
+
 ## C 
 
 ```c

problems/0063.不同路径II.md

@@ -184,8 +184,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n × m)$，n、m 分别为obstacleGrid 长度和宽度
+* 时间复杂度：O(n × m)，n、m 分别为obstacleGrid 长度和宽度
-* 空间复杂度：$O(m)$
+* 空间复杂度：O(m)
 
 
 ## 总结

problems/0123.买卖股票的最佳时机III.md

@@ -148,8 +148,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n)$
+* 时间复杂度：O(n)
-* 空间复杂度：$O(n × 5)$
+* 空间复杂度：O(n × 5)
 
 当然，大家可以看到力扣官方题解里的一种优化空间写法，我这里给出对应的C++版本：
 
@@ -173,8 +173,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n)$
+* 时间复杂度：O(n)
-* 空间复杂度：$O(1)$
+* 空间复杂度：O(1)
 
 大家会发现dp[2]利用的是当天的dp[1]。 但结果也是对的。
 

problems/0127.单词接龙.md

@@ -134,7 +134,29 @@ public int ladderLength(String beginWord, String endWord, List<String> wordList)
 ```
 
 ## Python 
-
+```
+class Solution:
+    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
+        wordSet = set(wordList)
+        if len(wordSet)== 0 or endWord not in wordSet:
+            return 0
+        mapping = {beginWord:1}
+        queue = deque([beginWord]) 
+        while queue:
+            word = queue.popleft()
+            path = mapping[word]
+            for i in range(len(word)):
+                word_list = list(word)
+                for j in range(26):
+                    word_list[i] = chr(ord('a')+j)
+                    newWord = "".join(word_list)
+                    if newWord == endWord:
+                        return path+1
+                    if newWord in wordSet and newWord not in mapping:
+                        mapping[newWord] = path+1
+                        queue.append(newWord)                      
+        return 0
+```
 ## Go 
 
 ## JavaScript

problems/0134.加油站.md

@@ -239,6 +239,30 @@ class Solution {
 
 ### Python 
 ```python
+# 解法1
+class Solution:
+    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
+        n = len(gas)
+        cur_sum = 0
+        min_sum = float('inf')
+        
+        for i in range(n):
+            cur_sum += gas[i] - cost[i]
+            min_sum = min(min_sum, cur_sum)
+        
+        if cur_sum < 0: return -1
+        if min_sum >= 0: return 0
+        
+        for j in range(n - 1, 0, -1):
+            min_sum += gas[j] - cost[j]
+            if min_sum >= 0:
+                return j
+        
+        return -1
+```
+
+```python
+# 解法2
 class Solution:
     def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
         start = 0

problems/0139.单词拆分.md

@@ -207,7 +207,7 @@ public:
 };
 ```
 
-* 时间复杂度：O(n^3)，因为substr返回子串的副本是$O(n)$的复杂度（这里的n是substring的长度）
+* 时间复杂度：O(n^3)，因为substr返回子串的副本是O(n)的复杂度（这里的n是substring的长度）
 * 空间复杂度：O(n)
 
 

problems/0141.环形链表.md

@@ -106,6 +106,21 @@ class Solution:
 ## Go
 
 ```go
+func hasCycle(head *ListNode) bool {
+    if head==nil{
+        return false
+    } //空链表一定不会有环
+    fast:=head
+    slow:=head //快慢指针
+    for fast.Next!=nil&&fast.Next.Next!=nil{
+        fast=fast.Next.Next
+        slow=slow.Next
+        if fast==slow{
+            return true  //快慢指针相遇则有环
+        }
+    }
+    return false
+}
 ```
 
 ### JavaScript

problems/0151.翻转字符串里的单词.md

@@ -79,7 +79,7 @@ void removeExtraSpaces(string& s) {
 
 逻辑很简单，从前向后遍历，遇到空格了就erase。
 
-如果不仔细琢磨一下erase的时间复杂读，还以为以上的代码是$O(n)$的时间复杂度呢。
+如果不仔细琢磨一下erase的时间复杂读，还以为以上的代码是O(n)的时间复杂度呢。
 
 想一下真正的时间复杂度是多少，一个erase本来就是O(n)的操作，erase实现原理题目：[数组：就移除个元素很难么？](https://programmercarl.com/0027.移除元素.html)，最优的算法来移除元素也要O(n)。
 
@@ -222,7 +222,44 @@ public:
 效率：
 <img src='https://code-thinking.cdn.bcebos.com/pics/151_翻转字符串里的单词.png' width=600> </img></div>
 
+```CPP
+//版本二：
+//原理同版本1，更简洁实现。
+class Solution {
+public:
+    void reverse(string& s, int start, int end){ //翻转，区间写法：闭区间 []
+        for (int i = start, j = end; i < j; i++, j--) {
+            swap(s[i], s[j]);
+        }
+    }
 
+    void removeExtraSpaces(string& s) {//去除所有空格并在相邻单词之间添加空格, 快慢指针。
+        int slow = 0;   //整体思想参考Leetcode: 27. 移除元素：https://leetcode-cn.com/problems/remove-element/
+        for (int i = 0; i < s.size(); ++i) { //
+            if (s[i] != ' ') { //遇到非空格就处理，即删除所有空格。
+                if (slow != 0) s[slow++] = ' '; //手动控制空格，给单词之间添加空格。slow != 0说明不是第一个单词，需要在单词前添加空格。
+                while (i < s.size() && s[i] != ' ') { //补上该单词，遇到空格说明单词结束。
+                    s[slow++] = s[i++];
+                }
+            }
+        }
+        s.resize(slow); //slow的大小即为去除多余空格后的大小。
+    }
+
+    string reverseWords(string s) {
+        removeExtraSpaces(s); //去除多余空格，保证单词之间之只有一个空格，且字符串首尾没空格。
+        reverse(s, 0, s.size() - 1);
+        int start = 0; //removeExtraSpaces后保证第一个单词的开始下标一定是0。
+        for (int i = 0; i <= s.size(); ++i) {
+            if (i == s.size() || s[i] == ' ') { //到达空格或者串尾，说明一个单词结束。进行翻转。
+                reverse(s, start, i - 1); //翻转，注意是左闭右闭 []的翻转。
+                start = i + 1; //更新下一个单词的开始下标start
+            }
+        }
+        return s;
+    }
+};
+```
 
 ## 其他语言版本
 

problems/0189.旋转数组.md

@@ -124,6 +124,19 @@ class Solution:
 ## Go
 
 ```go
+func rotate(nums []int, k int)  {
+    l:=len(nums)
+    index:=l-k%l
+    reverse(nums)
+    reverse(nums[:l-index])
+    reverse(nums[l-index:])
+}
+func reverse(nums []int){
+    l:=len(nums)
+    for i:=0;i<l/2;i++{
+        nums[i],nums[l-1-i]=nums[l-1-i],nums[i]
+    }
+}
 ```
 
 ## JavaScript

problems/0216.组合总和III.md

@@ -396,6 +396,30 @@ var combinationSum3 = function(k, n) {
 };
 ```
 
+## TypeScript
+
+```typescript
+function combinationSum3(k: number, n: number): number[][] {
+    const resArr: number[][] = [];
+    function backTracking(k: number, n: number, sum: number, startIndex: number, tempArr: number[]): void {
+        if (sum > n) return;
+        if (tempArr.length === k) {
+            if (sum === n) {
+                resArr.push(tempArr.slice());
+            }
+            return;
+        }
+        for (let i = startIndex; i <= 9 - (k - tempArr.length) + 1; i++) {
+            tempArr.push(i);
+            backTracking(k, n, sum + i, i + 1, tempArr);
+            tempArr.pop();
+        }
+    }
+    backTracking(k, n, 0, 1, []);
+    return resArr;
+};
+```
+
 ## C
 
 ```c

problems/0332.重新安排行程.md

@@ -342,6 +342,64 @@ class Solution:
         return path
 ```
 
+### Go
+```go
+type pair struct {
+	target  string
+	visited bool
+}
+type pairs []*pair
+
+func (p pairs) Len() int {
+	return len(p)
+}
+func (p pairs) Swap(i, j int) {
+	p[i], p[j] = p[j], p[i]
+}
+func (p pairs) Less(i, j int) bool {
+	return p[i].target < p[j].target
+}
+
+func findItinerary(tickets [][]string) []string {
+	result := []string{}
+	// map[出发机场] pair{目的地,是否被访问过}
+	targets := make(map[string]pairs)
+	for _, ticket := range tickets {
+		if targets[ticket[0]] == nil {
+			targets[ticket[0]] = make(pairs, 0)
+		}
+		targets[ticket[0]] = append(targets[ticket[0]], &pair{target: ticket[1], visited: false})
+	}
+	for k, _ := range targets {
+		sort.Sort(targets[k])
+	}
+	result = append(result, "JFK")
+	var backtracking func() bool
+	backtracking = func() bool {
+		if len(tickets)+1 == len(result) {
+			return true
+		}
+		// 取出起飞航班对应的目的地
+		for _, pair := range targets[result[len(result)-1]] {
+			if pair.visited == false {
+				result = append(result, pair.target)
+				pair.visited = true
+				if backtracking() {
+					return true
+				}
+				result = result[:len(result)-1]
+				pair.visited = false
+			}
+		}
+		return false
+	}
+
+	backtracking()
+
+	return result
+}
+```
+
 ### C语言 
 
 ```C
@@ -568,5 +626,77 @@ for line in tickets {
 }
 ```
 
+### Go 
+```Go
+
+// 先排序，然后找到第一条路径即可返回
+func findItinerary(tickets [][]string) []string {
+	var path []string	// 用来保存搜索的路径
+	data := make(map[string]ticketSlice)   // 用来保存tickets排序后的结果
+
+	var search func(airport string) bool
+	search = func(airport string) bool {
+		if len(path) == len(tickets) {
+			path = append(path, airport)
+			return true
+		}
+		to := data[airport]
+		for _, item := range to {
+			if item.Count == 0 {
+				// 已用完
+				continue
+			}
+
+			path = append(path, airport)
+			item.Count--
+			if search(item.To) { return true }
+			item.Count++
+			path = path[:len(path) - 1]
+		}
+
+		return false
+	}
+
+	// 排序
+	// 感觉这段代码有点啰嗦，不知道能不能简化一下
+	tmp := make(map[string]map[string]int)
+	for _, ticket := range tickets {
+		if to, ok := tmp[ticket[0]]; ok {
+			if _, ok2 := to[ticket[1]]; ok2 {
+				to[ticket[1]]++
+			} else {
+				to[ticket[1]] = 1
+			}
+		} else {
+			tmp[ticket[0]] = map[string]int{
+				ticket[1]: 1,
+			}
+		}
+	}
+	for from, to := range tmp {
+		var tmp ticketSlice
+		for to, num := range to {
+			tmp = append(tmp, &ticketStat{To: to, Count: num})
+		}
+		sort.Sort(tmp)
+		data[from] = tmp
+	}
+
+	search("JFK")
+	return path
+}
+
+type ticketStat struct {
+	To string
+	Count int
+}
+type ticketSlice []*ticketStat
+
+func (p ticketSlice) Len() int           { return len(p) }
+func (p ticketSlice) Less(i, j int) bool { return strings.Compare(p[i].To, p[j].To) == -1 }
+func (p ticketSlice) Swap(i, j int)      { p[i], p[j] = p[j], p[i] }
+
+```
+
 -----------------------
 <div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>

problems/0343.整数拆分.md

@@ -119,8 +119,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n^2)$
+* 时间复杂度：O(n^2)
-* 空间复杂度：$O(n)$
+* 空间复杂度：O(n)
 
 ### 贪心
 

problems/0450.删除二叉搜索树中的节点.md

@@ -51,7 +51,7 @@ if (root == nullptr) return root;
 
 * 确定单层递归的逻辑
 
-这里就把平衡二叉树中删除节点遇到的情况都搞清楚。
+这里就把二叉搜索树中删除节点遇到的情况都搞清楚。
 
 有以下五种情况：
 

problems/0503.下一个更大元素II.md

@@ -68,7 +68,7 @@ public:
 
 这种写法确实比较直观，但做了很多无用操作，例如修改了nums数组，而且最后还要把result数组resize回去。
 
-resize倒是不费时间，是$O(1)$的操作，但扩充nums数组相当于多了一个$O(n)$的操作。
+resize倒是不费时间，是O(1)的操作，但扩充nums数组相当于多了一个O(n)的操作。
 
 其实也可以不扩充nums，而是在遍历的过程中模拟走了两边nums。
 

problems/0674.最长连续递增序列.md

@@ -107,8 +107,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n)$
+* 时间复杂度：O(n)
-* 空间复杂度：$O(n)$
+* 空间复杂度：O(n)
 
 ### 贪心
 
@@ -135,12 +135,12 @@ public:
     }
 };
 ```
-* 时间复杂度：$O(n)$
+* 时间复杂度：O(n)
-* 空间复杂度：$O(1)$
+* 空间复杂度：O(1)
 
 ## 总结
 
-本题也是动规里子序列问题的经典题目，但也可以用贪心来做，大家也会发现贪心好像更简单一点，而且空间复杂度仅是$O(1)$。
+本题也是动规里子序列问题的经典题目，但也可以用贪心来做，大家也会发现贪心好像更简单一点，而且空间复杂度仅是O(1)。
 
 在动规分析中，关键是要理解和[动态规划：300.最长递增子序列](https://programmercarl.com/0300.最长上升子序列.html)的区别。
 

problems/0714.买卖股票的最佳时机含手续费（动态规划）.md

@@ -38,8 +38,8 @@
 
 使用贪心算法，的性能是：
 
-* 时间复杂度：$O(n)$
+* 时间复杂度：O(n)
-* 空间复杂度：$O(1)$
+* 空间复杂度：O(1)
 
 那么我们再来看看是使用动规的方法如何解题。
 
@@ -87,8 +87,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n)$
+* 时间复杂度：O(n)
-* 空间复杂度：$O(n)$
+* 空间复杂度：O(n)
 
 ## 其他语言版本
 

problems/0844.比较含退格的字符串.md

@@ -71,7 +71,7 @@ public:
     }
 };
 ```
-* 时间复杂度:O(n + m)，n为S的长度，m为T的长度 ，也可以理解是$O(n)$的时间复杂度
+* 时间复杂度:O(n + m)，n为S的长度，m为T的长度 ，也可以理解是O(n)的时间复杂度
 * 空间复杂度:O(n + m)
 
 当然以上代码，大家可以发现有重复的逻辑处理S，处理T，可以把这块公共逻辑抽离出来，代码精简如下：

problems/0922.按奇偶排序数组II.md

@@ -112,7 +112,7 @@ public:
 * 时间复杂度：O(n)
 * 空间复杂度：O(1)
 
-这里时间复杂度并不是$O(n^2)$，因为偶数位和奇数位都只操作一次，不是n/2 * n/2的关系，而是n/2 + n/2的关系！
+这里时间复杂度并不是O(n^2)，因为偶数位和奇数位都只操作一次，不是n/2 * n/2的关系，而是n/2 + n/2的关系！
 
 
 ## 其他语言版本

problems/O(n)的算法居然超时了，此时的n究竟是多大？.md

@@ -148,7 +148,7 @@ O(nlogn)的算法，1s内大概计算机可以运行 2 * (10^7)次计算，符
 
 ![程序超时1](https://img-blog.csdnimg.cn/20201208231559175.png)
 
-至于$O(\log n)$和$O(n^3)$ 等等这些时间复杂度在1s内可以处理的多大的数据规模，大家可以自己写一写代码去测一下了。
+至于O(log n)和O(n^3) 等等这些时间复杂度在1s内可以处理的多大的数据规模，大家可以自己写一写代码去测一下了。
 
 # 完整测试代码
 

problems/关于时间复杂度，你不知道的都在这里！.md

@@ -24,7 +24,7 @@
 
 算法导论给出的解释：**大O用来表示上界的**，当用它作为算法的最坏情况运行时间的上界，就是对任意数据输入的运行时间的上界。
 
-同样算法导论给出了例子：拿插入排序来说，插入排序的时间复杂度我们都说是$O(n^2)$ 。
+同样算法导论给出了例子：拿插入排序来说，插入排序的时间复杂度我们都说是O(n^2) 。
 
 输入数据的形式对程序运算时间是有很大影响的，在数据本来有序的情况下时间复杂度是O(n)，但如果数据是逆序的话，插入排序的时间复杂度就是O(n^2)，也就对于所有输入情况来说，最坏是O(n^2) 的时间复杂度，所以称插入排序的时间复杂度为O(n^2)。
 
@@ -44,7 +44,7 @@
 
 ![时间复杂度，不同数据规模的差异](https://img-blog.csdnimg.cn/20200728191447384.png)
 
-在决定使用哪些算法的时候，不是时间复杂越低的越好（因为简化后的时间复杂度忽略了常数项等等），要考虑数据规模，如果数据规模很小甚至可以用$O(n^2)$的算法比$O(n)$的更合适（在有常数项的时候）。
+在决定使用哪些算法的时候，不是时间复杂越低的越好（因为简化后的时间复杂度忽略了常数项等等），要考虑数据规模，如果数据规模很小甚至可以用O(n^2)的算法比O(n)的更合适（在有常数项的时候）。
 
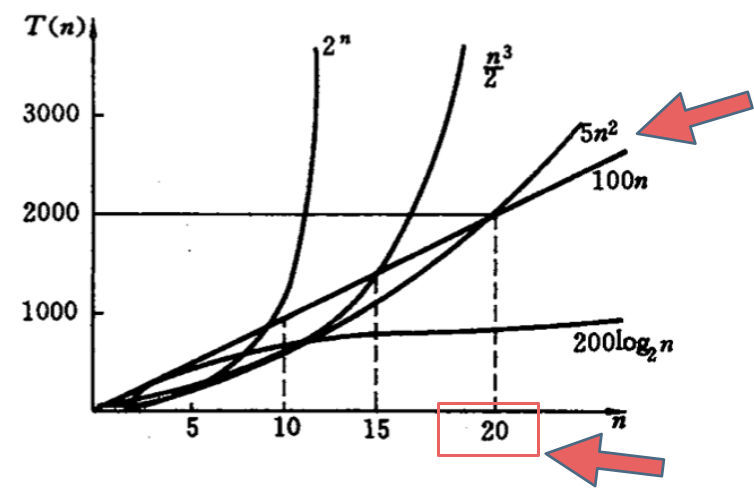
 就像上图中 O(5n^2) 和 O(100n) 在n为20之前 很明显 O(5n^2)是更优的，所花费的时间也是最少的。
 
@@ -125,7 +125,7 @@ O(2 × n^2 + 10 × n + 1000)  < O(3 × n^2)，所以说最后省略掉常数项
 
 如果是暴力枚举的话，时间复杂度是多少呢，是O(n^2)么？
 
-这里一些同学会忽略了字符串比较的时间消耗，这里并不像int 型数字做比较那么简单，除了n^2次的遍历次数外，字符串比较依然要消耗m次操作（m也就是字母串的长度），所以时间复杂度是$O(m × n × n)$。
+这里一些同学会忽略了字符串比较的时间消耗，这里并不像int 型数字做比较那么简单，除了n^2次的遍历次数外，字符串比较依然要消耗m次操作（m也就是字母串的长度），所以时间复杂度是O(m × n × n)。
 
 接下来再想一下其他解题思路。
 

problems/前序/关于时间复杂度，你不知道的都在这里！.md

@@ -9,7 +9,7 @@
 * 什么是大O
 * 不同数据规模的差异
 * 复杂表达式的化简
-* $O(\log n)$中的log是以什么为底？
+* O(log n)中的log是以什么为底？
 * 举一个例子
 
 
@@ -23,21 +23,21 @@
 
 那么该如何估计程序运行时间呢，通常会估算算法的操作单元数量来代表程序消耗的时间，这里默认CPU的每个单元运行消耗的时间都是相同的。
 
-假设算法的问题规模为n，那么操作单元数量便用函数f(n)来表示，随着数据规模n的增大，算法执行时间的增长率和f(n)的增长率相同，这称作为算法的渐近时间复杂度，简称时间复杂度，记为 $O(f(n)$)。
+假设算法的问题规模为n，那么操作单元数量便用函数f(n)来表示，随着数据规模n的增大，算法执行时间的增长率和f(n)的增长率相同，这称作为算法的渐近时间复杂度，简称时间复杂度，记为 O(f(n))。
 
 ## 什么是大O
 
-这里的大O是指什么呢，说到时间复杂度，**大家都知道$O(n)$，$O(n^2)$，却说不清什么是大O**。
+这里的大O是指什么呢，说到时间复杂度，**大家都知道O(n)，O(n^2)，却说不清什么是大O**。
 
 算法导论给出的解释：**大O用来表示上界的**，当用它作为算法的最坏情况运行时间的上界，就是对任意数据输入的运行时间的上界。
 
-同样算法导论给出了例子：拿插入排序来说，插入排序的时间复杂度我们都说是$O(n^2)$ 。
+同样算法导论给出了例子：拿插入排序来说，插入排序的时间复杂度我们都说是O(n^2) 。
 
-输入数据的形式对程序运算时间是有很大影响的，在数据本来有序的情况下时间复杂度是$O(n)$，但如果数据是逆序的话，插入排序的时间复杂度就是$O(n^2)$，也就对于所有输入情况来说，最坏是$O(n^2)$ 的时间复杂度，所以称插入排序的时间复杂度为$O(n^2)$。
+输入数据的形式对程序运算时间是有很大影响的，在数据本来有序的情况下时间复杂度是O(n)，但如果数据是逆序的话，插入排序的时间复杂度就是O(n^2)，也就对于所有输入情况来说，最坏是O(n^2) 的时间复杂度，所以称插入排序的时间复杂度为O(n^2)。
 
-同样的同理再看一下快速排序，都知道快速排序是$O(n\log n)$，但是当数据已经有序情况下，快速排序的时间复杂度是$O(n^2)$ 的，**所以严格从大O的定义来讲，快速排序的时间复杂度应该是$O(n^2)$**。
+同样的同理再看一下快速排序，都知道快速排序是O(nlogn)，但是当数据已经有序情况下，快速排序的时间复杂度是O(n^2) 的，**所以严格从大O的定义来讲，快速排序的时间复杂度应该是O(n^2)**。
 
-**但是我们依然说快速排序是$O(n\log n)$的时间复杂度，这个就是业内的一个默认规定，这里说的O代表的就是一般情况，而不是严格的上界**。如图所示：
+**但是我们依然说快速排序是O(nlogn)的时间复杂度，这个就是业内的一个默认规定，这里说的O代表的就是一般情况，而不是严格的上界**。如图所示：
 ![时间复杂度4，一般情况下的时间复杂度](https://img-blog.csdnimg.cn/20200728185745611.png)
 
 我们主要关心的还是一般情况下的数据形式。
@@ -51,11 +51,11 @@
 
 ![时间复杂度，不同数据规模的差异](https://img-blog.csdnimg.cn/20200728191447384.png)
 
-在决定使用哪些算法的时候，不是时间复杂越低的越好（因为简化后的时间复杂度忽略了常数项等等），要考虑数据规模，如果数据规模很小甚至可以用$O(n^2)$的算法比$O(n)$的更合适（在有常数项的时候）。
+在决定使用哪些算法的时候，不是时间复杂越低的越好（因为简化后的时间复杂度忽略了常数项等等），要考虑数据规模，如果数据规模很小甚至可以用O(n^2)的算法比O(n)的更合适（在有常数项的时候）。
 
-就像上图中 $O(5n^2)$ 和 $O(100n)$ 在n为20之前 很明显 $O(5n^2)$是更优的，所花费的时间也是最少的。
+就像上图中 O(5n^2) 和 O(100n) 在n为20之前 很明显 O(5n^2)是更优的，所花费的时间也是最少的。
 
-那为什么在计算时间复杂度的时候要忽略常数项系数呢，也就说$O(100n)$ 就是$O(n)$的时间复杂度，$O(5n^2)$ 就是$O(n^2)$的时间复杂度，而且要默认$O(n)$ 优于$O(n^2)$ 呢 ？
+那为什么在计算时间复杂度的时候要忽略常数项系数呢，也就说O(100n) 就是O(n)的时间复杂度，O(5n^2) 就是O(n^2)的时间复杂度，而且要默认O(n) 优于O(n^2) 呢 ？
 
 这里就又涉及到大O的定义，**因为大O就是数据量级突破一个点且数据量级非常大的情况下所表现出的时间复杂度，这个数据量也就是常数项系数已经不起决定性作用的数据量**。
 
@@ -63,13 +63,13 @@
 
 **所以我们说的时间复杂度都是省略常数项系数的，是因为一般情况下都是默认数据规模足够的大，基于这样的事实，给出的算法时间复杂的的一个排行如下所示**：
 
-O(1)常数阶 < $O(\log n)$对数阶 < $O(n)$线性阶 < $O(n^2)$平方阶 < $O(n^3)$立方阶 < $O(2^n)$指数阶
+O(1)常数阶 < O(logn)对数阶 < O(n)线性阶 < O(n^2)平方阶 < O(n^3)立方阶 < O(2^n)指数阶
 
 但是也要注意大常数，如果这个常数非常大，例如10^7 ，10^9 ，那么常数就是不得不考虑的因素了。
 
 ## 复杂表达式的化简
 
-有时候我们去计算时间复杂度的时候发现不是一个简单的$O(n)$ 或者$O(n^2)$， 而是一个复杂的表达式，例如：
+有时候我们去计算时间复杂度的时候发现不是一个简单的O(n) 或者O(n^2)， 而是一个复杂的表达式，例如：
 
 ```
 O(2*n^2 + 10*n + 1000)
@@ -95,19 +95,19 @@ O(n^2 + n)
 O(n^2)
 ```
 
-如果这一步理解有困难，那也可以做提取n的操作，变成$O(n(n+1)$) ，省略加法常数项后也就别变成了：
+如果这一步理解有困难，那也可以做提取n的操作，变成O(n(n+1)) ，省略加法常数项后也就别变成了：
 
 ```
 O(n^2)
 ```
 
-所以最后我们说：这个算法的算法时间复杂度是$O(n^2)$ 。
+所以最后我们说：这个算法的算法时间复杂度是O(n^2) 。
 
 
-也可以用另一种简化的思路，其实当n大于40的时候， 这个复杂度会恒小于$O(3 × n^2)$，
+也可以用另一种简化的思路，其实当n大于40的时候， 这个复杂度会恒小于O(3 × n^2)，
-$O(2 × n^2 + 10 × n + 1000) < O(3 × n^2)$，所以说最后省略掉常数项系数最终时间复杂度也是$O(n^2)$。
+O(2 × n^2 + 10 × n + 1000) < O(3 × n^2)，所以说最后省略掉常数项系数最终时间复杂度也是O(n^2)。
 
-## $O(\log n)$中的log是以什么为底？
+## O(logn)中的log是以什么为底？
 
 平时说这个算法的时间复杂度是logn的，那么一定是log 以2为底n的对数么？
 
@@ -130,21 +130,21 @@ $O(2 × n^2 + 10 × n + 1000) < O(3 × n^2)$，所以说最后省略掉常数项
 
 通过这道面试题目，来分析一下时间复杂度。题目描述：找出n个字符串中相同的两个字符串（假设这里只有两个相同的字符串）。
 
-如果是暴力枚举的话，时间复杂度是多少呢，是$O(n^2)$么？
+如果是暴力枚举的话，时间复杂度是多少呢，是O(n^2)么？
 
-这里一些同学会忽略了字符串比较的时间消耗，这里并不像int 型数字做比较那么简单，除了n^2 次的遍历次数外，字符串比较依然要消耗m次操作（m也就是字母串的长度），所以时间复杂度是$O(m × n × n)$。
+这里一些同学会忽略了字符串比较的时间消耗，这里并不像int 型数字做比较那么简单，除了n^2 次的遍历次数外，字符串比较依然要消耗m次操作（m也就是字母串的长度），所以时间复杂度是O(m × n × n)。
 
 接下来再想一下其他解题思路。
 
 先排对n个字符串按字典序来排序，排序后n个字符串就是有序的，意味着两个相同的字符串就是挨在一起，然后在遍历一遍n个字符串，这样就找到两个相同的字符串了。
 
-那看看这种算法的时间复杂度，快速排序时间复杂度为$O(n\log n)$，依然要考虑字符串的长度是m，那么快速排序每次的比较都要有m次的字符比较的操作，就是$O(m × n × \log n)$  。
+那看看这种算法的时间复杂度，快速排序时间复杂度为O(nlogn)，依然要考虑字符串的长度是m，那么快速排序每次的比较都要有m次的字符比较的操作，就是O(m × n × log n) 。
 
-之后还要遍历一遍这n个字符串找出两个相同的字符串，别忘了遍历的时候依然要比较字符串，所以总共的时间复杂度是 $O(m × n × \log n + n × m)$。
+之后还要遍历一遍这n个字符串找出两个相同的字符串，别忘了遍历的时候依然要比较字符串，所以总共的时间复杂度是 O(m × n × logn + n × m)。
 
-我们对$O(m × n × \log n + n × m)$ 进行简化操作，把$m × n$提取出来变成 $O(m × n × (\log n + 1)$)，再省略常数项最后的时间复杂度是 $O(m × n × \log n)$。
+我们对O(m × n × log n + n × m) 进行简化操作，把m × n提取出来变成 O(m × n × (logn + 1))，再省略常数项最后的时间复杂度是 O(m × n × log n)。
 
-最后很明显$O(m × n × \log n)$ 要优于$O(m × n × n)$！
+最后很明显O(m × n × logn) 要优于O(m × n × n)！
 
 所以先把字符串集合排序再遍历一遍找到两个相同字符串的方法要比直接暴力枚举的方式更快。
 

problems/前序/关于空间复杂度，可能有几个疑问？.md

@@ -3,14 +3,14 @@
 # 空间复杂度分析
 
 * [关于时间复杂度，你不知道的都在这里！](https://programmercarl.com/前序/关于时间复杂度，你不知道的都在这里！.html)
-* [$O(n)$的算法居然超时了，此时的n究竟是多大？](https://programmercarl.com/前序/On的算法居然超时了，此时的n究竟是多大？.html)
+* [O(n)的算法居然超时了，此时的n究竟是多大？](https://programmercarl.com/前序/On的算法居然超时了，此时的n究竟是多大？.html)
 * [通过一道面试题目，讲一讲递归算法的时间复杂度！](https://programmercarl.com/前序/通过一道面试题目，讲一讲递归算法的时间复杂度！.html)
 
 那么一直还没有讲空间复杂度，所以打算陆续来补上，内容不难，大家可以读一遍文章就有整体的了解了。
 
 什么是空间复杂度呢？
 
-是对一个算法在运行过程中占用内存空间大小的量度，记做$S(n)=O(f(n)$。
+是对一个算法在运行过程中占用内存空间大小的量度，记做S(n)=O(f(n)。
 
 空间复杂度(Space Complexity)记作S(n) 依然使用大O来表示。利用程序的空间复杂度，可以对程序运行中需要多少内存有个预先估计。
 
@@ -41,11 +41,11 @@ for (int i = 0; i < n; i++) {
 }
 
 ```
-第一段代码可以看出，随着n的变化，所需开辟的内存空间并不会随着n的变化而变化。即此算法空间复杂度为一个常量，所以表示为大$O(1)$。
+第一段代码可以看出，随着n的变化，所需开辟的内存空间并不会随着n的变化而变化。即此算法空间复杂度为一个常量，所以表示为大O(1)。
 
-什么时候的空间复杂度是$O(n)$？
+什么时候的空间复杂度是O(n)？
 
-当消耗空间和输入参数n保持线性增长，这样的空间复杂度为$O(n)$，来看一下这段C++代码
+当消耗空间和输入参数n保持线性增长，这样的空间复杂度为O(n)，来看一下这段C++代码
 ```CPP
 int* a = new int(n);
 for (int i = 0; i < n; i++) {
@@ -53,9 +53,9 @@ for (int i = 0; i < n; i++) {
 }
 ```
 
-我们定义了一个数组出来，这个数组占用的大小为n，虽然有一个for循环，但没有再分配新的空间，因此，这段代码的空间复杂度主要看第一行即可，随着n的增大，开辟的内存大小呈线性增长，即 $O(n)$。
+我们定义了一个数组出来，这个数组占用的大小为n，虽然有一个for循环，但没有再分配新的空间，因此，这段代码的空间复杂度主要看第一行即可，随着n的增大，开辟的内存大小呈线性增长，即 O(n)。
 
-其他的 $O(n^2)$， $O(n^3)$ 我想大家应该都可以以此例举出来了，**那么思考一下 什么时候空间复杂度是 $O(\log n)$呢？**
+其他的 O(n^2)， O(n^3) 我想大家应该都可以以此例举出来了，**那么思考一下 什么时候空间复杂度是 O(logn)呢？**
 
 空间复杂度是logn的情况确实有些特殊，其实是在**递归的时候，会出现空间复杂度为logn的情况**。
 

problems/前序/编程素养部分的吹毛求疵.md

@@ -13,7 +13,7 @@
 
 - 左孩子和右孩子的下标不太好理解。我给出证明过程：
 
-  如果父节点在第$k$层，第$m,m \in [0,2^k]$个节点，则其左孩子所在的位置必然为$k+1$层，第$2*(m-1)+1$个节点。
+  如果父节点在第k层，第$m,m \in [0,2^k]$个节点，则其左孩子所在的位置必然为$k+1$层，第$2*(m-1)+1$个节点。
 
   - 计算父节点在数组中的索引：
     $$

problems/前序/递归算法的时间与空间复杂度分析.md

@@ -26,7 +26,7 @@ int fibonacci(int i) {
 
 在讲解递归时间复杂度的时候，我们提到了递归算法的时间复杂度本质上是要看: **递归的次数 * 每次递归的时间复杂度**。
 
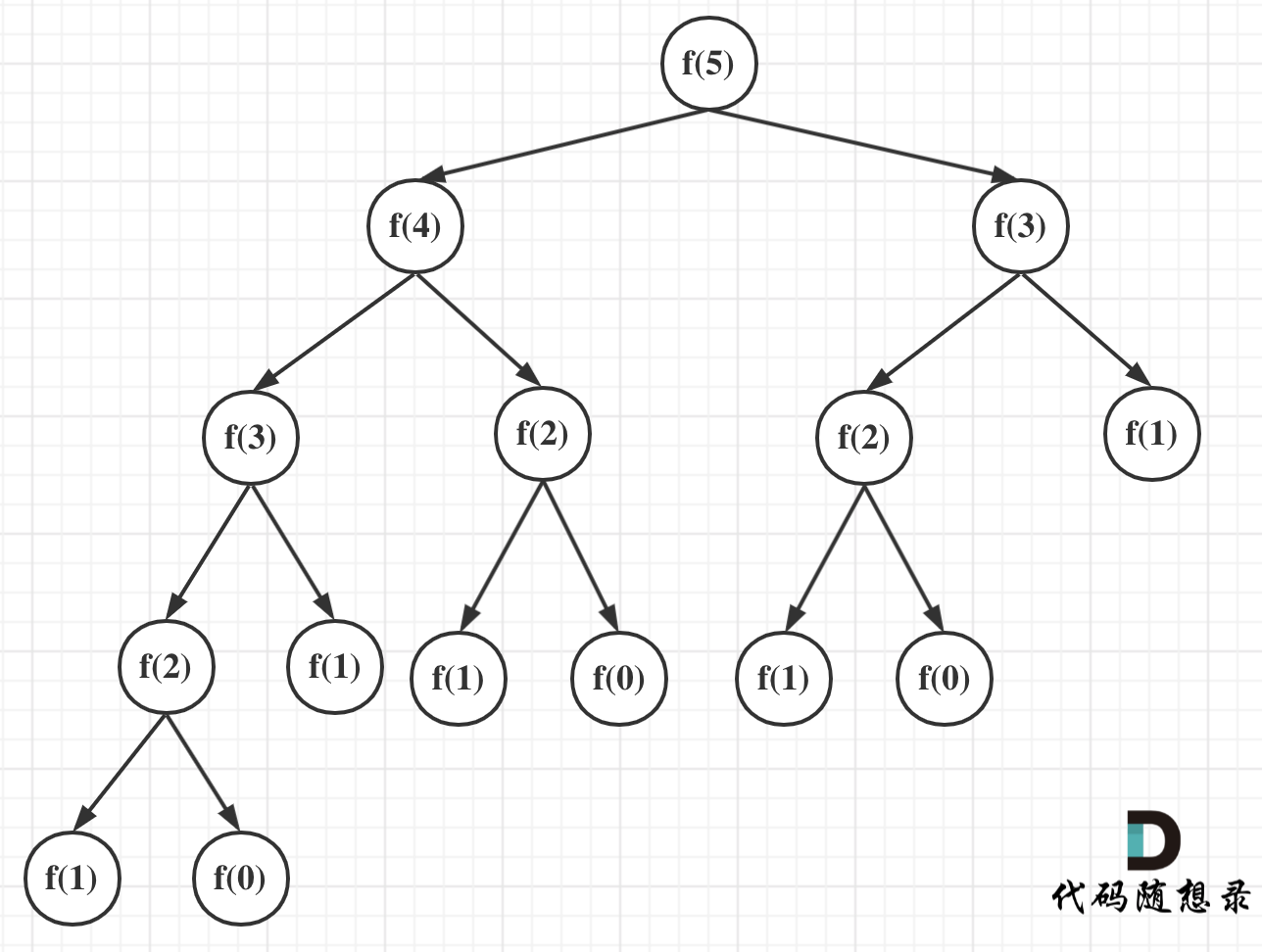
-可以看出上面的代码每次递归都是$O(1)$的操作。再来看递归了多少次，这里将i为5作为输入的递归过程 抽象成一棵递归树，如图：
+可以看出上面的代码每次递归都是O(1)的操作。再来看递归了多少次，这里将i为5作为输入的递归过程 抽象成一棵递归树，如图：
 
 ![递归空间复杂度分析](https://img-blog.csdnimg.cn/20210305093200104.png)
 
@@ -36,7 +36,7 @@ int fibonacci(int i) {
 
 我们之前也有说到，一棵深度（按根节点深度为1）为k的二叉树最多可以有 2^k - 1 个节点。
 
-所以该递归算法的时间复杂度为$O(2^n)$，这个复杂度是非常大的，随着n的增大，耗时是指数上升的。
+所以该递归算法的时间复杂度为O(2^n)，这个复杂度是非常大的，随着n的增大，耗时是指数上升的。
 
 来做一个实验，大家可以有一个直观的感受。
 
@@ -85,7 +85,7 @@ int main()
 * n = 40，耗时：837 ms
 * n = 50，耗时：110306 ms
 
-可以看出，$O(2^n)$这种指数级别的复杂度是非常大的。
+可以看出，O(2^n)这种指数级别的复杂度是非常大的。
 
 所以这种求斐波那契数的算法看似简洁，其实时间复杂度非常高，一般不推荐这样来实现斐波那契。
 
@@ -119,14 +119,14 @@ int fibonacci(int first, int second, int n) {
 
 这里相当于用first和second来记录当前相加的两个数值，此时就不用两次递归了。
 
-因为每次递归的时候n减1，即只是递归了n次，所以时间复杂度是 $O(n)$。
+因为每次递归的时候n减1，即只是递归了n次，所以时间复杂度是 O(n)。
 
-同理递归的深度依然是n，每次递归所需的空间也是常数，所以空间复杂度依然是$O(n)$。
+同理递归的深度依然是n，每次递归所需的空间也是常数，所以空间复杂度依然是O(n)。
 
 代码（版本二）的复杂度如下：
 
-* 时间复杂度：$O(n)$
+* 时间复杂度：O(n)
-* 空间复杂度：$O(n)$
+* 空间复杂度：O(n)
 
 此时再来测一下耗时情况验证一下：
 
@@ -198,7 +198,7 @@ int main()
 
 递归第n个斐波那契数的话，递归调用栈的深度就是n。
 
-那么每次递归的空间复杂度是$O(1)$， 调用栈深度为n，所以这段递归代码的空间复杂度就是$O(n)$。
+那么每次递归的空间复杂度是O(1)， 调用栈深度为n，所以这段递归代码的空间复杂度就是O(n)。
 
 ```CPP
 int fibonacci(int i) {
@@ -233,24 +233,24 @@ int binary_search( int arr[], int l, int r, int x) {
 }
 ```
 
-都知道二分查找的时间复杂度是$O(\log n)$，那么递归二分查找的空间复杂度是多少呢？
+都知道二分查找的时间复杂度是O(logn)，那么递归二分查找的空间复杂度是多少呢？
 
 我们依然看 **每次递归的空间复杂度和递归的深度**
 
 每次递归的空间复杂度可以看出主要就是参数里传入的这个arr数组，但需要注意的是在C/C++中函数传递数组参数，不是整个数组拷贝一份传入函数而是传入的数组首元素地址。
 
-**也就是说每一层递归都是公用一块数组地址空间的**，所以 每次递归的空间复杂度是常数即：$O(1)$。
+**也就是说每一层递归都是公用一块数组地址空间的**，所以 每次递归的空间复杂度是常数即：O(1)。
 
-再来看递归的深度，二分查找的递归深度是logn ，递归深度就是调用栈的长度，那么这段代码的空间复杂度为 $1 * logn = O(logn)$。
+再来看递归的深度，二分查找的递归深度是logn ，递归深度就是调用栈的长度，那么这段代码的空间复杂度为 1 * logn = O(logn)。
 
-大家要注意自己所用的语言在传递函数参数的时，是拷贝整个数值还是拷贝地址，如果是拷贝整个数值那么该二分法的空间复杂度就是$O(n\log n)$。
+大家要注意自己所用的语言在传递函数参数的时，是拷贝整个数值还是拷贝地址，如果是拷贝整个数值那么该二分法的空间复杂度就是O(nlogn)。
 
 
 ## 总结
 
 本章我们详细分析了递归实现的求斐波那契和二分法的空间复杂度，同时也对时间复杂度做了分析。
 
-特别是两种递归实现的求斐波那契数列，其时间复杂度截然不容，我们还做了实验，验证了时间复杂度为$O(2^n)$是非常耗时的。
+特别是两种递归实现的求斐波那契数列，其时间复杂度截然不容，我们还做了实验，验证了时间复杂度为O(2^n)是非常耗时的。
 
 通过本篇大家应该对递归算法的时间复杂度和空间复杂度有更加深刻的理解了。
 

problems/前序/通过一道面试题目，讲一讲递归算法的时间复杂度！.md

@@ -5,13 +5,13 @@
 
 相信很多同学对递归算法的时间复杂度都很模糊，那么这篇来给大家通透的讲一讲。
 
-**同一道题目，同样使用递归算法，有的同学会写出了$O(n)$的代码，有的同学就写出了$O(\log n)$的代码**。
+**同一道题目，同样使用递归算法，有的同学会写出了O(n)的代码，有的同学就写出了O(logn)的代码**。
 
 这是为什么呢？
 
 如果对递归的时间复杂度理解的不够深入的话，就会这样！
 
-那么我通过一道简单的面试题，模拟面试的场景，来带大家逐步分析递归算法的时间复杂度，最后找出最优解，来看看同样是递归，怎么就写成了$O(n)$的代码。
+那么我通过一道简单的面试题，模拟面试的场景，来带大家逐步分析递归算法的时间复杂度，最后找出最优解，来看看同样是递归，怎么就写成了O(n)的代码。
 
 面试题：求x的n次方
 
@@ -26,7 +26,7 @@ int function1(int x, int n) {
     return result;
 }
 ```
-时间复杂度为$O(n)$，此时面试官会说，有没有效率更好的算法呢。
+时间复杂度为O(n)，此时面试官会说，有没有效率更好的算法呢。
 
 **如果此时没有思路，不要说：我不会，我不知道了等等**。
 
@@ -44,11 +44,11 @@ int function2(int x, int n) {
 ```
 面试官问：“那么这个代码的时间复杂度是多少？”。
 
-一些同学可能一看到递归就想到了$O(\log n)$，其实并不是这样，递归算法的时间复杂度本质上是要看: **递归的次数 * 每次递归中的操作次数**。
+一些同学可能一看到递归就想到了O(log n)，其实并不是这样，递归算法的时间复杂度本质上是要看: **递归的次数 * 每次递归中的操作次数**。
 
 那再来看代码，这里递归了几次呢？
 
-每次n-1，递归了n次时间复杂度是$O(n)$，每次进行了一个乘法操作，乘法操作的时间复杂度一个常数项$O(1)$，所以这份代码的时间复杂度是 $n × 1 = O(n)$。
+每次n-1，递归了n次时间复杂度是O(n)，每次进行了一个乘法操作，乘法操作的时间复杂度一个常数项O(1)，所以这份代码的时间复杂度是 n × 1 = O(n)。
 
 这个时间复杂度就没有达到面试官的预期。于是又写出了如下的递归算法的代码：
 
@@ -81,11 +81,11 @@ int function3(int x, int n) {
 
 ![递归求时间复杂度](https://img-blog.csdnimg.cn/20200728195531892.png)
 
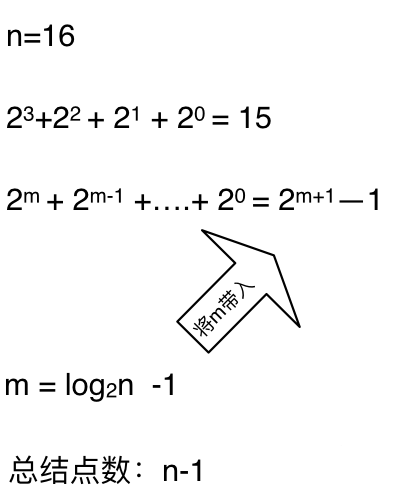
-**时间复杂度忽略掉常数项`-1`之后，这个递归算法的时间复杂度依然是$O(n)$**。对，你没看错，依然是$O(n)$的时间复杂度！
+**时间复杂度忽略掉常数项`-1`之后，这个递归算法的时间复杂度依然是O(n)**。对，你没看错，依然是O(n)的时间复杂度！
 
-此时面试官就会说：“这个递归的算法依然还是$O(n)$啊”， 很明显没有达到面试官的预期。
+此时面试官就会说：“这个递归的算法依然还是O(n)啊”， 很明显没有达到面试官的预期。
 
-那么$O(\log n)$的递归算法应该怎么写呢？
+那么O(logn)的递归算法应该怎么写呢？
 
 想一想刚刚给出的那份递归算法的代码，是不是有哪里比较冗余呢，其实有重复计算的部分。
 
@@ -108,7 +108,7 @@ int function4(int x, int n) {
 
 依然还是看他递归了多少次，可以看到这里仅仅有一个递归调用，且每次都是n/2 ，所以这里我们一共调用了log以2为底n的对数次。
 
-**每次递归了做都是一次乘法操作，这也是一个常数项的操作，那么这个递归算法的时间复杂度才是真正的$O(\log n)$**。
+**每次递归了做都是一次乘法操作，这也是一个常数项的操作，那么这个递归算法的时间复杂度才是真正的O(logn)**。
 
 此时大家最后写出了这样的代码并且将时间复杂度分析的非常清晰，相信面试官是比较满意的。
 
@@ -116,11 +116,11 @@ int function4(int x, int n) {
 
 对于递归的时间复杂度，毕竟初学者有时候会迷糊，刷过很多题的老手依然迷糊。
 
-**本篇我用一道非常简单的面试题目：求x的n次方，来逐步分析递归算法的时间复杂度，注意不要一看到递归就想到了$O(\log n)$！**
+**本篇我用一道非常简单的面试题目：求x的n次方，来逐步分析递归算法的时间复杂度，注意不要一看到递归就想到了O(logn)！**
 
-同样使用递归，有的同学可以写出$O(\log n)$的代码，有的同学还可以写出$O(n)$的代码。
+同样使用递归，有的同学可以写出O(logn)的代码，有的同学还可以写出O(n)的代码。
 
-对于function3 这样的递归实现，很容易让人感觉这是$O(\log n)$的时间复杂度，其实这是$O(n)$的算法！
+对于function3 这样的递归实现，很容易让人感觉这是O(log n)的时间复杂度，其实这是O(n)的算法！
 
 ```CPP
 int function3(int x, int n) {

problems/剑指Offer58-II.左旋转字符串.md

@@ -86,7 +86,7 @@ public:
 # 题外话
 
 一些同学热衷于使用substr，来做这道题。
-其实使用substr 和 反转 时间复杂度是一样的 ，都是$O(n)$，但是使用substr申请了额外空间，所以空间复杂度是$O(n)$，而反转方法的空间复杂度是$O(1)$。
+其实使用substr 和 反转 时间复杂度是一样的 ，都是O(n)，但是使用substr申请了额外空间，所以空间复杂度是O(n)，而反转方法的空间复杂度是O(1)。
 
 **如果想让这套题目有意义，就不要申请额外空间。**
 

problems/双指针总结.md

@@ -89,7 +89,7 @@ for (int i = 0; i < array.size(); i++) {
 
 # 总结 
 
-本文中一共介绍了leetcode上九道使用双指针解决问题的经典题目，除了链表一些题目一定要使用双指针，其他题目都是使用双指针来提高效率，一般是将$O(n^2)$的时间复杂度，降为$O(n)$。
+本文中一共介绍了leetcode上九道使用双指针解决问题的经典题目，除了链表一些题目一定要使用双指针，其他题目都是使用双指针来提高效率，一般是将O(n^2)的时间复杂度，降为$O(n)$。
 
 建议大家可以把文中涉及到的题目在好好做一做，琢磨琢磨，基本对双指针法就不在话下了。
 

problems/周总结/20200927二叉树周末总结.md

@@ -44,7 +44,7 @@ a->right = NULL;
 
 在介绍前中后序遍历的时候，有递归和迭代（非递归），还有一种牛逼的遍历方式：morris遍历。
 
-morris遍历是二叉树遍历算法的超强进阶算法，morris遍历可以将非递归遍历中的空间复杂度降为$O(1)$，感兴趣大家就去查一查学习学习，比较小众，面试几乎不会考。我其实也没有研究过，就不做过多介绍了。
+morris遍历是二叉树遍历算法的超强进阶算法，morris遍历可以将非递归遍历中的空间复杂度降为O(1)，感兴趣大家就去查一查学习学习，比较小众，面试几乎不会考。我其实也没有研究过，就不做过多介绍了。
 
 ## 周二
 

problems/周总结/20201126贪心周末总结.md

@@ -41,7 +41,7 @@
 
 一些录友不清楚[贪心算法：分发饼干](https://programmercarl.com/0455.分发饼干.html)中时间复杂度是怎么来的？
 
-就是快排$O(n\log n)$，遍历$O(n)$，加一起就是还是$O(n\log n)$。
+就是快排O(nlog n)，遍历O(n)，加一起就是还是O(nlogn)。
 
 ## 周三
 

problems/周总结/20201210复杂度分析周末总结.md

@@ -70,9 +70,9 @@
 
 # 周三
 
-在[$O(n)$的算法居然超时了，此时的n究竟是多大？](https://programmercarl.com/前序/On的算法居然超时了，此时的n究竟是多大？.html)中介绍了大家在leetcode上提交代码经常遇到的一个问题-超时！
+在[O(n)的算法居然超时了，此时的n究竟是多大？](https://programmercarl.com/前序/On的算法居然超时了，此时的n究竟是多大？.html)中介绍了大家在leetcode上提交代码经常遇到的一个问题-超时！
 
-估计很多录友知道算法超时了，但没有注意过 $O(n)$的算法，如果1s内出结果，这个n究竟是多大？
+估计很多录友知道算法超时了，但没有注意过 O(n)的算法，如果1s内出结果，这个n究竟是多大？
 
 文中从计算机硬件出发，分析计算机的计算性能，然后亲自做实验，整理出数据如下：
 
@@ -95,7 +95,7 @@
 
 文中给出了四个版本的代码实现，并逐一分析了其时间复杂度。
 
-此时大家就会发现，同一道题目，同样使用递归算法，有的同学会写出了$O(n)$的代码，有的同学就写出了$O(\log n)$的代码。
+此时大家就会发现，同一道题目，同样使用递归算法，有的同学会写出了O(n)的代码，有的同学就写出了$O(\log n)$的代码。
 
 其本质是要对递归的时间复杂度有清晰的认识，才能运用递归来有效的解决问题！
 

problems/周总结/20201217贪心周末总结.md

@@ -8,7 +8,7 @@
 
 在[贪心算法：加油站](https://programmercarl.com/0134.加油站.html)中给出每一个加油站的汽油和开到这个加油站的消耗，问汽车能不能开一圈。
 
-这道题目咋眼一看，感觉是一道模拟题，模拟一下汽车从每一个节点出发看看能不能开一圈，时间复杂度是$O(n^2)$。
+这道题目咋眼一看，感觉是一道模拟题，模拟一下汽车从每一个节点出发看看能不能开一圈，时间复杂度是O(n^2)。
 
 即使用模拟这种情况，也挺考察代码技巧的。
 

problems/周总结/20210225动规周末总结.md

@@ -211,8 +211,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n^2)$
+* 时间复杂度：O(n^2)
-* 空间复杂度：$O(1)$
+* 空间复杂度：O(1)
 
 贪心解法代码如下：
 
@@ -233,8 +233,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n)$
+* 时间复杂度：O(n)
-* 空间复杂度：$O(1)$
+* 空间复杂度：O(1)
 
 动规解法，版本一，代码如下：
 
@@ -256,8 +256,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n)$
+* 时间复杂度：O(n)
-* 空间复杂度：$O(n)$
+* 空间复杂度：O(n)
 
 从递推公式可以看出，dp[i]只是依赖于dp[i - 1]的状态。
 
@@ -282,8 +282,8 @@ public:
 };
 ```
 
-* 时间复杂度：$O(n)$
+* 时间复杂度：O(n)
-* 空间复杂度：$O(1)$
+* 空间复杂度：O(1)
 
 
 建议先写出版本一，然后在版本一的基础上优化成版本二，而不是直接就写出版本二。

problems/哈希表理论基础.md

@@ -22,7 +22,7 @@
 
 例如要查询一个名字是否在这所学校里。
 
-要枚举的话时间复杂度是$O(n)$，但如果使用哈希表的话， 只需要$O(1)$就可以做到。
+要枚举的话时间复杂度是O(n)，但如果使用哈希表的话， 只需要O(1)就可以做到。
 
 我们只需要初始化把这所学校里学生的名字都存在哈希表里，在查询的时候通过索引直接就可以知道这位同学在不在这所学校里了。
 
@@ -88,17 +88,17 @@
 
 |集合 |底层实现 | 是否有序 |数值是否可以重复 | 能否更改数值|查询效率 |增删效率|
 |---|---| --- |---| --- | --- | ---|
-|std::set |红黑树 |有序 |否 |否 | $O(\log n)$|$O(\log n)$ |
+|std::set |红黑树 |有序 |否 |否 | O(log n)|O(log n) |
-|std::multiset | 红黑树|有序 |是 | 否| $O(\log n)$ |$O(\log n)$ |
+|std::multiset | 红黑树|有序 |是 | 否| O(logn) |O(logn) |
-|std::unordered_set |哈希表 |无序 |否 |否 |$O(1)$ | $O(1)$|
+|std::unordered_set |哈希表 |无序 |否 |否 |O(1) | O(1)|
 
 std::unordered_set底层实现为哈希表，std::set 和std::multiset 的底层实现是红黑树，红黑树是一种平衡二叉搜索树，所以key值是有序的，但key不可以修改，改动key值会导致整棵树的错乱，所以只能删除和增加。
 
 |映射 |底层实现 | 是否有序 |数值是否可以重复 | 能否更改数值|查询效率 |增删效率|
 |---|---| --- |---| --- | --- | ---|
-|std::map |红黑树 |key有序 |key不可重复 |key不可修改 | $O(\log n)$|$O(\log n)$ |
+|std::map |红黑树 |key有序 |key不可重复 |key不可修改 | O(logn)|O(logn) |
-|std::multimap | 红黑树|key有序 | key可重复 | key不可修改|$O(\log n)$ |$O(\log n)$ |
+|std::multimap | 红黑树|key有序 | key可重复 | key不可修改|O(log n) |O(log n) |
-|std::unordered_map |哈希表 | key无序 |key不可重复 |key不可修改 |$O(1)$ | $O(1)$|
+|std::unordered_map |哈希表 | key无序 |key不可重复 |key不可修改 |O(1) | O(1)|
 
 std::unordered_map 底层实现为哈希表，std::map 和std::multimap 的底层实现是红黑树。同理，std::map 和std::multimap 的key也是有序的（这个问题也经常作为面试题，考察对语言容器底层的理解）。
 

problems/回溯总结.md

@@ -302,7 +302,7 @@ if (startIndex >= nums.size()) { // 终止条件可以不加
 
 **而使用used数组在时间复杂度上几乎没有额外负担！**
 
-**使用set去重，不仅时间复杂度高了，空间复杂度也高了**，在[本周小结！（回溯算法系列三）](https://programmercarl.com/周总结/20201112回溯周末总结.html)中分析过，组合，子集，排列问题的空间复杂度都是O(n)，但如果使用set去重，空间复杂度就变成了$O(n^2)$，因为每一层递归都有一个set集合，系统栈空间是n，每一个空间都有set集合。
+**使用set去重，不仅时间复杂度高了，空间复杂度也高了**，在[本周小结！（回溯算法系列三）](https://programmercarl.com/周总结/20201112回溯周末总结.html)中分析过，组合，子集，排列问题的空间复杂度都是O(n)，但如果使用set去重，空间复杂度就变成了O(n^2)，因为每一层递归都有一个set集合，系统栈空间是n，每一个空间都有set集合。
 
 那有同学可能疑惑 用used数组也是占用O(n)的空间啊？ 
 

problems/数组总结篇.md

@@ -102,7 +102,7 @@
 
 本题中，主要要理解滑动窗口如何移动 窗口起始位置，达到动态更新窗口大小的，从而得出长度最小的符合条件的长度。
 
-**滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将$O(n^2)$的暴力解法降为$O(n)$。**
+**滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。**
 
 如果没有接触过这一类的方法，很难想到类似的解题思路，滑动窗口方法还是很巧妙的。
 

problems/根据身高重建队列（vector原理讲解）.md

@@ -151,7 +151,7 @@ public:
 
 大家应该发现了，编程语言中一个普通容器的insert，delete的使用，都可能对写出来的算法的有很大影响！
 
-如果抛开语言谈算法，除非从来不用代码写算法纯分析，**否则的话，语言功底不到位O(n)的算法可以写出$O(n^2)$的性能**，哈哈。
+如果抛开语言谈算法，除非从来不用代码写算法纯分析，**否则的话，语言功底不到位O(n)的算法可以写出O(n^2)的性能**，哈哈。
 
 相信在这里学习算法的录友们，都是想在软件行业长远发展的，都是要从事编程的工作，那么一定要深耕好一门编程语言，这个非常重要！
 

problems/贪心算法总结篇.md

@@ -127,9 +127,9 @@ Carl个人认为：如果找出局部最优并可以推出全局最优，就是
 
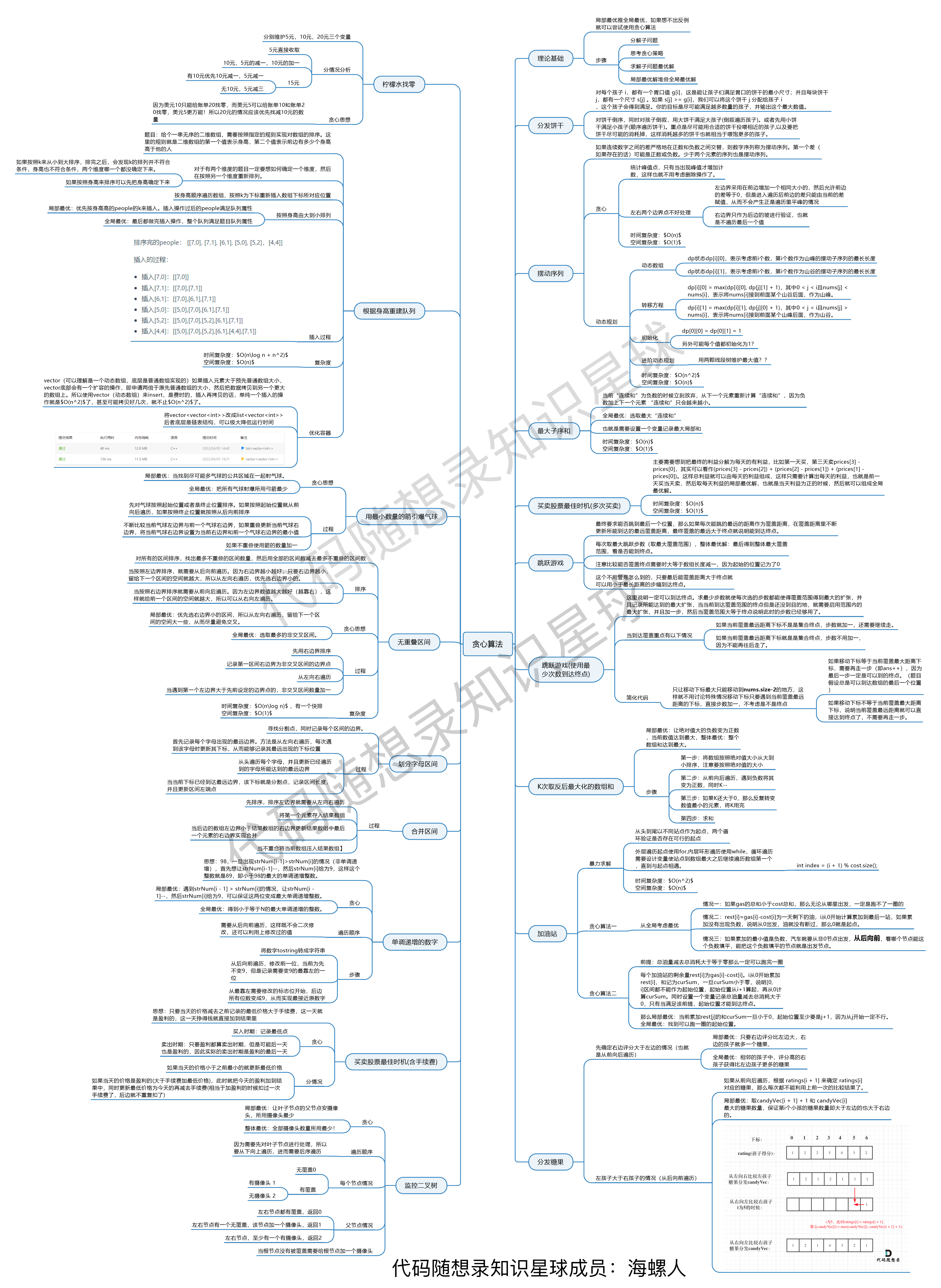
 贪心专题汇聚为一张图： 
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20211110121605.png) 
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/贪心总结water.png)
 
-这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员：[青](https://wx.zsxq.com/dweb2/index/footprint/185251215558842)所画，总结的非常好，分享给大家。
+这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员：[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412)所画，总结的非常好，分享给大家。
 
 很多没有接触过贪心的同学都会感觉贪心有啥可学的，但只要跟着「代码随想录」坚持下来之后，就会发现，贪心是一种很重要的算法思维而且并不简单，贪心往往妙的出其不意，触不及防！
 
@@ -145,18 +145,6 @@ Carl个人认为：如果找出局部最优并可以推出全局最优，就是
 
 **一个系列的结束，又是一个新系列的开始，我们将在明年第一个工作日正式开始动态规划，来不及解释了，录友们上车别掉队，我们又要开始新的征程！**
 
-## 其他语言版本
-
-
-Java：
-
-
-Python：
-
-
-Go：
-
-
 
 
 -----------------------