mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-13 06:06:11 +08:00
Merge branch 'youngyangyang04:master' into master
This commit is contained in:
@ -62,7 +62,7 @@
|
||||
如果你是算法老手,这篇攻略也是复习的最佳资料,如果把每个系列对应的总结篇,快速过一遍,整个算法知识体系以及各种解法就重现脑海了。
|
||||
|
||||
|
||||
目前「代码随想录」刷题攻略更新了:**200多篇文章,精讲了200道经典算法题目,共60w字的详细图解,部分难点题目还搭配了20分钟左右的视频讲解**。
|
||||
目前「代码随想录」刷题攻略更新了:**200多篇文章,精讲了200道经典算法题目,共60w字的详细图解,大部分题目都搭配了20分钟左右的视频讲解**,视频质量很好,口碑很好,大家可以去看看,视频列表:[代码随想录视频讲解](https://www.bilibili.com/video/BV1fA4y1o715)。
|
||||
|
||||
**这里每一篇题解,都是精品,值得仔细琢磨**。
|
||||
|
||||
|
||||
@ -216,6 +216,26 @@ impl Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
Rust
|
||||
|
||||
```
|
||||
use std::collections::HashMap;
|
||||
|
||||
impl Solution {
|
||||
pub fn two_sum(nums: Vec<i32>, target: i32) -> Vec<i32> {
|
||||
let mut hm: HashMap<i32, i32> = HashMap::new();
|
||||
for i in 0..nums.len() {
|
||||
let j = target - nums[i];
|
||||
if hm.contains_key(&j) {
|
||||
return vec![*hm.get(&j).unwrap(), i as i32]
|
||||
} else {
|
||||
hm.insert(nums[i], i as i32);
|
||||
}
|
||||
}
|
||||
vec![-1, -1]
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Javascript
|
||||
|
||||
|
||||
@ -135,6 +135,9 @@ public:
|
||||
};
|
||||
|
||||
```
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
技巧性的东西没有固定的学习方法,还是要多看多练,自己灵活运用了。
|
||||
|
||||
|
||||
|
||||
@ -4,10 +4,9 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
> 相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不少,做好心里准备!
|
||||
|
||||
> 相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不少,做好心里准备!
|
||||
|
||||
# 45.跳跃游戏II
|
||||
# 45.跳跃游戏 II
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/jump-game-ii/)
|
||||
|
||||
@ -18,13 +17,17 @@
|
||||
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
|
||||
|
||||
示例:
|
||||
* 输入: [2,3,1,1,4]
|
||||
* 输出: 2
|
||||
* 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
|
||||
|
||||
- 输入: [2,3,1,1,4]
|
||||
- 输出: 2
|
||||
- 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
|
||||
|
||||
说明:
|
||||
假设你总是可以到达数组的最后一个位置。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,最少跳几步还得看覆盖范围 | LeetCode: 45.跳跃游戏 II](https://www.bilibili.com/video/BV1Y24y1r7XZ),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
@ -46,7 +49,6 @@
|
||||
|
||||
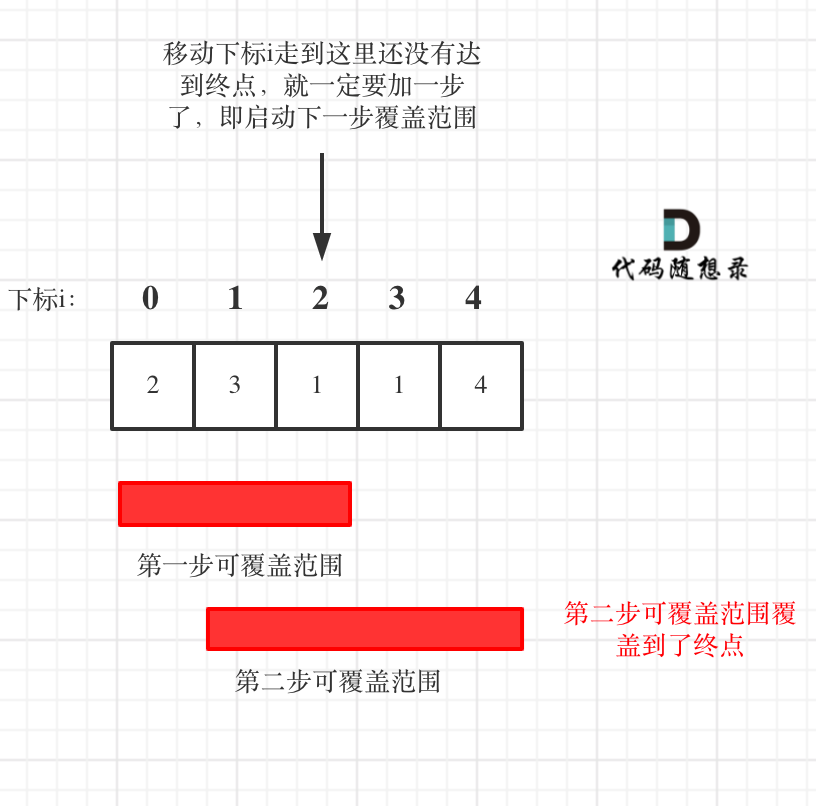
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
**图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)**
|
||||
@ -57,8 +59,8 @@
|
||||
|
||||
这里还是有个特殊情况需要考虑,当移动下标达到了当前覆盖的最远距离下标时
|
||||
|
||||
* 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。
|
||||
* 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
|
||||
- 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。
|
||||
- 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
|
||||
|
||||
C++代码如下:(详细注释)
|
||||
|
||||
@ -74,11 +76,9 @@ public:
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖最远距离下标
|
||||
if (i == curDistance) { // 遇到当前覆盖最远距离下标
|
||||
if (curDistance < nums.size() - 1) { // 如果当前覆盖最远距离下标不是终点
|
||||
ans++; // 需要走下一步
|
||||
curDistance = nextDistance; // 更新当前覆盖最远距离下标(相当于加油了)
|
||||
if (nextDistance >= nums.size() - 1) break; // 下一步的覆盖范围已经可以达到终点,结束循环
|
||||
} else break; // 当前覆盖最远距到达集合终点,不用做ans++操作了,直接结束
|
||||
ans++; // 需要走下一步
|
||||
curDistance = nextDistance; // 更新当前覆盖最远距离下标(相当于加油了)
|
||||
if (nextDistance >= nums.size() - 1) break; // 当前覆盖最远距到达集合终点,不用做ans++操作了,直接结束
|
||||
}
|
||||
}
|
||||
return ans;
|
||||
@ -86,20 +86,24 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
|
||||
|
||||
## 方法二
|
||||
|
||||
依然是贪心,思路和方法一差不多,代码可以简洁一些。
|
||||
|
||||
**针对于方法一的特殊情况,可以统一处理**,即:移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不考虑是不是终点的情况。
|
||||
|
||||
想要达到这样的效果,只要让移动下标,最大只能移动到nums.size - 2的地方就可以了。
|
||||
想要达到这样的效果,只要让移动下标,最大只能移动到 nums.size - 2 的地方就可以了。
|
||||
|
||||
因为当移动下标指向nums.size - 2时:
|
||||
因为当移动下标指向 nums.size - 2 时:
|
||||
|
||||
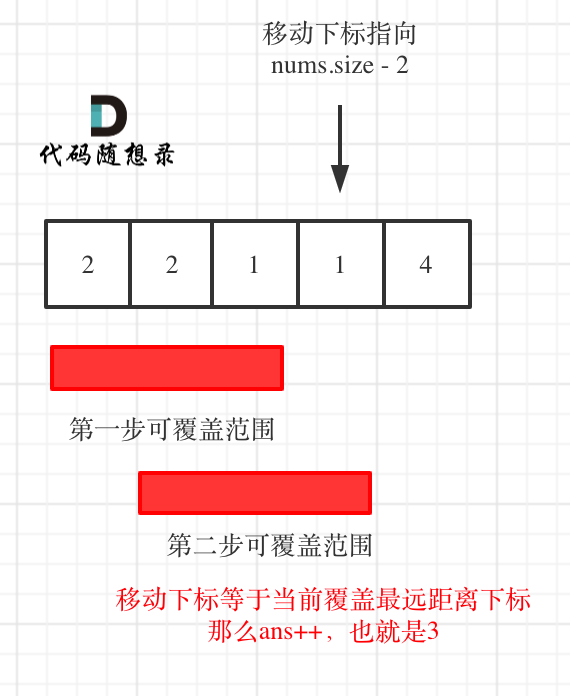
* 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
|
||||
|
||||
- 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即 ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
|
||||

|
||||
|
||||
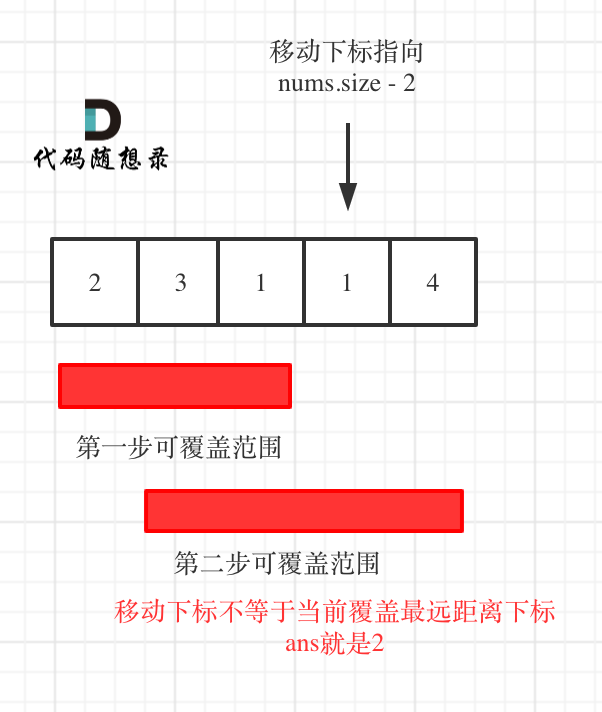
* 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
|
||||
- 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
|
||||
|
||||
|
||||
|
||||
@ -125,9 +129,14 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
|
||||
|
||||
|
||||
可以看出版本二的代码相对于版本一简化了不少!
|
||||
|
||||
**其精髓在于控制移动下标i只移动到nums.size() - 2的位置**,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。
|
||||
**其精髓在于控制移动下标 i 只移动到 nums.size() - 2 的位置**,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。
|
||||
|
||||
## 总结
|
||||
|
||||
@ -137,11 +146,10 @@ public:
|
||||
|
||||
理解本题的关键在于:**以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点**,这个范围内最小步数一定可以跳到,不用管具体是怎么跳的,不纠结于一步究竟跳一个单位还是两个单位。
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Java
|
||||
```Java
|
||||
// 版本一
|
||||
class Solution {
|
||||
@ -207,7 +215,7 @@ class Solution:
|
||||
nextDistance = 0
|
||||
for i in range(len(nums)):
|
||||
nextDistance = max(i + nums[i], nextDistance)
|
||||
if i == curDistance:
|
||||
if i == curDistance:
|
||||
if curDistance != len(nums) - 1:
|
||||
ans += 1
|
||||
curDistance = nextDistance
|
||||
@ -230,9 +238,25 @@ class Solution:
|
||||
step += 1
|
||||
return step
|
||||
```
|
||||
```python
|
||||
# 贪心版本三 - 类似‘55-跳跃游戏’写法
|
||||
class Solution:
|
||||
def jump(self, nums) -> int:
|
||||
if len(nums)==1: return 0
|
||||
i = 0
|
||||
count = 0
|
||||
cover = 0
|
||||
while i<=cover:
|
||||
for i in range(i,cover+1):
|
||||
cover = max(nums[i]+i,cover)
|
||||
if cover>=len(nums)-1: return count+1
|
||||
count+=1
|
||||
|
||||
```
|
||||
|
||||
```python
|
||||
# 动态规划做法
|
||||
class Solution:
|
||||
class Solution:
|
||||
def jump(self, nums: List[int]) -> int:
|
||||
result = [10**4+1]*len(nums)
|
||||
result[0]=0
|
||||
@ -244,7 +268,6 @@ class Solution:
|
||||
|
||||
```
|
||||
|
||||
|
||||
### Go
|
||||
|
||||
```go
|
||||
@ -331,21 +354,21 @@ var jump = function(nums) {
|
||||
|
||||
```typescript
|
||||
function jump(nums: number[]): number {
|
||||
const length: number = nums.length;
|
||||
let curFarthestIndex: number = 0,
|
||||
nextFarthestIndex: number = 0;
|
||||
let curIndex: number = 0;
|
||||
let stepNum: number = 0;
|
||||
while (curIndex < length - 1) {
|
||||
nextFarthestIndex = Math.max(nextFarthestIndex, curIndex + nums[curIndex]);
|
||||
if (curIndex === curFarthestIndex) {
|
||||
curFarthestIndex = nextFarthestIndex;
|
||||
stepNum++;
|
||||
}
|
||||
curIndex++;
|
||||
const length: number = nums.length;
|
||||
let curFarthestIndex: number = 0,
|
||||
nextFarthestIndex: number = 0;
|
||||
let curIndex: number = 0;
|
||||
let stepNum: number = 0;
|
||||
while (curIndex < length - 1) {
|
||||
nextFarthestIndex = Math.max(nextFarthestIndex, curIndex + nums[curIndex]);
|
||||
if (curIndex === curFarthestIndex) {
|
||||
curFarthestIndex = nextFarthestIndex;
|
||||
stepNum++;
|
||||
}
|
||||
return stepNum;
|
||||
};
|
||||
curIndex++;
|
||||
}
|
||||
return stepNum;
|
||||
}
|
||||
```
|
||||
|
||||
### Scala
|
||||
@ -427,7 +450,6 @@ impl Solution {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
|
||||
@ -158,6 +158,19 @@ if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
|
||||
|
||||
所以我通过举[1,1,1]的例子,把这两个去重的逻辑分别抽象成树形结构,大家可以一目了然:为什么两种写法都可以以及哪一种效率更高!
|
||||
|
||||
这里可能大家又有疑惑,既然 `used[i - 1] == false`也行而`used[i - 1] == true`也行,那为什么还要写这个条件呢?
|
||||
|
||||
直接这样写 不就完事了?
|
||||
|
||||
```cpp
|
||||
if (i > 0 && nums[i] == nums[i - 1]) {
|
||||
continue;
|
||||
}
|
||||
```
|
||||
|
||||
其实并不行,一定要加上 `used[i - 1] == false`或者`used[i - 1] == true`,因为 used[i - 1] 要一直是 true 或者一直是false 才可以,而不是 一会是true 一会又是false。 所以这个条件要写上。
|
||||
|
||||
|
||||
是不是豁然开朗了!!
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
@ -4,7 +4,6 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
# 53. 最大子序和
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/maximum-subarray/)
|
||||
@ -12,17 +11,19 @@
|
||||
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
|
||||
|
||||
示例:
|
||||
* 输入: [-2,1,-3,4,-1,2,1,-5,4]
|
||||
* 输出: 6
|
||||
* 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
|
||||
|
||||
- 输入: [-2,1,-3,4,-1,2,1,-5,4]
|
||||
- 输出: 6
|
||||
- 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法的巧妙需要慢慢体会!LeetCode:53. 最大子序和](https://www.bilibili.com/video/BV1aY4y1Z7ya),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 暴力解法
|
||||
|
||||
暴力解法的思路,第一层for 就是设置起始位置,第二层for循环遍历数组寻找最大值
|
||||
暴力解法的思路,第一层 for 就是设置起始位置,第二层 for 循环遍历数组寻找最大值
|
||||
|
||||
* 时间复杂度:O(n^2)
|
||||
* 空间复杂度:O(1)
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -41,14 +42,17 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度:O(n^2)
|
||||
* 空间复杂度:O(1)
|
||||
|
||||
以上暴力的解法C++勉强可以过,其他语言就不确定了。
|
||||
|
||||
以上暴力的解法 C++勉强可以过,其他语言就不确定了。
|
||||
|
||||
## 贪心解法
|
||||
|
||||
**贪心贪的是哪里呢?**
|
||||
|
||||
如果 -2 1 在一起,计算起点的时候,一定是从1开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
|
||||
如果 -2 1 在一起,计算起点的时候,一定是从 1 开始计算,因为负数只会拉低总和,这就是贪心贪的地方!
|
||||
|
||||
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
|
||||
|
||||
@ -56,29 +60,27 @@ public:
|
||||
|
||||
**局部最优的情况下,并记录最大的“连续和”,可以推出全局最优**。
|
||||
|
||||
|
||||
从代码角度上来讲:遍历nums,从头开始用count累积,如果count一旦加上nums[i]变为负数,那么就应该从nums[i+1]开始从0累积count了,因为已经变为负数的count,只会拖累总和。
|
||||
从代码角度上来讲:遍历 nums,从头开始用 count 累积,如果 count 一旦加上 nums[i]变为负数,那么就应该从 nums[i+1]开始从 0 累积 count 了,因为已经变为负数的 count,只会拖累总和。
|
||||
|
||||
**这相当于是暴力解法中的不断调整最大子序和区间的起始位置**。
|
||||
|
||||
|
||||
**那有同学问了,区间终止位置不用调整么? 如何才能得到最大“连续和”呢?**
|
||||
|
||||
区间的终止位置,其实就是如果count取到最大值了,及时记录下来了。例如如下代码:
|
||||
区间的终止位置,其实就是如果 count 取到最大值了,及时记录下来了。例如如下代码:
|
||||
|
||||
```
|
||||
if (count > result) result = count;
|
||||
```
|
||||
|
||||
**这样相当于是用result记录最大子序和区间和(变相的算是调整了终止位置)**。
|
||||
**这样相当于是用 result 记录最大子序和区间和(变相的算是调整了终止位置)**。
|
||||
|
||||
如动画所示:
|
||||
|
||||

|
||||
|
||||
红色的起始位置就是贪心每次取count为正数的时候,开始一个区间的统计。
|
||||
红色的起始位置就是贪心每次取 count 为正数的时候,开始一个区间的统计。
|
||||
|
||||
那么不难写出如下C++代码(关键地方已经注释)
|
||||
那么不难写出如下 C++代码(关键地方已经注释)
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -97,39 +99,34 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1)
|
||||
- 时间复杂度:O(n)
|
||||
- 空间复杂度:O(1)
|
||||
|
||||
当然题目没有说如果数组为空,应该返回什么,所以数组为空的话返回啥都可以了。
|
||||
|
||||
## 常见误区
|
||||
|
||||
## 常见误区
|
||||
|
||||
误区一:
|
||||
|
||||
不少同学认为 如果输入用例都是-1,或者 都是负数,这个贪心算法跑出来的结果是0, 这是**又一次证明脑洞模拟不靠谱的经典案例**,建议大家把代码运行一下试一试,就知道了,也会理解 为什么 result 要初始化为最小负数了。
|
||||
误区一:
|
||||
|
||||
不少同学认为 如果输入用例都是-1,或者 都是负数,这个贪心算法跑出来的结果是 0, 这是**又一次证明脑洞模拟不靠谱的经典案例**,建议大家把代码运行一下试一试,就知道了,也会理解 为什么 result 要初始化为最小负数了。
|
||||
|
||||
误区二:
|
||||
|
||||
大家在使用贪心算法求解本题,经常陷入的误区,就是分不清,是遇到 负数就选择起始位置,还是连续和为负选择起始位置。
|
||||
大家在使用贪心算法求解本题,经常陷入的误区,就是分不清,是遇到 负数就选择起始位置,还是连续和为负选择起始位置。
|
||||
|
||||
在动画演示用,大家可以发现, 4,遇到 -1 的时候,我们依然累加了,为什么呢?
|
||||
在动画演示用,大家可以发现, 4,遇到 -1 的时候,我们依然累加了,为什么呢?
|
||||
|
||||
因为和为3,只要连续和还是正数就会 对后面的元素 起到增大总和的作用。 所以只要连续和为正数我们就保留。
|
||||
|
||||
这里也会有录友疑惑,那 4 + -1 之后 不就变小了吗? 会不会错过 4 成为最大连续和的可能性?
|
||||
|
||||
其实并不会,因为还有一个变量result 一直在更新 最大的连续和,只要有更大的连续和出现,result就更新了,那么result已经把4更新了,后面 连续和变成3,也不会对最后结果有影响。
|
||||
因为和为 3,只要连续和还是正数就会 对后面的元素 起到增大总和的作用。 所以只要连续和为正数我们就保留。
|
||||
|
||||
这里也会有录友疑惑,那 4 + -1 之后 不就变小了吗? 会不会错过 4 成为最大连续和的可能性?
|
||||
|
||||
其实并不会,因为还有一个变量 result 一直在更新 最大的连续和,只要有更大的连续和出现,result 就更新了,那么 result 已经把 4 更新了,后面 连续和变成 3,也不会对最后结果有影响。
|
||||
|
||||
## 动态规划
|
||||
|
||||
当然本题还可以用动态规划来做,当前[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png)主要讲解贪心系列,后续到动态规划系列的时候会详细讲解本题的dp方法。
|
||||
当然本题还可以用动态规划来做,当前[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png)主要讲解贪心系列,后续到动态规划系列的时候会详细讲解本题的 dp 方法。
|
||||
|
||||
那么先给出我的dp代码如下,有时间的录友可以提前做一做:
|
||||
那么先给出我的 dp 代码如下,有时间的录友可以提前做一做:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -148,8 +145,8 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(n)
|
||||
- 时间复杂度:O(n)
|
||||
- 空间复杂度:O(n)
|
||||
|
||||
## 总结
|
||||
|
||||
@ -159,8 +156,8 @@ public:
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
### Java
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int maxSubArray(int[] nums) {
|
||||
@ -201,6 +198,7 @@ class Solution {
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def maxSubArray(self, nums: List[int]) -> int:
|
||||
@ -233,6 +231,7 @@ func maxSubArray(nums []int) int {
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
```rust
|
||||
pub fn max_sub_array(nums: Vec<i32>) -> i32 {
|
||||
let mut max_sum = i32::MIN;
|
||||
@ -247,6 +246,7 @@ pub fn max_sub_array(nums: Vec<i32>) -> i32 {
|
||||
```
|
||||
|
||||
### Javascript:
|
||||
|
||||
```Javascript
|
||||
var maxSubArray = function(nums) {
|
||||
let result = -Infinity
|
||||
@ -264,14 +264,15 @@ var maxSubArray = function(nums) {
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
### C:
|
||||
|
||||
贪心:
|
||||
|
||||
```c
|
||||
int maxSubArray(int* nums, int numsSize){
|
||||
int maxVal = INT_MIN;
|
||||
int subArrSum = 0;
|
||||
|
||||
|
||||
int i;
|
||||
for(i = 0; i < numsSize; ++i) {
|
||||
subArrSum += nums[i];
|
||||
@ -286,6 +287,7 @@ int maxSubArray(int* nums, int numsSize){
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```c
|
||||
/**
|
||||
* 解题思路:动态规划:
|
||||
@ -324,15 +326,15 @@ int maxSubArray(int* nums, int numsSize){
|
||||
|
||||
```typescript
|
||||
function maxSubArray(nums: number[]): number {
|
||||
let curSum: number = 0;
|
||||
let resMax: number = -Infinity;
|
||||
for (let i = 0, length = nums.length; i < length; i++) {
|
||||
curSum += nums[i];
|
||||
resMax = Math.max(curSum, resMax);
|
||||
if (curSum < 0) curSum = 0;
|
||||
}
|
||||
return resMax;
|
||||
};
|
||||
let curSum: number = 0;
|
||||
let resMax: number = -Infinity;
|
||||
for (let i = 0, length = nums.length; i < length; i++) {
|
||||
curSum += nums[i];
|
||||
resMax = Math.max(curSum, resMax);
|
||||
if (curSum < 0) curSum = 0;
|
||||
}
|
||||
return resMax;
|
||||
}
|
||||
```
|
||||
|
||||
**动态规划**
|
||||
@ -340,17 +342,17 @@ function maxSubArray(nums: number[]): number {
|
||||
```typescript
|
||||
// 动态规划
|
||||
function maxSubArray(nums: number[]): number {
|
||||
const length = nums.length;
|
||||
if (length === 0) return 0;
|
||||
const dp: number[] = [];
|
||||
dp[0] = nums[0];
|
||||
let resMax: number = nums[0];
|
||||
for (let i = 1; i < length; i++) {
|
||||
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
|
||||
resMax = Math.max(resMax, dp[i]);
|
||||
}
|
||||
return resMax;
|
||||
};
|
||||
const length = nums.length;
|
||||
if (length === 0) return 0;
|
||||
const dp: number[] = [];
|
||||
dp[0] = nums[0];
|
||||
let resMax: number = nums[0];
|
||||
for (let i = 1; i < length; i++) {
|
||||
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
|
||||
resMax = Math.max(resMax, dp[i]);
|
||||
}
|
||||
return resMax;
|
||||
}
|
||||
```
|
||||
|
||||
### Scala
|
||||
|
||||
@ -4,7 +4,6 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
# 55. 跳跃游戏
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/jump-game/)
|
||||
@ -15,20 +14,25 @@
|
||||
|
||||
判断你是否能够到达最后一个位置。
|
||||
|
||||
示例 1:
|
||||
* 输入: [2,3,1,1,4]
|
||||
* 输出: true
|
||||
* 解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
|
||||
示例 1:
|
||||
|
||||
示例 2:
|
||||
* 输入: [3,2,1,0,4]
|
||||
* 输出: false
|
||||
* 解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
|
||||
- 输入: [2,3,1,1,4]
|
||||
- 输出: true
|
||||
- 解释: 我们可以先跳 1 步,从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
|
||||
|
||||
示例 2:
|
||||
|
||||
- 输入: [3,2,1,0,4]
|
||||
- 输出: false
|
||||
- 解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,怎么跳跃不重要,关键在覆盖范围 | LeetCode:55.跳跃游戏](https://www.bilibili.com/video/BV1VG4y1X7kB),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
刚看到本题一开始可能想:当前位置元素如果是3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
|
||||
刚看到本题一开始可能想:当前位置元素如果是 3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢?
|
||||
|
||||
其实跳几步无所谓,关键在于可跳的覆盖范围!
|
||||
|
||||
@ -46,14 +50,14 @@
|
||||
|
||||
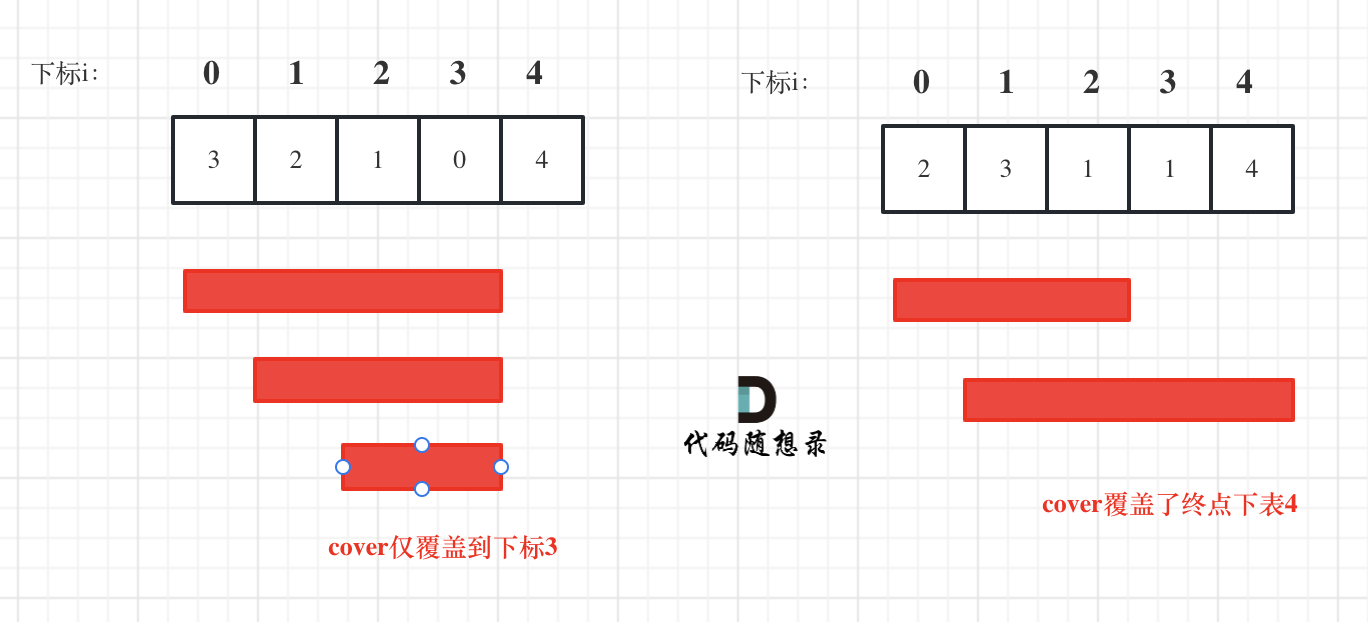
如图:
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
i每次移动只能在cover的范围内移动,每移动一个元素,cover得到该元素数值(新的覆盖范围)的补充,让i继续移动下去。
|
||||
i 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。
|
||||
|
||||
而cover每次只取 max(该元素数值补充后的范围, cover本身范围)。
|
||||
而 cover 每次只取 max(该元素数值补充后的范围, cover 本身范围)。
|
||||
|
||||
如果cover大于等于了终点下标,直接return true就可以了。
|
||||
如果 cover 大于等于了终点下标,直接 return true 就可以了。
|
||||
|
||||
C++代码如下:
|
||||
|
||||
@ -71,6 +75,11 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
这道题目关键点在于:不用拘泥于每次究竟跳几步,而是看覆盖范围,覆盖范围内一定是可以跳过来的,不用管是怎么跳的。
|
||||
@ -83,8 +92,8 @@ public:
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Java
|
||||
```Java
|
||||
class Solution {
|
||||
public boolean canJump(int[] nums) {
|
||||
@ -106,6 +115,7 @@ class Solution {
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def canJump(self, nums: List[int]) -> bool:
|
||||
@ -156,9 +166,7 @@ func max(a, b int ) int {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### Javascript
|
||||
### Javascript
|
||||
|
||||
```Javascript
|
||||
var canJump = function(nums) {
|
||||
@ -196,6 +204,7 @@ impl Solution {
|
||||
```
|
||||
|
||||
### C
|
||||
|
||||
```c
|
||||
#define max(a, b) (((a) > (b)) ? (a) : (b))
|
||||
|
||||
@ -217,23 +226,23 @@ bool canJump(int* nums, int numsSize){
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
### TypeScript
|
||||
|
||||
```typescript
|
||||
function canJump(nums: number[]): boolean {
|
||||
let farthestIndex: number = 0;
|
||||
let cur: number = 0;
|
||||
while (cur <= farthestIndex) {
|
||||
farthestIndex = Math.max(farthestIndex, cur + nums[cur]);
|
||||
if (farthestIndex >= nums.length - 1) return true;
|
||||
cur++;
|
||||
}
|
||||
return false;
|
||||
};
|
||||
let farthestIndex: number = 0;
|
||||
let cur: number = 0;
|
||||
while (cur <= farthestIndex) {
|
||||
farthestIndex = Math.max(farthestIndex, cur + nums[cur]);
|
||||
if (farthestIndex >= nums.length - 1) return true;
|
||||
cur++;
|
||||
}
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
### Scala
|
||||
|
||||
```scala
|
||||
object Solution {
|
||||
def canJump(nums: Array[Int]): Boolean = {
|
||||
@ -250,7 +259,6 @@ object Solution {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
|
||||
@ -22,6 +22,9 @@
|
||||
* 解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
|
||||
* 注意:输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,合并区间有细节!LeetCode:56.合并区间](https://www.bilibili.com/video/BV1wx4y157nD),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
@ -70,6 +73,10 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(nlogn)
|
||||
* 空间复杂度: O(logn),排序需要的空间开销
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
@ -106,7 +113,6 @@ class Solution {
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
```
|
||||
```java
|
||||
// 版本2
|
||||
@ -174,6 +180,34 @@ func max(a, b int) int {
|
||||
return b
|
||||
}
|
||||
```
|
||||
```go
|
||||
// 版本2
|
||||
func merge(intervals [][]int) [][]int {
|
||||
if len(intervals) == 1 {
|
||||
return intervals
|
||||
}
|
||||
sort.Slice(intervals, func(i, j int) bool {
|
||||
return intervals[i][0] < intervals[j][0]
|
||||
})
|
||||
res := make([][]int, 0)
|
||||
res = append(res, intervals[0])
|
||||
for i := 1; i < len(intervals); i++ {
|
||||
if intervals[i][0] <= res[len(res)-1][1]{
|
||||
res[len(res)-1][1] = max56(res[len(res)-1][1],intervals[i][1])
|
||||
} else {
|
||||
res = append(res, intervals[i])
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
func max56(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
### Javascript
|
||||
```javascript
|
||||
@ -277,24 +311,22 @@ object Solution {
|
||||
|
||||
```Rust
|
||||
impl Solution {
|
||||
fn max(a: i32, b: i32) -> i32 {
|
||||
if a > b { a } else { b }
|
||||
}
|
||||
|
||||
pub fn merge(intervals: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
|
||||
let mut intervals = intervals;
|
||||
let mut result = Vec::new();
|
||||
if intervals.len() == 0 { return result; }
|
||||
intervals.sort_by(|a, b| a[0].cmp(&b[0]));
|
||||
result.push(intervals[0].clone());
|
||||
for i in 1..intervals.len() {
|
||||
if result.last_mut().unwrap()[1] >= intervals[i][0] {
|
||||
result.last_mut().unwrap()[1] = Self::max(result.last_mut().unwrap()[1], intervals[i][1]);
|
||||
pub fn merge(mut intervals: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
|
||||
let mut res = vec![];
|
||||
if intervals.is_empty() {
|
||||
return res;
|
||||
}
|
||||
intervals.sort_by_key(|a| a[0]);
|
||||
res.push(intervals[0].clone());
|
||||
for interval in intervals.into_iter().skip(1) {
|
||||
let res_last_ele = res.last_mut().unwrap();
|
||||
if res_last_ele[1] >= interval[0] {
|
||||
res_last_ele[1] = interval[1].max(res_last_ele[1]);
|
||||
} else {
|
||||
result.push(intervals[i].clone());
|
||||
res.push(interval);
|
||||
}
|
||||
}
|
||||
result
|
||||
res
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -395,21 +395,14 @@ function uniquePaths(m: number, n: number): number {
|
||||
```Rust
|
||||
impl Solution {
|
||||
pub fn unique_paths(m: i32, n: i32) -> i32 {
|
||||
let m = m as usize;
|
||||
let n = n as usize;
|
||||
let mut dp = vec![vec![0; n]; m];
|
||||
for i in 0..m {
|
||||
dp[i][0] = 1;
|
||||
let (m, n) = (m as usize, n as usize);
|
||||
let mut dp = vec![vec![1; n]; m];
|
||||
for i in 1..m {
|
||||
for j in 1..n {
|
||||
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
|
||||
}
|
||||
for j in 0..n {
|
||||
dp[0][j] = 1;
|
||||
}
|
||||
for i in 1..m {
|
||||
for j in 1..n {
|
||||
dp[i][j] = dp[i-1][j] + dp[i][j-1];
|
||||
}
|
||||
}
|
||||
dp[m-1][n-1]
|
||||
}
|
||||
dp[m - 1][n - 1]
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
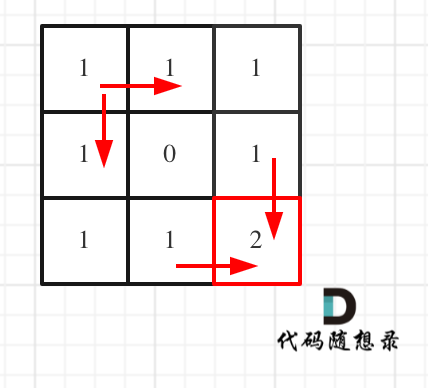
@ -135,7 +135,7 @@ for (int i = 1; i < m; i++) {
|
||||
|
||||
|
||||
|
||||
如果这个图看不同,建议在理解一下递归公式,然后照着文章中说的遍历顺序,自己推导一下!
|
||||
如果这个图看不懂,建议再理解一下递归公式,然后照着文章中说的遍历顺序,自己推导一下!
|
||||
|
||||
动规五部分分析完毕,对应C++代码如下:
|
||||
|
||||
|
||||
@ -72,7 +72,7 @@ dp[i]: 爬到第i层楼梯,有dp[i]种方法
|
||||
|
||||
3. dp数组如何初始化
|
||||
|
||||
再回顾一下dp[i]的定义:爬到第i层楼梯,有dp[i]中方法。
|
||||
再回顾一下dp[i]的定义:爬到第i层楼梯,有dp[i]种方法。
|
||||
|
||||
那么i为0,dp[i]应该是多少呢,这个可以有很多解释,但基本都是直接奔着答案去解释的。
|
||||
|
||||
@ -454,18 +454,32 @@ public class Solution {
|
||||
```rust
|
||||
impl Solution {
|
||||
pub fn climb_stairs(n: i32) -> i32 {
|
||||
if n <= 2 {
|
||||
if n <= 1 {
|
||||
return n;
|
||||
}
|
||||
let mut a = 1;
|
||||
let mut b = 2;
|
||||
let mut f = 0;
|
||||
for i in 2..n {
|
||||
let (mut a, mut b, mut f) = (1, 1, 0);
|
||||
for _ in 2..=n {
|
||||
f = a + b;
|
||||
a = b;
|
||||
b = f;
|
||||
}
|
||||
return f;
|
||||
f
|
||||
}
|
||||
```
|
||||
|
||||
dp 数组
|
||||
|
||||
```rust
|
||||
impl Solution {
|
||||
pub fn climb_stairs(n: i32) -> i32 {
|
||||
let n = n as usize;
|
||||
let mut dp = vec![0; n + 1];
|
||||
dp[0] = 1;
|
||||
dp[1] = 1;
|
||||
for i in 2..=n {
|
||||
dp[i] = dp[i - 1] + dp[i - 2];
|
||||
}
|
||||
dp[n]
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -101,6 +101,11 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(nm)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
|
||||
|
||||
代码中m表示最多可以爬m个台阶,代码中把m改成2就是本题70.爬楼梯可以AC的代码了。
|
||||
|
||||
## 总结
|
||||
|
||||
@ -218,6 +218,10 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n * m)
|
||||
* 空间复杂度: O(n * m)
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
@ -38,7 +38,7 @@
|
||||
本题可以使用前序(中左右),也可以使用后序遍历(左右中),使用前序求的就是深度,使用后序求的是高度。
|
||||
|
||||
* 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)
|
||||
* 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数后者节点数(取决于高度从0开始还是从1开始)
|
||||
* 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数或者节点数(取决于高度从0开始还是从1开始)
|
||||
|
||||
**而根节点的高度就是二叉树的最大深度**,所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。
|
||||
|
||||
@ -50,7 +50,7 @@
|
||||
|
||||
代码如下:
|
||||
```CPP
|
||||
int getdepth(treenode* node)
|
||||
int getdepth(TreeNode* node)
|
||||
```
|
||||
|
||||
2. 确定终止条件:如果为空节点的话,就返回0,表示高度为0。
|
||||
@ -76,14 +76,14 @@ return depth;
|
||||
```CPP
|
||||
class solution {
|
||||
public:
|
||||
int getdepth(treenode* node) {
|
||||
int getdepth(TreeNode* node) {
|
||||
if (node == NULL) return 0;
|
||||
int leftdepth = getdepth(node->left); // 左
|
||||
int rightdepth = getdepth(node->right); // 右
|
||||
int depth = 1 + max(leftdepth, rightdepth); // 中
|
||||
return depth;
|
||||
}
|
||||
int maxdepth(treenode* root) {
|
||||
int maxDepth(TreeNode* root) {
|
||||
return getdepth(root);
|
||||
}
|
||||
};
|
||||
@ -93,9 +93,9 @@ public:
|
||||
```CPP
|
||||
class solution {
|
||||
public:
|
||||
int maxdepth(treenode* root) {
|
||||
int maxDepth(TreeNode* root) {
|
||||
if (root == null) return 0;
|
||||
return 1 + max(maxdepth(root->left), maxdepth(root->right));
|
||||
return 1 + max(maxDepth(root->left), maxDepth(root->right));
|
||||
}
|
||||
};
|
||||
|
||||
@ -110,7 +110,7 @@ public:
|
||||
class solution {
|
||||
public:
|
||||
int result;
|
||||
void getdepth(treenode* node, int depth) {
|
||||
void getdepth(TreeNode* node, int depth) {
|
||||
result = depth > result ? depth : result; // 中
|
||||
|
||||
if (node->left == NULL && node->right == NULL) return ;
|
||||
@ -127,7 +127,7 @@ public:
|
||||
}
|
||||
return ;
|
||||
}
|
||||
int maxdepth(treenode* root) {
|
||||
int maxDepth(TreeNode* root) {
|
||||
result = 0;
|
||||
if (root == NULL) return result;
|
||||
getdepth(root, 1);
|
||||
@ -144,7 +144,7 @@ public:
|
||||
class solution {
|
||||
public:
|
||||
int result;
|
||||
void getdepth(treenode* node, int depth) {
|
||||
void getdepth(TreeNode* node, int depth) {
|
||||
result = depth > result ? depth : result; // 中
|
||||
if (node->left == NULL && node->right == NULL) return ;
|
||||
if (node->left) { // 左
|
||||
@ -155,7 +155,7 @@ public:
|
||||
}
|
||||
return ;
|
||||
}
|
||||
int maxdepth(treenode* root) {
|
||||
int maxDepth(TreeNode* root) {
|
||||
result = 0;
|
||||
if (root == 0) return result;
|
||||
getdepth(root, 1);
|
||||
@ -182,16 +182,16 @@ c++代码如下:
|
||||
```CPP
|
||||
class solution {
|
||||
public:
|
||||
int maxdepth(treenode* root) {
|
||||
int maxDepth(TreeNode* root) {
|
||||
if (root == NULL) return 0;
|
||||
int depth = 0;
|
||||
queue<treenode*> que;
|
||||
queue<TreeNode*> que;
|
||||
que.push(root);
|
||||
while(!que.empty()) {
|
||||
int size = que.size();
|
||||
depth++; // 记录深度
|
||||
for (int i = 0; i < size; i++) {
|
||||
treenode* node = que.front();
|
||||
TreeNode* node = que.front();
|
||||
que.pop();
|
||||
if (node->left) que.push(node->left);
|
||||
if (node->right) que.push(node->right);
|
||||
@ -230,11 +230,11 @@ c++代码:
|
||||
```CPP
|
||||
class solution {
|
||||
public:
|
||||
int maxdepth(node* root) {
|
||||
int maxDepth(Node* root) {
|
||||
if (root == 0) return 0;
|
||||
int depth = 0;
|
||||
for (int i = 0; i < root->children.size(); i++) {
|
||||
depth = max (depth, maxdepth(root->children[i]));
|
||||
depth = max (depth, maxDepth(root->children[i]));
|
||||
}
|
||||
return depth + 1;
|
||||
}
|
||||
@ -247,15 +247,15 @@ public:
|
||||
```CPP
|
||||
class solution {
|
||||
public:
|
||||
int maxdepth(node* root) {
|
||||
queue<node*> que;
|
||||
int maxDepth(Node* root) {
|
||||
queue<Node*> que;
|
||||
if (root != NULL) que.push(root);
|
||||
int depth = 0;
|
||||
while (!que.empty()) {
|
||||
int size = que.size();
|
||||
depth++; // 记录深度
|
||||
for (int i = 0; i < size; i++) {
|
||||
node* node = que.front();
|
||||
Node* node = que.front();
|
||||
que.pop();
|
||||
for (int j = 0; j < node->children.size(); j++) {
|
||||
if (node->children[j]) que.push(node->children[j]);
|
||||
|
||||
@ -170,11 +170,14 @@ class Solution {
|
||||
private:
|
||||
int result;
|
||||
void getdepth(TreeNode* node, int depth) {
|
||||
if (node->left == NULL && node->right == NULL) {
|
||||
result = min(depth, result);
|
||||
// 函数递归终止条件
|
||||
if (root == nullptr) {
|
||||
return;
|
||||
}
|
||||
// 中 只不过中没有处理的逻辑
|
||||
// 中,处理逻辑:判断是不是叶子结点
|
||||
if (root -> left == nullptr && root->right == nullptr) {
|
||||
res = min(res, depth);
|
||||
}
|
||||
if (node->left) { // 左
|
||||
getdepth(node->left, depth + 1);
|
||||
}
|
||||
@ -186,7 +189,9 @@ private:
|
||||
|
||||
public:
|
||||
int minDepth(TreeNode* root) {
|
||||
if (root == NULL) return 0;
|
||||
if (root == nullptr) {
|
||||
return 0;
|
||||
}
|
||||
result = INT_MAX;
|
||||
getdepth(root, 1);
|
||||
return result;
|
||||
|
||||
@ -17,7 +17,7 @@
|
||||
示例:
|
||||
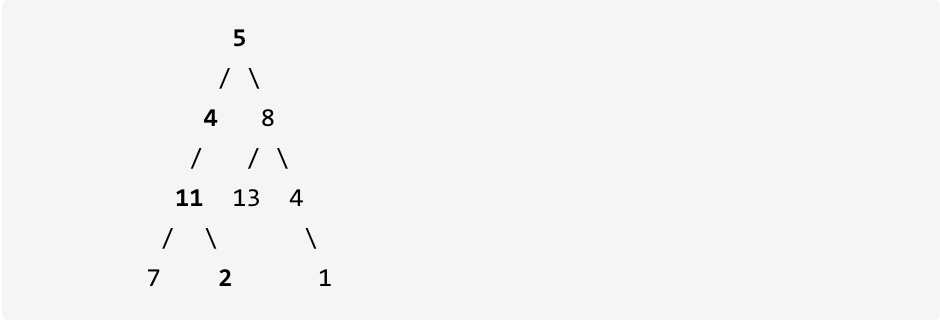
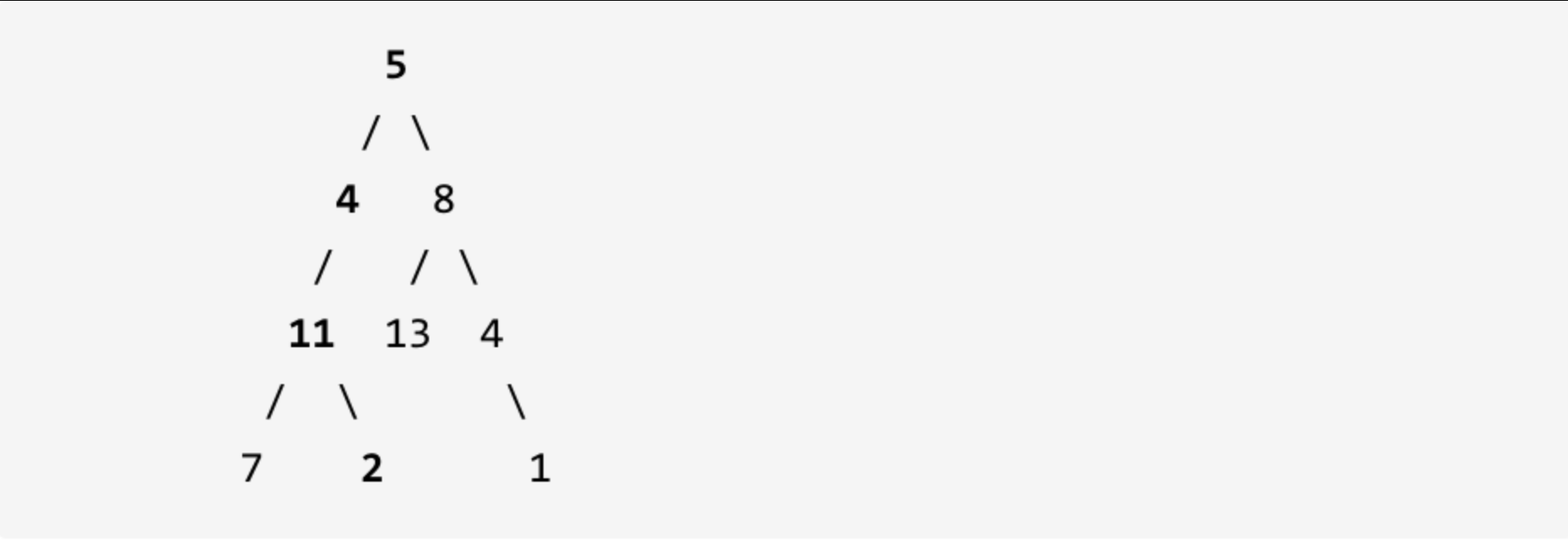
给定如下二叉树,以及目标和 sum = 22,
|
||||
|
||||
|
||||
|
||||
|
||||
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
|
||||
|
||||
@ -250,7 +250,7 @@ private:
|
||||
vector<vector<int>> result;
|
||||
vector<int> path;
|
||||
// 递归函数不需要返回值,因为我们要遍历整个树
|
||||
void traversal(treenode* cur, int count) {
|
||||
void traversal(TreeNode* cur, int count) {
|
||||
if (!cur->left && !cur->right && count == 0) { // 遇到了叶子节点且找到了和为sum的路径
|
||||
result.push_back(path);
|
||||
return;
|
||||
@ -276,10 +276,10 @@ private:
|
||||
}
|
||||
|
||||
public:
|
||||
vector<vector<int>> pathsum(treenode* root, int sum) {
|
||||
vector<vector<int>> pathSum(TreeNode* root, int sum) {
|
||||
result.clear();
|
||||
path.clear();
|
||||
if (root == null) return result;
|
||||
if (root == NULL) return result;
|
||||
path.push_back(root->val); // 把根节点放进路径
|
||||
traversal(root, sum - root->val);
|
||||
return result;
|
||||
@ -475,6 +475,12 @@ class solution:
|
||||
return false # 别忘记处理空treenode
|
||||
else:
|
||||
return isornot(root, targetsum - root.val)
|
||||
|
||||
class Solution: # 简洁版
|
||||
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
|
||||
if not root: return False
|
||||
if root.left==root.right==None and root.val == targetSum: return True
|
||||
return self.hasPathSum(root.left,targetSum-root.val) or self.hasPathSum(root.right,targetSum-root.val)
|
||||
```
|
||||
|
||||
**迭代 - 层序遍历**
|
||||
@ -560,6 +566,26 @@ class Solution:
|
||||
return result
|
||||
```
|
||||
|
||||
**迭代法,前序遍历**
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
|
||||
if not root: return []
|
||||
stack, path_stack,result = [[root,root.val]],[[root.val]],[]
|
||||
while stack:
|
||||
cur,cursum = stack.pop()
|
||||
path = path_stack.pop()
|
||||
if cur.left==cur.right==None:
|
||||
if cursum==targetSum: result.append(path)
|
||||
if cur.right:
|
||||
stack.append([cur.right,cursum+cur.right.val])
|
||||
path_stack.append(path+[cur.right.val])
|
||||
if cur.left:
|
||||
stack.append([cur.left,cursum+cur.left.val])
|
||||
path_stack.append(path+[cur.left.val])
|
||||
return result
|
||||
```
|
||||
## go
|
||||
|
||||
### 112. 路径总和
|
||||
|
||||
@ -149,6 +149,11 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n * m)
|
||||
* 空间复杂度: O(n * m)
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
|
||||
@ -4,43 +4,49 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
# 122.买卖股票的最佳时机II
|
||||
# 122.买卖股票的最佳时机 II
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/)
|
||||
|
||||
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
|
||||
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
|
||||
|
||||
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
|
||||
|
||||
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
|
||||
|
||||
|
||||
示例 1:
|
||||
* 输入: [7,1,5,3,6,4]
|
||||
* 输出: 7
|
||||
* 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
|
||||
|
||||
- 输入: [7,1,5,3,6,4]
|
||||
- 输出: 7
|
||||
- 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
|
||||
|
||||
示例 2:
|
||||
* 输入: [1,2,3,4,5]
|
||||
* 输出: 4
|
||||
* 解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
|
||||
|
||||
示例 3:
|
||||
* 输入: [7,6,4,3,1]
|
||||
* 输出: 0
|
||||
* 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
|
||||
- 输入: [1,2,3,4,5]
|
||||
- 输出: 4
|
||||
- 解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
|
||||
|
||||
示例 3:
|
||||
|
||||
- 输入: [7,6,4,3,1]
|
||||
- 输出: 0
|
||||
- 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
|
||||
|
||||
提示:
|
||||
* 1 <= prices.length <= 3 * 10 ^ 4
|
||||
* 0 <= prices[i] <= 10 ^ 4
|
||||
|
||||
- 1 <= prices.length <= 3 \* 10 ^ 4
|
||||
- 0 <= prices[i] <= 10 ^ 4
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法也能解决股票问题!LeetCode:122.买卖股票最佳时机 II](https://www.bilibili.com/video/BV1ev4y1C7na),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
本题首先要清楚两点:
|
||||
|
||||
* 只有一只股票!
|
||||
* 当前只有买股票或者卖股票的操作
|
||||
- 只有一只股票!
|
||||
- 当前只有买股票或者卖股票的操作
|
||||
|
||||
想获得利润至少要两天为一个交易单元。
|
||||
|
||||
@ -52,17 +58,16 @@
|
||||
|
||||
如何分解呢?
|
||||
|
||||
假如第0天买入,第3天卖出,那么利润为:prices[3] - prices[0]。
|
||||
假如第 0 天买入,第 3 天卖出,那么利润为:prices[3] - prices[0]。
|
||||
|
||||
相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。
|
||||
|
||||
**此时就是把利润分解为每天为单位的维度,而不是从0天到第3天整体去考虑!**
|
||||
**此时就是把利润分解为每天为单位的维度,而不是从 0 天到第 3 天整体去考虑!**
|
||||
|
||||
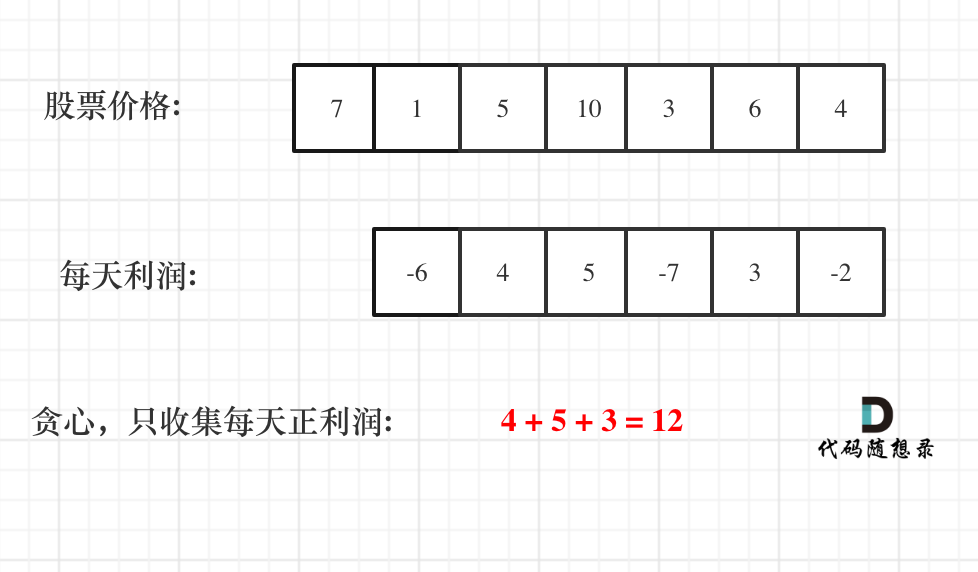
那么根据prices可以得到每天的利润序列:(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。
|
||||
那么根据 prices 可以得到每天的利润序列:(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
一些同学陷入:第一天怎么就没有利润呢,第一天到底算不算的困惑中。
|
||||
@ -77,7 +82,7 @@
|
||||
|
||||
局部最优可以推出全局最优,找不出反例,试一试贪心!
|
||||
|
||||
对应C++代码如下:
|
||||
对应 C++代码如下:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -92,12 +97,12 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1)
|
||||
- 时间复杂度:O(n)
|
||||
- 空间复杂度:O(1)
|
||||
|
||||
### 动态规划
|
||||
|
||||
动态规划将在下一个系列详细讲解,本题解先给出我的C++代码(带详细注释),感兴趣的同学可以自己先学习一下。
|
||||
动态规划将在下一个系列详细讲解,本题解先给出我的 C++代码(带详细注释),感兴趣的同学可以自己先学习一下。
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -119,8 +124,8 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:$O(n)$
|
||||
* 空间复杂度:$O(n)$
|
||||
- 时间复杂度:$O(n)$
|
||||
- 空间复杂度:$O(n)$
|
||||
|
||||
## 总结
|
||||
|
||||
@ -134,9 +139,10 @@ public:
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java:
|
||||
### Java:
|
||||
|
||||
贪心:
|
||||
|
||||
```java
|
||||
// 贪心思路
|
||||
class Solution {
|
||||
@ -151,6 +157,7 @@ class Solution {
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```java
|
||||
class Solution { // 动态规划
|
||||
public int maxProfit(int[] prices) {
|
||||
@ -172,8 +179,10 @@ class Solution { // 动态规划
|
||||
}
|
||||
```
|
||||
|
||||
### Python:
|
||||
### Python:
|
||||
|
||||
贪心:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def maxProfit(self, prices: List[int]) -> int:
|
||||
@ -184,6 +193,7 @@ class Solution:
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def maxProfit(self, prices: List[int]) -> int:
|
||||
@ -200,6 +210,7 @@ class Solution:
|
||||
### Go:
|
||||
|
||||
贪心算法
|
||||
|
||||
```go
|
||||
func maxProfit(prices []int) int {
|
||||
var sum int
|
||||
@ -212,7 +223,9 @@ func maxProfit(prices []int) int {
|
||||
return sum
|
||||
}
|
||||
```
|
||||
|
||||
动态规划
|
||||
|
||||
```go
|
||||
func maxProfit(prices []int) int {
|
||||
dp := make([][]int, len(prices))
|
||||
@ -226,7 +239,7 @@ func maxProfit(prices []int) int {
|
||||
dp[i][1] = max(dp[i-1][0] - prices[i], dp[i-1][1])
|
||||
}
|
||||
return dp[len(prices)-1][0]
|
||||
|
||||
|
||||
}
|
||||
func max(a, b int) int {
|
||||
if a > b {
|
||||
@ -239,6 +252,7 @@ func max(a, b int) int {
|
||||
### Javascript:
|
||||
|
||||
贪心
|
||||
|
||||
```Javascript
|
||||
var maxProfit = function(prices) {
|
||||
let result = 0
|
||||
@ -249,27 +263,28 @@ var maxProfit = function(prices) {
|
||||
};
|
||||
```
|
||||
|
||||
动态规划
|
||||
动态规划
|
||||
|
||||
```javascript
|
||||
const maxProfit = (prices) => {
|
||||
let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
|
||||
// dp[i][0] 表示第i天持有股票所得现金。
|
||||
// dp[i][1] 表示第i天不持有股票所得最多现金
|
||||
dp[0][0] = 0 - prices[0];
|
||||
dp[0][1] = 0;
|
||||
for(let i = 1; i < prices.length; i++) {
|
||||
// 如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
|
||||
// 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
|
||||
// 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
|
||||
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] - prices[i]);
|
||||
|
||||
// 在来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
|
||||
// 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
|
||||
// 第i天卖出股票,所得现金就是按照今天股票佳价格卖出后所得现金即:prices[i] + dp[i - 1][0]
|
||||
dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i]);
|
||||
}
|
||||
let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
|
||||
// dp[i][0] 表示第i天持有股票所得现金。
|
||||
// dp[i][1] 表示第i天不持有股票所得最多现金
|
||||
dp[0][0] = 0 - prices[0];
|
||||
dp[0][1] = 0;
|
||||
for (let i = 1; i < prices.length; i++) {
|
||||
// 如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
|
||||
// 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
|
||||
// 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
|
||||
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
|
||||
|
||||
return dp[prices.length -1][1];
|
||||
// 在来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
|
||||
// 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
|
||||
// 第i天卖出股票,所得现金就是按照今天股票佳价格卖出后所得现金即:prices[i] + dp[i - 1][0]
|
||||
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
|
||||
}
|
||||
|
||||
return dp[prices.length - 1][1];
|
||||
};
|
||||
```
|
||||
|
||||
@ -278,12 +293,12 @@ const maxProfit = (prices) => {
|
||||
贪心
|
||||
```typescript
|
||||
function maxProfit(prices: number[]): number {
|
||||
let resProfit: number = 0;
|
||||
for (let i = 1, length = prices.length; i < length; i++) {
|
||||
resProfit += Math.max(prices[i] - prices[i - 1], 0);
|
||||
}
|
||||
return resProfit;
|
||||
};
|
||||
let resProfit: number = 0;
|
||||
for (let i = 1, length = prices.length; i < length; i++) {
|
||||
resProfit += Math.max(prices[i] - prices[i - 1], 0);
|
||||
}
|
||||
return resProfit;
|
||||
}
|
||||
```
|
||||
|
||||
动态规划
|
||||
@ -304,6 +319,7 @@ function maxProfit(prices: number[]): number {
|
||||
### Rust
|
||||
|
||||
贪心:
|
||||
|
||||
```Rust
|
||||
impl Solution {
|
||||
fn max(a: i32, b: i32) -> i32 {
|
||||
@ -320,6 +336,7 @@ impl Solution {
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```Rust
|
||||
impl Solution {
|
||||
fn max(a: i32, b: i32) -> i32 {
|
||||
@ -339,7 +356,9 @@ impl Solution {
|
||||
```
|
||||
|
||||
### C:
|
||||
|
||||
贪心:
|
||||
|
||||
```c
|
||||
int maxProfit(int* prices, int pricesSize){
|
||||
int result = 0;
|
||||
@ -355,6 +374,7 @@ int maxProfit(int* prices, int pricesSize){
|
||||
```
|
||||
|
||||
动态规划:
|
||||
|
||||
```c
|
||||
#define max(a, b) (((a) > (b)) ? (a) : (b))
|
||||
|
||||
@ -379,6 +399,7 @@ int maxProfit(int* prices, int pricesSize){
|
||||
### Scala
|
||||
|
||||
贪心:
|
||||
|
||||
```scala
|
||||
object Solution {
|
||||
def maxProfit(prices: Array[Int]): Int = {
|
||||
|
||||
@ -289,7 +289,45 @@ class Solution:
|
||||
## Go
|
||||
|
||||
```go
|
||||
func minCut(s string) int {
|
||||
isValid := make([][]bool, len(s))
|
||||
for i := 0; i < len(isValid); i++ {
|
||||
isValid[i] = make([]bool, len(s))
|
||||
isValid[i][i] = true
|
||||
}
|
||||
for i := len(s) - 1; i >= 0; i-- {
|
||||
for j := i + 1; j < len(s); j++ {
|
||||
if s[i] == s[j] && (isValid[i + 1][j - 1] || j - i == 1) {
|
||||
isValid[i][j] = true
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
dp := make([]int, len(s))
|
||||
for i := 0; i < len(s); i++ {
|
||||
dp[i] = math.MaxInt
|
||||
}
|
||||
for i := 0; i < len(s); i++ {
|
||||
if isValid[0][i] {
|
||||
dp[i] = 0
|
||||
continue
|
||||
}
|
||||
for j := 0; j < i; j++ {
|
||||
if isValid[j + 1][i] {
|
||||
dp[i] = min(dp[i], dp[j] + 1)
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[len(s) - 1]
|
||||
}
|
||||
|
||||
func min(i, j int) int {
|
||||
if i < j {
|
||||
return i
|
||||
} else {
|
||||
return j
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
## JavaScript
|
||||
|
||||
@ -45,6 +45,10 @@
|
||||
* 解释:
|
||||
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油。开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油。开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油。你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。因此,无论怎样,你都不可能绕环路行驶一周。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,得这么加油才能跑完全程!LeetCode :134.加油站](https://www.bilibili.com/video/BV1jA411r7WX),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 暴力方法
|
||||
|
||||
|
||||
@ -28,6 +28,10 @@
|
||||
* 输出: 4
|
||||
* 解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。第三个孩子只得到 1 颗糖果,这已满足上述两个条件。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,两者兼顾很容易顾此失彼!LeetCode:135.分发糖果](https://www.bilibili.com/video/BV1ev4y1r7wN),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
@ -117,6 +121,11 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
这在leetcode上是一道困难的题目,其难点就在于贪心的策略,如果在考虑局部的时候想两边兼顾,就会顾此失彼。
|
||||
|
||||
@ -351,7 +351,17 @@ class Solution:
|
||||
dp[j] = dp[j] or (dp[j - len(word)] and word == s[j - len(word):j])
|
||||
return dp[len(s)]
|
||||
```
|
||||
|
||||
```python
|
||||
class Solution: # 和视频中写法一致(和最上面C++写法一致)
|
||||
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
|
||||
dp = [False]*(len(s)+1)
|
||||
dp[0]=True
|
||||
for j in range(1,len(s)+1):
|
||||
for i in range(j):
|
||||
word = s[i:j]
|
||||
if word in wordDict and dp[i]: dp[j]=True
|
||||
return dp[-1]
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
@ -113,6 +113,9 @@ public:
|
||||
};
|
||||
|
||||
```
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
|
||||
## 题外话
|
||||
|
||||
|
||||
@ -970,6 +970,49 @@ pub fn remove_extra_spaces(s: &mut Vec<char>) {
|
||||
}
|
||||
}
|
||||
```
|
||||
C:
|
||||
|
||||
```C
|
||||
// 翻转字符串中指定范围的字符
|
||||
void reverse(char* s, int start, int end) {
|
||||
for (int i = start, j = end; i < j; i++, j--) {
|
||||
int tmp = s[i];
|
||||
s[i] = s[j];
|
||||
s[j] = tmp;
|
||||
}
|
||||
}
|
||||
|
||||
// 删除字符串两端和中间多余的空格
|
||||
void removeExtraSpace(char* s) {
|
||||
int start = 0; // 指向字符串开头的指针
|
||||
int end = strlen(s) - 1; // 指向字符串结尾的指针
|
||||
while (s[start] == ' ') start++; // 移动指针 start,直到找到第一个非空格字符
|
||||
while (s[end] == ' ') end--; // 移动指针 end,直到找到第一个非空格字符
|
||||
int slow = 0; // 指向新字符串的下一个写入位置的指针
|
||||
for (int i = start; i <= end; i++) { // 遍历整个字符串
|
||||
if (s[i] == ' ' && s[i+1] == ' ') { // 如果当前字符是空格,并且下一个字符也是空格,则跳过
|
||||
continue;
|
||||
}
|
||||
s[slow] = s[i]; // 否则,将当前字符复制到新字符串的 slow 位置
|
||||
slow++; // 将 slow 指针向后移动
|
||||
}
|
||||
s[slow] = '\0'; // 在新字符串的末尾添加一个空字符
|
||||
}
|
||||
|
||||
// 翻转字符串中的单词
|
||||
char * reverseWords(char * s){
|
||||
removeExtraSpace(s); // 先删除字符串两端和中间的多余空格
|
||||
reverse(s, 0, strlen(s) - 1); // 翻转整个字符串
|
||||
int slow = 0; // 指向每个单词的开头位置的指针
|
||||
for (int i = 0; i <= strlen(s); i++) { // 遍历整个字符串
|
||||
if (s[i] ==' ' || s[i] == '\0') { // 如果当前字符是空格或空字符,说明一个单词结束了
|
||||
reverse(s, slow, i-1); // 翻转单词
|
||||
slow = i + 1; // 将 slow 指针指向下一个单词的开头位置
|
||||
}
|
||||
}
|
||||
return s; // 返回处理后的字符串
|
||||
}
|
||||
```
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
|
||||
@ -156,6 +156,11 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n * k),其中 n 为 prices 的长度
|
||||
* 空间复杂度: O(n * k)
|
||||
|
||||
|
||||
|
||||
当然有的解法是定义一个三维数组dp[i][j][k],第i天,第j次买卖,k表示买还是卖的状态,从定义上来讲是比较直观。
|
||||
|
||||
但感觉三维数组操作起来有些麻烦,我是直接用二维数组来模拟三维数组的情况,代码看起来也清爽一些。
|
||||
@ -323,6 +328,42 @@ func max(a, b int) int {
|
||||
}
|
||||
```
|
||||
|
||||
版本二: 三维 dp数组
|
||||
```go
|
||||
func maxProfit(k int, prices []int) int {
|
||||
length := len(prices)
|
||||
if length == 0 {
|
||||
return 0
|
||||
}
|
||||
// [天数][交易次数][是否持有股票]
|
||||
// 1表示不持有/卖出, 0表示持有/买入
|
||||
dp := make([][][]int, length)
|
||||
for i := 0; i < length; i++ {
|
||||
dp[i] = make([][]int, k+1)
|
||||
for j := 0; j <= k; j++ {
|
||||
dp[i][j] = make([]int, 2)
|
||||
}
|
||||
}
|
||||
for j := 0; j <= k; j++ {
|
||||
dp[0][j][0] = -prices[0]
|
||||
}
|
||||
for i := 1; i < length; i++ {
|
||||
for j := 1; j <= k; j++ {
|
||||
dp[i][j][0] = max188(dp[i-1][j][0], dp[i-1][j-1][1]-prices[i])
|
||||
dp[i][j][1] = max188(dp[i-1][j][1], dp[i-1][j][0]+prices[i])
|
||||
}
|
||||
}
|
||||
return dp[length-1][k][1]
|
||||
}
|
||||
|
||||
func max188(a, b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
```
|
||||
|
||||
Javascript:
|
||||
|
||||
```javascript
|
||||
|
||||
@ -108,6 +108,9 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
## 总结
|
||||
|
||||
打家劫舍是DP解决的经典题目,这道题也是打家劫舍入门级题目,后面我们还会变种方式来打劫的。
|
||||
@ -150,7 +153,17 @@ class Solution:
|
||||
dp[i] = max(dp[i-2]+nums[i], dp[i-1])
|
||||
return dp[-1]
|
||||
```
|
||||
|
||||
```python
|
||||
class Solution: # 二维dp数组写法
|
||||
def rob(self, nums: List[int]) -> int:
|
||||
dp = [[0,0] for _ in range(len(nums))]
|
||||
dp[0][1] = nums[0]
|
||||
for i in range(1,len(nums)):
|
||||
dp[i][0] = max(dp[i-1][1],dp[i-1][0])
|
||||
dp[i][1] = dp[i-1][0]+nums[i]
|
||||
print(dp)
|
||||
return max(dp[-1])
|
||||
```
|
||||
Go:
|
||||
```Go
|
||||
func rob(nums []int) int {
|
||||
|
||||
@ -316,8 +316,8 @@ class Solution:
|
||||
def removeElements(self, head: ListNode, val: int) -> ListNode:
|
||||
dummy_head = ListNode(next=head) #添加一个虚拟节点
|
||||
cur = dummy_head
|
||||
while(cur.next!=None):
|
||||
if(cur.next.val == val):
|
||||
while cur.next:
|
||||
if cur.next.val == val:
|
||||
cur.next = cur.next.next #删除cur.next节点
|
||||
else:
|
||||
cur = cur.next
|
||||
|
||||
@ -82,6 +82,11 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
成环之后还是难了一些的, 不少题解没有把“考虑房间”和“偷房间”说清楚。
|
||||
@ -142,7 +147,20 @@ class Solution:
|
||||
dp[i]=max(dp[i-1],dp[i-2]+nums[i])
|
||||
return dp[-1]
|
||||
```
|
||||
|
||||
```python
|
||||
class Solution: # 二维dp数组写法
|
||||
def rob(self, nums: List[int]) -> int:
|
||||
if len(nums)<3: return max(nums)
|
||||
return max(self.default(nums[:-1]),self.default(nums[1:]))
|
||||
def default(self,nums):
|
||||
dp = [[0,0] for _ in range(len(nums))]
|
||||
dp[0][1] = nums[0]
|
||||
for i in range(1,len(nums)):
|
||||
dp[i][0] = max(dp[i-1])
|
||||
dp[i][1] = dp[i-1][0] + nums[i]
|
||||
return max(dp[-1])
|
||||
|
||||
```
|
||||
Go:
|
||||
|
||||
```go
|
||||
|
||||
@ -111,6 +111,8 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: push为O(n),其他为O(1)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
# 优化
|
||||
|
||||
@ -156,6 +158,9 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: push为O(n),其他为O(1)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
|
||||
# 其他语言版本
|
||||
|
||||
|
||||
@ -112,6 +112,10 @@ public:
|
||||
|
||||
```
|
||||
|
||||
* 时间复杂度: push和empty为O(1), pop和peek为O(n)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
|
||||
## 拓展
|
||||
|
||||
可以看出peek()的实现,直接复用了pop(), 要不然,对stOut判空的逻辑又要重写一遍。
|
||||
|
||||
@ -184,6 +184,9 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(k)
|
||||
|
||||
|
||||
再来看一下时间复杂度,使用单调队列的时间复杂度是 O(n)。
|
||||
|
||||
|
||||
@ -205,6 +205,19 @@ var isAnagram = function(s, t) {
|
||||
}
|
||||
return true;
|
||||
};
|
||||
|
||||
var isAnagram = function(s, t) {
|
||||
if(s.length !== t.length) return false;
|
||||
let char_count = new Map();
|
||||
for(let item of s) {
|
||||
char_count.set(item, (char_count.get(item) || 0) + 1) ;
|
||||
}
|
||||
for(let item of t) {
|
||||
if(!char_count.get(item)) return false;
|
||||
char_count.set(item, char_count.get(item)-1);
|
||||
}
|
||||
return true;
|
||||
};
|
||||
```
|
||||
|
||||
TypeScript:
|
||||
|
||||
@ -127,6 +127,10 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n * √n)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
|
||||
同样我在给出先遍历物品,在遍历背包的代码,一样的可以AC的。
|
||||
|
||||
```CPP
|
||||
@ -145,6 +149,8 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 同上
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
|
||||
@ -106,6 +106,10 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n^2)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
|
||||
@ -133,6 +133,11 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n * amount),其中 n 为 coins 的长度
|
||||
* 空间复杂度: O(amount)
|
||||
|
||||
|
||||
|
||||
对于遍历方式遍历背包放在外循环,遍历物品放在内循环也是可以的,我就直接给出代码了
|
||||
|
||||
```CPP
|
||||
@ -154,6 +159,8 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 同上
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
|
||||
@ -380,7 +380,33 @@ class Solution:
|
||||
backtracking("JFK")
|
||||
return path
|
||||
```
|
||||
|
||||
python - 使用used数组 - 神似之前几题写法
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
|
||||
global used,path,results
|
||||
used = [0]*len(tickets)
|
||||
path = ['JFK']
|
||||
results = []
|
||||
tickets.sort() # 先排序,这样一旦找到第一个可行路径,一定是字母排序最小的
|
||||
self.backtracking(tickets,'JFK')
|
||||
return results[0]
|
||||
def backtracking(self,tickets,cur):
|
||||
if sum(used) == len(tickets):
|
||||
results.append(path[:])
|
||||
return True # 只要找到就返回
|
||||
for i in range(len(tickets)):
|
||||
if tickets[i][0]==cur and used[i]==0:
|
||||
used[i]=1
|
||||
path.append(tickets[i][1])
|
||||
state = self.backtracking(tickets,tickets[i][1])
|
||||
path.pop()
|
||||
used[i]=0
|
||||
if state: return True # 只要找到就返回,不继续搜索了
|
||||
```
|
||||
|
||||
### GO
|
||||
```go
|
||||
type pair struct {
|
||||
|
||||
@ -79,8 +79,6 @@
|
||||
|
||||
|
||||
```CPP
|
||||
// 时间复杂度:O(nlogk)
|
||||
// 空间复杂度:O(n)
|
||||
class Solution {
|
||||
public:
|
||||
// 小顶堆
|
||||
@ -120,6 +118,10 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(nlogk)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
# 拓展
|
||||
大家对这个比较运算在建堆时是如何应用的,为什么左大于右就会建立小顶堆,反而建立大顶堆比较困惑。
|
||||
|
||||
|
||||
@ -4,7 +4,6 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
> 本周讲解了[贪心理论基础](https://programmercarl.com/贪心算法理论基础.html),以及第一道贪心的题目:[贪心算法:分发饼干](https://programmercarl.com/0455.分发饼干.html),可能会给大家一种贪心算法比较简单的错觉,好了,接下来几天的题目难度要上来了,哈哈。
|
||||
|
||||
# 376. 摆动序列
|
||||
@ -13,25 +12,32 @@
|
||||
|
||||
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
|
||||
|
||||
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
|
||||
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
|
||||
|
||||
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
|
||||
|
||||
示例 1:
|
||||
* 输入: [1,7,4,9,2,5]
|
||||
* 输出: 6
|
||||
* 解释: 整个序列均为摆动序列。
|
||||
|
||||
- 输入: [1,7,4,9,2,5]
|
||||
- 输出: 6
|
||||
- 解释: 整个序列均为摆动序列。
|
||||
|
||||
示例 2:
|
||||
* 输入: [1,17,5,10,13,15,10,5,16,8]
|
||||
* 输出: 7
|
||||
* 解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
|
||||
|
||||
- 输入: [1,17,5,10,13,15,10,5,16,8]
|
||||
- 输出: 7
|
||||
- 解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
|
||||
|
||||
示例 3:
|
||||
* 输入: [1,2,3,4,5,6,7,8,9]
|
||||
* 输出: 2
|
||||
|
||||
## 思路1(贪心解法)
|
||||
- 输入: [1,2,3,4,5,6,7,8,9]
|
||||
- 输出: 2
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,寻找摆动有细节!| LeetCode:376.摆动序列](https://www.bilibili.com/video/BV17M411b7NS),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路 1(贪心解法)
|
||||
|
||||
本题要求通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
|
||||
|
||||
@ -53,63 +59,61 @@
|
||||
|
||||
**实际操作上,其实连删除的操作都不用做,因为题目要求的是最长摆动子序列的长度,所以只需要统计数组的峰值数量就可以了(相当于是删除单一坡度上的节点,然后统计长度)**
|
||||
|
||||
**这就是贪心所贪的地方,让峰值尽可能的保持峰值,然后删除单一坡度上的节点**
|
||||
**这就是贪心所贪的地方,让峰值尽可能的保持峰值,然后删除单一坡度上的节点**
|
||||
|
||||
在计算是否有峰值的时候,大家知道遍历的下标i ,计算prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i]),如果`prediff < 0 && curdiff > 0` 或者 `prediff > 0 && curdiff < 0` 此时就有波动就需要统计。
|
||||
在计算是否有峰值的时候,大家知道遍历的下标 i ,计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i]),如果`prediff < 0 && curdiff > 0` 或者 `prediff > 0 && curdiff < 0` 此时就有波动就需要统计。
|
||||
|
||||
这是我们思考本题的一个大题思路,但本题要考虑三种情况:
|
||||
|
||||
1. 情况一:上下坡中有平坡
|
||||
2. 情况二:数组首尾两端
|
||||
1. 情况一:上下坡中有平坡
|
||||
2. 情况二:数组首尾两端
|
||||
3. 情况三:单调坡中有平坡
|
||||
|
||||
### 情况一:上下坡中有平坡
|
||||
|
||||
例如 [1,2,2,2,1]这样的数组,如图:
|
||||
例如 [1,2,2,2,1]这样的数组,如图:
|
||||
|
||||
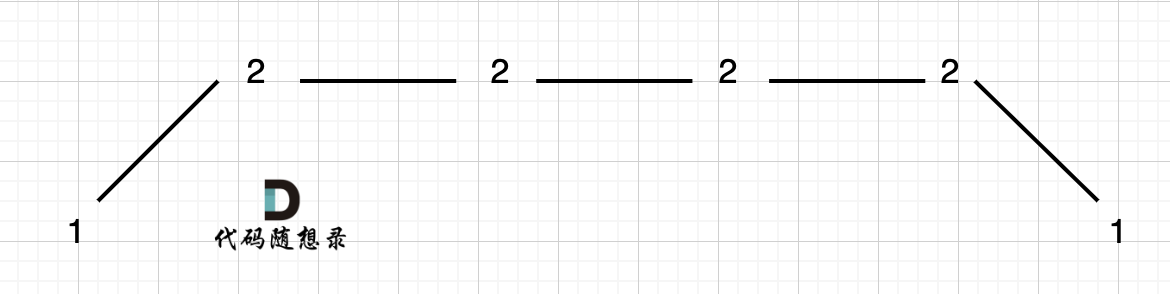
|
||||
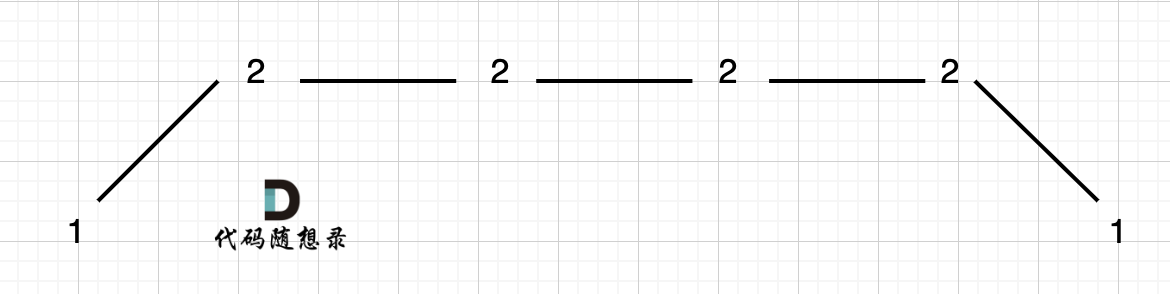
|
||||
|
||||
它的摇摆序列长度是多少呢? **其实是长度是3**,也就是我们在删除的时候 要不删除左面的三个2,要不就删除右边的三个2。
|
||||
它的摇摆序列长度是多少呢? **其实是长度是 3**,也就是我们在删除的时候 要不删除左面的三个 2,要不就删除右边的三个 2。
|
||||
|
||||
如图,可以统一规则,删除左边的三个2:
|
||||
如图,可以统一规则,删除左边的三个 2:
|
||||
|
||||
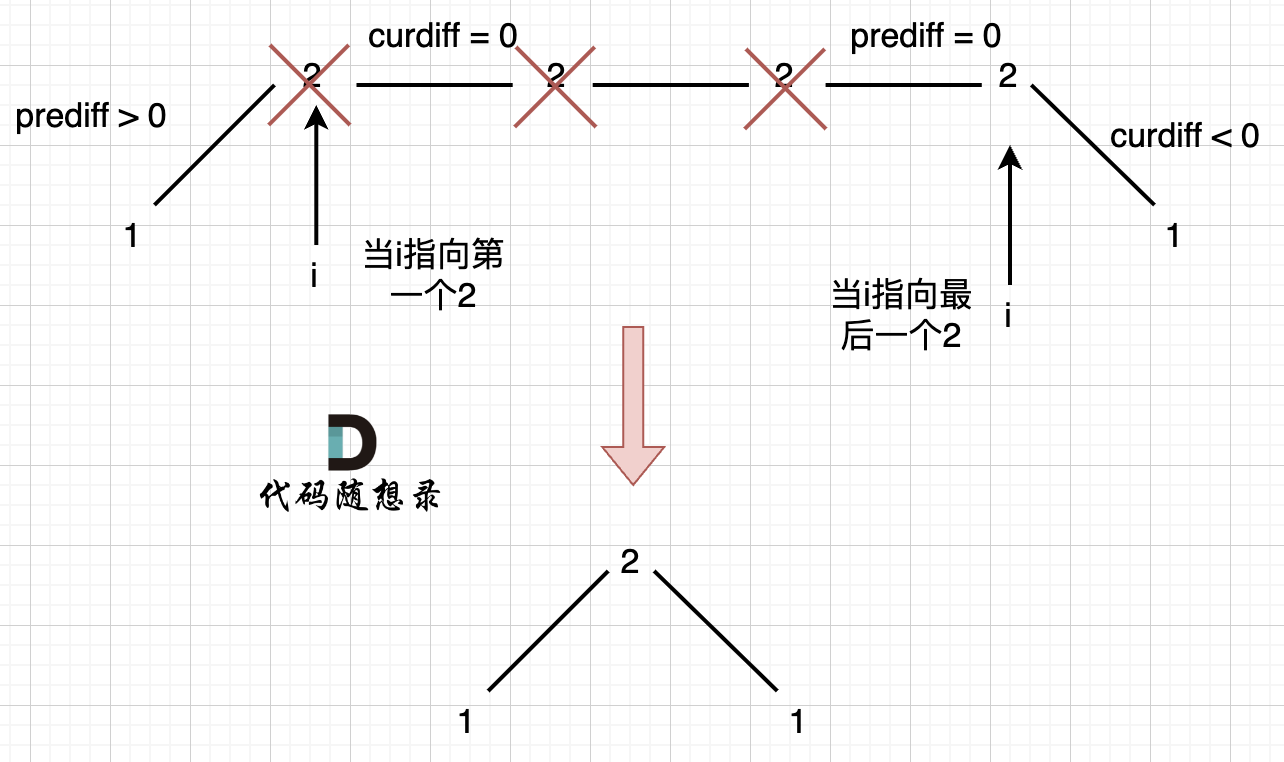
|
||||
|
||||
在图中,当i指向第一个2的时候,`prediff > 0 && curdiff = 0` ,当 i 指向最后一个2的时候 `prediff = 0 && curdiff < 0`。
|
||||
在图中,当 i 指向第一个 2 的时候,`prediff > 0 && curdiff = 0` ,当 i 指向最后一个 2 的时候 `prediff = 0 && curdiff < 0`。
|
||||
|
||||
如果我们采用,删左面三个2的规则,那么 当 `prediff = 0 && curdiff < 0` 也要记录一个峰值,因为他是把之前相同的元素都删掉留下的峰值。
|
||||
如果我们采用,删左面三个 2 的规则,那么 当 `prediff = 0 && curdiff < 0` 也要记录一个峰值,因为他是把之前相同的元素都删掉留下的峰值。
|
||||
|
||||
所以我们记录峰值的条件应该是: `(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)`,为什么这里允许 prediff == 0 ,就是为了 上面我说的这种情况。
|
||||
所以我们记录峰值的条件应该是: `(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)`,为什么这里允许 prediff == 0 ,就是为了 上面我说的这种情况。
|
||||
|
||||
### 情况二:数组首尾两端
|
||||
|
||||
### 情况二:数组首尾两端
|
||||
所以本题统计峰值的时候,数组最左面和最右面如何统计呢?
|
||||
|
||||
题目中说了,如果只有两个不同的元素,那摆动序列也是 2。
|
||||
|
||||
所以本题统计峰值的时候,数组最左面和最右面如果统计呢?
|
||||
|
||||
题目中说了,如果只有两个不同的元素,那摆动序列也是2。
|
||||
|
||||
例如序列[2,5],如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。
|
||||
例如序列[2,5],如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。
|
||||
|
||||
因为我们在计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i])的时候,至少需要三个数字才能计算,而数组只有两个数字。
|
||||
|
||||
这里我们可以写死,就是 如果只有两个元素,且元素不同,那么结果为2。
|
||||
这里我们可以写死,就是 如果只有两个元素,且元素不同,那么结果为 2。
|
||||
|
||||
不写死的话,如果和我们的判断规则结合在一起呢?
|
||||
不写死的话,如果和我们的判断规则结合在一起呢?
|
||||
|
||||
可以假设,数组最前面还有一个数字,那这个数字应该是什么呢?
|
||||
可以假设,数组最前面还有一个数字,那这个数字应该是什么呢?
|
||||
|
||||
之前我们在 讨论 情况一:相同数字连续 的时候, prediff = 0 ,curdiff < 0 或者 >0 也记为波谷。
|
||||
之前我们在 讨论 情况一:相同数字连续 的时候, prediff = 0 ,curdiff < 0 或者 >0 也记为波谷。
|
||||
|
||||
那么为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即preDiff = 0,如图:
|
||||
那么为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即 preDiff = 0,如图:
|
||||
|
||||
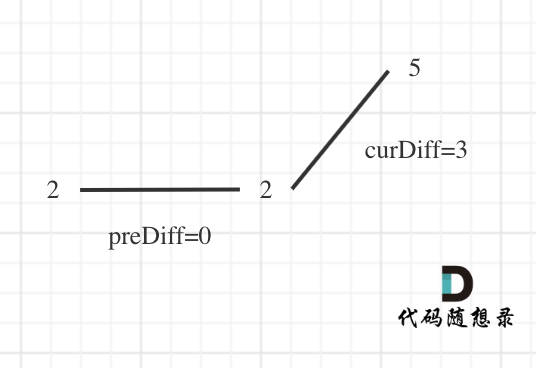
|
||||
|
||||
针对以上情形,result初始为1(默认最右面有一个峰值),此时curDiff > 0 && preDiff <= 0,那么result++(计算了左面的峰值),最后得到的result就是2(峰值个数为2即摆动序列长度为2)
|
||||
针对以上情形,result 初始为 1(默认最右面有一个峰值),此时 curDiff > 0 && preDiff <= 0,那么 result++(计算了左面的峰值),最后得到的 result 就是 2(峰值个数为 2 即摆动序列长度为 2)
|
||||
|
||||
经过以上分析后,我们可以写出如下代码:
|
||||
|
||||
```CPP
|
||||
```CPP
|
||||
// 版本一
|
||||
class Solution {
|
||||
public:
|
||||
@ -129,33 +133,34 @@ public:
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1)
|
||||
```
|
||||
|
||||
此时大家是不是发现 以上代码提交也不能通过本题?
|
||||
- 时间复杂度:O(n)
|
||||
- 空间复杂度:O(1)
|
||||
|
||||
此时大家是不是发现 以上代码提交也不能通过本题?
|
||||
|
||||
所以此时我们要讨论情况三!
|
||||
|
||||
### 情况三:单调坡度有平坡
|
||||
### 情况三:单调坡度有平坡
|
||||
|
||||
在版本一中,我们忽略了一种情况,即 如果在一个单调坡度上有平坡,例如[1,2,2,2,3,4],如图:
|
||||
在版本一中,我们忽略了一种情况,即 如果在一个单调坡度上有平坡,例如[1,2,2,2,3,4],如图:
|
||||
|
||||
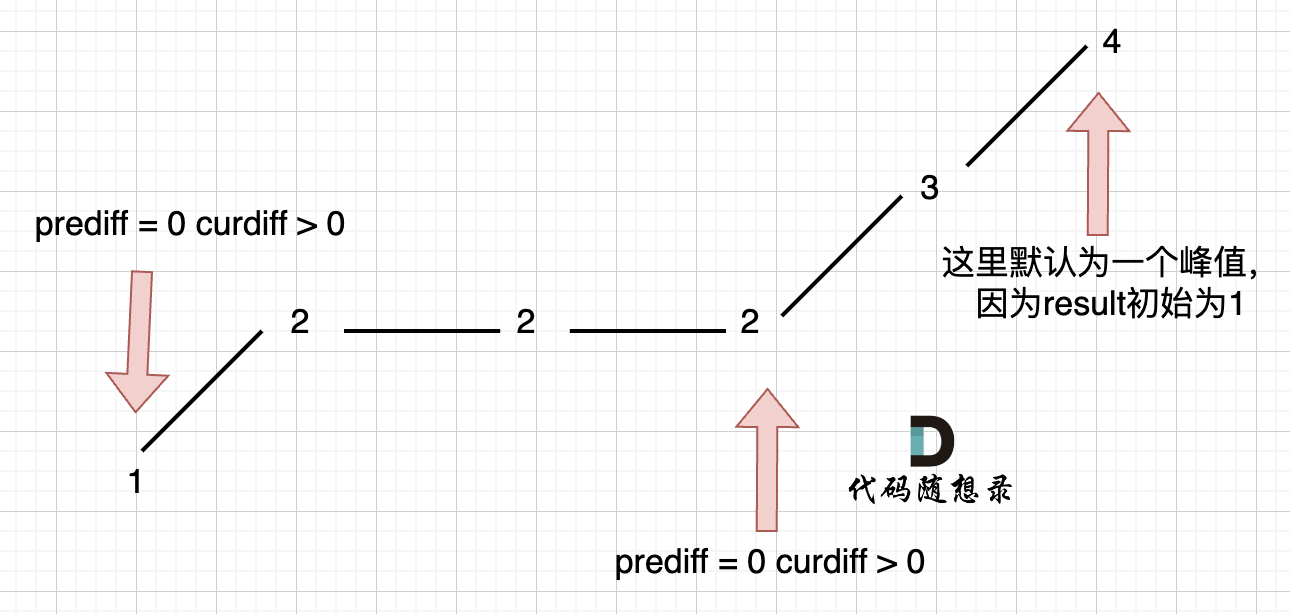
|
||||
|
||||
图中,我们可以看出,版本一的代码在三个地方记录峰值,但其实结果因为是2,因为 单调中的平坡 不能算峰值(即摆动)。
|
||||
图中,我们可以看出,版本一的代码在三个地方记录峰值,但其实结果因为是 2,因为 单调中的平坡 不能算峰值(即摆动)。
|
||||
|
||||
之所以版本一会出问题,是因为我们实时更新了 prediff。
|
||||
之所以版本一会出问题,是因为我们实时更新了 prediff。
|
||||
|
||||
那么我们应该什么时候更新prediff呢?
|
||||
那么我们应该什么时候更新 prediff 呢?
|
||||
|
||||
我们只需要在 这个坡度 摆动变化的时候,更新prediff就行,这样prediff在 单调区间有平坡的时候 就不会发生变化,造成我们的误判。
|
||||
我们只需要在 这个坡度 摆动变化的时候,更新 prediff 就行,这样 prediff 在 单调区间有平坡的时候 就不会发生变化,造成我们的误判。
|
||||
|
||||
所以本题的最终代码为:
|
||||
|
||||
```CPP
|
||||
|
||||
// 版本二
|
||||
// 版本二
|
||||
class Solution {
|
||||
public:
|
||||
int wiggleMaxLength(vector<int>& nums) {
|
||||
@ -168,7 +173,7 @@ public:
|
||||
// 出现峰值
|
||||
if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
|
||||
result++;
|
||||
preDiff = curDiff; // 注意这里,只在摆动变化的时候更新prediff
|
||||
preDiff = curDiff; // 注意这里,只在摆动变化的时候更新prediff
|
||||
}
|
||||
}
|
||||
return result;
|
||||
@ -176,25 +181,25 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
其实本题看起来好像简单,但需要考虑的情况还是很复杂的,而且很难一次性想到位。
|
||||
其实本题看起来好像简单,但需要考虑的情况还是很复杂的,而且很难一次性想到位。
|
||||
|
||||
**本题异常情况的本质,就是要考虑平坡**, 平坡分两种,一个是 上下中间有平坡,一个是单调有平坡,如图:
|
||||
**本题异常情况的本质,就是要考虑平坡**, 平坡分两种,一个是 上下中间有平坡,一个是单调有平坡,如图:
|
||||
|
||||
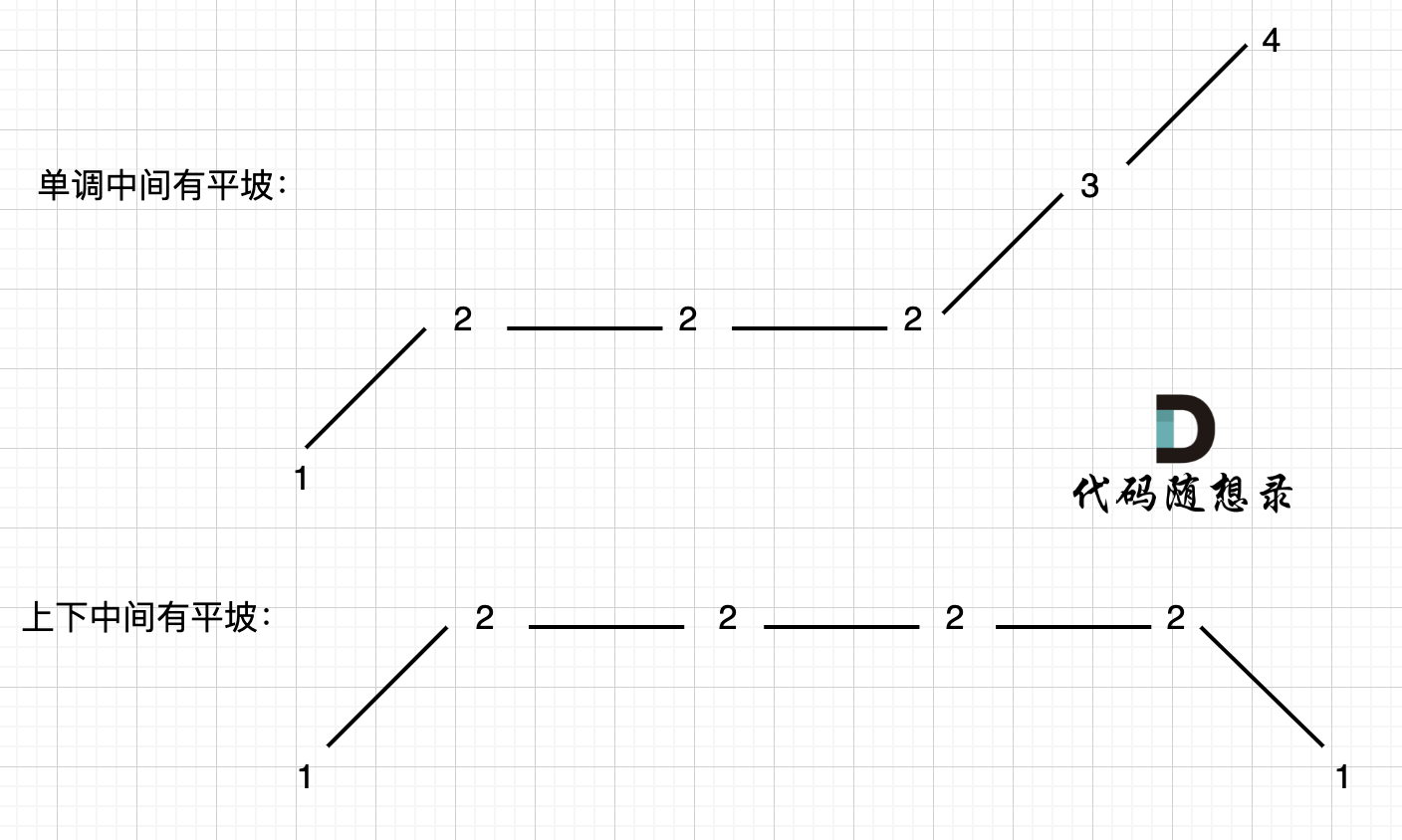
|
||||
|
||||
## 思路2(动态规划)
|
||||
## 思路 2(动态规划)
|
||||
|
||||
考虑用动态规划的思想来解决这个问题。
|
||||
|
||||
很容易可以发现,对于我们当前考虑的这个数,要么是作为山峰(即nums[i] > nums[i-1]),要么是作为山谷(即nums[i] < nums[i - 1])。
|
||||
很容易可以发现,对于我们当前考虑的这个数,要么是作为山峰(即 nums[i] > nums[i-1]),要么是作为山谷(即 nums[i] < nums[i - 1])。
|
||||
|
||||
* 设dp状态`dp[i][0]`,表示考虑前i个数,第i个数作为山峰的摆动子序列的最长长度
|
||||
* 设dp状态`dp[i][1]`,表示考虑前i个数,第i个数作为山谷的摆动子序列的最长长度
|
||||
- 设 dp 状态`dp[i][0]`,表示考虑前 i 个数,第 i 个数作为山峰的摆动子序列的最长长度
|
||||
- 设 dp 状态`dp[i][1]`,表示考虑前 i 个数,第 i 个数作为山谷的摆动子序列的最长长度
|
||||
|
||||
则转移方程为:
|
||||
|
||||
* `dp[i][0] = max(dp[i][0], dp[j][1] + 1)`,其中`0 < j < i`且`nums[j] < nums[i]`,表示将nums[i]接到前面某个山谷后面,作为山峰。
|
||||
* `dp[i][1] = max(dp[i][1], dp[j][0] + 1)`,其中`0 < j < i`且`nums[j] > nums[i]`,表示将nums[i]接到前面某个山峰后面,作为山谷。
|
||||
- `dp[i][0] = max(dp[i][0], dp[j][1] + 1)`,其中`0 < j < i`且`nums[j] < nums[i]`,表示将 nums[i]接到前面某个山谷后面,作为山峰。
|
||||
- `dp[i][1] = max(dp[i][1], dp[j][0] + 1)`,其中`0 < j < i`且`nums[j] > nums[i]`,表示将 nums[i]接到前面某个山峰后面,作为山谷。
|
||||
|
||||
初始状态:
|
||||
|
||||
@ -223,28 +228,25 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度:O(n^2)
|
||||
* 空间复杂度:O(n)
|
||||
- 时间复杂度:O(n^2)
|
||||
- 空间复杂度:O(n)
|
||||
|
||||
**进阶**
|
||||
|
||||
可以用两棵线段树来维护区间的最大值
|
||||
|
||||
* 每次更新`dp[i][0]`,则在`tree1`的`nums[i]`位置值更新为`dp[i][0]`
|
||||
* 每次更新`dp[i][1]`,则在`tree2`的`nums[i]`位置值更新为`dp[i][1]`
|
||||
* 则dp转移方程中就没有必要j从0遍历到i-1,可以直接在线段树中查询指定区间的值即可。
|
||||
- 每次更新`dp[i][0]`,则在`tree1`的`nums[i]`位置值更新为`dp[i][0]`
|
||||
- 每次更新`dp[i][1]`,则在`tree2`的`nums[i]`位置值更新为`dp[i][1]`
|
||||
- 则 dp 转移方程中就没有必要 j 从 0 遍历到 i-1,可以直接在线段树中查询指定区间的值即可。
|
||||
|
||||
时间复杂度:O(nlog n)
|
||||
|
||||
空间复杂度:O(n)
|
||||
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
### Java
|
||||
```Java
|
||||
class Solution {
|
||||
public int wiggleMaxLength(int[] nums) {
|
||||
@ -270,6 +272,7 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```java
|
||||
// DP
|
||||
class Solution {
|
||||
@ -300,7 +303,7 @@ class Solution {
|
||||
}
|
||||
```
|
||||
|
||||
### Python
|
||||
### Python
|
||||
|
||||
**贪心**
|
||||
|
||||
@ -332,7 +335,7 @@ class Solution:
|
||||
# nums[i] 为波谷
|
||||
if nums[j] > nums[i]:
|
||||
dp[i][1] = max(dp[i][1], dp[j][0] + 1)
|
||||
# nums[i] 为波峰
|
||||
# nums[i] 为波峰
|
||||
if nums[j] < nums[i]:
|
||||
dp[i][0] = max(dp[i][0], dp[j][1] + 1)
|
||||
return max(dp[-1][0], dp[-1][1])
|
||||
@ -357,9 +360,10 @@ class Solution:
|
||||
return max(up, down)
|
||||
```
|
||||
|
||||
### Go
|
||||
### Go
|
||||
|
||||
**贪心**
|
||||
|
||||
```go
|
||||
func wiggleMaxLength(nums []int) int {
|
||||
n := len(nums)
|
||||
@ -383,6 +387,7 @@ func wiggleMaxLength(nums []int) int {
|
||||
```
|
||||
|
||||
**动态规划**
|
||||
|
||||
```go
|
||||
func wiggleMaxLength(nums []int) int {
|
||||
n := len(nums)
|
||||
@ -419,8 +424,10 @@ func max(a, b int) int {
|
||||
}
|
||||
```
|
||||
|
||||
### Javascript
|
||||
### Javascript
|
||||
|
||||
**贪心**
|
||||
|
||||
```Javascript
|
||||
var wiggleMaxLength = function(nums) {
|
||||
if(nums.length <= 1) return nums.length
|
||||
@ -437,10 +444,12 @@ var wiggleMaxLength = function(nums) {
|
||||
return result
|
||||
};
|
||||
```
|
||||
|
||||
**动态规划**
|
||||
|
||||
```Javascript
|
||||
var wiggleMaxLength = function(nums) {
|
||||
if (nums.length === 1) return 1;
|
||||
if (nums.length === 1) return 1;
|
||||
// 考虑前i个数,当第i个值作为峰谷时的情况(则第i-1是峰顶)
|
||||
let down = 1;
|
||||
// 考虑前i个数,当第i个值作为峰顶时的情况(则第i-1是峰谷)
|
||||
@ -458,7 +467,9 @@ var wiggleMaxLength = function(nums) {
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
**贪心**
|
||||
|
||||
```Rust
|
||||
impl Solution {
|
||||
pub fn wiggle_max_length(nums: Vec<i32>) -> i32 {
|
||||
@ -504,11 +515,12 @@ impl Solution {
|
||||
```
|
||||
|
||||
### C
|
||||
|
||||
**贪心**
|
||||
|
||||
```c
|
||||
int wiggleMaxLength(int* nums, int numsSize){
|
||||
if(numsSize <= 1)
|
||||
if(numsSize <= 1)
|
||||
return numsSize;
|
||||
|
||||
int length = 1;
|
||||
@ -568,54 +580,49 @@ int wiggleMaxLength(int* nums, int numsSize){
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### TypeScript
|
||||
|
||||
**贪心**
|
||||
|
||||
```typescript
|
||||
function wiggleMaxLength(nums: number[]): number {
|
||||
let length: number = nums.length;
|
||||
if (length <= 1) return length;
|
||||
let preDiff: number = 0;
|
||||
let curDiff: number = 0;
|
||||
let count: number = 1;
|
||||
for (let i = 1; i < length; i++) {
|
||||
curDiff = nums[i] - nums[i - 1];
|
||||
if (
|
||||
(preDiff <= 0 && curDiff > 0) ||
|
||||
(preDiff >= 0 && curDiff < 0)
|
||||
) {
|
||||
preDiff = curDiff;
|
||||
count++;
|
||||
}
|
||||
let length: number = nums.length;
|
||||
if (length <= 1) return length;
|
||||
let preDiff: number = 0;
|
||||
let curDiff: number = 0;
|
||||
let count: number = 1;
|
||||
for (let i = 1; i < length; i++) {
|
||||
curDiff = nums[i] - nums[i - 1];
|
||||
if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
|
||||
preDiff = curDiff;
|
||||
count++;
|
||||
}
|
||||
return count;
|
||||
};
|
||||
}
|
||||
return count;
|
||||
}
|
||||
```
|
||||
|
||||
**动态规划**
|
||||
|
||||
```typescript
|
||||
function wiggleMaxLength(nums: number[]): number {
|
||||
const length: number = nums.length;
|
||||
if (length <= 1) return length;
|
||||
const dp: number[][] = new Array(length).fill(0).map(_ => []);
|
||||
dp[0][0] = 1; // 第一个数作为波峰
|
||||
dp[0][1] = 1; // 第一个数作为波谷
|
||||
for (let i = 1; i < length; i++) {
|
||||
dp[i][0] = 1;
|
||||
dp[i][1] = 1;
|
||||
for (let j = 0; j < i; j++) {
|
||||
if (nums[j] < nums[i]) dp[i][0] = Math.max(dp[i][0], dp[j][1] + 1);
|
||||
}
|
||||
for (let j = 0; j < i; j++) {
|
||||
if (nums[j] > nums[i]) dp[i][1] = Math.max(dp[i][1], dp[j][0] + 1);
|
||||
}
|
||||
const length: number = nums.length;
|
||||
if (length <= 1) return length;
|
||||
const dp: number[][] = new Array(length).fill(0).map((_) => []);
|
||||
dp[0][0] = 1; // 第一个数作为波峰
|
||||
dp[0][1] = 1; // 第一个数作为波谷
|
||||
for (let i = 1; i < length; i++) {
|
||||
dp[i][0] = 1;
|
||||
dp[i][1] = 1;
|
||||
for (let j = 0; j < i; j++) {
|
||||
if (nums[j] < nums[i]) dp[i][0] = Math.max(dp[i][0], dp[j][1] + 1);
|
||||
}
|
||||
return Math.max(dp[length - 1][0], dp[length - 1][1]);
|
||||
};
|
||||
for (let j = 0; j < i; j++) {
|
||||
if (nums[j] > nums[i]) dp[i][1] = Math.max(dp[i][1], dp[j][0] + 1);
|
||||
}
|
||||
}
|
||||
return Math.max(dp[length - 1][0], dp[length - 1][1]);
|
||||
}
|
||||
```
|
||||
|
||||
### Scala
|
||||
@ -648,3 +655,4 @@ object Solution {
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
@ -1,145 +0,0 @@
|
||||
# 完全背包的排列问题模拟
|
||||
|
||||
#### Problem
|
||||
|
||||
1. 排列问题是完全背包中十分棘手的问题。
|
||||
2. 其在迭代过程中需要先迭代背包容量,再迭代物品个数,使得其在代码理解上较难入手。
|
||||
|
||||
#### Contribution
|
||||
|
||||
本文档以力扣上[组合总和IV](https://leetcode.cn/problems/combination-sum-iv/)为例,提供一个二维dp的代码例子,并提供模拟过程以便于理解
|
||||
|
||||
#### Code
|
||||
|
||||
```cpp
|
||||
int combinationSum4(vector<int>& nums, int target) {
|
||||
// 定义背包容量为target,物品个数为nums.size()的dp数组
|
||||
// dp[i][j]表示将第0-i个物品添加入排列中,和为j的排列方式
|
||||
vector<vector<int>> dp (nums.size(), vector(target+1,0));
|
||||
|
||||
// 表示有0,1,...,n个物品可选择的情况下,和为0的选择方法为1:什么都不取
|
||||
for(int i = 0; i < nums.size(); i++) dp[i][0] = 1;
|
||||
|
||||
// 必须按列遍历,因为右边数组需要知道左边数组最低部的信息(排列问题)
|
||||
// 后面的模拟可以更清楚的表现这么操作的原因
|
||||
for(int i = 1; i <= target; i++){
|
||||
for(int j = 0; j < nums.size(); j++){
|
||||
// 只有nums[j]可以取的情况
|
||||
if(j == 0){
|
||||
if(nums[j] > i) dp[j][i] = 0;
|
||||
// 如果背包容量放不下 那么此时没有排列方式
|
||||
else dp[j][i] = dp[nums.size()-1][i-nums[j]];
|
||||
// 如果背包容量放的下 全排列方式为dp[最底层][容量-该物品容量]排列方式后面放一个nums[j]
|
||||
}
|
||||
// 有多个nums数可以取
|
||||
else{
|
||||
// 如果背包容量放不下 那么沿用0-j-1个物品的排列方式
|
||||
if(nums[j] > i) dp[j][i] = dp[j-1][i];
|
||||
// 如果背包容量放得下 在dp[最底层][容量-该物品容量]排列方式后面放一个nums[j]后面放个nums[j]
|
||||
// INT_MAX避免溢出
|
||||
else if(i >= nums[j] && dp[j-1][i] < INT_MAX - dp[nums.size()-1][i-nums[j]])
|
||||
dp[j][i] = dp[j-1][i] + dp[nums.size()-1][i-nums[j]];
|
||||
}
|
||||
}
|
||||
}
|
||||
// 打印dp数组
|
||||
for(int i = 0; i < nums.size(); i++){
|
||||
for(int j = 0; j <= target; j++){
|
||||
cout<<dp[i][j]<<" ";
|
||||
}
|
||||
cout<<endl;
|
||||
}
|
||||
return dp[nums.size()-1][target];
|
||||
}
|
||||
```
|
||||
|
||||
#### Simulation
|
||||
|
||||
##### 样例 nums = [2,3,4], target = 6
|
||||
|
||||
##### 1. 初始化一个3x7的dp数组
|
||||
|
||||
1 0 0 0 0 0 0
|
||||
1 0 0 0 0 0 0
|
||||
1 0 0 0 0 0 0
|
||||
|
||||
dp\[0-2\]\[0\] = 1,含义是有nums[0-2]物品时使得背包容量为0的取法为1,作用是在取到nums[i]物品使得背包容量为nums[i]时取法为1。
|
||||
|
||||
##### 2.迭代方式
|
||||
|
||||
必须列优先,因为右边的数组在迭代时需要最左下的数组最终结果。
|
||||
|
||||
##### 3. 模拟过程
|
||||
|
||||
i = 1, j = 0 dp\[0\]\[1\] = 0,表示在物品集合{2}中无法组成和为1
|
||||
i = 1, j = 1 dp\[1\]\[1\] = 0,表示在物品集合{2,3}中无法组成和为1
|
||||
i = 1, j = 2 dp\[2\]\[1\] = 0,表示在物品集合{2,3,4}中无法组成和为1
|
||||
|
||||
1 0 0 0 0 0 0
|
||||
1 0 0 0 0 0 0
|
||||
1 **0** 0 0 0 0 0
|
||||
|
||||
此时dp\[2\]\[1\]作为第1列最底部的元素,表示所有物品都有的情况下组成和为1的排列方式为0
|
||||
|
||||
————————————————————————————
|
||||
|
||||
i = 2, j = 0 dp\[0\]\[2\] = 1,表示在物品集合{2}中取出和为2的排列有{2}
|
||||
i = 2, j = 1 dp\[1\]\[2\] = 1,表示在物品集合{2,3}中取出和为2的排列有{2}
|
||||
i = 2, j = 2 dp\[2\]\[2\] = 1,表示在物品集合{2,3,4}中取出和为2的排列有{2}
|
||||
|
||||
1 0 1 0 0 0 0
|
||||
1 0 1 0 0 0 0
|
||||
1 0 **1** 0 0 0 0
|
||||
|
||||
此时dp\[2\]\[2\]作为第2列最底部的元素,表示所有物品都有的情况下和为2的排列方式有1个 (类比成一维dp即dp[2]=dp[0])
|
||||
|
||||
————————————————————————————
|
||||
|
||||
i = 3, j = 0 dp\[0\]\[3\] = 0,表示在物品集合{2}中无法取出和为3
|
||||
i = 3, j = 1 dp\[1\]\[3\] = 1,表示在物品集合{2,3}中取出和为3的排列有{3}
|
||||
i = 3, j = 2 dp\[2\]\[3\] = 1,表示在物品集合{2,3,4}中取出和为3的排列有{3}
|
||||
|
||||
1 0 1 0 0 0 0
|
||||
1 0 1 1 0 0 0
|
||||
1 0 1 **1** 0 0 0
|
||||
|
||||
此时dp\[2\]\[3\]作为第3列最底部的元素,表示所有物品都有的情况下和为3的排列方式有1个(类比成一维dp即dp[3]=dp[0])
|
||||
|
||||
————————————————————————————
|
||||
|
||||
i = 4, j = 0 dp\[0\]\[4\] = 1,表示在物品集合{2}中取出和为4的排列有在原有的排列{2}后添加一个2成为{2,2}(从第2列底部信息继承获得)
|
||||
i = 4, j = 1 dp\[1\]\[4\] = 1,表示在物品集合{2,3}中取出和为4的排列有{2,2}
|
||||
i = 4, j = 2 dp\[2\]\[4\] = 2,表示在物品集合{2,3,4}中取出和为4的排列有{{2,2},{4}}({2,2}的信息从该列头上获得)
|
||||
|
||||
1 0 1 0 1 0 0
|
||||
1 0 1 1 1 0 0
|
||||
1 0 1 1 **2** 0 0
|
||||
|
||||
此时dp\[2\]\[4\]作为第4列最底部的元素,表示所有物品都有的情况下和为4的排列方式有2个
|
||||
|
||||
————————————————————————————
|
||||
|
||||
i = 5, j = 0 dp\[0\]\[5\] = 1,表示在物品集合{2}中取出和为5的排列有{3,2} **(3的信息由dp[2]\[3]获得,即将2放在3的右边)**
|
||||
i = 5, j = 1 dp\[1\]\[5\] = 2,表示在物品集合{2,3}中取出和为5的排列有{{2,3},{3,2}} **({3,2}由上一行信息继承,{2,3}是从dp[2] [2]获得,将3放在2的右边)**
|
||||
i = 5, j = 2 dp\[2\]\[5\] = 2,表示在物品集合{2,3,4}中取出和为5的排列有{{2,3},{3,2}}
|
||||
|
||||
1 0 1 0 1 1 0
|
||||
1 0 1 1 1 2 0
|
||||
1 0 1 1 2 **2** 0
|
||||
|
||||
此时dp\[2\]\[5\]作为第5列最底部的元素,表示所有物品都有的情况下和为5的排列方式有2个
|
||||
|
||||
————————————————————————————
|
||||
|
||||
i = 6, j = 0 dp\[0\]\[6\] = 2,表示在物品集合{2}中取出和为6的排列有{{2,2,2},{4,2}} **(信息由dp[2]\[4]获得,即将2放在{2,2}和{4}的右边)**
|
||||
i = 6, j = 1 dp\[1\]\[6\] = 3,表示在物品集合{2,3}中取出和为6的排列有{{2,2,2},{4,2},{3,3}} **({2,2,2},{4,2}由上一行信息继承,{3,3}是从dp[2] [3]获得,将3放在3的右边)**
|
||||
i = 6, j = 2 dp\[2\]\[6\] = 4,表示在物品集合{2,3,4}中取出和为6的排列有{{2,2,2},{4,2},{3,3},{2,4}} **({2,2,2},{4,2},{3,3}由上一行继承,{2,4}从dp[2]获得,将4放在2的右边)**
|
||||
|
||||
1 0 1 0 1 1 2
|
||||
1 0 1 1 1 2 3
|
||||
1 0 1 1 2 2 **4**
|
||||
|
||||
此时dp\[2\]\[6\]作为第6列最底部的元素,表示所有物品都有的情况下和为6的排列方式有4个,为{2,2,2},{4,2},{3,3},{2,4}。
|
||||
|
||||
|
||||
|
||||
@ -1,145 +0,0 @@
|
||||
# 完全背包的排列问题模拟
|
||||
|
||||
#### Problem
|
||||
|
||||
1. 排列问题是完全背包中十分棘手的问题。
|
||||
2. 其在迭代过程中需要先迭代背包容量,再迭代物品个数,使得其在代码理解上较难入手。
|
||||
|
||||
#### Contribution
|
||||
|
||||
本文档以力扣上[组合总和IV](https://leetcode.cn/problems/combination-sum-iv/)为例,提供一个二维dp的代码例子,并提供模拟过程以便于理解
|
||||
|
||||
#### Code
|
||||
|
||||
```cpp
|
||||
int combinationSum4(vector<int>& nums, int target) {
|
||||
// 定义背包容量为target,物品个数为nums.size()的dp数组
|
||||
// dp[i][j]表示将第0-i个物品添加入排列中,和为j的排列方式
|
||||
vector<vector<int>> dp (nums.size(), vector(target+1,0));
|
||||
|
||||
// 表示有0,1,...,n个物品可选择的情况下,和为0的选择方法为1:什么都不取
|
||||
for(int i = 0; i < nums.size(); i++) dp[i][0] = 1;
|
||||
|
||||
// 必须按列遍历,因为右边数组需要知道左边数组最低部的信息(排列问题)
|
||||
// 后面的模拟可以更清楚的表现这么操作的原因
|
||||
for(int i = 1; i <= target; i++){
|
||||
for(int j = 0; j < nums.size(); j++){
|
||||
// 只有nums[j]可以取的情况
|
||||
if(j == 0){
|
||||
if(nums[j] > i) dp[j][i] = 0;
|
||||
// 如果背包容量放不下 那么此时没有排列方式
|
||||
else dp[j][i] = dp[nums.size()-1][i-nums[j]];
|
||||
// 如果背包容量放的下 全排列方式为dp[最底层][容量-该物品容量]排列方式后面放一个nums[j]
|
||||
}
|
||||
// 有多个nums数可以取
|
||||
else{
|
||||
// 如果背包容量放不下 那么沿用0-j-1个物品的排列方式
|
||||
if(nums[j] > i) dp[j][i] = dp[j-1][i];
|
||||
// 如果背包容量放得下 在dp[最底层][容量-该物品容量]排列方式后面放一个nums[j]后面放个nums[j]
|
||||
// INT_MAX避免溢出
|
||||
else if(i >= nums[j] && dp[j-1][i] < INT_MAX - dp[nums.size()-1][i-nums[j]])
|
||||
dp[j][i] = dp[j-1][i] + dp[nums.size()-1][i-nums[j]];
|
||||
}
|
||||
}
|
||||
}
|
||||
// 打印dp数组
|
||||
for(int i = 0; i < nums.size(); i++){
|
||||
for(int j = 0; j <= target; j++){
|
||||
cout<<dp[i][j]<<" ";
|
||||
}
|
||||
cout<<endl;
|
||||
}
|
||||
return dp[nums.size()-1][target];
|
||||
}
|
||||
```
|
||||
|
||||
#### Simulation
|
||||
|
||||
##### 样例 nums = [2,3,4], target = 6
|
||||
|
||||
##### 1. 初始化一个3x7的dp数组
|
||||
|
||||
1 0 0 0 0 0 0
|
||||
1 0 0 0 0 0 0
|
||||
1 0 0 0 0 0 0
|
||||
|
||||
dp\[0-2\]\[0\] = 1,含义是有nums[0-2]物品时使得背包容量为0的取法为1,作用是在取到nums[i]物品使得背包容量为nums[i]时取法为1。
|
||||
|
||||
##### 2.迭代方式
|
||||
|
||||
必须列优先,因为右边的数组在迭代时需要最左下的数组最终结果。
|
||||
|
||||
##### 3. 模拟过程
|
||||
|
||||
i = 1, j = 0 dp\[0\]\[1\] = 0,表示在物品集合{2}中无法组成和为1
|
||||
i = 1, j = 1 dp\[1\]\[1\] = 0,表示在物品集合{2,3}中无法组成和为1
|
||||
i = 1, j = 2 dp\[2\]\[1\] = 0,表示在物品集合{2,3,4}中无法组成和为1
|
||||
|
||||
1 0 0 0 0 0 0
|
||||
1 0 0 0 0 0 0
|
||||
1 **0** 0 0 0 0 0
|
||||
|
||||
此时dp\[2\]\[1\]作为第1列最底部的元素,表示所有物品都有的情况下组成和为1的排列方式为0
|
||||
|
||||
————————————————————————————
|
||||
|
||||
i = 2, j = 0 dp\[0\]\[2\] = 1,表示在物品集合{2}中取出和为2的排列有{2}
|
||||
i = 2, j = 1 dp\[1\]\[2\] = 1,表示在物品集合{2,3}中取出和为2的排列有{2}
|
||||
i = 2, j = 2 dp\[2\]\[2\] = 1,表示在物品集合{2,3,4}中取出和为2的排列有{2}
|
||||
|
||||
1 0 1 0 0 0 0
|
||||
1 0 1 0 0 0 0
|
||||
1 0 **1** 0 0 0 0
|
||||
|
||||
此时dp\[2\]\[2\]作为第2列最底部的元素,表示所有物品都有的情况下和为2的排列方式有1个 (类比成一维dp即dp[2]=dp[0])
|
||||
|
||||
————————————————————————————
|
||||
|
||||
i = 3, j = 0 dp\[0\]\[3\] = 0,表示在物品集合{2}中无法取出和为3
|
||||
i = 3, j = 1 dp\[1\]\[3\] = 1,表示在物品集合{2,3}中取出和为3的排列有{3}
|
||||
i = 3, j = 2 dp\[2\]\[3\] = 1,表示在物品集合{2,3,4}中取出和为3的排列有{3}
|
||||
|
||||
1 0 1 0 0 0 0
|
||||
1 0 1 1 0 0 0
|
||||
1 0 1 **1** 0 0 0
|
||||
|
||||
此时dp\[2\]\[3\]作为第3列最底部的元素,表示所有物品都有的情况下和为3的排列方式有1个(类比成一维dp即dp[3]=dp[0])
|
||||
|
||||
————————————————————————————
|
||||
|
||||
i = 4, j = 0 dp\[0\]\[4\] = 1,表示在物品集合{2}中取出和为4的排列有在原有的排列{2}后添加一个2成为{2,2}(从第2列底部信息继承获得)
|
||||
i = 4, j = 1 dp\[1\]\[4\] = 1,表示在物品集合{2,3}中取出和为4的排列有{2,2}
|
||||
i = 4, j = 2 dp\[2\]\[4\] = 2,表示在物品集合{2,3,4}中取出和为4的排列有{{2,2},{4}}({2,2}的信息从该列头上获得)
|
||||
|
||||
1 0 1 0 1 0 0
|
||||
1 0 1 1 1 0 0
|
||||
1 0 1 1 **2** 0 0
|
||||
|
||||
此时dp\[2\]\[4\]作为第4列最底部的元素,表示所有物品都有的情况下和为4的排列方式有2个
|
||||
|
||||
————————————————————————————
|
||||
|
||||
i = 5, j = 0 dp\[0\]\[5\] = 1,表示在物品集合{2}中取出和为5的排列有{3,2} **(3的信息由dp[2]\[3]获得,即将2放在3的右边)**
|
||||
i = 5, j = 1 dp\[1\]\[5\] = 2,表示在物品集合{2,3}中取出和为5的排列有{{2,3},{3,2}} **({3,2}由上一行信息继承,{2,3}是从dp[2] [2]获得,将3放在2的右边)**
|
||||
i = 5, j = 2 dp\[2\]\[5\] = 2,表示在物品集合{2,3,4}中取出和为5的排列有{{2,3},{3,2}}
|
||||
|
||||
1 0 1 0 1 1 0
|
||||
1 0 1 1 1 2 0
|
||||
1 0 1 1 2 **2** 0
|
||||
|
||||
此时dp\[2\]\[5\]作为第5列最底部的元素,表示所有物品都有的情况下和为5的排列方式有2个
|
||||
|
||||
————————————————————————————
|
||||
|
||||
i = 6, j = 0 dp\[0\]\[6\] = 2,表示在物品集合{2}中取出和为6的排列有{{2,2,2},{4,2}} **(信息由dp[2]\[4]获得,即将2放在{2,2}和{4}的右边)**
|
||||
i = 6, j = 1 dp\[1\]\[6\] = 3,表示在物品集合{2,3}中取出和为6的排列有{{2,2,2},{4,2},{3,3}} **({2,2,2},{4,2}由上一行信息继承,{3,3}是从dp[2] [3]获得,将3放在3的右边)**
|
||||
i = 6, j = 2 dp\[2\]\[6\] = 4,表示在物品集合{2,3,4}中取出和为6的排列有{{2,2,2},{4,2},{3,3},{2,4}} **({2,2,2},{4,2},{3,3}由上一行继承,{2,4}从dp[2]获得,将4放在2的右边)**
|
||||
|
||||
1 0 1 0 1 1 2
|
||||
1 0 1 1 1 2 3
|
||||
1 0 1 1 2 2 **4**
|
||||
|
||||
此时dp\[2\]\[6\]作为第6列最底部的元素,表示所有物品都有的情况下和为6的排列方式有4个,为{2,2,2},{4,2},{3,3},{2,4}。
|
||||
|
||||
|
||||
|
||||
@ -130,6 +130,11 @@ public:
|
||||
|
||||
```
|
||||
|
||||
* 时间复杂度: O(target * n),其中 n 为 nums 的长度
|
||||
* 空间复杂度: O(target)
|
||||
|
||||
|
||||
|
||||
C++测试用例有两个数相加超过int的数据,所以需要在if里加上dp[i] < INT_MAX - dp[i - num]。
|
||||
|
||||
但java就不用考虑这个限制,java里的int也是四个字节吧,也有可能leetcode后台对不同语言的测试数据不一样。
|
||||
|
||||
@ -37,6 +37,10 @@
|
||||
|
||||
题目数据确保队列可以被重建
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,不要两边一起贪,会顾此失彼 | LeetCode:406.根据身高重建队列](https://www.bilibili.com/video/BV1EA411675Y),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
本题有两个维度,h和k,看到这种题目一定要想如何确定一个维度,然后再按照另一个维度重新排列。
|
||||
|
||||
@ -30,6 +30,10 @@
|
||||
* 输出: 0
|
||||
* 解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,依然是判断重叠区间 | LeetCode:435.无重叠区间](https://www.bilibili.com/video/BV1A14y1c7E1),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
**相信很多同学看到这道题目都冥冥之中感觉要排序,但是究竟是按照右边界排序,还是按照左边界排序呢?**
|
||||
@ -395,18 +399,20 @@ object Solution {
|
||||
```Rust
|
||||
impl Solution {
|
||||
pub fn erase_overlap_intervals(intervals: Vec<Vec<i32>>) -> i32 {
|
||||
if intervals.len() == 0 { return 0; }
|
||||
let mut intervals = intervals;
|
||||
intervals.sort_by(|a, b| a[1].cmp(&b[1]));
|
||||
if intervals.is_empty() {
|
||||
return 0;
|
||||
}
|
||||
intervals.sort_by_key(|interval| interval[1]);
|
||||
let mut count = 1;
|
||||
let mut end = intervals[0][1];
|
||||
for i in 1..intervals.len() {
|
||||
if end <= intervals[i][0] {
|
||||
end = intervals[i][1];
|
||||
for v in intervals.iter().skip(1) {
|
||||
if end <= v[0] {
|
||||
end = v[1];
|
||||
count += 1;
|
||||
}
|
||||
}
|
||||
intervals.len() as i32 - count
|
||||
|
||||
(intervals.len() - count) as i32
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -42,6 +42,10 @@
|
||||
* points[i].length == 2
|
||||
* -2^31 <= xstart < xend <= 2^31 - 1
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,判断重叠区间问题 | LeetCode:452.用最少数量的箭引爆气球](https://www.bilibili.com/video/BV1SA41167xe),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
如何使用最少的弓箭呢?
|
||||
@ -173,7 +177,23 @@ class Solution:
|
||||
points[i][1] = min(points[i - 1][1], points[i][1]) # 更新重叠气球最小右边界
|
||||
return result
|
||||
```
|
||||
```python
|
||||
class Solution: # 不改变原数组
|
||||
def findMinArrowShots(self, points: List[List[int]]) -> int:
|
||||
points.sort(key = lambda x: x[0])
|
||||
sl,sr = points[0][0],points[0][1]
|
||||
count = 1
|
||||
for i in points:
|
||||
if i[0]>sr:
|
||||
count+=1
|
||||
sl,sr = i[0],i[1]
|
||||
else:
|
||||
sl = max(sl,i[0])
|
||||
sr = min(sr,i[1])
|
||||
return count
|
||||
|
||||
|
||||
```
|
||||
### Go
|
||||
```go
|
||||
func findMinArrowShots(points [][]int) int {
|
||||
|
||||
@ -97,26 +97,25 @@ Java:
|
||||
```Java
|
||||
class Solution {
|
||||
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
|
||||
Map<Integer, Integer> map = new HashMap<>();
|
||||
int temp;
|
||||
int res = 0;
|
||||
Map<Integer, Integer> map = new HashMap<Integer, Integer>();
|
||||
//统计两个数组中的元素之和,同时统计出现的次数,放入map
|
||||
for (int i : nums1) {
|
||||
for (int j : nums2) {
|
||||
temp = i + j;
|
||||
if (map.containsKey(temp)) {
|
||||
map.put(temp, map.get(temp) + 1);
|
||||
int tmp = map.getOrDefault(i + j, 0);
|
||||
if (tmp == 0) {
|
||||
map.put(i + j, 1);
|
||||
} else {
|
||||
map.put(temp, 1);
|
||||
map.replace(i + j, tmp + 1);
|
||||
}
|
||||
}
|
||||
}
|
||||
//统计剩余的两个元素的和,在map中找是否存在相加为0的情况,同时记录次数
|
||||
for (int i : nums3) {
|
||||
for (int j : nums4) {
|
||||
temp = i + j;
|
||||
if (map.containsKey(0 - temp)) {
|
||||
res += map.get(0 - temp);
|
||||
int tmp = map.getOrDefault(0 - i - j, 0);
|
||||
if (tmp != 0) {
|
||||
res += tmp;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
@ -4,31 +4,35 @@
|
||||
</a>
|
||||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
|
||||
# 455.分发饼干
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/assign-cookies/)
|
||||
|
||||
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
|
||||
|
||||
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
|
||||
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
|
||||
|
||||
示例 1:
|
||||
* 输入: g = [1,2,3], s = [1,1]
|
||||
* 输出: 1
|
||||
解释:你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。所以你应该输出1。
|
||||
示例 1:
|
||||
|
||||
示例 2:
|
||||
* 输入: g = [1,2], s = [1,2,3]
|
||||
* 输出: 2
|
||||
* 解释:你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出2.
|
||||
- 输入: g = [1,2,3], s = [1,1]
|
||||
- 输出: 1
|
||||
解释:你有三个孩子和两块小饼干,3 个孩子的胃口值分别是:1,2,3。虽然你有两块小饼干,由于他们的尺寸都是 1,你只能让胃口值是 1 的孩子满足。所以你应该输出 1。
|
||||
|
||||
示例 2:
|
||||
|
||||
- 输入: g = [1,2], s = [1,2,3]
|
||||
- 输出: 2
|
||||
- 解释:你有两个孩子和三块小饼干,2 个孩子的胃口值分别是 1,2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出 2.
|
||||
|
||||
提示:
|
||||
* 1 <= g.length <= 3 * 10^4
|
||||
* 0 <= s.length <= 3 * 10^4
|
||||
* 1 <= g[i], s[j] <= 2^31 - 1
|
||||
|
||||
- 1 <= g.length <= 3 \* 10^4
|
||||
- 0 <= s.length <= 3 \* 10^4
|
||||
- 1 <= g[i], s[j] <= 2^31 - 1
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,你想先喂哪个小孩?| LeetCode:455.分发饼干](https://www.bilibili.com/video/BV1MM411b7cq),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
@ -44,18 +48,14 @@
|
||||
|
||||
如图:
|
||||
|
||||

|
||||
|
||||
|
||||
这个例子可以看出饼干9只有喂给胃口为7的小孩,这样才是整体最优解,并想不出反例,那么就可以撸代码了。
|
||||
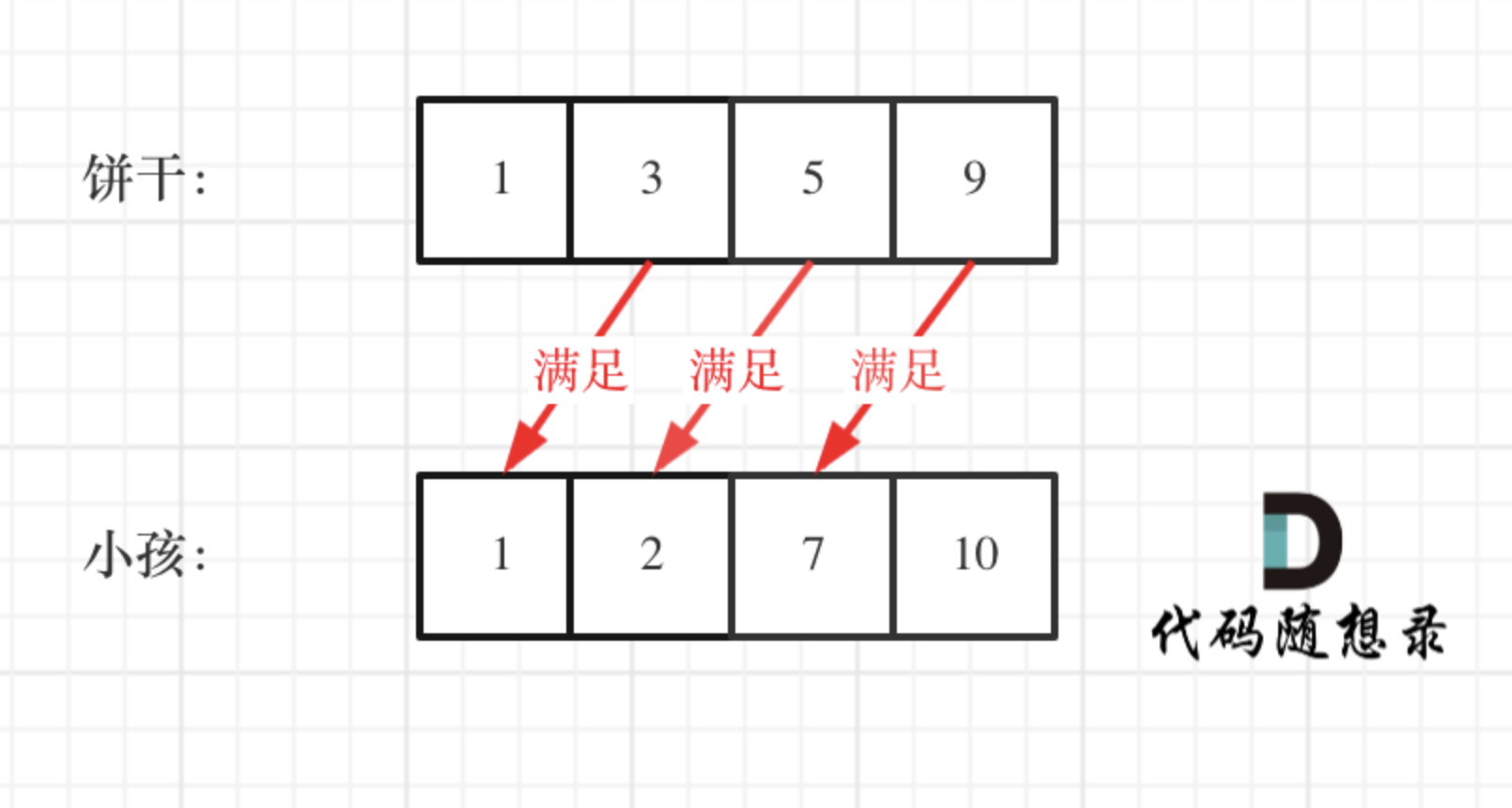
|
||||
|
||||
这个例子可以看出饼干 9 只有喂给胃口为 7 的小孩,这样才是整体最优解,并想不出反例,那么就可以撸代码了。
|
||||
|
||||
C++代码整体如下:
|
||||
|
||||
```CPP
|
||||
// 版本一
|
||||
// 时间复杂度:O(nlogn)
|
||||
// 空间复杂度:O(1)
|
||||
// 版本一
|
||||
class Solution {
|
||||
public:
|
||||
int findContentChildren(vector<int>& g, vector<int>& s) {
|
||||
@ -63,8 +63,8 @@ public:
|
||||
sort(s.begin(), s.end());
|
||||
int index = s.size() - 1; // 饼干数组的下标
|
||||
int result = 0;
|
||||
for (int i = g.size() - 1; i >= 0; i--) { // 遍历胃口
|
||||
if (index >= 0 && s[index] >= g[i]) { // 遍历饼干
|
||||
for (int i = g.size() - 1; i >= 0; i--) { // 遍历胃口
|
||||
if (index >= 0 && s[index] >= g[i]) { // 遍历饼干
|
||||
result++;
|
||||
index--;
|
||||
}
|
||||
@ -73,28 +73,29 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
从代码中可以看出我用了一个index来控制饼干数组的遍历,遍历饼干并没有再起一个for循环,而是采用自减的方式,这也是常用的技巧。
|
||||
|
||||
有的同学看到要遍历两个数组,就想到用两个for循环,那样逻辑其实就复杂了。
|
||||
* 时间复杂度:O(nlogn)
|
||||
* 空间复杂度:O(1)
|
||||
|
||||
|
||||
### 注意事项
|
||||
从代码中可以看出我用了一个 index 来控制饼干数组的遍历,遍历饼干并没有再起一个 for 循环,而是采用自减的方式,这也是常用的技巧。
|
||||
|
||||
注意版本一的代码中,可以看出来,是先遍历的胃口,在遍历的饼干,那么可不可以 先遍历 饼干,在遍历胃口呢?
|
||||
有的同学看到要遍历两个数组,就想到用两个 for 循环,那样逻辑其实就复杂了。
|
||||
|
||||
其实是不可以的。
|
||||
### 注意事项
|
||||
|
||||
外面的for 是里的下标i 是固定移动的,而if里面的下标 index 是符合条件才移动的。
|
||||
注意版本一的代码中,可以看出来,是先遍历的胃口,在遍历的饼干,那么可不可以 先遍历 饼干,在遍历胃口呢?
|
||||
|
||||
如果 for 控制的是饼干, if 控制胃口,就是出现如下情况 :
|
||||
其实是不可以的。
|
||||
|
||||
外面的 for 是里的下标 i 是固定移动的,而 if 里面的下标 index 是符合条件才移动的。
|
||||
|
||||
如果 for 控制的是饼干, if 控制胃口,就是出现如下情况 :
|
||||
|
||||
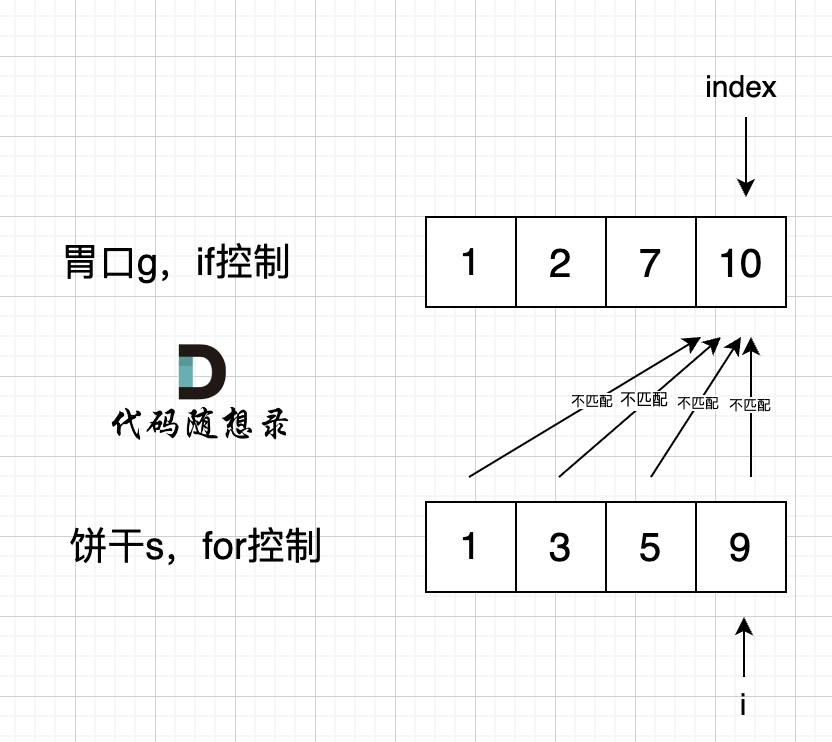
|
||||
|
||||
if 里的 index 指向 胃口 10, for里的i指向饼干9,因为 饼干9 满足不了 胃口10,所以 i 持续向前移动,而index 走不到` s[index] >= g[i]` 的逻辑,所以index不会移动,那么当i 持续向前移动,最后所有的饼干都匹配不上。
|
||||
|
||||
所以 一定要for 控制 胃口,里面的if控制饼干。
|
||||
if 里的 index 指向 胃口 10, for 里的 i 指向饼干 9,因为 饼干 9 满足不了 胃口 10,所以 i 持续向前移动,而 index 走不到` s[index] >= g[i]` 的逻辑,所以 index 不会移动,那么当 i 持续向前移动,最后所有的饼干都匹配不上。
|
||||
|
||||
所以 一定要 for 控制 胃口,里面的 if 控制饼干。
|
||||
|
||||
### 其他思路
|
||||
|
||||
@ -117,11 +118,14 @@ public:
|
||||
return index;
|
||||
}
|
||||
};
|
||||
```
|
||||
```
|
||||
* 时间复杂度:O(nlogn)
|
||||
* 空间复杂度:O(1)
|
||||
|
||||
细心的录友可以发现,这种写法,两个循环的顺序改变了,先遍历的饼干,在遍历的胃口,这是因为遍历顺序变了,我们是从小到大遍历。
|
||||
|
||||
理由在上面 “注意事项”中 已经讲过。
|
||||
细心的录友可以发现,这种写法,两个循环的顺序改变了,先遍历的饼干,在遍历的胃口,这是因为遍历顺序变了,我们是从小到大遍历。
|
||||
|
||||
理由在上面 “注意事项”中 已经讲过。
|
||||
|
||||
## 总结
|
||||
|
||||
@ -131,8 +135,8 @@ public:
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
### Java
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
// 思路1:优先考虑饼干,小饼干先喂饱小胃口
|
||||
@ -151,6 +155,7 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
// 思路2:优先考虑胃口,先喂饱大胃口
|
||||
@ -172,6 +177,7 @@ class Solution {
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
# 思路1:优先考虑小胃口
|
||||
@ -184,6 +190,7 @@ class Solution:
|
||||
res += 1
|
||||
return res
|
||||
```
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
# 思路2:优先考虑大胃口
|
||||
@ -199,6 +206,7 @@ class Solution:
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
```golang
|
||||
//排序后,局部最优
|
||||
func findContentChildren(g []int, s []int) int {
|
||||
@ -218,6 +226,7 @@ func findContentChildren(g []int, s []int) int {
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
```rust
|
||||
pub fn find_content_children(mut children: Vec<i32>, mut cookie: Vec<i32>) -> i32 {
|
||||
children.sort();
|
||||
@ -236,21 +245,21 @@ pub fn find_content_children(mut children: Vec<i32>, mut cookie: Vec<i32>) -> i3
|
||||
```
|
||||
|
||||
### Javascript
|
||||
```js
|
||||
var findContentChildren = function(g, s) {
|
||||
g = g.sort((a, b) => a - b)
|
||||
s = s.sort((a, b) => a - b)
|
||||
let result = 0
|
||||
let index = s.length - 1
|
||||
for(let i = g.length - 1; i >= 0; i--) {
|
||||
if(index >= 0 && s[index] >= g[i]) {
|
||||
result++
|
||||
index--
|
||||
}
|
||||
}
|
||||
return result
|
||||
};
|
||||
|
||||
```js
|
||||
var findContentChildren = function (g, s) {
|
||||
g = g.sort((a, b) => a - b);
|
||||
s = s.sort((a, b) => a - b);
|
||||
let result = 0;
|
||||
let index = s.length - 1;
|
||||
for (let i = g.length - 1; i >= 0; i--) {
|
||||
if (index >= 0 && s[index] >= g[i]) {
|
||||
result++;
|
||||
index--;
|
||||
}
|
||||
}
|
||||
return result;
|
||||
};
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
@ -258,41 +267,41 @@ var findContentChildren = function(g, s) {
|
||||
```typescript
|
||||
// 大饼干尽量喂胃口大的
|
||||
function findContentChildren(g: number[], s: number[]): number {
|
||||
g.sort((a, b) => a - b);
|
||||
s.sort((a, b) => a - b);
|
||||
const childLength: number = g.length,
|
||||
cookieLength: number = s.length;
|
||||
let curChild: number = childLength - 1,
|
||||
curCookie: number = cookieLength - 1;
|
||||
let resCount: number = 0;
|
||||
while (curChild >= 0 && curCookie >= 0) {
|
||||
if (g[curChild] <= s[curCookie]) {
|
||||
curCookie--;
|
||||
resCount++;
|
||||
}
|
||||
curChild--;
|
||||
g.sort((a, b) => a - b);
|
||||
s.sort((a, b) => a - b);
|
||||
const childLength: number = g.length,
|
||||
cookieLength: number = s.length;
|
||||
let curChild: number = childLength - 1,
|
||||
curCookie: number = cookieLength - 1;
|
||||
let resCount: number = 0;
|
||||
while (curChild >= 0 && curCookie >= 0) {
|
||||
if (g[curChild] <= s[curCookie]) {
|
||||
curCookie--;
|
||||
resCount++;
|
||||
}
|
||||
return resCount;
|
||||
};
|
||||
curChild--;
|
||||
}
|
||||
return resCount;
|
||||
}
|
||||
```
|
||||
|
||||
```typescript
|
||||
// 小饼干先喂饱小胃口的
|
||||
function findContentChildren(g: number[], s: number[]): number {
|
||||
g.sort((a, b) => a - b);
|
||||
s.sort((a, b) => a - b);
|
||||
const childLength: number = g.length,
|
||||
cookieLength: number = s.length;
|
||||
let curChild: number = 0,
|
||||
curCookie: number = 0;
|
||||
while (curChild < childLength && curCookie < cookieLength) {
|
||||
if (g[curChild] <= s[curCookie]) {
|
||||
curChild++;
|
||||
}
|
||||
curCookie++;
|
||||
g.sort((a, b) => a - b);
|
||||
s.sort((a, b) => a - b);
|
||||
const childLength: number = g.length,
|
||||
cookieLength: number = s.length;
|
||||
let curChild: number = 0,
|
||||
curCookie: number = 0;
|
||||
while (curChild < childLength && curCookie < cookieLength) {
|
||||
if (g[curChild] <= s[curCookie]) {
|
||||
curChild++;
|
||||
}
|
||||
return curChild;
|
||||
};
|
||||
curCookie++;
|
||||
}
|
||||
return curChild;
|
||||
}
|
||||
```
|
||||
|
||||
### C
|
||||
|
||||
@ -156,6 +156,11 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(kmn),k 为strs的长度
|
||||
* 空间复杂度: O(mn)
|
||||
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
不少同学刷过这道题,可能没有总结这究竟是什么背包。
|
||||
|
||||
@ -347,26 +347,32 @@ int fib(int n){
|
||||
### Rust
|
||||
动态规划:
|
||||
```Rust
|
||||
pub fn fib(n: i32) -> i32 {
|
||||
let n = n as usize;
|
||||
let mut dp = vec![0; 31];
|
||||
dp[1] = 1;
|
||||
for i in 2..=n {
|
||||
dp[i] = dp[i - 1] + dp[i - 2];
|
||||
impl Solution {
|
||||
pub fn fib(n: i32) -> i32 {
|
||||
if n <= 1 {
|
||||
return n;
|
||||
}
|
||||
let n = n as usize;
|
||||
let mut dp = vec![0; n + 1];
|
||||
dp[1] = 1;
|
||||
for i in 2..=n {
|
||||
dp[i] = dp[i - 2] + dp[i - 1];
|
||||
}
|
||||
dp[n]
|
||||
}
|
||||
dp[n]
|
||||
}
|
||||
```
|
||||
|
||||
递归实现:
|
||||
```Rust
|
||||
pub fn fib(n: i32) -> i32 {
|
||||
//若n小于等于1,返回n
|
||||
f n <= 1 {
|
||||
return n;
|
||||
impl Solution {
|
||||
pub fn fib(n: i32) -> i32 {
|
||||
if n <= 1 {
|
||||
n
|
||||
} else {
|
||||
Self::fib(n - 1) + Self::fib(n - 2)
|
||||
}
|
||||
}
|
||||
//否则返回fib(n-1) + fib(n-2)
|
||||
return fib(n - 1) + fib(n - 2);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
@ -144,6 +144,11 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n^2)
|
||||
* 空间复杂度: O(n^2)
|
||||
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
@ -179,6 +179,11 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(mn),其中 m 是amount,n 是 coins 的长度
|
||||
* 空间复杂度: O(m)
|
||||
|
||||
|
||||
是不是发现代码如此精简,哈哈
|
||||
|
||||
## 总结
|
||||
@ -215,6 +220,27 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
```Java
|
||||
// 二维dp数组版本,方便理解
|
||||
class Solution {
|
||||
public int change(int amount, int[] coins) {
|
||||
int[][] dp = new int[coins.length][amount + 1];
|
||||
// 只有一种硬币的情况
|
||||
for (int i = 0; i <= amount; i += coins[0]) {
|
||||
dp[0][i] = 1;
|
||||
}
|
||||
for (int i = 1; i < coins.length; i++) {
|
||||
for (int j = 0; j <= amount; j++) {
|
||||
// 第i种硬币使用0~k次,求和
|
||||
for (int k = 0; k * coins[i] <= j; k++) {
|
||||
dp[i][j] += dp[i - 1][j - k * coins[i]];
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[coins.length - 1][amount];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Python:
|
||||
|
||||
|
||||
@ -221,8 +221,27 @@ class Solution:
|
||||
for i in range(len(res)-1): // 统计有序数组的最小差值
|
||||
r = min(abs(res[i]-res[i+1]),r)
|
||||
return r
|
||||
|
||||
|
||||
class Solution: # 双指针法,不用数组 (同Carl写法) - 更快
|
||||
def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
|
||||
global pre,minval
|
||||
pre = None
|
||||
minval = 10**5
|
||||
self.traversal(root)
|
||||
return minval
|
||||
|
||||
def traversal(self,root):
|
||||
global pre,minval
|
||||
if not root: return None
|
||||
self.traversal(root.left)
|
||||
if pre and root.val-pre.val<minval:
|
||||
minval = root.val-pre.val
|
||||
pre = root
|
||||
self.traversal(root.right)
|
||||
```
|
||||
|
||||
|
||||
迭代法-中序遍历
|
||||
```python
|
||||
class Solution:
|
||||
|
||||
@ -234,6 +234,26 @@ class Solution:
|
||||
return root
|
||||
|
||||
```
|
||||
**迭代**
|
||||
```python
|
||||
class Solution:
|
||||
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
|
||||
if not root: return root
|
||||
stack = []
|
||||
result = []
|
||||
cur = root
|
||||
pre = 0
|
||||
while cur or stack:
|
||||
if cur:
|
||||
stack.append(cur)
|
||||
cur = cur.right
|
||||
else:
|
||||
cur = stack.pop()
|
||||
cur.val+= pre
|
||||
pre = cur.val
|
||||
cur =cur.left
|
||||
return root
|
||||
```
|
||||
|
||||
## Go
|
||||
|
||||
|
||||
@ -104,6 +104,10 @@ public:
|
||||
};
|
||||
|
||||
```
|
||||
* 时间复杂度: O(n * m)
|
||||
* 空间复杂度: O(n * m)
|
||||
|
||||
|
||||
|
||||
### 动态规划二
|
||||
|
||||
@ -127,6 +131,10 @@ public:
|
||||
};
|
||||
|
||||
```
|
||||
* 时间复杂度: O(n * m)
|
||||
* 空间复杂度: O(n * m)
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
@ -26,6 +26,10 @@
|
||||
|
||||
说明: N 是在 [0, 10^9] 范围内的一个整数。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,思路不难想,但代码不好写!LeetCode:738.单调自增的数字](https://www.bilibili.com/video/BV1Kv4y1x7tP),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 暴力解法
|
||||
|
||||
@ -276,18 +280,20 @@ object Solution {
|
||||
```Rust
|
||||
impl Solution {
|
||||
pub fn monotone_increasing_digits(n: i32) -> i32 {
|
||||
let mut str_num = n.to_string().chars().map(|x| x.to_digit(10).unwrap() as i32).collect::<Vec<i32>>();
|
||||
let mut flag = str_num.len();
|
||||
for i in (1..str_num.len()).rev() {
|
||||
if str_num[i - 1] > str_num[i] {
|
||||
let mut n_bytes = n.to_string().into_bytes();
|
||||
let mut flag = n_bytes.len();
|
||||
for i in (1..n_bytes.len()).rev() {
|
||||
if n_bytes[i - 1] > n_bytes[i] {
|
||||
flag = i;
|
||||
str_num[i - 1] -= 1;
|
||||
n_bytes[i - 1] -= 1;
|
||||
}
|
||||
}
|
||||
for i in flag..str_num.len() {
|
||||
str_num[i] = 9;
|
||||
for v in n_bytes.iter_mut().skip(flag) {
|
||||
*v = 57;
|
||||
}
|
||||
str_num.iter().fold(0, |acc, x| acc * 10 + x)
|
||||
n_bytes
|
||||
.into_iter()
|
||||
.fold(0, |acc, x| acc * 10 + x as i32 - 48)
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -271,6 +271,7 @@ class Solution {
|
||||
```
|
||||
|
||||
Python:
|
||||
> 未精简版本
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
@ -291,6 +292,21 @@ class Solution:
|
||||
return answer
|
||||
```
|
||||
|
||||
> 精简版本
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
|
||||
answer = [0]*len(temperatures)
|
||||
stack = []
|
||||
for i in range(len(temperatures)):
|
||||
while len(stack)>0 and temperatures[i] > temperatures[stack[-1]]:
|
||||
answer[stack[-1]] = i - stack[-1]
|
||||
stack.pop()
|
||||
stack.append(i)
|
||||
return answer
|
||||
```
|
||||
|
||||
Go:
|
||||
|
||||
> 暴力法
|
||||
|
||||
@ -92,7 +92,7 @@ dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
|
||||
|
||||
这里就要说明本题力扣为什么改题意,而且修改题意之后 就清晰很多的原因了。
|
||||
|
||||
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 从 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
|
||||
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
|
||||
|
||||
所以初始化 dp[0] = 0,dp[1] = 0;
|
||||
|
||||
@ -312,17 +312,30 @@ func min(a, b int) int {
|
||||
```
|
||||
|
||||
|
||||
### Javascript
|
||||
```Javascript
|
||||
### JavaScript
|
||||
|
||||
```JavaScript
|
||||
var minCostClimbingStairs = function(cost) {
|
||||
const n = cost.length;
|
||||
const dp = new Array(n + 1);
|
||||
dp[0] = dp[1] = 0;
|
||||
for (let i = 2; i <= n; ++i) {
|
||||
dp[i] = Math.min(dp[i -1] + cost[i - 1], dp[i - 2] + cost[i - 2])
|
||||
const dp = [0, 0]
|
||||
for (let i = 2; i <= cost.length; ++i) {
|
||||
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
|
||||
}
|
||||
return dp[cost.length]
|
||||
};
|
||||
```
|
||||
|
||||
不使用 dp 数组
|
||||
|
||||
```JavaScript
|
||||
var minCostClimbingStairs = function(cost) {
|
||||
let dpBefore = 0,
|
||||
dpAfter = 0
|
||||
for(let i = 2;i <= cost.length;i++){
|
||||
let dpi = Math.min(dpBefore + cost[i - 2],dpAfter + cost[i - 1])
|
||||
dpBefore = dpAfter
|
||||
dpAfter = dpi
|
||||
}
|
||||
|
||||
return dp[n]
|
||||
return dpAfter
|
||||
};
|
||||
```
|
||||
|
||||
@ -330,38 +343,55 @@ var minCostClimbingStairs = function(cost) {
|
||||
|
||||
```typescript
|
||||
function minCostClimbingStairs(cost: number[]): number {
|
||||
/**
|
||||
dp[i]: 走到第i阶需要花费的最少金钱
|
||||
dp[0]: 0;
|
||||
dp[1]: 0;
|
||||
...
|
||||
dp[i]: min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
|
||||
*/
|
||||
const dp = [];
|
||||
const length = cost.length;
|
||||
dp[0] = 0;
|
||||
dp[1] = 0;
|
||||
for (let i = 2; i <= length; i++) {
|
||||
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
|
||||
}
|
||||
return dp[length];
|
||||
};
|
||||
const dp = [0, 0]
|
||||
for (let i = 2; i <= cost.length; i++) {
|
||||
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
|
||||
}
|
||||
return dp[cost.length]
|
||||
}
|
||||
```
|
||||
|
||||
不使用 dp 数组
|
||||
|
||||
```typescript
|
||||
function minCostClimbingStairs(cost: number[]): number {
|
||||
let dpBefore = 0,
|
||||
dpAfter = 0
|
||||
for (let i = 2; i <= cost.length; i++) {
|
||||
let dpi = Math.min(dpBefore + cost[i - 2], dpAfter + cost[i - 1])
|
||||
dpBefore = dpAfter
|
||||
dpAfter = dpi
|
||||
}
|
||||
return dpAfter
|
||||
}
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
```Rust
|
||||
use std::cmp::min;
|
||||
impl Solution {
|
||||
pub fn min_cost_climbing_stairs(cost: Vec<i32>) -> i32 {
|
||||
let len = cost.len();
|
||||
let mut dp = vec![0; len];
|
||||
dp[0] = cost[0];
|
||||
dp[1] = cost[1];
|
||||
for i in 2..len {
|
||||
dp[i] = min(dp[i-1], dp[i-2]) + cost[i];
|
||||
let mut dp = vec![0; cost.len() + 1];
|
||||
for i in 2..=cost.len() {
|
||||
dp[i] = (dp[i - 1] + cost[i - 1]).min(dp[i - 2] + cost[i - 2]);
|
||||
}
|
||||
min(dp[len-1], dp[len-2])
|
||||
dp[cost.len()]
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
不使用 dp 数组
|
||||
|
||||
```rust
|
||||
impl Solution {
|
||||
pub fn min_cost_climbing_stairs(cost: Vec<i32>) -> i32 {
|
||||
let (mut dp_before, mut dp_after) = (0, 0);
|
||||
for i in 2..=cost.len() {
|
||||
let dpi = (dp_before + cost[i - 2]).min(dp_after + cost[i - 1]);
|
||||
dp_before = dp_after;
|
||||
dp_after = dpi;
|
||||
}
|
||||
dp_after
|
||||
}
|
||||
}
|
||||
```
|
||||
@ -369,18 +399,29 @@ impl Solution {
|
||||
### C
|
||||
|
||||
```c
|
||||
int minCostClimbingStairs(int* cost, int costSize){
|
||||
//开辟dp数组,大小为costSize
|
||||
int *dp = (int *)malloc(sizeof(int) * costSize);
|
||||
//初始化dp[0] = cost[0], dp[1] = cost[1]
|
||||
dp[0] = cost[0], dp[1] = cost[1];
|
||||
#include <math.h>
|
||||
int minCostClimbingStairs(int *cost, int costSize) {
|
||||
int dp[costSize + 1];
|
||||
dp[0] = dp[1] = 0;
|
||||
for (int i = 2; i <= costSize; i++) {
|
||||
dp[i] = fmin(dp[i - 2] + cost[i - 2], dp[i - 1] + cost[i - 1]);
|
||||
}
|
||||
return dp[costSize];
|
||||
}
|
||||
```
|
||||
|
||||
int i;
|
||||
for(i = 2; i < costSize; ++i) {
|
||||
dp[i] = (dp[i-1] < dp[i-2] ? dp[i-1] : dp[i-2]) + cost[i];
|
||||
}
|
||||
//选出倒数2层楼梯中较小的
|
||||
return dp[i-1] < dp[i-2] ? dp[i-1] : dp[i-2];
|
||||
不使用 dp 数组
|
||||
|
||||
```c
|
||||
#include <math.h>
|
||||
int minCostClimbingStairs(int *cost, int costSize) {
|
||||
int dpBefore = 0, dpAfter = 0;
|
||||
for (int i = 2; i <= costSize; i++) {
|
||||
int dpi = fmin(dpBefore + cost[i - 2], dpAfter + cost[i - 1]);
|
||||
dpBefore = dpAfter;
|
||||
dpAfter = dpi;
|
||||
}
|
||||
return dpAfter;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
@ -24,6 +24,10 @@
|
||||
* S的长度在[1, 500]之间。
|
||||
* S只包含小写字母 'a' 到 'z' 。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,寻找最远的出现位置! LeetCode:763.划分字母区间](https://www.bilibili.com/video/BV18G4y1K7d5),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
一想到分割字符串就想到了回溯,但本题其实不用回溯去暴力搜索。
|
||||
@ -408,28 +412,22 @@ object Solution {
|
||||
### Rust
|
||||
|
||||
```Rust
|
||||
use std::collections::HashMap;
|
||||
impl Solution {
|
||||
fn max (a: usize, b: usize) -> usize {
|
||||
if a > b { a } else { b }
|
||||
}
|
||||
pub fn partition_labels(s: String) -> Vec<i32> {
|
||||
let s = s.chars().collect::<Vec<char>>();
|
||||
let mut hash: HashMap<char, usize> = HashMap::new();
|
||||
for i in 0..s.len() {
|
||||
hash.insert(s[i], i);
|
||||
let mut hash = vec![0; 26];
|
||||
for (i, &c) in s.as_bytes().iter().enumerate() {
|
||||
hash[(c - b'a') as usize] = i;
|
||||
}
|
||||
let mut result: Vec<i32> = Vec::new();
|
||||
let mut left: usize = 0;
|
||||
let mut right: usize = 0;
|
||||
for i in 0..s.len() {
|
||||
right = Self::max(right, hash[&s[i]]);
|
||||
let mut res = vec![];
|
||||
let (mut left, mut right) = (0, 0);
|
||||
for (i, &c) in s.as_bytes().iter().enumerate() {
|
||||
right = right.max(hash[(c - b'a') as usize]);
|
||||
if i == right {
|
||||
result.push((right - left + 1) as i32);
|
||||
res.push((right - left + 1) as i32);
|
||||
left = i + 1;
|
||||
}
|
||||
}
|
||||
result
|
||||
res
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -535,8 +535,57 @@ function getIndexAfterDel(s: string, startIndex: number): number {
|
||||
}
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
> 双指针
|
||||
|
||||
```rust
|
||||
impl Solution {
|
||||
pub fn backspace_compare(s: String, t: String) -> bool {
|
||||
let (s, t) = (
|
||||
s.chars().collect::<Vec<char>>(),
|
||||
t.chars().collect::<Vec<char>>(),
|
||||
);
|
||||
Self::get_string(s) == Self::get_string(t)
|
||||
}
|
||||
|
||||
pub fn get_string(mut chars: Vec<char>) -> Vec<char> {
|
||||
let mut slow = 0;
|
||||
for i in 0..chars.len() {
|
||||
if chars[i] == '#' {
|
||||
slow = (slow as u32).saturating_sub(1) as usize;
|
||||
} else {
|
||||
chars[slow] = chars[i];
|
||||
slow += 1;
|
||||
}
|
||||
}
|
||||
chars.truncate(slow);
|
||||
chars
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
> 双栈法
|
||||
|
||||
```rust
|
||||
impl Solution {
|
||||
pub fn backspace_compare(s: String, t: String) -> bool {
|
||||
Self::get_string(s) == Self::get_string(t)
|
||||
}
|
||||
|
||||
pub fn get_string(string: String) -> String {
|
||||
let mut s = String::new();
|
||||
for c in string.chars() {
|
||||
if c != '#' {
|
||||
s.push(c);
|
||||
} else if !s.is_empty() {
|
||||
s.pop();
|
||||
}
|
||||
}
|
||||
s
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
|
||||
@ -50,6 +50,10 @@
|
||||
* 0 <= bills.length <= 10000
|
||||
* bills[i] 不是 5 就是 10 或是 20
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,看上去复杂,其实逻辑都是固定的!LeetCode:860.柠檬水找零](https://www.bilibili.com/video/BV12x4y1j7DD),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
这是前几天的leetcode每日一题,感觉不错,给大家讲一下。
|
||||
@ -111,6 +115,9 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
|
||||
@ -38,6 +38,10 @@
|
||||
* 给定树的节点数的范围是 [1, 1000]。
|
||||
* 每个节点的值都是 0。
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,二叉树与贪心的结合,有点难...... LeetCode:968.监督二叉树](https://www.bilibili.com/video/BV1SA411U75i),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
@ -299,6 +303,11 @@ public:
|
||||
|
||||
```
|
||||
|
||||
* 时间复杂度: O(n),需要遍历二叉树上的每个节点
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
|
||||
|
||||
大家可能会惊讶,居然可以这么简短,**其实就是在版本一的基础上,使用else把一些情况直接覆盖掉了**。
|
||||
|
||||
在网上关于这道题解可以搜到很多这种神级别的代码,但都没讲不清楚,如果直接看代码的话,指定越看越晕,**所以建议大家对着版本一的代码一步一步来,版本二中看不中用!**。
|
||||
|
||||
@ -252,6 +252,36 @@ var commonChars = function (words) {
|
||||
}
|
||||
return res
|
||||
};
|
||||
|
||||
// 方法二:map()
|
||||
var commonChars = function(words) {
|
||||
let min_count = new Map()
|
||||
// 统计字符串中字符出现的最小频率,以第一个字符串初始化
|
||||
for(let str of words[0]) {
|
||||
min_count.set(str, ((min_count.get(str) || 0) + 1))
|
||||
}
|
||||
// 从第二个单词开始统计字符出现次数
|
||||
for(let i = 1; i < words.length; i++) {
|
||||
let char_count = new Map()
|
||||
for(let str of words[i]) { // 遍历字母
|
||||
char_count.set(str, (char_count.get(str) || 0) + 1)
|
||||
}
|
||||
// 比较出最小的字符次数
|
||||
for(let value of min_count) { // 注意这里遍历min_count!而不是单词
|
||||
min_count.set(value[0], Math.min((min_count.get(value[0]) || 0), (char_count.get(value[0]) || 0)))
|
||||
}
|
||||
}
|
||||
// 遍历map
|
||||
let res = []
|
||||
min_count.forEach((value, key) => {
|
||||
if(value) {
|
||||
for(let i=0; i<value; i++) {
|
||||
res.push(key)
|
||||
}
|
||||
}
|
||||
})
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
TypeScript
|
||||
|
||||
@ -34,6 +34,10 @@
|
||||
* 1 <= K <= 10000
|
||||
* -100 <= A[i] <= 100
|
||||
|
||||
# 视频讲解
|
||||
|
||||
**《代码随想录》算法视频公开课:[贪心算法,这不就是常识?还能叫贪心?LeetCode:1005.K次取反后最大化的数组和](https://www.bilibili.com/video/BV138411G7LY),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
本题思路其实比较好想了,如何可以让数组和最大呢?
|
||||
@ -81,6 +85,10 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
* 时间复杂度: O(nlogn)
|
||||
* 空间复杂度: O(1)
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
贪心的题目如果简单起来,会让人简单到开始怀疑:本来不就应该这么做么?这也算是算法?我认为这不是贪心?
|
||||
|
||||
@ -62,6 +62,10 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n * m)
|
||||
* 空间复杂度: O(n * m)
|
||||
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
|
||||
@ -77,6 +77,9 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(n)
|
||||
|
||||
|
||||
当然可以拿字符串直接作为栈,这样省去了栈还要转为字符串的操作。
|
||||
|
||||
@ -99,6 +102,8 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1),返回值不计空间复杂度
|
||||
|
||||
## 题外话
|
||||
|
||||
|
||||
@ -124,6 +124,10 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度: O(n * m),其中 n 和 m 分别为 text1 和 text2 的长度
|
||||
* 空间复杂度: O(n * m)
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
@ -54,9 +54,9 @@ int function2(int x, int n) {
|
||||
|
||||
```CPP
|
||||
int function3(int x, int n) {
|
||||
if (n == 0) {
|
||||
return 1;
|
||||
}
|
||||
if (n == 0) return 1;
|
||||
if (n == 1) return x;
|
||||
|
||||
if (n % 2 == 1) {
|
||||
return function3(x, n / 2) * function3(x, n / 2)*x;
|
||||
}
|
||||
@ -93,9 +93,8 @@ int function3(int x, int n) {
|
||||
|
||||
```CPP
|
||||
int function4(int x, int n) {
|
||||
if (n == 0) {
|
||||
return 1;
|
||||
}
|
||||
if (n == 0) return 1;
|
||||
if (n == 1) return x;
|
||||
int t = function4(x, n / 2);// 这里相对于function3,是把这个递归操作抽取出来
|
||||
if (n % 2 == 1) {
|
||||
return t * t * x;
|
||||
@ -124,9 +123,8 @@ int function4(int x, int n) {
|
||||
|
||||
```CPP
|
||||
int function3(int x, int n) {
|
||||
if (n == 0) {
|
||||
return 1;
|
||||
}
|
||||
if (n == 0) return 1;
|
||||
if (n == 1) return x;
|
||||
if (n % 2 == 1) {
|
||||
return function3(x, n / 2) * function3(x, n / 2)*x;
|
||||
}
|
||||
|
||||
@ -146,7 +146,7 @@ public:
|
||||
|
||||
**这也体现了刷题顺序的重要性**。
|
||||
|
||||
先遍历背包,在遍历物品:
|
||||
先遍历背包,再遍历物品:
|
||||
|
||||
```CPP
|
||||
// 版本一
|
||||
@ -165,7 +165,7 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
先遍历物品,在遍历背包:
|
||||
先遍历物品,再遍历背包:
|
||||
|
||||
```CPP
|
||||
// 版本二
|
||||
|
||||
@ -89,7 +89,7 @@
|
||||
在C++中,set 和 map 分别提供以下三种数据结构,其底层实现以及优劣如下表所示:
|
||||
|
||||
| 集合 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|
||||
| ------------------ | -------- | -------- | ---------------- | ------------ | -------- | -------- |
|
||||
| --- | --- | ---- | --- | --- | --- | --- |
|
||||
| std::set | 红黑树 | 有序 | 否 | 否 | O(log n) | O(log n) |
|
||||
| std::multiset | 红黑树 | 有序 | 是 | 否 | O(logn) | O(logn) |
|
||||
| std::unordered_set | 哈希表 | 无序 | 否 | 否 | O(1) | O(1) |
|
||||
@ -97,11 +97,12 @@
|
||||
std::unordered_set底层实现为哈希表,std::set 和std::multiset 的底层实现是红黑树,红黑树是一种平衡二叉搜索树,所以key值是有序的,但key不可以修改,改动key值会导致整棵树的错乱,所以只能删除和增加。
|
||||
|
||||
| 映射 | 底层实现 | 是否有序 | 数值是否可以重复 | 能否更改数值 | 查询效率 | 增删效率 |
|
||||
| ------------------ | -------- | -------- | ---------------- | ------------ | -------- | -------- |
|
||||
| --- | --- | --- | --- | --- | --- | --- |
|
||||
| std::map | 红黑树 | key有序 | key不可重复 | key不可修改 | O(logn) | O(logn) |
|
||||
| std::multimap | 红黑树 | key有序 | key可重复 | key不可修改 | O(log n) | O(log n) |
|
||||
| std::unordered_map | 哈希表 | key无序 | key不可重复 | key不可修改 | O(1) | O(1) |
|
||||
|
||||
|
||||
std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底层实现是红黑树。同理,std::map 和std::multimap 的key也是有序的(这个问题也经常作为面试题,考察对语言容器底层的理解)。
|
||||
|
||||
当我们要使用集合来解决哈希问题的时候,优先使用unordered_set,因为它的查询和增删效率是最优的,如果需要集合是有序的,那么就用set,如果要求不仅有序还要有重复数据的话,那么就用multiset。
|
||||
|
||||
@ -177,6 +177,35 @@ Java:
|
||||
|
||||
Python:
|
||||
|
||||
Rust:
|
||||
|
||||
```rust
|
||||
// 版本二,使用list(链表)
|
||||
use std::collections::LinkedList;
|
||||
impl Solution{
|
||||
pub fn reconstruct_queue(mut people: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
|
||||
let mut queue = LinkedList::new();
|
||||
people.sort_by(|a, b| {
|
||||
if a[0] == b[0] {
|
||||
return a[1].cmp(&b[1]);
|
||||
}
|
||||
b[0].cmp(&a[0])
|
||||
});
|
||||
queue.push_back(people[0].clone());
|
||||
for v in people.iter().skip(1) {
|
||||
if queue.len() > v[1] as usize {
|
||||
let mut back_link = queue.split_off(v[1] as usize);
|
||||
queue.push_back(v.clone());
|
||||
queue.append(&mut back_link);
|
||||
} else {
|
||||
queue.push_back(v.clone());
|
||||
}
|
||||
}
|
||||
queue.into_iter().collect()
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
Go:
|
||||
|
||||
|
||||
@ -41,7 +41,7 @@
|
||||
* [动态规划:关于01背包问题,你该了解这些!](https://programmercarl.com/背包理论基础01背包-1.html)
|
||||
* [动态规划:关于01背包问题,你该了解这些!(滚动数组)](https://programmercarl.com/背包理论基础01背包-2.html)
|
||||
|
||||
首先在回顾一下01背包的核心代码
|
||||
首先再回顾一下01背包的核心代码
|
||||
```cpp
|
||||
for(int i = 0; i < weight.size(); i++) { // 遍历物品
|
||||
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
|
||||
@ -173,7 +173,7 @@ int main() {
|
||||
|
||||
别急,下一篇就是了!哈哈
|
||||
|
||||
最后,**又可以出一道面试题了,就是纯完全背包,要求先用二维dp数组实现,然后再用一维dp数组实现,最后在问,两个for循环的先后是否可以颠倒?为什么?**
|
||||
最后,**又可以出一道面试题了,就是纯完全背包,要求先用二维dp数组实现,然后再用一维dp数组实现,最后再问,两个for循环的先后是否可以颠倒?为什么?**
|
||||
这个简单的完全背包问题,估计就可以难住不少候选人了。
|
||||
|
||||
|
||||
|
||||
Reference in New Issue
Block a user