Update

problems/0416.分割等和子集.md

@@ -60,7 +60,7 @@
 * [动态规划：关于01背包问题，你该了解这些！](https://programmercarl.com/背包理论基础01背包-1.html)
 * [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)
 
-### 01背包问题
+## 01背包问题
 
 01背包问题，大家都知道，有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
 
@@ -92,7 +92,7 @@
 
 动规五部曲分析如下：
 
-1. 确定dp数组以及下标的含义
+### 1. 确定dp数组以及下标的含义
 
 01背包中，dp[j] 表示： 容量（所能装的重量）为j的背包，所背的物品价值最大可以为dp[j]。
 
@@ -104,7 +104,7 @@
 
 而dp[6] 就可以等于6了，放进1 和 5，那么dp[6] == 6，说明背包装满了。
 
-2. 确定递推公式
+### 2. 确定递推公式
 
 01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
 
@@ -113,7 +113,7 @@
 所以递推公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
 
 
-3. dp数组如何初始化
+### 3. dp数组如何初始化
 
 在01背包，一维dp如何初始化，已经讲过，
 
@@ -133,7 +133,7 @@
 vector<int> dp(10001, 0);
 ```
 
-4. 确定遍历顺序
+### 4. 确定遍历顺序
 
 在[动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://programmercarl.com/背包理论基础01背包-2.html)中就已经说明：如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！
 
@@ -148,7 +148,7 @@ for(int i = 0; i < nums.size(); i++) {
 }
 ```
 
-5. 举例推导dp数组
+### 5. 举例推导dp数组
 
 dp[j]的数值一定是小于等于j的。
 

problems/0695.岛屿的最大面积.md

@@ -44,7 +44,7 @@
 
 这里其实涉及到dfs的两种写法。
 
-写法一，dfs只处理下一个节点，即在主函数遇到岛屿就计数为1，dfs处理接下来的相邻陆地
+写法一，dfs处理当前节点的相邻节点，即在主函数遇到岛屿就计数为1，dfs处理接下来的相邻陆地
 
 ```CPP 
 // 版本一
@@ -87,7 +87,7 @@ public:
 };
 ```
 
-写法二，dfs处理当前节点，即即在主函数遇到岛屿就计数为0，dfs处理接下来的全部陆地
+写法二，dfs处理当前节点，即在主函数遇到岛屿就计数为0，dfs处理接下来的全部陆地
 
 dfs 
 ```CPP 

problems/kamacoder/0098.所有可达路径.md

@@ -7,7 +7,7 @@
 
 【题目描述】
 
-给定一个有 n 个节点的有向无环图，节点编号从 1 到 n。请编写一个函数，找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
+给定一个有 n 个节点的有向无环图，节点编号从 1 到 n。请编写一个程序，找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
 
 【输入描述】
 

problems/kamacoder/0099.岛屿的数量广搜.md

@@ -72,7 +72,7 @@
 
 如果从队列拿出节点，再去标记这个节点走过，就会发生下图所示的结果，会导致很多节点重复加入队列。
 
-![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220727100846.png)
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20250124094043.png)
 
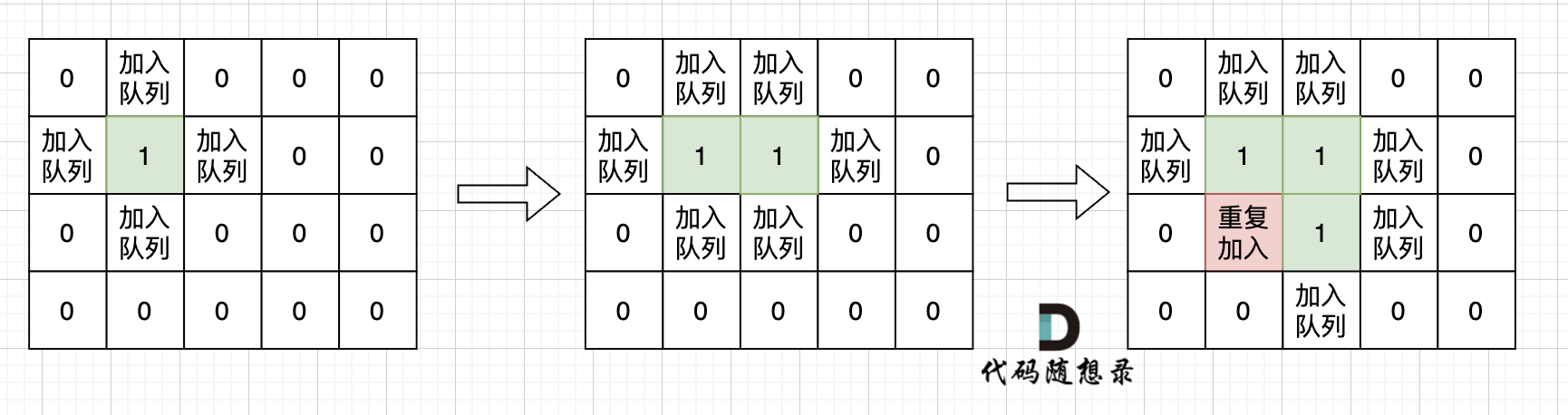
 超时写法 （从队列中取出节点再标记，注意代码注释的地方）
 

problems/kamacoder/0100.岛屿的最大面积.md

@@ -63,7 +63,7 @@
 
 这里其实涉及到dfs的两种写法。
 
-写法一，dfs只处理下一个节点，即在主函数遇到岛屿就计数为1，dfs处理接下来的相邻陆地
+写法一，dfs处理当前节点的相邻节点，即在主函数遇到岛屿就计数为1，dfs处理接下来的相邻陆地
 
 ```CPP 
 // 版本一

problems/kamacoder/0101.孤岛的总面积.md

@@ -72,10 +72,8 @@
 #include <vector>
 using namespace std;
 int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
-int count; // 统计符合题目要求的陆地空格数量
 void dfs(vector<vector<int>>& grid, int x, int y) {
     grid[x][y] = 0;
-    count++;
     for (int i = 0; i < 4; i++) { // 向四个方向遍历
         int nextx = x + dir[i][0];
         int nexty = y + dir[i][1];
@@ -109,16 +107,17 @@ int main() {
         if (grid[0][j] == 1) dfs(grid, 0, j);
         if (grid[n - 1][j] == 1) dfs(grid, n - 1, j);
     }
-    count = 0;
+    int count = 0;
     for (int i = 0; i < n; i++) {
         for (int j = 0; j < m; j++) {
-            if (grid[i][j] == 1) dfs(grid, i, j);
+            if (grid[i][j] == 1) count++;
         }
     }
     cout << count << endl;
 }
 ```
 
+
 采用广度优先搜索的代码如下：
 
 ```CPP 
@@ -126,13 +125,11 @@ int main() {
 #include <vector>
 #include <queue>
 using namespace std;
-int count = 0;
 int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
 void bfs(vector<vector<int>>& grid, int x, int y) {
     queue<pair<int, int>> que;
     que.push({x, y});
     grid[x][y] = 0; // 只要加入队列，立刻标记
-    count++;
     while(!que.empty()) {
         pair<int ,int> cur = que.front(); que.pop();
         int curx = cur.first;
@@ -143,7 +140,6 @@ void bfs(vector<vector<int>>& grid, int x, int y) {
             if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 越界了，直接跳过
             if (grid[nextx][nexty] == 1) {
                 que.push({nextx, nexty});
-                count++;
                 grid[nextx][nexty] = 0; // 只要加入队列立刻标记
             }
         }
@@ -169,15 +165,16 @@ int main() {
         if (grid[0][j] == 1) bfs(grid, 0, j);
         if (grid[n - 1][j] == 1) bfs(grid, n - 1, j);
     }
-    count = 0;
+    int count = 0;
     for (int i = 0; i < n; i++) {
         for (int j = 0; j < m; j++) {
-            if (grid[i][j] == 1) bfs(grid, i, j);
+            if (grid[i][j] == 1) count++;
         }
     }
 
     cout << count << endl;
 }
+
 ```
 
 

problems/kamacoder/图论深搜理论基础.md

@@ -162,7 +162,7 @@ if (终止条件) {
 
 终止添加不仅是结束本层递归，同时也是我们收获结果的时候。 
 
-另外，其实很多dfs写法，没有写终止条件，其实终止条件写在了， 下面dfs递归的逻辑里了，也就是不符合条件，直接不会向下递归。这里如果大家不理解的话，没关系，后面会有具体题目来讲解。
+另外，其实很多dfs写法，没有写终止条件，其实终止条件写在了， 隐藏在下面dfs递归的逻辑里了，也就是不符合条件，直接不会向下递归。这里如果大家不理解的话，没关系，后面会有具体题目来讲解。
 
 3. 处理目前搜索节点出发的路径 
 

problems/kamacoder/图论理论基础.md

@@ -128,6 +128,29 @@
 
 主要是 朴素存储、邻接表和邻接矩阵。 
 
+关于朴素存储，这是我自创的名字，因为这种存储方式，就是将所有边存下来。 
+
+例如图：  
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240511112951.png)
+
+图中有8条边，我们就定义 8 * 2的数组，即有n条边就申请n * 2，这么大的数组： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20250110114348.png)
+
+数组第一行：6 7，就表示节点6 指向 节点7，以此类推。 
+
+当然可以不用数组，用map，或者用 类 到可以表示出 这种边的关系。
+
+这种表示方式的好处就是直观，把节点与节点之间关系很容易展现出来。
+
+但如果我们想知道 节点1 和 节点6 是否相连，我们就需要把存储空间都枚举一遍才行。
+
+这是明显的缺点，同时，我们在深搜和广搜的时候，都不会使用这种存储方式。
+
+因为 搜索中，需要知道 节点与其他节点的链接情况，而这种朴素存储，都需要全部枚举才知道链接情况。 
+
+在图论章节的后面文章讲解中，我会举例说明的。大家先有个印象。
 
 ### 邻接矩阵