mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-10 04:06:51 +08:00
Merge branch 'youngyangyang04:master' into master
This commit is contained in:
46
README.md
46
README.md
@ -132,6 +132,7 @@
|
||||
8. [计算机专业要不要读研!](https://mp.weixin.qq.com/s/c9v1L3IjqiXtkNH7sOMAdg)
|
||||
9. [秋招和提前批都越来越提前了....](https://mp.weixin.qq.com/s/SNFiRDx8CKyjhTPlys6ywQ)
|
||||
10. [你的简历里「专业技能」写的够专业么?](https://mp.weixin.qq.com/s/bp6y-e5FVN28H9qc8J9zrg)
|
||||
11. [对于秋招,实习生也有烦恼....](https://mp.weixin.qq.com/s/ka07IPryFnfmIjByFFcXDg)
|
||||
|
||||
|
||||
## 数组
|
||||
@ -274,10 +275,10 @@
|
||||
16. [回溯算法:排列问题(二)](./problems/0047.全排列II.md)
|
||||
17. [本周小结!(回溯算法系列三)](./problems/周总结/20201112回溯周末总结.md)
|
||||
18. [回溯算法去重问题的另一种写法](./problems/回溯算法去重问题的另一种写法.md)
|
||||
23. [回溯算法:重新安排行程](./problems/0332.重新安排行程.md)
|
||||
24. [回溯算法:N皇后问题](./problems/0051.N皇后.md)
|
||||
25. [回溯算法:解数独](./problems/0037.解数独.md)
|
||||
26. [一篇总结带你彻底搞透回溯算法!](./problems/回溯总结.md)
|
||||
19. [回溯算法:重新安排行程](./problems/0332.重新安排行程.md)
|
||||
20. [回溯算法:N皇后问题](./problems/0051.N皇后.md)
|
||||
21. [回溯算法:解数独](./problems/0037.解数独.md)
|
||||
22. [一篇总结带你彻底搞透回溯算法!](./problems/回溯总结.md)
|
||||
|
||||
## 贪心算法
|
||||
|
||||
@ -364,40 +365,43 @@
|
||||
|
||||
32. [动态规划:买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
|
||||
33. [动态规划:本周我们都讲了这些(系列六)](./problems/周总结/20210225动规周末总结.md)
|
||||
33. [动态规划:买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II(动态规划).md)
|
||||
34. [动态规划:买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
|
||||
35. [动态规划:买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
|
||||
36. [动态规划:最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
|
||||
37. [动态规划:本周我们都讲了这些(系列七)](./problems/周总结/20210304动规周末总结.md)
|
||||
38. [动态规划:买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费(动态规划).md)
|
||||
39. [动态规划:股票系列总结篇](./problems/动态规划-股票问题总结篇.md)
|
||||
34. [动态规划:买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II(动态规划).md)
|
||||
35. [动态规划:买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
|
||||
36. [动态规划:买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
|
||||
37. [动态规划:最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
|
||||
38. [动态规划:本周我们都讲了这些(系列七)](./problems/周总结/20210304动规周末总结.md)
|
||||
39. [动态规划:买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费(动态规划).md)
|
||||
40. [动态规划:股票系列总结篇](./problems/动态规划-股票问题总结篇.md)
|
||||
|
||||
子序列系列:
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/动态规划-子序列问题总结.jpg' width=500 alt=''> </img></div>
|
||||
|
||||
|
||||
40. [动态规划:最长递增子序列](./problems/0300.最长上升子序列.md)
|
||||
41. [动态规划:最长连续递增序列](./problems/0674.最长连续递增序列.md)
|
||||
42. [动态规划:最长重复子数组](./problems/0718.最长重复子数组.md)
|
||||
43. [动态规划:最长公共子序列](./problems/1143.最长公共子序列.md)
|
||||
41. [动态规划:最长递增子序列](./problems/0300.最长上升子序列.md)
|
||||
42. [动态规划:最长连续递增序列](./problems/0674.最长连续递增序列.md)
|
||||
43. [动态规划:最长重复子数组](./problems/0718.最长重复子数组.md)
|
||||
44. [动态规划:最长公共子序列](./problems/1143.最长公共子序列.md)
|
||||
45. [动态规划:不相交的线](./problems/1035.不相交的线.md)
|
||||
46. [动态规划:最大子序和](./problems/0053.最大子序和(动态规划).md)
|
||||
47. [动态规划:判断子序列](./problems/0392.判断子序列.md)
|
||||
48. [动态规划:不同的子序列](./problems/0115.不同的子序列.md)
|
||||
49. [动态规划:两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
|
||||
51. [动态规划:编辑距离](./problems/0072.编辑距离.md)
|
||||
52. [为了绝杀编辑距离,Carl做了三步铺垫,你都知道么?](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
|
||||
53. [动态规划:回文子串](./problems/0647.回文子串.md)
|
||||
54. [动态规划:最长回文子序列](./problems/0516.最长回文子序列.md)
|
||||
55. [动态规划总结篇](./problems/动态规划总结篇.md)
|
||||
50. [动态规划:编辑距离](./problems/0072.编辑距离.md)
|
||||
51. [为了绝杀编辑距离,Carl做了三步铺垫,你都知道么?](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
|
||||
52. [动态规划:回文子串](./problems/0647.回文子串.md)
|
||||
53. [动态规划:最长回文子序列](./problems/0516.最长回文子序列.md)
|
||||
54. [动态规划总结篇](./problems/动态规划总结篇.md)
|
||||
|
||||
(持续更新中....)
|
||||
|
||||
## 单调栈
|
||||
|
||||
1. [单调栈:每日温度](./problems/0739.每日温度.md)
|
||||
2. [单调栈:下一个更大元素I](./problems/0496.下一个更大元素I.md)
|
||||
3. [单调栈:下一个更大元素II](./problems/0503.下一个更大元素II.md)
|
||||
4. [单调栈:接雨水](./problems/0042.接雨水.md)
|
||||
|
||||
(持续更新中....)
|
||||
|
||||
## 图论
|
||||
|
||||
|
||||
357
problems/0042.接雨水.md
Normal file
357
problems/0042.接雨水.md
Normal file
@ -0,0 +1,357 @@
|
||||
|
||||
|
||||
# 42. 接雨水
|
||||
|
||||
题目链接:https://leetcode-cn.com/problems/trapping-rain-water/
|
||||
|
||||
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
|
||||
|
||||
示例 1:
|
||||
|
||||

|
||||
|
||||
* 输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
|
||||
* 输出:6
|
||||
* 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
|
||||
|
||||
示例 2:
|
||||
|
||||
* 输入:height = [4,2,0,3,2,5]
|
||||
* 输出:9
|
||||
|
||||
|
||||
# 思路
|
||||
|
||||
接雨水问题在面试中还是常见题目的,有必要好好讲一讲。
|
||||
|
||||
本文深度讲解如下三种方法:
|
||||
* 双指针法
|
||||
* 动态规划
|
||||
* 单调栈
|
||||
|
||||
## 双指针解法
|
||||
|
||||
这道题目使用双指针法并不简单,我们来看一下思路。
|
||||
|
||||
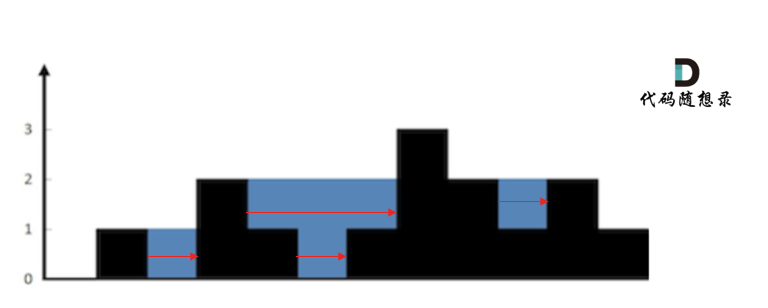
首先要明确,要按照行来计算,还是按照列来计算。
|
||||
|
||||
按照行来计算如图:
|
||||
|
||||
|
||||
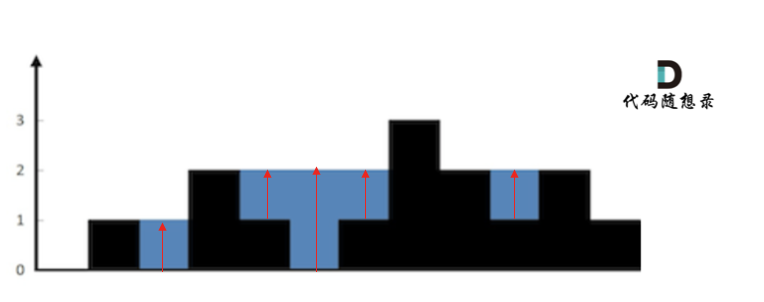
按照列来计算如图:
|
||||
|
||||
|
||||
一些同学在实现的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
|
||||
|
||||
我个人倾向于按照列来计算,比较容易理解,接下来看一下按照列如何计算。
|
||||
|
||||
首先,**如果按照列来计算的话,宽度一定是1了,我们再把每一列的雨水的高度求出来就可以了。**
|
||||
|
||||
可以看出每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
|
||||
|
||||
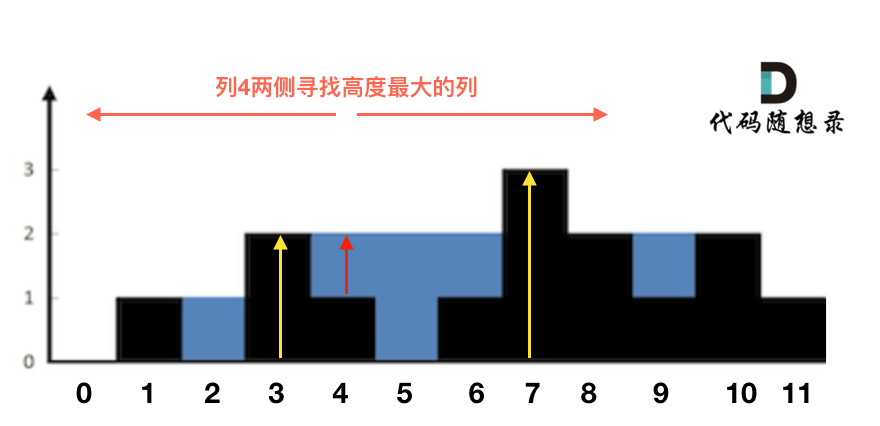
这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
|
||||
|
||||
|
||||
|
||||
列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
|
||||
|
||||
列4 右侧最高的柱子是列7,高度为3(以下用rHeight表示)。
|
||||
|
||||
列4 柱子的高度为1(以下用height表示)
|
||||
|
||||
那么列4的雨水高度为 列3和列7的高度最小值减列4高度,即: min(lHeight, rHeight) - height。
|
||||
|
||||
列4的雨水高度求出来了,宽度为1,相乘就是列4的雨水体积了。
|
||||
|
||||
此时求出了列4的雨水体积。
|
||||
|
||||
一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
|
||||
|
||||
首先从头遍历所有的列,并且**要注意第一个柱子和最后一个柱子不接雨水**,代码如下:
|
||||
```C++
|
||||
for (int i = 0; i < height.size(); i++) {
|
||||
// 第一个柱子和最后一个柱子不接雨水
|
||||
if (i == 0 || i == height.size() - 1) continue;
|
||||
}
|
||||
```
|
||||
|
||||
在for循环中求左右两边最高柱子,代码如下:
|
||||
|
||||
```C++
|
||||
int rHeight = height[i]; // 记录右边柱子的最高高度
|
||||
int lHeight = height[i]; // 记录左边柱子的最高高度
|
||||
for (int r = i + 1; r < height.size(); r++) {
|
||||
if (height[r] > rHeight) rHeight = height[r];
|
||||
}
|
||||
for (int l = i - 1; l >= 0; l--) {
|
||||
if (height[l] > lHeight) lHeight = height[l];
|
||||
}
|
||||
```
|
||||
|
||||
最后,计算该列的雨水高度,代码如下:
|
||||
|
||||
```C++
|
||||
int h = min(lHeight, rHeight) - height[i];
|
||||
if (h > 0) sum += h; // 注意只有h大于零的时候,在统计到总和中
|
||||
```
|
||||
|
||||
整体代码如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int trap(vector<int>& height) {
|
||||
int sum = 0;
|
||||
for (int i = 0; i < height.size(); i++) {
|
||||
// 第一个柱子和最后一个柱子不接雨水
|
||||
if (i == 0 || i == height.size() - 1) continue;
|
||||
|
||||
int rHeight = height[i]; // 记录右边柱子的最高高度
|
||||
int lHeight = height[i]; // 记录左边柱子的最高高度
|
||||
for (int r = i + 1; r < height.size(); r++) {
|
||||
if (height[r] > rHeight) rHeight = height[r];
|
||||
}
|
||||
for (int l = i - 1; l >= 0; l--) {
|
||||
if (height[l] > lHeight) lHeight = height[l];
|
||||
}
|
||||
int h = min(lHeight, rHeight) - height[i];
|
||||
if (h > 0) sum += h;
|
||||
}
|
||||
return sum;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
因为每次遍历列的时候,还要向两边寻找最高的列,所以时间复杂度为O(n^2)。
|
||||
空间复杂度为O(1)。
|
||||
|
||||
## 动态规划解法
|
||||
|
||||
在上一节的双指针解法中,我们可以看到只要记录左边柱子的最高高度 和 右边柱子的最高高度,就可以计算当前位置的雨水面积,这就是通过列来计算。
|
||||
|
||||
当前列雨水面积:min(左边柱子的最高高度,记录右边柱子的最高高度) - 当前柱子高度。
|
||||
|
||||
为了的到两边的最高高度,使用了双指针来遍历,每到一个柱子都向两边遍历一遍,这其实是有重复计算的。我们把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight)。这样就避免了重复计算,这就用到了动态规划。
|
||||
|
||||
当前位置,左边的最高高度是前一个位置的左边最高高度和本高度的最大值。
|
||||
|
||||
即从左向右遍历:maxLeft[i] = max(height[i], maxLeft[i - 1]);
|
||||
|
||||
从右向左遍历:maxRight[i] = max(height[i], maxRight[i + 1]);
|
||||
|
||||
这样就找到递推公式。
|
||||
|
||||
代码如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int trap(vector<int>& height) {
|
||||
if (height.size() <= 2) return 0;
|
||||
vector<int> maxLeft(height.size(), 0);
|
||||
vector<int> maxRight(height.size(), 0);
|
||||
int size = maxRight.size();
|
||||
|
||||
// 记录每个柱子左边柱子最大高度
|
||||
maxLeft[0] = height[0];
|
||||
for (int i = 1; i < size; i++) {
|
||||
maxLeft[i] = max(height[i], maxLeft[i - 1]);
|
||||
}
|
||||
// 记录每个柱子右边柱子最大高度
|
||||
maxRight[size - 1] = height[size - 1];
|
||||
for (int i = size - 2; i >= 0; i--) {
|
||||
maxRight[i] = max(height[i], maxRight[i + 1]);
|
||||
}
|
||||
// 求和
|
||||
int sum = 0;
|
||||
for (int i = 0; i < size; i++) {
|
||||
int count = min(maxLeft[i], maxRight[i]) - height[i];
|
||||
if (count > 0) sum += count;
|
||||
}
|
||||
return sum;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
## 单调栈解法
|
||||
|
||||
这个解法可以说是最不好理解的了,所以下面我花了大量的篇幅来介绍这种方法。
|
||||
|
||||
单调栈就是保持栈内元素有序。和[栈与队列:单调队列](https://mp.weixin.qq.com/s/Xgcqx5eBa3xZabt_LurnNQ)一样,需要我们自己维持顺序,没有现成的容器可以用。
|
||||
|
||||
|
||||
### 准备工作
|
||||
|
||||
那么本题使用单调栈有如下几个问题:
|
||||
|
||||
1. 首先单调栈是按照行方向来计算雨水,如图:
|
||||
|
||||

|
||||
|
||||
知道这一点,后面的就可以理解了。
|
||||
|
||||
2. 使用单调栈内元素的顺序
|
||||
|
||||
从大到小还是从小打到呢?
|
||||
|
||||
从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。
|
||||
|
||||
因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
|
||||
|
||||
如图:
|
||||
|
||||

|
||||
|
||||
|
||||
3. 遇到相同高度的柱子怎么办。
|
||||
|
||||
遇到相同的元素,更新栈内下标,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。
|
||||
|
||||
例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出,把第二个5添加到栈中。
|
||||
|
||||
**因为我们要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度**。
|
||||
|
||||
如图所示:
|
||||
|
||||

|
||||
|
||||
4. 栈里要保存什么数值
|
||||
|
||||
是用单调栈,其实是通过 长 * 宽 来计算雨水面积的。
|
||||
|
||||
长就是通过柱子的高度来计算,宽是通过柱子之间的下标来计算,
|
||||
|
||||
那么栈里有没有必要存一个pair<int, int>类型的元素,保存柱子的高度和下标呢。
|
||||
|
||||
其实不用,栈里就存放int类型的元素就行了,表示下标,想要知道对应的高度,通过height[stack.top()] 就知道弹出的下标对应的高度了。
|
||||
|
||||
所以栈的定义如下:
|
||||
|
||||
```
|
||||
stack<int> st; // 存着下标,计算的时候用下标对应的柱子高度
|
||||
```
|
||||
|
||||
明确了如上几点,我们再来看处理逻辑。
|
||||
|
||||
### 单调栈处理逻辑
|
||||
|
||||
先将下标0的柱子加入到栈中,`st.push(0);`。
|
||||
|
||||
然后开始从下标1开始遍历所有的柱子,`for (int i = 1; i < height.size(); i++)`。
|
||||
|
||||
如果当前遍历的元素(柱子)高度小于栈顶元素的高度,就把这个元素加入栈中,因为栈里本来就要保持从小到大的顺序(从栈头到栈底)。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
if (height[i] < height[st.top()]) st.push(i);
|
||||
```
|
||||
|
||||
如果当前遍历的元素(柱子)高度等于栈顶元素的高度,要跟更新栈顶元素,因为遇到相相同高度的柱子,需要使用最右边的柱子来计算宽度。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况
|
||||
st.pop();
|
||||
st.push(i);
|
||||
}
|
||||
```
|
||||
|
||||
如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:
|
||||
|
||||

|
||||
|
||||
取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下标记为mid,对应的高度为height[mid](就是图中的高度1)。
|
||||
|
||||
此时的栈顶元素st.top(),就是凹槽的左边位置,下标为st.top(),对应的高度为height[st.top()](就是图中的高度2)。
|
||||
|
||||
当前遍历的元素i,就是凹槽右边的位置,下标为i,对应的高度为height[i](就是图中的高度3)。
|
||||
|
||||
此时大家应该可以发现其实就是**栈顶和栈顶的下一个元素以及要入栈的三个元素来接水!**
|
||||
|
||||
那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:`int h = min(height[st.top()], height[i]) - height[mid];`
|
||||
|
||||
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度),代码为:`int w = i - st.top() - 1 ;`
|
||||
|
||||
当前凹槽雨水的体积就是:`h * w`。
|
||||
|
||||
求当前凹槽雨水的体积代码如下:
|
||||
|
||||
```C++
|
||||
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while,持续跟新栈顶元素
|
||||
int mid = st.top();
|
||||
st.pop();
|
||||
if (!st.empty()) {
|
||||
int h = min(height[st.top()], height[i]) - height[mid];
|
||||
int w = i - st.top() - 1; // 注意减一,只求中间宽度
|
||||
sum += h * w;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
关键部分讲完了,整体代码如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int trap(vector<int>& height) {
|
||||
if (height.size() <= 2) return 0; // 可以不加
|
||||
stack<int> st; // 存着下标,计算的时候用下标对应的柱子高度
|
||||
st.push(0);
|
||||
int sum = 0;
|
||||
for (int i = 1; i < height.size(); i++) {
|
||||
if (height[i] < height[st.top()]) { // 情况一
|
||||
st.push(i);
|
||||
} if (height[i] == height[st.top()]) { // 情况二
|
||||
st.pop(); // 其实这一句可以不加,效果是一样的,但处理相同的情况的思路却变了。
|
||||
st.push(i);
|
||||
} else { // 情况三
|
||||
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while
|
||||
int mid = st.top();
|
||||
st.pop();
|
||||
if (!st.empty()) {
|
||||
int h = min(height[st.top()], height[i]) - height[mid];
|
||||
int w = i - st.top() - 1; // 注意减一,只求中间宽度
|
||||
sum += h * w;
|
||||
}
|
||||
}
|
||||
st.push(i);
|
||||
}
|
||||
}
|
||||
return sum;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
以上代码冗余了一些,但是思路是清晰的,下面我将代码精简一下,如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int trap(vector<int>& height) {
|
||||
stack<int> st;
|
||||
st.push(0);
|
||||
int sum = 0;
|
||||
for (int i = 1; i < height.size(); i++) {
|
||||
while (!st.empty() && height[i] > height[st.top()]) {
|
||||
int mid = st.top();
|
||||
st.pop();
|
||||
if (!st.empty()) {
|
||||
int h = min(height[st.top()], height[i]) - height[mid];
|
||||
int w = i - st.top() - 1;
|
||||
sum += h * w;
|
||||
}
|
||||
}
|
||||
st.push(i);
|
||||
}
|
||||
return sum;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
精简之后的代码,大家就看不出去三种情况的处理了,貌似好像只处理的情况三,其实是把情况一和情况二融合了。 这样的代码不太利于理解。
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
@ -5,6 +5,7 @@
|
||||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a>
|
||||
</p>
|
||||
<p align="center"><strong>欢迎大家<a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
# 排列问题(二)
|
||||
|
||||
## 47.全排列 II
|
||||
@ -222,6 +223,43 @@ class Solution:
|
||||
return res
|
||||
```
|
||||
|
||||
Go:
|
||||
|
||||
```go
|
||||
var res [][]int
|
||||
func permute(nums []int) [][]int {
|
||||
res = [][]int{}
|
||||
sort.Ints(nums)
|
||||
dfs(nums, make([]int, 0), make([]bool, len(nums)))
|
||||
return res
|
||||
}
|
||||
|
||||
func dfs(nums, path []int, used []bool) {
|
||||
if len(path) == len(nums) {
|
||||
res = append(res, append([]int{}, path...))
|
||||
return
|
||||
}
|
||||
|
||||
m := make(map[int]bool)
|
||||
for i := 0; i < len(nums); i++ {
|
||||
// used 从剩余 nums 中选
|
||||
if used[i] {
|
||||
continue
|
||||
}
|
||||
// m 集合间去重
|
||||
if _, ok := m[nums[i]]; ok {
|
||||
continue
|
||||
}
|
||||
m[nums[i]] = true
|
||||
path = append(path, nums[i])
|
||||
used[i] = true
|
||||
dfs(nums, path, used)
|
||||
used[i] = false
|
||||
path = path[:len(path)-1]
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Javascript:
|
||||
|
||||
```javascript
|
||||
@ -258,7 +296,45 @@ var permuteUnique = function (nums) {
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
Go:
|
||||
回溯+本层去重+下层去重
|
||||
```golang
|
||||
func permuteUnique(nums []int) [][]int {
|
||||
var subRes []int
|
||||
var res [][]int
|
||||
sort.Ints(nums)
|
||||
used:=make([]bool,len(nums))
|
||||
backTring(nums,subRes,&res,used)
|
||||
return res
|
||||
}
|
||||
func backTring(nums,subRes []int,res *[][]int,used []bool){
|
||||
if len(subRes)==len(nums){
|
||||
tmp:=make([]int,len(nums))
|
||||
copy(tmp,subRes)
|
||||
*res=append(*res,tmp)
|
||||
return
|
||||
}
|
||||
// used[i - 1] == true,说明同一树支candidates[i - 1]使用过
|
||||
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
|
||||
for i:=0;i<len(nums);i++{
|
||||
if i>0&&nums[i]==nums[i-1]&&used[i-1]==false{//当本层元素相同且前一个被使用过,则继续向后找(本层去重)
|
||||
continue
|
||||
}
|
||||
//到达这里有两种情况:1.该层前后元素不同;2.该层前后元素相同但该层没有使用过
|
||||
//所以只能对该层没有被使用过的抽取
|
||||
if used[i]==false{
|
||||
//首先将该元素置为使用过(即同一树枝使用过),下一层的元素就不能选择重复使用过的元素(下层去重)
|
||||
used[i]=true
|
||||
subRes=append(subRes,nums[i])
|
||||
backTring(nums,subRes,res,used)
|
||||
//回溯
|
||||
//回溯回来,将该元素置为false,表示该元素在该层使用过
|
||||
used[i]=false
|
||||
subRes=subRes[:len(subRes)-1]
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
@ -307,6 +307,32 @@ func Min(args ...int) int {
|
||||
```
|
||||
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
const minDistance = (word1, word2) => {
|
||||
let dp = Array.from(Array(word1.length + 1), () => Array(word2.length+1).fill(0));
|
||||
|
||||
for(let i = 1; i <= word1.length; i++) {
|
||||
dp[i][0] = i;
|
||||
}
|
||||
|
||||
for(let j = 1; j <= word2.length; j++) {
|
||||
dp[0][j] = j;
|
||||
}
|
||||
|
||||
for(let i = 1; i <= word1.length; i++) {
|
||||
for(let j = 1; j <= word2.length; j++) {
|
||||
if(word1[i-1] === word2[j-1]) {
|
||||
dp[i][j] = dp[i-1][j-1];
|
||||
} else {
|
||||
dp[i][j] = Math.min(dp[i-1][j] + 1, dp[i][j-1] + 1, dp[i-1][j-1] + 1);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return dp[word1.length][word2.length];
|
||||
};
|
||||
```
|
||||
|
||||
-----------------------
|
||||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||||
|
||||
@ -32,7 +32,7 @@
|
||||
|
||||
可以递归中序遍历将二叉搜索树转变成一个数组,代码如下:
|
||||
|
||||
```
|
||||
```C++
|
||||
vector<int> vec;
|
||||
void traversal(TreeNode* root) {
|
||||
if (root == NULL) return;
|
||||
@ -44,7 +44,7 @@ void traversal(TreeNode* root) {
|
||||
|
||||
然后只要比较一下,这个数组是否是有序的,**注意二叉搜索树中不能有重复元素**。
|
||||
|
||||
```
|
||||
```C++
|
||||
traversal(root);
|
||||
for (int i = 1; i < vec.size(); i++) {
|
||||
// 注意要小于等于,搜索树里不能有相同元素
|
||||
@ -55,7 +55,7 @@ return true;
|
||||
|
||||
整体代码如下:
|
||||
|
||||
```
|
||||
```C++
|
||||
class Solution {
|
||||
private:
|
||||
vector<int> vec;
|
||||
@ -162,7 +162,8 @@ return left && right;
|
||||
```
|
||||
|
||||
整体代码如下:
|
||||
```
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
long long maxVal = LONG_MIN; // 因为后台测试数据中有int最小值
|
||||
@ -188,7 +189,7 @@ public:
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
TreeNode* pre = NULL; // 用来记录前一个节点
|
||||
@ -213,7 +214,7 @@ public:
|
||||
|
||||
迭代法中序遍历稍加改动就可以了,代码如下:
|
||||
|
||||
```
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
bool isValidBST(TreeNode* root) {
|
||||
@ -343,7 +344,7 @@ Python:
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
//递归法
|
||||
# 递归法
|
||||
class Solution:
|
||||
def isValidBST(self, root: TreeNode) -> bool:
|
||||
res = [] //把二叉搜索树按中序遍历写成list
|
||||
@ -355,6 +356,35 @@ class Solution:
|
||||
return res
|
||||
buildalist(root)
|
||||
return res == sorted(res) and len(set(res)) == len(res) //检查list里的数有没有重复元素,以及是否按从小到大排列
|
||||
|
||||
# 简单递归法
|
||||
class Solution:
|
||||
def isValidBST(self, root: TreeNode) -> bool:
|
||||
def isBST(root, min_val, max_val):
|
||||
if not root: return True
|
||||
if root.val >= max_val or root.val <= min_val:
|
||||
return False
|
||||
return isBST(root.left, min_val, root.val) and isBST(root.right, root.val, max_val)
|
||||
return isBST(root, float("-inf"), float("inf"))
|
||||
|
||||
# 迭代-中序遍历
|
||||
class Solution:
|
||||
def isValidBST(self, root: TreeNode) -> bool:
|
||||
stack = []
|
||||
cur = root
|
||||
pre = None
|
||||
while cur or stack:
|
||||
if cur: # 指针来访问节点,访问到最底层
|
||||
stack.append(cur)
|
||||
cur = cur.left
|
||||
else: # 逐一处理节点
|
||||
cur = stack.pop()
|
||||
if pre and cur.val <= pre.val: # 比较当前节点和前节点的值的大小
|
||||
return False
|
||||
pre = cur
|
||||
cur = cur.right
|
||||
return True
|
||||
|
||||
```
|
||||
Go:
|
||||
```Go
|
||||
|
||||
@ -35,7 +35,7 @@
|
||||
|
||||
## 题外话
|
||||
|
||||
咋眼一看这道题目和[二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)很像,其实有很大区别。
|
||||
咋眼一看这道题目和[104.二叉树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)很像,其实有很大区别。
|
||||
|
||||
这里强调一波概念:
|
||||
|
||||
@ -50,11 +50,11 @@
|
||||
|
||||
因为求深度可以从上到下去查 所以需要前序遍历(中左右),而高度只能从下到上去查,所以只能后序遍历(左右中)
|
||||
|
||||
有的同学一定疑惑,为什么[二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中求的是二叉树的最大深度,也用的是后序遍历。
|
||||
有的同学一定疑惑,为什么[104.二叉树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中求的是二叉树的最大深度,也用的是后序遍历。
|
||||
|
||||
**那是因为代码的逻辑其实是求的根节点的高度,而根节点的高度就是这颗树的最大深度,所以才可以使用后序遍历。**
|
||||
|
||||
在[二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中,如果真正求取二叉树的最大深度,代码应该写成如下:(前序遍历)
|
||||
在[104.二叉树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中,如果真正求取二叉树的最大深度,代码应该写成如下:(前序遍历)
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
@ -227,7 +227,7 @@ public:
|
||||
|
||||
### 迭代
|
||||
|
||||
在[二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中我们可以使用层序遍历来求深度,但是就不能直接用层序遍历来求高度了,这就体现出求高度和求深度的不同。
|
||||
在[104.二叉树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中我们可以使用层序遍历来求深度,但是就不能直接用层序遍历来求高度了,这就体现出求高度和求深度的不同。
|
||||
|
||||
本题的迭代方式可以先定义一个函数,专门用来求高度。
|
||||
|
||||
@ -448,7 +448,6 @@ class Solution {
|
||||
/**
|
||||
* 优化迭代法,针对暴力迭代法的getHeight方法做优化,利用TreeNode.val来保存当前结点的高度,这样就不会有重复遍历
|
||||
* 获取高度算法时间复杂度可以降到O(1),总的时间复杂度降为O(n)。
|
||||
* <p>
|
||||
* 时间复杂度:O(n)
|
||||
*/
|
||||
public boolean isBalanced(TreeNode root) {
|
||||
@ -493,7 +492,6 @@ class Solution {
|
||||
return height;
|
||||
}
|
||||
}
|
||||
// LeetCode题解链接:https://leetcode-cn.com/problems/balanced-binary-tree/solution/110-ping-heng-er-cha-shu-di-gui-fa-bao-l-yqr3/
|
||||
```
|
||||
|
||||
Python:
|
||||
@ -590,6 +588,7 @@ func abs(a int)int{
|
||||
return a
|
||||
}
|
||||
```
|
||||
|
||||
JavaScript:
|
||||
```javascript
|
||||
var isBalanced = function(root) {
|
||||
|
||||
@ -222,7 +222,28 @@ class SolutionDP2:
|
||||
|
||||
Go:
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
const numDistinct = (s, t) => {
|
||||
let dp = Array.from(Array(s.length + 1), () => Array(t.length +1).fill(0));
|
||||
|
||||
for(let i = 0; i <=s.length; i++) {
|
||||
dp[i][0] = 1;
|
||||
}
|
||||
|
||||
for(let i = 1; i <= s.length; i++) {
|
||||
for(let j = 1; j<= t.length; j++) {
|
||||
if(s[i-1] === t[j-1]) {
|
||||
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
|
||||
} else {
|
||||
dp[i][j] = dp[i-1][j]
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return dp[s.length][t.length];
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -201,6 +201,29 @@ class Solution:
|
||||
|
||||
Go:
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
const maxProfit = (prices) => {
|
||||
let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
|
||||
// dp[i][0] 表示第i天持有股票所得现金。
|
||||
// dp[i][1] 表示第i天不持有股票所得最多现金
|
||||
dp[0][0] = 0 - prices[0];
|
||||
dp[0][1] = 0;
|
||||
for(let i = 1; i < prices.length; i++) {
|
||||
// 如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
|
||||
// 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
|
||||
// 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
|
||||
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] - prices[i]);
|
||||
|
||||
// 在来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
|
||||
// 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
|
||||
// 第i天卖出股票,所得现金就是按照今天股票佳价格卖出后所得现金即:prices[i] + dp[i - 1][0]
|
||||
dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i]);
|
||||
}
|
||||
|
||||
return dp[prices.length -1][0];
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
@ -193,35 +193,49 @@ dp[1] = max(dp[1], dp[0] - prices[i]); 如果dp[1]取dp[1],即保持买入股
|
||||
Java:
|
||||
|
||||
```java
|
||||
class Solution { // 动态规划
|
||||
// 版本一
|
||||
class Solution {
|
||||
public int maxProfit(int[] prices) {
|
||||
// 可交易次数
|
||||
int k = 2;
|
||||
int len = prices.length;
|
||||
// 边界判断, 题目中 length >= 1, 所以可省去
|
||||
if (prices.length == 0) return 0;
|
||||
|
||||
// [天数][交易次数][是否持有股票]
|
||||
int[][][] dp = new int[prices.length][k + 1][2];
|
||||
/*
|
||||
* 定义 5 种状态:
|
||||
* 0: 没有操作, 1: 第一次买入, 2: 第一次卖出, 3: 第二次买入, 4: 第二次卖出
|
||||
*/
|
||||
int[][] dp = new int[len][5];
|
||||
dp[0][1] = -prices[0];
|
||||
// 初始化第二次买入的状态是确保 最后结果是最多两次买卖的最大利润
|
||||
dp[0][3] = -prices[0];
|
||||
|
||||
// badcase
|
||||
dp[0][0][0] = 0;
|
||||
dp[0][0][1] = Integer.MIN_VALUE;
|
||||
dp[0][1][0] = 0;
|
||||
dp[0][1][1] = -prices[0];
|
||||
dp[0][2][0] = 0;
|
||||
dp[0][2][1] = Integer.MIN_VALUE;
|
||||
for (int i = 1; i < len; i++) {
|
||||
dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
|
||||
dp[i][2] = Math.max(dp[i - 1][2], dp[i][1] + prices[i]);
|
||||
dp[i][3] = Math.max(dp[i - 1][3], dp[i][2] - prices[i]);
|
||||
dp[i][4] = Math.max(dp[i - 1][4], dp[i][3] + prices[i]);
|
||||
}
|
||||
|
||||
for (int i = 1; i < prices.length; i++) {
|
||||
for (int j = 2; j >= 1; j--) {
|
||||
// dp公式
|
||||
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
|
||||
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
|
||||
return dp[len - 1][4];
|
||||
}
|
||||
}
|
||||
|
||||
int res = 0;
|
||||
for (int i = 1; i < 3; i++) {
|
||||
res = Math.max(res, dp[prices.length - 1][i][0]);
|
||||
// 版本二: 空间优化
|
||||
class Solution {
|
||||
public int maxProfit(int[] prices) {
|
||||
int len = prices.length;
|
||||
int[] dp = new int[5];
|
||||
dp[1] = -prices[0];
|
||||
dp[3] = -prices[0];
|
||||
|
||||
for (int i = 1; i < len; i++) {
|
||||
dp[1] = Math.max(dp[1], dp[0] - prices[i]);
|
||||
dp[2] = Math.max(dp[2], dp[1] + prices[i]);
|
||||
dp[3] = Math.max(dp[3], dp[2] - prices[i]);
|
||||
dp[4] = Math.max(dp[4], dp[3] + prices[i]);
|
||||
}
|
||||
return res;
|
||||
|
||||
return dp[4];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@ -170,48 +170,61 @@ public:
|
||||
Java:
|
||||
|
||||
```java
|
||||
class Solution { //动态规划
|
||||
// 版本一: 三维 dp数组
|
||||
class Solution {
|
||||
public int maxProfit(int k, int[] prices) {
|
||||
if (prices == null || prices.length < 2 || k == 0) {
|
||||
return 0;
|
||||
}
|
||||
if (prices.length == 0) return 0;
|
||||
|
||||
// [天数][交易次数][是否持有股票]
|
||||
int[][][] dp = new int[prices.length][k + 1][2];
|
||||
int len = prices.length;
|
||||
int[][][] dp = new int[len][k + 1][2];
|
||||
|
||||
// bad case
|
||||
dp[0][0][0] = 0;
|
||||
dp[0][0][1] = Integer.MIN_VALUE;
|
||||
dp[0][1][0] = 0;
|
||||
dp[0][1][1] = -prices[0];
|
||||
// dp[0][j][0] 都均为0
|
||||
// dp[0][j][1] 异常值都取Integer.MIN_VALUE;
|
||||
for (int i = 2; i < k + 1; i++) {
|
||||
dp[0][i][0] = 0;
|
||||
dp[0][i][1] = Integer.MIN_VALUE;
|
||||
// dp数组初始化
|
||||
// 初始化所有的交易次数是为确保 最后结果是最多 k 次买卖的最大利润
|
||||
for (int i = 0; i <= k; i++) {
|
||||
dp[0][i][1] = -prices[0];
|
||||
}
|
||||
|
||||
for (int i = 1; i < prices.length; i++) {
|
||||
for (int j = k; j >= 1; j--) {
|
||||
// dp公式
|
||||
for (int i = 1; i < len; i++) {
|
||||
for (int j = 1; j <= k; j++) {
|
||||
// dp方程, 0表示不持有/卖出, 1表示持有/买入
|
||||
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
|
||||
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
|
||||
}
|
||||
}
|
||||
|
||||
int res = 0;
|
||||
for (int i = 1; i < k + 1; i++) {
|
||||
res = Math.max(res, dp[prices.length - 1][i][0]);
|
||||
return dp[len - 1][k][0];
|
||||
}
|
||||
}
|
||||
|
||||
return res;
|
||||
// 版本二: 空间优化
|
||||
class Solution {
|
||||
public int maxProfit(int k, int[] prices) {
|
||||
if (prices.length == 0) return 0;
|
||||
|
||||
// [天数][股票状态]
|
||||
// 股票状态: 奇数表示第 k 次交易持有/买入, 偶数表示第 k 次交易不持有/卖出, 0 表示没有操作
|
||||
int len = prices.length;
|
||||
int[][] dp = new int[len][k*2 + 1];
|
||||
|
||||
// dp数组的初始化, 与版本一同理
|
||||
for (int i = 1; i < k*2; i += 2) {
|
||||
dp[0][i] = -prices[0];
|
||||
}
|
||||
|
||||
for (int i = 1; i < len; i++) {
|
||||
for (int j = 0; j < k*2 - 1; j += 2) {
|
||||
dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
|
||||
dp[i][j + 2] = Math.max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
|
||||
}
|
||||
}
|
||||
return dp[len - 1][k*2];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
Python:
|
||||
|
||||
版本一
|
||||
```python
|
||||
class Solution:
|
||||
def maxProfit(self, k: int, prices: List[int]) -> int:
|
||||
@ -226,11 +239,49 @@ class Solution:
|
||||
dp[i][j+2] = max(dp[i-1][j+2], dp[i-1][j+1] + prices[i])
|
||||
return dp[-1][2*k]
|
||||
```
|
||||
|
||||
版本二
|
||||
```python3
|
||||
class Solution:
|
||||
def maxProfit(self, k: int, prices: List[int]) -> int:
|
||||
if len(prices) == 0: return 0
|
||||
dp = [0] * (2*k + 1)
|
||||
for i in range(1,2*k,2):
|
||||
dp[i] = -prices[0]
|
||||
for i in range(1,len(prices)):
|
||||
for j in range(1,2*k + 1):
|
||||
if j % 2:
|
||||
dp[j] = max(dp[j],dp[j-1]-prices[i])
|
||||
else:
|
||||
dp[j] = max(dp[j],dp[j-1]+prices[i])
|
||||
return dp[2*k]
|
||||
```
|
||||
Go:
|
||||
|
||||
|
||||
Javascript:
|
||||
|
||||
```javascript
|
||||
const maxProfit = (k,prices) => {
|
||||
if (prices == null || prices.length < 2 || k == 0) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
let dp = Array.from(Array(prices.length), () => Array(2*k+1).fill(0));
|
||||
|
||||
for (let j = 1; j < 2 * k; j += 2) {
|
||||
dp[0][j] = 0 - prices[0];
|
||||
}
|
||||
|
||||
for(let i = 1; i < prices.length; i++) {
|
||||
for (let j = 0; j < 2 * k; j += 2) {
|
||||
dp[i][j+1] = Math.max(dp[i-1][j+1], dp[i-1][j] - prices[i]);
|
||||
dp[i][j+2] = Math.max(dp[i-1][j+2], dp[i-1][j+1] + prices[i]);
|
||||
}
|
||||
}
|
||||
|
||||
return dp[prices.length - 1][2 * k];
|
||||
};
|
||||
```
|
||||
|
||||
-----------------------
|
||||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||||
|
||||
@ -170,6 +170,25 @@ func lengthOfLIS(nums []int ) int {
|
||||
return len(dp)
|
||||
}
|
||||
```
|
||||
|
||||
Javascript
|
||||
```javascript
|
||||
const lengthOfLIS = (nums) => {
|
||||
let dp = Array(nums.length).fill(1);
|
||||
let result = 1;
|
||||
|
||||
for(let i = 1; i < nums.length; i++) {
|
||||
for(let j = 0; j < i; j++) {
|
||||
if(nums[i] > nums[j]) {
|
||||
dp[i] = Math.max(dp[i], dp[j]+1);
|
||||
}
|
||||
}
|
||||
result = Math.max(result, dp[i]);
|
||||
}
|
||||
|
||||
return result;
|
||||
};
|
||||
```
|
||||
*复杂度分析*
|
||||
- 时间复杂度:O(nlogn)。数组 nums 的长度为 n,我们依次用数组中的元素去更新 dp 数组,相当于插入最后递增的元素,而更新 dp 数组时需要进行 O(logn) 的二分搜索,所以总时间复杂度为 O(nlogn)。
|
||||
- 空间复杂度:O(n),需要额外使用长度为 n 的 dp 数组。
|
||||
|
||||
@ -207,7 +207,29 @@ class Solution:
|
||||
|
||||
Go:
|
||||
|
||||
Javascript:
|
||||
|
||||
```javascript
|
||||
const maxProfit = (prices) => {
|
||||
if(prices.length < 2) {
|
||||
return 0
|
||||
} else if(prices.length < 3) {
|
||||
return Math.max(0, prices[1] - prices[0]);
|
||||
}
|
||||
|
||||
let dp = Array.from(Array(prices.length), () => Array(4).fill(0));
|
||||
dp[0][0] = 0 - prices[0];
|
||||
|
||||
for(i = 1; i < prices.length; i++) {
|
||||
dp[i][0] = Math.max(dp[i - 1][0], Math.max(dp[i-1][1], dp[i-1][3]) - prices[i]);
|
||||
dp[i][1] = Math.max(dp[i -1][1], dp[i - 1][3]);
|
||||
dp[i][2] = dp[i-1][0] + prices[i];
|
||||
dp[i][3] = dp[i-1][2];
|
||||
}
|
||||
|
||||
return Math.max(dp[prices.length - 1][1], dp[prices.length - 1][2], dp[prices.length - 1][3]);
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -173,7 +173,7 @@ return {val2, val1};
|
||||
|
||||
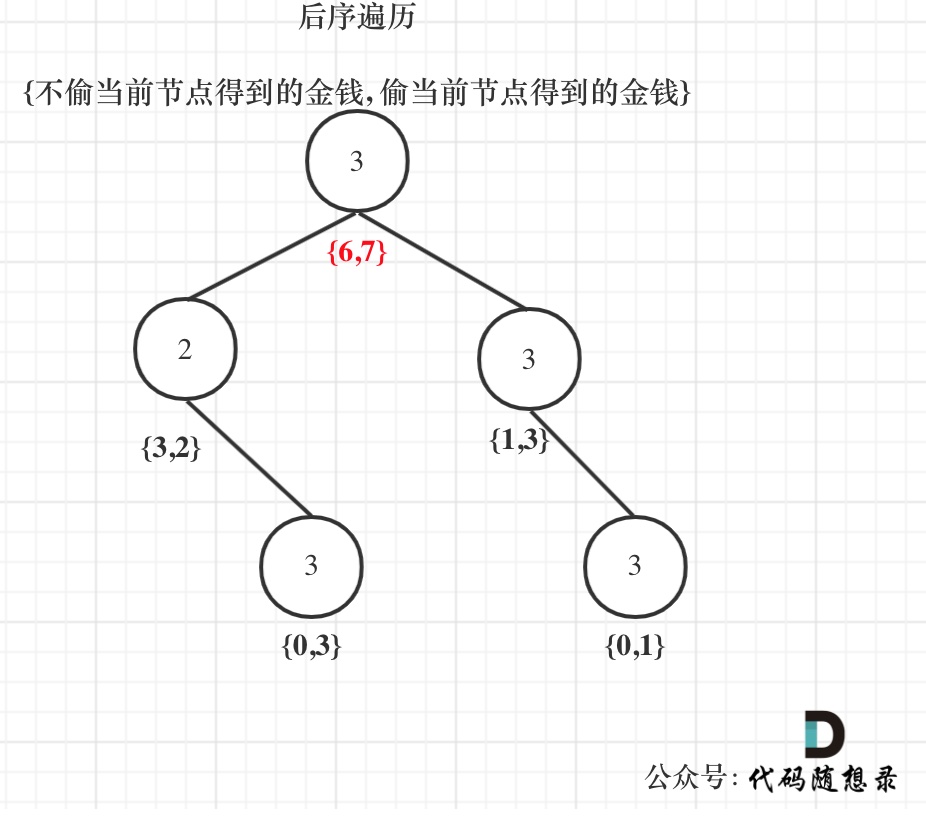
以示例1为例,dp数组状态如下:(**注意用后序遍历的方式推导**)
|
||||
|
||||
|
||||

|
||||
|
||||
**最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱**。
|
||||
|
||||
|
||||
@ -18,18 +18,18 @@ https://leetcode-cn.com/problems/top-k-frequent-elements/
|
||||
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
|
||||
|
||||
示例 1:
|
||||
输入: nums = [1,1,1,2,2,3], k = 2
|
||||
输出: [1,2]
|
||||
* 输入: nums = [1,1,1,2,2,3], k = 2
|
||||
* 输出: [1,2]
|
||||
|
||||
示例 2:
|
||||
输入: nums = [1], k = 1
|
||||
输出: [1]
|
||||
* 输入: nums = [1], k = 1
|
||||
* 输出: [1]
|
||||
|
||||
提示:
|
||||
你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
|
||||
你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
|
||||
题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
|
||||
你可以按任意顺序返回答案。
|
||||
* 你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
|
||||
* 你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
|
||||
* 题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
|
||||
* 你可以按任意顺序返回答案。
|
||||
|
||||
# 思路
|
||||
|
||||
@ -70,7 +70,7 @@ https://leetcode-cn.com/problems/top-k-frequent-elements/
|
||||
|
||||
寻找前k个最大元素流程如图所示:(图中的频率只有三个,所以正好构成一个大小为3的小顶堆,如果频率更多一些,则用这个小顶堆进行扫描)
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
我们来看一下C++代码:
|
||||
@ -126,10 +126,7 @@ public:
|
||||
优先级队列的定义正好反过来了,可能和优先级队列的源码实现有关(我没有仔细研究),我估计是底层实现上优先队列队首指向后面,队尾指向最前面的缘故!
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
# 其他语言版本
|
||||
|
||||
|
||||
Java:
|
||||
|
||||
@ -435,7 +435,7 @@ Python:
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
//递归法
|
||||
# 递归法
|
||||
class Solution:
|
||||
def findMode(self, root: TreeNode) -> List[int]:
|
||||
if not root: return
|
||||
@ -460,6 +460,66 @@ class Solution:
|
||||
return
|
||||
findNumber(root)
|
||||
return self.res
|
||||
|
||||
|
||||
# 迭代法-中序遍历-使用额外空间map的方法:
|
||||
class Solution:
|
||||
def findMode(self, root: TreeNode) -> List[int]:
|
||||
stack = []
|
||||
cur = root
|
||||
pre = None
|
||||
dist = {}
|
||||
while cur or stack:
|
||||
if cur: # 指针来访问节点,访问到最底层
|
||||
stack.append(cur)
|
||||
cur = cur.left
|
||||
else: # 逐一处理节点
|
||||
cur = stack.pop()
|
||||
if cur.val in dist:
|
||||
dist[cur.val] += 1
|
||||
else:
|
||||
dist[cur.val] = 1
|
||||
pre = cur
|
||||
cur = cur.right
|
||||
|
||||
# 找出字典中最大的key
|
||||
res = []
|
||||
for key, value in dist.items():
|
||||
if (value == max(dist.values())):
|
||||
res.append(key)
|
||||
return res
|
||||
|
||||
# 迭代法-中序遍历-不使用额外空间,利用二叉搜索树特性:
|
||||
class Solution:
|
||||
def findMode(self, root: TreeNode) -> List[int]:
|
||||
stack = []
|
||||
cur = root
|
||||
pre = None
|
||||
maxCount, count = 0, 0
|
||||
res = []
|
||||
while cur or stack:
|
||||
if cur: # 指针来访问节点,访问到最底层
|
||||
stack.append(cur)
|
||||
cur = cur.left
|
||||
else: # 逐一处理节点
|
||||
cur = stack.pop()
|
||||
if pre == None: # 第一个节点
|
||||
count = 1
|
||||
elif pre.val == cur.val: # 与前一个节点数值相同
|
||||
count += 1
|
||||
else:
|
||||
count = 1
|
||||
if count == maxCount:
|
||||
res.append(cur.val)
|
||||
if count > maxCount:
|
||||
maxCount = count
|
||||
res.clear()
|
||||
res.append(cur.val)
|
||||
|
||||
pre = cur
|
||||
cur = cur.right
|
||||
return res
|
||||
|
||||
```
|
||||
Go:
|
||||
暴力法(非BSL)
|
||||
|
||||
103
problems/0503.下一个更大元素II.md
Normal file
103
problems/0503.下一个更大元素II.md
Normal file
@ -0,0 +1,103 @@
|
||||
|
||||
# 503.下一个更大元素II
|
||||
|
||||
链接:https://leetcode-cn.com/problems/next-greater-element-ii/
|
||||
|
||||
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
|
||||
|
||||
示例 1:
|
||||
|
||||
* 输入: [1,2,1]
|
||||
* 输出: [2,-1,2]
|
||||
* 解释: 第一个 1 的下一个更大的数是 2;数字 2 找不到下一个更大的数;第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
|
||||
|
||||
|
||||
# 思路
|
||||
|
||||
做本题之前建议先做[739. 每日温度](https://mp.weixin.qq.com/s/YeQ7eE0-hZpxJfJJziq25Q) 和 [496.下一个更大元素 I](https://mp.weixin.qq.com/s/U0O6XkFOe-RMXthPS16sWQ)。
|
||||
|
||||
这道题和[739. 每日温度](https://mp.weixin.qq.com/s/YeQ7eE0-hZpxJfJJziq25Q)也几乎如出一辙。
|
||||
|
||||
不同的时候本题要循环数组了。
|
||||
|
||||
关于单调栈的讲解我在题解[739. 每日温度](https://mp.weixin.qq.com/s/YeQ7eE0-hZpxJfJJziq25Q)中已经详细讲解了。
|
||||
|
||||
本篇我侧重与说一说,如何处理循环数组。
|
||||
|
||||
相信不少同学看到这道题,就想那我直接把两个数组拼接在一起,然后使用单调栈求下一个最大值不就行了!
|
||||
|
||||
确实可以!
|
||||
|
||||
讲两个nums数组拼接在一起,使用单调栈计算出每一个元素的下一个最大值,最后再把结果集即result数组resize到原数组大小就可以了。
|
||||
|
||||
代码如下:
|
||||
|
||||
```C++
|
||||
// 版本一
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> nextGreaterElements(vector<int>& nums) {
|
||||
// 拼接一个新的nums
|
||||
vector<int> nums1(nums.begin(), nums.end());
|
||||
nums.insert(nums.end(), nums1.begin(), nums1.end());
|
||||
// 用新的nums大小来初始化result
|
||||
vector<int> result(nums.size(), -1);
|
||||
if (nums.size() == 0) return result;
|
||||
|
||||
// 开始单调栈
|
||||
stack<int> st;
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
while (!st.empty() && nums[i] > nums[st.top()]) {
|
||||
result[st.top()] = nums[i];
|
||||
st.pop();
|
||||
}
|
||||
st.push(i);
|
||||
}
|
||||
// 最后再把结果集即result数组resize到原数组大小
|
||||
result.resize(nums.size() / 2);
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
这种写法确实比较直观,但做了很多无用操作,例如修改了nums数组,而且最后还要把result数组resize回去。
|
||||
|
||||
resize倒是不费时间,是O(1)的操作,但扩充nums数组相当于多了一个O(n)的操作。
|
||||
|
||||
其实也可以不扩充nums,而是在遍历的过程中模拟走了两边nums。
|
||||
|
||||
代码如下:
|
||||
|
||||
```C++
|
||||
// 版本二
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> nextGreaterElements(vector<int>& nums) {
|
||||
vector<int> result(nums.size(), -1);
|
||||
if (nums.size() == 0) return result;
|
||||
stack<int> st;
|
||||
for (int i = 0; i < nums.size() * 2; i++) {
|
||||
// 模拟遍历两边nums,注意一下都是用i % nums.size()来操作
|
||||
while (!st.empty() && nums[i % nums.size()] > nums[st.top()]) {
|
||||
result[st.top()] = nums[i % nums.size()];
|
||||
st.pop();
|
||||
}
|
||||
st.push(i % nums.size());
|
||||
}
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
可以版本二不仅代码精简了,也比版本一少做了无用功!
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
Java:
|
||||
|
||||
Python:
|
||||
|
||||
Go:
|
||||
|
||||
JavaScript:
|
||||
@ -37,7 +37,7 @@
|
||||
|
||||
如果使用递归法,如何判断是最后一行呢,其实就是深度最大的叶子节点一定是最后一行。
|
||||
|
||||
如果对二叉树深度和高度还有点疑惑的话,请看:[二叉树:我平衡么?](https://mp.weixin.qq.com/s/isUS-0HDYknmC0Rr4R8mww)。
|
||||
如果对二叉树深度和高度还有点疑惑的话,请看:[110.平衡二叉树](https://mp.weixin.qq.com/s/isUS-0HDYknmC0Rr4R8mww)。
|
||||
|
||||
所以要找深度最大的叶子节点。
|
||||
|
||||
@ -207,7 +207,7 @@ public:
|
||||
|
||||
本题涉及如下几点:
|
||||
|
||||
* 递归求深度的写法,我们在[二叉树:我平衡么?](https://mp.weixin.qq.com/s/isUS-0HDYknmC0Rr4R8mww)中详细的分析了深度应该怎么求,高度应该怎么求。
|
||||
* 递归求深度的写法,我们在[110.平衡二叉树](https://mp.weixin.qq.com/s/isUS-0HDYknmC0Rr4R8mww)中详细的分析了深度应该怎么求,高度应该怎么求。
|
||||
* 递归中其实隐藏了回溯,在[二叉树:以为使用了递归,其实还隐藏着回溯](https://mp.weixin.qq.com/s/ivLkHzWdhjQQD1rQWe6zWA)中讲解了究竟哪里使用了回溯,哪里隐藏了回溯。
|
||||
* 层次遍历,在[二叉树:层序遍历登场!](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)深度讲解了二叉树层次遍历。
|
||||
所以本题涉及到的点,我们之前都讲解过,这些知识点需要同学们灵活运用,这样就举一反三了。
|
||||
|
||||
@ -222,6 +222,26 @@ class Solution:
|
||||
for i in range(len(res)-1): // 统计有序数组的最小差值
|
||||
r = min(abs(res[i]-res[i+1]),r)
|
||||
return r
|
||||
|
||||
# 迭代法-中序遍历
|
||||
class Solution:
|
||||
def getMinimumDifference(self, root: TreeNode) -> int:
|
||||
stack = []
|
||||
cur = root
|
||||
pre = None
|
||||
result = float('inf')
|
||||
while cur or stack:
|
||||
if cur: # 指针来访问节点,访问到最底层
|
||||
stack.append(cur)
|
||||
cur = cur.left
|
||||
else: # 逐一处理节点
|
||||
cur = stack.pop()
|
||||
if pre: # 当前节点和前节点的值的差值
|
||||
result = min(result, cur.val - pre.val)
|
||||
pre = cur
|
||||
cur = cur.right
|
||||
return result
|
||||
|
||||
```
|
||||
Go:
|
||||
> 中序遍历,然后计算最小差值
|
||||
|
||||
@ -73,7 +73,7 @@ for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
|
||||
|
||||
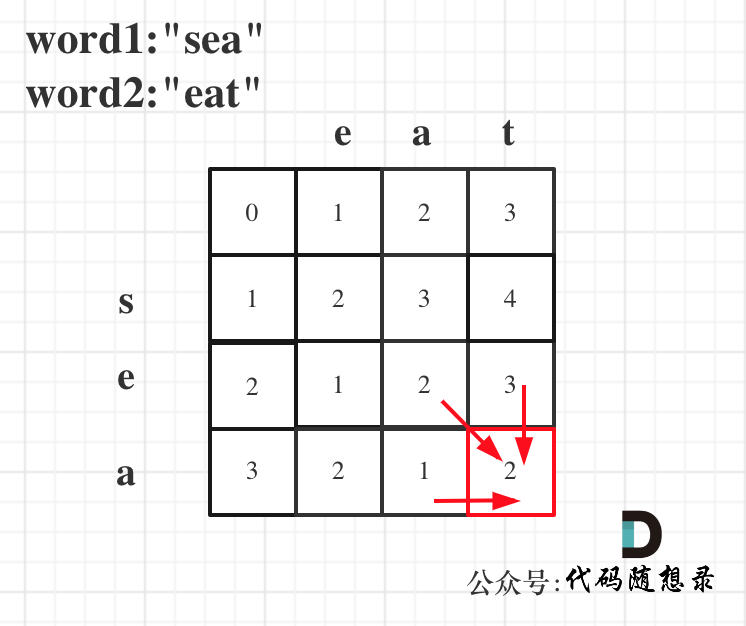
以word1:"sea",word2:"eat"为例,推导dp数组状态图如下:
|
||||
|
||||
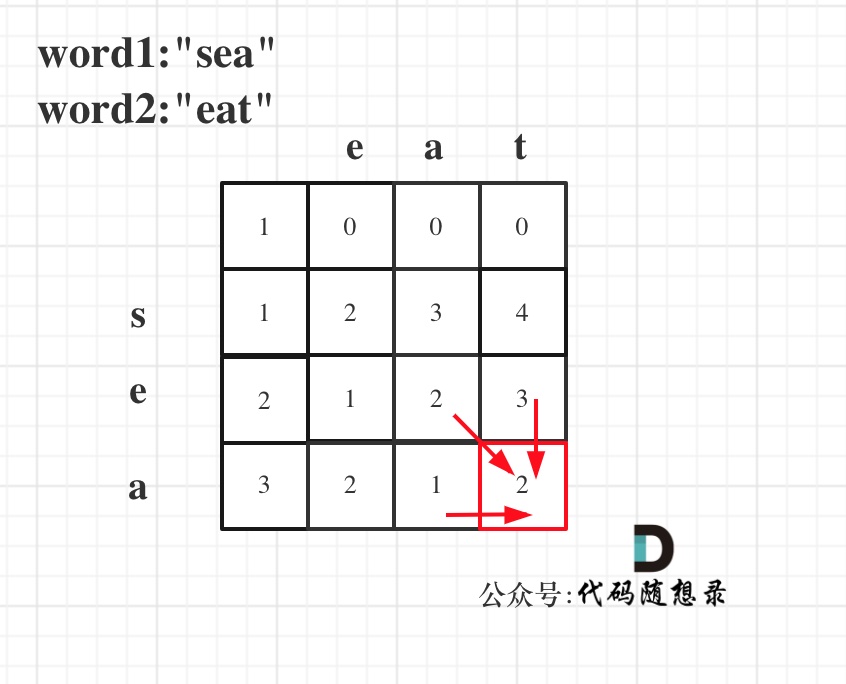
|
||||
|
||||
|
||||
|
||||
以上分析完毕,代码如下:
|
||||
@ -149,6 +149,32 @@ class Solution:
|
||||
Go:
|
||||
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
const minDistance = (word1, word2) => {
|
||||
let dp = Array.from(Array(word1.length + 1), () => Array(word2.length+1).fill(0));
|
||||
|
||||
for(let i = 1; i <= word1.length; i++) {
|
||||
dp[i][0] = i;
|
||||
}
|
||||
|
||||
for(let j = 1; j <= word2.length; j++) {
|
||||
dp[0][j] = j;
|
||||
}
|
||||
|
||||
for(let i = 1; i <= word1.length; i++) {
|
||||
for(let j = 1; j <= word2.length; j++) {
|
||||
if(word1[i-1] === word2[j-1]) {
|
||||
dp[i][j] = dp[i-1][j-1];
|
||||
} else {
|
||||
dp[i][j] = Math.min(dp[i-1][j] + 1, dp[i][j-1] + 1, dp[i-1][j-1] + 2);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return dp[word1.length][word2.length];
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -361,7 +361,51 @@ func countSubstrings(s string) int {
|
||||
}
|
||||
```
|
||||
|
||||
Javascript
|
||||
> 动态规划
|
||||
```javascript
|
||||
const countSubstrings = (s) => {
|
||||
const strLen = s.length;
|
||||
let numOfPalindromicStr = 0;
|
||||
let dp = Array.from(Array(strLen), () => Array(strLen).fill(false));
|
||||
|
||||
for(let j = 0; j < strLen; j++) {
|
||||
for(let i = 0; i <= j; i++) {
|
||||
if(s[i] === s[j]) {
|
||||
if((j - i) < 2) {
|
||||
dp[i][j] = true;
|
||||
} else {
|
||||
dp[i][j] = dp[i+1][j-1];
|
||||
}
|
||||
numOfPalindromicStr += dp[i][j] ? 1 : 0;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return numOfPalindromicStr;
|
||||
}
|
||||
```
|
||||
|
||||
> 双指针法:
|
||||
```javascript
|
||||
const countSubstrings = (s) => {
|
||||
const strLen = s.length;
|
||||
let numOfPalindromicStr = 0;
|
||||
|
||||
for(let i = 0; i < 2 * strLen - 1; i++) {
|
||||
let left = Math.floor(i/2);
|
||||
let right = left + i % 2;
|
||||
|
||||
while(left >= 0 && right < strLen && s[left] === s[right]){
|
||||
numOfPalindromicStr++;
|
||||
left--;
|
||||
right++;
|
||||
}
|
||||
}
|
||||
|
||||
return numOfPalindromicStr;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -218,6 +218,49 @@ class Solution:
|
||||
|
||||
Go:
|
||||
|
||||
Javascript:
|
||||
|
||||
> 动态规划:
|
||||
```javascript
|
||||
const findLengthOfLCIS = (nums) => {
|
||||
let dp = Array(nums.length).fill(1);
|
||||
|
||||
|
||||
for(let i = 0; i < nums.length - 1; i++) {
|
||||
if(nums[i+1] > nums[i]) {
|
||||
dp[i+1] = dp[i]+ 1;
|
||||
}
|
||||
}
|
||||
|
||||
return Math.max(...dp);
|
||||
};
|
||||
```
|
||||
|
||||
> 贪心法:
|
||||
```javascript
|
||||
const findLengthOfLCIS = (nums) => {
|
||||
if(nums.length === 1) {
|
||||
return 1;
|
||||
}
|
||||
|
||||
let maxLen = 1;
|
||||
let curMax = 1;
|
||||
let cur = nums[0];
|
||||
|
||||
for(let num of nums) {
|
||||
if(num > cur) {
|
||||
curMax += 1;
|
||||
maxLen = Math.max(maxLen, curMax);
|
||||
} else {
|
||||
curMax = 1;
|
||||
}
|
||||
cur = num;
|
||||
}
|
||||
|
||||
return maxLen;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@ -153,7 +153,18 @@ class Solution:
|
||||
|
||||
Go:
|
||||
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
const maxProfit = (prices,fee) => {
|
||||
let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
|
||||
dp[0][0] = 0 - prices[0];
|
||||
for (let i = 1; i < prices.length; i++) {
|
||||
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
|
||||
dp[i][1] = Math.max(dp[i - 1][0] + prices[i] - fee, dp[i - 1][1]);
|
||||
}
|
||||
return Math.max(dp[prices.length - 1][0], dp[prices.length - 1][1]);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -20,7 +20,7 @@ B: [3,2,1,4,7]
|
||||
输出:3
|
||||
解释:
|
||||
长度最长的公共子数组是 [3, 2, 1] 。
|
||||
|
||||
|
||||
提示:
|
||||
|
||||
* 1 <= len(A), len(B) <= 1000
|
||||
@ -155,6 +155,7 @@ public:
|
||||
|
||||
Java:
|
||||
```java
|
||||
// 版本一
|
||||
class Solution {
|
||||
public int findLength(int[] nums1, int[] nums2) {
|
||||
int result = 0;
|
||||
@ -164,7 +165,7 @@ class Solution {
|
||||
for (int j = 1; j < nums2.length + 1; j++) {
|
||||
if (nums1[i - 1] == nums2[j - 1]) {
|
||||
dp[i][j] = dp[i - 1][j - 1] + 1;
|
||||
max = Math.max(max, dp[i][j]);
|
||||
result = Math.max(result, dp[i][j]);
|
||||
}
|
||||
}
|
||||
}
|
||||
@ -172,6 +173,26 @@ class Solution {
|
||||
return result;
|
||||
}
|
||||
}
|
||||
|
||||
// 版本二: 滚动数组
|
||||
class Solution {
|
||||
public int findLength(int[] nums1, int[] nums2) {
|
||||
int[] dp = new int[nums2.length + 1];
|
||||
int result = 0;
|
||||
|
||||
for (int i = 1; i <= nums1.length; i++) {
|
||||
for (int j = nums2.length; j > 0; j--) {
|
||||
if (nums1[i - 1] == nums2[j - 1]) {
|
||||
dp[j] = dp[j - 1] + 1;
|
||||
} else {
|
||||
dp[j] = 0;
|
||||
}
|
||||
result = Math.max(result, dp[j]);
|
||||
}
|
||||
}
|
||||
return result;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Python:
|
||||
|
||||
@ -99,6 +99,33 @@ public:
|
||||
|
||||
|
||||
Java:
|
||||
```java
|
||||
class Solution {
|
||||
public int largestSumAfterKNegations(int[] nums, int K) {
|
||||
// 将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
|
||||
nums = IntStream.of(nums)
|
||||
.boxed()
|
||||
.sorted((o1, o2) -> Math.abs(o2) - Math.abs(o1))
|
||||
.mapToInt(Integer::intValue).toArray();
|
||||
int len = nums.length;
|
||||
for (int i = 0; i < len; i++) {
|
||||
//从前向后遍历,遇到负数将其变为正数,同时K--
|
||||
if (nums[i] < 0 && k > 0) {
|
||||
nums[i] = -nums[i];
|
||||
k--;
|
||||
}
|
||||
}
|
||||
// 如果K还大于0,那么反复转变数值最小的元素,将K用完
|
||||
if (k % 2 == 1) nums[len - 1] = -nums[len - 1];
|
||||
int result = 0;
|
||||
for (int a : nums) {
|
||||
result += a;
|
||||
}
|
||||
return result;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int largestSumAfterKNegations(int[] A, int K) {
|
||||
|
||||
@ -8,6 +8,8 @@
|
||||
|
||||
## 1035.不相交的线
|
||||
|
||||
题目链接: https://leetcode-cn.com/problems/uncrossed-lines/
|
||||
|
||||
我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。
|
||||
|
||||
现在,我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线,只要 A[i] == B[j],且我们绘制的直线不与任何其他连线(非水平线)相交。
|
||||
|
||||
@ -8,6 +8,8 @@
|
||||
|
||||
## 1143.最长公共子序列
|
||||
|
||||
题目链接: https://leetcode-cn.com/problems/longest-common-subsequence/
|
||||
|
||||
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
|
||||
|
||||
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
|
||||
@ -195,7 +197,24 @@ func max(a,b int)int {
|
||||
}
|
||||
```
|
||||
|
||||
Javascript:
|
||||
```javascript
|
||||
const longestCommonSubsequence = (text1, text2) => {
|
||||
let dp = Array.from(Array(text1.length+1), () => Array(text2.length+1).fill(0));
|
||||
|
||||
for(let i = 1; i <= text1.length; i++) {
|
||||
for(let j = 1; j <= text2.length; j++) {
|
||||
if(text1[i-1] === text2[j-1]) {
|
||||
dp[i][j] = dp[i-1][j-1] +1;;
|
||||
} else {
|
||||
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1])
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return dp[text1.length][text2.length];
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
-----------------------
|
||||
|
||||
@ -5,6 +5,7 @@
|
||||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a>
|
||||
</p>
|
||||
<p align="center"><strong>欢迎大家<a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||||
|
||||
# 二叉树理论基础篇
|
||||
|
||||
我们要开启新的征程了,大家跟上!
|
||||
|
||||
@ -111,7 +111,7 @@ void traversal(TreeNode* cur, vector<int>& vec) {
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
# 其他语言版本
|
||||
|
||||
|
||||
Java:
|
||||
|
||||
@ -125,7 +125,7 @@ dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化
|
||||
|
||||
其实从递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是又左上方数值推导出来了,那么 其他下标初始为什么数值都可以,因为都会被覆盖。
|
||||
|
||||
初始-1,初始-2,初始100,都可以!
|
||||
**初始-1,初始-2,初始100,都可以!**
|
||||
|
||||
但只不过一开始就统一把dp数组统一初始为0,更方便一些。
|
||||
|
||||
|
||||
Reference in New Issue
Block a user