
欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+ # 排列问题(二) ## 47.全排列 II @@ -222,6 +223,43 @@ class Solution: return res ``` +Go: + +```go +var res [][]int +func permute(nums []int) [][]int { + res = [][]int{} + sort.Ints(nums) + dfs(nums, make([]int, 0), make([]bool, len(nums))) + return res +} + +func dfs(nums, path []int, used []bool) { + if len(path) == len(nums) { + res = append(res, append([]int{}, path...)) + return + } + + m := make(map[int]bool) + for i := 0; i < len(nums); i++ { + // used 从剩余 nums 中选 + if used[i] { + continue + } + // m 集合间去重 + if _, ok := m[nums[i]]; ok { + continue + } + m[nums[i]] = true + path = append(path, nums[i]) + used[i] = true + dfs(nums, path, used) + used[i] = false + path = path[:len(path)-1] + } +} +``` + Javascript: ```javascript @@ -258,7 +296,45 @@ var permuteUnique = function (nums) { }; ``` - +Go: +回溯+本层去重+下层去重 +```golang +func permuteUnique(nums []int) [][]int { + var subRes []int + var res [][]int + sort.Ints(nums) + used:=make([]bool,len(nums)) + backTring(nums,subRes,&res,used) + return res +} +func backTring(nums,subRes []int,res *[][]int,used []bool){ + if len(subRes)==len(nums){ + tmp:=make([]int,len(nums)) + copy(tmp,subRes) + *res=append(*res,tmp) + return + } + // used[i - 1] == true,说明同一树支candidates[i - 1]使用过 + // used[i - 1] == false,说明同一树层candidates[i - 1]使用过 + for i:=0;i
* 时间复杂度:O(n)
*/
public boolean isBalanced(TreeNode root) {
@@ -493,7 +492,6 @@ class Solution {
return height;
}
}
-// LeetCode题解链接:https://leetcode-cn.com/problems/balanced-binary-tree/solution/110-ping-heng-er-cha-shu-di-gui-fa-bao-l-yqr3/
```
Python:
@@ -590,6 +588,7 @@ func abs(a int)int{
return a
}
```
+
JavaScript:
```javascript
var isBalanced = function(root) {
diff --git a/problems/0112.路径总和.md b/problems/0112.路径总和.md
index d798ca90..ae9a9267 100644
--- a/problems/0112.路径总和.md
+++ b/problems/0112.路径总和.md
@@ -13,8 +13,8 @@
接下来我通过详细讲解如下两道题,来回答这个问题:
-* 112. 路径总和
-* 113. 路径总和II
+* 112.路径总和
+* 113.路径总和II
## 112. 路径总和
diff --git a/problems/0115.不同的子序列.md b/problems/0115.不同的子序列.md
index 62af9d0f..014eb3cd 100644
--- a/problems/0115.不同的子序列.md
+++ b/problems/0115.不同的子序列.md
@@ -222,7 +222,28 @@ class SolutionDP2:
Go:
+Javascript:
+```javascript
+const numDistinct = (s, t) => {
+ let dp = Array.from(Array(s.length + 1), () => Array(t.length +1).fill(0));
+ for(let i = 0; i <=s.length; i++) {
+ dp[i][0] = 1;
+ }
+
+ for(let i = 1; i <= s.length; i++) {
+ for(let j = 1; j<= t.length; j++) {
+ if(s[i-1] === t[j-1]) {
+ dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
+ } else {
+ dp[i][j] = dp[i-1][j]
+ }
+ }
+ }
+
+ return dp[s.length][t.length];
+};
+```
-----------------------
diff --git a/problems/0122.买卖股票的最佳时机II(动态规划).md b/problems/0122.买卖股票的最佳时机II(动态规划).md
index 1215025e..8ed70063 100644
--- a/problems/0122.买卖股票的最佳时机II(动态规划).md
+++ b/problems/0122.买卖股票的最佳时机II(动态规划).md
@@ -201,6 +201,29 @@ class Solution:
Go:
+Javascript:
+```javascript
+const maxProfit = (prices) => {
+ let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
+ // dp[i][0] 表示第i天持有股票所得现金。
+ // dp[i][1] 表示第i天不持有股票所得最多现金
+ dp[0][0] = 0 - prices[0];
+ dp[0][1] = 0;
+ for(let i = 1; i < prices.length; i++) {
+ // 如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
+ // 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
+ // 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
+ dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] - prices[i]);
+
+ // 在来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
+ // 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
+ // 第i天卖出股票,所得现金就是按照今天股票佳价格卖出后所得现金即:prices[i] + dp[i - 1][0]
+ dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i]);
+ }
+
+ return dp[prices.length -1][0];
+};
+```
diff --git a/problems/0123.买卖股票的最佳时机III.md b/problems/0123.买卖股票的最佳时机III.md
index fccb187d..7ff1bfe2 100644
--- a/problems/0123.买卖股票的最佳时机III.md
+++ b/problems/0123.买卖股票的最佳时机III.md
@@ -193,35 +193,49 @@ dp[1] = max(dp[1], dp[0] - prices[i]); 如果dp[1]取dp[1],即保持买入股
Java:
```java
-class Solution { // 动态规划
+// 版本一
+class Solution {
public int maxProfit(int[] prices) {
- // 可交易次数
- int k = 2;
+ int len = prices.length;
+ // 边界判断, 题目中 length >= 1, 所以可省去
+ if (prices.length == 0) return 0;
- // [天数][交易次数][是否持有股票]
- int[][][] dp = new int[prices.length][k + 1][2];
+ /*
+ * 定义 5 种状态:
+ * 0: 没有操作, 1: 第一次买入, 2: 第一次卖出, 3: 第二次买入, 4: 第二次卖出
+ */
+ int[][] dp = new int[len][5];
+ dp[0][1] = -prices[0];
+ // 初始化第二次买入的状态是确保 最后结果是最多两次买卖的最大利润
+ dp[0][3] = -prices[0];
- // badcase
- dp[0][0][0] = 0;
- dp[0][0][1] = Integer.MIN_VALUE;
- dp[0][1][0] = 0;
- dp[0][1][1] = -prices[0];
- dp[0][2][0] = 0;
- dp[0][2][1] = Integer.MIN_VALUE;
-
- for (int i = 1; i < prices.length; i++) {
- for (int j = 2; j >= 1; j--) {
- // dp公式
- dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
- dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
- }
+ for (int i = 1; i < len; i++) {
+ dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
+ dp[i][2] = Math.max(dp[i - 1][2], dp[i][1] + prices[i]);
+ dp[i][3] = Math.max(dp[i - 1][3], dp[i][2] - prices[i]);
+ dp[i][4] = Math.max(dp[i - 1][4], dp[i][3] + prices[i]);
}
- int res = 0;
- for (int i = 1; i < 3; i++) {
- res = Math.max(res, dp[prices.length - 1][i][0]);
+ return dp[len - 1][4];
+ }
+}
+
+// 版本二: 空间优化
+class Solution {
+ public int maxProfit(int[] prices) {
+ int len = prices.length;
+ int[] dp = new int[5];
+ dp[1] = -prices[0];
+ dp[3] = -prices[0];
+
+ for (int i = 1; i < len; i++) {
+ dp[1] = Math.max(dp[1], dp[0] - prices[i]);
+ dp[2] = Math.max(dp[2], dp[1] + prices[i]);
+ dp[3] = Math.max(dp[3], dp[2] - prices[i]);
+ dp[4] = Math.max(dp[4], dp[3] + prices[i]);
}
- return res;
+
+ return dp[4];
}
}
```
diff --git a/problems/0188.买卖股票的最佳时机IV.md b/problems/0188.买卖股票的最佳时机IV.md
index 431c292b..46c6f7f0 100644
--- a/problems/0188.买卖股票的最佳时机IV.md
+++ b/problems/0188.买卖股票的最佳时机IV.md
@@ -170,48 +170,61 @@ public:
Java:
```java
-class Solution { //动态规划
+// 版本一: 三维 dp数组
+class Solution {
public int maxProfit(int k, int[] prices) {
- if (prices == null || prices.length < 2 || k == 0) {
- return 0;
+ if (prices.length == 0) return 0;
+
+ // [天数][交易次数][是否持有股票]
+ int len = prices.length;
+ int[][][] dp = new int[len][k + 1][2];
+
+ // dp数组初始化
+ // 初始化所有的交易次数是为确保 最后结果是最多 k 次买卖的最大利润
+ for (int i = 0; i <= k; i++) {
+ dp[0][i][1] = -prices[0];
}
- // [天数][交易次数][是否持有股票]
- int[][][] dp = new int[prices.length][k + 1][2];
-
- // bad case
- dp[0][0][0] = 0;
- dp[0][0][1] = Integer.MIN_VALUE;
- dp[0][1][0] = 0;
- dp[0][1][1] = -prices[0];
- // dp[0][j][0] 都均为0
- // dp[0][j][1] 异常值都取Integer.MIN_VALUE;
- for (int i = 2; i < k + 1; i++) {
- dp[0][i][0] = 0;
- dp[0][i][1] = Integer.MIN_VALUE;
- }
-
- for (int i = 1; i < prices.length; i++) {
- for (int j = k; j >= 1; j--) {
- // dp公式
+ for (int i = 1; i < len; i++) {
+ for (int j = 1; j <= k; j++) {
+ // dp方程, 0表示不持有/卖出, 1表示持有/买入
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
}
}
+ return dp[len - 1][k][0];
+ }
+}
- int res = 0;
- for (int i = 1; i < k + 1; i++) {
- res = Math.max(res, dp[prices.length - 1][i][0]);
+// 版本二: 空间优化
+class Solution {
+ public int maxProfit(int k, int[] prices) {
+ if (prices.length == 0) return 0;
+
+ // [天数][股票状态]
+ // 股票状态: 奇数表示第 k 次交易持有/买入, 偶数表示第 k 次交易不持有/卖出, 0 表示没有操作
+ int len = prices.length;
+ int[][] dp = new int[len][k*2 + 1];
+
+ // dp数组的初始化, 与版本一同理
+ for (int i = 1; i < k*2; i += 2) {
+ dp[0][i] = -prices[0];
}
- return res;
+ for (int i = 1; i < len; i++) {
+ for (int j = 0; j < k*2 - 1; j += 2) {
+ dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
+ dp[i][j + 2] = Math.max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
+ }
+ }
+ return dp[len - 1][k*2];
}
}
```
Python:
-
+版本一
```python
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
@@ -226,11 +239,49 @@ class Solution:
dp[i][j+2] = max(dp[i-1][j+2], dp[i-1][j+1] + prices[i])
return dp[-1][2*k]
```
-
+版本二
+```python3
+class Solution:
+ def maxProfit(self, k: int, prices: List[int]) -> int:
+ if len(prices) == 0: return 0
+ dp = [0] * (2*k + 1)
+ for i in range(1,2*k,2):
+ dp[i] = -prices[0]
+ for i in range(1,len(prices)):
+ for j in range(1,2*k + 1):
+ if j % 2:
+ dp[j] = max(dp[j],dp[j-1]-prices[i])
+ else:
+ dp[j] = max(dp[j],dp[j-1]+prices[i])
+ return dp[2*k]
+```
Go:
+Javascript:
+```javascript
+const maxProfit = (k,prices) => {
+ if (prices == null || prices.length < 2 || k == 0) {
+ return 0;
+ }
+
+ let dp = Array.from(Array(prices.length), () => Array(2*k+1).fill(0));
+
+ for (let j = 1; j < 2 * k; j += 2) {
+ dp[0][j] = 0 - prices[0];
+ }
+
+ for(let i = 1; i < prices.length; i++) {
+ for (let j = 0; j < 2 * k; j += 2) {
+ dp[i][j+1] = Math.max(dp[i-1][j+1], dp[i-1][j] - prices[i]);
+ dp[i][j+2] = Math.max(dp[i-1][j+2], dp[i-1][j+1] + prices[i]);
+ }
+ }
+
+ return dp[prices.length - 1][2 * k];
+};
+```
-----------------------
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
diff --git a/problems/0300.最长上升子序列.md b/problems/0300.最长上升子序列.md
index 8b4ad5b1..9a7c543b 100644
--- a/problems/0300.最长上升子序列.md
+++ b/problems/0300.最长上升子序列.md
@@ -170,6 +170,25 @@ func lengthOfLIS(nums []int ) int {
return len(dp)
}
```
+
+Javascript
+```javascript
+const lengthOfLIS = (nums) => {
+ let dp = Array(nums.length).fill(1);
+ let result = 1;
+
+ for(let i = 1; i < nums.length; i++) {
+ for(let j = 0; j < i; j++) {
+ if(nums[i] > nums[j]) {
+ dp[i] = Math.max(dp[i], dp[j]+1);
+ }
+ }
+ result = Math.max(result, dp[i]);
+ }
+
+ return result;
+};
+```
*复杂度分析*
- 时间复杂度:O(nlogn)。数组 nums 的长度为 n,我们依次用数组中的元素去更新 dp 数组,相当于插入最后递增的元素,而更新 dp 数组时需要进行 O(logn) 的二分搜索,所以总时间复杂度为 O(nlogn)。
- 空间复杂度:O(n),需要额外使用长度为 n 的 dp 数组。
diff --git a/problems/0309.最佳买卖股票时机含冷冻期.md b/problems/0309.最佳买卖股票时机含冷冻期.md
index 4667c122..e28e8369 100644
--- a/problems/0309.最佳买卖股票时机含冷冻期.md
+++ b/problems/0309.最佳买卖股票时机含冷冻期.md
@@ -207,7 +207,29 @@ class Solution:
Go:
+Javascript:
+```javascript
+const maxProfit = (prices) => {
+ if(prices.length < 2) {
+ return 0
+ } else if(prices.length < 3) {
+ return Math.max(0, prices[1] - prices[0]);
+ }
+
+ let dp = Array.from(Array(prices.length), () => Array(4).fill(0));
+ dp[0][0] = 0 - prices[0];
+
+ for(i = 1; i < prices.length; i++) {
+ dp[i][0] = Math.max(dp[i - 1][0], Math.max(dp[i-1][1], dp[i-1][3]) - prices[i]);
+ dp[i][1] = Math.max(dp[i -1][1], dp[i - 1][3]);
+ dp[i][2] = dp[i-1][0] + prices[i];
+ dp[i][3] = dp[i-1][2];
+ }
+
+ return Math.max(dp[prices.length - 1][1], dp[prices.length - 1][2], dp[prices.length - 1][3]);
+};
+```
-----------------------
diff --git a/problems/0337.打家劫舍III.md b/problems/0337.打家劫舍III.md
index 3504a574..197841e9 100644
--- a/problems/0337.打家劫舍III.md
+++ b/problems/0337.打家劫舍III.md
@@ -173,7 +173,7 @@ return {val2, val1};
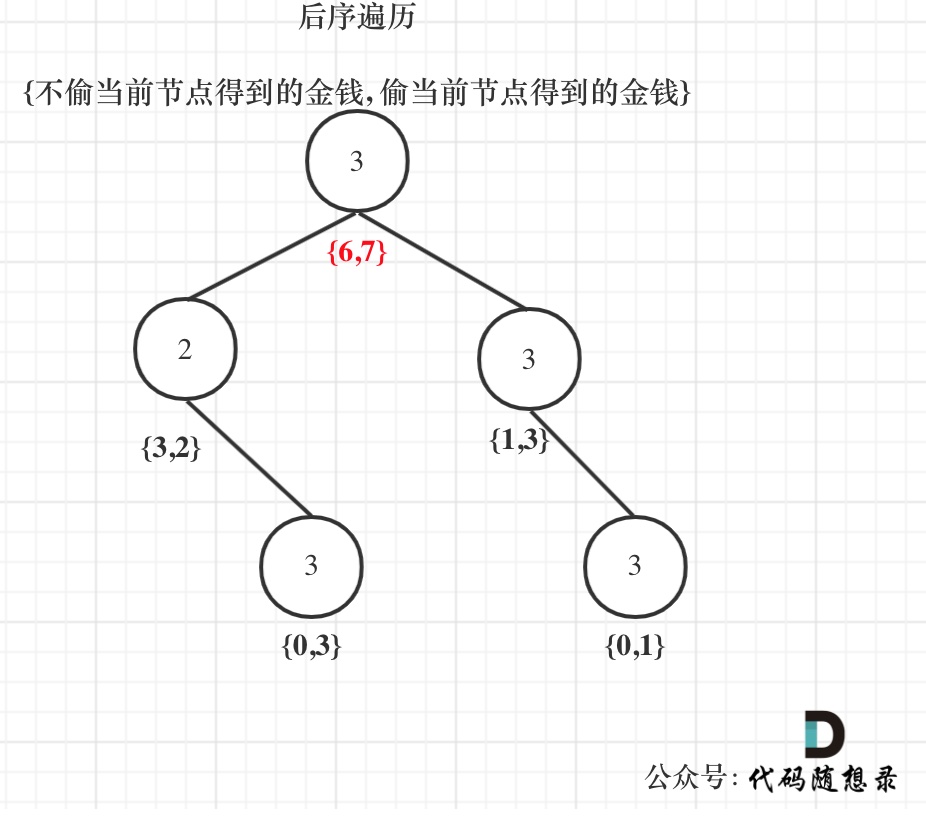
以示例1为例,dp数组状态如下:(**注意用后序遍历的方式推导**)
-
+
**最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱**。
diff --git a/problems/0347.前K个高频元素.md b/problems/0347.前K个高频元素.md
index 71af618e..6b07c258 100644
--- a/problems/0347.前K个高频元素.md
+++ b/problems/0347.前K个高频元素.md
@@ -18,18 +18,18 @@ https://leetcode-cn.com/problems/top-k-frequent-elements/
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例 1:
-输入: nums = [1,1,1,2,2,3], k = 2
-输出: [1,2]
+* 输入: nums = [1,1,1,2,2,3], k = 2
+* 输出: [1,2]
示例 2:
-输入: nums = [1], k = 1
-输出: [1]
+* 输入: nums = [1], k = 1
+* 输出: [1]
提示:
-你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
-你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
-题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
-你可以按任意顺序返回答案。
+* 你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
+* 你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
+* 题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
+* 你可以按任意顺序返回答案。
# 思路
@@ -70,7 +70,7 @@ https://leetcode-cn.com/problems/top-k-frequent-elements/
寻找前k个最大元素流程如图所示:(图中的频率只有三个,所以正好构成一个大小为3的小顶堆,如果频率更多一些,则用这个小顶堆进行扫描)
-
+
我们来看一下C++代码:
@@ -126,10 +126,7 @@ public:
优先级队列的定义正好反过来了,可能和优先级队列的源码实现有关(我没有仔细研究),我估计是底层实现上优先队列队首指向后面,队尾指向最前面的缘故!
-
-
-
-## 其他语言版本
+# 其他语言版本
Java:
diff --git a/problems/0501.二叉搜索树中的众数.md b/problems/0501.二叉搜索树中的众数.md
index 66be790f..ac7ff603 100644
--- a/problems/0501.二叉搜索树中的众数.md
+++ b/problems/0501.二叉搜索树中的众数.md
@@ -435,7 +435,7 @@ Python:
# self.val = val
# self.left = left
# self.right = right
-//递归法
+# 递归法
class Solution:
def findMode(self, root: TreeNode) -> List[int]:
if not root: return
@@ -460,6 +460,66 @@ class Solution:
return
findNumber(root)
return self.res
+
+
+# 迭代法-中序遍历-使用额外空间map的方法:
+class Solution:
+ def findMode(self, root: TreeNode) -> List[int]:
+ stack = []
+ cur = root
+ pre = None
+ dist = {}
+ while cur or stack:
+ if cur: # 指针来访问节点,访问到最底层
+ stack.append(cur)
+ cur = cur.left
+ else: # 逐一处理节点
+ cur = stack.pop()
+ if cur.val in dist:
+ dist[cur.val] += 1
+ else:
+ dist[cur.val] = 1
+ pre = cur
+ cur = cur.right
+
+ # 找出字典中最大的key
+ res = []
+ for key, value in dist.items():
+ if (value == max(dist.values())):
+ res.append(key)
+ return res
+
+# 迭代法-中序遍历-不使用额外空间,利用二叉搜索树特性:
+class Solution:
+ def findMode(self, root: TreeNode) -> List[int]:
+ stack = []
+ cur = root
+ pre = None
+ maxCount, count = 0, 0
+ res = []
+ while cur or stack:
+ if cur: # 指针来访问节点,访问到最底层
+ stack.append(cur)
+ cur = cur.left
+ else: # 逐一处理节点
+ cur = stack.pop()
+ if pre == None: # 第一个节点
+ count = 1
+ elif pre.val == cur.val: # 与前一个节点数值相同
+ count += 1
+ else:
+ count = 1
+ if count == maxCount:
+ res.append(cur.val)
+ if count > maxCount:
+ maxCount = count
+ res.clear()
+ res.append(cur.val)
+
+ pre = cur
+ cur = cur.right
+ return res
+
```
Go:
暴力法(非BSL)
diff --git a/problems/0503.下一个更大元素II.md b/problems/0503.下一个更大元素II.md
new file mode 100644
index 00000000..3980cb0e
--- /dev/null
+++ b/problems/0503.下一个更大元素II.md
@@ -0,0 +1,103 @@
+
+# 503.下一个更大元素II
+
+链接:https://leetcode-cn.com/problems/next-greater-element-ii/
+
+给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
+
+示例 1:
+
+* 输入: [1,2,1]
+* 输出: [2,-1,2]
+* 解释: 第一个 1 的下一个更大的数是 2;数字 2 找不到下一个更大的数;第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
+
+
+# 思路
+
+做本题之前建议先做[739. 每日温度](https://mp.weixin.qq.com/s/YeQ7eE0-hZpxJfJJziq25Q) 和 [496.下一个更大元素 I](https://mp.weixin.qq.com/s/U0O6XkFOe-RMXthPS16sWQ)。
+
+这道题和[739. 每日温度](https://mp.weixin.qq.com/s/YeQ7eE0-hZpxJfJJziq25Q)也几乎如出一辙。
+
+不同的时候本题要循环数组了。
+
+关于单调栈的讲解我在题解[739. 每日温度](https://mp.weixin.qq.com/s/YeQ7eE0-hZpxJfJJziq25Q)中已经详细讲解了。
+
+本篇我侧重与说一说,如何处理循环数组。
+
+相信不少同学看到这道题,就想那我直接把两个数组拼接在一起,然后使用单调栈求下一个最大值不就行了!
+
+确实可以!
+
+讲两个nums数组拼接在一起,使用单调栈计算出每一个元素的下一个最大值,最后再把结果集即result数组resize到原数组大小就可以了。
+
+代码如下:
+
+```C++
+// 版本一
+class Solution {
+public:
+ vector
欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+ # 二叉树理论基础篇 我们要开启新的征程了,大家跟上! diff --git a/problems/二叉树的递归遍历.md b/problems/二叉树的递归遍历.md index 68f17257..2b5a44dd 100644 --- a/problems/二叉树的递归遍历.md +++ b/problems/二叉树的递归遍历.md @@ -111,7 +111,7 @@ void traversal(TreeNode* cur, vector -40. [动态规划:最长递增子序列](./problems/0300.最长上升子序列.md)
-41. [动态规划:最长连续递增序列](./problems/0674.最长连续递增序列.md)
-42. [动态规划:最长重复子数组](./problems/0718.最长重复子数组.md)
-43. [动态规划:最长公共子序列](./problems/1143.最长公共子序列.md)
+41. [动态规划:最长递增子序列](./problems/0300.最长上升子序列.md)
+42. [动态规划:最长连续递增序列](./problems/0674.最长连续递增序列.md)
+43. [动态规划:最长重复子数组](./problems/0718.最长重复子数组.md)
+44. [动态规划:最长公共子序列](./problems/1143.最长公共子序列.md)
45. [动态规划:不相交的线](./problems/1035.不相交的线.md)
46. [动态规划:最大子序和](./problems/0053.最大子序和(动态规划).md)
47. [动态规划:判断子序列](./problems/0392.判断子序列.md)
48. [动态规划:不同的子序列](./problems/0115.不同的子序列.md)
49. [动态规划:两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
-51. [动态规划:编辑距离](./problems/0072.编辑距离.md)
-52. [为了绝杀编辑距离,Carl做了三步铺垫,你都知道么?](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
-53. [动态规划:回文子串](./problems/0647.回文子串.md)
-54. [动态规划:最长回文子序列](./problems/0516.最长回文子序列.md)
-55. [动态规划总结篇](./problems/动态规划总结篇.md)
+50. [动态规划:编辑距离](./problems/0072.编辑距离.md)
+51. [为了绝杀编辑距离,Carl做了三步铺垫,你都知道么?](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
+52. [动态规划:回文子串](./problems/0647.回文子串.md)
+53. [动态规划:最长回文子序列](./problems/0516.最长回文子序列.md)
+54. [动态规划总结篇](./problems/动态规划总结篇.md)
-(持续更新中....)
## 单调栈
1. [单调栈:每日温度](./problems/0739.每日温度.md)
2. [单调栈:下一个更大元素I](./problems/0496.下一个更大元素I.md)
+3. [单调栈:下一个更大元素II](./problems/0503.下一个更大元素II.md)
+4. [单调栈:接雨水](./problems/0042.接雨水.md)
+
+(持续更新中....)
## 图论
diff --git a/problems/0042.接雨水.md b/problems/0042.接雨水.md
new file mode 100644
index 00000000..55a5c522
--- /dev/null
+++ b/problems/0042.接雨水.md
@@ -0,0 +1,357 @@
+
+
+# 42. 接雨水
+
+题目链接:https://leetcode-cn.com/problems/trapping-rain-water/
+
+给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
+
+示例 1:
+
+
+
+* 输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
+* 输出:6
+* 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
+
+示例 2:
+
+* 输入:height = [4,2,0,3,2,5]
+* 输出:9
+
+
+# 思路
+
+接雨水问题在面试中还是常见题目的,有必要好好讲一讲。
+
+本文深度讲解如下三种方法:
+* 双指针法
+* 动态规划
+* 单调栈
+
+## 双指针解法
+
+这道题目使用双指针法并不简单,我们来看一下思路。
+
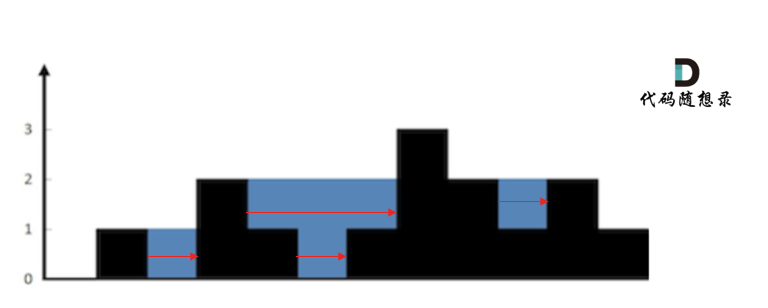
+首先要明确,要按照行来计算,还是按照列来计算。
+
+按照行来计算如图:
+
+
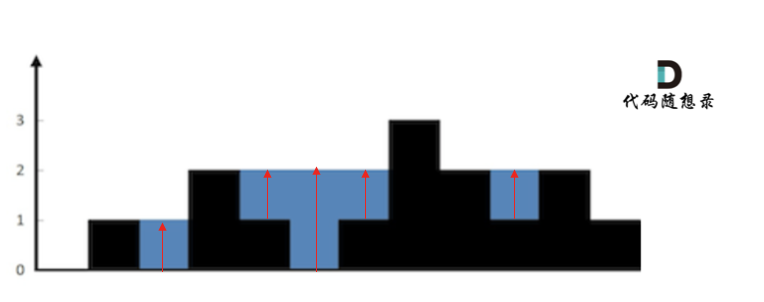
+按照列来计算如图:
+
+
+一些同学在实现的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
+
+我个人倾向于按照列来计算,比较容易理解,接下来看一下按照列如何计算。
+
+首先,**如果按照列来计算的话,宽度一定是1了,我们再把每一列的雨水的高度求出来就可以了。**
+
+可以看出每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
+
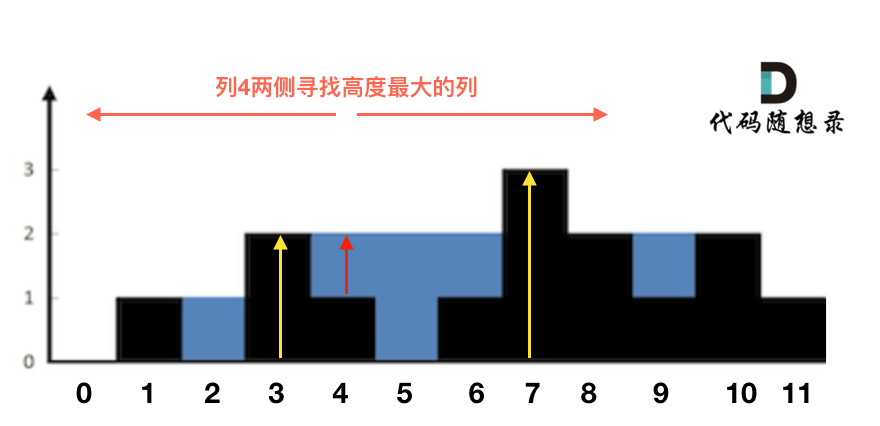
+这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
+
+
+
+列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
+
+列4 右侧最高的柱子是列7,高度为3(以下用rHeight表示)。
+
+列4 柱子的高度为1(以下用height表示)
+
+那么列4的雨水高度为 列3和列7的高度最小值减列4高度,即: min(lHeight, rHeight) - height。
+
+列4的雨水高度求出来了,宽度为1,相乘就是列4的雨水体积了。
+
+此时求出了列4的雨水体积。
+
+一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
+
+首先从头遍历所有的列,并且**要注意第一个柱子和最后一个柱子不接雨水**,代码如下:
+```C++
+for (int i = 0; i < height.size(); i++) {
+ // 第一个柱子和最后一个柱子不接雨水
+ if (i == 0 || i == height.size() - 1) continue;
+}
+```
+
+在for循环中求左右两边最高柱子,代码如下:
+
+```C++
+int rHeight = height[i]; // 记录右边柱子的最高高度
+int lHeight = height[i]; // 记录左边柱子的最高高度
+for (int r = i + 1; r < height.size(); r++) {
+ if (height[r] > rHeight) rHeight = height[r];
+}
+for (int l = i - 1; l >= 0; l--) {
+ if (height[l] > lHeight) lHeight = height[l];
+}
+```
+
+最后,计算该列的雨水高度,代码如下:
+
+```C++
+int h = min(lHeight, rHeight) - height[i];
+if (h > 0) sum += h; // 注意只有h大于零的时候,在统计到总和中
+```
+
+整体代码如下:
+
+```C++
+class Solution {
+public:
+ int trap(vector
-40. [动态规划:最长递增子序列](./problems/0300.最长上升子序列.md)
-41. [动态规划:最长连续递增序列](./problems/0674.最长连续递增序列.md)
-42. [动态规划:最长重复子数组](./problems/0718.最长重复子数组.md)
-43. [动态规划:最长公共子序列](./problems/1143.最长公共子序列.md)
+41. [动态规划:最长递增子序列](./problems/0300.最长上升子序列.md)
+42. [动态规划:最长连续递增序列](./problems/0674.最长连续递增序列.md)
+43. [动态规划:最长重复子数组](./problems/0718.最长重复子数组.md)
+44. [动态规划:最长公共子序列](./problems/1143.最长公共子序列.md)
45. [动态规划:不相交的线](./problems/1035.不相交的线.md)
46. [动态规划:最大子序和](./problems/0053.最大子序和(动态规划).md)
47. [动态规划:判断子序列](./problems/0392.判断子序列.md)
48. [动态规划:不同的子序列](./problems/0115.不同的子序列.md)
49. [动态规划:两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
-51. [动态规划:编辑距离](./problems/0072.编辑距离.md)
-52. [为了绝杀编辑距离,Carl做了三步铺垫,你都知道么?](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
-53. [动态规划:回文子串](./problems/0647.回文子串.md)
-54. [动态规划:最长回文子序列](./problems/0516.最长回文子序列.md)
-55. [动态规划总结篇](./problems/动态规划总结篇.md)
+50. [动态规划:编辑距离](./problems/0072.编辑距离.md)
+51. [为了绝杀编辑距离,Carl做了三步铺垫,你都知道么?](./problems/为了绝杀编辑距离,卡尔做了三步铺垫.md)
+52. [动态规划:回文子串](./problems/0647.回文子串.md)
+53. [动态规划:最长回文子序列](./problems/0516.最长回文子序列.md)
+54. [动态规划总结篇](./problems/动态规划总结篇.md)
-(持续更新中....)
## 单调栈
1. [单调栈:每日温度](./problems/0739.每日温度.md)
2. [单调栈:下一个更大元素I](./problems/0496.下一个更大元素I.md)
+3. [单调栈:下一个更大元素II](./problems/0503.下一个更大元素II.md)
+4. [单调栈:接雨水](./problems/0042.接雨水.md)
+
+(持续更新中....)
## 图论
diff --git a/problems/0042.接雨水.md b/problems/0042.接雨水.md
new file mode 100644
index 00000000..55a5c522
--- /dev/null
+++ b/problems/0042.接雨水.md
@@ -0,0 +1,357 @@
+
+
+# 42. 接雨水
+
+题目链接:https://leetcode-cn.com/problems/trapping-rain-water/
+
+给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
+
+示例 1:
+
+
+
+* 输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
+* 输出:6
+* 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
+
+示例 2:
+
+* 输入:height = [4,2,0,3,2,5]
+* 输出:9
+
+
+# 思路
+
+接雨水问题在面试中还是常见题目的,有必要好好讲一讲。
+
+本文深度讲解如下三种方法:
+* 双指针法
+* 动态规划
+* 单调栈
+
+## 双指针解法
+
+这道题目使用双指针法并不简单,我们来看一下思路。
+
+首先要明确,要按照行来计算,还是按照列来计算。
+
+按照行来计算如图:
+
+
+按照列来计算如图:
+
+
+一些同学在实现的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
+
+我个人倾向于按照列来计算,比较容易理解,接下来看一下按照列如何计算。
+
+首先,**如果按照列来计算的话,宽度一定是1了,我们再把每一列的雨水的高度求出来就可以了。**
+
+可以看出每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
+
+这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
+
+
+
+列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
+
+列4 右侧最高的柱子是列7,高度为3(以下用rHeight表示)。
+
+列4 柱子的高度为1(以下用height表示)
+
+那么列4的雨水高度为 列3和列7的高度最小值减列4高度,即: min(lHeight, rHeight) - height。
+
+列4的雨水高度求出来了,宽度为1,相乘就是列4的雨水体积了。
+
+此时求出了列4的雨水体积。
+
+一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
+
+首先从头遍历所有的列,并且**要注意第一个柱子和最后一个柱子不接雨水**,代码如下:
+```C++
+for (int i = 0; i < height.size(); i++) {
+ // 第一个柱子和最后一个柱子不接雨水
+ if (i == 0 || i == height.size() - 1) continue;
+}
+```
+
+在for循环中求左右两边最高柱子,代码如下:
+
+```C++
+int rHeight = height[i]; // 记录右边柱子的最高高度
+int lHeight = height[i]; // 记录左边柱子的最高高度
+for (int r = i + 1; r < height.size(); r++) {
+ if (height[r] > rHeight) rHeight = height[r];
+}
+for (int l = i - 1; l >= 0; l--) {
+ if (height[l] > lHeight) lHeight = height[l];
+}
+```
+
+最后,计算该列的雨水高度,代码如下:
+
+```C++
+int h = min(lHeight, rHeight) - height[i];
+if (h > 0) sum += h; // 注意只有h大于零的时候,在统计到总和中
+```
+
+整体代码如下:
+
+```C++
+class Solution {
+public:
+ int trap(vector