mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-06 15:09:40 +08:00
Merge branch 'youngyangyang04:master' into master
This commit is contained in:
7
.gitignore
vendored
Normal file
7
.gitignore
vendored
Normal file
@ -0,0 +1,7 @@
|
||||
.idea/
|
||||
.DS_Store
|
||||
.vscode
|
||||
.temp
|
||||
.cache
|
||||
*.iml
|
||||
__pycache__
|
||||
@ -106,8 +106,8 @@
|
||||
4. [数组:977.有序数组的平方](./problems/0977.有序数组的平方.md)
|
||||
5. [数组:209.长度最小的子数组](./problems/0209.长度最小的子数组.md)
|
||||
6. [数组:区间和](./problems/kamacoder/0058.区间和.md)
|
||||
6. [数组:59.螺旋矩阵II](./problems/0059.螺旋矩阵II.md)
|
||||
8. [数组:开发商购买土地](./problems/kamacoder/0044.开发商购买土地.md)
|
||||
7. [数组:开发商购买土地](./problems/kamacoder/0044.开发商购买土地.md)
|
||||
8. [数组:59.螺旋矩阵II](./problems/0059.螺旋矩阵II.md)
|
||||
9. [数组:总结篇](./problems/数组总结篇.md)
|
||||
|
||||
## 链表
|
||||
@ -196,7 +196,6 @@
|
||||
12. [二叉树:110.平衡二叉树](./problems/0110.平衡二叉树.md)
|
||||
13. [二叉树:257.二叉树的所有路径](./problems/0257.二叉树的所有路径.md)
|
||||
14. [本周总结!(二叉树)](./problems/周总结/20201003二叉树周末总结.md)
|
||||
15. [二叉树:二叉树中递归带着回溯](./problems/二叉树中递归带着回溯.md)
|
||||
16. [二叉树:404.左叶子之和](./problems/0404.左叶子之和.md)
|
||||
17. [二叉树:513.找树左下角的值](./problems/0513.找树左下角的值.md)
|
||||
18. [二叉树:112.路径总和](./problems/0112.路径总和.md)
|
||||
@ -400,7 +399,7 @@
|
||||
24. [图论:Bellman_ford 算法](./problems/kamacoder/0094.城市间货物运输I.md)
|
||||
25. [图论:Bellman_ford 队列优化算法(又名SPFA)](./problems/kamacoder/0094.城市间货物运输I-SPFA.md)
|
||||
26. [图论:Bellman_ford之判断负权回路](./problems/kamacoder/0095.城市间货物运输II.md)
|
||||
27. [图论:Bellman_ford之单源有限最短路](./problems/kamacoder/0095.城市间货物运输II.md)
|
||||
27. [图论:Bellman_ford之单源有限最短路](./problems/kamacoder/0096.城市间货物运输III.md)
|
||||
28. [图论:Floyd 算法](./problems/kamacoder/0097.小明逛公园.md)
|
||||
29. [图论:A * 算法](./problems/kamacoder/0126.骑士的攻击astar.md)
|
||||
30. [图论:最短路算法总结篇](./problems/kamacoder/最短路问题总结篇.md)
|
||||
|
||||
@ -256,7 +256,60 @@ public:
|
||||
* 时间复杂度:O(n^2)
|
||||
* 空间复杂度:O(1)
|
||||
|
||||
### Manacher 算法
|
||||
|
||||
Manacher 算法的关键在于高效利用回文的对称性,通过插入分隔符和维护中心、边界等信息,在线性时间内找到最长回文子串。这种方法避免了重复计算,是处理回文问题的最优解。
|
||||
|
||||
```c++
|
||||
//Manacher 算法
|
||||
class Solution {
|
||||
public:
|
||||
string longestPalindrome(string s) {
|
||||
// 预处理字符串,在每个字符之间插入 '#'
|
||||
string t = "#";
|
||||
for (char c : s) {
|
||||
t += c; // 添加字符
|
||||
t += '#';// 添加分隔符
|
||||
}
|
||||
int n = t.size();// 新字符串的长度
|
||||
vector<int> p(n, 0);// p[i] 表示以 t[i] 为中心的回文半径
|
||||
int center = 0, right = 0;// 当前回文的中心和右边界
|
||||
|
||||
|
||||
// 遍历预处理后的字符串
|
||||
for (int i = 0; i < n; i++) {
|
||||
// 如果当前索引在右边界内,利用对称性初始化 p[i]
|
||||
if (i < right) {
|
||||
p[i] = min(right - i, p[2 * center - i]);
|
||||
}
|
||||
// 尝试扩展回文
|
||||
while (i - p[i] - 1 >= 0 && i + p[i] + 1 < n && t[i - p[i] - 1] == t[i + p[i] + 1]) {
|
||||
p[i]++;// 增加回文半径
|
||||
}
|
||||
// 如果当前回文扩展超出右边界,更新中心和右边界
|
||||
if (i + p[i] > right) {
|
||||
center = i;// 更新中心
|
||||
right = i + p[i];// 更新右边界
|
||||
}
|
||||
}
|
||||
// 找到最大回文半径和对应的中心
|
||||
int maxLen = 0, centerIndex = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (p[i] > maxLen) {
|
||||
maxLen = p[i];// 更新最大回文长度
|
||||
centerIndex = i;// 更新中心索引
|
||||
}
|
||||
}
|
||||
// 计算原字符串中回文子串的起始位置并返回
|
||||
return s.substr((centerIndex - maxLen) / 2, maxLen);
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(n)
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
@ -682,3 +735,4 @@ public class Solution {
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
@ -201,6 +201,7 @@ class Solution {
|
||||
public void backtrack(int[] nums, LinkedList<Integer> path) {
|
||||
if (path.size() == nums.length) {
|
||||
result.add(new ArrayList<>(path));
|
||||
return;
|
||||
}
|
||||
for (int i =0; i < nums.length; i++) {
|
||||
// 如果path中已有,则跳过
|
||||
@ -524,3 +525,4 @@ public class Solution
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
@ -214,6 +214,7 @@ class Solution:
|
||||
return result
|
||||
|
||||
```
|
||||
贪心法
|
||||
```python
|
||||
class Solution:
|
||||
def maxSubArray(self, nums):
|
||||
@ -226,9 +227,55 @@ class Solution:
|
||||
if count <= 0: # 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
|
||||
count = 0
|
||||
return result
|
||||
|
||||
|
||||
```
|
||||
动态规划
|
||||
```python
|
||||
class Solution:
|
||||
def maxSubArray(self, nums: List[int]) -> int:
|
||||
dp = [0] * len(nums)
|
||||
dp[0] = nums[0]
|
||||
res = nums[0]
|
||||
for i in range(1, len(nums)):
|
||||
dp[i] = max(dp[i-1] + nums[i], nums[i])
|
||||
res = max(res, dp[i])
|
||||
return res
|
||||
```
|
||||
|
||||
动态规划
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def maxSubArray(self, nums):
|
||||
if not nums:
|
||||
return 0
|
||||
dp = [0] * len(nums) # dp[i]表示包括i之前的最大连续子序列和
|
||||
dp[0] = nums[0]
|
||||
result = dp[0]
|
||||
for i in range(1, len(nums)):
|
||||
dp[i] = max(dp[i-1]+nums[i], nums[i]) # 状态转移公式
|
||||
if dp[i] > result:
|
||||
result = dp[i] # result 保存dp[i]的最大值
|
||||
return result
|
||||
```
|
||||
|
||||
动态规划优化
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def maxSubArray(self, nums: List[int]) -> int:
|
||||
max_sum = float("-inf") # 初始化结果为负无穷大,方便比较取最大值
|
||||
current_sum = 0 # 初始化当前连续和
|
||||
|
||||
for num in nums:
|
||||
|
||||
# 更新当前连续和
|
||||
# 如果原本的连续和加上当前数字之后没有当前数字大,说明原本的连续和是负数,那么就直接从当前数字开始重新计算连续和
|
||||
current_sum = max(current_sum+num, num)
|
||||
max_sum = max(max_sum, current_sum) # 更新结果
|
||||
|
||||
return max_sum
|
||||
```
|
||||
|
||||
### Go
|
||||
贪心法
|
||||
```go
|
||||
|
||||
@ -143,6 +143,23 @@ class Solution:
|
||||
return False
|
||||
```
|
||||
|
||||
```python
|
||||
## 基于当前最远可到达位置判断
|
||||
class Solution:
|
||||
def canJump(self, nums: List[int]) -> bool:
|
||||
far = nums[0]
|
||||
for i in range(len(nums)):
|
||||
# 要考虑两个情况
|
||||
# 1. i <= far - 表示 当前位置i 可以到达
|
||||
# 2. i > far - 表示 当前位置i 无法到达
|
||||
if i > far:
|
||||
return False
|
||||
far = max(far, nums[i]+i)
|
||||
# 如果循环正常结束,表示最后一个位置也可以到达,否则会在中途直接退出
|
||||
# 关键点在于,要想明白其实列表中的每个位置都是需要验证能否到达的
|
||||
return True
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
```go
|
||||
|
||||
@ -184,6 +184,16 @@ if __name__ == '__main__':
|
||||
|
||||
### Go:
|
||||
```go
|
||||
package main
|
||||
|
||||
import (
|
||||
"bufio"
|
||||
"fmt"
|
||||
"os"
|
||||
"strconv"
|
||||
"strings"
|
||||
)
|
||||
|
||||
func climbStairs(n int, m int) int {
|
||||
dp := make([]int, n+1)
|
||||
dp[0] = 1
|
||||
|
||||
@ -376,9 +376,8 @@ class Solution {
|
||||
// 剪枝:ip段的长度最大是3,并且ip段处于[0,255]
|
||||
for (int i = start; i < s.length() && i - start < 3 && Integer.parseInt(s.substring(start, i + 1)) >= 0
|
||||
&& Integer.parseInt(s.substring(start, i + 1)) <= 255; i++) {
|
||||
// 如果ip段的长度大于1,并且第一位为0的话,continue
|
||||
if (i + 1 - start > 1 && s.charAt(start) - '0' == 0) {
|
||||
continue;
|
||||
break;
|
||||
}
|
||||
stringBuilder.append(s.substring(start, i + 1));
|
||||
// 当stringBuilder里的网段数量小于3时,才会加点;如果等于3,说明已经有3段了,最后一段不需要再加点
|
||||
@ -467,9 +466,37 @@ class Solution:
|
||||
num = int(s[start:end+1])
|
||||
return 0 <= num <= 255
|
||||
|
||||
回溯(版本三)
|
||||
|
||||
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def restoreIpAddresses(self, s: str) -> List[str]:
|
||||
result = []
|
||||
self.backtracking(s, 0, [], result)
|
||||
return result
|
||||
|
||||
def backtracking(self, s, startIndex, path, result):
|
||||
if startIndex == len(s):
|
||||
result.append('.'.join(path[:]))
|
||||
return
|
||||
|
||||
for i in range(startIndex, min(startIndex+3, len(s))):
|
||||
# 如果 i 往后遍历了,并且当前地址的第一个元素是 0 ,就直接退出
|
||||
if i > startIndex and s[startIndex] == '0':
|
||||
break
|
||||
# 比如 s 长度为 5,当前遍历到 i = 3 这个元素
|
||||
# 因为还没有执行任何操作,所以此时剩下的元素数量就是 5 - 3 = 2 ,即包括当前的 i 本身
|
||||
# path 里面是当前包含的子串,所以有几个元素就表示储存了几个地址
|
||||
# 所以 (4 - len(path)) * 3 表示当前路径至多能存放的元素个数
|
||||
# 4 - len(path) 表示至少要存放的元素个数
|
||||
if (4 - len(path)) * 3 < len(s) - i or 4 - len(path) > len(s) - i:
|
||||
break
|
||||
if i - startIndex == 2:
|
||||
if not int(s[startIndex:i+1]) <= 255:
|
||||
break
|
||||
path.append(s[startIndex:i+1])
|
||||
self.backtracking(s, i+1, path, result)
|
||||
path.pop()
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
@ -609,10 +609,13 @@ class Solution:
|
||||
while stack:
|
||||
node = stack.pop()
|
||||
if node:
|
||||
stack.append(node)
|
||||
stack.append(node) # 中
|
||||
stack.append(None)
|
||||
if node.left: stack.append(node.left)
|
||||
if node.right: stack.append(node.right)
|
||||
# 采用数组进行迭代,先将右节点加入,保证左节点能够先出栈
|
||||
if node.right: # 右
|
||||
stack.append(node.right)
|
||||
if node.left: # 左
|
||||
stack.append(node.left)
|
||||
else:
|
||||
real_node = stack.pop()
|
||||
left, right = height_map.get(real_node.left, 0), height_map.get(real_node.right, 0)
|
||||
|
||||
@ -564,10 +564,10 @@ class Solution:
|
||||
|
||||
return False
|
||||
|
||||
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
|
||||
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
|
||||
if root is None:
|
||||
return False
|
||||
return self.traversal(root, sum - root.val)
|
||||
return self.traversal(root, targetSum - root.val)
|
||||
```
|
||||
|
||||
(版本二) 递归 + 精简
|
||||
@ -579,12 +579,12 @@ class Solution:
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
|
||||
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
|
||||
if not root:
|
||||
return False
|
||||
if not root.left and not root.right and sum == root.val:
|
||||
if not root.left and not root.right and targetSum == root.val:
|
||||
return True
|
||||
return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)
|
||||
return self.hasPathSum(root.left, targetSum - root.val) or self.hasPathSum(root.right, targetSum - root.val)
|
||||
|
||||
```
|
||||
(版本三) 迭代
|
||||
@ -596,7 +596,7 @@ class Solution:
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
|
||||
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
|
||||
if not root:
|
||||
return False
|
||||
# 此时栈里要放的是pair<节点指针,路径数值>
|
||||
@ -659,13 +659,13 @@ class Solution:
|
||||
|
||||
return
|
||||
|
||||
def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
|
||||
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
|
||||
self.result.clear()
|
||||
self.path.clear()
|
||||
if not root:
|
||||
return self.result
|
||||
self.path.append(root.val) # 把根节点放进路径
|
||||
self.traversal(root, sum - root.val)
|
||||
self.traversal(root, targetSum - root.val)
|
||||
return self.result
|
||||
```
|
||||
|
||||
@ -678,7 +678,7 @@ class Solution:
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def pathSum(self, root: TreeNode, targetSum: int) -> List[List[int]]:
|
||||
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
|
||||
|
||||
result = []
|
||||
self.traversal(root, targetSum, [], result)
|
||||
@ -703,7 +703,7 @@ class Solution:
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def pathSum(self, root: TreeNode, targetSum: int) -> List[List[int]]:
|
||||
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
|
||||
if not root:
|
||||
return []
|
||||
stack = [(root, [root.val])]
|
||||
|
||||
@ -251,6 +251,27 @@ func max(a, b int) int {
|
||||
}
|
||||
```
|
||||
|
||||
```go
|
||||
// 动态规划 版本二 滚动数组
|
||||
func maxProfit(prices []int) int {
|
||||
dp := [2][2]int{} // 注意这里只开辟了一个2 * 2大小的二维数组
|
||||
dp[0][0] = -prices[0]
|
||||
dp[0][1] = 0
|
||||
for i := 1; i < len(prices); i++ {
|
||||
dp[i%2][0] = max(dp[(i-1)%2][0], dp[(i - 1) % 2][1] - prices[i])
|
||||
dp[i%2][1] = max(dp[(i-1)%2][1], dp[(i-1)%2][0] + prices[i])
|
||||
}
|
||||
return dp[(len(prices)-1)%2][1]
|
||||
}
|
||||
|
||||
func max(x, y int) int {
|
||||
if x > y {
|
||||
return x
|
||||
}
|
||||
return y
|
||||
}
|
||||
```
|
||||
|
||||
### JavaScript:
|
||||
|
||||
```javascript
|
||||
|
||||
@ -317,6 +317,7 @@ class Solution:
|
||||
### Go:
|
||||
|
||||
```go
|
||||
// 版本一
|
||||
func maxProfit(prices []int) int {
|
||||
dp := make([][]int, len(prices))
|
||||
for i := 0; i < len(prices); i++ {
|
||||
@ -344,6 +345,58 @@ func max(a, b int) int {
|
||||
}
|
||||
```
|
||||
|
||||
```go
|
||||
// 版本二
|
||||
func maxProfit(prices []int) int {
|
||||
if len(prices) == 0 {
|
||||
return 0
|
||||
}
|
||||
dp := make([]int, 5)
|
||||
dp[1] = -prices[0]
|
||||
dp[3] = -prices[0]
|
||||
for i := 1; i < len(prices); i++ {
|
||||
dp[1] = max(dp[1], dp[0] - prices[i])
|
||||
dp[2] = max(dp[2], dp[1] + prices[i])
|
||||
dp[3] = max(dp[3], dp[2] - prices[i])
|
||||
dp[4] = max(dp[4], dp[3] + prices[i])
|
||||
}
|
||||
return dp[4]
|
||||
}
|
||||
|
||||
func max(x, y int) int {
|
||||
if x > y {
|
||||
return x
|
||||
}
|
||||
return y
|
||||
}
|
||||
```
|
||||
|
||||
```go
|
||||
// 版本三
|
||||
func maxProfit(prices []int) int {
|
||||
if len(prices) == 0 {
|
||||
return 0
|
||||
}
|
||||
dp := make([][5]int, len(prices))
|
||||
dp[0][1] = -prices[0]
|
||||
dp[0][3] = -prices[0]
|
||||
for i := 1; i < len(prices); i++ {
|
||||
dp[i][1] = max(dp[i-1][1], 0 - prices[i])
|
||||
dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i])
|
||||
dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i])
|
||||
dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i])
|
||||
}
|
||||
return dp[len(prices)-1][4]
|
||||
}
|
||||
|
||||
func max(x, y int) int {
|
||||
if x > y {
|
||||
return x
|
||||
}
|
||||
return y
|
||||
}
|
||||
```
|
||||
|
||||
### JavaScript:
|
||||
|
||||
> 版本一:
|
||||
|
||||
@ -158,7 +158,7 @@ i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i
|
||||
|
||||
如果 curSum<0 说明 区间和1 + 区间和2 < 0, 那么 假设从上图中的位置开始计数curSum不会小于0的话,就是 区间和2>0。
|
||||
|
||||
区间和1 + 区间和2 < 0 同时 区间和2>0,只能说明区间和1 < 0, 那么就会从假设的箭头初就开始从新选择其实位置了。
|
||||
区间和1 + 区间和2 < 0 同时 区间和2>0,只能说明区间和1 < 0, 那么就会从假设的箭头初就开始从新选择起始位置了。
|
||||
|
||||
|
||||
**那么局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置**。
|
||||
|
||||
@ -177,21 +177,20 @@ class Solution {
|
||||
```python
|
||||
class Solution:
|
||||
def candy(self, ratings: List[int]) -> int:
|
||||
candyVec = [1] * len(ratings)
|
||||
n = len(ratings)
|
||||
candies = [1] * n
|
||||
|
||||
# 从前向后遍历,处理右侧比左侧评分高的情况
|
||||
for i in range(1, len(ratings)):
|
||||
# Forward pass: handle cases where right rating is higher than left
|
||||
for i in range(1, n):
|
||||
if ratings[i] > ratings[i - 1]:
|
||||
candyVec[i] = candyVec[i - 1] + 1
|
||||
candies[i] = candies[i - 1] + 1
|
||||
|
||||
# 从后向前遍历,处理左侧比右侧评分高的情况
|
||||
for i in range(len(ratings) - 2, -1, -1):
|
||||
# Backward pass: handle cases where left rating is higher than right
|
||||
for i in range(n - 2, -1, -1):
|
||||
if ratings[i] > ratings[i + 1]:
|
||||
candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1)
|
||||
candies[i] = max(candies[i], candies[i + 1] + 1)
|
||||
|
||||
# 统计结果
|
||||
result = sum(candyVec)
|
||||
return result
|
||||
return sum(candies)
|
||||
|
||||
```
|
||||
|
||||
|
||||
@ -108,7 +108,7 @@ public:
|
||||
}
|
||||
}
|
||||
|
||||
int result = st.top();
|
||||
long long result = st.top();
|
||||
st.pop(); // 把栈里最后一个元素弹出(其实不弹出也没事)
|
||||
return result;
|
||||
}
|
||||
|
||||
@ -440,11 +440,10 @@ class Solution {
|
||||
```Python
|
||||
class Solution:
|
||||
def reverseWords(self, s: str) -> str:
|
||||
# 删除前后空白
|
||||
s = s.strip()
|
||||
# 反转整个字符串
|
||||
s = s[::-1]
|
||||
# 将字符串拆分为单词,并反转每个单词
|
||||
# split()函数能够自动忽略多余的空白字符
|
||||
s = ' '.join(word[::-1] for word in s.split())
|
||||
return s
|
||||
|
||||
@ -475,7 +474,45 @@ class Solution:
|
||||
words = words[::-1] # 反转单词
|
||||
return ' '.join(words) #列表转换成字符串
|
||||
```
|
||||
(版本四) 将字符串转换为列表后,使用双指针去除空格
|
||||
```python
|
||||
class Solution:
|
||||
def single_reverse(self, s, start: int, end: int):
|
||||
while start < end:
|
||||
s[start], s[end] = s[end], s[start]
|
||||
start += 1
|
||||
end -= 1
|
||||
|
||||
def reverseWords(self, s: str) -> str:
|
||||
result = ""
|
||||
fast = 0
|
||||
# 1. 首先将原字符串反转并且除掉空格, 并且加入到新的字符串当中
|
||||
# 由于Python字符串的不可变性,因此只能转换为列表进行处理
|
||||
s = list(s)
|
||||
s.reverse()
|
||||
while fast < len(s):
|
||||
if s[fast] != " ":
|
||||
if len(result) != 0:
|
||||
result += " "
|
||||
while s[fast] != " " and fast < len(s):
|
||||
result += s[fast]
|
||||
fast += 1
|
||||
else:
|
||||
fast += 1
|
||||
# 2.其次将每个单词进行翻转操作
|
||||
slow = 0
|
||||
fast = 0
|
||||
result = list(result)
|
||||
while fast <= len(result):
|
||||
if fast == len(result) or result[fast] == " ":
|
||||
self.single_reverse(result, slow, fast - 1)
|
||||
slow = fast + 1
|
||||
fast += 1
|
||||
else:
|
||||
fast += 1
|
||||
|
||||
return "".join(result)
|
||||
```
|
||||
### Go:
|
||||
|
||||
版本一:
|
||||
@ -991,3 +1028,4 @@ public string ReverseWords(string s) {
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
@ -199,7 +199,17 @@ function reverseByRange(nums: number[], left: number, right: number): void {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
### Rust
|
||||
```rust
|
||||
impl Solution {
|
||||
pub fn rotate(nums: &mut Vec<i32>, k: i32) {
|
||||
let k = k as usize % nums.len();
|
||||
nums.reverse();
|
||||
nums[..k].reverse();
|
||||
nums[k..].reverse();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
<p align="center">
|
||||
|
||||
@ -534,6 +534,30 @@ public class Solution {
|
||||
}
|
||||
```
|
||||
|
||||
### Ruby:
|
||||
|
||||
```ruby
|
||||
# @param {Integer} n
|
||||
# @return {Boolean}
|
||||
def is_happy(n)
|
||||
@occurred_nums = Set.new
|
||||
|
||||
while true
|
||||
n = next_value(n)
|
||||
|
||||
return true if n == 1
|
||||
|
||||
return false if @occurred_nums.include?(n)
|
||||
|
||||
@occurred_nums << n
|
||||
end
|
||||
end
|
||||
|
||||
def next_value(n)
|
||||
n.to_s.chars.sum { |char| char.to_i ** 2 }
|
||||
end
|
||||
```
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
|
||||
@ -459,11 +459,10 @@ class Solution:
|
||||
|
||||
queue = collections.deque([root])
|
||||
while queue:
|
||||
for i in range(len(queue)):
|
||||
node = queue.popleft()
|
||||
node.left, node.right = node.right, node.left
|
||||
if node.left: queue.append(node.left)
|
||||
if node.right: queue.append(node.right)
|
||||
node = queue.popleft()
|
||||
node.left, node.right = node.right, node.left
|
||||
if node.left: queue.append(node.left)
|
||||
if node.right: queue.append(node.right)
|
||||
return root
|
||||
|
||||
```
|
||||
@ -1033,4 +1032,3 @@ public TreeNode InvertTree(TreeNode root) {
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
@ -454,7 +454,11 @@ impl Solution {
|
||||
p: Option<Rc<RefCell<TreeNode>>>,
|
||||
q: Option<Rc<RefCell<TreeNode>>>,
|
||||
) -> Option<Rc<RefCell<TreeNode>>> {
|
||||
if root == p || root == q || root.is_none() {
|
||||
if root.is_none() {
|
||||
return root;
|
||||
}
|
||||
if Rc::ptr_eq(root.as_ref().unwrap(), p.as_ref().unwrap())
|
||||
|| Rc::ptr_eq(root.as_ref().unwrap(), q.as_ref().unwrap()) {
|
||||
return root;
|
||||
}
|
||||
let left = Self::lowest_common_ancestor(
|
||||
|
||||
@ -169,7 +169,20 @@ void moveZeroes(int* nums, int numsSize){
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
### Rust
|
||||
```rust
|
||||
impl Solution {
|
||||
pub fn move_zeroes(nums: &mut Vec<i32>) {
|
||||
let mut slow = 0;
|
||||
for fast in 0..nums.len() {
|
||||
if nums[fast] != 0 {
|
||||
nums.swap(slow, fast);
|
||||
slow += 1;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
@ -337,6 +337,29 @@ pub fn length_of_lis(nums: Vec<i32>) -> i32 {
|
||||
}
|
||||
```
|
||||
|
||||
### Cangjie:
|
||||
|
||||
```cangjie
|
||||
func lengthOfLIS(nums: Array<Int64>): Int64 {
|
||||
let n = nums.size
|
||||
if (n <= 1) {
|
||||
return n
|
||||
}
|
||||
|
||||
let dp = Array(n, item: 1)
|
||||
var res = 0
|
||||
for (i in 1..n) {
|
||||
for (j in 0..i) {
|
||||
if (nums[i] > nums[j]) {
|
||||
dp[i] = max(dp[i], dp[j] + 1)
|
||||
}
|
||||
}
|
||||
res = max(dp[i], res)
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
|
||||
@ -388,6 +388,90 @@ class Solution:
|
||||
|
||||
### Go
|
||||
|
||||
暴力递归
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
func rob(root *TreeNode) int {
|
||||
if root == nil {
|
||||
return 0
|
||||
}
|
||||
if root.Left == nil && root.Right == nil {
|
||||
return root.Val
|
||||
}
|
||||
// 偷父节点
|
||||
val1 := root.Val
|
||||
if root.Left != nil {
|
||||
val1 += rob(root.Left.Left) + rob(root.Left.Right) // 跳过root->left,相当于不考虑左孩子了
|
||||
}
|
||||
if root.Right != nil {
|
||||
val1 += rob(root.Right.Left) + rob(root.Right.Right) // 跳过root->right,相当于不考虑右孩子了
|
||||
}
|
||||
// 不偷父节点
|
||||
val2 := rob(root.Left) + rob(root.Right) // 考虑root的左右孩子
|
||||
return max(val1, val2)
|
||||
}
|
||||
|
||||
func max(x, y int) int {
|
||||
if x > y {
|
||||
return x
|
||||
}
|
||||
return y
|
||||
}
|
||||
```
|
||||
|
||||
记忆化递推
|
||||
|
||||
```go
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* type TreeNode struct {
|
||||
* Val int
|
||||
* Left *TreeNode
|
||||
* Right *TreeNode
|
||||
* }
|
||||
*/
|
||||
var umap = make(map[*TreeNode]int)
|
||||
|
||||
func rob(root *TreeNode) int {
|
||||
if root == nil {
|
||||
return 0
|
||||
}
|
||||
if root.Left == nil && root.Right == nil {
|
||||
return root.Val
|
||||
}
|
||||
if val, ok := umap[root]; ok {
|
||||
return val // 如果umap里已经有记录则直接返回
|
||||
}
|
||||
// 偷父节点
|
||||
val1 := root.Val
|
||||
if root.Left != nil {
|
||||
val1 += rob(root.Left.Left) + rob(root.Left.Right) // 跳过root->left,相当于不考虑左孩子了
|
||||
}
|
||||
if root.Right != nil {
|
||||
val1 += rob(root.Right.Left) + rob(root.Right.Right) // 跳过root->right,相当于不考虑右孩子了
|
||||
}
|
||||
// 不偷父节点
|
||||
val2 := rob(root.Left) + rob(root.Right) // 考虑root的左右孩子
|
||||
umap[root] = max(val1, val2) // umap记录一下结果
|
||||
return max(val1, val2)
|
||||
}
|
||||
|
||||
func max(x, y int) int {
|
||||
if x > y {
|
||||
return x
|
||||
}
|
||||
return y
|
||||
}
|
||||
```
|
||||
|
||||
动态规划
|
||||
|
||||
```go
|
||||
|
||||
@ -243,6 +243,29 @@ class Solution {
|
||||
}
|
||||
}
|
||||
```
|
||||
贪心
|
||||
```Java
|
||||
class Solution {
|
||||
public int integerBreak(int n) {
|
||||
// with 贪心
|
||||
// 通过数学原理拆出更多的3乘积越大,则
|
||||
/**
|
||||
@Param: an int, the integer we need to break.
|
||||
@Return: an int, the maximum integer after breaking
|
||||
@Method: Using math principle to solve this problem
|
||||
@Time complexity: O(1)
|
||||
**/
|
||||
if(n == 2) return 1;
|
||||
if(n == 3) return 2;
|
||||
int result = 1;
|
||||
while(n > 4) {
|
||||
n-=3;
|
||||
result *=3;
|
||||
}
|
||||
return result*n;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Python
|
||||
动态规划(版本一)
|
||||
|
||||
@ -176,7 +176,7 @@ class Solution:
|
||||
|
||||
for x in ransomNote:
|
||||
value = hashmap.get(x)
|
||||
if not value or not value:
|
||||
if not value:
|
||||
return False
|
||||
else:
|
||||
hashmap[x] -= 1
|
||||
|
||||
@ -47,7 +47,13 @@
|
||||
|
||||
那么只要找到集合里能够出现 sum / 2 的子集总和,就算是可以分割成两个相同元素和子集了。
|
||||
|
||||
本题是可以用回溯暴力搜索出所有答案的,但最后超时了,也不想再优化了,放弃回溯,直接上01背包吧。
|
||||
本题是可以用回溯暴力搜索出所有答案的,但最后超时了,也不想再优化了,放弃回溯。
|
||||
|
||||
是否有其他解法可以解决此题。
|
||||
|
||||
本题的本质是,能否把容量为 sum / 2的背包装满。
|
||||
|
||||
**这是 背包算法可以解决的经典类型题目**。
|
||||
|
||||
如果对01背包不够了解,建议仔细看完如下两篇:
|
||||
|
||||
@ -56,7 +62,7 @@
|
||||
|
||||
### 01背包问题
|
||||
|
||||
背包问题,大家都知道,有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
|
||||
01背包问题,大家都知道,有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
|
||||
|
||||
**背包问题有多种背包方式,常见的有:01背包、完全背包、多重背包、分组背包和混合背包等等。**
|
||||
|
||||
@ -64,32 +70,33 @@
|
||||
|
||||
**即一个商品如果可以重复多次放入是完全背包,而只能放入一次是01背包,写法还是不一样的。**
|
||||
|
||||
**要明确本题中我们要使用的是01背包,因为元素我们只能用一次。**
|
||||
**元素我们只能用一次,如果使用背包,那么也是01背包**
|
||||
|
||||
回归主题:首先,本题要求集合里能否出现总和为 sum / 2 的子集。
|
||||
|
||||
那么来一一对应一下本题,看看背包问题如何来解决。
|
||||
既有一个 只能装重量为 sum / 2 的背包,商品为数字,这些数字能不能把 这个背包装满。
|
||||
|
||||
**只有确定了如下四点,才能把01背包问题套到本题上来。**
|
||||
那每一件商品是数字的话,对应的重量 和 价值是多少呢?
|
||||
|
||||
* 背包的体积为sum / 2
|
||||
* 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
|
||||
* 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
|
||||
* 背包中每一个元素是不可重复放入。
|
||||
一个数字只有一个维度,即 重量等于价值。
|
||||
|
||||
以上分析完,我们就可以套用01背包,来解决这个问题了。
|
||||
当数字 可以装满 承载重量为 sum / 2 的背包的背包时,这个背包的价值也是 sum / 2。
|
||||
|
||||
那么这道题就是 装满 承载重量为 sum / 2 的背包,价值最大是多少?
|
||||
|
||||
如果最大价值是 sum / 2,说明正好被商品装满了。
|
||||
|
||||
因为商品是数字,重量和对应的价值是相同的。
|
||||
|
||||
以上分析完,我们就可以直接用01背包 来解决这个问题了。
|
||||
|
||||
动规五部曲分析如下:
|
||||
|
||||
1. 确定dp数组以及下标的含义
|
||||
|
||||
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
|
||||
01背包中,dp[j] 表示: 容量(所能装的重量)为j的背包,所背的物品价值最大可以为dp[j]。
|
||||
|
||||
本题中每一个元素的数值既是重量,也是价值。
|
||||
|
||||
**套到本题,dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]**。
|
||||
|
||||
那么如果背包容量为target, dp[target]就是装满 背包之后的重量,所以 当 dp[target] == target 的时候,背包就装满了。
|
||||
如果背包所载重量为target, dp[target]就是装满 背包之后的总价值,因为 本题中每一个元素的数值既是重量,也是价值,所以,当 dp[target] == target 的时候,背包就装满了。
|
||||
|
||||
有录友可能想,那还有装不满的时候?
|
||||
|
||||
@ -192,12 +199,11 @@ public:
|
||||
|
||||
## 总结
|
||||
|
||||
这道题目就是一道01背包应用类的题目,需要我们拆解题目,然后套入01背包的场景。
|
||||
这道题目就是一道01背包经典应用类的题目,需要我们拆解题目,然后才能发现可以使用01背包。
|
||||
|
||||
01背包相对于本题,主要要理解,题目中物品是nums[i],重量是nums[i],价值也是nums[i],背包体积是sum/2。
|
||||
|
||||
看代码的话,就可以发现,基本就是按照01背包的写法来的。
|
||||
|
||||
做完本题后,需要大家清晰:背包问题,不仅可以求 背包能被的最大价值,还可以求这个背包是否可以装满。
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
|
||||
@ -26,7 +26,7 @@
|
||||
|
||||
## 算法公开课
|
||||
|
||||
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[调整二叉树的结构最难!| LeetCode:450.删除二叉搜索树中的节点](https://www.bilibili.com/video/BV1tP41177us?share_source=copy_web),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||||
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[调整二叉树的结构最难!| LeetCode:450.删除二叉搜索树中的节点](https://www.bilibili.com/video/BV1tP41177us?share_source=copy_web),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||||
|
||||
## 思路
|
||||
|
||||
|
||||
@ -110,7 +110,7 @@ public:
|
||||
```
|
||||
|
||||
* 时间复杂度:O(nlog n),因为有一个快排
|
||||
* 空间复杂度:O(1),有一个快排,最差情况(倒序)时,需要n次递归调用。因此确实需要O(n)的栈空间
|
||||
* 空间复杂度:O(n),有一个快排,最差情况(倒序)时,需要n次递归调用。因此确实需要O(n)的栈空间
|
||||
|
||||
可以看出代码并不复杂。
|
||||
|
||||
@ -180,19 +180,25 @@ class Solution:
|
||||
```python
|
||||
class Solution: # 不改变原数组
|
||||
def findMinArrowShots(self, points: List[List[int]]) -> int:
|
||||
if len(points) == 0:
|
||||
return 0
|
||||
|
||||
points.sort(key = lambda x: x[0])
|
||||
sl,sr = points[0][0],points[0][1]
|
||||
|
||||
# points已经按照第一个坐标正序排列,因此只需要设置一个变量,记录右侧坐标(阈值)
|
||||
# 考虑一个气球范围包含两个不相交气球的情况:气球1: [1, 10], 气球2: [2, 5], 气球3: [6, 10]
|
||||
curr_min_right = points[0][1]
|
||||
count = 1
|
||||
|
||||
for i in points:
|
||||
if i[0]>sr:
|
||||
count+=1
|
||||
sl,sr = i[0],i[1]
|
||||
if i[0] > curr_min_right:
|
||||
# 当气球左侧大于这个阈值,那么一定就需要在发射一只箭,并且将阈值更新为当前气球的右侧
|
||||
count += 1
|
||||
curr_min_right = i[1]
|
||||
else:
|
||||
sl = max(sl,i[0])
|
||||
sr = min(sr,i[1])
|
||||
# 否则的话,我们只需要求阈值和当前气球的右侧的较小值来更新阈值
|
||||
curr_min_right = min(curr_min_right, i[1])
|
||||
return count
|
||||
|
||||
|
||||
```
|
||||
### Go
|
||||
```go
|
||||
|
||||
@ -488,6 +488,44 @@ int fourSumCount(int* nums1, int nums1Size, int* nums2, int nums2Size, int* nums
|
||||
}
|
||||
```
|
||||
|
||||
### Ruby:
|
||||
|
||||
```ruby
|
||||
# @param {Integer[]} nums1
|
||||
# @param {Integer[]} nums2
|
||||
# @param {Integer[]} nums3
|
||||
# @param {Integer[]} nums4
|
||||
# @return {Integer}
|
||||
# 新思路:和版主的思路基本相同,只是对后面两个数组的二重循环,用一个方法调用外加一重循环替代,简化了一点。
|
||||
# 简单的说,就是把四数和变成了两个两数和的统计(结果放到两个 hash 中),然后再来一次两数和为0.
|
||||
# 把四个数分成两组两个数,然后分别计算每组可能的和情况,分别存入 hash 中,key 是 和,value 是 数量;
|
||||
# 最后,得到的两个 hash 只需要遍历一次,符合和为零的 value 相乘并加总。
|
||||
def four_sum_count(nums1, nums2, nums3, nums4)
|
||||
num_to_count_1 = two_sum_mapping(nums1, nums2)
|
||||
num_to_count_2 = two_sum_mapping(nums3, nums4)
|
||||
|
||||
count_sum = 0
|
||||
|
||||
num_to_count_1.each do |num, count|
|
||||
count_sum += num_to_count_2[-num] * count # 反查另一个 hash,看有没有匹配的,没有的话,hash 默认值为 0,不影响加总;有匹配的,乘积就是可能的情况
|
||||
end
|
||||
|
||||
count_sum
|
||||
end
|
||||
|
||||
def two_sum_mapping(nums1, nums2)
|
||||
num_to_count = Hash.new(0)
|
||||
|
||||
nums1.each do |num1|
|
||||
nums2.each do |nums2|
|
||||
num_to_count[num1 + nums2] += 1 # 统计和为 num1 + nums2 的有几个
|
||||
end
|
||||
end
|
||||
|
||||
num_to_count
|
||||
end
|
||||
```
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
|
||||
@ -56,10 +56,66 @@
|
||||
|
||||
|
||||
|
||||
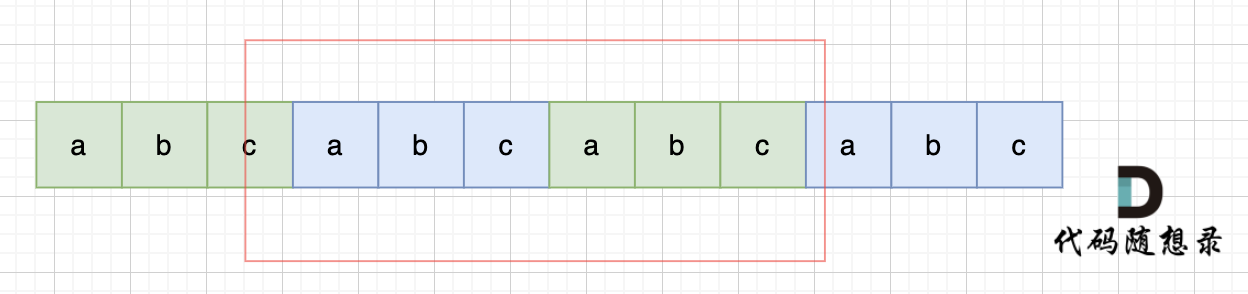
所以判断字符串s是否由重复子串组成,只要两个s拼接在一起,里面还出现一个s的话,就说明是由重复子串组成。
|
||||
|
||||
当然,我们在判断 s + s 拼接的字符串里是否出现一个s的的时候,**要刨除 s + s 的首字符和尾字符**,这样避免在s+s中搜索出原来的s,我们要搜索的是中间拼接出来的s。
|
||||
|
||||
|
||||
以上证明的充分性,接下来证明必要性:
|
||||
|
||||
如果有一个字符串s,在 s + s 拼接后, 不算首尾字符,如果能凑成s字符串,说明s 一定是重复子串组成。
|
||||
|
||||
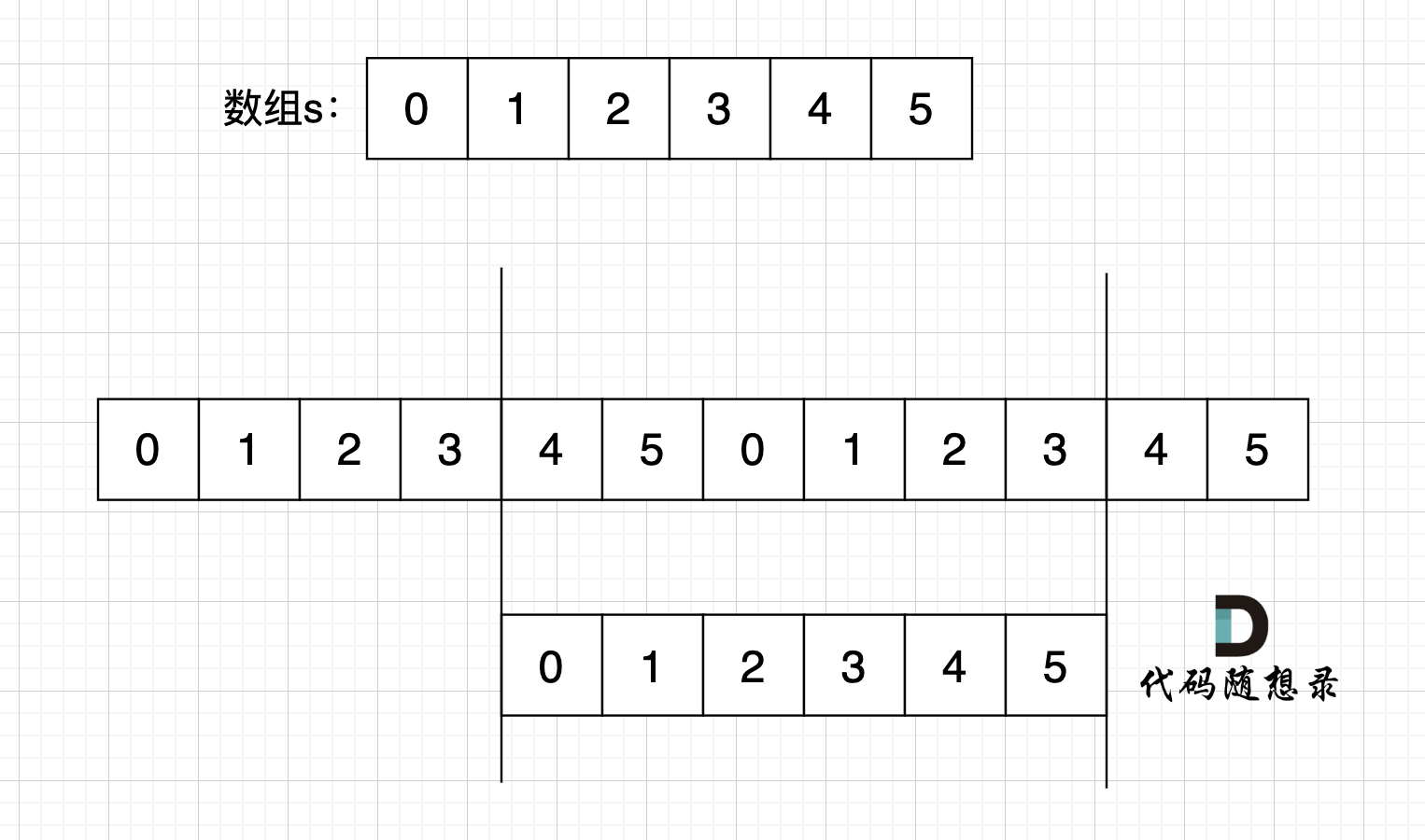
如图,字符串s,图中数字为数组下标,在 s + s 拼接后, 不算首尾字符,中间凑成s字符串。 (图中数字为数组下标)
|
||||
|
||||
|
||||
|
||||
图中,因为中间拼接成了s,根据红色框 可以知道 s[4] = s[0], s[5] = s[1], s[0] = s[2], s[1] = s[3] s[2] = s[4] ,s[3] = s[5]
|
||||
|
||||

|
||||
|
||||
以上相等关系我们串联一下:
|
||||
|
||||
s[4] = s[0] = s[2]
|
||||
|
||||
s[5] = s[1] = s[3]
|
||||
|
||||
|
||||
即:s[4],s[5] = s[0],s[1] = s[2],s[3]
|
||||
|
||||
**说明这个字符串,是由 两个字符 s[0] 和 s[1] 重复组成的**!
|
||||
|
||||
这里可以有录友想,凭什么就是这样组成的s呢,我换一个方式组成s 行不行,如图:
|
||||
|
||||

|
||||
|
||||
s[3] = s[0],s[4] = s[1] ,s[5] = s[2],s[0] = s[3],s[1] = s[4],s[2] = s[5]
|
||||
|
||||
以上相等关系串联:
|
||||
|
||||
s[3] = s[0]
|
||||
|
||||
s[1] = s[4]
|
||||
|
||||
s[2] = s[5]
|
||||
|
||||
s[0] s[1] s[2] = s[3] s[4] s[5]
|
||||
|
||||
和以上推导过程一样,最后可以推导出,这个字符串是由 s[0] ,s[1] ,s[2] 重复组成。
|
||||
|
||||
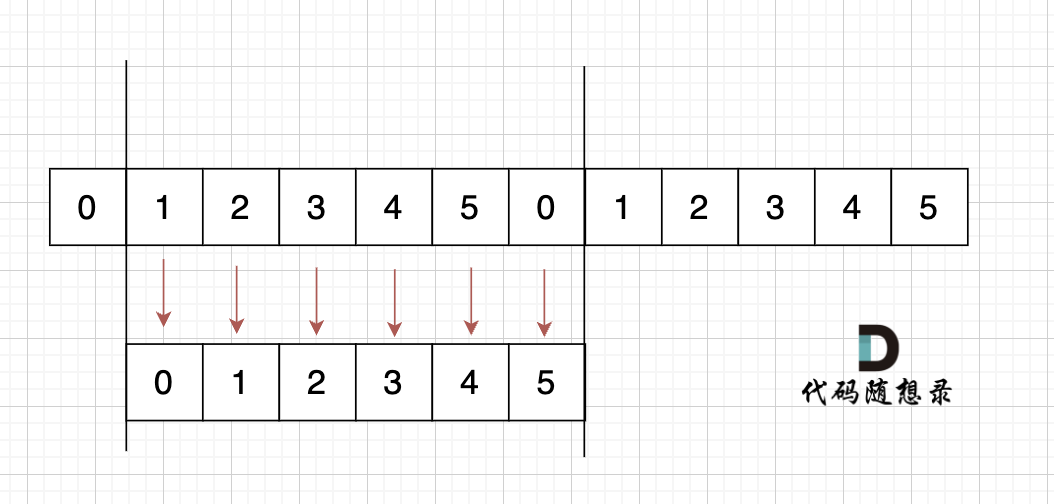
如果是这样的呢,如图:
|
||||
|
||||
|
||||
|
||||
s[1] = s[0],s[2] = s[1] ,s[3] = s[2],s[4] = s[3],s[5] = s[4],s[0] = s[5]
|
||||
|
||||
以上相等关系串联
|
||||
|
||||
s[0] = s[1] = s[2] = s[3] = s[4] = s[5]
|
||||
|
||||
最后可以推导出,这个字符串是由 s[0] 重复组成。
|
||||
|
||||
以上 充分和必要性都证明了,所以判断字符串s是否由重复子串组成,只要两个s拼接在一起,里面还出现一个s的话,就说明是由重复子串组成。
|
||||
|
||||
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
@ -76,13 +132,14 @@ public:
|
||||
* 时间复杂度: O(n)
|
||||
* 空间复杂度: O(1)
|
||||
|
||||
不过这种解法还有一个问题,就是 我们最终还是要判断 一个字符串(s + s)是否出现过 s 的过程,大家可能直接用contains,find 之类的库函数。 却忽略了实现这些函数的时间复杂度(暴力解法是m * n,一般库函数实现为 O(m + n))。
|
||||
不过这种解法还有一个问题,就是 我们最终还是要判断 一个字符串(s + s)是否出现过 s 的过程,大家可能直接用contains,find 之类的库函数, 却忽略了实现这些函数的时间复杂度(暴力解法是m * n,一般库函数实现为 O(m + n))。
|
||||
|
||||
如果我们做过 [28.实现strStr](https://programmercarl.com/0028.实现strStr.html) 题目的话,其实就知道,**实现一个 高效的算法来判断 一个字符串中是否出现另一个字符串是很复杂的**,这里就涉及到了KMP算法。
|
||||
|
||||
### KMP
|
||||
|
||||
#### 为什么会使用KMP
|
||||
|
||||
以下使用KMP方式讲解,强烈建议大家先把以下两个视频看了,理解KMP算法,再来看下面讲解,否则会很懵。
|
||||
|
||||
* [视频讲解版:帮你把KMP算法学个通透!(理论篇)](https://www.bilibili.com/video/BV1PD4y1o7nd/)
|
||||
@ -91,7 +148,9 @@ public:
|
||||
|
||||
在一个串中查找是否出现过另一个串,这是KMP的看家本领。那么寻找重复子串怎么也涉及到KMP算法了呢?
|
||||
|
||||
KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一个匹配过的位置继续匹配,靠的是有计算好的前缀表。 前缀表里,统计了各个位置为终点字符串的最长相同前后缀的长度。
|
||||
KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一个匹配过的位置继续匹配,靠的是有计算好的前缀表。
|
||||
|
||||
前缀表里,统计了各个位置为终点字符串的最长相同前后缀的长度。
|
||||
|
||||
那么 最长相同前后缀和重复子串的关系又有什么关系呢。
|
||||
|
||||
@ -100,16 +159,61 @@ KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一
|
||||
* 前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串;
|
||||
* 后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串
|
||||
|
||||
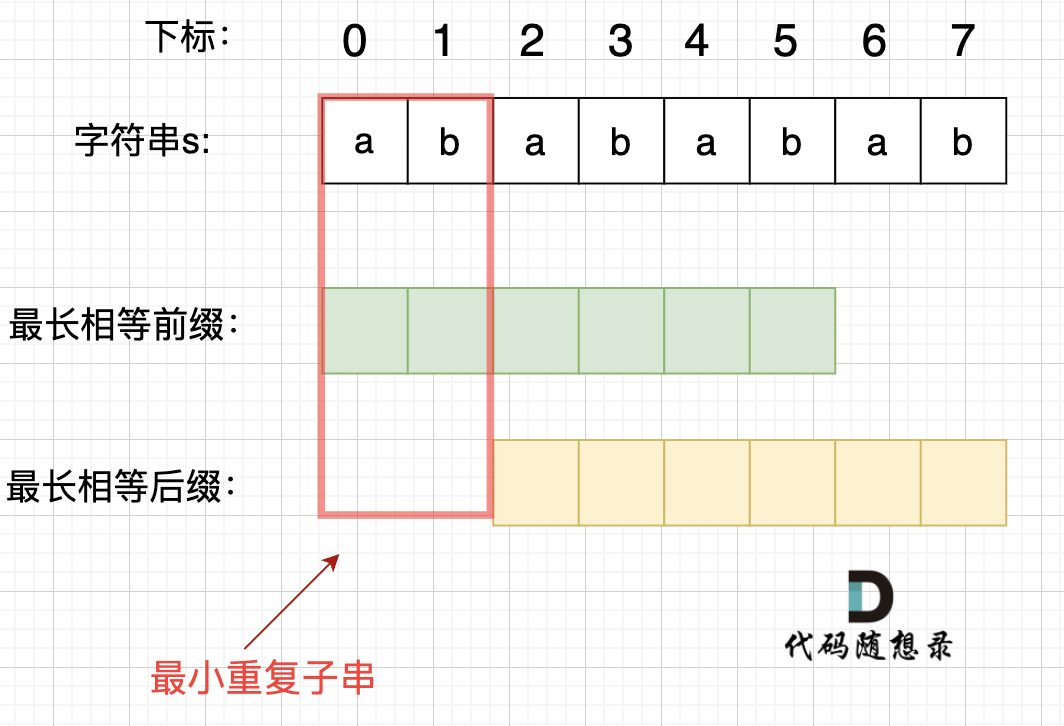
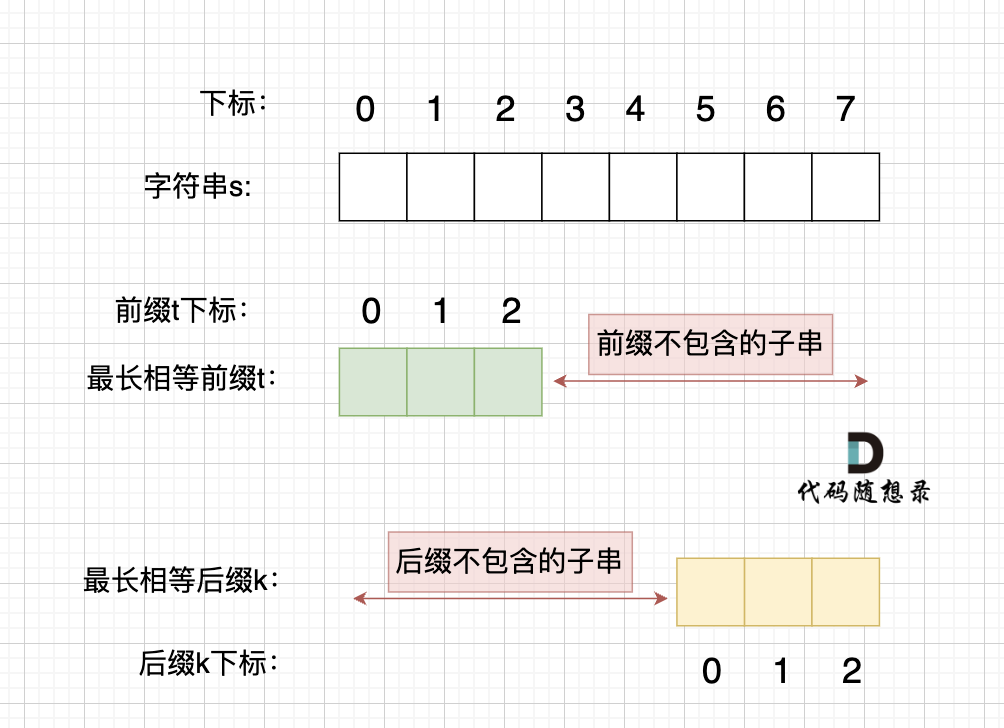
在由重复子串组成的字符串中,最长相等前后缀不包含的子串就是最小重复子串,这里拿字符串s:abababab 来举例,ab就是最小重复单位,如图所示:
|
||||
#### 充分性证明
|
||||
|
||||
|
||||
如果一个字符串s是由重复子串组成,那么 最长相等前后缀不包含的子串一定是字符串s的最小重复子串。
|
||||
|
||||
如果s 是由最小重复子串p组成,即 s = n * p
|
||||
|
||||
#### 如何找到最小重复子串
|
||||
那么相同前后缀可以是这样:
|
||||
|
||||
这里有同学就问了,为啥一定是开头的ab呢。 其实最关键还是要理解 最长相等前后缀,如图:
|
||||

|
||||
|
||||
|
||||
也可以是这样:
|
||||
|
||||

|
||||
|
||||
最长的相等前后缀,也就是这样:
|
||||
|
||||

|
||||
|
||||
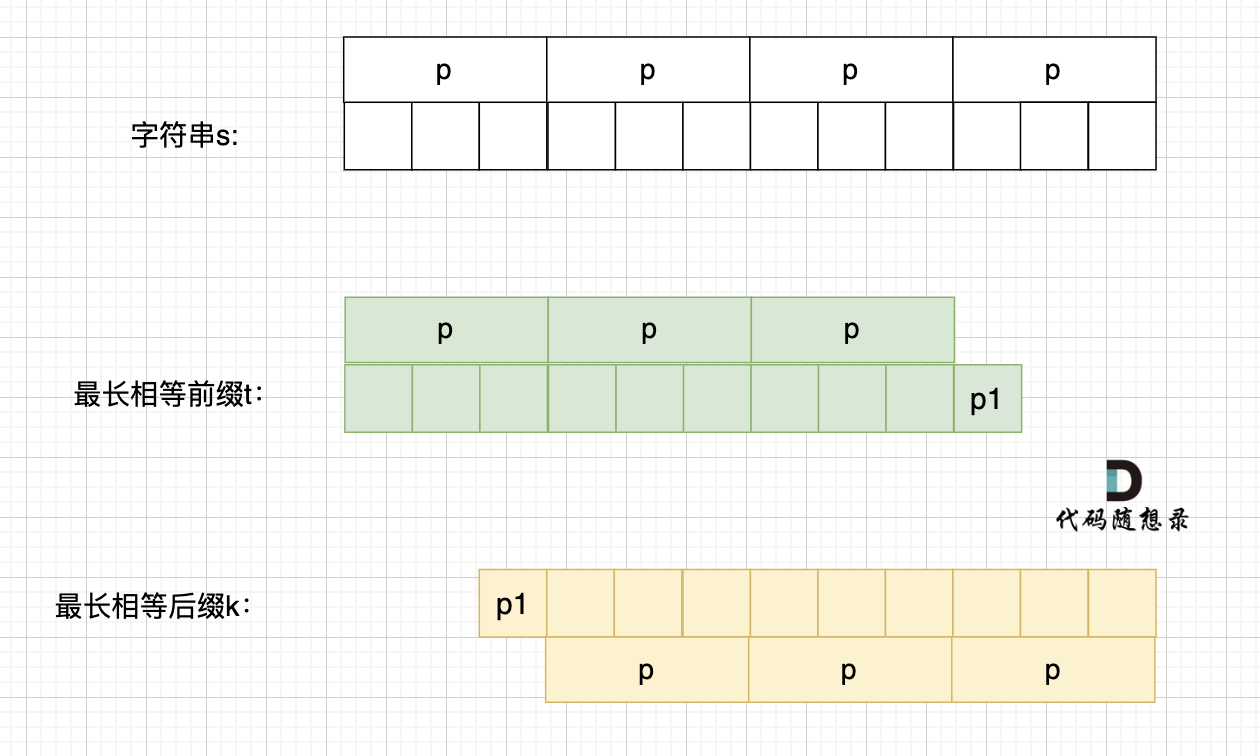
这里有录友就想:如果字符串s 是由最小重复子串p组成,最长相等前后缀就不能更长一些? 例如这样:
|
||||
|
||||
|
||||
|
||||
如果这样的话,因为前后缀要相同,所以 p2 = p1,p3 = p2,如图:
|
||||
|
||||
|
||||
|
||||
p2 = p1,p3 = p2 即: p1 = p2 = p3
|
||||
|
||||
说明 p = p1 * 3。
|
||||
|
||||
这样p 就不是最小重复子串了,不符合我们定义的条件。
|
||||
|
||||
所以,**如果这个字符串s是由重复子串组成,那么最长相等前后缀不包含的子串是字符串s的最小重复子串**。
|
||||
|
||||
#### 必要性证明
|
||||
|
||||
以上是充分性证明,以下是必要性证明:
|
||||
|
||||
**如果 最长相等前后缀不包含的子串是字符串s的最小重复子串, 那么字符串s一定由重复子串组成吗**?
|
||||
|
||||
最长相等前后缀不包含的子串已经是字符串s的最小重复子串,那么字符串s一定由重复子串组成,这个不需要证明了。
|
||||
|
||||
关键是要证明:最长相等前后缀不包含的子串什么时候才是字符串s的最小重复子串呢。
|
||||
|
||||
情况一, 最长相等前后缀不包含的子串的长度 比 字符串s的一半的长度还大,那一定不是字符串s的重复子串,如图:
|
||||
|
||||
|
||||
|
||||
图中:前后缀不包含的子串的长度 大于 字符串s的长度的 二分之一
|
||||
|
||||
--------------
|
||||
|
||||
情况二,最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除,如图:
|
||||
|
||||
|
||||
|
||||
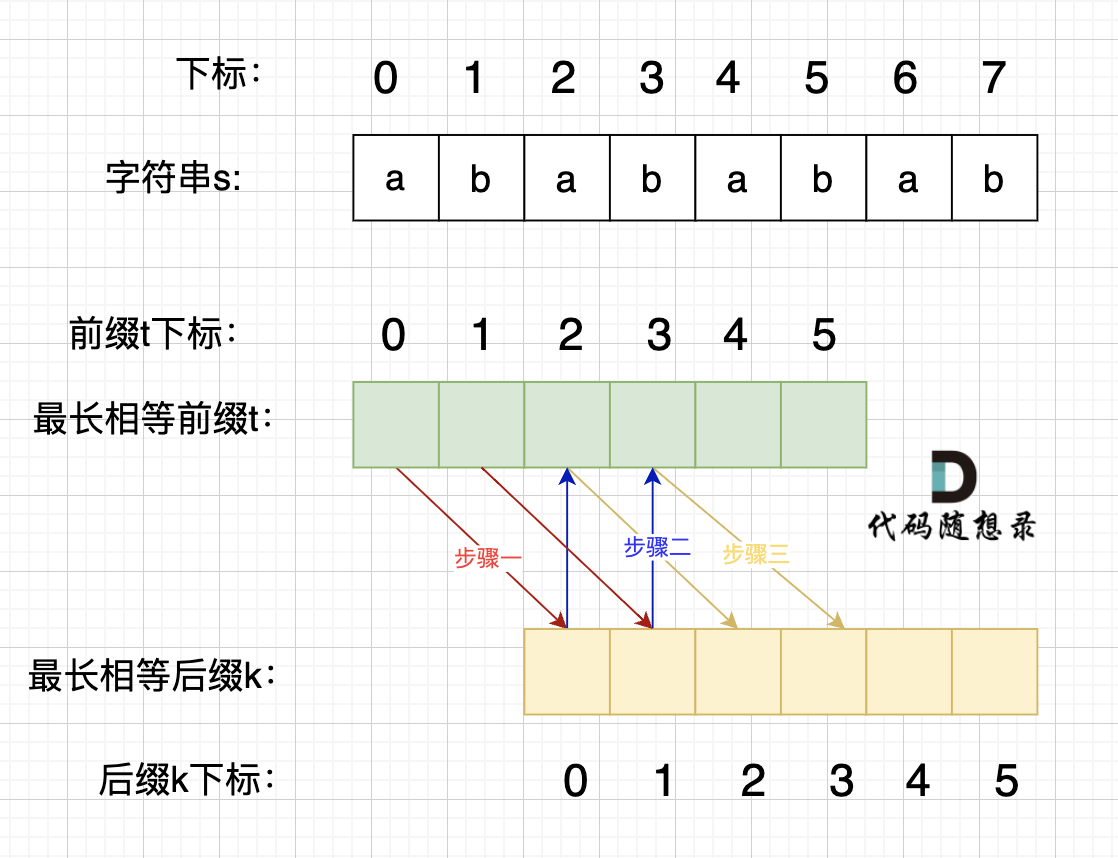
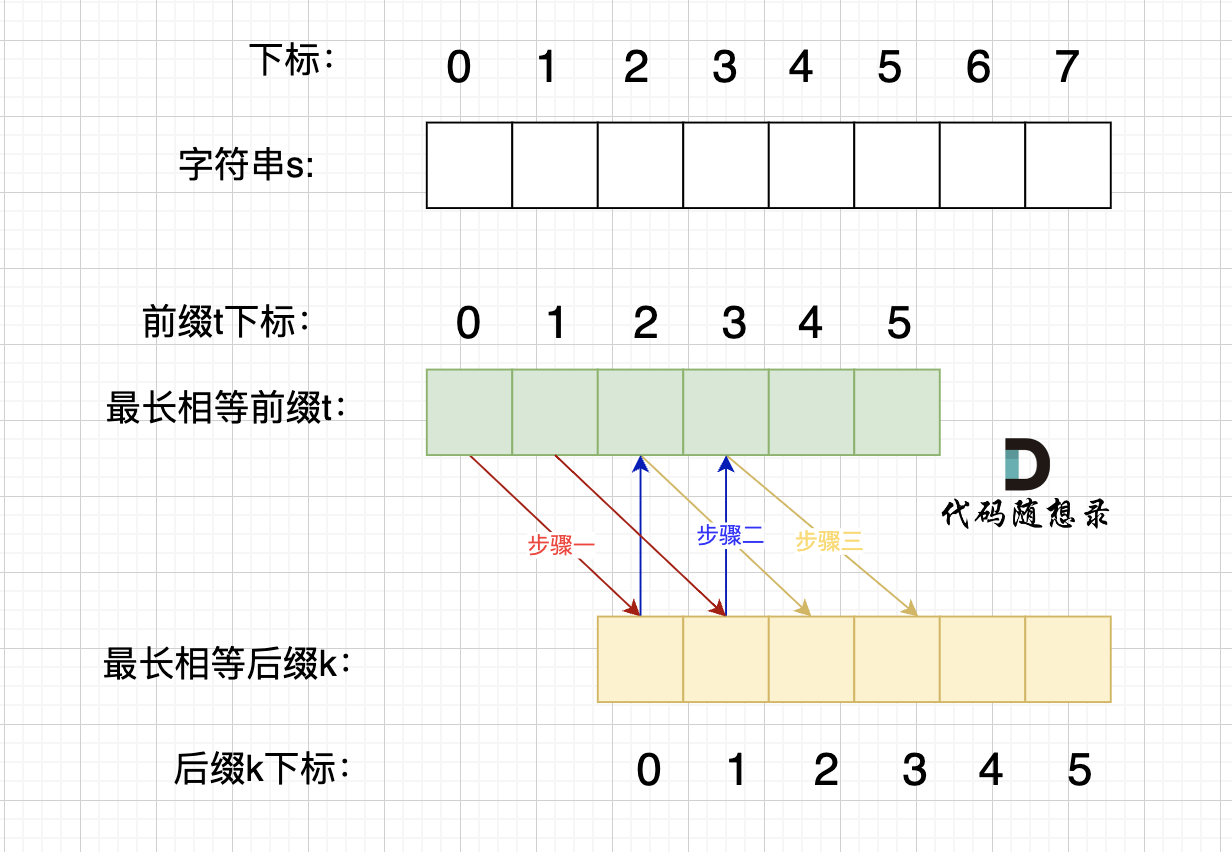
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,所以 s[0] 一定和 s[2]相同,s[1] 一定和 s[3]相同,即:,s[0]s[1]与s[2]s[3]相同 。
|
||||
|
||||
@ -121,28 +225,79 @@ KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一
|
||||
|
||||
所以字符串s,s[0]s[1]与s[2]s[3]相同, s[2]s[3] 与 s[4]s[5]相同,s[4]s[5] 与 s[6]s[7] 相同。
|
||||
|
||||
正是因为 最长相等前后缀的规则,当一个字符串由重复子串组成的,最长相等前后缀不包含的子串就是最小重复子串。
|
||||
可以推出,在由重复子串组成的字符串中,最长相等前后缀不包含的子串就是最小重复子串。
|
||||
|
||||
#### 简单推理
|
||||
即 s[0]s[1] 是最小重复子串
|
||||
|
||||
这里再给出一个数学推导,就容易理解很多。
|
||||
|
||||
假设字符串s使用多个重复子串构成(这个子串是最小重复单位),重复出现的子字符串长度是x,所以s是由n * x组成。
|
||||
以上推导中,录友可能想,你怎么知道 s[0] 和 s[1] 就不相同呢? s[0] 为什么就不能是最小重复子串。
|
||||
|
||||
因为字符串s的最长相同前后缀的长度一定是不包含s本身,所以 最长相同前后缀长度必然是m * x,而且 n - m = 1,(这里如果不懂,看上面的推理)
|
||||
如果 s[0] 和 s[1] 也相同,同时 s[0]s[1]与s[2]s[3]相同,s[2]s[3] 与 s[4]s[5]相同,s[4]s[5] 与 s[6]s[7] 相同,那么这个字符串就是有一个字符构成的字符串。
|
||||
|
||||
所以如果 nx % (n - m)x = 0,就可以判定有重复出现的子字符串。
|
||||
那么它的最长相同前后缀,就不是上图中的前后缀,而是这样的的前后缀:
|
||||
|
||||
next 数组记录的就是最长相同前后缀 [字符串:KMP算法精讲](https://programmercarl.com/0028.实现strStr.html) 这里介绍了什么是前缀,什么是后缀,什么又是最长相同前后缀), 如果 next[len - 1] != -1,则说明字符串有最长相同的前后缀(就是字符串里的前缀子串和后缀子串相同的最长长度)。
|
||||
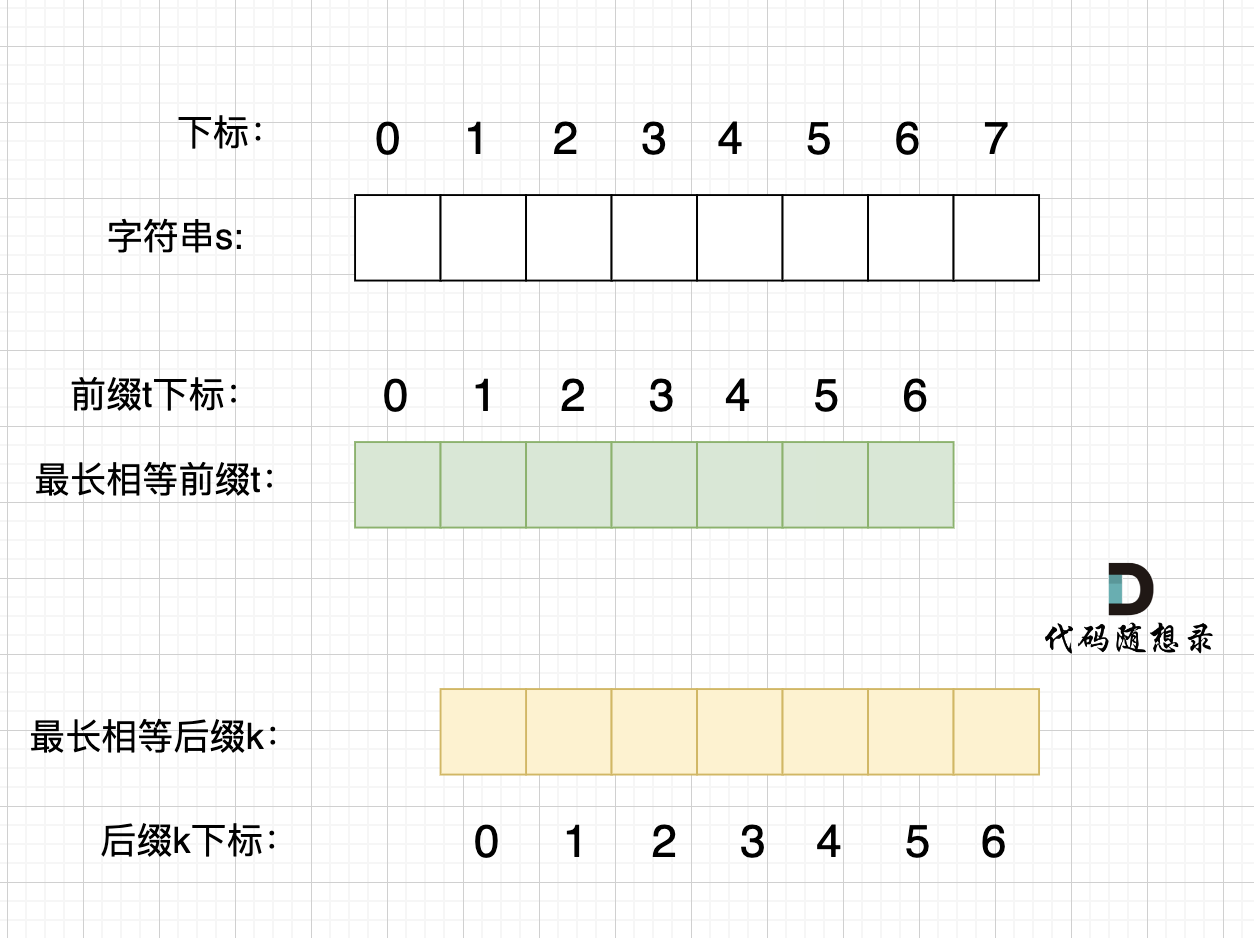
|
||||
|
||||
最长相等前后缀的长度为:next[len - 1] + 1。(这里的next数组是以统一减一的方式计算的,因此需要+1,两种计算next数组的具体区别看这里:[字符串:KMP算法精讲](https://programmercarl.com/0028.实现strStr.html))
|
||||
录友可能再问,由一个字符组成的字符串,最长相等前后缀凭什么就是这样的。
|
||||
|
||||
有这种疑惑的录友,就是还不知道 最长相等前后缀 是怎么算的。
|
||||
|
||||
可以看这里:[KMP讲解](https://programmercarl.com/0028.%E5%AE%9E%E7%8E%B0strStr.html),再去回顾一下。
|
||||
|
||||
或者说,自己举个例子,`aaaaaa`,这个字符串,他的最长相等前后缀是什么?
|
||||
|
||||
同上以上推导,最长相等前后缀不包含的子串的长度只要被 字符串s的长度整除,最长相等前后缀不包含的子串一定是最小重复子串。
|
||||
|
||||
----------------
|
||||
|
||||
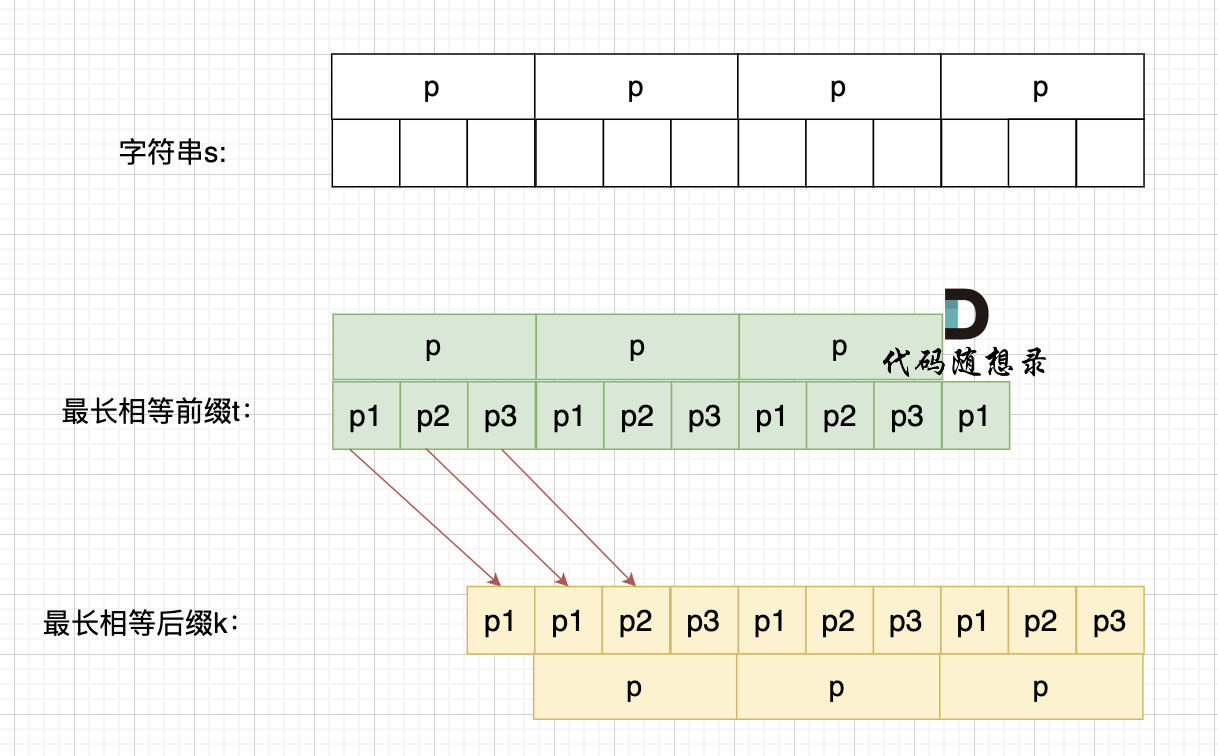
**情况三,最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除得情况**,如图:
|
||||
|
||||
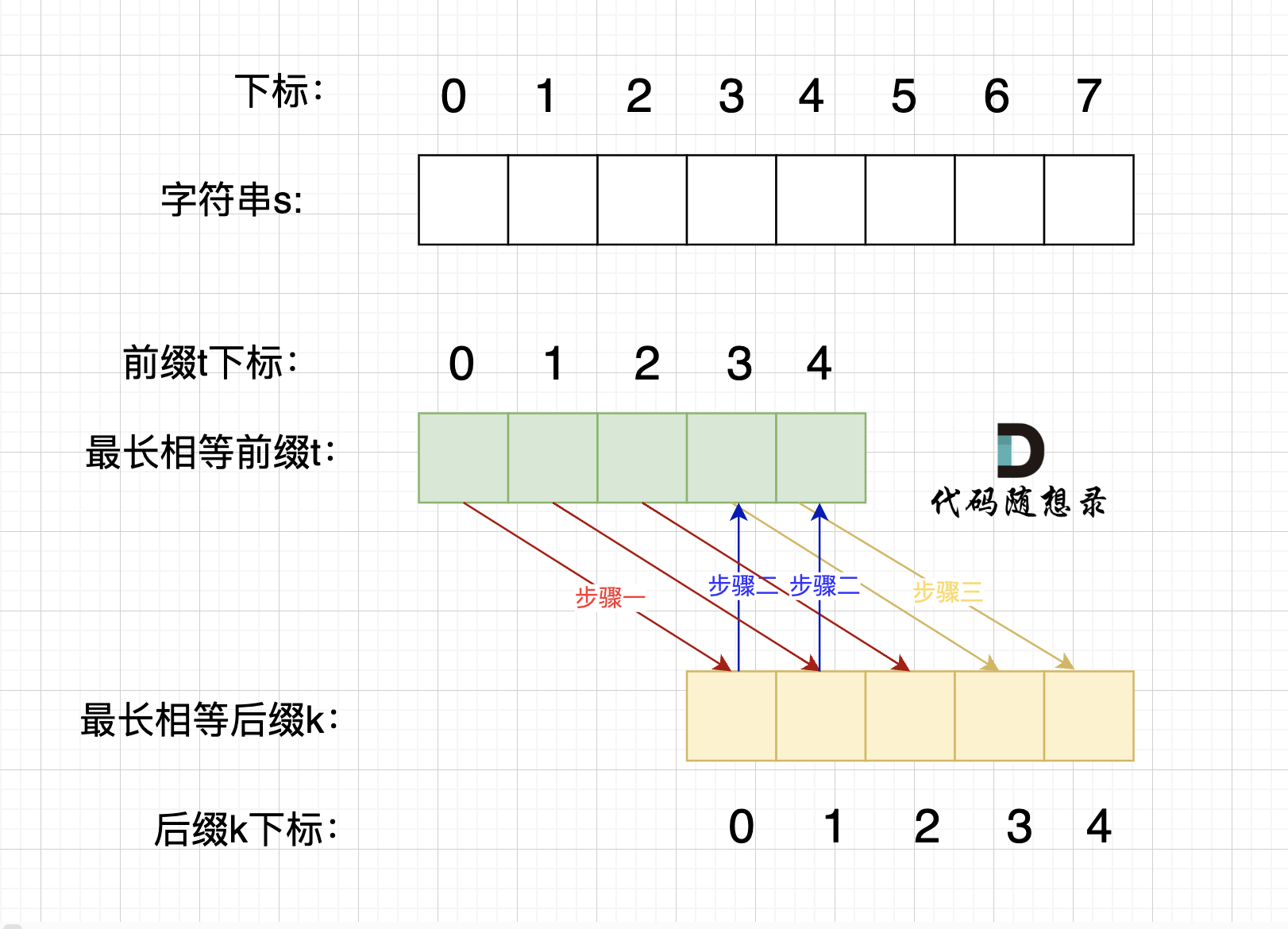
|
||||
|
||||
|
||||
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,t[2] 与 k[2]相同。
|
||||
|
||||
所以 s[0] 与 s[3]相同,s[1] 与 s[4]相同,s[2] 与s[5],即:,s[0]s[1]与s[2]s[3]相同 。
|
||||
|
||||
步骤二: 因为在同一个字符串位置,所以 t[3] 与 k[0]相同,t[4] 与 k[1]相同。
|
||||
|
||||
|
||||
步骤三: 因为 这是相等的前缀和后缀,t[3] 与 k[3]相同 ,t[4]与k[5] 相同,所以,s[3]一定和s[6]相同,s[4]一定和s[7]相同,即:s[3]s[4] 与 s[6]s[7]相同。
|
||||
|
||||
|
||||
以上推导,可以得出 s[0],s[1],s[2] 与 s[3],s[4],s[5] 相同,s[3]s[4] 与 s[6]s[7]相同。
|
||||
|
||||
那么 最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除 ,最长相等前后缀不包含的子串就不是s的重复子串
|
||||
|
||||
-----------
|
||||
|
||||
充分条件:如果字符串s是由重复子串组成,那么 最长相等前后缀不包含的子串 一定是 s的最小重复子串。
|
||||
|
||||
必要条件:如果字符串s的最长相等前后缀不包含的子串 是 s最小重复子串,那么 s是由重复子串组成。
|
||||
|
||||
在必要条件,这个是 显而易见的,都已经假设 最长相等前后缀不包含的子串 是 s的最小重复子串了,那s必然是重复子串。
|
||||
|
||||
**关键是需要证明, 字符串s的最长相等前后缀不包含的子串 什么时候才是 s最小重复子串**。
|
||||
|
||||
同上我们证明了,当 最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除,那么不包含的子串 就是s的最小重复子串。
|
||||
|
||||
|
||||
-------------
|
||||
|
||||
|
||||
### 代码分析
|
||||
|
||||
next 数组记录的就是最长相同前后缀( [字符串:KMP算法精讲](https://programmercarl.com/0028.实现strStr.html)), 如果 `next[len - 1] != -1`,则说明字符串有最长相同的前后缀(就是字符串里的前缀子串和后缀子串相同的最长长度)。
|
||||
|
||||
最长相等前后缀的长度为:`next[len - 1] + 1`。(这里的next数组是以统一减一的方式计算的,因此需要+1,两种计算next数组的具体区别看这里:[字符串:KMP算法精讲](https://programmercarl.com/0028.实现strStr.html))
|
||||
|
||||
数组长度为:len。
|
||||
|
||||
如果len % (len - (next[len - 1] + 1)) == 0 ,则说明数组的长度正好可以被 (数组长度-最长相等前后缀的长度) 整除 ,说明该字符串有重复的子字符串。
|
||||
`len - (next[len - 1] + 1)` 是最长相等前后缀不包含的子串的长度。
|
||||
|
||||
**数组长度减去最长相同前后缀的长度相当于是第一个周期的长度,也就是一个周期的长度,如果这个周期可以被整除,就说明整个数组就是这个周期的循环。**
|
||||
如果`len % (len - (next[len - 1] + 1)) == 0` ,则说明数组的长度正好可以被 最长相等前后缀不包含的子串的长度 整除 ,说明该字符串有重复的子字符串。
|
||||
|
||||
### 打印数组
|
||||
|
||||
**强烈建议大家把next数组打印出来,看看next数组里的规律,有助于理解KMP算法**
|
||||
|
||||
@ -150,11 +305,15 @@ next 数组记录的就是最长相同前后缀 [字符串:KMP算法精讲](ht
|
||||
|
||||

|
||||
|
||||
next[len - 1] = 7,next[len - 1] + 1 = 8,8就是此时字符串asdfasdfasdf的最长相同前后缀的长度。
|
||||
`next[len - 1] = 7`,`next[len - 1] + 1 = 8`,8就是此时字符串asdfasdfasdf的最长相同前后缀的长度。
|
||||
|
||||
(len - (next[len - 1] + 1)) 也就是: 12(字符串的长度) - 8(最长公共前后缀的长度) = 4, 4正好可以被 12(字符串的长度) 整除,所以说明有重复的子字符串(asdf)。
|
||||
`(len - (next[len - 1] + 1))` 也就是: 12(字符串的长度) - 8(最长公共前后缀的长度) = 4, 为最长相同前后缀不包含的子串长度
|
||||
|
||||
|
||||
4可以被 12(字符串的长度) 整除,所以说明有重复的子字符串(asdf)。
|
||||
|
||||
### 代码实现
|
||||
|
||||
C++代码如下:(这里使用了前缀表统一减一的实现方式)
|
||||
|
||||
```CPP
|
||||
@ -725,3 +884,4 @@ public int[] GetNext(string s)
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
@ -61,7 +61,7 @@
|
||||
|
||||
left + right = sum,而sum是固定的。right = sum - left
|
||||
|
||||
公式来了, left - (sum - left) = target 推导出 left = (target + sum)/2 。
|
||||
left - (sum - left) = target 推导出 left = (target + sum)/2 。
|
||||
|
||||
target是固定的,sum是固定的,left就可以求出来。
|
||||
|
||||
@ -126,7 +126,7 @@ public:
|
||||
|
||||
x = (target + sum) / 2
|
||||
|
||||
**此时问题就转化为,装满容量为x的背包,有几种方法**。
|
||||
**此时问题就转化为,用nums装满容量为x的背包,有几种方法**。
|
||||
|
||||
这里的x,就是bagSize,也就是我们后面要求的背包容量。
|
||||
|
||||
@ -161,6 +161,8 @@ if (abs(target) > sum) return 0; // 此时没有方案
|
||||
|
||||
我们先手动推导一下,这个二维数组里面的数值。
|
||||
|
||||
------------
|
||||
|
||||
先只考虑物品0,如图:
|
||||
|
||||

|
||||
@ -173,6 +175,8 @@ if (abs(target) > sum) return 0; // 此时没有方案
|
||||
|
||||
装满背包容量为2 的方法个数是0,目前没有办法能装满容量为2的背包。
|
||||
|
||||
--------------
|
||||
|
||||
接下来 考虑 物品0 和 物品1,如图:
|
||||
|
||||
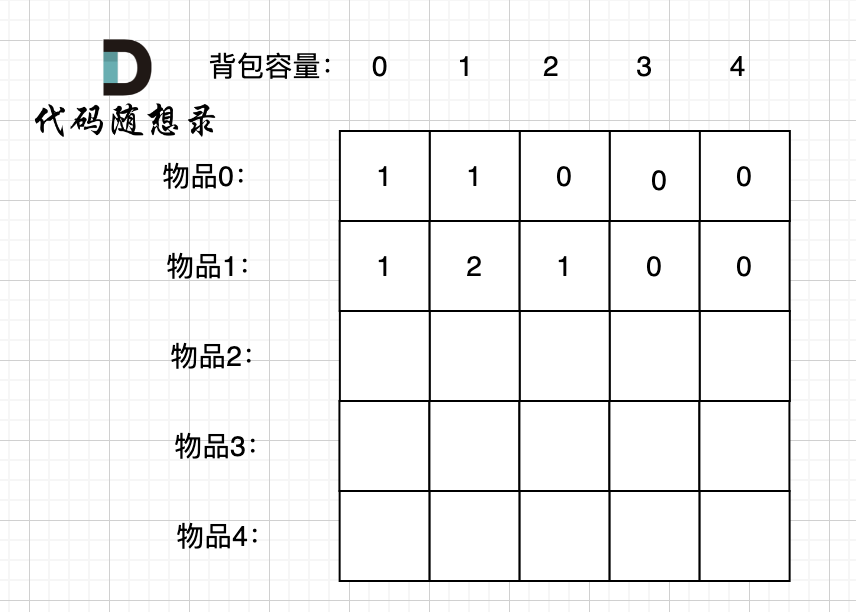
|
||||
@ -185,6 +189,8 @@ if (abs(target) > sum) return 0; // 此时没有方案
|
||||
|
||||
其他容量都不能装满,所以方法是0。
|
||||
|
||||
-----------------
|
||||
|
||||
接下来 考虑 物品0 、物品1 和 物品2 ,如图:
|
||||
|
||||
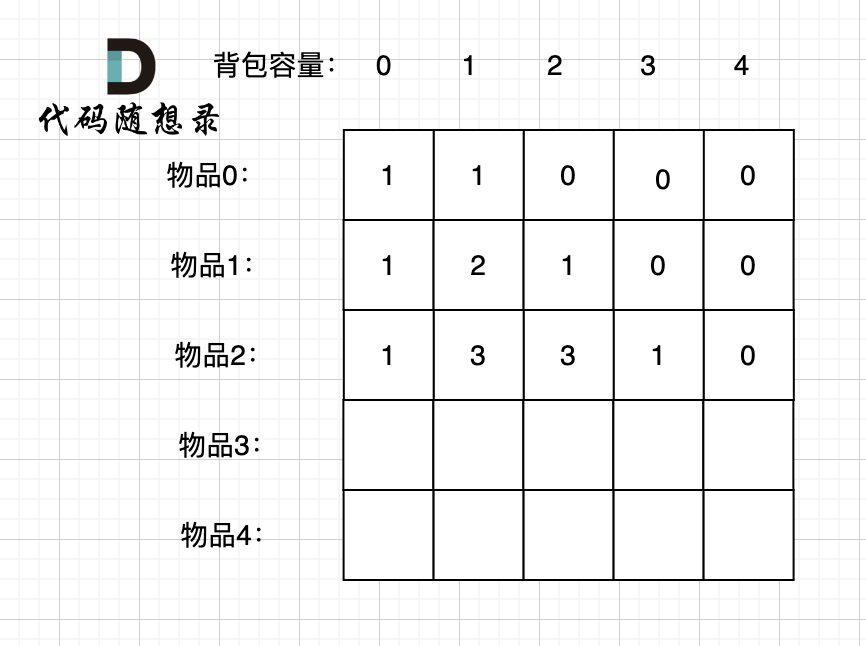
|
||||
@ -193,10 +199,12 @@ if (abs(target) > sum) return 0; // 此时没有方案
|
||||
|
||||
装满背包容量为1 的方法个数是3,即 放物品0 或者 放物品1 或者 放物品2。
|
||||
|
||||
装满背包容量为2 的方法个数是3,即 放物品0 和 放物品1、放物品0 和 物品 2、 放物品1 和 物品2。
|
||||
装满背包容量为2 的方法个数是3,即 放物品0 和 放物品1、放物品0 和 物品2、放物品1 和 物品2。
|
||||
|
||||
装满背包容量为3的方法个数是1,即 放物品0 和 物品1 和 物品2。
|
||||
|
||||
---------------
|
||||
|
||||
通过以上举例,我们来看 dp[2][2] 可以有哪些方向推出来。
|
||||
|
||||
如图红色部分:
|
||||
@ -229,7 +237,7 @@ dp[2][2] = 3,即 放物品0 和 放物品1、放物品0 和 物品 2、放物
|
||||
|
||||
在上面图中,你把物品2补上就好,同样是两种方法。
|
||||
|
||||
dp[2][2] = 容量为2的背包不放物品2有几种方法 + 容量为2的背包不放物品2有几种方法
|
||||
dp[2][2] = 容量为2的背包不放物品2有几种方法 + 容量为2的背包放物品2有几种方法
|
||||
|
||||
所以 dp[2][2] = dp[1][2] + dp[1][1] ,如图:
|
||||
|
||||
@ -284,6 +292,29 @@ dp[0][j]:只放物品0, 把容量为j的背包填满有几种方法。
|
||||
|
||||
即 dp[i][0] = 1
|
||||
|
||||
但这里有例外,就是如果 物品数值就是0呢?
|
||||
|
||||
如果有两个物品,物品0为0, 物品1为0,装满背包容量为0的方法有几种。
|
||||
|
||||
* 放0件物品
|
||||
* 放物品0
|
||||
* 放物品1
|
||||
* 放物品0 和 物品1
|
||||
|
||||
此时是有4种方法。
|
||||
|
||||
其实就是算数组里有t个0,然后按照组合数量求,即 2^t 。
|
||||
|
||||
初始化如下:
|
||||
|
||||
```CPP
|
||||
int numZero = 0;
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
if (nums[i] == 0) numZero++;
|
||||
dp[i][0] = (int) pow(2.0, numZero);
|
||||
}
|
||||
```
|
||||
|
||||
4. 确定遍历顺序
|
||||
|
||||
在明确递推方向时,我们知道 当前值 是由上方和左上方推出。
|
||||
@ -675,6 +706,57 @@ class Solution:
|
||||
```
|
||||
|
||||
### Go
|
||||
二维dp
|
||||
```go
|
||||
func findTargetSumWays(nums []int, target int) int {
|
||||
sum := 0
|
||||
for _, v := range nums {
|
||||
sum += v
|
||||
}
|
||||
if math.Abs(float64(target)) > float64(sum) {
|
||||
return 0 // 此时没有方案
|
||||
}
|
||||
if (target + sum) % 2 == 1 {
|
||||
return 0 // 此时没有方案
|
||||
}
|
||||
bagSize := (target + sum) / 2
|
||||
|
||||
dp := make([][]int, len(nums))
|
||||
for i := range dp {
|
||||
dp[i] = make([]int, bagSize + 1)
|
||||
}
|
||||
|
||||
// 初始化最上行
|
||||
if nums[0] <= bagSize {
|
||||
dp[0][nums[0]] = 1
|
||||
}
|
||||
|
||||
// 初始化最左列,最左列其他数值在递推公式中就完成了赋值
|
||||
dp[0][0] = 1
|
||||
|
||||
var numZero float64
|
||||
for i := range nums {
|
||||
if nums[i] == 0 {
|
||||
numZero++
|
||||
}
|
||||
dp[i][0] = int(math.Pow(2, numZero))
|
||||
}
|
||||
|
||||
// 以下遍历顺序行列可以颠倒
|
||||
for i := 1; i < len(nums); i++ { // 行,遍历物品
|
||||
for j := 0; j <= bagSize; j++ { // 列,遍历背包
|
||||
if nums[i] > j {
|
||||
dp[i][j] = dp[i-1][j]
|
||||
} else {
|
||||
dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]]
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[len(nums)-1][bagSize]
|
||||
}
|
||||
```
|
||||
|
||||
一维dp
|
||||
```go
|
||||
func findTargetSumWays(nums []int, target int) int {
|
||||
sum := 0
|
||||
|
||||
@ -55,7 +55,7 @@
|
||||
|
||||
参数必须有要遍历的树的根节点,还有就是一个int型的变量用来记录最长深度。 这里就不需要返回值了,所以递归函数的返回类型为void。
|
||||
|
||||
本题还需要类里的两个全局变量,maxLen用来记录最大深度,result记录最大深度最左节点的数值。
|
||||
本题还需要类里的两个全局变量,maxDepth用来记录最大深度,result记录最大深度最左节点的数值。
|
||||
|
||||
代码如下:
|
||||
|
||||
|
||||
@ -168,23 +168,43 @@ for (int j = 0; j <= amount; j++) { // 遍历背包容量
|
||||
class Solution {
|
||||
public:
|
||||
int change(int amount, vector<int>& coins) {
|
||||
vector<int> dp(amount + 1, 0);
|
||||
dp[0] = 1;
|
||||
vector<uint64_t> dp(amount + 1, 0); // 防止相加数据超int
|
||||
dp[0] = 1; // 只有一种方式达到0
|
||||
for (int i = 0; i < coins.size(); i++) { // 遍历物品
|
||||
for (int j = coins[i]; j <= amount; j++) { // 遍历背包
|
||||
dp[j] += dp[j - coins[i]];
|
||||
}
|
||||
}
|
||||
return dp[amount];
|
||||
return dp[amount]; // 返回组合数
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
C++测试用例有两个数相加超过int的数据,所以需要在if里加上dp[i] < INT_MAX - dp[i - num]。
|
||||
|
||||
* 时间复杂度: O(mn),其中 m 是amount,n 是 coins 的长度
|
||||
* 空间复杂度: O(m)
|
||||
|
||||
为了防止相加的数据 超int 也可以这么写:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
int change(int amount, vector<int>& coins) {
|
||||
vector<int> dp(amount + 1, 0);
|
||||
dp[0] = 1; // 只有一种方式达到0
|
||||
for (int i = 0; i < coins.size(); i++) { // 遍历物品
|
||||
for (int j = coins[i]; j <= amount; j++) { // 遍历背包
|
||||
if (dp[j] < INT_MAX - dp[j - coins[i]]) { //防止相加数据超int
|
||||
dp[j] += dp[j - coins[i]];
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[amount]; // 返回组合数
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
是不是发现代码如此精简
|
||||
|
||||
## 总结
|
||||
|
||||
@ -268,6 +288,7 @@ class Solution:
|
||||
|
||||
### Go:
|
||||
|
||||
一维dp
|
||||
```go
|
||||
func change(amount int, coins []int) int {
|
||||
// 定义dp数组
|
||||
@ -286,6 +307,29 @@ func change(amount int, coins []int) int {
|
||||
return dp[amount]
|
||||
}
|
||||
```
|
||||
二维dp
|
||||
```go
|
||||
func change(amount int, coins []int) int {
|
||||
dp := make([][]int, len(coins))
|
||||
for i := range dp {
|
||||
dp[i] = make([]int, amount + 1)
|
||||
dp[i][0] = 1
|
||||
}
|
||||
for j := coins[0]; j <= amount; j++ {
|
||||
dp[0][j] += dp[0][j-coins[0]]
|
||||
}
|
||||
for i := 1; i < len(coins); i++ {
|
||||
for j := 1; j <= amount; j++ {
|
||||
if j < coins[i] {
|
||||
dp[i][j] = dp[i-1][j]
|
||||
} else {
|
||||
dp[i][j] = dp[i][j-coins[i]] + dp[i-1][j]
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[len(coins)-1][amount]
|
||||
}
|
||||
```
|
||||
|
||||
### Rust:
|
||||
|
||||
|
||||
@ -37,7 +37,7 @@
|
||||
|
||||
因为要找的也就是每2 * k 区间的起点,这样写,程序会高效很多。
|
||||
|
||||
**所以当需要固定规律一段一段去处理字符串的时候,要想想在在for循环的表达式上做做文章。**
|
||||
**所以当需要固定规律一段一段去处理字符串的时候,要想想在for循环的表达式上做做文章。**
|
||||
|
||||
性能如下:
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/541_反转字符串II.png' width=600> </img></div>
|
||||
@ -505,3 +505,4 @@ impl Solution {
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
@ -492,6 +492,25 @@ int findLengthOfLCIS(int* nums, int numsSize) {
|
||||
}
|
||||
```
|
||||
|
||||
### Cangjie
|
||||
|
||||
```cangjie
|
||||
func findLengthOfLCIS(nums: Array<Int64>): Int64 {
|
||||
let n = nums.size
|
||||
if (n <= 1) {
|
||||
return n
|
||||
}
|
||||
let dp = Array(n, repeat: 1)
|
||||
var res = 0
|
||||
for (i in 1..n) {
|
||||
if (nums[i] > nums[i - 1]) {
|
||||
dp[i] = dp[i - 1] + 1
|
||||
}
|
||||
res = max(res, dp[i])
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
@ -43,7 +43,7 @@
|
||||
|
||||
在[贪心算法:122.买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II.html)中使用贪心策略不用关心具体什么时候买卖,只要收集每天的正利润,最后稳稳的就是最大利润了。
|
||||
|
||||
而本题有了手续费,就要关系什么时候买卖了,因为计算所获得利润,需要考虑买卖利润可能不足以手续费的情况。
|
||||
而本题有了手续费,就要关心什么时候买卖了,因为计算所获得利润,需要考虑买卖利润可能不足以扣减手续费的情况。
|
||||
|
||||
如果使用贪心策略,就是最低值买,最高值(如果算上手续费还盈利)就卖。
|
||||
|
||||
@ -122,7 +122,7 @@ public:
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(n)
|
||||
|
||||
当然可以对空间经行优化,因为当前状态只是依赖前一个状态。
|
||||
当然可以对空间进行优化,因为当前状态只是依赖前一个状态。
|
||||
|
||||
C++ 代码如下:
|
||||
|
||||
|
||||
@ -46,7 +46,7 @@
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1)
|
||||
|
||||
本题使用贪心算法并不好理解,也很容易出错,那么我们再来看看是使用动规的方法如何解题。
|
||||
本题使用贪心算法并不好理解,也很容易出错,那么我们再来看看使用动规的方法如何解题。
|
||||
|
||||
相对于[动态规划:122.买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II(动态规划).html),本题只需要在计算卖出操作的时候减去手续费就可以了,代码几乎是一样的。
|
||||
|
||||
@ -54,7 +54,7 @@
|
||||
|
||||
这里重申一下dp数组的含义:
|
||||
|
||||
dp[i][0] 表示第i天持有股票所省最多现金。
|
||||
dp[i][0] 表示第i天持有股票所得最多现金。
|
||||
dp[i][1] 表示第i天不持有股票所得最多现金
|
||||
|
||||
|
||||
|
||||
@ -581,6 +581,25 @@ int findLength(int* nums1, int nums1Size, int* nums2, int nums2Size) {
|
||||
}
|
||||
```
|
||||
|
||||
### Cangjie
|
||||
|
||||
```cangjie
|
||||
func findLength(nums1: Array<Int64>, nums2: Array<Int64>): Int64 {
|
||||
let n = nums1.size
|
||||
let m = nums2.size
|
||||
let dp = Array(n + 1, {_ => Array(m + 1, item: 0)})
|
||||
var res = 0
|
||||
for (i in 1..=n) {
|
||||
for (j in 1..=m) {
|
||||
if (nums1[i - 1] == nums2[j - 1]) {
|
||||
dp[i][j] = dp[i - 1][j - 1] + 1
|
||||
}
|
||||
res = max(res, dp[i][j])
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
<p align="center">
|
||||
|
||||
@ -196,7 +196,22 @@ public class Solution {
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
### Rust
|
||||
```rust
|
||||
impl Solution {
|
||||
pub fn valid_mountain_array(arr: Vec<i32>) -> bool {
|
||||
let mut i = 0;
|
||||
let mut j = arr.len() - 1;
|
||||
while i < arr.len() - 1 && arr[i] < arr[i + 1] {
|
||||
i += 1;
|
||||
}
|
||||
while j > 0 && arr[j] < arr[j - 1] {
|
||||
j -= 1;
|
||||
}
|
||||
i > 0 && j < arr.len() - 1 && i == j
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
|
||||
@ -100,6 +100,7 @@ public:
|
||||
## 其他语言版本
|
||||
|
||||
### Java:
|
||||
|
||||
排序法
|
||||
```Java
|
||||
class Solution {
|
||||
@ -209,6 +210,43 @@ class Solution:
|
||||
return new_list[::-1]
|
||||
```
|
||||
|
||||
```python3
|
||||
(双指针优化版本) 三步优化
|
||||
class Solution:
|
||||
def sortedSquares(self, nums: List[int]) -> List[int]:
|
||||
"""
|
||||
整体思想:有序数组的绝对值最大值永远在两头,比较两头,平方大的插到新数组的最后
|
||||
优 化:1. 优化所有元素为非正或非负的情况
|
||||
2. 头尾平方的大小比较直接将头尾相加与0进行比较即可
|
||||
3. 新的平方排序数组的插入索引可以用倒序插入实现(针对for循环,while循环不适用)
|
||||
"""
|
||||
|
||||
# 特殊情况, 元素都非负(优化1)
|
||||
if nums[0] >= 0:
|
||||
return [num ** 2 for num in nums] # 按顺序平方即可
|
||||
# 最后一个非正,全负有序的
|
||||
if nums[-1] <= 0:
|
||||
return [x ** 2 for x in nums[::-1]] # 倒序平方后的数组
|
||||
|
||||
# 一般情况, 有正有负
|
||||
i = 0 # 原数组头索引
|
||||
j = len(nums) - 1 # 原数组尾部索引
|
||||
new_nums = [0] * len(nums) # 新建一个等长数组用于保存排序后的结果
|
||||
# end_index = len(nums) - 1 # 新的排序数组(是新数组)尾插索引, 每次需要减一(优化3优化了)
|
||||
|
||||
for end_index in range(len(nums)-1, -1, -1): # (优化3,倒序,不用单独创建变量)
|
||||
# if nums[i] ** 2 >= nums[j] ** 2:
|
||||
if nums[i] + nums[j] <= 0: # (优化2)
|
||||
new_nums[end_index] = nums[i] ** 2
|
||||
i += 1
|
||||
# end_index -= 1 (优化3)
|
||||
else:
|
||||
new_nums[end_index] = nums[j] ** 2
|
||||
j -= 1
|
||||
# end_index -= 1 (优化3)
|
||||
return new_nums
|
||||
```
|
||||
|
||||
### Go:
|
||||
|
||||
```Go
|
||||
|
||||
@ -164,7 +164,7 @@ class Solution {
|
||||
int top = -1;
|
||||
for (int i = 0; i < s.length(); i++) {
|
||||
char c = s.charAt(i);
|
||||
// 当 top > 0,即栈中有字符时,当前字符如果和栈中字符相等,弹出栈顶字符,同时 top--
|
||||
// 当 top >= 0,即栈中有字符时,当前字符如果和栈中字符相等,弹出栈顶字符,同时 top--
|
||||
if (top >= 0 && res.charAt(top) == c) {
|
||||
res.deleteCharAt(top);
|
||||
top--;
|
||||
|
||||
@ -399,6 +399,25 @@ int longestCommonSubsequence(char* text1, char* text2) {
|
||||
}
|
||||
```
|
||||
|
||||
### Cangjie
|
||||
|
||||
```cangjie
|
||||
func longestCommonSubsequence(text1: String, text2: String): Int64 {
|
||||
let n = text1.size
|
||||
let m = text2.size
|
||||
let dp = Array(n + 1, {_ => Array(m + 1, repeat: 0)})
|
||||
for (i in 1..=n) {
|
||||
for (j in 1..=m) {
|
||||
if (text1[i - 1] == text2[j - 1]) {
|
||||
dp[i][j] = dp[i - 1][j - 1] + 1
|
||||
} else {
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[n][m]
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
<p align="center">
|
||||
|
||||
@ -221,6 +221,28 @@ func uniqueOccurrences(arr []int) bool {
|
||||
}
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
```rust
|
||||
use std::collections::{HashMap, HashSet};
|
||||
impl Solution {
|
||||
pub fn unique_occurrences(arr: Vec<i32>) -> bool {
|
||||
let mut hash = HashMap::<i32, i32>::new();
|
||||
for x in arr {
|
||||
*hash.entry(x).or_insert(0) += 1;
|
||||
}
|
||||
let mut set = HashSet::<i32>::new();
|
||||
for (_k, v) in hash {
|
||||
if set.contains(&v) {
|
||||
return false
|
||||
} else {
|
||||
set.insert(v);
|
||||
}
|
||||
}
|
||||
true
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
@ -260,6 +260,22 @@ function smallerNumbersThanCurrent(nums: number[]): number[] {
|
||||
};
|
||||
```
|
||||
|
||||
### rust
|
||||
```rust
|
||||
use std::collections::HashMap;
|
||||
impl Solution {
|
||||
pub fn smaller_numbers_than_current(nums: Vec<i32>) -> Vec<i32> {
|
||||
let mut v = nums.clone();
|
||||
v.sort();
|
||||
let mut hash = HashMap::new();
|
||||
for i in 0..v.len() {
|
||||
// rust中使用or_insert插入值, 如果存在就不插入,可以使用正序遍历
|
||||
hash.entry(v[i]).or_insert(i as i32);
|
||||
}
|
||||
nums.into_iter().map(|x| *hash.get(&x).unwrap()).collect()
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
<p align="center">
|
||||
|
||||
BIN
.DS_Store → problems/kamacoder/.DS_Store
vendored
BIN
.DS_Store → problems/kamacoder/.DS_Store
vendored
Binary file not shown.
@ -578,7 +578,7 @@ int main() {
|
||||
更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
|
||||
|
||||
* 源点到节点2的最短距离为100,小于原minDist[2]的数值max,更新minDist[2] = 100
|
||||
* 源点到节点3的最短距离为1,小于原minDist[3]的数值max,更新minDist[4] = 1
|
||||
* 源点到节点3的最短距离为1,小于原minDist[3]的数值max,更新minDist[3] = 1
|
||||
|
||||
-------------------
|
||||
|
||||
@ -869,6 +869,65 @@ if __name__ == "__main__":
|
||||
|
||||
### Javascript
|
||||
|
||||
```js
|
||||
function dijkstra(grid, start, end) {
|
||||
const visited = Array.from({length: end + 1}, () => false)
|
||||
const minDist = Array.from({length: end + 1}, () => Number.MAX_VALUE)
|
||||
minDist[start] = 0
|
||||
|
||||
for (let i = 1 ; i < end + 1 ; i++) {
|
||||
let cur = -1
|
||||
let tempMinDist = Number.MAX_VALUE
|
||||
// 1. 找尋與起始點距離最近且未被訪的節點
|
||||
for (let j = 1 ; j < end + 1 ; j++) {
|
||||
if (!visited[j] && minDist[j] < tempMinDist) {
|
||||
cur = j
|
||||
tempMinDist = minDist[j]
|
||||
}
|
||||
}
|
||||
if (cur === -1) break;
|
||||
|
||||
// 2. 更新節點狀態為已拜訪
|
||||
visited[cur] = true
|
||||
|
||||
// 3. 更新未拜訪節點與起始點的最短距離
|
||||
for (let j = 1 ; j < end + 1 ; j++) {
|
||||
if(!visited[j] && grid[cur][j] != Number.MAX_VALUE
|
||||
&& grid[cur][j] + minDist[cur] < minDist[j]
|
||||
) {
|
||||
minDist[j] = grid[cur][j] + minDist[cur]
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return minDist[end] === Number.MAX_VALUE ? -1 : minDist[end]
|
||||
}
|
||||
|
||||
|
||||
async function main() {
|
||||
// 輸入
|
||||
const rl = require('readline').createInterface({ input: process.stdin })
|
||||
const iter = rl[Symbol.asyncIterator]()
|
||||
const readline = async () => (await iter.next()).value
|
||||
const [n, m] = (await readline()).split(" ").map(Number)
|
||||
const grid = Array.from({length: n + 1},
|
||||
() => Array.from({length:n + 1}, () => Number.MAX_VALUE))
|
||||
for (let i = 0 ; i < m ; i++) {
|
||||
const [s, e, w] = (await readline()).split(" ").map(Number)
|
||||
grid[s][e] = w
|
||||
}
|
||||
|
||||
// dijkstra
|
||||
const result = dijkstra(grid, 1, n)
|
||||
|
||||
// 輸出
|
||||
console.log(result)
|
||||
}
|
||||
|
||||
|
||||
main()
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
@ -549,6 +549,62 @@ if __name__ == "__main__":
|
||||
|
||||
### Javascript
|
||||
|
||||
```js
|
||||
function kruskal(v, edges) {
|
||||
const father = Array.from({ length: v + 1 }, (_, i) => i)
|
||||
|
||||
function find(u){
|
||||
if (u === father[u]) {
|
||||
return u
|
||||
} else {
|
||||
father[u] = find(father[u])
|
||||
return father[u]
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
function isSame(u, v) {
|
||||
let s = find(u)
|
||||
let t = find(v)
|
||||
return s === t
|
||||
}
|
||||
|
||||
function join(u, v) {
|
||||
let s = find(u)
|
||||
let t = find(v)
|
||||
if (s !== t) {
|
||||
father[s] = t
|
||||
}
|
||||
}
|
||||
|
||||
edges.sort((a, b) => a[2] - b[2])
|
||||
let result = 0
|
||||
for (const [v1, v2, w] of edges) {
|
||||
if (!isSame(v1, v2)) {
|
||||
result += w
|
||||
join(v1 ,v2)
|
||||
}
|
||||
}
|
||||
console.log(result)
|
||||
}
|
||||
|
||||
|
||||
async function main() {
|
||||
const rl = require('readline').createInterface({ input: process.stdin })
|
||||
const iter = rl[Symbol.asyncIterator]()
|
||||
const readline = async () => (await iter.next()).value
|
||||
const [v, e] = (await readline()).split(" ").map(Number)
|
||||
const edges = []
|
||||
for (let i = 0 ; i < e ; i++) {
|
||||
edges.push((await readline()).split(" ").map(Number))
|
||||
}
|
||||
kruskal(v, edges)
|
||||
}
|
||||
|
||||
|
||||
main()
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
@ -562,4 +618,145 @@ if __name__ == "__main__":
|
||||
### Dart
|
||||
|
||||
### C
|
||||
并查集方法一
|
||||
```c
|
||||
#include <stdio.h>
|
||||
#include <stdlib.h>
|
||||
|
||||
// 定义边结构体,包含两个顶点vex1和vex2以及它们之间的权重val
|
||||
struct Edge
|
||||
{
|
||||
int vex1, vex2, val;
|
||||
};
|
||||
|
||||
// 冒泡排序函数,用于按边的权重val不减序排序边数组
|
||||
void bubblesort(struct Edge *a, int numsize)
|
||||
{
|
||||
for (int i = 0; i < numsize - 1; ++i)
|
||||
{
|
||||
|
||||
for (int j = 0; j < numsize - i - 1; ++j)
|
||||
{
|
||||
if (a[j].val > a[j + 1].val)
|
||||
{
|
||||
struct Edge temp = a[j];
|
||||
a[j] = a[j + 1];
|
||||
a[j + 1] = temp;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
int main()
|
||||
{
|
||||
int v, e;
|
||||
int v1, v2, val;
|
||||
int ret = 0;
|
||||
|
||||
scanf("%d%d", &v, &e);
|
||||
struct Edge *edg = (struct Edge *)malloc(sizeof(struct Edge) * e);
|
||||
int *conne_gra = (int *)malloc(sizeof(int) * (v + 1));
|
||||
|
||||
// 初始化连通图数组,每个顶点初始时只与自己相连通
|
||||
for (int i = 0; i <= v; ++i)
|
||||
{
|
||||
conne_gra[i] = i;
|
||||
}
|
||||
|
||||
// 读取所有边的信息并存储到edg(存储所有边的)数组中
|
||||
for (int i = 0; i < e; ++i)
|
||||
{
|
||||
scanf("%d%d%d", &v1, &v2, &val);
|
||||
edg[i].vex1 = v1;
|
||||
edg[i].vex2 = v2;
|
||||
edg[i].val = val;
|
||||
}
|
||||
bubblesort(edg, e); // 调用冒泡排序函数对边进行排序
|
||||
|
||||
// 遍历所有边,执行Kruskal算法来找到最小生成树
|
||||
for (int i = 0; i < e; ++i)
|
||||
{
|
||||
if (conne_gra[edg[i].vex1] != conne_gra[edg[i].vex2])
|
||||
{ // 如果当前边的两个顶点不在同一个连通分量中
|
||||
int tmp1 = conne_gra[edg[i].vex1], tmp2 = conne_gra[edg[i].vex2];
|
||||
for (int k = 1; k <= v; ++k)
|
||||
{ // 将所有属于tmp2的顶点合并到tmp1的连通分量中
|
||||
if (conne_gra[k] == tmp2)
|
||||
conne_gra[k] = tmp1;
|
||||
}
|
||||
ret += edg[i].val; // 将当前边的权重加到最小生成树的权重中
|
||||
}
|
||||
}
|
||||
printf("%d", ret);
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
并查集方法二
|
||||
```c
|
||||
#include <stdio.h>
|
||||
#include <stdlib.h>
|
||||
|
||||
// 定义边结构体,包含两个顶点vex1和vex2以及它们之间的权重val (略,同上)
|
||||
// 冒泡排序函数,用于按边的权重val不减序排序边数组(略,同上)
|
||||
|
||||
// 并查集的查找操作
|
||||
int find(int m, int *father)
|
||||
{ // 如果当前节点是其自身的父节点,则直接返回该节点
|
||||
// 否则递归查找其父节点的根,并将当前节点直接连接到根节点
|
||||
return (m == father[m]) ? m : (father[m] = find(father[m], father)); // 路径压缩
|
||||
}
|
||||
|
||||
// 并查集的加入集合
|
||||
void Union(int m, int n, int *father)
|
||||
{
|
||||
int x = find(m, father);
|
||||
int y = find(n, father);
|
||||
if (x == y)
|
||||
return; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
|
||||
father[y] = x;
|
||||
}
|
||||
|
||||
int main()
|
||||
{
|
||||
int v, e;
|
||||
int v1, v2, val;
|
||||
int ret = 0;
|
||||
|
||||
scanf("%d%d", &v, &e);
|
||||
struct Edge *edg = (struct Edge *)malloc(sizeof(struct Edge) * e);
|
||||
int *conne_gra = (int *)malloc(sizeof(int) * (v + 1));
|
||||
|
||||
// 初始化连通图数组,每个顶点初始时只与自己相连通
|
||||
for (int i = 0; i <= v; ++i)
|
||||
{
|
||||
conne_gra[i] = i;
|
||||
}
|
||||
// 读取所有边的信息并存储到edg(存储所有边的)数组中
|
||||
for (int i = 0; i < e; ++i)
|
||||
{
|
||||
scanf("%d%d%d", &v1, &v2, &val);
|
||||
edg[i].vex1 = v1;
|
||||
edg[i].vex2 = v2;
|
||||
edg[i].val = val;
|
||||
}
|
||||
|
||||
bubblesort(edg, e); // 调用冒泡排序函数对边进行排序
|
||||
|
||||
// Kruskal算法的实现,通过边数组构建最小生成树
|
||||
int j = 0, count = 0;
|
||||
while (v > 1)
|
||||
{
|
||||
if (find(edg[j].vex1, conne_gra) != find(edg[j].vex2, conne_gra))
|
||||
{
|
||||
ret += edg[j].val; // 将当前边的权重加到最小生成树的权重中
|
||||
Union(edg[j].vex1, edg[j].vex2, conne_gra);
|
||||
v--;
|
||||
}
|
||||
j++;
|
||||
}
|
||||
printf("%d", ret);
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
@ -9,17 +9,17 @@
|
||||
|
||||
在世界的某个区域,有一些分散的神秘岛屿,每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路,方便运输。
|
||||
|
||||
不同岛屿之间,路途距离不同,国王希望你可以规划建公路的方案,如何可以以最短的总公路距离将 所有岛屿联通起来。
|
||||
不同岛屿之间,路途距离不同,国王希望你可以规划建公路的方案,如何可以以最短的总公路距离将所有岛屿联通起来。
|
||||
|
||||
给定一张地图,其中包括了所有的岛屿,以及它们之间的距离。以最小化公路建设长度,确保可以链接到所有岛屿。
|
||||
|
||||
输入描述:
|
||||
|
||||
第一行包含两个整数V 和 E,V代表顶点数,E代表边数 。顶点编号是从1到V。例如:V=2,一个有两个顶点,分别是1和2。
|
||||
第一行包含两个整数V和E,V代表顶点数,E代表边数。顶点编号是从1到V。例如:V=2,一个有两个顶点,分别是1和2。
|
||||
|
||||
接下来共有 E 行,每行三个整数 v1,v2 和 val,v1 和 v2 为边的起点和终点,val代表边的权值。
|
||||
接下来共有E行,每行三个整数v1,v2和val,v1和v2为边的起点和终点,val代表边的权值。
|
||||
|
||||
输出描述:
|
||||
输出描述:
|
||||
|
||||
输出联通所有岛屿的最小路径总距离
|
||||
|
||||
@ -38,65 +38,65 @@
|
||||
5 6 2
|
||||
5 7 1
|
||||
6 7 1
|
||||
```
|
||||
```
|
||||
|
||||
输出示例:
|
||||
输出示例:
|
||||
|
||||
6
|
||||
|
||||
|
||||
## 解题思路
|
||||
## 解题思路
|
||||
|
||||
本题是最小生成树的模板题,那么我们来讲一讲最小生成树。
|
||||
本题是最小生成树的模板题,那么我们来讲一讲最小生成树。
|
||||
|
||||
最小生成树 可以使用 prim算法 也可以使用 kruskal算法计算出来。
|
||||
最小生成树可以使用prim算法也可以使用kruskal算法计算出来。
|
||||
|
||||
本篇我们先讲解 prim算法。
|
||||
本篇我们先讲解prim算法。
|
||||
|
||||
最小生成树是所有节点的最小连通子图, 即:以最小的成本(边的权值)将图中所有节点链接到一起。
|
||||
最小生成树是所有节点的最小连通子图,即:以最小的成本(边的权值)将图中所有节点链接到一起。
|
||||
|
||||
图中有n个节点,那么一定可以用 n - 1 条边将所有节点连接到一起。
|
||||
图中有n个节点,那么一定可以用n-1条边将所有节点连接到一起。
|
||||
|
||||
那么如何选择 这 n-1 条边 就是 最小生成树算法的任务所在。
|
||||
那么如何选择这n-1条边就是最小生成树算法的任务所在。
|
||||
|
||||
例如本题示例中的无向有权图为:
|
||||
例如本题示例中的无向有权图为:
|
||||
|
||||
|
||||
|
||||
那么在这个图中,如何选取 n-1 条边 使得 图中所有节点连接到一起,并且边的权值和最小呢?
|
||||
那么在这个图中,如何选取n-1条边使得图中所有节点连接到一起,并且边的权值和最小呢?
|
||||
|
||||
(图中为n为7,即7个节点,那么只需要 n-1 即 6条边就可以讲所有顶点连接到一起)
|
||||
(图中为n为7,即7个节点,那么只需要n-1即6条边就可以讲所有顶点连接到一起)
|
||||
|
||||
prim算法 是从节点的角度 采用贪心的策略 每次寻找距离 最小生成树最近的节点 并加入到最小生成树中。
|
||||
prim算法是从节点的角度采用贪心的策略每次寻找距离最小生成树最近的节点并加入到最小生成树中。
|
||||
|
||||
prim算法核心就是三步,我称为**prim三部曲**,大家一定要熟悉这三步,代码相对会好些很多:
|
||||
prim算法核心就是三步,我称为**prim三部曲**,大家一定要熟悉这三步,代码相对会好些很多:
|
||||
|
||||
1. 第一步,选距离生成树最近节点
|
||||
2. 第二步,最近节点加入生成树
|
||||
2. 第二步,最近节点加入生成树
|
||||
3. 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
现在录友们会对这三步很陌生,不知道这是干啥的,没关系,下面将会画图举例来带大家把这**prim三部曲**理解到位。
|
||||
现在录友们会对这三步很陌生,不知道这是干啥的,没关系,下面将会画图举例来带大家把这**prim三部曲**理解到位。
|
||||
|
||||
在prim算法中,有一个数组特别重要,这里我起名为:minDist。
|
||||
|
||||
刚刚我有讲过 “每次寻找距离 最小生成树最近的节点 并加入到最小生成树中”,那么如何寻找距离最小生成树最近的节点呢?
|
||||
刚刚我有讲过“每次寻找距离最小生成树最近的节点并加入到最小生成树中”,那么如何寻找距离最小生成树最近的节点呢?
|
||||
|
||||
这就用到了 minDist 数组, 它用来作什么呢?
|
||||
这就用到了minDist数组,它用来作什么呢?
|
||||
|
||||
**minDist数组 用来记录 每一个节点距离最小生成树的最近距离**。 理解这一点非常重要,这也是 prim算法最核心要点所在,很多录友看不懂prim算法的代码,都是因为没有理解透 这个数组的含义。
|
||||
**minDist数组用来记录每一个节点距离最小生成树的最近距离**。理解这一点非常重要,这也是prim算法最核心要点所在,很多录友看不懂prim算法的代码,都是因为没有理解透这个数组的含义。
|
||||
|
||||
接下来,我们来通过一步一步画图,来带大家巩固 **prim三部曲** 以及 minDist数组 的作用。
|
||||
接下来,我们来通过一步一步画图,来带大家巩固**prim三部曲**以及minDist数组的作用。
|
||||
|
||||
(**示例中节点编号是从1开始,所以为了让大家看的不晕,minDist数组下标我也从 1 开始计数,下标0 就不使用了,这样 下标和节点标号就可以对应上了,避免大家搞混**)
|
||||
(**示例中节点编号是从1开始,所以为了让大家看的不晕,minDist数组下标我也从1开始计数,下标0就不使用了,这样下标和节点标号就可以对应上了,避免大家搞混**)
|
||||
|
||||
|
||||
### 1 初始状态
|
||||
### 1 初始状态
|
||||
|
||||
minDist 数组 里的数值初始化为 最大数,因为本题 节点距离不会超过 10000,所以 初始化最大数为 10001就可以。
|
||||
minDist数组里的数值初始化为最大数,因为本题节点距离不会超过10000,所以初始化最大数为10001就可以。
|
||||
|
||||
相信这里录友就要问了,为什么这么做?
|
||||
相信这里录友就要问了,为什么这么做?
|
||||
|
||||
现在 还没有最小生成树,默认每个节点距离最小生成树是最大的,这样后面我们在比较的时候,发现更近的距离,才能更新到 minDist 数组上。
|
||||
现在还没有最小生成树,默认每个节点距离最小生成树是最大的,这样后面我们在比较的时候,发现更近的距离,才能更新到minDist数组上。
|
||||
|
||||
如图:
|
||||
|
||||
@ -108,125 +108,125 @@ minDist 数组 里的数值初始化为 最大数,因为本题 节点距离不
|
||||
|
||||
1、prim三部曲,第一步:选距离生成树最近节点
|
||||
|
||||
选择距离最小生成树最近的节点,加入到最小生成树,刚开始还没有最小生成树,所以随便选一个节点加入就好(因为每一个节点一定会在最小生成树里,所以随便选一个就好),那我们选择节点1 (符合遍历数组的习惯,第一个遍历的也是节点1)
|
||||
选择距离最小生成树最近的节点,加入到最小生成树,刚开始还没有最小生成树,所以随便选一个节点加入就好(因为每一个节点一定会在最小生成树里,所以随便选一个就好),那我们选择节点1(符合遍历数组的习惯,第一个遍历的也是节点1)
|
||||
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
|
||||
此时 节点1 已经算最小生成树的节点。
|
||||
此时节点1已经算最小生成树的节点。
|
||||
|
||||
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
接下来,我们要更新所有节点距离最小生成树的距离,如图:
|
||||
接下来,我们要更新所有节点距离最小生成树的距离,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
注意下标0,我们就不管它了,下标 1 与节点 1 对应,这样可以避免大家把节点搞混。
|
||||
注意下标0,我们就不管它了,下标1与节点1对应,这样可以避免大家把节点搞混。
|
||||
|
||||
此时所有非生成树的节点距离 最小生成树(节点1)的距离都已经跟新了 。
|
||||
此时所有非生成树的节点距离最小生成树(节点1)的距离都已经跟新了。
|
||||
|
||||
* 节点2 与 节点1 的距离为1,比原先的 距离值10001小,所以更新minDist[2]。
|
||||
* 节点3 和 节点1 的距离为1,比原先的 距离值10001小,所以更新minDist[3]。
|
||||
* 节点5 和 节点1 的距离为2,比原先的 距离值10001小,所以更新minDist[5]。
|
||||
* 节点2与节点1的距离为1,比原先的距离值10001小,所以更新minDist[2]。
|
||||
* 节点3和节点1的距离为1,比原先的距离值10001小,所以更新minDist[3]。
|
||||
* 节点5和节点1的距离为2,比原先的距离值10001小,所以更新minDist[5]。
|
||||
|
||||
**注意图中我标记了 minDist数组里更新的权值**,是哪两个节点之间的权值,例如 minDist[2] =1 ,这个 1 是 节点1 与 节点2 之间的连线,清楚这一点对最后我们记录 最小生成树的权值总和很重要。
|
||||
**注意图中我标记了minDist数组里更新的权值**,是哪两个节点之间的权值,例如minDist[2]=1,这个1是节点1与节点2之间的连线,清楚这一点对最后我们记录最小生成树的权值总和很重要。
|
||||
|
||||
(我在后面依然会不断重复 prim三部曲,可能基础好的录友会感觉有点啰嗦,但也是让大家感觉这三部曲求解的过程)
|
||||
(我在后面依然会不断重复prim三部曲,可能基础好的录友会感觉有点啰嗦,但也是让大家感觉这三部曲求解的过程)
|
||||
|
||||
### 3
|
||||
### 3
|
||||
|
||||
1、prim三部曲,第一步:选距离生成树最近节点
|
||||
|
||||
选取一个距离 最小生成树(节点1) 最近的非生成树里的节点,节点2,3,5 距离 最小生成树(节点1) 最近,选节点 2(其实选 节点3或者节点2都可以,距离一样的)加入最小生成树。
|
||||
选取一个距离最小生成树(节点1)最近的非生成树里的节点,节点2,3,5距离最小生成树(节点1)最近,选节点2(其实选节点3或者节点2都可以,距离一样的)加入最小生成树。
|
||||
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
|
||||
此时 节点1 和 节点2,已经算最小生成树的节点。
|
||||
此时节点1和节点2,已经算最小生成树的节点。
|
||||
|
||||
|
||||
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
接下来,我们要更新节点距离最小生成树的距离,如图:
|
||||
接下来,我们要更新节点距离最小生成树的距离,如图:
|
||||
|
||||
|
||||

|
||||
|
||||
此时所有非生成树的节点距离 最小生成树(节点1、节点2)的距离都已经跟新了 。
|
||||
此时所有非生成树的节点距离最小生成树(节点1、节点2)的距离都已经跟新了。
|
||||
|
||||
* 节点3 和 节点2 的距离为2,和原先的距离值1 小,所以不用更新。
|
||||
* 节点4 和 节点2 的距离为2,比原先的距离值10001小,所以更新minDist[4]。
|
||||
* 节点5 和 节点2 的距离为10001(不连接),所以不用更新。
|
||||
* 节点6 和 节点2 的距离为1,比原先的距离值10001小,所以更新minDist[6]。
|
||||
* 节点3和节点2的距离为2,和原先的距离值1小,所以不用更新。
|
||||
* 节点4和节点2的距离为2,比原先的距离值10001小,所以更新minDist[4]。
|
||||
* 节点5和节点2的距离为10001(不连接),所以不用更新。
|
||||
* 节点6和节点2的距离为1,比原先的距离值10001小,所以更新minDist[6]。
|
||||
|
||||
### 4
|
||||
### 4
|
||||
|
||||
1、prim三部曲,第一步:选距离生成树最近节点
|
||||
|
||||
选择一个距离 最小生成树(节点1、节点2) 最近的非生成树里的节点,节点3,6 距离 最小生成树(节点1、节点2) 最近,选节点3 (选节点6也可以,距离一样)加入最小生成树。
|
||||
选择一个距离最小生成树(节点1、节点2)最近的非生成树里的节点,节点3,6距离最小生成树(节点1、节点2)最近,选节点3(选节点6也可以,距离一样)加入最小生成树。
|
||||
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
|
||||
此时 节点1 、节点2 、节点3 算是最小生成树的节点。
|
||||
此时节点1、节点2、节点3算是最小生成树的节点。
|
||||
|
||||
|
||||
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
接下来更新节点距离最小生成树的距离,如图:
|
||||
接下来更新节点距离最小生成树的距离,如图:
|
||||
|
||||

|
||||

|
||||
|
||||
所有非生成树的节点距离 最小生成树(节点1、节点2、节点3 )的距离都已经跟新了 。
|
||||
所有非生成树的节点距离最小生成树(节点1、节点2、节点3)的距离都已经跟新了。
|
||||
|
||||
* 节点 4 和 节点 3的距离为 1,和原先的距离值 2 小,所以更新minDist[4]为1。
|
||||
* 节点4和节点3的距离为1,和原先的距离值2小,所以更新minDist[4]为1。
|
||||
|
||||
上面为什么我们只比较 节点4 和 节点3 的距离呢?
|
||||
上面为什么我们只比较节点4和节点3的距离呢?
|
||||
|
||||
因为节点3加入 最小生成树后,非 生成树节点 只有 节点 4 和 节点3是链接的,所以需要重新更新一下 节点4距离最小生成树的距离,其他节点距离最小生成树的距离 都不变。
|
||||
因为节点3加入最小生成树后,非生成树节点只有节点4和节点3是链接的,所以需要重新更新一下节点4距离最小生成树的距离,其他节点距离最小生成树的距离都不变。
|
||||
|
||||
### 5
|
||||
### 5
|
||||
|
||||
1、prim三部曲,第一步:选距离生成树最近节点
|
||||
|
||||
继续选择一个距离 最小生成树(节点1、节点2、节点3) 最近的非生成树里的节点,为了巩固大家对 minDist数组的理解,这里我再啰嗦一遍:
|
||||
继续选择一个距离最小生成树(节点1、节点2、节点3)最近的非生成树里的节点,为了巩固大家对minDist数组的理解,这里我再啰嗦一遍:
|
||||
|
||||
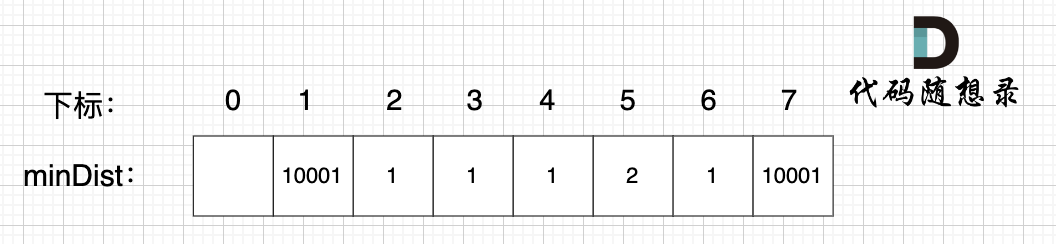
|
||||

|
||||
|
||||
**minDist数组 是记录了 所有非生成树节点距离生成树的最小距离**,所以 从数组里我们能看出来,非生成树节点 4 和 节点 6 距离 生成树最近。
|
||||
**minDist数组是记录了所有非生成树节点距离生成树的最小距离**,所以从数组里我们能看出来,非生成树节点4和节点6距离生成树最近。
|
||||
|
||||
|
||||
任选一个加入生成树,我们选 节点4(选节点6也行) 。
|
||||
任选一个加入生成树,我们选节点4(选节点6也行)。
|
||||
|
||||
**注意**,我们根据 minDist数组,选取距离 生成树 最近的节点 加入生成树,那么 **minDist数组里记录的其实也是 最小生成树的边的权值**(我在图中把权值对应的是哪两个节点也标记出来了)。
|
||||
**注意**,我们根据minDist数组,选取距离生成树最近的节点加入生成树,那么**minDist数组里记录的其实也是最小生成树的边的权值**(我在图中把权值对应的是哪两个节点也标记出来了)。
|
||||
|
||||
如果大家不理解,可以跟着我们下面的讲解,看 minDist数组的变化, minDist数组 里记录的权值对应的哪条边。
|
||||
如果大家不理解,可以跟着我们下面的讲解,看minDist数组的变化,minDist数组里记录的权值对应的哪条边。
|
||||
|
||||
理解这一点很重要,因为 最后我们要求 最小生成树里所有边的权值和。
|
||||
理解这一点很重要,因为最后我们要求最小生成树里所有边的权值和。
|
||||
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
|
||||
此时 节点1、节点2、节点3、节点4 算是 最小生成树的节点。
|
||||
此时节点1、节点2、节点3、节点4算是最小生成树的节点。
|
||||
|
||||
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
接下来更新节点距离最小生成树的距离,如图:
|
||||
接下来更新节点距离最小生成树的距离,如图:
|
||||
|
||||
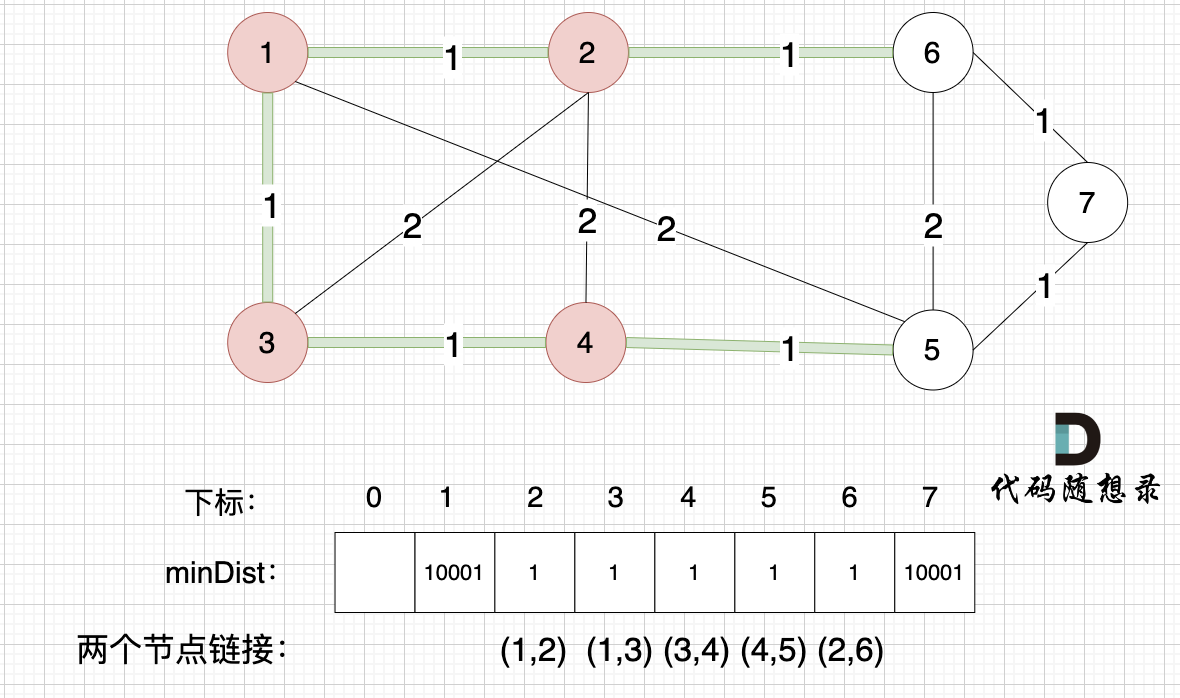
|
||||

|
||||
|
||||
minDist数组已经更新了 所有非生成树的节点距离 最小生成树(节点1、节点2、节点3、节点4 )的距离 。
|
||||
minDist数组已经更新了所有非生成树的节点距离最小生成树(节点1、节点2、节点3、节点4)的距离。
|
||||
|
||||
* 节点 5 和 节点 4的距离为 1,和原先的距离值 2 小,所以更新minDist[5]为1。
|
||||
* 节点5和节点4的距离为1,和原先的距离值2小,所以更新minDist[5]为1。
|
||||
|
||||
### 6
|
||||
### 6
|
||||
|
||||
1、prim三部曲,第一步:选距离生成树最近节点
|
||||
|
||||
继续选距离 最小生成树(节点1、节点2、节点3、节点4 )最近的非生成树里的节点,只有 节点 5 和 节点6。
|
||||
继续选距离最小生成树(节点1、节点2、节点3、节点4)最近的非生成树里的节点,只有节点5和节点6。
|
||||
|
||||
|
||||
选节点5 (选节点6也可以)加入 生成树。
|
||||
选节点5(选节点6也可以)加入生成树。
|
||||
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
|
||||
节点1、节点2、节点3、节点4、节点5 算是 最小生成树的节点。
|
||||
节点1、节点2、节点3、节点4、节点5算是最小生成树的节点。
|
||||
|
||||
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
@ -234,44 +234,44 @@ minDist数组已经更新了 所有非生成树的节点距离 最小生成树
|
||||
|
||||
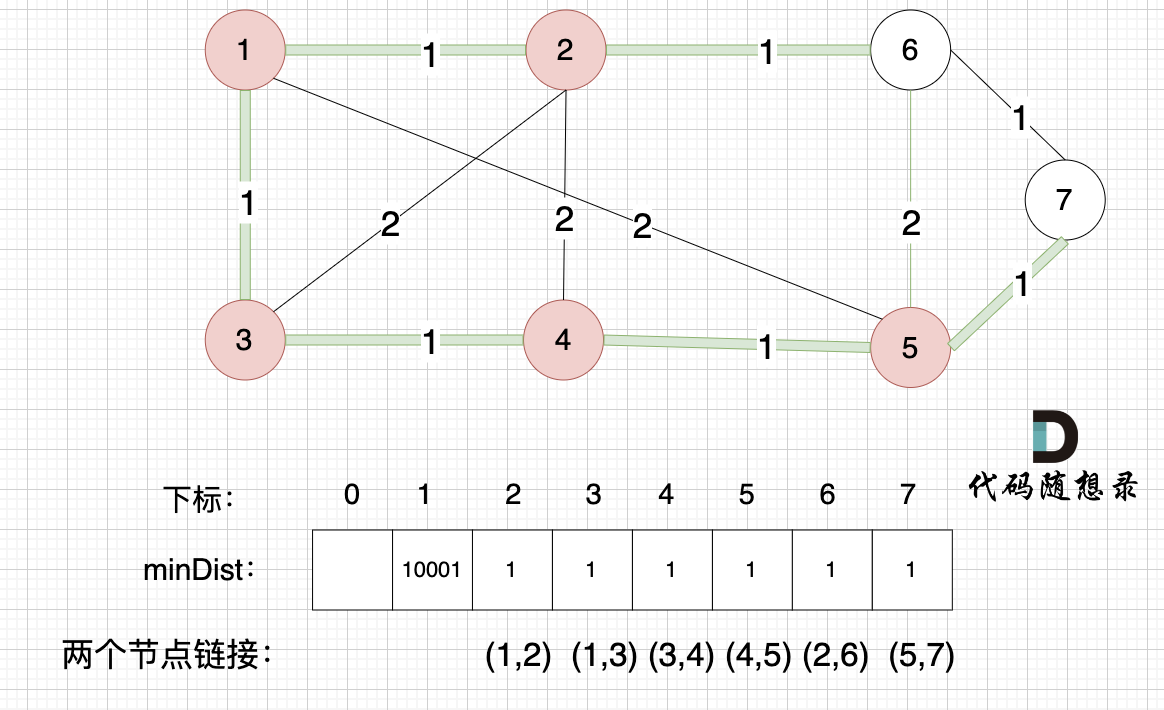
|
||||
|
||||
minDist数组已经更新了 所有非生成树的节点距离 最小生成树(节点1、节点2、节点3、节点4 、节点5)的距离 。
|
||||
minDist数组已经更新了所有非生成树的节点距离最小生成树(节点1、节点2、节点3、节点4、节点5)的距离。
|
||||
|
||||
* 节点 6 和 节点 5 距离为 2,比原先的距离值 1 大,所以不更新
|
||||
* 节点 7 和 节点 5 距离为 1,比原先的距离值 10001小,更新 minDist[7]
|
||||
* 节点6和节点5距离为2,比原先的距离值1大,所以不更新
|
||||
* 节点7和节点5距离为1,比原先的距离值10001小,更新minDist[7]
|
||||
|
||||
### 7
|
||||
### 7
|
||||
|
||||
1、prim三部曲,第一步:选距离生成树最近节点
|
||||
|
||||
继续选距离 最小生成树(节点1、节点2、节点3、节点4 、节点5)最近的非生成树里的节点,只有 节点 6 和 节点7。
|
||||
继续选距离最小生成树(节点1、节点2、节点3、节点4、节点5)最近的非生成树里的节点,只有节点6和节点7。
|
||||
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
|
||||
选节点6 (选节点7也行,距离一样的)加入生成树。
|
||||
选节点6(选节点7也行,距离一样的)加入生成树。
|
||||
|
||||
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
节点1、节点2、节点3、节点4、节点5、节点6 算是 最小生成树的节点 ,接下来更新节点距离最小生成树的距离,如图:
|
||||
节点1、节点2、节点3、节点4、节点5、节点6算是最小生成树的节点,接下来更新节点距离最小生成树的距离,如图:
|
||||
|
||||
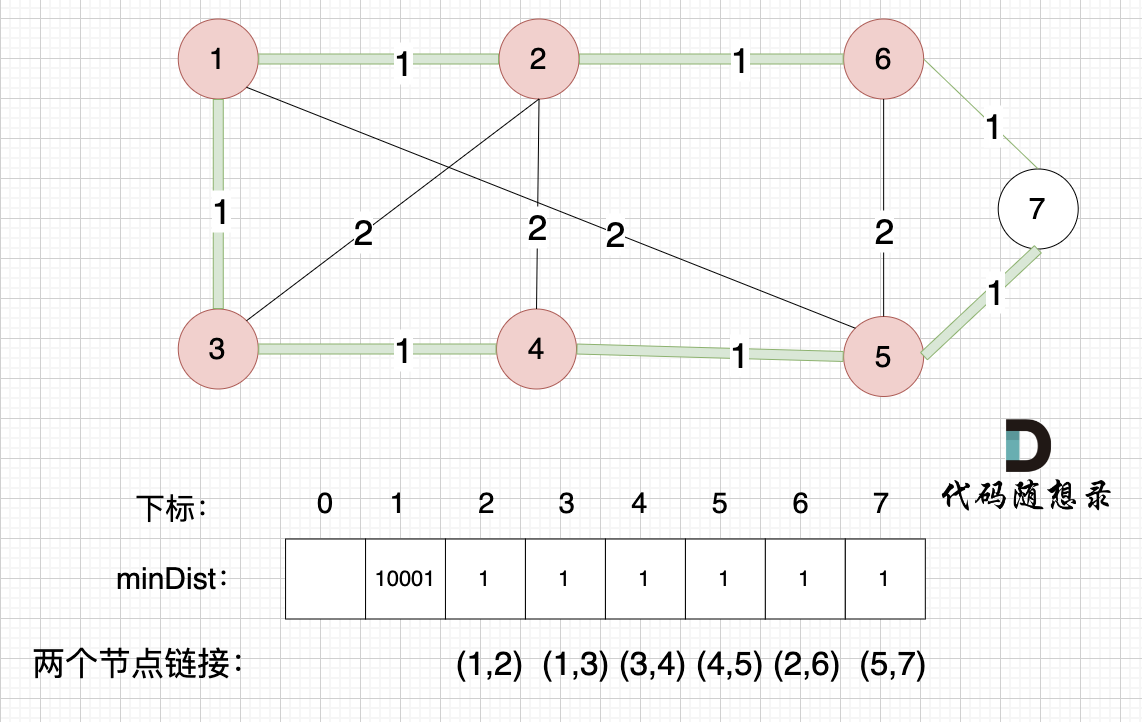
|
||||
|
||||
这里就不在重复描述了,大家类推,最后,节点7加入生成树,如图:
|
||||
这里就不在重复描述了,大家类推,最后,节点7加入生成树,如图:
|
||||
|
||||
|
||||

|
||||
|
||||
### 最后
|
||||
### 最后
|
||||
|
||||
最后我们就生成了一个 最小生成树, 绿色的边将所有节点链接到一起,并且 保证权值是最小的,因为我们在更新 minDist 数组的时候,都是选距离 最小生成树最近的点 加入到树中。
|
||||
最后我们就生成了一个最小生成树,绿色的边将所有节点链接到一起,并且保证权值是最小的,因为我们在更新minDist数组的时候,都是选距离最小生成树最近的点加入到树中。
|
||||
|
||||
讲解上面的模拟过程的时候,我已经强调多次 minDist数组 是记录了 所有非生成树节点距离生成树的最小距离。
|
||||
讲解上面的模拟过程的时候,我已经强调多次minDist数组是记录了所有非生成树节点距离生成树的最小距离。
|
||||
|
||||
最后,minDist数组 也就是记录的是最小生成树所有边的权值。
|
||||
最后,minDist数组也就是记录的是最小生成树所有边的权值。
|
||||
|
||||
我在图中,特别把 每条边的权值对应的是哪两个节点 标记出来(例如minDist[7] = 1,对应的是节点5 和 节点7之间的边,而不是 节点6 和 节点7),为了就是让大家清楚, minDist里的每一个值 对应的是哪条边。
|
||||
我在图中,特别把每条边的权值对应的是哪两个节点标记出来(例如minDist[7]=1,对应的是节点5和节点7之间的边,而不是节点6和节点7),为了就是让大家清楚,minDist里的每一个值对应的是哪条边。
|
||||
|
||||
那么我们要求最小生成树里边的权值总和 就是 把 最后的 minDist 数组 累加一起。
|
||||
那么我们要求最小生成树里边的权值总和就是把最后的minDist数组累加一起。
|
||||
|
||||
以下代码,我对 prim三部曲,做了重点注释,大家根据这三步,就可以 透彻理解prim。
|
||||
以下代码,我对prim三部曲,做了重点注释,大家根据这三步,就可以透彻理解prim。
|
||||
|
||||
```CPP
|
||||
#include<iostream>
|
||||
@ -338,52 +338,52 @@ int main() {
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
```
|
||||
|
||||
时间复杂度为 O(n^2),其中 n 为节点数量。
|
||||
时间复杂度为O(n^2),其中n为节点数量。
|
||||
|
||||
## 拓展
|
||||
|
||||
上面讲解的是记录了最小生成树 所有边的权值,如果让打印出来 最小生成树的每条边呢? 或者说 要把这个最小生成树画出来呢?
|
||||
上面讲解的是记录了最小生成树所有边的权值,如果让打印出来最小生成树的每条边呢?或者说要把这个最小生成树画出来呢?
|
||||
|
||||
|
||||
此时我们就需要把 最小生成树里每一条边记录下来。
|
||||
此时我们就需要把最小生成树里每一条边记录下来。
|
||||
|
||||
此时有两个问题:
|
||||
此时有两个问题:
|
||||
|
||||
* 1、用什么结构来记录
|
||||
* 2、如何记录
|
||||
* 1、用什么结构来记录
|
||||
* 2、如何记录
|
||||
|
||||
如果记录边,其实就是记录两个节点就可以,两个节点连成一条边。
|
||||
如果记录边,其实就是记录两个节点就可以,两个节点连成一条边。
|
||||
|
||||
如何记录两个节点呢?
|
||||
|
||||
我们使用一维数组就可以记录。 parent[节点编号] = 节点编号, 这样就把一条边记录下来了。(当然如果节点编号非常大,可以考虑使用map)
|
||||
我们使用一维数组就可以记录。parent[节点编号] = 节点编号,这样就把一条边记录下来了。(当然如果节点编号非常大,可以考虑使用map)
|
||||
|
||||
使用一维数组记录是有向边,不过我们这里不需要记录方向,所以只关注两条边是连接的就行。
|
||||
使用一维数组记录是有向边,不过我们这里不需要记录方向,所以只关注两条边是连接的就行。
|
||||
|
||||
parent数组初始化代码:
|
||||
parent数组初始化代码:
|
||||
|
||||
```CPP
|
||||
vector<int> parent(v + 1, -1);
|
||||
```
|
||||
|
||||
接下来就是第二个问题,如何记录?
|
||||
接下来就是第二个问题,如何记录?
|
||||
|
||||
我们再来回顾一下 prim三部曲,
|
||||
我们再来回顾一下prim三部曲,
|
||||
|
||||
1. 第一步,选距离生成树最近节点
|
||||
2. 第二步,最近节点加入生成树
|
||||
2. 第二步,最近节点加入生成树
|
||||
3. 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
大家先思考一下,我们是在第几步,可以记录 最小生成树的边呢?
|
||||
大家先思考一下,我们是在第几步,可以记录最小生成树的边呢?
|
||||
|
||||
在本面上半篇 我们讲解过:“我们根据 minDist数组,选组距离 生成树 最近的节点 加入生成树,那么 **minDist数组里记录的其实也是 最小生成树的边的权值**。”
|
||||
在本面上半篇我们讲解过:“我们根据minDist数组,选组距离生成树最近的节点加入生成树,那么**minDist数组里记录的其实也是最小生成树的边的权值**。”
|
||||
|
||||
既然 minDist数组 记录了 最小生成树的边,是不是就是在更新 minDist数组 的时候,去更新parent数组来记录一下对应的边呢。
|
||||
既然minDist数组记录了最小生成树的边,是不是就是在更新minDist数组的时候,去更新parent数组来记录一下对应的边呢。
|
||||
|
||||
|
||||
所以 在 prim三部曲中的第三步,更新 parent数组,代码如下:
|
||||
所以在prim三部曲中的第三步,更新parent数组,代码如下:
|
||||
|
||||
```CPP
|
||||
for (int j = 1; j <= v; j++) {
|
||||
@ -394,23 +394,23 @@ for (int j = 1; j <= v; j++) {
|
||||
}
|
||||
```
|
||||
|
||||
代码中注释中,我强调了 数组指向的顺序很重要。 因为不少录友在这里会写成这样: `parent[cur] = j` 。
|
||||
代码中注释中,我强调了数组指向的顺序很重要。因为不少录友在这里会写成这样: `parent[cur] = j` 。
|
||||
|
||||
这里估计大家会疑惑了,parent[节点编号A] = 节点编号B, 就表示A 和 B 相连,我们这里就不用在意方向,代码中 为什么 只能 `parent[j] = cur` 而不能 `parent[cur] = j` 这么写呢?
|
||||
这里估计大家会疑惑了,parent[节点编号A] = 节点编号B,就表示A和B相连,我们这里就不用在意方向,代码中为什么只能 `parent[j] = cur` 而不能 `parent[cur] = j` 这么写呢?
|
||||
|
||||
如果写成 `parent[cur] = j`,在 for 循环中,有多个 j 满足要求, 那么 parent[cur] 就会被反复覆盖,因为 cur 是一个固定值。
|
||||
如果写成 `parent[cur] = j`,在for循环中,有多个j满足要求,那么 parent[cur] 就会被反复覆盖,因为cur是一个固定值。
|
||||
|
||||
举个例子,cur = 1, 在 for循环中,可能 就 j = 2, j = 3,j =4 都符合条件,那么本来应该记录 节点1 与 节点 2、节点3、节点4相连的。
|
||||
举个例子,cur=1,在for循环中,可能就j=2,j=3,j=4都符合条件,那么本来应该记录节点1与节点2、节点3、节点4相连的。
|
||||
|
||||
如果 `parent[cur] = j` 这么写,最后更新的逻辑是 parent[1] = 2, parent[1] = 3, parent[1] = 4, 最后只能记录 节点1 与节点 4 相连,其他相连情况都被覆盖了。
|
||||
如果 `parent[cur] = j` 这么写,最后更新的逻辑是 parent[1] = 2, parent[1] = 3, parent[1] = 4,最后只能记录节点1与节点4相连,其他相连情况都被覆盖了。
|
||||
|
||||
如果这么写 `parent[j] = cur`, 那就是 parent[2] = 1, parent[3] = 1, parent[4] = 1 ,这样 才能完整表示出 节点1 与 其他节点都是链接的,才没有被覆盖。
|
||||
如果这么写 `parent[j] = cur`,那就是 parent[2] = 1, parent[3] = 1, parent[4] = 1 ,这样才能完整表示出节点1与其他节点都是链接的,才没有被覆盖。
|
||||
|
||||
主要问题也是我们使用了一维数组来记录。
|
||||
|
||||
如果是二维数组,来记录两个点链接,例如 parent[节点编号A][节点编号B] = 1 ,parent[节点编号B][节点编号A] = 1,来表示 节点A 与 节点B 相连,那就没有上面说的这个注意事项了,当然这么做的话,就是多开辟的内存空间。
|
||||
如果是二维数组,来记录两个点链接,例如 parent[节点编号A][节点编号B] = 1 ,parent[节点编号B][节点编号A] = 1,来表示节点A与节点B相连,那就没有上面说的这个注意事项了,当然这么做的话,就是多开辟的内存空间。
|
||||
|
||||
以下是输出最小生成树边的代码,不算最后输出, 就额外添加了两行代码,我都注释标记了:
|
||||
以下是输出最小生成树边的代码,不算最后输出,就额外添加了两行代码,我都注释标记了:
|
||||
|
||||
```CPP
|
||||
#include<iostream>
|
||||
@ -460,7 +460,7 @@ int main() {
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
```
|
||||
|
||||
按照本题示例,代码输入如下:
|
||||
|
||||
@ -476,40 +476,40 @@ int main() {
|
||||
|
||||
注意,这里是无向图,我在输出上添加了箭头仅仅是为了方便大家看出是边的意思。
|
||||
|
||||
大家可以和我们本题最后生成的最小生成树的图 去对比一下 边的链接情况:
|
||||
大家可以和我们本题最后生成的最小生成树的图去对比一下边的链接情况:
|
||||
|
||||
|
||||
|
||||
绿色的边 是最小生成树,和我们的 输出完全一致。
|
||||
绿色的边是最小生成树,和我们的输出完全一致。
|
||||
|
||||
## 总结
|
||||
## 总结
|
||||
|
||||
此时我就把prim算法讲解完毕了,我们再来回顾一下。
|
||||
此时我就把prim算法讲解完毕了,我们再来回顾一下。
|
||||
|
||||
关于 prim算法,我自创了三部曲,来帮助大家理解:
|
||||
关于prim算法,我自创了三部曲,来帮助大家理解:
|
||||
|
||||
1. 第一步,选距离生成树最近节点
|
||||
2. 第二步,最近节点加入生成树
|
||||
2. 第二步,最近节点加入生成树
|
||||
3. 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
大家只要理解这三部曲, prim算法 至少是可以写出一个框架出来,然后在慢慢补充细节,这样不至于 自己在写prim的时候 两眼一抹黑 完全凭感觉去写。
|
||||
这也为什么很多录友感觉 prim算法比较难,而且每次学会来,隔一段时间 又不会写了,主要是 没有一个纲领。
|
||||
大家只要理解这三部曲,prim算法至少是可以写出一个框架出来,然后在慢慢补充细节,这样不至于自己在写prim的时候两眼一抹黑完全凭感觉去写。
|
||||
这也为什么很多录友感觉prim算法比较难,而且每次学会来,隔一段时间又不会写了,主要是没有一个纲领。
|
||||
|
||||
理解这三部曲之后,更重要的 就是理解 minDist数组。
|
||||
理解这三部曲之后,更重要的就是理解minDist数组。
|
||||
|
||||
**minDist数组 是prim算法的灵魂,它帮助 prim算法完成最重要的一步,就是如何找到 距离最小生成树最近的点**。
|
||||
**minDist数组是prim算法的灵魂,它帮助prim算法完成最重要的一步,就是如何找到距离最小生成树最近的点**。
|
||||
|
||||
再来帮大家回顾 minDist数组 的含义:记录 每一个节点距离最小生成树的最近距离。
|
||||
再来帮大家回顾minDist数组的含义:记录每一个节点距离最小生成树的最近距离。
|
||||
|
||||
理解 minDist数组 ,至少大家看prim算法的代码不会懵。
|
||||
理解minDist数组,至少大家看prim算法的代码不会懵。
|
||||
|
||||
也正是 因为 minDist数组 的作用,我们根据 minDist数组,选取距离 生成树 最近的节点 加入生成树,那么 **minDist数组里记录的其实也是 最小生成树的边的权值**。
|
||||
也正是因为minDist数组的作用,我们根据minDist数组,选取距离生成树最近的节点加入生成树,那么**minDist数组里记录的其实也是最小生成树的边的权值**。
|
||||
|
||||
所以我们求 最小生成树的权值和 就是 计算后的 minDist数组 数值总和。
|
||||
所以我们求最小生成树的权值和就是计算后的minDist数组数值总和。
|
||||
|
||||
最后我们拓展了如何求职 最小生成树 的每一条边,其实 添加的代码很简单,主要是理解 为什么使用 parent数组 来记录边 以及 在哪里 更新parent数组。
|
||||
最后我们拓展了如何获得最小生成树的每一条边,其实添加的代码很简单,主要是理解为什么使用parent数组来记录边以及在哪里更新parent数组。
|
||||
|
||||
同时,因为使用一维数组,数组的下标和数组 如何赋值很重要,不要搞反,导致结果被覆盖。
|
||||
同时,因为使用一维数组,数组的下标和数组如何赋值很重要,不要搞反,导致结果被覆盖。
|
||||
|
||||
好了,以上为总结,录友们学习愉快。
|
||||
|
||||
@ -693,6 +693,55 @@ if __name__ == "__main__":
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
```js
|
||||
function prim(v, edges) {
|
||||
const grid = Array.from({ length: v + 1 }, () => new Array(v + 1).fill(10001)); // Fixed grid initialization
|
||||
const minDist = new Array(v + 1).fill(10001)
|
||||
const isInTree = new Array(v + 1).fill(false)
|
||||
// 建構鄰接矩陣
|
||||
for(const [v1, v2, w] of edges) {
|
||||
grid[v1][v2] = w
|
||||
grid[v2][v1] = w
|
||||
}
|
||||
// prim 演算法
|
||||
for (let i = 1 ; i < v ; i++) {
|
||||
let cur = -1
|
||||
let tempMinDist = Number.MAX_VALUE
|
||||
// 1. 尋找距離生成樹最近的節點
|
||||
for (let j = 1 ; j < v + 1 ; j++) {
|
||||
if (!isInTree[j] && minDist[j] < tempMinDist) {
|
||||
tempMinDist = minDist[j]
|
||||
cur = j
|
||||
}
|
||||
}
|
||||
// 2. 將節點放入生成樹
|
||||
isInTree[cur] = true
|
||||
// 3. 更新非生成樹節點與生成樹的最短距離
|
||||
for (let j = 1 ; j < v + 1 ; j++) {
|
||||
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
|
||||
minDist[j] = grid[cur][j]
|
||||
}
|
||||
}
|
||||
}
|
||||
console.log(minDist.slice(2).reduce((acc, cur) => acc + cur, 0))
|
||||
}
|
||||
|
||||
|
||||
async function main() {
|
||||
const rl = require('readline').createInterface({ input: process.stdin })
|
||||
const iter = rl[Symbol.asyncIterator]()
|
||||
const readline = async () => (await iter.next()).value
|
||||
const [v, e] = (await readline()).split(" ").map(Number)
|
||||
const edges = []
|
||||
for (let i = 0 ; i < e ; i++) {
|
||||
edges.push((await readline()).split(" ").map(Number))
|
||||
}
|
||||
prim(v, edges)
|
||||
}
|
||||
|
||||
|
||||
main()
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
|
||||
@ -425,13 +425,99 @@ public class Main {
|
||||
```
|
||||
|
||||
### Python
|
||||
```Python
|
||||
import collections
|
||||
|
||||
def main():
|
||||
n, m = map(int, input().strip().split())
|
||||
edges = [[] for _ in range(n + 1)]
|
||||
for _ in range(m):
|
||||
src, dest, weight = map(int, input().strip().split())
|
||||
edges[src].append([dest, weight])
|
||||
|
||||
minDist = [float("inf")] * (n + 1)
|
||||
minDist[1] = 0
|
||||
que = collections.deque([1])
|
||||
visited = [False] * (n + 1)
|
||||
visited[1] = True
|
||||
|
||||
while que:
|
||||
cur = que.popleft()
|
||||
visited[cur] = False
|
||||
for dest, weight in edges[cur]:
|
||||
if minDist[cur] != float("inf") and minDist[cur] + weight < minDist[dest]:
|
||||
minDist[dest] = minDist[cur] + weight
|
||||
if visited[dest] == False:
|
||||
que.append(dest)
|
||||
visited[dest] = True
|
||||
|
||||
if minDist[-1] == float("inf"):
|
||||
return "unconnected"
|
||||
return minDist[-1]
|
||||
|
||||
if __name__ == "__main__":
|
||||
print(main())
|
||||
```
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
```js
|
||||
async function main() {
|
||||
// 輸入
|
||||
const rl = require('readline').createInterface({ input: process.stdin })
|
||||
const iter = rl[Symbol.asyncIterator]()
|
||||
const readline = async () => (await iter.next()).value
|
||||
const [n, m] = (await readline()).split(" ").map(Number)
|
||||
const grid = {}
|
||||
for (let i = 0 ; i < m ; i++) {
|
||||
const [src, desc, w] = (await readline()).split(" ").map(Number)
|
||||
if (grid.hasOwnProperty(src)) {
|
||||
grid[src].push([desc, w])
|
||||
} else {
|
||||
grid[src] = [[desc, w]]
|
||||
}
|
||||
}
|
||||
const minDist = Array.from({length: n + 1}, () => Number.MAX_VALUE)
|
||||
|
||||
// 起始點
|
||||
minDist[1] = 0
|
||||
|
||||
const q = [1]
|
||||
const visited = Array.from({length: n + 1}, () => false)
|
||||
|
||||
while (q.length) {
|
||||
const src = q.shift()
|
||||
const neighbors = grid[src]
|
||||
visited[src] = false
|
||||
if (neighbors) {
|
||||
for (const [desc, w] of neighbors) {
|
||||
if (minDist[src] !== Number.MAX_VALUE
|
||||
&& minDist[src] + w < minDist[desc]) {
|
||||
minDist[desc] = minDist[src] + w
|
||||
if (!visited[desc]) {
|
||||
q.push(desc)
|
||||
visited[desc] = true
|
||||
}
|
||||
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 輸出
|
||||
if (minDist[n] === Number.MAX_VALUE) {
|
||||
console.log('unconnected')
|
||||
} else {
|
||||
console.log(minDist[n])
|
||||
}
|
||||
}
|
||||
|
||||
main()
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
@ -451,6 +451,33 @@ public class Main {
|
||||
```
|
||||
|
||||
### Python
|
||||
```Python
|
||||
def main():
|
||||
n, m = map(int, input().strip().split())
|
||||
edges = []
|
||||
for _ in range(m):
|
||||
src, dest, weight = map(int, input().strip().split())
|
||||
edges.append([src, dest, weight])
|
||||
|
||||
minDist = [float("inf")] * (n + 1)
|
||||
minDist[1] = 0 # 起点处距离为0
|
||||
|
||||
for i in range(1, n):
|
||||
updated = False
|
||||
for src, dest, weight in edges:
|
||||
if minDist[src] != float("inf") and minDist[src] + weight < minDist[dest]:
|
||||
minDist[dest] = minDist[src] + weight
|
||||
updated = True
|
||||
if not updated: # 若边不再更新,即停止回圈
|
||||
break
|
||||
|
||||
if minDist[-1] == float("inf"): # 返还终点权重
|
||||
return "unconnected"
|
||||
return minDist[-1]
|
||||
|
||||
if __name__ == "__main__":
|
||||
print(main())
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
@ -458,6 +485,45 @@ public class Main {
|
||||
|
||||
### Javascript
|
||||
|
||||
```js
|
||||
async function main() {
|
||||
// 輸入
|
||||
const rl = require('readline').createInterface({ input: process.stdin })
|
||||
const iter = rl[Symbol.asyncIterator]()
|
||||
const readline = async () => (await iter.next()).value
|
||||
const [n, m] = (await readline()).split(" ").map(Number)
|
||||
const edges = []
|
||||
for (let i = 0 ; i < m ; i++) {
|
||||
edges.push((await readline()).split(" ").map(Number))
|
||||
}
|
||||
const minDist = Array.from({length: n + 1}, () => Number.MAX_VALUE)
|
||||
// 起始點
|
||||
minDist[1] = 0
|
||||
|
||||
for (let i = 1 ; i < n ; i++) {
|
||||
let update = false
|
||||
for (const [src, desc, w] of edges) {
|
||||
if (minDist[src] !== Number.MAX_VALUE && minDist[src] + w < minDist[desc]) {
|
||||
minDist[desc] = minDist[src] + w
|
||||
update = true
|
||||
}
|
||||
}
|
||||
if (!update) {
|
||||
break;
|
||||
}
|
||||
}
|
||||
|
||||
// 輸出
|
||||
if (minDist[n] === Number.MAX_VALUE) {
|
||||
console.log('unconnected')
|
||||
} else {
|
||||
console.log(minDist[n])
|
||||
}
|
||||
}
|
||||
|
||||
main()
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
@ -54,7 +54,7 @@ circle
|
||||
|
||||
## 思路
|
||||
|
||||
本题是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 延伸题目。
|
||||
本题是 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 延伸题目。
|
||||
|
||||
本题是要我们判断 负权回路,也就是图中出现环且环上的边总权值为负数。
|
||||
|
||||
@ -64,7 +64,7 @@ circle
|
||||
|
||||
接下来我们来看 如何使用 bellman_ford 算法来判断 负权回路。
|
||||
|
||||
在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 中 我们讲了 bellman_ford 算法的核心就是一句话:对 所有边 进行 n-1 次松弛。 同时文中的 【拓展】部分, 我们也讲了 松弛n次以上 会怎么样?
|
||||
在 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 中 我们讲了 bellman_ford 算法的核心就是一句话:对 所有边 进行 n-1 次松弛。 同时文中的 【拓展】部分, 我们也讲了 松弛n次以上 会怎么样?
|
||||
|
||||
在没有负权回路的图中,松弛 n 次以上 ,结果不会有变化。
|
||||
|
||||
@ -72,7 +72,7 @@ circle
|
||||
|
||||
那么每松弛一次,都会更新最短路径,所以结果会一直有变化。
|
||||
|
||||
(如果对于 bellman_ford 不了解的录友,建议详细看这里:[kama94.城市间货物运输I](./kama94.城市间货物运输I.md))
|
||||
(如果对于 bellman_ford 不了解的录友,建议详细看这里:[kama94.城市间货物运输I](./0094.城市间货物运输I.md))
|
||||
|
||||
以上为理论分析,接下来我们再画图举例。
|
||||
|
||||
@ -94,13 +94,13 @@ circle
|
||||
|
||||
如果在负权回路多绕两圈,三圈,无穷圈,那么我们的总成本就会无限小, 如果要求最小成本的话,你会发现本题就无解了。
|
||||
|
||||
在 bellman_ford 算法中,松弛 n-1 次所有的边 就可以求得 起点到任何节点的最短路径,松弛 n 次以上,minDist数组(记录起到到其他节点的最短距离)中的结果也不会有改变 (如果对 bellman_ford 算法 不了解,也不知道 minDist 是什么,建议详看上篇讲解[kama94.城市间货物运输I](./kama94.城市间货物运输I.md))
|
||||
在 bellman_ford 算法中,松弛 n-1 次所有的边 就可以求得 起点到任何节点的最短路径,松弛 n 次以上,minDist数组(记录起到到其他节点的最短距离)中的结果也不会有改变 (如果对 bellman_ford 算法 不了解,也不知道 minDist 是什么,建议详看上篇讲解[kama94.城市间货物运输I](./0094.城市间货物运输I.md))
|
||||
|
||||
而本题有负权回路的情况下,一直都会有更短的最短路,所以 松弛 第n次,minDist数组 也会发生改变。
|
||||
|
||||
那么解决本题的 核心思路,就是在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 的基础上,再多松弛一次,看minDist数组 是否发生变化。
|
||||
那么解决本题的 核心思路,就是在 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 的基础上,再多松弛一次,看minDist数组 是否发生变化。
|
||||
|
||||
代码和 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 基本是一样的,如下:(关键地方已注释)
|
||||
代码和 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 基本是一样的,如下:(关键地方已注释)
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
|
||||
@ -51,15 +51,15 @@
|
||||
|
||||
## 思路
|
||||
|
||||
本题为单源有限最短路问题,同样是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 延伸题目。
|
||||
本题为单源有限最短路问题,同样是 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 延伸题目。
|
||||
|
||||
注意题目中描述是 **最多经过 k 个城市的条件下,而不是一定经过k个城市,也可以经过的城市数量比k小,但要最短的路径**。
|
||||
|
||||
在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 中我们讲了:**对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离**。
|
||||
在 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 中我们讲了:**对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离**。
|
||||
|
||||
节点数量为n,起点到终点,最多是 n-1 条边相连。 那么对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。
|
||||
|
||||
(如果对以上讲解看不懂,建议详看 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) )
|
||||
(如果对以上讲解看不懂,建议详看 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) )
|
||||
|
||||
本题是最多经过 k 个城市, 那么是 k + 1条边相连的节点。 这里可能有录友想不懂为什么是k + 1,来看这个图:
|
||||
|
||||
@ -71,7 +71,7 @@
|
||||
|
||||
对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离,那么对所有边松弛 k + 1次,就是求 起点到达 与起点k + 1条边相连的节点的 最短距离。
|
||||
|
||||
**注意**: 本题是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 的拓展题,如果对 bellman_ford 没有深入了解,强烈建议先看 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 再做本题。
|
||||
**注意**: 本题是 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 的拓展题,如果对 bellman_ford 没有深入了解,强烈建议先看 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 再做本题。
|
||||
|
||||
理解以上内容,其实本题代码就很容易了,bellman_ford 标准写法是松弛 n-1 次,本题就松弛 k + 1次就好。
|
||||
|
||||
@ -215,9 +215,9 @@ int main() {
|
||||

|
||||
|
||||
|
||||
边:节点3 -> 节点4,权值为1 ,minDist[4] > minDist[3] + 1,更新 minDist[4] = 0 + (-1) = -1 ,如图:
|
||||
边:节点3 -> 节点4,权值为1 ,minDist[4] > minDist[3] + 1,更新 minDist[4] = 0 + 1 = 1 ,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
以上是对所有边进行的第一次松弛,最后 minDist数组为 :-1 -1 0 1 ,(从下标1算起)
|
||||
@ -366,19 +366,19 @@ int main() {
|
||||
|
||||
## 拓展二(本题本质)
|
||||
|
||||
那么前面讲解过的 [94.城市间货物运输I](./kama94.城市间货物运输I.md) 和 [95.城市间货物运输II](./kama95.城市间货物运输II.md) 也是bellman_ford经典算法,也没使用 minDist_copy,怎么就没问题呢?
|
||||
那么前面讲解过的 [94.城市间货物运输I](./0094.城市间货物运输I.md) 和 [95.城市间货物运输II](./0095.城市间货物运输II.md) 也是bellman_ford经典算法,也没使用 minDist_copy,怎么就没问题呢?
|
||||
|
||||
> 如果没看过我上面这两篇讲解的话,建议详细学习上面两篇,再看我下面讲的区别,否则容易看不懂。
|
||||
|
||||
[94.城市间货物运输I](./kama94.城市间货物运输I.md), 是没有 负权回路的,那么 多松弛多少次,对结果都没有影响。
|
||||
[94.城市间货物运输I](./0094.城市间货物运输I.md), 是没有 负权回路的,那么 多松弛多少次,对结果都没有影响。
|
||||
|
||||
求 节点1 到 节点n 的最短路径,松弛n-1 次就够了,松弛 大于 n-1次,结果也不会变。
|
||||
|
||||
那么在对所有边进行第一次松弛的时候,如果基于 本次计算的 minDist 来计算 minDist (相当于多做松弛了),也是对最终结果没影响。
|
||||
|
||||
[95.城市间货物运输II](./kama95.城市间货物运输II.md) 是判断是否有 负权回路,一旦有负权回路, 对所有边松弛 n-1 次以后,在做松弛 minDist 数值一定会变,根据这一点来判断是否有负权回路。
|
||||
[95.城市间货物运输II](./0095.城市间货物运输II.md) 是判断是否有 负权回路,一旦有负权回路, 对所有边松弛 n-1 次以后,在做松弛 minDist 数值一定会变,根据这一点来判断是否有负权回路。
|
||||
|
||||
所以,[95.城市间货物运输II](./kama95.城市间货物运输II.md) 只需要判断minDist数值变化了就行,而 minDist 的数值对不对,并不是我们关心的。
|
||||
所以,[95.城市间货物运输II](./0095.城市间货物运输II.md) 只需要判断minDist数值变化了就行,而 minDist 的数值对不对,并不是我们关心的。
|
||||
|
||||
那么本题 为什么计算minDist 一定要基于上次 的 minDist 数值。
|
||||
|
||||
@ -703,6 +703,42 @@ public class Main {
|
||||
```
|
||||
|
||||
### Python
|
||||
```python
|
||||
def main():
|
||||
# 輸入
|
||||
n, m = map(int, input().split())
|
||||
edges = list()
|
||||
for _ in range(m):
|
||||
edges.append(list(map(int, input().split() )))
|
||||
|
||||
start, end, k = map(int, input().split())
|
||||
min_dist = [float('inf') for _ in range(n + 1)]
|
||||
min_dist[start] = 0
|
||||
|
||||
# 只能經過k個城市,所以從起始點到中間有(k + 1)個邊連接
|
||||
# 需要鬆弛(k + 1)次
|
||||
|
||||
for _ in range(k + 1):
|
||||
update = False
|
||||
min_dist_copy = min_dist.copy()
|
||||
for src, desc, w in edges:
|
||||
if (min_dist_copy[src] != float('inf') and
|
||||
min_dist_copy[src] + w < min_dist[desc]):
|
||||
min_dist[desc] = min_dist_copy[src] + w
|
||||
update = True
|
||||
if not update:
|
||||
break
|
||||
# 輸出
|
||||
if min_dist[end] == float('inf'):
|
||||
print('unreachable')
|
||||
else:
|
||||
print(min_dist[end])
|
||||
|
||||
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
|
||||
@ -277,7 +277,7 @@ ACM格式大家在输出结果的时候,要关注看看格式问题,特别
|
||||
|
||||
有录友可能会想,ACM格式就是麻烦,有空格没有空格有什么影响,结果对了不就行了?
|
||||
|
||||
ACM模式相对于核心代码模式(力扣) 更考验大家对代码的掌控能力。 例如工程代码里,输出输出都是要自己控制的。这也是为什么大公司笔试,都是ACM模式。
|
||||
ACM模式相对于核心代码模式(力扣) 更考验大家对代码的掌控能力。 例如工程代码里,输入输出都是要自己控制的。这也是为什么大公司笔试,都是ACM模式。
|
||||
|
||||
以上代码中,结果都存在了 result数组里(二维数组,每一行是一个结果),最后将其打印出来。(重点看注释)
|
||||
|
||||
|
||||
@ -191,10 +191,57 @@ int main() {
|
||||
### Java
|
||||
|
||||
```java
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
public static int[][] dir = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};//下右上左逆时针遍历
|
||||
|
||||
public static void bfs(int[][] grid, boolean[][] visited, int x, int y) {
|
||||
Queue<pair> queue = new LinkedList<pair>();//定义坐标队列,没有现成的pair类,在下面自定义了
|
||||
queue.add(new pair(x, y));
|
||||
visited[x][y] = true;//遇到入队直接标记为优先,
|
||||
// 否则出队时才标记的话会导致重复访问,比如下方节点会在右下顺序的时候被第二次访问入队
|
||||
while (!queue.isEmpty()) {
|
||||
int curX = queue.peek().first;
|
||||
int curY = queue.poll().second;//当前横纵坐标
|
||||
for (int i = 0; i < 4; i++) {
|
||||
//顺时针遍历新节点next,下面记录坐标
|
||||
int nextX = curX + dir[i][0];
|
||||
int nextY = curY + dir[i][1];
|
||||
if (nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) {
|
||||
continue;
|
||||
}//去除越界部分
|
||||
if (!visited[nextX][nextY] && grid[nextX][nextY] == 1) {
|
||||
queue.add(new pair(nextX, nextY));
|
||||
visited[nextX][nextY] = true;//逻辑同上
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int m = sc.nextInt();
|
||||
int n = sc.nextInt();
|
||||
int[][] grid = new int[m][n];
|
||||
boolean[][] visited = new boolean[m][n];
|
||||
int ans = 0;
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
grid[i][j] = sc.nextInt();
|
||||
}
|
||||
}
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (!visited[i][j] && grid[i][j] == 1) {
|
||||
ans++;
|
||||
bfs(grid, visited, i, j);
|
||||
}
|
||||
}
|
||||
}
|
||||
System.out.println(ans);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
@ -452,6 +499,55 @@ main();
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
```scala
|
||||
import scala.collection.mutable.Queue
|
||||
import util.control.Breaks._
|
||||
|
||||
// Dev on LeetCode: https://leetcode.cn/problems/number-of-islands/description/
|
||||
object Solution {
|
||||
def numIslands(grid: Array[Array[Char]]): Int = {
|
||||
val row = grid.length
|
||||
val col = grid(0).length
|
||||
val dir = List((-1,0), (0,-1), (1,0), (0,1)) // 四个方向
|
||||
var visited = Array.fill(row)(Array.fill(col)(false))
|
||||
var counter = 0
|
||||
var que = Queue.empty[Tuple2[Int, Int]]
|
||||
|
||||
(0 until row).map{ r =>
|
||||
(0 until col).map{ c =>
|
||||
breakable {
|
||||
if (!visited(r)(c) && grid(r)(c) == '1') {
|
||||
que.enqueue((r, c))
|
||||
visited(r)(c) // 只要加入队列,立刻标记
|
||||
} else break // 不是岛屿不进入queue,也不记录
|
||||
|
||||
while (!que.isEmpty) {
|
||||
val cur = que.head
|
||||
que.dequeue()
|
||||
val x = cur(0)
|
||||
val y = cur(1)
|
||||
dir.map{ d =>
|
||||
val nextX = x + d(0)
|
||||
val nextY = y + d(1)
|
||||
breakable {
|
||||
// 越界就跳过
|
||||
if (nextX < 0 || nextX >= row || nextY < 0 || nextY >= col) break
|
||||
if (!visited(nextX)(nextY) && grid(nextX)(nextY) == '1') {
|
||||
visited(nextX)(nextY) = true // 只要加入队列,立刻标记
|
||||
que.enqueue((nextX, nextY))
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
counter = counter + 1 // 找完一个岛屿后记录一下
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
counter
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### C#
|
||||
|
||||
|
||||
@ -182,7 +182,52 @@ int main() {
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
```java
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static int[][] dir ={{0,1},{1,0},{-1,0},{0,-1}};
|
||||
public static void dfs(boolean[][] visited,int x,int y ,int [][]grid)
|
||||
{
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextX=x+dir[i][0];
|
||||
int nextY=y+dir[i][1];
|
||||
if(nextY<0||nextX<0||nextX>= grid.length||nextY>=grid[0].length)
|
||||
continue;
|
||||
if(!visited[nextX][nextY]&&grid[nextX][nextY]==1)
|
||||
{
|
||||
visited[nextX][nextY]=true;
|
||||
dfs(visited,nextX,nextY,grid);
|
||||
}
|
||||
}
|
||||
}
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int m= sc.nextInt();
|
||||
int n = sc.nextInt();
|
||||
int[][] grid = new int[m][n];
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
grid[i][j]=sc.nextInt();
|
||||
}
|
||||
}
|
||||
boolean[][]visited =new boolean[m][n];
|
||||
int ans = 0;
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
if(!visited[i][j]&&grid[i][j]==1)
|
||||
{
|
||||
ans++;
|
||||
visited[i][j]=true;
|
||||
dfs(visited,i,j,grid);
|
||||
}
|
||||
}
|
||||
}
|
||||
System.out.println(ans);
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
### Python
|
||||
|
||||
版本一
|
||||
@ -367,6 +412,46 @@ const dfs = (graph, visited, x, y) => {
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
```scala
|
||||
import util.control.Breaks._
|
||||
|
||||
object Solution {
|
||||
val dir = List((-1,0), (0,-1), (1,0), (0,1)) // 四个方向
|
||||
|
||||
def dfs(grid: Array[Array[Char]], visited: Array[Array[Boolean]], row: Int, col: Int): Unit = {
|
||||
(0 until 4).map { x =>
|
||||
val nextR = row + dir(x)(0)
|
||||
val nextC = col + dir(x)(1)
|
||||
breakable {
|
||||
if(nextR < 0 || nextR >= grid.length || nextC < 0 || nextC >= grid(0).length) break
|
||||
if (!visited(nextR)(nextC) && grid(nextR)(nextC) == '1') {
|
||||
visited(nextR)(nextC) = true // 经过就记录
|
||||
dfs(grid, visited, nextR, nextC)
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
def numIslands(grid: Array[Array[Char]]): Int = {
|
||||
val row = grid.length
|
||||
val col = grid(0).length
|
||||
var visited = Array.fill(row)(Array.fill(col)(false))
|
||||
var counter = 0
|
||||
|
||||
(0 until row).map{ r =>
|
||||
(0 until col).map{ c =>
|
||||
if (!visited(r)(c) && grid(r)(c) == '1') {
|
||||
visited(r)(c) = true // 经过就记录
|
||||
dfs(grid, visited, r, c)
|
||||
counter += 1
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
counter
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### C#
|
||||
|
||||
|
||||
@ -222,8 +222,128 @@ public:
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
### Java
|
||||
|
||||
```java
|
||||
import java.util.*;
|
||||
import java.math.*;
|
||||
|
||||
/**
|
||||
* DFS版
|
||||
*/
|
||||
public class Main{
|
||||
|
||||
static final int[][] dir={{0,1},{1,0},{0,-1},{-1,0}};
|
||||
static int result=0;
|
||||
static int count=0;
|
||||
|
||||
public static void main(String[] args){
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int m = scanner.nextInt();
|
||||
int[][] map = new int[n][m];
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
map[i][j]=scanner.nextInt();
|
||||
}
|
||||
}
|
||||
boolean[][] visited = new boolean[n][m];
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if(!visited[i][j]&&map[i][j]==1){
|
||||
count=0;
|
||||
dfs(map,visited,i,j);
|
||||
result= Math.max(count, result);
|
||||
}
|
||||
}
|
||||
}
|
||||
System.out.println(result);
|
||||
}
|
||||
|
||||
static void dfs(int[][] map,boolean[][] visited,int x,int y){
|
||||
count++;
|
||||
visited[x][y]=true;
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextX=x+dir[i][0];
|
||||
int nextY=y+dir[i][1];
|
||||
//水或者已经访问过的跳过
|
||||
if(nextX<0||nextY<0
|
||||
||nextX>=map.length||nextY>=map[0].length
|
||||
||visited[nextX][nextY]||map[nextX][nextY]==0)continue;
|
||||
|
||||
dfs(map,visited,nextX,nextY);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```java
|
||||
import java.util.*;
|
||||
import java.math.*;
|
||||
|
||||
/**
|
||||
* BFS版
|
||||
*/
|
||||
public class Main {
|
||||
static class Node {
|
||||
int x;
|
||||
int y;
|
||||
|
||||
public Node(int x, int y) {
|
||||
this.x = x;
|
||||
this.y = y;
|
||||
}
|
||||
}
|
||||
|
||||
static final int[][] dir = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
|
||||
static int result = 0;
|
||||
static int count = 0;
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int m = scanner.nextInt();
|
||||
int[][] map = new int[n][m];
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
map[i][j] = scanner.nextInt();
|
||||
}
|
||||
}
|
||||
boolean[][] visited = new boolean[n][m];
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (!visited[i][j] && map[i][j] == 1) {
|
||||
count = 0;
|
||||
bfs(map, visited, i, j);
|
||||
result = Math.max(count, result);
|
||||
|
||||
}
|
||||
}
|
||||
}
|
||||
System.out.println(result);
|
||||
}
|
||||
|
||||
static void bfs(int[][] map, boolean[][] visited, int x, int y) {
|
||||
Queue<Node> q = new LinkedList<>();
|
||||
q.add(new Node(x, y));
|
||||
visited[x][y] = true;
|
||||
count++;
|
||||
while (!q.isEmpty()) {
|
||||
Node node = q.remove();
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextX = node.x + dir[i][0];
|
||||
int nextY = node.y + dir[i][1];
|
||||
if (nextX < 0 || nextY < 0 || nextX >= map.length || nextY >= map[0].length || visited[nextX][nextY] || map[nextX][nextY] == 0)
|
||||
continue;
|
||||
q.add(new Node(nextX, nextY));
|
||||
visited[nextX][nextY] = true;
|
||||
count++;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
### Python
|
||||
|
||||
DFS
|
||||
@ -389,6 +509,144 @@ func main() {
|
||||
|
||||
|
||||
### Rust
|
||||
DFS
|
||||
|
||||
``` rust
|
||||
use std::io;
|
||||
use std::cmp;
|
||||
|
||||
// 定义四个方向
|
||||
const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];
|
||||
|
||||
fn dfs(grid: &Vec<Vec<i32>>, visited: &mut Vec<Vec<bool>>, x: usize, y: usize, count: &mut i32) {
|
||||
if visited[x][y] || grid[x][y] == 0 {
|
||||
return; // 终止条件:已访问或者遇到海水
|
||||
}
|
||||
visited[x][y] = true; // 标记已访问
|
||||
*count += 1;
|
||||
|
||||
for &(dx, dy) in DIRECTIONS.iter() {
|
||||
let new_x = x as i32 + dx;
|
||||
let new_y = y as i32 + dy;
|
||||
|
||||
// 检查边界条件
|
||||
if new_x >= 0 && new_x < grid.len() as i32 && new_y >= 0 && new_y < grid[0].len() as i32 {
|
||||
dfs(grid, visited, new_x as usize, new_y as usize, count);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
fn main() {
|
||||
let mut input = String::new();
|
||||
|
||||
// 读取 n 和 m
|
||||
io::stdin().read_line(&mut input);
|
||||
let dims: Vec<usize> = input.trim().split_whitespace().map(|s| s.parse().unwrap()).collect();
|
||||
let (n, m) = (dims[0], dims[1]);
|
||||
|
||||
// 读取 grid
|
||||
let mut grid = vec![];
|
||||
for _ in 0..n {
|
||||
input.clear();
|
||||
io::stdin().read_line(&mut input);
|
||||
let row: Vec<i32> = input.trim().split_whitespace().map(|s| s.parse().unwrap()).collect();
|
||||
grid.push(row);
|
||||
}
|
||||
|
||||
// 初始化访问记录
|
||||
let mut visited = vec![vec![false; m]; n];
|
||||
let mut result = 0;
|
||||
|
||||
// 遍历所有格子
|
||||
for i in 0..n {
|
||||
for j in 0..m {
|
||||
if !visited[i][j] && grid[i][j] == 1 {
|
||||
let mut count = 0;
|
||||
dfs(&grid, &mut visited, i, j, &mut count);
|
||||
result = cmp::max(result, count);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 输出结果
|
||||
println!("{}", result);
|
||||
}
|
||||
|
||||
```
|
||||
BFS
|
||||
```rust
|
||||
use std::io;
|
||||
use std::collections::VecDeque;
|
||||
|
||||
// 定义四个方向
|
||||
const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];
|
||||
|
||||
fn bfs(grid: &Vec<Vec<i32>>, visited: &mut Vec<Vec<bool>>, x: usize, y: usize) -> i32 {
|
||||
let mut count = 0;
|
||||
let mut queue = VecDeque::new();
|
||||
queue.push_back((x, y));
|
||||
visited[x][y] = true; // 标记已访问
|
||||
|
||||
while let Some((cur_x, cur_y)) = queue.pop_front() {
|
||||
count += 1; // 增加计数
|
||||
|
||||
for &(dx, dy) in DIRECTIONS.iter() {
|
||||
let new_x = cur_x as i32 + dx;
|
||||
let new_y = cur_y as i32 + dy;
|
||||
|
||||
// 检查边界条件
|
||||
if new_x >= 0 && new_x < grid.len() as i32 && new_y >= 0 && new_y < grid[0].len() as i32 {
|
||||
let new_x_usize = new_x as usize;
|
||||
let new_y_usize = new_y as usize;
|
||||
|
||||
// 如果未访问且是陆地,加入队列
|
||||
if !visited[new_x_usize][new_y_usize] && grid[new_x_usize][new_y_usize] == 1 {
|
||||
visited[new_x_usize][new_y_usize] = true; // 标记已访问
|
||||
queue.push_back((new_x_usize, new_y_usize));
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
count
|
||||
}
|
||||
|
||||
fn main() {
|
||||
let mut input = String::new();
|
||||
|
||||
// 读取 n 和 m
|
||||
io::stdin().read_line(&mut input).expect("Failed to read line");
|
||||
let dims: Vec<usize> = input.trim().split_whitespace().map(|s| s.parse().unwrap()).collect();
|
||||
let (n, m) = (dims[0], dims[1]);
|
||||
|
||||
// 读取 grid
|
||||
let mut grid = vec![];
|
||||
for _ in 0..n {
|
||||
input.clear();
|
||||
io::stdin().read_line(&mut input).expect("Failed to read line");
|
||||
let row: Vec<i32> = input.trim().split_whitespace().map(|s| s.parse().unwrap()).collect();
|
||||
grid.push(row);
|
||||
}
|
||||
|
||||
// 初始化访问记录
|
||||
let mut visited = vec![vec![false; m]; n];
|
||||
let mut result = 0;
|
||||
|
||||
// 遍历所有格子
|
||||
for i in 0..n {
|
||||
for j in 0..m {
|
||||
if !visited[i][j] && grid[i][j] == 1 {
|
||||
let count = bfs(&grid, &mut visited, i, j);
|
||||
result = result.max(count);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 输出结果
|
||||
println!("{}", result);
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
### Javascript
|
||||
|
||||
@ -480,7 +738,84 @@ const bfs = (graph, visited, x, y) => {
|
||||
})()
|
||||
```
|
||||
|
||||
```javascript
|
||||
|
||||
// 深搜版
|
||||
|
||||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||||
// 创建readline接口
|
||||
let iter = r1[Symbol.asyncIterator]();
|
||||
// 创建异步迭代器
|
||||
const readline = async () => (await iter.next()).value;
|
||||
|
||||
let graph // 地图
|
||||
let N, M // 地图大小
|
||||
let visited // 访问过的节点
|
||||
let result = 0 // 最大岛屿面积
|
||||
let count = 0 // 岛屿内节点数
|
||||
const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
|
||||
|
||||
// 读取输入,初始化地图
|
||||
const initGraph = async () => {
|
||||
let line = await readline();
|
||||
[N, M] = line.split(' ').map(Number);
|
||||
graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
|
||||
visited = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||||
|
||||
for (let i = 0; i < N; i++) {
|
||||
line = await readline()
|
||||
line = line.split(' ').map(Number)
|
||||
for (let j = 0; j < M; j++) {
|
||||
graph[i][j] = line[j]
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
/**
|
||||
* @description: 从(x, y)开始深度优先遍历
|
||||
* @param {*} graph 地图
|
||||
* @param {*} visited 访问过的节点
|
||||
* @param {*} x 开始搜索节点的下标
|
||||
* @param {*} y 开始搜索节点的下标
|
||||
* @return {*}
|
||||
*/
|
||||
const dfs = (graph, visited, x, y) => {
|
||||
for (let i = 0; i < 4; i++) {
|
||||
let nextx = x + dir[i][0]
|
||||
let nexty = y + dir[i][1]
|
||||
if(nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue
|
||||
if(!visited[nextx][nexty] && graph[nextx][nexty] === 1){
|
||||
count++
|
||||
visited[nextx][nexty] = true
|
||||
dfs(graph, visited, nextx, nexty)
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
(async function () {
|
||||
|
||||
// 读取输入,初始化地图
|
||||
await initGraph()
|
||||
|
||||
// 统计最大岛屿面积
|
||||
for (let i = 0; i < N; i++) {
|
||||
for (let j = 0; j < M; j++) {
|
||||
if (!visited[i][j] && graph[i][j] === 1) { //遇到没有访问过的陆地
|
||||
// 重新计算面积
|
||||
count = 1
|
||||
visited[i][j] = true
|
||||
|
||||
// 深度优先遍历,统计岛屿内节点数,并将岛屿标记为已访问
|
||||
dfs(graph, visited, i, j)
|
||||
|
||||
// 更新最大岛屿面积
|
||||
result = Math.max(result, count)
|
||||
}
|
||||
}
|
||||
}
|
||||
console.log(result);
|
||||
})()
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
|
||||
@ -307,6 +307,71 @@ for i in range(n):
|
||||
|
||||
print(count)
|
||||
```
|
||||
|
||||
```python
|
||||
direction = [[1, 0], [-1, 0], [0, 1], [0, -1]]
|
||||
result = 0
|
||||
|
||||
# 深度搜尋
|
||||
def dfs(grid, y, x):
|
||||
grid[y][x] = 0
|
||||
global result
|
||||
result += 1
|
||||
|
||||
for i, j in direction:
|
||||
next_x = x + j
|
||||
next_y = y + i
|
||||
if (next_x < 0 or next_y < 0 or
|
||||
next_x >= len(grid[0]) or next_y >= len(grid)
|
||||
):
|
||||
continue
|
||||
if grid[next_y][next_x] == 1 and not visited[next_y][next_x]:
|
||||
visited[next_y][next_x] = True
|
||||
dfs(grid, next_y, next_x)
|
||||
|
||||
|
||||
# 讀取輸入值
|
||||
n, m = map(int, input().split())
|
||||
grid = []
|
||||
visited = [[False] * m for _ in range(n)]
|
||||
|
||||
for i in range(n):
|
||||
grid.append(list(map(int, input().split())))
|
||||
|
||||
# 處理邊界
|
||||
for j in range(m):
|
||||
# 上邊界
|
||||
if grid[0][j] == 1 and not visited[0][j]:
|
||||
visited[0][j] = True
|
||||
dfs(grid, 0, j)
|
||||
# 下邊界
|
||||
if grid[n - 1][j] == 1 and not visited[n - 1][j]:
|
||||
visited[n - 1][j] = True
|
||||
dfs(grid, n - 1, j)
|
||||
|
||||
for i in range(n):
|
||||
# 左邊界
|
||||
if grid[i][0] == 1 and not visited[i][0]:
|
||||
visited[i][0] = True
|
||||
dfs(grid, i, 0)
|
||||
# 右邊界
|
||||
if grid[i][m - 1] == 1 and not visited[i][m - 1]:
|
||||
visited[i][m - 1] = True
|
||||
dfs(grid, i, m - 1)
|
||||
|
||||
# 計算孤島總面積
|
||||
result = 0 # 初始化,避免使用到處理邊界時所產生的累加值
|
||||
|
||||
for i in range(n):
|
||||
for j in range(m):
|
||||
if grid[i][j] == 1 and not visited[i][j]:
|
||||
visited[i][j] = True
|
||||
dfs(grid, i, j)
|
||||
|
||||
# 輸出孤島的總面積
|
||||
print(result)
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
``` go
|
||||
|
||||
@ -294,37 +294,52 @@ int main() {
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
public static List<List<Integer>> adjList = new ArrayList<>();
|
||||
|
||||
public static void dfs(List<List<Integer>> graph, int key, boolean[] visited) {
|
||||
for (int neighbor : graph.get(key)) {
|
||||
if (!visited[neighbor]) { // Check if the next node is not visited
|
||||
visited[neighbor] = true;
|
||||
dfs(graph, neighbor, visited);
|
||||
public static void dfs(boolean[] visited, int key) {
|
||||
if (visited[key]) {
|
||||
return;
|
||||
}
|
||||
visited[key] = true;
|
||||
List<Integer> nextKeys = adjList.get(key);
|
||||
for (int nextKey : nextKeys) {
|
||||
dfs(visited, nextKey);
|
||||
}
|
||||
}
|
||||
|
||||
public static void bfs(boolean[] visited, int key) {
|
||||
Queue<Integer> queue = new LinkedList<Integer>();
|
||||
queue.add(key);
|
||||
visited[key] = true;
|
||||
while (!queue.isEmpty()) {
|
||||
int curKey = queue.poll();
|
||||
List<Integer> list = adjList.get(curKey);
|
||||
for (int nextKey : list) {
|
||||
if (!visited[nextKey]) {
|
||||
queue.add(nextKey);
|
||||
visited[nextKey] = true;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int m = scanner.nextInt();
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int vertices_num = sc.nextInt();
|
||||
int line_num = sc.nextInt();
|
||||
for (int i = 0; i < vertices_num; i++) {
|
||||
adjList.add(new LinkedList<>());
|
||||
}//Initialization
|
||||
for (int i = 0; i < line_num; i++) {
|
||||
int s = sc.nextInt();
|
||||
int t = sc.nextInt();
|
||||
adjList.get(s - 1).add(t - 1);
|
||||
}//构造邻接表
|
||||
boolean[] visited = new boolean[vertices_num];
|
||||
dfs(visited, 0);
|
||||
// bfs(visited, 0);
|
||||
|
||||
List<List<Integer>> graph = new ArrayList<>();
|
||||
for (int i = 0; i <= n; i++) {
|
||||
graph.add(new ArrayList<>());
|
||||
}
|
||||
|
||||
for (int i = 0; i < m; i++) {
|
||||
int s = scanner.nextInt();
|
||||
int t = scanner.nextInt();
|
||||
graph.get(s).add(t);
|
||||
}
|
||||
|
||||
boolean[] visited = new boolean[n + 1];
|
||||
visited[1] = true; // Process node 1 beforehand
|
||||
dfs(graph, 1, visited);
|
||||
|
||||
for (int i = 1; i <= n; i++) {
|
||||
for (int i = 0; i < vertices_num; i++) {
|
||||
if (!visited[i]) {
|
||||
System.out.println(-1);
|
||||
return;
|
||||
@ -334,7 +349,6 @@ public class Main {
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
```
|
||||
|
||||
|
||||
|
||||
@ -7,9 +7,15 @@
|
||||
|
||||
题目描述
|
||||
|
||||
树可以看成是一个图(拥有 n 个节点和 n - 1 条边的连通无环无向图)。
|
||||
有一个图,它是一棵树,他是拥有 n 个节点(节点编号1到n)和 n - 1 条边的连通无环无向图(其实就是一个线形图),如图:
|
||||
|
||||
现给定一个拥有 n 个节点(节点编号从 1 到 n)和 n 条边的连通无向图,请找出一条可以删除的边,删除后图可以变成一棵树。
|
||||

|
||||
|
||||
现在在这棵树上的基础上,添加一条边(依然是n个节点,但有n条边),使这个图变成了有环图,如图
|
||||
|
||||
|
||||
|
||||
先请你找出冗余边,删除后,使该图可以重新变成一棵树。
|
||||
|
||||
输入描述
|
||||
|
||||
@ -60,12 +66,11 @@
|
||||
|
||||
那么我们就可以从前向后遍历每一条边(因为优先让前面的边连上),边的两个节点如果不在同一个集合,就加入集合(即:同一个根节点)。
|
||||
|
||||
如图所示:
|
||||
|
||||
如图所示,节点A 和节点 B 不在同一个集合,那么就可以将两个 节点连在一起。
|
||||
|
||||
|
||||
|
||||
节点A 和节点 B 不在同一个集合,那么就可以将两个 节点连在一起。
|
||||
|
||||
如果边的两个节点已经出现在同一个集合里,说明着边的两个节点已经连在一起了,再加入这条边一定就出现环了。
|
||||
|
||||
如图所示:
|
||||
@ -127,6 +132,44 @@ int main() {
|
||||
|
||||
可以看出,主函数的代码很少,就判断一下边的两个节点在不在同一个集合就可以了。
|
||||
|
||||
## 拓展
|
||||
|
||||
题目要求 “请删除标准输入中最后出现的那条边” ,不少录友疑惑,这代码分明是遇到在同一个根的两个节点立刻就返回了,怎么就求出 最后出现的那条边 了呢。
|
||||
|
||||
有这种疑惑的录友是 认为发现一条冗余边后,后面还可能会有一条冗余边。
|
||||
|
||||
其实并不会。
|
||||
|
||||
题目是在 树的基础上 添加一条边,所以冗余边仅仅是一条。
|
||||
|
||||
到这一条可能靠前出现,可能靠后出现。
|
||||
|
||||
例如,题目输入示例:
|
||||
|
||||
输入示例
|
||||
|
||||
```
|
||||
3
|
||||
1 2
|
||||
2 3
|
||||
1 3
|
||||
```
|
||||
|
||||
图:
|
||||
|
||||
|
||||
|
||||
输出示例
|
||||
|
||||
1 3
|
||||
|
||||
当我们从前向后遍历,优先让前面的边连上,最后判断冗余边就是 1 3。
|
||||
|
||||
如果我们从后向前便利,优先让后面的边连上,最后判断的冗余边就是 1 2。
|
||||
|
||||
题目要求“请删除标准输入中最后出现的那条边”,所以 1 3 这条边才是我们要求的。
|
||||
|
||||
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
@ -135,6 +178,45 @@ int main() {
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
father = list()
|
||||
|
||||
def find(u):
|
||||
if u == father[u]:
|
||||
return u
|
||||
else:
|
||||
father[u] = find(father[u])
|
||||
return father[u]
|
||||
|
||||
def is_same(u, v):
|
||||
u = find(u)
|
||||
v = find(v)
|
||||
return u == v
|
||||
|
||||
def join(u, v):
|
||||
u = find(u)
|
||||
v = find(v)
|
||||
if u != v:
|
||||
father[u] = v
|
||||
|
||||
if __name__ == "__main__":
|
||||
# 輸入
|
||||
n = int(input())
|
||||
for i in range(n + 1):
|
||||
father.append(i)
|
||||
# 尋找冗余邊
|
||||
result = None
|
||||
for i in range(n):
|
||||
s, t = map(int, input().split())
|
||||
if is_same(s, t):
|
||||
result = str(s) + ' ' + str(t)
|
||||
else:
|
||||
join(s, t)
|
||||
|
||||
# 輸出
|
||||
print(result)
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
@ -251,8 +251,218 @@ int main() {
|
||||
|
||||
### Java
|
||||
|
||||
```java
|
||||
import java.util.*;
|
||||
|
||||
/*
|
||||
* 冗余连接II。主要问题是存在入度为2或者成环,也可能两个问题同时存在。
|
||||
* 1.判断入度为2的边
|
||||
* 2.判断是否成环(并查集)
|
||||
*/
|
||||
|
||||
public class Main {
|
||||
/**
|
||||
* 并查集模板
|
||||
*/
|
||||
static class Disjoint {
|
||||
|
||||
private final int[] father;
|
||||
|
||||
public Disjoint(int n) {
|
||||
father = new int[n];
|
||||
for (int i = 0; i < n; i++) {
|
||||
father[i] = i;
|
||||
}
|
||||
}
|
||||
|
||||
public void join(int n, int m) {
|
||||
n = find(n);
|
||||
m = find(m);
|
||||
if (n == m) return;
|
||||
father[n] = m;
|
||||
}
|
||||
|
||||
public int find(int n) {
|
||||
return father[n] == n ? n : (father[n] = find(father[n]));
|
||||
}
|
||||
|
||||
public boolean isSame(int n, int m) {
|
||||
return find(n) == find(m);
|
||||
}
|
||||
}
|
||||
|
||||
static class Edge {
|
||||
int s;
|
||||
int t;
|
||||
|
||||
public Edge(int s, int t) {
|
||||
this.s = s;
|
||||
this.t = t;
|
||||
}
|
||||
}
|
||||
|
||||
static class Node {
|
||||
int id;
|
||||
int in;
|
||||
int out;
|
||||
}
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
List<Edge> edges = new ArrayList<>();
|
||||
Node[] nodeMap = new Node[n + 1];
|
||||
for (int i = 1; i <= n; i++) {
|
||||
nodeMap[i] = new Node();
|
||||
}
|
||||
Integer doubleIn = null;
|
||||
for (int i = 0; i < n; i++) {
|
||||
int s = scanner.nextInt();
|
||||
int t = scanner.nextInt();
|
||||
//记录入度
|
||||
nodeMap[t].in++;
|
||||
if (!(nodeMap[t].in < 2)) doubleIn = t;
|
||||
Edge edge = new Edge(s, t);
|
||||
edges.add(edge);
|
||||
}
|
||||
Edge result = null;
|
||||
//存在入度为2的节点,既要消除入度为2的问题同时解除可能存在的环
|
||||
if (doubleIn != null) {
|
||||
List<Edge> doubleInEdges = new ArrayList<>();
|
||||
for (Edge edge : edges) {
|
||||
if (edge.t == doubleIn) doubleInEdges.add(edge);
|
||||
if (doubleInEdges.size() == 2) break;
|
||||
}
|
||||
Edge edge = doubleInEdges.get(1);
|
||||
if (isTreeWithExclude(edges, edge, nodeMap)) {
|
||||
result = edge;
|
||||
} else {
|
||||
result = doubleInEdges.get(0);
|
||||
}
|
||||
} else {
|
||||
//不存在入度为2的节点,则只需要解除环即可
|
||||
result = getRemoveEdge(edges, nodeMap);
|
||||
}
|
||||
|
||||
System.out.println(result.s + " " + result.t);
|
||||
}
|
||||
|
||||
public static boolean isTreeWithExclude(List<Edge> edges, Edge exculdEdge, Node[] nodeMap) {
|
||||
Disjoint disjoint = new Disjoint(nodeMap.length + 1);
|
||||
for (Edge edge : edges) {
|
||||
if (edge == exculdEdge) continue;
|
||||
//成环则不是树
|
||||
if (disjoint.isSame(edge.s, edge.t)) {
|
||||
return false;
|
||||
}
|
||||
disjoint.join(edge.s, edge.t);
|
||||
}
|
||||
return true;
|
||||
}
|
||||
|
||||
public static Edge getRemoveEdge(List<Edge> edges, Node[] nodeMap) {
|
||||
int length = nodeMap.length;
|
||||
Disjoint disjoint = new Disjoint(length);
|
||||
|
||||
for (Edge edge : edges) {
|
||||
if (disjoint.isSame(edge.s, edge.t)) return edge;
|
||||
disjoint.join(edge.s, edge.t);
|
||||
}
|
||||
return null;
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
from collections import defaultdict
|
||||
|
||||
father = list()
|
||||
|
||||
|
||||
def find(u):
|
||||
if u == father[u]:
|
||||
return u
|
||||
else:
|
||||
father[u] = find(father[u])
|
||||
return father[u]
|
||||
|
||||
|
||||
def is_same(u, v):
|
||||
u = find(u)
|
||||
v = find(v)
|
||||
return u == v
|
||||
|
||||
|
||||
def join(u, v):
|
||||
u = find(u)
|
||||
v = find(v)
|
||||
if u != v:
|
||||
father[u] = v
|
||||
|
||||
|
||||
def is_tree_after_remove_edge(edges, edge, n):
|
||||
# 初始化并查集
|
||||
global father
|
||||
father = [i for i in range(n + 1)]
|
||||
|
||||
for i in range(len(edges)):
|
||||
if i == edge:
|
||||
continue
|
||||
s, t = edges[i]
|
||||
if is_same(s, t): # 成環,即不是有向樹
|
||||
return False
|
||||
else: # 將s,t放入集合中
|
||||
join(s, t)
|
||||
return True
|
||||
|
||||
|
||||
def get_remove_edge(edges):
|
||||
# 初始化并查集
|
||||
global father
|
||||
father = [i for i in range(n + 1)]
|
||||
|
||||
for s, t in edges:
|
||||
if is_same(s, t):
|
||||
print(s, t)
|
||||
return
|
||||
else:
|
||||
join(s, t)
|
||||
|
||||
|
||||
if __name__ == "__main__":
|
||||
# 輸入
|
||||
n = int(input())
|
||||
edges = list()
|
||||
in_degree = defaultdict(int)
|
||||
|
||||
for i in range(n):
|
||||
s, t = map(int, input().split())
|
||||
in_degree[t] += 1
|
||||
edges.append([s, t])
|
||||
|
||||
# 尋找入度為2的邊,並紀錄其下標(index)
|
||||
vec = list()
|
||||
for i in range(n - 1, -1, -1):
|
||||
if in_degree[edges[i][1]] == 2:
|
||||
vec.append(i)
|
||||
|
||||
# 輸出
|
||||
if len(vec) > 0:
|
||||
# 情況一:刪除輸出順序靠後的邊
|
||||
if is_tree_after_remove_edge(edges, vec[0], n):
|
||||
print(edges[vec[0]][0], edges[vec[0]][1])
|
||||
# 情況二:只能刪除特定的邊
|
||||
else:
|
||||
print(edges[vec[1]][0], edges[vec[1]][1])
|
||||
else:
|
||||
# 情況三: 原圖有環
|
||||
get_remove_edge(edges)
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
@ -152,66 +152,70 @@ int main() {
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
### Java
|
||||
|
||||
```Java
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
// BFS方法
|
||||
public static int ladderLength(String beginWord, String endWord, List<String> wordList) {
|
||||
// 使用set作为查询容器,效率更高
|
||||
HashSet<String> set = new HashSet<>(wordList);
|
||||
|
||||
// 声明一个queue存储每次变更一个字符得到的且存在于容器中的新字符串
|
||||
Queue<String> queue = new LinkedList<>();
|
||||
|
||||
// 声明一个hashMap存储遍历到的字符串以及所走过的路径path
|
||||
HashMap<String, Integer> visitMap = new HashMap<>();
|
||||
queue.offer(beginWord);
|
||||
visitMap.put(beginWord, 1);
|
||||
|
||||
while (!queue.isEmpty()) {
|
||||
String curWord = queue.poll();
|
||||
int path = visitMap.get(curWord);
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
scanner.nextLine();
|
||||
String beginStr = scanner.next();
|
||||
String endStr = scanner.next();
|
||||
scanner.nextLine();
|
||||
List<String> wordList = new ArrayList<>();
|
||||
wordList.add(beginStr);
|
||||
wordList.add(endStr);
|
||||
for (int i = 0; i < n; i++) {
|
||||
wordList.add(scanner.nextLine());
|
||||
}
|
||||
int count = bfs(beginStr, endStr, wordList);
|
||||
System.out.println(count);
|
||||
}
|
||||
|
||||
for (int i = 0; i < curWord.length(); i++) {
|
||||
char[] ch = curWord.toCharArray();
|
||||
// 每个位置尝试26个字母
|
||||
for (char k = 'a'; k <= 'z'; k++) {
|
||||
ch[i] = k;
|
||||
|
||||
String newWord = new String(ch);
|
||||
if (newWord.equals(endWord)) return path + 1;
|
||||
|
||||
// 如果这个新字符串存在于容器且之前未被访问到
|
||||
if (set.contains(newWord) && !visitMap.containsKey(newWord)) {
|
||||
visitMap.put(newWord, path + 1);
|
||||
queue.offer(newWord);
|
||||
/**
|
||||
* 广度优先搜索-寻找最短路径
|
||||
*/
|
||||
public static int bfs(String beginStr, String endStr, List<String> wordList) {
|
||||
int len = 1;
|
||||
Set<String> set = new HashSet<>(wordList);
|
||||
Set<String> visited = new HashSet<>();
|
||||
Queue<String> q = new LinkedList<>();
|
||||
visited.add(beginStr);
|
||||
q.add(beginStr);
|
||||
q.add(null);
|
||||
while (!q.isEmpty()) {
|
||||
String node = q.remove();
|
||||
//上一层结束,若下一层还有节点进入下一层
|
||||
if (node == null) {
|
||||
if (!q.isEmpty()) {
|
||||
len++;
|
||||
q.add(null);
|
||||
}
|
||||
continue;
|
||||
}
|
||||
char[] charArray = node.toCharArray();
|
||||
//寻找邻接节点
|
||||
for (int i = 0; i < charArray.length; i++) {
|
||||
//记录旧值,用于回滚修改
|
||||
char old = charArray[i];
|
||||
for (char j = 'a'; j <= 'z'; j++) {
|
||||
charArray[i] = j;
|
||||
String newWord = new String(charArray);
|
||||
if (set.contains(newWord) && !visited.contains(newWord)) {
|
||||
q.add(newWord);
|
||||
visited.add(newWord);
|
||||
//找到结尾
|
||||
if (newWord.equals(endStr)) return len + 1;
|
||||
}
|
||||
}
|
||||
charArray[i] = old;
|
||||
}
|
||||
}
|
||||
|
||||
return 0;
|
||||
}
|
||||
|
||||
public static void main (String[] args) {
|
||||
/* code */
|
||||
// 接收输入
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int N = sc.nextInt();
|
||||
sc.nextLine();
|
||||
String[] strs = sc.nextLine().split(" ");
|
||||
|
||||
List<String> wordList = new ArrayList<>();
|
||||
for (int i = 0; i < N; i++) {
|
||||
wordList.add(sc.nextLine());
|
||||
}
|
||||
|
||||
// wordList.add(strs[1]);
|
||||
|
||||
// 打印结果
|
||||
int result = ladderLength(strs[0], strs[1], wordList);
|
||||
System.out.println(result);
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
@ -1,27 +0,0 @@
|
||||
|
||||
# 111. 构造二阶行列式
|
||||
|
||||
暴力模拟就好,每个数不超过 20, 暴力枚举其实也没多大。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
for (int x = 1; x <= 20; x++) {
|
||||
for (int y = 1; y <= 20; y++) {
|
||||
for (int i = 1; i <= 20; i++) {
|
||||
for (int j = 1; j <= 20; j++) {
|
||||
if ((x * j - y * i) == n) {
|
||||
cout << x << " " << y << endl;
|
||||
cout << i << " " << j << endl;
|
||||
return 0;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
cout << -1 << endl;
|
||||
}
|
||||
```
|
||||
@ -1,26 +0,0 @@
|
||||
|
||||
# 112. 挑战boss
|
||||
|
||||
本题题意有点绕,注意看一下 题目描述中的【提示信息】,但是在笔试中,是不给这样的提示信息的。
|
||||
|
||||
简单模拟:
|
||||
|
||||
```CPP
|
||||
#include<iostream>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n, a, b, k = 0;
|
||||
cin >> n >> a >> b;
|
||||
string s;
|
||||
cin >> s;
|
||||
int result = 0;
|
||||
for (int i = 0; i < s.size(); i++) {
|
||||
int cur = a + k * b;
|
||||
result += cur;
|
||||
++k;
|
||||
if (s[i] == 'x') k = 0;
|
||||
}
|
||||
cout << result << endl;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
@ -1,59 +0,0 @@
|
||||
|
||||
# 113.国际象棋
|
||||
|
||||
广搜,但本题如果广搜枚举马和象的话会超时。
|
||||
|
||||
广搜要只枚举马的走位,同时判断是否在对角巷直接走象
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
using namespace std;
|
||||
const int N = 100005, mod = 1000000007;
|
||||
using ll = long long;
|
||||
int n, ans;
|
||||
int dir[][2] = {{1, 2}, {1, -2}, {-1, 2}, {-1, -2}, {2, 1}, {2, -1}, {-2, -1}, {-2, 1}};
|
||||
int main() {
|
||||
int x1, y1, x2, y2;
|
||||
cin >> n;
|
||||
while (n--) {
|
||||
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
|
||||
if (x1 == x2 && y1 == y2) {
|
||||
cout << 0 << endl;
|
||||
continue;
|
||||
}
|
||||
// 判断象走一步到达
|
||||
int d = abs(x1 - x2) - abs(y1 - y2);
|
||||
if (!d) {cout << 1 << endl; continue;}
|
||||
// 判断马走一步到达
|
||||
bool one = 0;
|
||||
for (int i = 0; i < 8; ++i) {
|
||||
int dx = x1 + dir[i][0], dy = y1 + dir[i][1];
|
||||
if (dx == x2 && dy == y2) {
|
||||
cout << 1 << endl;
|
||||
one = true;
|
||||
break;
|
||||
}
|
||||
}
|
||||
if (one) continue;
|
||||
// 接下来为两步的逻辑, 象走两步或者马走一步,象走一步
|
||||
// 象直接两步可以到达,这个计算是不是同颜色的格子,象可以在两步到达所有同颜色的格子
|
||||
int d2 = abs(x1 - x2) + abs(y1 - y2);
|
||||
if (d2 % 2 == 0) {
|
||||
cout << 2 << endl;
|
||||
continue;
|
||||
}
|
||||
// 接下来判断马 + 象的组合
|
||||
bool two = 0;
|
||||
for (int i = 0; i < 8; ++i) {
|
||||
int dx = x1 + dir[i][0], dy = y1 + dir[i][1];
|
||||
int d = abs(dx - x2) - abs(dy - y2);
|
||||
if (!d) {cout << 2 << endl; two = true; break;}
|
||||
}
|
||||
if (two) continue;
|
||||
// 剩下的格子全都是三步到达的
|
||||
cout << 3 << endl;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
@ -1,29 +0,0 @@
|
||||
|
||||
# 114. 小欧的平均数
|
||||
|
||||
这道题非常的脑筋急转弯, 读题都要理解半天。
|
||||
|
||||
初步读题,感觉好像是求 如何最小加减,得到三个数的平均数。
|
||||
|
||||
但题意不是这样的。
|
||||
|
||||
小欧的说的三个数平衡,只是三个数里 任何两个数 相加都能被2整除, 那么 也就是说,这三个数 要么都是 奇数,要么都是偶数,才能达到小欧所说的平衡。
|
||||
|
||||
所以题目要求的,就是,三个数,最小加减1 几次 可以让三个数都变成奇数,或者都变成偶数。
|
||||
|
||||
所以最终的结果 不是1 就是0,没有其他的。
|
||||
|
||||
录友可能想,题目出的这么绕干啥? 没办法,企业的笔试题就是这样的。
|
||||
|
||||
```CPP
|
||||
#include<iostream>
|
||||
#include<algorithm>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int x, y, z;
|
||||
cin >> x >> y >> z;
|
||||
int count = (x % 2 == 0) + (y % 2 == 0) + (z % 2 == 0);
|
||||
cout << min(3 - count, count);
|
||||
}
|
||||
```
|
||||
|
||||
@ -1,67 +0,0 @@
|
||||
|
||||
# 115. 组装手机
|
||||
|
||||
这道题是比较难得哈希表题目。 把代码随想录哈希表章节理解透彻,做本题没问题。
|
||||
|
||||
思路是
|
||||
|
||||
1. 用哈希表记录 外壳售价 和 手机零件售价 出现的次数
|
||||
2. 记录总和出现的次数
|
||||
3. 遍历总和,减去 外壳售价,看 手机零件售价出现了几次
|
||||
4. 最后累加,取最大值
|
||||
|
||||
有一个需要注意的点: 数字可以重复,在计算个数的时候,如果计算重复的数字
|
||||
|
||||
例如 如果输入是
|
||||
|
||||
```
|
||||
4
|
||||
1 1 1 1
|
||||
1 1 1 1
|
||||
```
|
||||
那么输出应该是 4, 外壳售价 和 手机零件售价 是可以重复的。
|
||||
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <unordered_set>
|
||||
#include <unordered_map>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
vector<int> aVec(n, 0);
|
||||
vector<int> bVec(n, 0);
|
||||
unordered_map<int, int > aUmap;
|
||||
unordered_map<int, int > bUmap;
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> aVec[i];
|
||||
aUmap[aVec[i]]++;
|
||||
}
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> bVec[i];
|
||||
bUmap[bVec[i]]++;
|
||||
}
|
||||
unordered_set<int > uset;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < n; j++){
|
||||
uset.insert(aVec[i] + bVec[j]);
|
||||
}
|
||||
}
|
||||
int result = 0;
|
||||
for (int sum : uset) {
|
||||
//cout << p.first << endl;
|
||||
int count = 0;
|
||||
for (pair<int, int> p : aUmap) {
|
||||
//cout << p.first - aVec[i] << endl;
|
||||
if (sum - p.first > 0 && bUmap[sum - p.first] != 0) {
|
||||
count += min(bUmap[sum - p.first], p.second);
|
||||
}
|
||||
}
|
||||
result = max(result, count);
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
@ -1,91 +0,0 @@
|
||||
|
||||
<p align="center"><strong><a href="./qita/join.md">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!</strong></p>
|
||||
|
||||
# 大数减法
|
||||
|
||||
本题测试数据超过int 和 longlong了,所以考察的使用 string 来模拟 两个大数的 加减操作。
|
||||
|
||||
当然如果使用python或者Java 使用库函数都可以水过。
|
||||
|
||||
使用字符串来模拟过程,需要处理以下几个问题:
|
||||
|
||||
* 负号处理:要考虑正负数的处理,如果大数相减的结果是负数,需要在结果前加上负号。
|
||||
* 大数比较:在进行减法之前,需要确定哪个数大,以便知道结果是否需要添加负号。
|
||||
* 位数借位:处理大数相减时的借位问题,这类似于手动减法。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <string>
|
||||
#include <algorithm>
|
||||
using namespace std;
|
||||
|
||||
// 比较两个字符串表示的数字,返回1表示a > b,0表示a == b,-1表示a < b
|
||||
int compareStrings(const string& a, const string& b) {
|
||||
if (a.length() > b.length()) return 1;
|
||||
if (a.length() < b.length()) return -1;
|
||||
return a.compare(b);
|
||||
}
|
||||
|
||||
// 去除字符串左侧的前导零
|
||||
string removeLeadingZeros(const string& num) {
|
||||
size_t start = 0;
|
||||
while (start < num.size() && num[start] == '0') {
|
||||
start++;
|
||||
}
|
||||
return start == num.size() ? "0" : num.substr(start);
|
||||
}
|
||||
|
||||
// 大数相减,假设a >= b
|
||||
string subtractStrings(const string& a, const string& b) {
|
||||
string result;
|
||||
int len1 = a.length(), len2 = b.length();
|
||||
int carry = 0;
|
||||
|
||||
for (int i = 0; i < len1; i++) {
|
||||
int digitA = a[len1 - 1 - i] - '0';
|
||||
int digitB = i < len2 ? b[len2 - 1 - i] - '0' : 0;
|
||||
|
||||
int digit = digitA - digitB - carry;
|
||||
if (digit < 0) {
|
||||
digit += 10;
|
||||
carry = 1;
|
||||
} else {
|
||||
carry = 0;
|
||||
}
|
||||
|
||||
result.push_back(digit + '0');
|
||||
}
|
||||
|
||||
// 去除结果中的前导零
|
||||
reverse(result.begin(), result.end());
|
||||
return removeLeadingZeros(result);
|
||||
}
|
||||
|
||||
string subtractLargeNumbers(const string& num1, const string& num2) {
|
||||
string a = num1, b = num2;
|
||||
|
||||
// 比较两个数的大小
|
||||
int cmp = compareStrings(a, b);
|
||||
|
||||
if (cmp == 0) {
|
||||
return "0"; // 如果两个数相等,结果为0
|
||||
} else if (cmp < 0) {
|
||||
// 如果a < b,交换它们并在结果前加上负号
|
||||
swap(a, b);
|
||||
return "-" + subtractStrings(a, b);
|
||||
} else {
|
||||
return subtractStrings(a, b);
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
string num1, num2;
|
||||
cin >> num1 >> num2;
|
||||
|
||||
string result = subtractLargeNumbers(num1, num2);
|
||||
cout << result << endl;
|
||||
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
@ -1,132 +0,0 @@
|
||||
|
||||
# 121. 小红的区间翻转
|
||||
|
||||
比较暴力的方式,就是直接模拟, 枚举所有 区间,然后检查其翻转的情况。
|
||||
|
||||
在检查翻转的时候,需要一些代码优化,否则容易超时。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
|
||||
bool canTransform(const vector<int>& a, const vector<int>& b, int left, int right) {
|
||||
// 提前检查翻转区间的值是否可以匹配
|
||||
for (int i = left, j = right; i <= right; i++, j--) {
|
||||
if (a[i] != b[j]) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
// 检查翻转区间外的值是否匹配
|
||||
for (int i = 0; i < left; i++) {
|
||||
if (a[i] != b[i]) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
for (int i = right + 1; i < a.size(); i++) {
|
||||
if (a[i] != b[i]) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
|
||||
vector<int> a(n);
|
||||
vector<int> b(n);
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> a[i];
|
||||
}
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> b[i];
|
||||
}
|
||||
|
||||
int count = 0;
|
||||
|
||||
// 遍历所有可能的区间
|
||||
for (int left = 0; left < n; left++) {
|
||||
for (int right = left; right < n; right++) {
|
||||
// 检查翻转区间 [left, right] 后,a 是否可以变成 b
|
||||
if (canTransform(a, b, left, right)) {
|
||||
count++;
|
||||
}
|
||||
}
|
||||
}
|
||||
cout << count << endl;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
也可以事先计算好,最长公共前缀,和最长公共后缀。
|
||||
|
||||
在公共前缀和公共后缀之间的部分进行翻转操作,这样我们可以减少很多不必要的翻转尝试。
|
||||
|
||||
通过在公共前缀和后缀之间的部分,找到可以通过翻转使得 a 和 b 相等的区间。
|
||||
|
||||
以下 为评论区 卡码网用户:码鬼的C++代码
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
vector<int> a(n), b(n);
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> a[i];
|
||||
}
|
||||
for (int i = 0; i < n; i++) {
|
||||
cin >> b[i];
|
||||
}
|
||||
|
||||
vector<int> prefix(n, 0), suffix(n, 0);
|
||||
|
||||
// 计算前缀相等的位置
|
||||
int p = 0;
|
||||
while (p < n && a[p] == b[p]) {
|
||||
prefix[p] = 1;
|
||||
p++;
|
||||
}
|
||||
|
||||
// 计算后缀相等的位置
|
||||
int s = n - 1;
|
||||
while (s >= 0 && a[s] == b[s]) {
|
||||
suffix[s] = 1;
|
||||
s--;
|
||||
}
|
||||
|
||||
int count = 0;
|
||||
|
||||
// 遍历所有可能的区间
|
||||
for (int i = 0; i < n - 1; i++) {
|
||||
for (int j = i + 1; j < n; j++) {
|
||||
// 判断前缀和后缀是否相等
|
||||
if ((i == 0 || prefix[i - 1] == 1) && (j == n - 1 || suffix[j + 1] == 1)) {
|
||||
// 判断翻转后的子数组是否和目标数组相同
|
||||
bool is_palindrome = true;
|
||||
for (int k = 0; k <= (j - i) / 2; k++) {
|
||||
if (a[i + k] != b[j - k]) {
|
||||
is_palindrome = false;
|
||||
break;
|
||||
}
|
||||
}
|
||||
if (is_palindrome) {
|
||||
count++;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
cout << count << endl;
|
||||
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
@ -1,127 +0,0 @@
|
||||
|
||||
# 滑动窗口最大值
|
||||
|
||||
本题是 [代码随想录:滑动窗口最大值](https://www.programmercarl.com/0239.%E6%BB%91%E5%8A%A8%E7%AA%97%E5%8F%A3%E6%9C%80%E5%A4%A7%E5%80%BC.html) 的升级版。
|
||||
|
||||
在[代码随想录:滑动窗口最大值](https://www.programmercarl.com/0239.%E6%BB%91%E5%8A%A8%E7%AA%97%E5%8F%A3%E6%9C%80%E5%A4%A7%E5%80%BC.html) 中详细讲解了如何求解 滑动窗口的最大值。
|
||||
|
||||
那么求滑动窗口的最小值原理也是一样的, 大家稍加思考,把优先级队列里的 大于 改成小于 就行了。
|
||||
|
||||
求最大值的优先级队列(从大到小)
|
||||
```
|
||||
while (!que.empty() && value > que.back()) {
|
||||
```
|
||||
|
||||
求最小值的优先级队列(从小到大)
|
||||
```
|
||||
while (!que.empty() && value > que.back()) {
|
||||
```
|
||||
|
||||
这样在滑动窗口里 最大值最小值都求出来了,遍历一遍找出 差值最大的就好。
|
||||
|
||||
至于输入,需要一波字符串处理,比较考察基本功。
|
||||
|
||||
CPP代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <sstream>
|
||||
#include <vector>
|
||||
#include <string>
|
||||
#include <deque>
|
||||
using namespace std;
|
||||
class MyBigQueue { //单调队列(从大到小)
|
||||
public:
|
||||
deque<int> que; // 使用deque来实现单调队列
|
||||
// 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
|
||||
// 同时pop之前判断队列当前是否为空。
|
||||
void pop(int value) {
|
||||
if (!que.empty() && value == que.front()) {
|
||||
que.pop_front();
|
||||
}
|
||||
}
|
||||
// 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
|
||||
// 这样就保持了队列里的数值是单调从大到小的了。
|
||||
void push(int value) {
|
||||
while (!que.empty() && value > que.back()) {
|
||||
que.pop_back();
|
||||
}
|
||||
que.push_back(value);
|
||||
|
||||
}
|
||||
// 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
|
||||
int front() {
|
||||
return que.front();
|
||||
}
|
||||
};
|
||||
|
||||
class MySmallQueue { //单调队列(从小到大)
|
||||
public:
|
||||
deque<int> que;
|
||||
|
||||
void pop(int value) {
|
||||
if (!que.empty() && value == que.front()) {
|
||||
que.pop_front();
|
||||
}
|
||||
}
|
||||
|
||||
// 和上面队列的区别是这里换成了小于,
|
||||
void push(int value) {
|
||||
while (!que.empty() && value < que.back()) {
|
||||
que.pop_back();
|
||||
}
|
||||
que.push_back(value);
|
||||
|
||||
}
|
||||
|
||||
int front() {
|
||||
return que.front();
|
||||
}
|
||||
};
|
||||
|
||||
int main() {
|
||||
string input;
|
||||
|
||||
getline(cin, input);
|
||||
|
||||
vector<int> nums;
|
||||
int k;
|
||||
|
||||
// 找到并截取nums的部分
|
||||
int numsStart = input.find('[');
|
||||
int numsEnd = input.find(']');
|
||||
string numsStr = input.substr(numsStart + 1, numsEnd - numsStart - 1);
|
||||
// cout << numsStr << endl;
|
||||
|
||||
// 用字符串流处理nums字符串,提取数字
|
||||
stringstream ss(numsStr);
|
||||
string temp;
|
||||
while (getline(ss, temp, ',')) {
|
||||
nums.push_back(stoi(temp));
|
||||
}
|
||||
|
||||
// 找到并提取k的值
|
||||
int kStart = input.find("k = ") + 4;
|
||||
k = stoi(input.substr(kStart));
|
||||
|
||||
MyBigQueue queB; // 获取区间最大值
|
||||
MySmallQueue queS; // 获取区间最小值
|
||||
// vector<int> result;
|
||||
for (int i = 0; i < k; i++) { // 先将前k的元素放进队列
|
||||
queB.push(nums[i]);
|
||||
queS.push(nums[i]);
|
||||
}
|
||||
|
||||
int result = queB.front() - queS.front();
|
||||
for (int i = k; i < nums.size(); i++) {
|
||||
queB.pop(nums[i - k]); // 滑动窗口移除最前面元素
|
||||
queB.push(nums[i]); // 滑动窗口前加入最后面的元素
|
||||
|
||||
queS.pop(nums[i - k]);
|
||||
queS.push(nums[i]);
|
||||
|
||||
result = max (result, queB.front() - queS.front());
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
@ -1,52 +0,0 @@
|
||||
|
||||
121. 小红的数组构造
|
||||
|
||||
本题大家不要想着真去模拟数组的情况,那样就想复杂了。
|
||||
|
||||
数组只能是:1k、2k、3k ... (n-1)k、nk,这样 总和就是最小的。
|
||||
|
||||
注意最后的和可能超过int,所以用 long long。
|
||||
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
using namespace std;
|
||||
int main () {
|
||||
long long result = 0;
|
||||
int n, k;
|
||||
cin >> n >> k;
|
||||
for (int i = 1; i <= n; i++) {
|
||||
result += i * k;
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
|
||||
优化思路:
|
||||
|
||||
|
||||
由于要计算1到n的整数之和,可以利用等差数列求和公式来优化计算。
|
||||
|
||||
和公式:1 + 2 + 3 + ... + n = n * (n + 1) / 2
|
||||
|
||||
因此,总和 result = k * (n * (n + 1) / 2)
|
||||
|
||||
```CPP
|
||||
|
||||
#include <iostream>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
long long result = 0;
|
||||
int n, k;
|
||||
cin >> n >> k;
|
||||
|
||||
// 使用等差数列求和公式进行计算
|
||||
result = k * (n * (n + 1LL) / 2);
|
||||
|
||||
cout << result << endl;
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
@ -1,38 +0,0 @@
|
||||
|
||||
|
||||
# 122.精华帖子
|
||||
|
||||
|
||||
开辟一个数组,默认都是0,把精华帖标记为1.
|
||||
|
||||
使用前缀和,快速计算出,k 范围内 有多少个精华帖。
|
||||
|
||||
前缀和要特别注意区间问题,即 vec[i+k] - vec[i] 求得区间和是 (i, i + k] 这个区间,注意这是一个左开右闭的区间。
|
||||
|
||||
所以前缀和 很容易漏掉 vec[0] 这个数值的计算
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n, m, k, l, r;
|
||||
cin >> n >> m >> k;
|
||||
vector<int> vec(n);
|
||||
while (m--) {
|
||||
cin >> l >> r;
|
||||
for (int i = l; i < r; i++) vec[i] = 1;
|
||||
}
|
||||
int result = 0;
|
||||
for (int i = 0; i < k; i++) result += vec[i]; // 提前预处理result,包含vec[0]的区间,否则前缀和容易漏掉这个区间
|
||||
|
||||
for (int i = 1; i < n; i++) {
|
||||
vec[i] += vec[i - 1];
|
||||
}
|
||||
|
||||
for (int i = 0; i < n - k; i++) {
|
||||
result = max (result, vec[i + k] - vec[i]);
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
@ -1,66 +0,0 @@
|
||||
|
||||
# 123.连续子数组最大和
|
||||
|
||||
这道题目可以说是 [代码随想录,动态规划:最大子序和](https://www.programmercarl.com/0053.%E6%9C%80%E5%A4%A7%E5%AD%90%E5%BA%8F%E5%92%8C%EF%BC%88%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%EF%BC%89.html) 的升级版。
|
||||
|
||||
题目求的是 可以替换一个数字 之后 的 连续子数组最大和。
|
||||
|
||||
如果替换的是数组下标 i 的元素。
|
||||
|
||||
那么可以用 [代码随想录,动态规划:最大子序和](https://www.programmercarl.com/0053.%E6%9C%80%E5%A4%A7%E5%AD%90%E5%BA%8F%E5%92%8C%EF%BC%88%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%EF%BC%89.html) 的方法,先求出 [0 - i) 区间的 最大子序和 dp1 和 (i, n)的最大子序和dp2 。
|
||||
|
||||
然后在遍历一遍i, 计算 dp1 + dp2 + vec[i] 的最大值就可以。
|
||||
|
||||
正序遍历,求出 [0 - i) 区间的 最大子序,dp[ i - 1] 表示 是 包括下标i - 1(以vec[i - 1]为结尾)的最大连续子序列和为dp[i - 1]。
|
||||
|
||||
所以 在计算区间 (i, n)即 dp2 的时候,我们要倒叙。 因为我们求的是以 包括下标i + 1 为起始位置的最大连续子序列和为dp[i + 1]。
|
||||
|
||||
这样 dp1 + dp2 + vec[i] 才是一个完整区间。
|
||||
|
||||
这里就体现出对 dp数组定义的把控,本题如果对 dp数组含义理解不清,其实是不容易做出来的。
|
||||
|
||||
代码:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <climits>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int t, n, x;
|
||||
cin >> t;
|
||||
while (t--) {
|
||||
cin >> n >> x;
|
||||
vector<int> vec(n);
|
||||
for (int i = 0; i < n; i++) cin >> vec[i];
|
||||
vector<int> dp1(n);
|
||||
dp1[0] = vec[0];
|
||||
int res = vec[0];
|
||||
// 从前向后统计最大子序和
|
||||
for (int i = 1; i < n; i++) {
|
||||
dp1[i] = max(dp1[i - 1] + vec[i], vec[i]); // 状态转移公式
|
||||
res = max(res, dp1[i]);
|
||||
}
|
||||
|
||||
res = max(res, vec[n - 1]);
|
||||
// 从后向前统计最大子序和
|
||||
vector<int> dp2(n);
|
||||
dp2[n - 1] = vec[n - 1];
|
||||
for (int i = n - 2; i >= 0; i--) {
|
||||
dp2[i] = max(dp2[i + 1] + vec[i], vec[i]);
|
||||
|
||||
}
|
||||
|
||||
for (int i = 0 ; i < n ; i++) {
|
||||
int dp1res = 0;
|
||||
if (i > 0) dp1res = max(dp1[i-1], 0);
|
||||
int dp2res = 0;
|
||||
if (i < n - 1 ) dp2res = max(dp2[i+1], 0);
|
||||
|
||||
res = max(res, dp1res + dp2res + x);
|
||||
}
|
||||
cout << res << endl;
|
||||
}
|
||||
|
||||
}
|
||||
```
|
||||
@ -173,7 +173,7 @@ int n=q.front();q.pop();
|
||||
|
||||
G:起点达到目前遍历节点的距离
|
||||
|
||||
F:目前遍历的节点到达终点的距离
|
||||
H:目前遍历的节点到达终点的距离
|
||||
|
||||
起点达到目前遍历节点的距离 + 目前遍历的节点到达终点的距离 就是起点到达终点的距离。
|
||||
|
||||
@ -337,12 +337,169 @@ IDA * 算法 对这一空间增长问题进行了优化,关于 IDA * 算法,
|
||||
|
||||
### Python
|
||||
|
||||
```Python
|
||||
import heapq
|
||||
|
||||
n = int(input())
|
||||
|
||||
moves = [(1, 2), (2, 1), (-1, 2), (2, -1), (1, -2), (-2, 1), (-1, -2), (-2, -1)]
|
||||
|
||||
def distance(a, b):
|
||||
return ((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2) ** 0.5
|
||||
|
||||
def bfs(start, end):
|
||||
q = [(distance(start, end), start)]
|
||||
step = {start: 0}
|
||||
|
||||
while q:
|
||||
d, cur = heapq.heappop(q)
|
||||
if cur == end:
|
||||
return step[cur]
|
||||
for move in moves:
|
||||
new = (move[0] + cur[0], move[1] + cur[1])
|
||||
if 1 <= new[0] <= 1000 and 1 <= new[1] <= 1000:
|
||||
step_new = step[cur] + 1
|
||||
if step_new < step.get(new, float('inf')):
|
||||
step[new] = step_new
|
||||
heapq.heappush(q, (distance(new, end) + step_new, new))
|
||||
return False
|
||||
|
||||
for _ in range(n):
|
||||
a1, a2, b1, b2 = map(int, input().split())
|
||||
print(bfs((a1, a2), (b1, b2)))
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
### Javascript
|
||||
|
||||
```js
|
||||
class MinHeap {
|
||||
constructor() {
|
||||
this.val = []
|
||||
}
|
||||
push(val) {
|
||||
this.val.push(val)
|
||||
if (this.val.length > 1) {
|
||||
this.bubbleUp()
|
||||
}
|
||||
}
|
||||
bubbleUp() {
|
||||
let pi = this.val.length - 1
|
||||
let pp = Math.floor((pi - 1) / 2)
|
||||
while (pi > 0 && this.val[pp][0] > this.val[pi][0]) {
|
||||
;[this.val[pi], this.val[pp]] = [this.val[pp], this.val[pi]]
|
||||
pi = pp
|
||||
pp = Math.floor((pi - 1) / 2)
|
||||
}
|
||||
}
|
||||
pop() {
|
||||
if (this.val.length > 1) {
|
||||
let pp = 0
|
||||
let pi = this.val.length - 1
|
||||
;[this.val[pi], this.val[pp]] = [this.val[pp], this.val[pi]]
|
||||
const min = this.val.pop()
|
||||
if (this.val.length > 1) {
|
||||
this.sinkDown(0)
|
||||
}
|
||||
return min
|
||||
} else if (this.val.length == 1) {
|
||||
return this.val.pop()
|
||||
}
|
||||
|
||||
}
|
||||
sinkDown(parentIdx) {
|
||||
let pp = parentIdx
|
||||
let plc = pp * 2 + 1
|
||||
let prc = pp * 2 + 2
|
||||
let pt = pp // temp pointer
|
||||
if (plc < this.val.length && this.val[pp][0] > this.val[plc][0]) {
|
||||
pt = plc
|
||||
}
|
||||
if (prc < this.val.length && this.val[pt][0] > this.val[prc][0]) {
|
||||
pt = prc
|
||||
}
|
||||
if (pt != pp) {
|
||||
;[this.val[pp], this.val[pt]] = [this.val[pt], this.val[pp]]
|
||||
this.sinkDown(pt)
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
const moves = [
|
||||
[1, 2],
|
||||
[2, 1],
|
||||
[-1, -2],
|
||||
[-2, -1],
|
||||
[-1, 2],
|
||||
[-2, 1],
|
||||
[1, -2],
|
||||
[2, -1]
|
||||
]
|
||||
|
||||
function dist(a, b) {
|
||||
return ((a[0] - b[0])**2 + (a[1] - b[1])**2)**0.5
|
||||
}
|
||||
|
||||
function isValid(x, y) {
|
||||
return x >= 1 && y >= 1 && x < 1001 && y < 1001
|
||||
}
|
||||
|
||||
function bfs(start, end) {
|
||||
const step = new Map()
|
||||
step.set(start.join(" "), 0)
|
||||
const q = new MinHeap()
|
||||
q.push([dist(start, end), start[0], start[1]])
|
||||
|
||||
while(q.val.length) {
|
||||
const [d, x, y] = q.pop()
|
||||
// if x and y correspond to end position output result
|
||||
if (x == end[0] && y == end[1]) {
|
||||
console.log(step.get(end.join(" ")))
|
||||
break;
|
||||
}
|
||||
for (const [dx, dy] of moves) {
|
||||
const nx = dx + x
|
||||
const ny = dy + y
|
||||
if (isValid(nx, ny)) {
|
||||
const newStep = step.get([x, y].join(" ")) + 1
|
||||
const newDist = dist([nx, ny], [...end])
|
||||
const s = step.get([nx, ny].join(" ")) ?
|
||||
step.get([nx, ny]) :
|
||||
Number.MAX_VALUE
|
||||
if (newStep < s) {
|
||||
q.push(
|
||||
[
|
||||
newStep + newDist,
|
||||
nx,
|
||||
ny
|
||||
]
|
||||
)
|
||||
step.set([nx, ny].join(" "), newStep)
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
async function main() {
|
||||
const rl = require('readline').createInterface({ input: process.stdin })
|
||||
const iter = rl[Symbol.asyncIterator]()
|
||||
const readline = async () => (await iter.next()).value
|
||||
const n = Number((await readline()))
|
||||
|
||||
// find min step
|
||||
for (let i = 0 ; i < n ; i++) {
|
||||
const [s1, s2, t1, t2] = (await readline()).split(" ").map(Number)
|
||||
bfs([s1, s2], [t1, t2])
|
||||
}
|
||||
}
|
||||
|
||||
main()
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
@ -1,29 +0,0 @@
|
||||
|
||||
# 小美的排列询问
|
||||
|
||||
模拟题,注意 x 和y 不分先后
|
||||
|
||||
```CPP
|
||||
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n, x, y;
|
||||
cin >> n;
|
||||
vector<int> vec(n, 0);
|
||||
for (int i =0; i < n; i++) {
|
||||
cin >> vec[i];
|
||||
}
|
||||
cin >> x >> y;
|
||||
for (int i = 0; i < n - 1; i++) {
|
||||
if (x == vec[i] && y == vec[i + 1]) || (y == vec[i] && x == vec[i + 1]) ) {
|
||||
cout << "Yes" << endl;
|
||||
return 0;
|
||||
}
|
||||
}
|
||||
cout << "No" << endl;
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
@ -1,35 +0,0 @@
|
||||
|
||||
# 小美走公路
|
||||
|
||||
在处理环形情况的时候,很多录友容易算懵了,不是多算一个数,就是少算一个数。
|
||||
|
||||
这里这样的题目,最好的方式是将 两个环展开,首尾相连,这样我们就可以通过 直线的思维去解题了
|
||||
|
||||
两个注意点:
|
||||
|
||||
1. x 可以比 y 大,题目没规定 x 和y 的大小顺序
|
||||
2. 累计相加的数可能超过int
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main () {
|
||||
int n;
|
||||
cin >> n;
|
||||
vector<int> vec(2* n + 1, 0);
|
||||
for (int i = 1; i <= n; i++) {
|
||||
cin >> vec[i];
|
||||
vec[n + i] = vec[i];
|
||||
}
|
||||
int x, y;
|
||||
cin >> x >> y;
|
||||
int xx = min(x ,y); // 注意点1:x 可以比 y 大
|
||||
int yy = max(x, y);
|
||||
long long a = 0, b = 0; // 注意点2:相加的数可能超过int
|
||||
for (int i = xx; i < yy; i++) a += vec[i];
|
||||
for (int i = yy; i < xx + n; i++ ) b += vec[i];
|
||||
cout << min(a, b) << endl;
|
||||
}
|
||||
```
|
||||
@ -1,51 +0,0 @@
|
||||
|
||||
# 小美的蛋糕切割
|
||||
|
||||
二维前缀和,不了解前缀和的录友 可以自行查一下,是一个很容易理解的算法思路
|
||||
|
||||
```CPP
|
||||
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <climits>
|
||||
|
||||
using namespace std;
|
||||
int main () {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
int sum = 0;
|
||||
vector<vector<int>> vec(n, vector<int>(m, 0)) ;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> vec[i][j];
|
||||
sum += vec[i][j];
|
||||
}
|
||||
}
|
||||
// 统计横向
|
||||
vector<int> horizontal(n, 0);
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0 ; j < m; j++) {
|
||||
horizontal[i] += vec[i][j];
|
||||
}
|
||||
}
|
||||
// 统计纵向
|
||||
vector<int> vertical(m , 0);
|
||||
for (int j = 0; j < m; j++) {
|
||||
for (int i = 0 ; i < n; i++) {
|
||||
vertical[j] += vec[i][j];
|
||||
}
|
||||
}
|
||||
int result = INT_MAX;
|
||||
int horizontalCut = 0;
|
||||
for (int i = 0 ; i < n; i++) {
|
||||
horizontalCut += horizontal[i];
|
||||
result = min(result, abs(sum - horizontalCut - horizontalCut));
|
||||
}
|
||||
int verticalCut = 0;
|
||||
for (int j = 0; j < m; j++) {
|
||||
verticalCut += vertical[j];
|
||||
result = min(result, abs(sum - verticalCut - verticalCut));
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
@ -1,78 +0,0 @@
|
||||
|
||||
# 130.小美的字符串变换
|
||||
|
||||
本题是[岛屿数量](./0099.岛屿的数量广搜.md)的进阶版,主要思路和代码都是一样的,统计一个图里岛屿的数量,也是染色问题。
|
||||
|
||||
1、 先枚举各个可能出现的矩阵
|
||||
2、 针对矩阵经行广搜染色(深搜,并查集一样可以)
|
||||
3、 统计岛屿数量最小的数量。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <climits>
|
||||
#include <vector>
|
||||
#include <queue>
|
||||
using namespace std;
|
||||
|
||||
// 广搜代码同 卡码网:99. 岛屿数量
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void bfs(const vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y, char a) {
|
||||
queue<pair<int, int>> que;
|
||||
que.push({x, y});
|
||||
visited[x][y] = true; // 只要加入队列,立刻标记
|
||||
while(!que.empty()) {
|
||||
pair<int ,int> cur = que.front(); que.pop();
|
||||
int curx = cur.first;
|
||||
int cury = cur.second;
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = curx + dir[i][0];
|
||||
int nexty = cury + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
|
||||
if (!visited[nextx][nexty] && grid[nextx][nexty] == a) {
|
||||
que.push({nextx, nexty});
|
||||
visited[nextx][nexty] = true; // 只要加入队列立刻标记
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
string s;
|
||||
cin >> n;
|
||||
int result = INT_MAX;
|
||||
cin >> s;
|
||||
for (int k = 1; k < n; k++) {
|
||||
if (n % k != 0) continue;
|
||||
// 计算出 矩阵的 行 和 列
|
||||
int x = n / k;
|
||||
int y = k;
|
||||
//cout << x << " " << y << endl;
|
||||
vector<vector<char>> vec(x, vector<char>(y, 0));
|
||||
// 填装矩阵
|
||||
int sCount = 0;
|
||||
for (int i = 0; i < x; i++) {
|
||||
for (int j = 0; j < y; j++) {
|
||||
vec[i][j] = s[sCount++];
|
||||
}
|
||||
}
|
||||
|
||||
// 开始广搜染色
|
||||
vector<vector<bool>> visited(x, vector<bool>(y, false));
|
||||
int count = 0;
|
||||
for (int i = 0; i < x; i++) {
|
||||
for (int j = 0; j < y; j++) {
|
||||
|
||||
if (!visited[i][j]) {
|
||||
count++; // 遇到没访问过的陆地,+1
|
||||
bfs(vec, visited, i, j, vec[i][j]); // 将与其链接的陆地都标记上 true
|
||||
}
|
||||
}
|
||||
}
|
||||
// 取岛屿数量最少的
|
||||
result = min (result, count);
|
||||
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
@ -1,134 +0,0 @@
|
||||
# 131. 小美的树上染色
|
||||
|
||||
本题为树形dp 稍有难度,主要在于 递推公式上。
|
||||
|
||||
dp数组的定义:
|
||||
|
||||
dp[cur][1] :当前节点染色,那么当前节点为根节点及其左右子节点中,可以染色的最大数量
|
||||
|
||||
dp[cur][0] :当前节点不染色,那么当前节点为根节点及其左右子节点中,可以染色的最大数量
|
||||
|
||||
关于 dp转移方程
|
||||
|
||||
1、 情况一:
|
||||
|
||||
如果当前节点不染色,那就去 子节点 染色 或者 不染色的最大值。
|
||||
|
||||
`dp[cur][0] += max(dp[child][0], dp[child][1]);`
|
||||
|
||||
|
||||
2、情况二:
|
||||
|
||||
那么当前节点染色的话,这种情况就不好想了。
|
||||
|
||||
首先这不是二叉树,每一个节点都有可能 会有n个子节点。
|
||||
|
||||
所以我们要分别讨论,每一个子节点的情况 对父节点的影响。
|
||||
|
||||
那么父节点 针对每种情况,就要去 最大值, 也就是 `dp[cur][1] = max(dp[cur][1], 每个自孩子的情况)`
|
||||
|
||||
如图,假如节点1 是我们要计算的父节点,节点2是我们这次要计算的子节点。
|
||||
|
||||

|
||||
|
||||
选中一个节点2 作为我们这次计算的子节点,父节点染色的话,子节点必染色。
|
||||
|
||||
接下来就是计算 父节点1和该子节点2染色的话, 以子节点2 为根的 染色节点的最大数量 。
|
||||
|
||||
是:节点2不染色 且 以节点2为根节点的最大 染色数量 + 2, + 2 是因为 节点 1 和 节点2 要颜色了,染色节点增加两个。
|
||||
|
||||
代码:`dp[child][0] + 2`
|
||||
|
||||
细心的录友会发现,那我们只计算了 红色框里面的,那么框外 最大的染色数量是多少呢?
|
||||
|
||||

|
||||
|
||||
|
||||
先看 作为子节点的节点2 为根节点的最大染色数量是多少? 取一个最值,即 节点2染色 或者 不染色取最大值。
|
||||
|
||||
代码:`max(dp[child][0], dp[child][1])`
|
||||
|
||||
那么红框以外的 染色最大节点数量 就是 `dp[cur][0] - max(dp[child][0], dp[child][1])`
|
||||
|
||||
(cur是节点1,child是节点2)
|
||||
|
||||
红框以外的染色最大数量 + 父节点1和该子节点2染色的话 以子节点2 为根的 染色节点的最大数量 就是 节点1 染色的最大节点数量。
|
||||
|
||||
代码:
|
||||
|
||||
`dp[cur][1] = max(dp[cur][1], dp[cur][0] - max(dp[child][0], dp[child][1]) + dp[child][0] + 2);`
|
||||
|
||||
整体代码如下:
|
||||
|
||||
```CPP
|
||||
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <cmath>
|
||||
#include <algorithm>
|
||||
#include <list>
|
||||
|
||||
using namespace std;
|
||||
|
||||
int maxN = 10005;
|
||||
vector<vector<int>> dp (maxN, vector<int>(2, 0));
|
||||
vector<list<int>> grid(maxN); // 邻接表
|
||||
vector<long> value(maxN); // 存储每个节点的权值
|
||||
|
||||
|
||||
// 在树上进行动态规划的函数
|
||||
void dpOnTheTree(int cur) {
|
||||
|
||||
for (int child : grid[cur]) {
|
||||
// 后序遍历,从下向上计算
|
||||
dpOnTheTree(child);
|
||||
// 情况一
|
||||
dp[cur][0] += max(dp[child][0], dp[child][1]);
|
||||
|
||||
}
|
||||
|
||||
// 计算dp[1] - 当前节点染色
|
||||
for (int child : grid[cur]) {
|
||||
long mul = value[cur] * value[child]; // 当前节点和相邻节点权值的乘积
|
||||
long sqrtNum = (long) sqrt(mul);
|
||||
|
||||
if (sqrtNum * sqrtNum == mul) { // 如果乘积是完全平方数
|
||||
// 情况二
|
||||
// dp[cur][0] 表示所有子节点 染色或者不染色的 最大染色数量
|
||||
// max(dp[child][0], dp[child][1]) 需要染色节点的孩子节点的最大染色数量
|
||||
// dp[cur][0] - max(dp[child][0], dp[child][1]) 除了要染色的节点及其子节点,其他孩子的最大染色数量
|
||||
// 最后 + dp[child][0] + 2 , 就是本节点染色的最大染色节点数量
|
||||
dp[cur][1] = max(dp[cur][1], dp[cur][0] - max(dp[child][0], dp[child][1]) + dp[child][0] + 2);
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
int main() {
|
||||
|
||||
int n;
|
||||
cin >> n; // 输入节点数量
|
||||
|
||||
// 读取节点权值
|
||||
for (int i = 1; i <= n; ++i) {
|
||||
cin >> value[i];
|
||||
}
|
||||
|
||||
// 构建树的邻接表
|
||||
for (int i = 1; i < n; ++i) {
|
||||
int x, y;
|
||||
cin >> x >> y;
|
||||
grid[x].push_back(y);
|
||||
}
|
||||
|
||||
// 从根节点(节点1)开始进行动态规划
|
||||
dpOnTheTree(1);
|
||||
|
||||
// 输出最大染色节点数量
|
||||
cout << max(dp[1][0], dp[1][1]) << endl;
|
||||
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
@ -1,47 +0,0 @@
|
||||
|
||||
# 132. 夹吃棋
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1209)
|
||||
|
||||
这道题是模拟题,但很多录友可能想复杂了。
|
||||
|
||||
行方向,白棋吃,只有这样的布局 `o*o`,黑棋吃,只有这样的布局 `*o*`
|
||||
|
||||
列方向也是同理的。
|
||||
|
||||
想到这一点,本题的代码就容易写了, C++代码如下:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
while (n--) {
|
||||
int black = 0, white = 0;
|
||||
vector<string> grid(3, "");
|
||||
// 判断行
|
||||
for (int i = 0; i < 3; i++) {
|
||||
cin >> grid[i];
|
||||
if (grid[i] == "o*o") white++;
|
||||
if (grid[i] == "*o*") black++;
|
||||
}
|
||||
// 判断列
|
||||
for (int i = 0; i < 3; i++) {
|
||||
string s;
|
||||
s += grid[0][i];
|
||||
s += grid[1][i];
|
||||
s += grid[2][i];
|
||||
if (s == "o*o") white++;
|
||||
if (s == "*o*") black++;
|
||||
}
|
||||
// 如果一个棋盘的局面没有一方被夹吃或者黑白双方都被对面夹吃,则认为是平局
|
||||
if ((!white && !black) || (white && black)) cout << "draw" << endl;
|
||||
// 白棋赢
|
||||
else if (white && !black) cout << "yukan" << endl;
|
||||
// 黑棋赢
|
||||
else cout << "kou" << endl;
|
||||
}
|
||||
}
|
||||
```
|
||||
@ -1,48 +0,0 @@
|
||||
|
||||
# 133. 小红买药
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1210)
|
||||
|
||||
本题是一道直观的模拟题,但也并不简单,很多情况容易漏了,笔试现场可能要多错几次 才能把情况都想到。
|
||||
|
||||
主要是三个情况:
|
||||
|
||||
* 小红没症状,药有副作用,统计加一,同时要给小红标记上症状
|
||||
* 小红有症状,药治不了,同时也没副症状 ,这时也要统计加一
|
||||
* 小红有症状,药可以治,给小红取消症状标记
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n, m, q, u;
|
||||
cin >> n;
|
||||
string s;
|
||||
cin >> s;
|
||||
cin >> m;
|
||||
vector<string> a(m + 1); // 因为后面u是从1开始的
|
||||
vector<string> b(m + 1);
|
||||
for (int i = 1; i <= m; i++) {
|
||||
cin >> a[i] >> b[i];
|
||||
}
|
||||
cin >> q;
|
||||
while (q--) {
|
||||
cin >> u;
|
||||
int num = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
// s 没症状,但b给了副作用,统计num的同时,要给s标记上症状
|
||||
if (s[i] == '0' && b[u][i] == '1') {
|
||||
num ++;
|
||||
s[i] = '1';
|
||||
}
|
||||
// s 有症状,但 a治不了,b也没副症状
|
||||
else if (s[i] == '1' && a[u][i] == '0' && a[u][i] == '0') num++;
|
||||
// s 有症状,a 可以治
|
||||
else if (s[i] == '1' && a[u][i] == '1') s[i] = '0';
|
||||
}
|
||||
cout << num << endl;
|
||||
}
|
||||
}
|
||||
```
|
||||
@ -1,77 +0,0 @@
|
||||
|
||||
# 134. 皇后移动的最小步数
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1211)
|
||||
|
||||
本题和 [代码随想录-不同路径](https://www.programmercarl.com/0062.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84.html) 有一些类似。
|
||||
|
||||
关键是弄清楚递推公式
|
||||
|
||||
一共分三个情况,
|
||||
|
||||
情况一,向右移动:
|
||||
|
||||
然后从 (i, j) 再向右走 到 (i, k)。 无论k 多大,步数只加1 :
|
||||
|
||||
`dp[i][k] = dp[i][j] + 1`
|
||||
|
||||
那么 `dp[i][k]` 也有可能 从其他方向得到,例如 从上到下, 或者斜上方到达 dp[i][k]
|
||||
|
||||
本题我们要求最小步数,所以取最小值:`dp[i][k] = min(dp[i][k], dp[i][j] + 1);`
|
||||
|
||||
情况二,向下移动:
|
||||
|
||||
从 (i, j) 再向下走 到 (k, j)。 无论k 多大,步数只加1 :
|
||||
|
||||
`dp[k][j] = dp[i][j] + 1;`
|
||||
|
||||
同理 `dp[i][k]` 也有可能 从其他方向得到,取最小值:`dp[k][j] = min(dp[k][j], dp[i][j] + 1);`
|
||||
|
||||
情况三,右下方移动:
|
||||
|
||||
从 (i, j) 再向右下方移动 到 (i + k, j + k)。 无论k 多大,步数只加1 :
|
||||
|
||||
`dp[i + k][j + k] = dp[i][j] + 1`
|
||||
|
||||
同理 `dp[i + k][j + k]` 也有可能 从其他方向得到,取最小值:`dp[i + k][j + k] = min(dp[i + k][j + k], dp[i][j] + 1);`
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
const int INF = 4e6; // 最多步数也就是 2000 * 2000
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
vector<vector<char>> grid(n, vector<char>(m));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
vector<vector<int>> dp(n, vector<int>(m, INF));
|
||||
dp[0][0] = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (grid[i][j] == '*') continue;
|
||||
// 向右移动k个格子
|
||||
for (int k = j + 1; k < m && grid[i][k] == '.'; k++) {
|
||||
dp[i][k] = min(dp[i][k], dp[i][j] + 1);
|
||||
}
|
||||
// 向下移动 k个格子
|
||||
for (int k = i + 1; k < n && grid[k][j] == '.'; k++) {
|
||||
dp[k][j] = min(dp[k][j], dp[i][j] + 1);
|
||||
}
|
||||
// 向右下移动k个格子
|
||||
for (int k = 1; i + k < n && j + k < m && grid[i + k][j + k] == '.'; k++) {
|
||||
dp[i + k][j + k] = min(dp[i + k][j + k], dp[i][j] + 1);
|
||||
}
|
||||
}
|
||||
}
|
||||
if (dp[n - 1][m - 1] == INF) cout << -1 << endl;
|
||||
else cout << dp[n - 1][m - 1] << endl;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
@ -1,147 +0,0 @@
|
||||
|
||||
# 135. 获取连通的相邻节点列表
|
||||
|
||||
本题是一个 “阅读理解”题,其实题目的算法很简单,但理解题意很费劲。
|
||||
|
||||
题目描述中的【提示信息】 是我后加上去了,华为笔试的时候没有这个 【提示信息】。
|
||||
|
||||
相信没有 【提示信息】大家理解题意 平均要多用半个小时。
|
||||
|
||||
思路:
|
||||
|
||||
1. 将第一行数据加入set中
|
||||
2. 后面输出数据,判断是否在 set里
|
||||
3. 最后把结果排个序
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <algorithm>
|
||||
#include <unordered_set>
|
||||
using namespace std;
|
||||
int main() {
|
||||
unordered_set<int> uset;
|
||||
int n, a;
|
||||
cin >> n;
|
||||
while (n--) {
|
||||
cin >> a;
|
||||
uset.insert(a);
|
||||
}
|
||||
int m, x, vlan_id;
|
||||
long long tb;
|
||||
vector<long long> vecTB;
|
||||
cin >> m;
|
||||
while(m--) {
|
||||
cin >> tb;
|
||||
cin >> x;
|
||||
vector<long long> vecVlan_id(x);
|
||||
for (int i = 0; i < x; i++) {
|
||||
cin >> vecVlan_id[i];
|
||||
}
|
||||
for (int i = 0; i < x; i++) {
|
||||
if (uset.find(vecVlan_id[i]) != uset.end()) {
|
||||
vecTB.push_back(tb);
|
||||
break;
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
cout << vecTB.size() << endl;
|
||||
if (vecTB.size() != 0) {
|
||||
sort(vecTB.begin(), vecTB.end());
|
||||
for (int i = 0; i < vecTB.size() ; i++) cout << vecTB[i] << " ";
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
Set<Integer> uset = new HashSet<>();
|
||||
int n = scanner.nextInt();
|
||||
while (n-- > 0) {
|
||||
int a = scanner.nextInt();
|
||||
uset.add(a);
|
||||
}
|
||||
|
||||
int m = scanner.nextInt();
|
||||
List<Long> vecTB = new ArrayList<>();
|
||||
while (m-- > 0) {
|
||||
long tb = scanner.nextLong();
|
||||
int x = scanner.nextInt();
|
||||
List<Integer> vecVlan_id = new ArrayList<>();
|
||||
for (int i = 0; i < x; i++) {
|
||||
vecVlan_id.add(scanner.nextInt());
|
||||
}
|
||||
for (int vlanId : vecVlan_id) {
|
||||
if (uset.contains(vlanId)) {
|
||||
vecTB.add(tb);
|
||||
break;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println(vecTB.size());
|
||||
if (!vecTB.isEmpty()) {
|
||||
Collections.sort(vecTB);
|
||||
for (long tb : vecTB) {
|
||||
System.out.print(tb + " ");
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
def main():
|
||||
import sys
|
||||
input = sys.stdin.read
|
||||
data = input().split()
|
||||
|
||||
index = 0
|
||||
n = int(data[index])
|
||||
index += 1
|
||||
uset = set()
|
||||
for _ in range(n):
|
||||
a = int(data[index])
|
||||
index += 1
|
||||
uset.add(a)
|
||||
|
||||
m = int(data[index])
|
||||
index += 1
|
||||
vecTB = []
|
||||
while m > 0:
|
||||
tb = int(data[index])
|
||||
index += 1
|
||||
x = int(data[index])
|
||||
index += 1
|
||||
vecVlan_id = []
|
||||
for _ in range(x):
|
||||
vecVlan_id.append(int(data[index]))
|
||||
index += 1
|
||||
for vlan_id in vecVlan_id:
|
||||
if vlan_id in uset:
|
||||
vecTB.append(tb)
|
||||
break
|
||||
m -= 1
|
||||
|
||||
print(len(vecTB))
|
||||
if vecTB:
|
||||
vecTB.sort()
|
||||
print(" ".join(map(str, vecTB)))
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
```
|
||||
@ -1,148 +0,0 @@
|
||||
|
||||
# 字符串处理器
|
||||
|
||||
纯模拟,但情况比较多,非常容易 空指针异常。
|
||||
|
||||
大家要注意,边界问题 以及 负数问题。
|
||||
|
||||
整体代码如下:
|
||||
|
||||
```CPP
|
||||
#include<bits/stdc++.h>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int index = 0;
|
||||
long long optNum;
|
||||
string s;
|
||||
string cmd;
|
||||
while(cin >> cmd){
|
||||
//cout << s << endl;
|
||||
if(cmd == "insert") {
|
||||
string buff;
|
||||
cin >> buff;
|
||||
s.insert(index, buff);
|
||||
index += buff.size();
|
||||
}
|
||||
else if(cmd == "move") {
|
||||
cin >> optNum;
|
||||
if(optNum > 0 && index + optNum <= s.size()) index += optNum;
|
||||
if(optNum < 0 && index >= -optNum) index += optNum;
|
||||
}
|
||||
else if(cmd == "delete") {
|
||||
cin >> optNum;
|
||||
if(index >= optNum && optNum > 0){
|
||||
s.erase(index - optNum, optNum);
|
||||
index -= optNum;
|
||||
}
|
||||
}
|
||||
else if(cmd == "copy") {
|
||||
if(index > 0) {
|
||||
string tmp = s.substr(0, index);
|
||||
s.insert(index, tmp);
|
||||
}
|
||||
}
|
||||
else if(cmd == "end") {
|
||||
for(int i = 0; i < index; i++) {
|
||||
cout << s[i];
|
||||
}
|
||||
cout << '|';
|
||||
for(int i = index; i < s.size(); i++) cout << s[i];
|
||||
|
||||
break;
|
||||
}
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
StringBuilder s = new StringBuilder();
|
||||
int index = 0;
|
||||
int optNum;
|
||||
|
||||
while (true) {
|
||||
String cmd = scanner.next();
|
||||
if (cmd.equals("insert")) {
|
||||
String buff = scanner.next();
|
||||
s.insert(index, buff);
|
||||
index += buff.length();
|
||||
} else if (cmd.equals("move")) {
|
||||
optNum = scanner.nextInt();
|
||||
if (optNum > 0 && index + optNum <= s.length()) index += optNum;
|
||||
if (optNum < 0 && index >= -optNum) index += optNum;
|
||||
} else if (cmd.equals("delete")) {
|
||||
optNum = scanner.nextInt();
|
||||
if (index >= optNum && optNum > 0) {
|
||||
s.delete(index - optNum, index);
|
||||
index -= optNum;
|
||||
}
|
||||
} else if (cmd.equals("copy")) {
|
||||
if (index > 0) {
|
||||
String tmp = s.substring(0, index);
|
||||
s.insert(index, tmp);
|
||||
}
|
||||
} else if (cmd.equals("end")) {
|
||||
System.out.print(s.substring(0, index) + '|' + s.substring(index));
|
||||
break;
|
||||
}
|
||||
}
|
||||
scanner.close();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
def main():
|
||||
import sys
|
||||
input = sys.stdin.read
|
||||
data = input().split()
|
||||
s = ""
|
||||
index = 0
|
||||
i = 0
|
||||
|
||||
while i < len(data):
|
||||
cmd = data[i]
|
||||
i += 1
|
||||
if cmd == "insert":
|
||||
buff = data[i]
|
||||
i += 1
|
||||
s = s[:index] + buff + s[index:]
|
||||
index += len(buff)
|
||||
elif cmd == "move":
|
||||
optNum = int(data[i])
|
||||
i += 1
|
||||
if optNum > 0 and index + optNum <= len(s):
|
||||
index += optNum
|
||||
elif optNum < 0 and index >= -optNum:
|
||||
index += optNum
|
||||
elif cmd == "delete":
|
||||
optNum = int(data[i])
|
||||
i += 1
|
||||
if index >= optNum and optNum > 0:
|
||||
s = s[:index - optNum] + s[index:]
|
||||
index -= optNum
|
||||
elif cmd == "copy":
|
||||
if index > 0:
|
||||
tmp = s[:index]
|
||||
s = s[:index] + tmp + s[index:]
|
||||
elif cmd == "end":
|
||||
print(s[:index] + '|' + s[index:])
|
||||
break
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
|
||||
|
||||
```
|
||||
@ -1,192 +0,0 @@
|
||||
|
||||
# 137. 消息传输
|
||||
|
||||
这道题目,普通广搜就可以解决。
|
||||
|
||||
这里说一下几点注意事项:
|
||||
|
||||
1、 题目描述中,注意 n 是列数,m是行数
|
||||
|
||||
这是造成很多录友周赛的时候提交 返回 【运行错误】的罪魁祸首,如果 输入用例是 正方形,那没问题,如果后台输入用例是矩形, n 和 m 搞反了,就会数组越界。
|
||||
|
||||
矩阵是 m * n ,但输入的顺序却是 先输入n 再输入 m。
|
||||
|
||||
这会让很多人把矩阵的 n 和 m 搞反。
|
||||
|
||||
其实规范出题,就应该是n 行,m列,然后 先输入n,在输入m。
|
||||
|
||||
只能说 大厂出题的人,也不是专业出题的,所以会在 非算法方面一不小心留下很多 “bug”,消耗大家的精力。
|
||||
|
||||
2、再写广搜的时候,可能担心会无限循环
|
||||
|
||||
即 A 走到 B,B又走到A,A又走到B ,这种情况,一般来说 广搜都是用一个 visit数组来标记的。
|
||||
|
||||
但本题不用,因为 不会重复走的,题图里的信号都是正数,根据距离判断大小 可以保证不走回头路。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <queue>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
const int inf = 1e6;
|
||||
int main () {
|
||||
int n, m, startx, starty;
|
||||
cin >> n >> m;
|
||||
cin >> startx >> starty;
|
||||
vector<vector<int>> grid(m, vector<int>(n));
|
||||
vector<vector<int>> dis(m, vector<int>(n, inf));
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
queue<pair<int, int>> que;
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
|
||||
que.push(pair<int, int>(startx, starty));
|
||||
dis[startx][starty] = 0;
|
||||
while(!que.empty()) {
|
||||
pair<int, int> cur = que.front(); que.pop();
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int newx = cur.first + dir[i][1];
|
||||
int newy = cur.second + dir[i][0];
|
||||
if (newx < 0 || newx >= m || newy < 0 || newy >= n || grid[cur.first][cur.second] == 0) continue;
|
||||
|
||||
if (dis[newx][newy] > dis[cur.first][cur.second] + grid[cur.first][cur.second]) {
|
||||
dis[newx][newy] = dis[cur.first][cur.second] + grid[cur.first][cur.second];
|
||||
que.push(pair<int, int>(newx, newy));
|
||||
}
|
||||
}
|
||||
}
|
||||
int result = 0;
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (dis[i][j] == inf) {
|
||||
cout << -1 << endl;
|
||||
return 0;
|
||||
}
|
||||
result = max(result, dis[i][j]);
|
||||
}
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
static final int INF = 1000000;
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int m = scanner.nextInt();
|
||||
int startX = scanner.nextInt();
|
||||
int startY = scanner.nextInt();
|
||||
|
||||
int[][] grid = new int[m][n];
|
||||
int[][] dis = new int[m][n];
|
||||
|
||||
for (int i = 0; i < m; i++) {
|
||||
Arrays.fill(dis[i], INF);
|
||||
for (int j = 0; j < n; j++) {
|
||||
grid[i][j] = scanner.nextInt();
|
||||
}
|
||||
}
|
||||
|
||||
Queue<int[]> queue = new LinkedList<>();
|
||||
int[][] directions = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};
|
||||
|
||||
queue.add(new int[]{startX, startY});
|
||||
dis[startX][startY] = 0;
|
||||
|
||||
while (!queue.isEmpty()) {
|
||||
int[] current = queue.poll();
|
||||
for (int[] dir : directions) {
|
||||
int newX = current[0] + dir[0];
|
||||
int newY = current[1] + dir[1];
|
||||
if (newX >= 0 && newX < m && newY >= 0 && newY < n && grid[current[0]][current[1]] != 0) {
|
||||
if (dis[newX][newY] > dis[current[0]][current[1]] + grid[current[0]][current[1]]) {
|
||||
dis[newX][newY] = dis[current[0]][current[1]] + grid[current[0]][current[1]];
|
||||
queue.add(new int[]{newX, newY});
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
int result = 0;
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (dis[i][j] == INF) {
|
||||
System.out.println(-1);
|
||||
return;
|
||||
}
|
||||
result = Math.max(result, dis[i][j]);
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println(result);
|
||||
scanner.close();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
```Python
|
||||
from collections import deque
|
||||
|
||||
inf = 1000000
|
||||
|
||||
def main():
|
||||
import sys
|
||||
input = sys.stdin.read
|
||||
data = input().split()
|
||||
index = 0
|
||||
|
||||
n = int(data[index])
|
||||
m = int(data[index+1])
|
||||
startx = int(data[index+2])
|
||||
starty = int(data[index+3])
|
||||
index += 4
|
||||
|
||||
grid = []
|
||||
dis = [[inf] * n for _ in range(m)]
|
||||
|
||||
for i in range(m):
|
||||
grid.append([int(data[index+j]) for j in range(n)])
|
||||
index += n
|
||||
|
||||
directions = [(0, 1), (1, 0), (-1, 0), (0, -1)]
|
||||
queue = deque()
|
||||
queue.append((startx, starty))
|
||||
dis[startx][starty] = 0
|
||||
|
||||
while queue:
|
||||
curx, cury = queue.popleft()
|
||||
for dx, dy in directions:
|
||||
newx, newy = curx + dx, cury + dy
|
||||
if 0 <= newx < m and 0 <= newy < n and grid[curx][cury] != 0:
|
||||
if dis[newx][newy] > dis[curx][cury] + grid[curx][cury]:
|
||||
dis[newx][newy] = dis[curx][cury] + grid[curx][cury]
|
||||
queue.append((newx, newy))
|
||||
|
||||
result = 0
|
||||
for i in range(m):
|
||||
for j in range(n):
|
||||
if dis[i][j] == inf:
|
||||
print(-1)
|
||||
return
|
||||
result = max(result, dis[i][j])
|
||||
|
||||
print(result)
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
|
||||
|
||||
```
|
||||
@ -1,101 +0,0 @@
|
||||
|
||||
# 可爱串
|
||||
|
||||
整体思路,就含有 子序列的字符串数量 减去 含有子串的字符串数量。
|
||||
|
||||
因为子序列数量已经是包含子串数量的。 剩下的就是 只有子序列 且没有子串的 字符串数量。
|
||||
|
||||
|
||||
需要注意我们求的不是 长度为 i 的字符串里有多少个 red 子序列。
|
||||
|
||||
**而是 可以有多少个 长度为i 的字符串 含有子序列 red**
|
||||
|
||||
同理,可以有多少个长度为i的字符串含有 red 子串
|
||||
|
||||
认清这一点很重要!
|
||||
|
||||
### 求子串
|
||||
|
||||
dp2[i][3] 长度为i 且 含有子串 red 的字符串数量 有多少
|
||||
|
||||
dp2[i][2] 长度为i 且 含有子串 re 的字符串数量有多少
|
||||
|
||||
dp2[i][1] 长度为 i 且 含有子串 r 的字符串数量有多少
|
||||
|
||||
dp2[1][0] 长度为 i 且 含有 只有 de, ee , e, d的字符串的字符串数量有多少。
|
||||
|
||||
```CPP
|
||||
// 求子串
|
||||
dp2[0][0] = 1;
|
||||
for(int i = 1;i <= n; i++) {
|
||||
dp2[i][0] = (dp2[i - 1][2] + dp2[i - 1][1] + dp2[i - 1][0] * 2) % mod; // 含有 re 的可以把 r改成d, 含有r 的可以改成
|
||||
dp2[i][1] = (dp2[i - 1][2] + dp2[i - 1][1] + dp2[i - 1][0]) % mod;
|
||||
dp2[i][2] = (dp2[i - 1][1]);
|
||||
dp2[i][3] = (dp2[i - 1][3] * 3 + dp2[i - 1][2]) % mod;
|
||||
}
|
||||
``
|
||||
|
||||
### 求子序列
|
||||
|
||||
dp1[i][3] 长度为i 且 含有子序列 red 的字符串数量 有多少
|
||||
|
||||
dp2[i][2] 长度为i 且 含有子序列 re 的字符串数量有多少
|
||||
|
||||
dp2[i][1] 长度为 i 且 含有子序列 r 的字符串数量有多少
|
||||
|
||||
dp2[1][0] 长度为 i 且 含有 只含有 e 和 d 的字符串的字符串数量有多少。
|
||||
|
||||
```CPP
|
||||
|
||||
// 求子序列
|
||||
dp1[0][0]=1;
|
||||
for(int i=1;i<=n;i++)
|
||||
{
|
||||
dp1[i][0] = (dp1[i - 1][0] * 2) % mod;
|
||||
dp1[i][1] = (dp1[i - 1][0] + dp1[i - 1][1] * 2) % mod;
|
||||
dp1[i][2] = (dp1[i - 1][1] + dp1[i - 1][2] * 2) % mod;
|
||||
dp1[i][3] = (dp1[i - 1][2] + dp1[i - 1][3] * 3) % mod;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
```CPP
|
||||
|
||||
#include <bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
using ll=long long;
|
||||
const int mod=1e9+7;
|
||||
|
||||
int main()
|
||||
{
|
||||
int n;
|
||||
|
||||
cin>>n;
|
||||
vector<vector<ll>> dp1(n + 1,vector<ll> (4,0));
|
||||
vector<vector<ll>> dp2(n + 1,vector<ll> (4,0));
|
||||
// 求子串
|
||||
dp2[0][0] = 1;
|
||||
for(int i = 1;i <= n; i++) {
|
||||
dp2[i][0] = (dp2[i - 1][2] + dp2[i - 1][1] + dp2[i - 1][0] * 2) % mod;
|
||||
dp2[i][1] = (dp2[i - 1][2] + dp2[i - 1][1] + dp2[i - 1][0]) % mod;
|
||||
dp2[i][2] = (dp2[i - 1][1]);
|
||||
dp2[i][3] = (dp2[i - 1][3] * 3 + dp2[i - 1][2]) % mod;
|
||||
}
|
||||
|
||||
// 求子序列
|
||||
dp1[0][0]=1;
|
||||
for(int i=1;i<=n;i++)
|
||||
{
|
||||
dp1[i][0] = (dp1[i - 1][0] * 2) % mod;
|
||||
dp1[i][1] = (dp1[i - 1][0] + dp1[i - 1][1] * 2) % mod;
|
||||
dp1[i][2] = (dp1[i - 1][1] + dp1[i - 1][2] * 2) % mod;
|
||||
dp1[i][3] = (dp1[i - 1][2] + dp1[i - 1][3] * 3) % mod;
|
||||
}
|
||||
|
||||
cout<<(dp1[n][3] - dp2[n][3])%mod;
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
@ -1,29 +0,0 @@
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int countOnes(long long num) {
|
||||
int zeroCount = 0;
|
||||
while (num > 0) {
|
||||
if (num % 10 != 0) { // 检查最低位是否为0
|
||||
zeroCount++;
|
||||
}
|
||||
num /= 10; // 移除最低位
|
||||
}
|
||||
return zeroCount;
|
||||
}
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
vector<int> vec(n);
|
||||
for (int i = 0; i < n; i++) cin >> vec[i];
|
||||
int result = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = i + 1; j < n; j++) {
|
||||
if (countOnes(vec[i] * vec[j]) == 1) result++;
|
||||
}
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
@ -1,104 +0,0 @@
|
||||
|
||||
本题和 [96.不同的二叉搜索树](https://www.programmercarl.com/0096.%E4%B8%8D%E5%90%8C%E7%9A%84%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91.html) 比较像
|
||||
|
||||
* 取模这里很容易出错
|
||||
* 过程中所用到的数值都有可能超过int,所以要改用longlong
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
|
||||
long long mod = 1e9 + 7;
|
||||
long long dp(int t, vector<long long>& memory) {
|
||||
if (t % 2 == 0) return 0;
|
||||
if (t == 1) return 1;
|
||||
if (memory[t] != -1) return memory[t];
|
||||
|
||||
long long result = 0;
|
||||
// 枚举左右子树节点的数量
|
||||
for (int i = 1; i < t; i += 2) {
|
||||
long long leftNum = dp(i, memory); // 左子树节点数量为i
|
||||
long long rightNum = dp(t - i - 1, memory); // 右子树节点数量为t - i - 1
|
||||
result += (leftNum * rightNum) % mod; // 注意这里是乘的关系
|
||||
result %= mod;
|
||||
}
|
||||
memory[t] = result;
|
||||
return result;
|
||||
}
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
vector<long long> memory(n + 1, -1);
|
||||
cout << dp(n, memory) << endl;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <cstring>
|
||||
|
||||
using namespace std;
|
||||
|
||||
const int MOD = 1000000007;
|
||||
|
||||
int main() {
|
||||
int num;
|
||||
cin >> num;
|
||||
|
||||
if (num % 2 == 0) {
|
||||
cout << 0 << endl;
|
||||
return 0;
|
||||
}
|
||||
|
||||
vector<long long> dp(num + 1, 0);
|
||||
dp[1] = 1;
|
||||
|
||||
for (int i = 3; i <= num; i += 2) {
|
||||
for (int j = 1; j <= i - 2; j += 2) {
|
||||
dp[i] = (dp[i] + dp[j] * dp[i - 1 - j]) % MOD;
|
||||
}
|
||||
}
|
||||
|
||||
cout << dp[num] << endl;
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
|
||||
第二题的代码
|
||||
|
||||
#include <bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
long fastexp(long base,long n,long mod){
|
||||
long answer = 1;
|
||||
while(n > 0){
|
||||
if(n % 2 == 1){
|
||||
answer = (answer * base) % mod;
|
||||
}
|
||||
base = (base * base) % mod;
|
||||
n /= 2;
|
||||
}
|
||||
return answer;
|
||||
}
|
||||
int kawaiiStrings(int n) {
|
||||
// write code here
|
||||
std::vector<long> f(n + 1), g(n + 1), h(n + 1);
|
||||
long mod = 1000000007;
|
||||
for (long i = 2; i <= n; i++) g[i] = (g[i - 1] * 2 + (i - 1) * fastexp(2,i-2,mod)) % mod;
|
||||
for (long i = 3; i <= n; i++) f[i] = ((f[i - 1] * 3) % mod + g[i - 1]) % mod;
|
||||
for (long i = 3; i <= n; i++) h[i] = (fastexp(3, i - 3, mod) + h[i - 1] * 3 - h[i - 3]) % mod;
|
||||
return (f[n]-h[n]+mod)%mod;
|
||||
|
||||
}
|
||||
|
||||
int main(){
|
||||
int n;
|
||||
cin >> n;
|
||||
cout << kawaiiStrings(n) << endl;
|
||||
return 0;
|
||||
}
|
||||
@ -1,108 +0,0 @@
|
||||
|
||||
# 142. 两个字符串的最小 ASCII 删除总和
|
||||
|
||||
本题和[代码随想录:两个字符串的删除操作](https://www.programmercarl.com/0583.%E4%B8%A4%E4%B8%AA%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%88%A0%E9%99%A4%E6%93%8D%E4%BD%9C.html) 思路基本是一样的。
|
||||
|
||||
属于编辑距离问题,如果想彻底了解,建议看看「代码随想录」的编辑距离总结篇。
|
||||
|
||||
本题dp数组含义:
|
||||
|
||||
dp[i][j] 表示 以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最小ASCII 删除总和。
|
||||
|
||||
如果 s1[i - 1] 与 s2[j - 1] 相同,则不用删:`dp[i][j] = dp[i - 1][j - 1]`
|
||||
|
||||
如果 s1[i - 1] 与 s2[j - 1] 不相同,删word1 的 最小删除和: `dp[i - 1][j] + s1[i - 1]` ,删word2的最小删除和: `dp[i][j - 1] + s2[j - 1]`
|
||||
|
||||
取最小值: `dp[i][j] = min(dp[i - 1][j] + s1[i - 1], dp[i][j - 1] + s2[j - 1])`
|
||||
|
||||
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int main() {
|
||||
string s1, s2;
|
||||
cin >> s1 >> s2;
|
||||
vector<vector<int>> dp(s1.size() + 1, vector<int>(s2.size() + 1, 0));
|
||||
|
||||
// s1 如果变成空串的最小删除ASCLL值综合
|
||||
for (int i = 1; i <= s1.size(); i++) dp[i][0] = dp[i - 1][0] + s1[i - 1];
|
||||
// s2 如果变成空串的最小删除ASCLL值综合
|
||||
for (int j = 1; j <= s2.size(); j++) dp[0][j] = dp[0][j - 1] + s2[j - 1];
|
||||
|
||||
for (int i = 1; i <= s1.size(); i++) {
|
||||
for (int j = 1; j <= s2.size(); j++) {
|
||||
if (s1[i - 1] == s2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
|
||||
else dp[i][j] = min(dp[i - 1][j] + s1[i - 1], dp[i][j - 1] + s2[j - 1]);
|
||||
}
|
||||
}
|
||||
cout << dp[s1.size()][s2.size()] << endl;
|
||||
}
|
||||
```
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
String s1 = scanner.nextLine();
|
||||
String s2 = scanner.nextLine();
|
||||
int[][] dp = new int[s1.length() + 1][s2.length() + 1];
|
||||
|
||||
// s1 如果变成空串的最小删除ASCII值综合
|
||||
for (int i = 1; i <= s1.length(); i++) {
|
||||
dp[i][0] = dp[i - 1][0] + s1.charAt(i - 1);
|
||||
}
|
||||
// s2 如果变成空串的最小删除ASCII值综合
|
||||
for (int j = 1; j <= s2.length(); j++) {
|
||||
dp[0][j] = dp[0][j - 1] + s2.charAt(j - 1);
|
||||
}
|
||||
|
||||
for (int i = 1; i <= s1.length(); i++) {
|
||||
for (int j = 1; j <= s2.length(); j++) {
|
||||
if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
|
||||
dp[i][j] = dp[i - 1][j - 1];
|
||||
} else {
|
||||
dp[i][j] = Math.min(dp[i - 1][j] + s1.charAt(i - 1), dp[i][j - 1] + s2.charAt(j - 1));
|
||||
}
|
||||
}
|
||||
}
|
||||
System.out.println(dp[s1.length()][s2.length()]);
|
||||
scanner.close();
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
```
|
||||
|
||||
### python
|
||||
|
||||
```python
|
||||
def min_delete_sum(s1: str, s2: str) -> int:
|
||||
dp = [[0] * (len(s2) + 1) for _ in range(len(s1) + 1)]
|
||||
|
||||
# s1 如果变成空串的最小删除ASCII值综合
|
||||
for i in range(1, len(s1) + 1):
|
||||
dp[i][0] = dp[i - 1][0] + ord(s1[i - 1])
|
||||
# s2 如果变成空串的最小删除ASCII值综合
|
||||
for j in range(1, len(s2) + 1):
|
||||
dp[0][j] = dp[0][j - 1] + ord(s2[j - 1])
|
||||
|
||||
for i in range(1, len(s1) + 1):
|
||||
for j in range(1, len(s2) + 1):
|
||||
if s1[i - 1] == s2[j - 1]:
|
||||
dp[i][j] = dp[i - 1][j - 1]
|
||||
else:
|
||||
dp[i][j] = min(dp[i - 1][j] + ord(s1[i - 1]), dp[i][j - 1] + ord(s2[j - 1]))
|
||||
|
||||
return dp[len(s1)][len(s2)]
|
||||
|
||||
if __name__ == "__main__":
|
||||
s1 = input().strip()
|
||||
s2 = input().strip()
|
||||
print(min_delete_sum(s1, s2))
|
||||
```
|
||||
@ -1,237 +0,0 @@
|
||||
|
||||
|
||||
# 143. 最长同值路径
|
||||
|
||||
|
||||
本题两个考点:
|
||||
|
||||
1. 层序遍历构造二叉树
|
||||
2. 树形dp,找出最长路径
|
||||
|
||||
对于写代码不多,或者动手能力比较差的录友,第一个 构造二叉树 基本就被卡主了。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <queue>
|
||||
#include <vector>
|
||||
|
||||
using namespace std;
|
||||
|
||||
// 定义二叉树节点结构
|
||||
struct TreeNode {
|
||||
int val;
|
||||
TreeNode* left;
|
||||
TreeNode* right;
|
||||
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
|
||||
};
|
||||
|
||||
// 根据层序遍历数组构建二叉树
|
||||
TreeNode* constructBinaryTree(const vector<string>& levelOrder) {
|
||||
if (levelOrder.empty()) return NULL;
|
||||
|
||||
TreeNode* root = new TreeNode(stoi(levelOrder[0]));
|
||||
queue<TreeNode*> q;
|
||||
q.push(root);
|
||||
int i = 1;
|
||||
|
||||
while (!q.empty() && i < levelOrder.size()) {
|
||||
TreeNode* current = q.front();
|
||||
q.pop();
|
||||
|
||||
if (i < levelOrder.size() && levelOrder[i] != "null") {
|
||||
current->left = new TreeNode(stoi(levelOrder[i]));
|
||||
q.push(current->left);
|
||||
}
|
||||
i++;
|
||||
|
||||
if (i < levelOrder.size() && levelOrder[i] != "null") {
|
||||
current->right = new TreeNode(stoi(levelOrder[i]));
|
||||
q.push(current->right);
|
||||
}
|
||||
i++;
|
||||
}
|
||||
|
||||
return root;
|
||||
}
|
||||
|
||||
int result = 0;
|
||||
|
||||
// 树形DP
|
||||
int dfs(TreeNode* node) {
|
||||
if (node == NULL) return 0;
|
||||
int leftPath = dfs(node->left);
|
||||
int rightPath = dfs(node->right);
|
||||
|
||||
int leftNum = 0, rightNum = 0;
|
||||
if (node->left != NULL && node->left->val == node->val) {
|
||||
leftNum = leftPath + 1;
|
||||
}
|
||||
if (node->right != NULL && node->right->val == node->val) {
|
||||
rightNum = rightPath + 1;
|
||||
}
|
||||
result = max(result, leftNum + rightNum);
|
||||
return max(leftNum, rightNum);
|
||||
|
||||
}
|
||||
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
vector<string> levelOrder(n);
|
||||
for (int i = 0; i < n ; i++) cin >> levelOrder[i];
|
||||
|
||||
TreeNode* root = constructBinaryTree(levelOrder);
|
||||
dfs(root);
|
||||
cout << result << endl;
|
||||
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
### Java
|
||||
|
||||
```Java
|
||||
import java.util.*;
|
||||
|
||||
class TreeNode {
|
||||
int val;
|
||||
TreeNode left, right;
|
||||
TreeNode(int x) {
|
||||
val = x;
|
||||
left = null;
|
||||
right = null;
|
||||
}
|
||||
}
|
||||
|
||||
public class Main {
|
||||
public static int result = 0;
|
||||
|
||||
public static TreeNode constructBinaryTree(List<String> levelOrder) {
|
||||
if (levelOrder.isEmpty()) return null;
|
||||
|
||||
TreeNode root = new TreeNode(Integer.parseInt(levelOrder.get(0)));
|
||||
Queue<TreeNode> queue = new LinkedList<>();
|
||||
queue.add(root);
|
||||
int i = 1;
|
||||
|
||||
while (!queue.isEmpty() && i < levelOrder.size()) {
|
||||
TreeNode current = queue.poll();
|
||||
|
||||
if (i < levelOrder.size() && !levelOrder.get(i).equals("null")) {
|
||||
current.left = new TreeNode(Integer.parseInt(levelOrder.get(i)));
|
||||
queue.add(current.left);
|
||||
}
|
||||
i++;
|
||||
|
||||
if (i < levelOrder.size() && !levelOrder.get(i).equals("null")) {
|
||||
current.right = new TreeNode(Integer.parseInt(levelOrder.get(i)));
|
||||
queue.add(current.right);
|
||||
}
|
||||
i++;
|
||||
}
|
||||
|
||||
return root;
|
||||
}
|
||||
|
||||
public static int dfs(TreeNode node) {
|
||||
if (node == null) return 0;
|
||||
int leftPath = dfs(node.left);
|
||||
int rightPath = dfs(node.right);
|
||||
|
||||
int leftNum = 0, rightNum = 0;
|
||||
if (node.left != null && node.left.val == node.val) {
|
||||
leftNum = leftPath + 1;
|
||||
}
|
||||
if (node.right != null && node.right.val == node.val) {
|
||||
rightNum = rightPath + 1;
|
||||
}
|
||||
result = Math.max(result, leftNum + rightNum);
|
||||
return Math.max(leftNum, rightNum);
|
||||
}
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int n = sc.nextInt();
|
||||
sc.nextLine(); // consume the newline character
|
||||
List<String> levelOrder = new ArrayList<>();
|
||||
for (int i = 0; i < n; i++) {
|
||||
levelOrder.add(sc.next());
|
||||
}
|
||||
TreeNode root = constructBinaryTree(levelOrder);
|
||||
dfs(root);
|
||||
System.out.println(result);
|
||||
sc.close();
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
### python
|
||||
|
||||
```python
|
||||
from typing import List, Optional
|
||||
from collections import deque
|
||||
import sys
|
||||
|
||||
class TreeNode:
|
||||
def __init__(self, val: int = 0, left: 'TreeNode' = None, right: 'TreeNode' = None):
|
||||
self.val = val
|
||||
self.left = left
|
||||
self.right = right
|
||||
|
||||
def construct_binary_tree(level_order: List[str]) -> Optional[TreeNode]:
|
||||
if not level_order:
|
||||
return None
|
||||
|
||||
root = TreeNode(int(level_order[0]))
|
||||
queue = deque([root])
|
||||
i = 1
|
||||
|
||||
while queue and i < len(level_order):
|
||||
current = queue.popleft()
|
||||
|
||||
if i < len(level_order) and level_order[i] != "null":
|
||||
current.left = TreeNode(int(level_order[i]))
|
||||
queue.append(current.left)
|
||||
i += 1
|
||||
|
||||
if i < len(level_order) and level_order[i] != "null":
|
||||
current.right = TreeNode(int(level_order[i]))
|
||||
queue.append(current.right)
|
||||
i += 1
|
||||
|
||||
return root
|
||||
|
||||
result = 0
|
||||
|
||||
def dfs(node: Optional[TreeNode]) -> int:
|
||||
global result
|
||||
if node is None:
|
||||
return 0
|
||||
|
||||
left_path = dfs(node.left)
|
||||
right_path = dfs(node.right)
|
||||
|
||||
left_num = right_num = 0
|
||||
if node.left is not None and node.left.val == node.val:
|
||||
left_num = left_path + 1
|
||||
if node.right is not None and node.right.val == node.val:
|
||||
right_num = right_path + 1
|
||||
|
||||
result = max(result, left_num + right_num)
|
||||
return max(left_num, right_num)
|
||||
|
||||
if __name__ == "__main__":
|
||||
input = sys.stdin.read
|
||||
data = input().strip().split()
|
||||
|
||||
n = int(data[0])
|
||||
level_order = data[1:]
|
||||
|
||||
root = construct_binary_tree(level_order)
|
||||
dfs(root)
|
||||
print(result)
|
||||
|
||||
|
||||
```
|
||||
@ -1,66 +0,0 @@
|
||||
|
||||
# 0144.字典序最小的01字符串
|
||||
|
||||
贪心思路:移动尽可能 移动前面的1 ,这样可以是 字典序最小
|
||||
|
||||
从前到后遍历,遇到 0 ,就用前面的 1 来交换
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <string>
|
||||
using namespace std;
|
||||
int main() {
|
||||
int n,k;
|
||||
cin >> n >> k;
|
||||
string s;
|
||||
cin >> s;
|
||||
for(int i = 0; i < n && k > 0; i++) {
|
||||
if(s[i] == '0') {
|
||||
// 开始用前面的 1 来交换
|
||||
int j = i;
|
||||
while(j > 0 && s[j - 1] == '1' && k > 0) {
|
||||
swap(s[j], s[j - 1]);
|
||||
--j;
|
||||
--k;
|
||||
}
|
||||
}
|
||||
}
|
||||
cout << s << endl;
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
Java:
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int k = scanner.nextInt();
|
||||
scanner.nextLine(); // 消耗掉换行符
|
||||
String s = scanner.nextLine();
|
||||
char[] ch = s.toCharArray();
|
||||
|
||||
for (int i = 0; i < n && k > 0; i++) {
|
||||
if (ch[i] == '0') {
|
||||
// 开始用前面的 1 来交换
|
||||
int j = i;
|
||||
while (j > 0 && ch[j - 1] == '1' && k > 0) {
|
||||
char tmp = ch[j];
|
||||
ch[j] = ch[j - 1];
|
||||
ch[j - 1] = tmp;
|
||||
j--;
|
||||
k--;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println(new String(ch));
|
||||
}
|
||||
}
|
||||
```
|
||||
@ -1,98 +0,0 @@
|
||||
|
||||
# 145. 数组子序列的排列
|
||||
|
||||
每个元素出现的次数相乘就可以了。
|
||||
|
||||
注意 “长度为 m 的数组,1 到 m 每个元素都出现过,且恰好出现 1 次。” ,题目中有n个元素,所以我们要统计的就是 1 到 n 元素出现的个数。
|
||||
|
||||
因为如果有一个元素x 大于n了, 那不可能出现 长度为x的数组 且 1 到 x 每个元素都出现过。
|
||||
|
||||
```CPP
|
||||
#include "bits/stdc++.h"
|
||||
using namespace std;
|
||||
int main(){
|
||||
int n;
|
||||
int x;
|
||||
cin >> n;
|
||||
unordered_map<int, int> umap;
|
||||
for(int i = 0; i < n; ++i){
|
||||
cin >> x;
|
||||
if(umap.find(x) != umap.end()) umap[x]++;
|
||||
else umap[x] = 1;
|
||||
}
|
||||
long long res = 0;
|
||||
long long num = 1;
|
||||
for (int i = 1; i <= n; i++) {
|
||||
if (umap.find(i) == umap.end()) break; // 如果i都没出现,后面得数也不能 1 到 m 每个元素都出现过
|
||||
num = (num * umap[i]) % 1000000007;
|
||||
res += num;
|
||||
res %= 1000000007;
|
||||
}
|
||||
cout << res << endl;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.HashMap;
|
||||
import java.util.Map;
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int n = sc.nextInt();
|
||||
Map<Integer, Integer> map = new HashMap<>();
|
||||
for (int i = 0; i < n; i++) {
|
||||
int x = sc.nextInt();
|
||||
map.put(x, map.getOrDefault(x, 0) + 1);
|
||||
}
|
||||
long res = 0;
|
||||
long num = 1;
|
||||
for (int i = 1; i <= n; i++) {
|
||||
if (!map.containsKey(i)) break; // 如果i都没出现,后面得数也不能1到m每个元素都出现过
|
||||
num = (num * map.get(i)) % 1000000007;
|
||||
res += num;
|
||||
res %= 1000000007;
|
||||
}
|
||||
System.out.println(res);
|
||||
sc.close();
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
|
||||
```python
|
||||
def main():
|
||||
import sys
|
||||
input = sys.stdin.read
|
||||
data = input().split()
|
||||
|
||||
n = int(data[0])
|
||||
umap = {}
|
||||
|
||||
for i in range(1, n + 1):
|
||||
x = int(data[i])
|
||||
if x in umap:
|
||||
umap[x] += 1
|
||||
else:
|
||||
umap[x] = 1
|
||||
|
||||
res = 0
|
||||
num = 1
|
||||
MOD = 1000000007
|
||||
|
||||
for i in range(1, n + 1):
|
||||
if i not in umap:
|
||||
break # 如果i都没出现,后面得数也不能1到m每个元素都出现过
|
||||
num = (num * umap[i]) % MOD
|
||||
res = (res + num) % MOD
|
||||
|
||||
print(res)
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
|
||||
```
|
||||
@ -1,65 +0,0 @@
|
||||
|
||||
|
||||
|
||||
|
||||
# 146. 传送树
|
||||
|
||||
本题题意是比较绕的,我后面给补上了 【提示信息】对 题目输出样例讲解一下,相对会容易理解的多。
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <algorithm>
|
||||
using namespace std;
|
||||
|
||||
vector<vector<int>> edge; // 邻接表来存图
|
||||
vector<int> nxt;
|
||||
int n;
|
||||
|
||||
/*
|
||||
* 递归函数,用于找到每个节点的下一个传送门节点,并记录在nxt数组中。
|
||||
* 遍历当前节点的所有子节点,递归调用findNext以确保子节点的nxt值已经计算出来。
|
||||
* 更新当前节点的nxt值为其子节点中编号最小的节点。
|
||||
* 如果当前节点是叶子节点(即没有子节点),则将其nxt值设置为自身。
|
||||
*/
|
||||
void findNext(int node) {
|
||||
for (int v : edge[node]) {
|
||||
findNext(v);
|
||||
if (nxt[node] == -1 || nxt[node] > min(v, nxt[v])) {
|
||||
nxt[node] = min(v, nxt[v]);
|
||||
}
|
||||
}
|
||||
|
||||
// 叶子节点
|
||||
if (nxt[node] == -1) {
|
||||
nxt[node] = node;
|
||||
}
|
||||
}
|
||||
|
||||
// 计算从节点u出发经过若干次传送门到达叶子节点所需的步数。
|
||||
// 通过不断访问nxt节点,直到到达叶子节点,记录访问的节点数。
|
||||
int get(int u) {
|
||||
int cnt = 1;
|
||||
while (nxt[u] != u) {
|
||||
cnt++;
|
||||
u = nxt[u];
|
||||
}
|
||||
return cnt;
|
||||
}
|
||||
|
||||
int main() {
|
||||
cin >> n;
|
||||
edge.resize(n + 1);
|
||||
nxt.resize(n + 1, -1);
|
||||
for (int i = 1; i <= n; ++i) {
|
||||
int a, b;
|
||||
cin >> a >> b;
|
||||
edge[a].push_back(b);
|
||||
}
|
||||
findNext(1);
|
||||
for (int i = 1; i <= n; ++i) {
|
||||
cout << get(i) << ' ';
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
@ -1,78 +0,0 @@
|
||||
|
||||
# 三珠互斥
|
||||
|
||||
1. 如果k * 3 大于 n 了,那说明一定没结果,如果没想明白,大家举个例子试试看
|
||||
2. 分别求出三个红珠子之间的距离
|
||||
3. 对这三段距离从小到大排序 y1, y2, y3
|
||||
4. 如果第一段距离y1 小于k,说明需要交换 k - y 次, 同理 第二段距离y2 小于k,说明需要交换 k - y2 次
|
||||
5. y1 y2 都调整好了,不用计算y3,因为 y3是距离最大
|
||||
|
||||
```CPP
|
||||
#include<bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
int main(){
|
||||
int t;
|
||||
cin >> t;
|
||||
int n, k, a1, a2, a3;
|
||||
vector<int> dis(3);
|
||||
|
||||
while (t--) {
|
||||
cin >> n >> k >> a1 >> a2 >> a3;
|
||||
if(k * 3 > n){
|
||||
cout << -1 << endl;
|
||||
continue;
|
||||
}
|
||||
dis[0] = min(abs(a1 - a2), n - abs(a1 - a2));
|
||||
dis[1] = min(abs(a1 - a3), n - abs(a1 - a3));
|
||||
dis[2] = min(abs(a3 - a2), n - abs(a3 - a2));
|
||||
|
||||
sort(dis.begin(), dis.end());
|
||||
|
||||
int result = 0;
|
||||
if (dis[0] < k) result += (k - dis[0]);
|
||||
if (dis[1] < k) result += (k - dis[1]);
|
||||
|
||||
cout << result << endl;
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Java代码:
|
||||
|
||||
```Java
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int t = scanner.nextInt();
|
||||
|
||||
while (t-- > 0) {
|
||||
int n = scanner.nextInt();
|
||||
int k = scanner.nextInt();
|
||||
int a1 = scanner.nextInt();
|
||||
int a2 = scanner.nextInt();
|
||||
int a3 = scanner.nextInt();
|
||||
if (k * 3 > n) {
|
||||
System.out.println(-1);
|
||||
continue;
|
||||
}
|
||||
|
||||
List<Integer> dis = new ArrayList<>(3);
|
||||
dis.add(Math.min(Math.abs(a1 - a2), n - Math.abs(a1 - a2)));
|
||||
dis.add(Math.min(Math.abs(a1 - a3), n - Math.abs(a1 - a3)));
|
||||
dis.add(Math.min(Math.abs(a3 - a2), n - Math.abs(a3 - a2)));
|
||||
|
||||
Collections.sort(dis);
|
||||
|
||||
int result = 0;
|
||||
if (dis.get(0) < k) result += (k - dis.get(0));
|
||||
if (dis.get(1) < k) result += (k - dis.get(1));
|
||||
|
||||
System.out.println(result);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
@ -1,122 +0,0 @@
|
||||
|
||||
# 扑克牌同花顺
|
||||
|
||||
首先我们要定义一个结构体,来存放我们的数据
|
||||
|
||||
`map<花色,{同一花色牌集合,同一花色的牌对应的牌数量}>`
|
||||
|
||||
再遍历 每一个花色下,每一个牌 的数量
|
||||
|
||||
代码如下详细注释:
|
||||
|
||||
|
||||
```CPP
|
||||
#include<bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
string cards[] = {"H","S","D","C"};
|
||||
typedef long long ll;
|
||||
struct color
|
||||
{
|
||||
set<int> st; // 同一花色 牌的集合
|
||||
map<int, ll> cnt; // 同一花色 牌对应的数量
|
||||
};
|
||||
unordered_map<string, color> umap;
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
for (int i = 0; i < n; i++) {
|
||||
int x, y;
|
||||
string card;
|
||||
cin >> x >> y >> card;
|
||||
umap[card].st.insert(x);
|
||||
umap[card].cnt[x] += y;
|
||||
}
|
||||
ll sum = 0;
|
||||
// 遍历每一个花色
|
||||
for (string cardOne : cards) {
|
||||
color colorOne = umap[cardOne];
|
||||
// 遍历 同花色 每一个牌
|
||||
for (int number : colorOne.st) {
|
||||
ll numberCount = colorOne.cnt[number]; // 获取牌为number的数量是 numberCount
|
||||
|
||||
// 统计 number 到 number + 4 都是否有牌,用cal 把 number 到number+4 的数量记下来
|
||||
ll cal = numberCount;
|
||||
for (int j = number + 1; j <= number + 4; j++) cal = min(cal, colorOne.cnt[j]);
|
||||
// 统计结果
|
||||
sum += cal;
|
||||
// 把统计过的同花顺数量减下去
|
||||
for (int j = number + 1; j <= number + 4; j++) colorOne.cnt[j] -= cal;
|
||||
}
|
||||
}
|
||||
cout << sum << endl;
|
||||
}
|
||||
```
|
||||
|
||||
Java代码如下:
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
static String[] cards = {"H", "S", "D", "C"}; // 花色数组
|
||||
|
||||
static class Color {
|
||||
Set<Integer> st; // 同一花色牌的集合
|
||||
Map<Integer, Long> cnt; // 同一花色牌对应的数量
|
||||
|
||||
Color() {
|
||||
st = new HashSet<>(); // 初始化集合
|
||||
cnt = new HashMap<>(); // 初始化映射
|
||||
}
|
||||
}
|
||||
|
||||
static Map<String, Color> umap = new HashMap<>(); // 用于存储每种花色对应的Color对象
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt(); // 读取牌的数量
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
int x = scanner.nextInt(); // 读取牌的值
|
||||
int y = scanner.nextInt(); // 读取牌的数量
|
||||
String card = scanner.next(); // 读取牌的花色
|
||||
|
||||
umap.putIfAbsent(card, new Color()); // 如果不存在该花色,则创建一个新的Color对象
|
||||
umap.get(card).st.add(x); // 将牌的值加入集合
|
||||
umap.get(card).cnt.put(x, umap.get(card).cnt.getOrDefault(x, 0L) + y); // 更新牌的数量
|
||||
}
|
||||
|
||||
long sum = 0; // 结果累加器
|
||||
|
||||
// 遍历每一种花色
|
||||
for (String cardOne : cards) {
|
||||
Color colorOne = umap.getOrDefault(cardOne, new Color()); // 获取对应花色的Color对象
|
||||
|
||||
// 遍历同花色的每一张牌
|
||||
for (int number : colorOne.st) {
|
||||
long numberCount = colorOne.cnt.get(number); // 获取当前牌的数量
|
||||
|
||||
// 计算从当前牌到number+4的最小数量
|
||||
long cal = numberCount;
|
||||
for (int j = number + 1; j <= number + 4; j++) {
|
||||
cal = Math.min(cal, colorOne.cnt.getOrDefault(j, 0L)); // 更新cal为最小值
|
||||
}
|
||||
|
||||
// 将结果累加到sum
|
||||
sum += cal;
|
||||
|
||||
// 将统计过的同花顺数量减去
|
||||
for (int j = number + 1; j <= number + 4; j++) {
|
||||
colorOne.cnt.put(j, colorOne.cnt.getOrDefault(j, 0L) - cal);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println(sum); // 输出结果
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
@ -1,102 +0,0 @@
|
||||
|
||||
# 149. 好数组
|
||||
|
||||
贪心思路:
|
||||
|
||||
整体思路是移动到中间位置(中位数),一定是 移动次数最小的。
|
||||
|
||||
有一个数可以不改变,对数组排序之后, 最小数 和 最大数 一定是移动次数最多的,所以分别保留最小 和 最大的不变。
|
||||
|
||||
中间可能有两个位置,所以要计算中间偏前 和 中间偏后的
|
||||
|
||||
代码如下:
|
||||
|
||||
```CPP
|
||||
#include<bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
vector<long> arr(n);
|
||||
for (int i = 0; i < n; ++i) {
|
||||
cin >> arr[i];
|
||||
}
|
||||
sort(arr.begin(), arr.end());
|
||||
|
||||
if (arr[0] == arr[n - 1]) {
|
||||
cout << 1 << endl;
|
||||
return 0;
|
||||
}
|
||||
long cnt = 0L;
|
||||
long cnt1 = 0L;
|
||||
|
||||
// 如果要保留一个不改变,要不不改最小的,要不不改最大的。
|
||||
|
||||
// 取中间偏前的位置
|
||||
long mid = arr[(n - 2) / 2];
|
||||
|
||||
// 不改最大的
|
||||
for (int i = 0; i < n - 1; i++) {
|
||||
cnt += abs(arr[i] - mid);
|
||||
}
|
||||
|
||||
// 取中间偏后的位置
|
||||
mid = arr[n / 2];
|
||||
|
||||
// 不改最小的
|
||||
for (int i = 1; i < n; i++) {
|
||||
cnt1 += abs(arr[i] - mid);
|
||||
}
|
||||
|
||||
cout << min(cnt, cnt1) << endl;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Java代码如下:
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
long[] arr = new long[n];
|
||||
for (int i = 0; i < n; ++i) {
|
||||
arr[i] = scanner.nextLong();
|
||||
}
|
||||
Arrays.sort(arr);
|
||||
|
||||
if (arr[0] == arr[n - 1]) {
|
||||
System.out.println(1);
|
||||
return;
|
||||
}
|
||||
long cnt = 0L;
|
||||
long cnt1 = 0L;
|
||||
|
||||
// 如果要保留一个不改变,要不不改最小的,要不不改最大的。
|
||||
|
||||
// 取中间偏前的位置
|
||||
long mid = arr[(n - 2) / 2];
|
||||
|
||||
// 不改最大的
|
||||
for (int i = 0; i < n - 1; i++) {
|
||||
cnt += Math.abs(arr[i] - mid);
|
||||
}
|
||||
|
||||
// 取中间偏后的位置
|
||||
mid = arr[n / 2];
|
||||
|
||||
// 不改最小的
|
||||
for (int i = 1; i < n; i++) {
|
||||
cnt1 += Math.abs(arr[i] - mid);
|
||||
}
|
||||
|
||||
System.out.println(Math.min(cnt, cnt1));
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
@ -1,66 +0,0 @@
|
||||
|
||||
# 150. 极长连续段的权值
|
||||
|
||||
动态规划,枚举最后边节点的情况:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <string>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int n;
|
||||
cin >> n;
|
||||
string s;
|
||||
cin >> s;
|
||||
|
||||
long long result = 1;
|
||||
long long a = 1;
|
||||
|
||||
for (int i = 1; i < n; ++i) {
|
||||
// 加上本身长度为1的子串
|
||||
if (s[i] == s[i - 1]) {
|
||||
a += 1;
|
||||
result += a;
|
||||
// 以最右节点为终点,每个子串的级长连续段都+1,再加本身长度为1的子串
|
||||
} else {
|
||||
a = a + i + 1;
|
||||
result += a;
|
||||
}
|
||||
}
|
||||
cout << result << endl;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
Java代码如下:
|
||||
|
||||
```Java
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
String s = scanner.next();
|
||||
|
||||
long result = 1;
|
||||
long a = 1;
|
||||
|
||||
for (int i = 1; i < n; ++i) {
|
||||
// 加上本身长度为1的子串
|
||||
if (s.charAt(i) == s.charAt(i - 1)) {
|
||||
a += 1;
|
||||
result += a;
|
||||
// 以最右节点为终点,每个子串的级长连续段都+1,再加本身长度为1的子串
|
||||
} else {
|
||||
a = a + i + 1;
|
||||
result += a;
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println(result);
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
@ -1,127 +0,0 @@
|
||||
# 151. 手机流畅运行的秘密
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1229)
|
||||
|
||||
先运行 能留下电量多的 任务,才能有余电运行其他任务。
|
||||
|
||||
任务1,1:10 ,运行完 能留下 9个电
|
||||
|
||||
任务2,2:12,运行完 能留下 10个电
|
||||
|
||||
任务3,3:10,运行完 能留下 7个电。
|
||||
|
||||
运行顺序: 任务2 -> 任务1 -> 任务3
|
||||
|
||||
按照 最低初始电量 - 耗电量,从大到小排序。
|
||||
|
||||
计算总电量,需要 从小到大 遍历, 不断取 总电量 + 任务耗电量 与 任务最低初始电量 的最大值。
|
||||
|
||||
```CPP
|
||||
#include<bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
bool cmp(const pair<int,int>& taskA, const pair<int,int>& taskB) {
|
||||
return (taskA.second - taskA.first) < (taskB.second - taskB.first);
|
||||
}
|
||||
int main() {
|
||||
string str, tmp;
|
||||
vector<pair<int,int>> tasks;
|
||||
|
||||
//处理输入
|
||||
getline(cin, str);
|
||||
stringstream ss(str);
|
||||
while (getline(ss, tmp, ',')) {
|
||||
int p = tmp.find(":");
|
||||
string a = tmp.substr(0, p);
|
||||
string b = tmp.substr(p + 1);
|
||||
tasks.push_back({stoi(a), stoi(b)});
|
||||
}
|
||||
|
||||
// 按照差值从小到大排序
|
||||
sort(tasks.begin(), tasks.end(), cmp);
|
||||
|
||||
// 收集结果
|
||||
int result = 0;
|
||||
for (int i = 0 ; i < tasks.size(); i++) {
|
||||
result = max(result + tasks[i].first, tasks[i].second);
|
||||
}
|
||||
|
||||
result = result <= 4800 ? result : -1;
|
||||
cout << result << endl;
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
Java版本:
|
||||
|
||||
```Java
|
||||
import java.util.*;
|
||||
import java.util.stream.Collectors;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
String str = sc.nextLine();
|
||||
String[] tasksArray = str.split(",");
|
||||
List<Pair> tasks = Arrays.stream(tasksArray)
|
||||
.map(task -> {
|
||||
String[] parts = task.split(":");
|
||||
return new Pair(Integer.parseInt(parts[0]), Integer.parseInt(parts[1]));
|
||||
})
|
||||
.collect(Collectors.toList());
|
||||
|
||||
// 按照差值从小到大排序
|
||||
Collections.sort(tasks, (taskA, taskB) ->
|
||||
(taskA.second - taskA.first) - (taskB.second - taskB.first)
|
||||
);
|
||||
|
||||
// 收集结果
|
||||
int result = 0;
|
||||
for (Pair task : tasks) {
|
||||
result = Math.max(result + task.first, task.second);
|
||||
}
|
||||
|
||||
result = result <= 4800 ? result : -1;
|
||||
System.out.println(result);
|
||||
}
|
||||
}
|
||||
|
||||
class Pair {
|
||||
int first;
|
||||
int second;
|
||||
|
||||
Pair(int first, int second) {
|
||||
this.first = first;
|
||||
this.second = second;
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
Python版本:
|
||||
|
||||
```python
|
||||
def main():
|
||||
import sys
|
||||
input = sys.stdin.read
|
||||
|
||||
str = input().strip()
|
||||
tasks = []
|
||||
for tmp in str.split(','):
|
||||
a, b = map(int, tmp.split(':'))
|
||||
tasks.append((a, b))
|
||||
|
||||
# 按照差值从小到大排序
|
||||
tasks.sort(key=lambda task: task[1] - task[0])
|
||||
|
||||
# 收集结果
|
||||
result = 0
|
||||
for task in tasks:
|
||||
result = max(result + task[0], task[1])
|
||||
|
||||
result = result if result <= 4800 else -1
|
||||
print(result)
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
```
|
||||
@ -1,121 +0,0 @@
|
||||
|
||||
|
||||
# 152. 小米手机通信校准
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1230)
|
||||
|
||||
一道模拟题,但比较考察 代码能力。
|
||||
|
||||
遍历去找 里 freq 最近的 freg就好, 需要记录刚遍历过的的freg和 loss,因为可能有 相邻一样的 freg。
|
||||
|
||||
```CPP
|
||||
#include <bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
int main() {
|
||||
int freq;
|
||||
cin >> freq;
|
||||
string data;
|
||||
double result = 0;
|
||||
int last_freg = 0; // 记录上一个 freg
|
||||
int last_loss = 0; // 记录上一个loss
|
||||
while(cin >> data) {
|
||||
int index = data.find(':');
|
||||
int freg = stoi(data.substr(0, index)); // 获取 freg 和 loss
|
||||
int loss = stoi(data.substr(index + 1));
|
||||
// 两遍一样
|
||||
if(abs(freg - freq) == abs(last_freg - freq)) {
|
||||
result = (double)(last_loss + loss)/2.0;
|
||||
} // 否则更新最新的result
|
||||
else if(abs(freg - freq) < abs(last_freg - freq)){
|
||||
result = (double)loss;
|
||||
}
|
||||
last_freg = freg;
|
||||
last_loss = loss;
|
||||
}
|
||||
printf("%.1lf\n", result);
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
Java 版本:
|
||||
|
||||
```Java
|
||||
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int freq = sc.nextInt();
|
||||
sc.nextLine(); // 读取换行符
|
||||
|
||||
String inputLine = sc.nextLine(); // 读取包含所有后续输入的行
|
||||
String[] data = inputLine.split(" "); // 根据空格分割输入
|
||||
|
||||
double result = 0;
|
||||
int lastFreq = 0; // 记录上一个 freg
|
||||
int lastLoss = 0; // 记录上一个 loss
|
||||
|
||||
for (String entry : data) {
|
||||
int index = entry.indexOf(':');
|
||||
int freg = Integer.parseInt(entry.substring(0, index)); // 获取 freg 和 loss
|
||||
int loss = Integer.parseInt(entry.substring(index + 1));
|
||||
|
||||
// 两遍一样
|
||||
if (Math.abs(freg - freq) == Math.abs(lastFreq - freq)) {
|
||||
result = (double) (lastLoss + loss) / 2.0;
|
||||
}
|
||||
// 否则更新最新的 result
|
||||
else if (Math.abs(freg - freq) < Math.abs(lastFreq - freq)) {
|
||||
result = (double) loss;
|
||||
}
|
||||
|
||||
lastFreq = freg;
|
||||
lastLoss = loss;
|
||||
}
|
||||
|
||||
System.out.printf("%.1f\n", result);
|
||||
sc.close();
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
Python版本:
|
||||
|
||||
```python
|
||||
def main():
|
||||
import sys
|
||||
input = sys.stdin.read
|
||||
data = input().split()
|
||||
|
||||
freq = int(data[0])
|
||||
result = 0
|
||||
last_freg = 0 # 记录上一个 freg
|
||||
last_loss = 0 # 记录上一个 loss
|
||||
|
||||
for i in range(1, len(data)):
|
||||
item = data[i]
|
||||
index = item.find(':')
|
||||
freg = int(item[:index]) # 获取 freg 和 loss
|
||||
loss = int(item[index + 1:])
|
||||
|
||||
# 两遍一样
|
||||
if abs(freg - freq) == abs(last_freg - freq):
|
||||
result = (last_loss + loss) / 2.0
|
||||
# 否则更新最新的 result
|
||||
elif abs(freg - freq) < abs(last_freg - freq):
|
||||
result = loss
|
||||
|
||||
last_freg = freg
|
||||
last_loss = loss
|
||||
|
||||
print(f"{result:.1f}")
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
|
||||
|
||||
```
|
||||
@ -1,95 +0,0 @@
|
||||
|
||||
|
||||
# 权值优势路径计数
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1231)
|
||||
|
||||
1、构建二叉树:首先根据层序遍历的序列构建二叉树。这可以通过使用队列来实现,队列中存储当前节点及其索引,确保可以正确地将子节点添加到父节点下。
|
||||
|
||||
2、路径遍历:使用深度优先搜索(DFS)遍历所有从根到叶子的路径。在遍历过程中,维护一个计数器跟踪当前路径中权值为 1 和权值为 0 的节点的数量。
|
||||
|
||||
3、计数满足条件的路径:每当到达一个叶子节点时,检查当前路径的权值 1 的节点数量是否比权值 0 的节点数量多 1。如果满足,递增一个全局计数器。
|
||||
|
||||
|
||||
```CPP
|
||||
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <queue>
|
||||
|
||||
using namespace std;
|
||||
|
||||
struct TreeNode {
|
||||
int val;
|
||||
TreeNode *left, *right;
|
||||
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
|
||||
};
|
||||
|
||||
// DFS遍历二叉树,并计算满足条件的路径数量
|
||||
void countPaths(TreeNode* node, int count1, int count0, int& result) {
|
||||
if (!node) return;
|
||||
|
||||
// 更新当前路径中1和0的数量
|
||||
node->val == 1 ? count1++ : count0++;
|
||||
|
||||
// 检查当前节点是否为叶子节点
|
||||
if (!node->left && !node->right) {
|
||||
// 检查1的数量是否比0的数量多1
|
||||
if (count1 == count0 + 1) {
|
||||
result++;
|
||||
}
|
||||
return;
|
||||
}
|
||||
|
||||
// 递归访问左右子节点
|
||||
countPaths(node->left, count1, count0, result);
|
||||
countPaths(node->right, count1, count0, result);
|
||||
}
|
||||
|
||||
int main() {
|
||||
int N;
|
||||
cin >> N;
|
||||
|
||||
vector<int> nums(N);
|
||||
for (int i = 0; i < N; ++i) {
|
||||
cin >> nums[i];
|
||||
}
|
||||
|
||||
if (nums.empty()) {
|
||||
cout << 0 << endl;
|
||||
return 0;
|
||||
}
|
||||
|
||||
// 根据层序遍历的输入构建二叉树
|
||||
queue<TreeNode*> q;
|
||||
TreeNode* root = new TreeNode(nums[0]);
|
||||
q.push(root);
|
||||
int index = 1;
|
||||
|
||||
while (!q.empty() && index < N) {
|
||||
TreeNode* node = q.front();
|
||||
q.pop();
|
||||
|
||||
if (index < N && nums[index] != -1) {
|
||||
node->left = new TreeNode(nums[index]);
|
||||
q.push(node->left);
|
||||
}
|
||||
index++;
|
||||
|
||||
if (index < N && nums[index] != -1) {
|
||||
node->right = new TreeNode(nums[index]);
|
||||
q.push(node->right);
|
||||
}
|
||||
index++;
|
||||
}
|
||||
|
||||
// 计算满足条件的路径数
|
||||
int result = 0;
|
||||
countPaths(root, 0, 0, result);
|
||||
|
||||
cout << result << endl;
|
||||
|
||||
return 0;
|
||||
}
|
||||
|
||||
```
|
||||
@ -1,68 +0,0 @@
|
||||
|
||||
# 序列中位数
|
||||
|
||||
[题目链接](https://kamacoder.com/problempage.php?pid=1232)
|
||||
|
||||
注意给的数组默认不是有序的!
|
||||
|
||||
模拟题,排序之后,取中位数,然后按照b数组 删 a数组中元素,再取中位数。
|
||||
|
||||
```CPP
|
||||
#include<bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
// 计算并返回中位数
|
||||
double findMedian(vector<int>& nums) {
|
||||
int n = nums.size();
|
||||
if (n % 2 == 1) {
|
||||
return nums[n / 2]; // 奇数长度,返回中间的元素
|
||||
} else {
|
||||
// 偶数长度,返回中间两个元素的平均值
|
||||
return (nums[n / 2] + nums[n / 2 - 1]) / 2.0;
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
int main(){
|
||||
int t;
|
||||
cin >> t;
|
||||
while(t--){
|
||||
int n;
|
||||
cin>> n;
|
||||
vector<int> a(n);
|
||||
vector<int> b(n - 1);
|
||||
for(int i = 0; i < n; i++){
|
||||
cin >> a[i];
|
||||
}
|
||||
for(int i = 0; i < n - 1; i++){
|
||||
cin >> b[i];
|
||||
}
|
||||
vector<int> nums = a;
|
||||
vector<double> answers;
|
||||
|
||||
sort(nums.begin(), nums.end());
|
||||
|
||||
// 把中位数放进结果集
|
||||
answers.push_back(findMedian(nums));
|
||||
|
||||
for(int i = 0; i < n - 1; i++){
|
||||
|
||||
int target = a[b[i]];
|
||||
// 删除目标值
|
||||
nums.erase(find(nums.begin(), nums.end(), target));
|
||||
// 把中位数放进结果集
|
||||
answers.push_back(findMedian(nums));
|
||||
|
||||
}
|
||||
|
||||
for(auto answer : answers){
|
||||
// 判断是否是整数
|
||||
if(answer == (int)answer) printf("%d ", (int)answer);
|
||||
else printf("%.1f ", answer);
|
||||
}
|
||||
cout << endl;
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
Some files were not shown because too many files have changed in this diff Show More
Reference in New Issue
Block a user