Merge branch 'master' of github.com:youngyangyang04/leetcode-master

2025-07-06 15:09:40 +08:00 · 2022-01-05 19:49:26 +08:00
parent 9a1788dbf8 f8c32ab25c
commit a7d9cf704b
1 changed files with 137 additions and 0 deletions
--- a/problems/0054.螺旋矩阵.md
+++ b/problems/0054.螺旋矩阵.md
@ -0,0 +1,137 @@
+<p align="center">
+<a href="https://programmercarl.com/other/kstar.html" target="_blank">
+  <img src="https://code-thinking-1253855093.file.myqcloud.com/pics/20210924105952.png" width="1000"/>
+</a>
+<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>
+
+
+
+## 54.螺旋矩阵
+
+[力扣题目链接](https://leetcode-cn.com/problems/spiral-matrix/)
+
+给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。
+
+示例1:
+
+输入: 
+[
+ [ 1, 2, 3 ],
+ [ 4, 5, 6 ],
+ [ 7, 8, 9 ]
+]
+输出:[1,2,3,6,9,8,7,4,5]
+
+## 思路
+
+本题解决思路继承自[59.螺旋矩阵II](https://www.programmercarl.com/0059.%E8%9E%BA%E6%97%8B%E7%9F%A9%E9%98%B5II.html)，建议看完59.螺旋矩阵II之后再看本题
+
+与59.螺旋矩阵II相同的是：两者都是模拟矩形的顺时针旋转，所以核心依然是依然是坚持循环不变量，按照左闭右开的原则
+
+模拟顺时针画矩阵的过程:
+
+* 填充上行从左到右
+* 填充右列从上到下
+* 填充下行从右到左
+* 填充左列从下到上
+
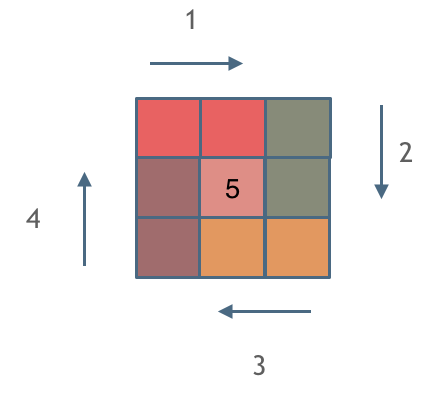
+由外向内一圈一圈这么画下去，如下所示：
+
+![螺旋矩阵](https://img-blog.csdnimg.cn/2020121623550681.png)
+
+这里每一种颜色，代表一条边，我们遍历的长度，可以看出每一个拐角处的处理规则，拐角处让给新的一条边来继续画。
+
+与59.螺旋矩阵II不同的是：前题中的螺旋矩阵是正方形，只有正方形的边长n一个边界条件，而本题中，需要考虑长方形的长和宽(m行和n列)两个边界条件。自然，m可以等于n，即前题可视为本题在m==n的特殊情况。
+
+我们从最一般的情况开始考虑，与59.螺旋矩阵II题解对比起来，m和n的带入，主要引来两方面的差异：
+
+* loop的计算：
+    本题的loop计算与59.螺旋矩阵II算法略微差异，因为存在rows和columns两个维度，可自行分析，loop只能取min(rows, columns)，例如rows = 5, columns = 7，那loop = 5 / 7 = 2
+* mid的计算及填充：
+    1、同样的原理，本题的mid计算也存在上述差异；
+    2、
+      如果min(rows, columns)为偶数，则不需要在最后单独考虑矩阵最中间位置的赋值
+      如果min(rows, columns)为奇数，则矩阵最中间位置不只是[mid][mid],而是会留下来一个特殊的中间行或者中间列，具体是中间行还是中间列，要看rows和columns的大小，如果rows > columns,则是中间列，相反，则是中间行
+
+代码如下，已经详细注释了每一步的目的，可以看出while循环里判断的情况是很多的，代码里处理的原则也是统一的左闭右开。
+
+整体C++代码如下：
+
+```CPP
+class Solution {
+public:
+    vector<int> spiralOrder(vector<vector<int>>& matrix) {
+        if (matrix.size() == 0 || matrix[0].size() == 0)
+            return {};
+        int rows = matrix.size(), columns = matrix[0].size();
+        int total = rows * columns;
+        vector<int> res(total); // 使用vector定义一个一维数组存放结果
+        int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
+        int loop = min(rows, columns) / 2; 
+        // 本题的loop计算与59.螺旋矩阵II算法略微差异，因为存在rows和columns两个维度，可自行分析，loop只能取min(rows, columns)，例如rows = 5, columns = 7，那loop = 5 / 7 = 2
+        int mid = min(rows, columns) / 2; 
+        // 1、同样的原理，本题的mid计算也存在上述差异；
+        // 2、
+            //如果min(rows, columns)为偶数，则不需要在最后单独考虑矩阵最中间位置的赋值
+            //如果min(rows, columns)为奇数，则矩阵最中间位置不只是[mid][mid],而是会留下来一个特殊的中间行或者中间列，具体是中间行还是中间列，要看rows和columns的大小，如果rows > columns,则是中间列，相反，则是中间行
+        //相信这一点不好理解，建议自行画图理解
+        int count = 0;// 用来给矩阵中每一个空格赋值
+        int offset = 1;// 每一圈循环，需要控制每一条边遍历的长度
+        int i,j;
+        while (loop --) {
+            i = startx;
+            j = starty;
+
+            // 下面开始的四个for就是模拟转了一圈
+            // 模拟填充上行从左到右(左闭右开)
+            for (j = starty; j < starty + columns - offset; j++) {
+                res[count++] = matrix[startx][j];
+            }
+            // 模拟填充右列从上到下(左闭右开)
+            for (i = startx; i < startx + rows - offset; i++) {
+                res[count++] = matrix[i][j];
+            }
+            // 模拟填充下行从右到左(左闭右开)
+            for (; j > starty; j--) {
+                res[count++] = matrix[i][j];
+            }
+            // 模拟填充左列从下到上(左闭右开)
+            for (; i > startx; i--) {
+                res[count++] = matrix[i][starty];
+            }
+
+            // 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
+            startx++;
+            starty++;
+
+            // offset 控制每一圈里每一条边遍历的长度
+            offset += 2;
+        }
+
+        // 如果min(rows, columns)为奇数的话，需要单独给矩阵最中间的位置赋值
+        if (min(rows, columns) % 2) {
+            if(rows > columns){
+                for (int i = mid; i < mid + rows - columns + 1; ++i) {
+                    res[count++] = matrix[i][mid];
+                }
+
+            } else {
+                for (int i = mid; i < mid + columns - rows + 1; ++i) {
+                    res[count++] = matrix[mid][i];
+                }
+            }
+        }
+        return res;
+    }
+};
+```
+
+## 类似题目
+
+* [59.螺旋矩阵II](https://leetcode-cn.com/problems/spiral-matrix-ii/)
+* [剑指Offer 29.顺时针打印矩阵](https://leetcode-cn.com/problems/shun-shi-zhen-da-yin-ju-zhen-lcof/)
+
+
+
+-----------------------
+<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>