mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-09 19:44:45 +08:00
Update
This commit is contained in:
@ -89,6 +89,7 @@
|
||||
* [二叉树:你真的会翻转二叉树么?](https://mp.weixin.qq.com/s/6gY1MiXrnm-khAAJiIb5Bg)
|
||||
* [本周小结!(二叉树)](https://mp.weixin.qq.com/s/JWmTeC7aKbBfGx4TY6uwuQ)
|
||||
* [二叉树:我对称么?](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)
|
||||
* [二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)
|
||||
|
||||
(持续更新中....)
|
||||
|
||||
@ -317,6 +318,7 @@
|
||||
|
||||
# 我的公众号
|
||||
|
||||
|
||||
更多精彩文章持续更新,微信搜索:「代码随想录」第一时间围观,关注后回复: 「简历模板」「java」「C++」「python」「算法与数据结构」 等关键字就可以获得我多年整理出来的学习资料。
|
||||
|
||||
**每天8:35准时为你推送一篇经典面试题目,帮你梳理算法知识体系,轻松学习算法!**,并且公众号里有大量学习资源,也有我自己的学习心得和方法总结,相信你一定会有所收获!
|
||||
|
||||
BIN
pics/111.二叉树的最小深度.png
Normal file
BIN
pics/111.二叉树的最小深度.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 83 KiB |
BIN
pics/111.二叉树的最小深度1.png
Normal file
BIN
pics/111.二叉树的最小深度1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 9.0 KiB |
@ -250,23 +250,27 @@ public:
|
||||
## C++代码
|
||||
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> largestValues(TreeNode* root) {
|
||||
queue<TreeNode*> que;
|
||||
if (root != NULL) que.push(root);
|
||||
vector<vector<int>> result;
|
||||
vector<int> result;
|
||||
while (!que.empty()) {
|
||||
int size = que.size();
|
||||
vector<int> vec;
|
||||
// 这里一定要使用固定大小size,不要使用que.size(),因为que.size是不断变化的
|
||||
int maxValue = INT_MIN; // 取每一层的最大值
|
||||
for (int i = 0; i < size; i++) {
|
||||
TreeNode* node = que.front();
|
||||
que.pop();
|
||||
vec.push_back(node->val);
|
||||
maxValue = node->val > maxValue ? node->val : maxValue;
|
||||
if (node->left) que.push(node->left);
|
||||
if (node->right) que.push(node->right);
|
||||
}
|
||||
result.push_back(vec);
|
||||
result.push_back(maxValue); // 把最大值放进数组
|
||||
}
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
# 116.填充每个节点的下一个右侧节点指针
|
||||
|
||||
@ -187,4 +187,38 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
使用栈来模拟后序遍历依然可以
|
||||
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
int maxDepth(TreeNode* root) {
|
||||
stack<TreeNode*> st;
|
||||
if (root != NULL) st.push(root);
|
||||
int depth = 0;
|
||||
int result = 0;
|
||||
while (!st.empty()) {
|
||||
TreeNode* node = st.top();
|
||||
if (node != NULL) {
|
||||
st.pop();
|
||||
st.push(node); // 中
|
||||
st.push(NULL);
|
||||
depth++;
|
||||
if (node->right) st.push(node->right); // 右
|
||||
if (node->left) st.push(node->left); // 左
|
||||
|
||||
} else {
|
||||
st.pop();
|
||||
node = st.top();
|
||||
st.pop();
|
||||
depth--;
|
||||
}
|
||||
result = result > depth ? result : depth;
|
||||
}
|
||||
return result;
|
||||
|
||||
}
|
||||
};
|
||||
```
|
||||
> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
|
||||
|
||||
@ -2,11 +2,39 @@
|
||||
## 题目地址
|
||||
https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/
|
||||
|
||||
## 思路
|
||||
> 和求最大深度一个套路?
|
||||
|
||||
看完了这篇[二叉树:看看这些树的最大深度](),再来看看如何求最小深度。
|
||||
# 111.二叉树的最小深度
|
||||
|
||||
直觉上好像和求最大深度差不多,其实还是差挺多的,一起来看一下。
|
||||
给定一个二叉树,找出其最小深度。
|
||||
|
||||
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
|
||||
|
||||
说明: 叶子节点是指没有子节点的节点。
|
||||
|
||||
示例:
|
||||
|
||||
给定二叉树 [3,9,20,null,null,15,7],
|
||||
|
||||
<img src='../pics/111.二叉树的最小深度1.png' width=600> </img></div>
|
||||
|
||||
返回它的最小深度 2.
|
||||
|
||||
# 思路
|
||||
|
||||
看完了这篇[二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg),再来看看如何求最小深度。
|
||||
|
||||
直觉上好像和求最大深度差不多,其实还是差不少的。
|
||||
|
||||
遍历顺序上依然是后序遍历(因为要比较递归返回之后的结果),但在处理中间节点的逻辑上,最大深度很容易理解,最小深度可有一个误区,如图:
|
||||
|
||||
<img src='../pics/111.二叉树的最小深度.png' width=600> </img></div>
|
||||
|
||||
这就重新审题了,题目中说的是:**最小深度是从根节点到最近叶子节点的最短路径上的节点数量。**,注意是**叶子节点**。
|
||||
|
||||
什么是叶子节点,左右孩子都为空的节点才是叶子节点!
|
||||
|
||||
## 递归法
|
||||
|
||||
来来来,一起递归三部曲:
|
||||
|
||||
@ -32,59 +60,63 @@ if (node == NULL) return 0;
|
||||
|
||||
3. 确定单层递归的逻辑
|
||||
|
||||
这块和求最大深度可就不一样了,一些同学可能会写如下代码
|
||||
|
||||
这块和求最大深度可就不一样了,一些同学可能会写如下代码:
|
||||
```
|
||||
int leftDepth = getDepth(node->left);
|
||||
int rightDepth = getDepth(node->right);
|
||||
if (node->left == NULL && node->right != NULL) {
|
||||
return 1 + rightDepth;
|
||||
}
|
||||
if (node->left != NULL && node->right == NULL) {
|
||||
return 1 + leftDepth;
|
||||
}
|
||||
return 1 + min(leftDepth, rightDepth);
|
||||
int result = 1 + min(leftDepth, rightDepth);
|
||||
return result;
|
||||
```
|
||||
|
||||
首先取左右子树的深度,如果左子树为空,右子树不为空,说明最小深度是 1 + 右子树的深度。
|
||||
这个代码就犯了此图中的误区:
|
||||
|
||||
反之,右子树为空,左子树不为空,最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空,返回左右子树深度最小值 + 1 就可以了。
|
||||
<img src='../pics/111.二叉树的最小深度.png' width=600> </img></div>
|
||||
|
||||
可以看出:求二叉树的最小深度和求二叉树的最大深度的差别主要在于处理左右孩子不为空的逻辑。
|
||||
如果这么求的话,没有左孩子的分支会算为最短深度。
|
||||
|
||||
所以,如果左子树为空,右子树不为空,说明最小深度是 1 + 右子树的深度。
|
||||
|
||||
反之,右子树为空,左子树不为空,最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空,返回左右子树深度最小值 + 1 。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
int leftDepth = getDepth(node->left);
|
||||
int rightDepth = getDepth(node->right);
|
||||
int leftDepth = getDepth(node->left); // 左
|
||||
int rightDepth = getDepth(node->right); // 右
|
||||
// 中
|
||||
// 当一个左子树为空,右不为空,这时并不是最低点
|
||||
if (node->left == NULL && node->right != NULL) {
|
||||
return 1 + rightDepth;
|
||||
}
|
||||
// 当一个右子树为空,左不为空,这时并不是最低点
|
||||
if (node->left != NULL && node->right == NULL) {
|
||||
return 1 + leftDepth;
|
||||
}
|
||||
return 1 + min(leftDepth, rightDepth);
|
||||
int result = 1 + min(leftDepth, rightDepth);
|
||||
return result;
|
||||
```
|
||||
|
||||
遍历的顺序为后序(左右中),可以看出:**求二叉树的最小深度和求二叉树的最大深度的差别主要在于处理左右孩子不为空的逻辑。**
|
||||
|
||||
整体递归代码如下:
|
||||
|
||||
## C++代码
|
||||
|
||||
### 递归
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
int getDepth(TreeNode* node) {
|
||||
if (node == NULL) return 0;
|
||||
int leftDepth = getDepth(node->left); // 左
|
||||
int rightDepth = getDepth(node->right); // 右
|
||||
// 中
|
||||
// 当一个左子树为空,右不为空,这时并不是最低点
|
||||
if (node->left == NULL && node->right != NULL) {
|
||||
return 1 + getDepth(node->right);
|
||||
}
|
||||
if (node->left == NULL && node->right != NULL) {
|
||||
return 1 + rightDepth;
|
||||
}
|
||||
// 当一个右子树为空,左不为空,这时并不是最低点
|
||||
if (node->left != NULL && node->right == NULL) {
|
||||
return 1 + getDepth(node->left);
|
||||
if (node->left != NULL && node->right == NULL) {
|
||||
return 1 + leftDepth;
|
||||
}
|
||||
return 1 + min(getDepth(node->left), getDepth(node->right));
|
||||
int result = 1 + min(leftDepth, rightDepth);
|
||||
return result;
|
||||
}
|
||||
|
||||
int minDepth(TreeNode* root) {
|
||||
@ -93,15 +125,36 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
### 迭代法
|
||||
精简之后代码如下:
|
||||
|
||||
可以使用二叉树的广度优先遍历(层序遍历),来做这道题目,其实这就是一道模板题了,二叉树的层序遍历模板在这道题解中[0102.二叉树的层序遍历](https://github.com/youngyangyang04/leetcode/blob/master/problems/0102.二叉树的层序遍历.md)
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
int minDepth(TreeNode* root) {
|
||||
if (root == NULL) return 0;
|
||||
if (root->left == NULL && root->right != NULL) {
|
||||
return 1 + minDepth(root->right);
|
||||
}
|
||||
if (root->left != NULL && root->right == NULL) {
|
||||
return 1 + minDepth(root->left);
|
||||
}
|
||||
return 1 + min(minDepth(root->left), minDepth(root->right));
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
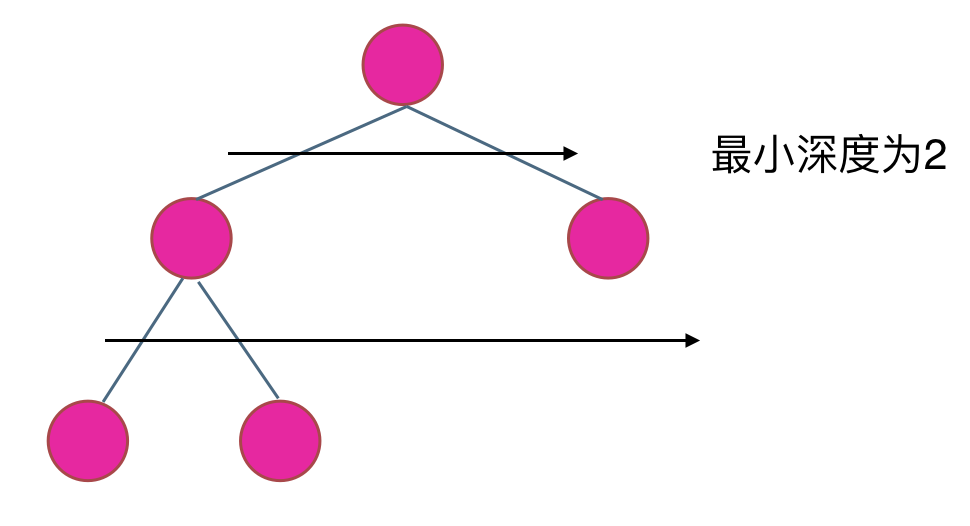
层序遍历如图所示:
|
||||
**精简之后的代码根本看不出是哪种遍历方式,所以依然还要强调一波:如果对二叉树的操作还不熟练,尽量不要直接照着精简代码来学。**
|
||||
|
||||
|
||||
## 迭代法
|
||||
|
||||
相对于[二叉树:看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg),本题还可以使用层序遍历的方式来解决,思路是一样的。
|
||||
|
||||
如果对层序遍历还不清楚的话,可以看这篇:[二叉树:层序遍历登场!](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)
|
||||
|
||||
**需要注意的是,只有当左右孩子都为空的时候,才说明遍历的最低点了。如果其中一个孩子为空则不是最低点**
|
||||
|
||||
代码如下:(详细注释)
|
||||
|
||||
```
|
||||
class Solution {
|
||||
public:
|
||||
@ -112,8 +165,8 @@ public:
|
||||
queue<TreeNode*> que;
|
||||
que.push(root);
|
||||
while(!que.empty()) {
|
||||
int size = que.size(); // 必须要这么写,要固定size大小
|
||||
depth++;
|
||||
int size = que.size();
|
||||
depth++; // 记录最小深度
|
||||
int flag = 0;
|
||||
for (int i = 0; i < size; i++) {
|
||||
TreeNode* node = que.front();
|
||||
|
||||
@ -40,7 +40,7 @@ public:
|
||||
for (int i = 0; i < size; i++) {
|
||||
TreeNode* node = que.front();
|
||||
que.pop();
|
||||
result++; // 记录遍历的层数
|
||||
result++; // 记录节点数量
|
||||
if (node->left) que.push(node->left);
|
||||
if (node->right) que.push(node->right);
|
||||
}
|
||||
|
||||
@ -11,7 +11,7 @@ https://leetcode-cn.com/problems/insert-into-a-binary-search-tree/
|
||||
|
||||
例如插入元素10 ,需要找到末尾节点插入便可,一样的道理来插入元素15,插入元素0,插入元素6,**需要调整二叉树的结构么? 并不需要。**只需要遍历二叉搜索树,找到空节点 插入元素就可以了, 那么这道题其实就非常简单了。
|
||||
|
||||
<video src='../video/701.二叉搜索树中的插入操作.mp4' controls='controls' width='640' height='320' autoplay='autoplay'> Your browser does not support the video tag.</video></div>
|
||||
<img src='../video/701.二叉搜索树中的插入操作.gif' width=600> </img></div>
|
||||
|
||||
接下来就是遍历二叉搜索树的过程了。
|
||||
|
||||
|
||||
BIN
video/701.二叉搜索树中的插入操作.gif
Normal file
BIN
video/701.二叉搜索树中的插入操作.gif
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 342 KiB |
Reference in New Issue
Block a user