mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-06 15:09:40 +08:00
Merge branch 'youngyangyang04:master' into master
This commit is contained in:
@ -34,7 +34,7 @@
|
||||
|
||||
### 哈希解法
|
||||
|
||||
两层for循环就可以确定 a 和b 的数值了,可以使用哈希法来确定 0-(a+b) 是否在 数组里出现过,其实这个思路是正确的,但是我们有一个非常棘手的问题,就是题目中说的不可以包含重复的三元组。
|
||||
两层for循环就可以确定 两个数值,可以使用哈希法来确定 第三个数 0-(a+b) 或者 0 - (a + c) 是否在 数组里出现过,其实这个思路是正确的,但是我们有一个非常棘手的问题,就是题目中说的不可以包含重复的三元组。
|
||||
|
||||
把符合条件的三元组放进vector中,然后再去重,这样是非常费时的,很容易超时,也是这道题目通过率如此之低的根源所在。
|
||||
|
||||
@ -48,35 +48,41 @@
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
// 在一个数组中找到3个数形成的三元组,它们的和为0,不能重复使用(三数下标互不相同),且三元组不能重复。
|
||||
// b(存储)== 0-(a+c)(检索)
|
||||
vector<vector<int>> threeSum(vector<int>& nums) {
|
||||
vector<vector<int>> result;
|
||||
sort(nums.begin(), nums.end());
|
||||
// 找出a + b + c = 0
|
||||
// a = nums[i], b = nums[j], c = -(a + b)
|
||||
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
// 排序之后如果第一个元素已经大于零,那么不可能凑成三元组
|
||||
if (nums[i] > 0) {
|
||||
// 如果a是正数,a<b<c,不可能形成和为0的三元组
|
||||
if (nums[i] > 0)
|
||||
break;
|
||||
}
|
||||
if (i > 0 && nums[i] == nums[i - 1]) { //三元组元素a去重
|
||||
|
||||
// [a, a, ...] 如果本轮a和上轮a相同,那么找到的b,c也是相同的,所以去重a
|
||||
if (i > 0 && nums[i] == nums[i - 1])
|
||||
continue;
|
||||
}
|
||||
|
||||
// 这个set的作用是存储b
|
||||
unordered_set<int> set;
|
||||
for (int j = i + 1; j < nums.size(); j++) {
|
||||
if (j > i + 2
|
||||
&& nums[j] == nums[j-1]
|
||||
&& nums[j-1] == nums[j-2]) { // 三元组元素b去重
|
||||
|
||||
for (int k = i + 1; k < nums.size(); k++) {
|
||||
// 去重b=c时的b和c
|
||||
if (k > i + 2 && nums[k] == nums[k - 1] && nums[k - 1] == nums[k - 2])
|
||||
continue;
|
||||
|
||||
// a+b+c=0 <=> b=0-(a+c)
|
||||
int target = 0 - (nums[i] + nums[k]);
|
||||
if (set.find(target) != set.end()) {
|
||||
result.push_back({nums[i], target, nums[k]}); // nums[k]成为c
|
||||
set.erase(target);
|
||||
}
|
||||
int c = 0 - (nums[i] + nums[j]);
|
||||
if (set.find(c) != set.end()) {
|
||||
result.push_back({nums[i], nums[j], c});
|
||||
set.erase(c);// 三元组元素c去重
|
||||
} else {
|
||||
set.insert(nums[j]);
|
||||
else {
|
||||
set.insert(nums[k]); // nums[k]成为b
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
@ -58,7 +58,7 @@
|
||||
|
||||
* fast和slow同时移动,直到fast指向末尾,如题:
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/19.%E5%88%A0%E9%99%A4%E9%93%BE%E8%A1%A8%E7%9A%84%E5%80%92%E6%95%B0%E7%AC%ACN%E4%B8%AA%E8%8A%82%E7%82%B92.png' width=600> </img></div>
|
||||
|
||||
//图片中有错别词:应该将“只到”改为“直到”
|
||||
* 删除slow指向的下一个节点,如图:
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/19.%E5%88%A0%E9%99%A4%E9%93%BE%E8%A1%A8%E7%9A%84%E5%80%92%E6%95%B0%E7%AC%ACN%E4%B8%AA%E8%8A%82%E7%82%B93.png' width=600> </img></div>
|
||||
|
||||
|
||||
@ -1456,6 +1456,70 @@ public int[] GetNext(string needle)
|
||||
}
|
||||
```
|
||||
|
||||
### C:
|
||||
|
||||
> 前缀表统一右移和减一
|
||||
|
||||
```c
|
||||
|
||||
int *build_next(char* needle, int len) {
|
||||
|
||||
int *next = (int *)malloc(len * sizeof(int));
|
||||
assert(next); // 确保分配成功
|
||||
|
||||
// 初始化next数组
|
||||
next[0] = -1; // next[0] 设置为 -1,表示没有有效前缀匹配
|
||||
if (len <= 1) { // 如果模式串长度小于等于 1,直接返回
|
||||
return next;
|
||||
}
|
||||
next[1] = 0; // next[1] 设置为 0,表示第一个字符没有公共前后缀
|
||||
|
||||
// 构建next数组, i 从模式串的第三个字符开始, j 指向当前匹配的最长前缀长度
|
||||
int i = 2, j = 0;
|
||||
while (i < len) {
|
||||
if (needle[i - 1] == needle[j]) {
|
||||
j++;
|
||||
next[i] = j;
|
||||
i++;
|
||||
} else if (j > 0) {
|
||||
// 如果不匹配且 j > 0, 回退到次长匹配前缀的长度
|
||||
j = next[j];
|
||||
} else {
|
||||
next[i] = 0;
|
||||
i++;
|
||||
}
|
||||
}
|
||||
return next;
|
||||
}
|
||||
|
||||
int strStr(char* haystack, char* needle) {
|
||||
|
||||
int needle_len = strlen(needle);
|
||||
int haystack_len = strlen(haystack);
|
||||
|
||||
int *next = build_next(needle, needle_len);
|
||||
|
||||
int i = 0, j = 0; // i 指向主串的当前起始位置, j 指向模式串的当前匹配位置
|
||||
while (i <= haystack_len - needle_len) {
|
||||
if (haystack[i + j] == needle[j]) {
|
||||
j++;
|
||||
if (j == needle_len) {
|
||||
free(next);
|
||||
next = NULL
|
||||
return i;
|
||||
}
|
||||
} else {
|
||||
i += j - next[j]; // 调整主串的起始位置
|
||||
j = j > 0 ? next[j] : 0;
|
||||
}
|
||||
}
|
||||
|
||||
free(next);
|
||||
next = NULL;
|
||||
return -1;
|
||||
}
|
||||
```
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
|
||||
@ -366,40 +366,56 @@ class Solution:
|
||||
"""
|
||||
Do not return anything, modify board in-place instead.
|
||||
"""
|
||||
self.backtracking(board)
|
||||
row_used = [set() for _ in range(9)]
|
||||
col_used = [set() for _ in range(9)]
|
||||
box_used = [set() for _ in range(9)]
|
||||
for row in range(9):
|
||||
for col in range(9):
|
||||
num = board[row][col]
|
||||
if num == ".":
|
||||
continue
|
||||
row_used[row].add(num)
|
||||
col_used[col].add(num)
|
||||
box_used[(row // 3) * 3 + col // 3].add(num)
|
||||
self.backtracking(0, 0, board, row_used, col_used, box_used)
|
||||
|
||||
def backtracking(self, board: List[List[str]]) -> bool:
|
||||
# 若有解,返回True;若无解,返回False
|
||||
for i in range(len(board)): # 遍历行
|
||||
for j in range(len(board[0])): # 遍历列
|
||||
# 若空格内已有数字,跳过
|
||||
if board[i][j] != '.': continue
|
||||
for k in range(1, 10):
|
||||
if self.is_valid(i, j, k, board):
|
||||
board[i][j] = str(k)
|
||||
if self.backtracking(board): return True
|
||||
board[i][j] = '.'
|
||||
# 若数字1-9都不能成功填入空格,返回False无解
|
||||
return False
|
||||
return True # 有解
|
||||
def backtracking(
|
||||
self,
|
||||
row: int,
|
||||
col: int,
|
||||
board: List[List[str]],
|
||||
row_used: List[List[int]],
|
||||
col_used: List[List[int]],
|
||||
box_used: List[List[int]],
|
||||
) -> bool:
|
||||
if row == 9:
|
||||
return True
|
||||
|
||||
def is_valid(self, row: int, col: int, val: int, board: List[List[str]]) -> bool:
|
||||
# 判断同一行是否冲突
|
||||
for i in range(9):
|
||||
if board[row][i] == str(val):
|
||||
return False
|
||||
# 判断同一列是否冲突
|
||||
for j in range(9):
|
||||
if board[j][col] == str(val):
|
||||
return False
|
||||
# 判断同一九宫格是否有冲突
|
||||
start_row = (row // 3) * 3
|
||||
start_col = (col // 3) * 3
|
||||
for i in range(start_row, start_row + 3):
|
||||
for j in range(start_col, start_col + 3):
|
||||
if board[i][j] == str(val):
|
||||
return False
|
||||
return True
|
||||
next_row, next_col = (row, col + 1) if col < 8 else (row + 1, 0)
|
||||
if board[row][col] != ".":
|
||||
return self.backtracking(
|
||||
next_row, next_col, board, row_used, col_used, box_used
|
||||
)
|
||||
|
||||
for num in map(str, range(1, 10)):
|
||||
if (
|
||||
num not in row_used[row]
|
||||
and num not in col_used[col]
|
||||
and num not in box_used[(row // 3) * 3 + col // 3]
|
||||
):
|
||||
board[row][col] = num
|
||||
row_used[row].add(num)
|
||||
col_used[col].add(num)
|
||||
box_used[(row // 3) * 3 + col // 3].add(num)
|
||||
if self.backtracking(
|
||||
next_row, next_col, board, row_used, col_used, box_used
|
||||
):
|
||||
return True
|
||||
board[row][col] = "."
|
||||
row_used[row].remove(num)
|
||||
col_used[col].remove(num)
|
||||
box_used[(row // 3) * 3 + col // 3].remove(num)
|
||||
return False
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
@ -474,7 +474,128 @@ class Solution:
|
||||
|
||||
### Go:
|
||||
|
||||
> 单调栈
|
||||
暴力解法
|
||||
|
||||
```go
|
||||
func largestRectangleArea(heights []int) int {
|
||||
sum := 0
|
||||
for i := 0; i < len(heights); i++ {
|
||||
left, right := i, i
|
||||
for left >= 0 {
|
||||
if heights[left] < heights[i] {
|
||||
break
|
||||
}
|
||||
left--
|
||||
}
|
||||
for right < len(heights) {
|
||||
if heights[right] < heights[i] {
|
||||
break
|
||||
}
|
||||
right++
|
||||
}
|
||||
w := right - left - 1
|
||||
h := heights[i]
|
||||
sum = max(sum, w * h)
|
||||
}
|
||||
return sum
|
||||
}
|
||||
|
||||
func max(x, y int) int {
|
||||
if x > y {
|
||||
return x
|
||||
}
|
||||
return y
|
||||
}
|
||||
```
|
||||
|
||||
双指针解法
|
||||
|
||||
```go
|
||||
func largestRectangleArea(heights []int) int {
|
||||
size := len(heights)
|
||||
minLeftIndex := make([]int, size)
|
||||
minRightIndex := make([]int, size)
|
||||
|
||||
// 记录每个柱子 左边第一个小于该柱子的下标
|
||||
minLeftIndex[0] = -1 // 注意这里初始化,防止下面while死循环
|
||||
for i := 1; i < size; i++ {
|
||||
t := i - 1
|
||||
// 这里不是用if,而是不断向左寻找的过程
|
||||
for t >= 0 && heights[t] >= heights[i] {
|
||||
t = minLeftIndex[t]
|
||||
}
|
||||
minLeftIndex[i] = t
|
||||
}
|
||||
// 记录每个柱子 右边第一个小于该柱子的下标
|
||||
minRightIndex[size - 1] = size; // 注意这里初始化,防止下面while死循环
|
||||
for i := size - 2; i >= 0; i-- {
|
||||
t := i + 1
|
||||
// 这里不是用if,而是不断向右寻找的过程
|
||||
for t < size && heights[t] >= heights[i] {
|
||||
t = minRightIndex[t]
|
||||
}
|
||||
minRightIndex[i] = t
|
||||
}
|
||||
// 求和
|
||||
result := 0
|
||||
for i := 0; i < size; i++ {
|
||||
sum := heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1)
|
||||
result = max(sum, result)
|
||||
}
|
||||
return result
|
||||
}
|
||||
|
||||
func max(x, y int) int {
|
||||
if x > y {
|
||||
return x
|
||||
}
|
||||
return y
|
||||
}
|
||||
```
|
||||
|
||||
单调栈
|
||||
|
||||
```go
|
||||
func largestRectangleArea(heights []int) int {
|
||||
result := 0
|
||||
heights = append([]int{0}, heights...) // 数组头部加入元素0
|
||||
heights = append(heights, 0) // 数组尾部加入元素0
|
||||
st := []int{0}
|
||||
|
||||
// 第一个元素已经入栈,从下标1开始
|
||||
for i := 1; i < len(heights); i++ {
|
||||
if heights[i] > heights[st[len(st)-1]] {
|
||||
st = append(st, i)
|
||||
} else if heights[i] == heights[st[len(st)-1]] {
|
||||
st = st[:len(st)-1]
|
||||
st = append(st, i)
|
||||
} else {
|
||||
for len(st) > 0 && heights[i] < heights[st[len(st)-1]] {
|
||||
mid := st[len(st)-1]
|
||||
st = st[:len(st)-1]
|
||||
if len(st) > 0 {
|
||||
left := st[len(st)-1]
|
||||
right := i
|
||||
w := right - left - 1
|
||||
h := heights[mid]
|
||||
result = max(result, w * h)
|
||||
}
|
||||
}
|
||||
st = append(st, i)
|
||||
}
|
||||
}
|
||||
return result
|
||||
}
|
||||
|
||||
func max(x, y int) int {
|
||||
if x > y {
|
||||
return x
|
||||
}
|
||||
return y
|
||||
}
|
||||
```
|
||||
|
||||
单调栈精简
|
||||
|
||||
```go
|
||||
func largestRectangleArea(heights []int) int {
|
||||
|
||||
@ -38,7 +38,7 @@ public:
|
||||
cur = head;
|
||||
int i = 1;
|
||||
int j = vec.size() - 1; // i j为之前前后的双指针
|
||||
int count = 0; // 计数,偶数去后面,奇数取前面
|
||||
int count = 0; // 计数,偶数取后面,奇数取前面
|
||||
while (i <= j) {
|
||||
if (count % 2 == 0) {
|
||||
cur->next = vec[j];
|
||||
@ -73,7 +73,7 @@ public:
|
||||
}
|
||||
|
||||
cur = head;
|
||||
int count = 0; // 计数,偶数去后面,奇数取前面
|
||||
int count = 0; // 计数,偶数取后面,奇数取前面
|
||||
ListNode* node;
|
||||
while(que.size()) {
|
||||
if (count % 2 == 0) {
|
||||
@ -338,8 +338,85 @@ class Solution:
|
||||
return pre
|
||||
```
|
||||
### Go
|
||||
|
||||
```go
|
||||
# 方法三 分割链表
|
||||
// 方法一 数组模拟
|
||||
/**
|
||||
* Definition for singly-linked list.
|
||||
* type ListNode struct {
|
||||
* Val int
|
||||
* Next *ListNode
|
||||
* }
|
||||
*/
|
||||
func reorderList(head *ListNode) {
|
||||
vec := make([]*ListNode, 0)
|
||||
cur := head
|
||||
if cur == nil {
|
||||
return
|
||||
}
|
||||
for cur != nil {
|
||||
vec = append(vec, cur)
|
||||
cur = cur.Next
|
||||
}
|
||||
cur = head
|
||||
i := 1
|
||||
j := len(vec) - 1 // i j为前后的双指针
|
||||
count := 0 // 计数,偶数取后面,奇数取前面
|
||||
for i <= j {
|
||||
if count % 2 == 0 {
|
||||
cur.Next = vec[j]
|
||||
j--
|
||||
} else {
|
||||
cur.Next = vec[i]
|
||||
i++
|
||||
}
|
||||
cur = cur.Next
|
||||
count++
|
||||
}
|
||||
cur.Next = nil // 注意结尾
|
||||
}
|
||||
```
|
||||
|
||||
```go
|
||||
// 方法二 双向队列模拟
|
||||
/**
|
||||
* Definition for singly-linked list.
|
||||
* type ListNode struct {
|
||||
* Val int
|
||||
* Next *ListNode
|
||||
* }
|
||||
*/
|
||||
func reorderList(head *ListNode) {
|
||||
que := make([]*ListNode, 0)
|
||||
cur := head
|
||||
if cur == nil {
|
||||
return
|
||||
}
|
||||
|
||||
for cur.Next != nil {
|
||||
que = append(que, cur.Next)
|
||||
cur = cur.Next
|
||||
}
|
||||
|
||||
cur = head
|
||||
count := 0 // 计数,偶数取后面,奇数取前面
|
||||
for len(que) > 0 {
|
||||
if count % 2 == 0 {
|
||||
cur.Next = que[len(que)-1]
|
||||
que = que[:len(que)-1]
|
||||
} else {
|
||||
cur.Next = que[0]
|
||||
que = que[1:]
|
||||
}
|
||||
count++
|
||||
cur = cur.Next
|
||||
}
|
||||
cur.Next = nil // 注意结尾
|
||||
}
|
||||
```
|
||||
|
||||
```go
|
||||
// 方法三 分割链表
|
||||
func reorderList(head *ListNode) {
|
||||
var slow=head
|
||||
var fast=head
|
||||
|
||||
@ -337,6 +337,37 @@ public ListNode removeElements(ListNode head, int val) {
|
||||
|
||||
```
|
||||
|
||||
递归
|
||||
|
||||
```java
|
||||
/**
|
||||
* 时间复杂度 O(n)
|
||||
* 空间复杂度 O(n)
|
||||
* @param head
|
||||
* @param val
|
||||
* @return
|
||||
*/
|
||||
class Solution {
|
||||
public ListNode removeElements(ListNode head, int val) {
|
||||
if (head == null) {
|
||||
return head;
|
||||
}
|
||||
|
||||
// 假设 removeElements() 返回后面完整的已经去掉val节点的子链表
|
||||
// 在当前递归层用当前节点接住后面的子链表
|
||||
// 随后判断当前层的node是否需要被删除,如果是,就返回
|
||||
// 也可以先判断是否需要删除当前node,但是这样条件语句会比较不好想
|
||||
head.next = removeElements(head.next, val);
|
||||
if (head.val == val) {
|
||||
return head.next;
|
||||
}
|
||||
return head;
|
||||
|
||||
// 实际上就是还原一个从尾部开始重新构建链表的过程
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Python:
|
||||
|
||||
```python
|
||||
|
||||
@ -45,7 +45,7 @@
|
||||
|
||||
那么二叉树如何可以自底向上查找呢?
|
||||
|
||||
回溯啊,二叉树回溯的过程就是从低到上。
|
||||
回溯啊,二叉树回溯的过程就是从底到上。
|
||||
|
||||
后序遍历(左右中)就是天然的回溯过程,可以根据左右子树的返回值,来处理中节点的逻辑。
|
||||
|
||||
|
||||
@ -172,7 +172,7 @@ if (result.size() == ticketNum + 1) {
|
||||
|
||||
回溯的过程中,如何遍历一个机场所对应的所有机场呢?
|
||||
|
||||
这里刚刚说过,在选择映射函数的时候,不能选择`unordered_map<string, multiset<string>> targets`, 因为一旦有元素增删multiset的迭代器就会失效,当然可能有牛逼的容器删除元素迭代器不会失效,这里就不在讨论了。
|
||||
这里刚刚说过,在选择映射函数的时候,不能选择`unordered_map<string, multiset<string>> targets`, 因为一旦有元素增删multiset的迭代器就会失效,当然可能有牛逼的容器删除元素迭代器不会失效,这里就不再讨论了。
|
||||
|
||||
**可以说本题既要找到一个对数据进行排序的容器,而且还要容易增删元素,迭代器还不能失效**。
|
||||
|
||||
|
||||
@ -72,7 +72,7 @@
|
||||
|
||||
#### 情况一:上下坡中有平坡
|
||||
|
||||
例如 [1,2,2,2,1]这样的数组,如图:
|
||||
例如 [1,2,2,2,2,1]这样的数组,如图:
|
||||
|
||||
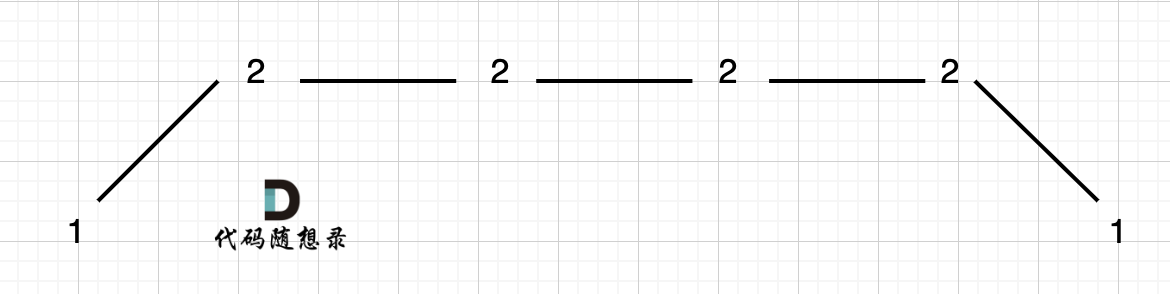
|
||||
|
||||
|
||||
@ -801,6 +801,40 @@ impl Solution {
|
||||
}
|
||||
```
|
||||
|
||||
### Ruby
|
||||
> 递归法:
|
||||
```ruby
|
||||
# @param {TreeNode} root
|
||||
# @param {Integer} key
|
||||
# @return {TreeNode}
|
||||
def delete_node(root, key)
|
||||
return nil if root.nil?
|
||||
|
||||
right = root.right
|
||||
left = root.left
|
||||
|
||||
if root.val == key
|
||||
return right if left.nil?
|
||||
return left if right.nil?
|
||||
|
||||
node = right
|
||||
while node.left
|
||||
node = node.left
|
||||
end
|
||||
node.left = left
|
||||
|
||||
return right
|
||||
end
|
||||
|
||||
if root.val > key
|
||||
root.left = delete_node(left, key)
|
||||
else
|
||||
root.right = delete_node(right, key)
|
||||
end
|
||||
|
||||
return root
|
||||
end
|
||||
```
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
|
||||
@ -706,6 +706,31 @@ class Solution:
|
||||
```
|
||||
|
||||
### Go
|
||||
回溯法思路
|
||||
```go
|
||||
func findTargetSumWays(nums []int, target int) int {
|
||||
var result int
|
||||
var backtracking func(nums []int, target int, index int, currentSum int)
|
||||
|
||||
backtracking = func(nums []int, target int, index int, currentSum int) {
|
||||
if index == len(nums) {
|
||||
if currentSum == target {
|
||||
result++
|
||||
}
|
||||
return
|
||||
}
|
||||
|
||||
// 选择加上当前数字
|
||||
backtracking(nums, target, index+1, currentSum+nums[index])
|
||||
|
||||
// 选择减去当前数字
|
||||
backtracking(nums, target, index+1, currentSum-nums[index])
|
||||
}
|
||||
|
||||
backtracking(nums, target, 0, 0)
|
||||
return result
|
||||
}
|
||||
```
|
||||
二维dp
|
||||
```go
|
||||
func findTargetSumWays(nums []int, target int) int {
|
||||
|
||||
@ -422,38 +422,38 @@ void myLinkedListFree(MyLinkedList* obj) {
|
||||
|
||||
```Java
|
||||
//单链表
|
||||
class ListNode {
|
||||
int val;
|
||||
ListNode next;
|
||||
ListNode(){}
|
||||
ListNode(int val) {
|
||||
this.val=val;
|
||||
}
|
||||
}
|
||||
class MyLinkedList {
|
||||
|
||||
class ListNode {
|
||||
int val;
|
||||
ListNode next;
|
||||
ListNode(int val) {
|
||||
this.val=val;
|
||||
}
|
||||
}
|
||||
//size存储链表元素的个数
|
||||
int size;
|
||||
//虚拟头结点
|
||||
ListNode head;
|
||||
private int size;
|
||||
//注意这里记录的是虚拟头结点
|
||||
private ListNode head;
|
||||
|
||||
//初始化链表
|
||||
public MyLinkedList() {
|
||||
size = 0;
|
||||
head = new ListNode(0);
|
||||
this.size = 0;
|
||||
this.head = new ListNode(0);
|
||||
}
|
||||
|
||||
//获取第index个节点的数值,注意index是从0开始的,第0个节点就是头结点
|
||||
//获取第index个节点的数值,注意index是从0开始的,第0个节点就是虚拟头结点
|
||||
public int get(int index) {
|
||||
//如果index非法,返回-1
|
||||
if (index < 0 || index >= size) {
|
||||
return -1;
|
||||
}
|
||||
ListNode currentNode = head;
|
||||
//包含一个虚拟头节点,所以查找第 index+1 个节点
|
||||
ListNode cur = head;
|
||||
//第0个节点是虚拟头节点,所以查找第 index+1 个节点
|
||||
for (int i = 0; i <= index; i++) {
|
||||
currentNode = currentNode.next;
|
||||
cur = cur.next;
|
||||
}
|
||||
return currentNode.val;
|
||||
return cur.val;
|
||||
}
|
||||
|
||||
public void addAtHead(int val) {
|
||||
@ -473,7 +473,6 @@ class MyLinkedList {
|
||||
while (cur.next != null) {
|
||||
cur = cur.next;
|
||||
}
|
||||
|
||||
cur.next = newNode;
|
||||
size++;
|
||||
|
||||
@ -485,55 +484,53 @@ class MyLinkedList {
|
||||
// 如果 index 等于链表的长度,则说明是新插入的节点为链表的尾结点
|
||||
// 如果 index 大于链表的长度,则返回空
|
||||
public void addAtIndex(int index, int val) {
|
||||
if (index > size) {
|
||||
if (index < 0 || index > size) {
|
||||
return;
|
||||
}
|
||||
if (index < 0) {
|
||||
index = 0;
|
||||
}
|
||||
size++;
|
||||
|
||||
//找到要插入节点的前驱
|
||||
ListNode pred = head;
|
||||
ListNode pre = head;
|
||||
for (int i = 0; i < index; i++) {
|
||||
pred = pred.next;
|
||||
pre = pre.next;
|
||||
}
|
||||
ListNode toAdd = new ListNode(val);
|
||||
toAdd.next = pred.next;
|
||||
pred.next = toAdd;
|
||||
ListNode newNode = new ListNode(val);
|
||||
newNode.next = pre.next;
|
||||
pre.next = newNode;
|
||||
size++;
|
||||
}
|
||||
|
||||
//删除第index个节点
|
||||
public void deleteAtIndex(int index) {
|
||||
if (index < 0 || index >= size) {
|
||||
return;
|
||||
}
|
||||
size--;
|
||||
//因为有虚拟头节点,所以不用对Index=0的情况进行特殊处理
|
||||
ListNode pred = head;
|
||||
|
||||
//因为有虚拟头节点,所以不用对index=0的情况进行特殊处理
|
||||
ListNode pre = head;
|
||||
for (int i = 0; i < index ; i++) {
|
||||
pred = pred.next;
|
||||
pre = pre.next;
|
||||
}
|
||||
pred.next = pred.next.next;
|
||||
pre.next = pre.next.next;
|
||||
size--;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```Java
|
||||
//双链表
|
||||
class ListNode{
|
||||
int val;
|
||||
ListNode next,prev;
|
||||
ListNode() {};
|
||||
ListNode(int val){
|
||||
this.val = val;
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
class MyLinkedList {
|
||||
|
||||
class ListNode{
|
||||
int val;
|
||||
ListNode next, prev;
|
||||
ListNode(int val){
|
||||
this.val = val;
|
||||
}
|
||||
}
|
||||
|
||||
//记录链表中元素的数量
|
||||
int size;
|
||||
private int size;
|
||||
//记录链表的虚拟头结点和尾结点
|
||||
ListNode head,tail;
|
||||
private ListNode head, tail;
|
||||
|
||||
public MyLinkedList() {
|
||||
//初始化操作
|
||||
@ -541,25 +538,25 @@ class MyLinkedList {
|
||||
this.head = new ListNode(0);
|
||||
this.tail = new ListNode(0);
|
||||
//这一步非常关键,否则在加入头结点的操作中会出现null.next的错误!!!
|
||||
head.next=tail;
|
||||
tail.prev=head;
|
||||
this.head.next = tail;
|
||||
this.tail.prev = head;
|
||||
}
|
||||
|
||||
public int get(int index) {
|
||||
//判断index是否有效
|
||||
if(index>=size){
|
||||
if(index < 0 || index >= size){
|
||||
return -1;
|
||||
}
|
||||
ListNode cur = this.head;
|
||||
ListNode cur = head;
|
||||
//判断是哪一边遍历时间更短
|
||||
if(index >= size / 2){
|
||||
//tail开始
|
||||
cur = tail;
|
||||
for(int i=0; i< size-index; i++){
|
||||
for(int i = 0; i < size - index; i++){
|
||||
cur = cur.prev;
|
||||
}
|
||||
}else{
|
||||
for(int i=0; i<= index; i++){
|
||||
for(int i = 0; i <= index; i++){
|
||||
cur = cur.next;
|
||||
}
|
||||
}
|
||||
@ -568,24 +565,23 @@ class MyLinkedList {
|
||||
|
||||
public void addAtHead(int val) {
|
||||
//等价于在第0个元素前添加
|
||||
addAtIndex(0,val);
|
||||
addAtIndex(0, val);
|
||||
}
|
||||
|
||||
public void addAtTail(int val) {
|
||||
//等价于在最后一个元素(null)前添加
|
||||
addAtIndex(size,val);
|
||||
addAtIndex(size, val);
|
||||
}
|
||||
|
||||
public void addAtIndex(int index, int val) {
|
||||
//index大于链表长度
|
||||
if(index>size){
|
||||
//判断index是否有效
|
||||
if(index < 0 || index > size){
|
||||
return;
|
||||
}
|
||||
|
||||
size++;
|
||||
//找到前驱
|
||||
ListNode pre = this.head;
|
||||
for(int i=0; i<index; i++){
|
||||
ListNode pre = head;
|
||||
for(int i = 0; i < index; i++){
|
||||
pre = pre.next;
|
||||
}
|
||||
//新建结点
|
||||
@ -594,22 +590,24 @@ class MyLinkedList {
|
||||
pre.next.prev = newNode;
|
||||
newNode.prev = pre;
|
||||
pre.next = newNode;
|
||||
size++;
|
||||
|
||||
}
|
||||
|
||||
public void deleteAtIndex(int index) {
|
||||
//判断索引是否有效
|
||||
if(index>=size){
|
||||
//判断index是否有效
|
||||
if(index < 0 || index >= size){
|
||||
return;
|
||||
}
|
||||
|
||||
//删除操作
|
||||
size--;
|
||||
ListNode pre = this.head;
|
||||
for(int i=0; i<index; i++){
|
||||
ListNode pre = head;
|
||||
for(int i = 0; i < index; i++){
|
||||
pre = pre.next;
|
||||
}
|
||||
pre.next.next.prev = pre;
|
||||
pre.next = pre.next.next;
|
||||
size--;
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
@ -190,9 +190,9 @@ class Solution:
|
||||
贪心(版本一)
|
||||
```python
|
||||
class Solution:
|
||||
def monotoneIncreasingDigits(self, N: int) -> int:
|
||||
def monotoneIncreasingDigits(self, n: int) -> int:
|
||||
# 将整数转换为字符串
|
||||
strNum = str(N)
|
||||
strNum = str(n)
|
||||
# flag用来标记赋值9从哪里开始
|
||||
# 设置为字符串长度,为了防止第二个for循环在flag没有被赋值的情况下执行
|
||||
flag = len(strNum)
|
||||
@ -216,9 +216,9 @@ class Solution:
|
||||
贪心(版本二)
|
||||
```python
|
||||
class Solution:
|
||||
def monotoneIncreasingDigits(self, N: int) -> int:
|
||||
def monotoneIncreasingDigits(self, n: int) -> int:
|
||||
# 将整数转换为字符串
|
||||
strNum = list(str(N))
|
||||
strNum = list(str(n))
|
||||
|
||||
# 从右往左遍历字符串
|
||||
for i in range(len(strNum) - 1, 0, -1):
|
||||
@ -238,9 +238,9 @@ class Solution:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def monotoneIncreasingDigits(self, N: int) -> int:
|
||||
def monotoneIncreasingDigits(self, n: int) -> int:
|
||||
# 将整数转换为字符串
|
||||
strNum = list(str(N))
|
||||
strNum = list(str(n))
|
||||
|
||||
# 从右往左遍历字符串
|
||||
for i in range(len(strNum) - 1, 0, -1):
|
||||
@ -258,8 +258,8 @@ class Solution:
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def monotoneIncreasingDigits(self, N: int) -> int:
|
||||
strNum = str(N)
|
||||
def monotoneIncreasingDigits(self, n: int) -> int:
|
||||
strNum = str(n)
|
||||
for i in range(len(strNum) - 1, 0, -1):
|
||||
# 如果当前字符比前一个字符小,说明需要修改前一个字符
|
||||
if strNum[i - 1] > strNum[i]:
|
||||
@ -272,12 +272,12 @@ class Solution:
|
||||
```
|
||||
### Go
|
||||
```go
|
||||
func monotoneIncreasingDigits(N int) int {
|
||||
func monotoneIncreasingDigits(n int) int {
|
||||
s := strconv.Itoa(N)//将数字转为字符串,方便使用下标
|
||||
ss := []byte(s)//将字符串转为byte数组,方便更改。
|
||||
n := len(ss)
|
||||
if n <= 1 {
|
||||
return N
|
||||
return n
|
||||
}
|
||||
for i := n-1; i > 0; i-- {
|
||||
if ss[i-1] > ss[i] { //前一个大于后一位,前一位减1,后面的全部置为9
|
||||
|
||||
@ -11,9 +11,9 @@
|
||||
|
||||
[力扣题目链接](https://leetcode.cn/problems/sort-array-by-parity-ii/)
|
||||
|
||||
给定一个非负整数数组 A, A 中一半整数是奇数,一半整数是偶数。
|
||||
给定一个非负整数数组 nums, nums 中一半整数是奇数,一半整数是偶数。
|
||||
|
||||
对数组进行排序,以便当 A[i] 为奇数时,i 也是奇数;当 A[i] 为偶数时, i 也是偶数。
|
||||
对数组进行排序,以便当 nums[i] 为奇数时,i 也是奇数;当 nums[i] 为偶数时, i 也是偶数。
|
||||
|
||||
你可以返回任何满足上述条件的数组作为答案。
|
||||
|
||||
@ -35,17 +35,17 @@
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> sortArrayByParityII(vector<int>& A) {
|
||||
vector<int> even(A.size() / 2); // 初始化就确定数组大小,节省开销
|
||||
vector<int> odd(A.size() / 2);
|
||||
vector<int> result(A.size());
|
||||
vector<int> sortArrayByParityII(vector<int>& nums) {
|
||||
vector<int> even(nums.size() / 2); // 初始化就确定数组大小,节省开销
|
||||
vector<int> odd(nums.size() / 2);
|
||||
vector<int> result(nums.size());
|
||||
int evenIndex = 0;
|
||||
int oddIndex = 0;
|
||||
int resultIndex = 0;
|
||||
// 把A数组放进偶数数组,和奇数数组
|
||||
for (int i = 0; i < A.size(); i++) {
|
||||
if (A[i] % 2 == 0) even[evenIndex++] = A[i];
|
||||
else odd[oddIndex++] = A[i];
|
||||
// 把nums数组放进偶数数组,和奇数数组
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
if (nums[i] % 2 == 0) even[evenIndex++] = nums[i];
|
||||
else odd[oddIndex++] = nums[i];
|
||||
}
|
||||
// 把偶数数组,奇数数组分别放进result数组中
|
||||
for (int i = 0; i < evenIndex; i++) {
|
||||
@ -62,22 +62,22 @@ public:
|
||||
|
||||
### 方法二
|
||||
|
||||
以上代码我是建了两个辅助数组,而且A数组还相当于遍历了两次,用辅助数组的好处就是思路清晰,优化一下就是不用这两个辅助树,代码如下:
|
||||
以上代码我是建了两个辅助数组,而且nums数组还相当于遍历了两次,用辅助数组的好处就是思路清晰,优化一下就是不用这两个辅助数组,代码如下:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> sortArrayByParityII(vector<int>& A) {
|
||||
vector<int> result(A.size());
|
||||
vector<int> sortArrayByParityII(vector<int>& nums) {
|
||||
vector<int> result(nums.size());
|
||||
int evenIndex = 0; // 偶数下标
|
||||
int oddIndex = 1; // 奇数下标
|
||||
for (int i = 0; i < A.size(); i++) {
|
||||
if (A[i] % 2 == 0) {
|
||||
result[evenIndex] = A[i];
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
if (nums[i] % 2 == 0) {
|
||||
result[evenIndex] = nums[i];
|
||||
evenIndex += 2;
|
||||
}
|
||||
else {
|
||||
result[oddIndex] = A[i];
|
||||
result[oddIndex] = nums[i];
|
||||
oddIndex += 2;
|
||||
}
|
||||
}
|
||||
@ -96,15 +96,15 @@ public:
|
||||
```CPP
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> sortArrayByParityII(vector<int>& A) {
|
||||
vector<int> sortArrayByParityII(vector<int>& nums) {
|
||||
int oddIndex = 1;
|
||||
for (int i = 0; i < A.size(); i += 2) {
|
||||
if (A[i] % 2 == 1) { // 在偶数位遇到了奇数
|
||||
while(A[oddIndex] % 2 != 0) oddIndex += 2; // 在奇数位找一个偶数
|
||||
swap(A[i], A[oddIndex]); // 替换
|
||||
for (int i = 0; i < nums.size(); i += 2) {
|
||||
if (nums[i] % 2 == 1) { // 在偶数位遇到了奇数
|
||||
while(nums[oddIndex] % 2 != 0) oddIndex += 2; // 在奇数位找一个偶数
|
||||
swap(nums[i], nums[oddIndex]); // 替换
|
||||
}
|
||||
}
|
||||
return A;
|
||||
return nums;
|
||||
}
|
||||
};
|
||||
```
|
||||
@ -253,6 +253,37 @@ func sortArrayByParityII(nums []int) []int {
|
||||
}
|
||||
return result;
|
||||
}
|
||||
|
||||
// 方法二
|
||||
func sortArrayByParityII(nums []int) []int {
|
||||
result := make([]int, len(nums))
|
||||
evenIndex := 0 // 偶数下标
|
||||
oddIndex := 1 // 奇数下标
|
||||
for _, v := range nums {
|
||||
if v % 2 == 0 {
|
||||
result[evenIndex] = v
|
||||
evenIndex += 2
|
||||
} else {
|
||||
result[oddIndex] = v
|
||||
oddIndex += 2
|
||||
}
|
||||
}
|
||||
return result
|
||||
}
|
||||
|
||||
// 方法三
|
||||
func sortArrayByParityII(nums []int) []int {
|
||||
oddIndex := 1
|
||||
for i := 0; i < len(nums); i += 2 {
|
||||
if nums[i] % 2 == 1 { // 在偶数位遇到了奇数
|
||||
for nums[oddIndex] % 2 != 0 {
|
||||
oddIndex += 2 // 在奇数位找一个偶数
|
||||
}
|
||||
nums[i], nums[oddIndex] = nums[oddIndex], nums[i]
|
||||
}
|
||||
}
|
||||
return nums
|
||||
}
|
||||
```
|
||||
|
||||
### JavaScript
|
||||
|
||||
@ -388,6 +388,62 @@ if __name__ == "__main__":
|
||||
main()
|
||||
|
||||
```
|
||||
|
||||
### JavaScript
|
||||
|
||||
前缀和
|
||||
```js
|
||||
function func() {
|
||||
const readline = require('readline')
|
||||
const rl = readline.createInterface({
|
||||
input: process.stdin,
|
||||
output: process.stdout
|
||||
})
|
||||
let inputLines = []
|
||||
rl.on('line', function (line) {
|
||||
inputLines.push(line.trim())
|
||||
})
|
||||
|
||||
rl.on('close', function () {
|
||||
let [n, m] = inputLines[0].split(" ").map(Number)
|
||||
let c = new Array(n).fill(0)
|
||||
let r = new Array(m).fill(0)
|
||||
let arr = new Array(n)
|
||||
let sum = 0//数组总和
|
||||
let min = Infinity//设置最小值的初始值为无限大
|
||||
//定义数组
|
||||
for (let s = 0; s < n; s++) {
|
||||
arr[s] = inputLines[s + 1].split(" ").map(Number)
|
||||
}
|
||||
//每一行的和
|
||||
for (let i = 0; i < n; i++) {
|
||||
for (let j = 0; j < m; j++) {
|
||||
c[i] += arr[i][j]
|
||||
sum += arr[i][j]
|
||||
}
|
||||
}
|
||||
//每一列的和
|
||||
for (let i = 0; i < n; i++) {
|
||||
for (let j = 0; j < m; j++) {
|
||||
r[j] += arr[i][j]
|
||||
}
|
||||
}
|
||||
let sum1 = 0, sum2 = 0
|
||||
//横向切割
|
||||
for (let i = 0; i < n; i++) {
|
||||
sum1 += c[i]
|
||||
min = min < Math.abs(sum - 2 * sum1) ? min : Math.abs(sum - 2 * sum1)
|
||||
}
|
||||
//纵向切割
|
||||
for (let j = 0; j < m; j++) {
|
||||
sum2 += r[j]
|
||||
min = min < Math.abs(sum - 2 * sum2) ? min : Math.abs(sum - 2 * sum2)
|
||||
}
|
||||
console.log(min);
|
||||
})
|
||||
}
|
||||
```
|
||||
|
||||
### C
|
||||
|
||||
前缀和
|
||||
|
||||
@ -333,6 +333,8 @@ public class Main {
|
||||
|
||||
### Python
|
||||
|
||||
Bellman-Ford方法求解含有负回路的最短路问题
|
||||
|
||||
```python
|
||||
import sys
|
||||
|
||||
@ -388,6 +390,52 @@ if __name__ == "__main__":
|
||||
|
||||
```
|
||||
|
||||
SPFA方法求解含有负回路的最短路问题
|
||||
|
||||
```python
|
||||
from collections import deque
|
||||
from math import inf
|
||||
|
||||
def main():
|
||||
n, m = [int(i) for i in input().split()]
|
||||
graph = [[] for _ in range(n+1)]
|
||||
min_dist = [inf for _ in range(n+1)]
|
||||
count = [0 for _ in range(n+1)] # 记录节点加入队列的次数
|
||||
for _ in range(m):
|
||||
s, t, v = [int(i) for i in input().split()]
|
||||
graph[s].append([t, v])
|
||||
|
||||
min_dist[1] = 0 # 初始化
|
||||
count[1] = 1
|
||||
d = deque([1])
|
||||
flag = False
|
||||
|
||||
while d: # 主循环
|
||||
cur_node = d.popleft()
|
||||
for next_node, val in graph[cur_node]:
|
||||
if min_dist[next_node] > min_dist[cur_node] + val:
|
||||
min_dist[next_node] = min_dist[cur_node] + val
|
||||
count[next_node] += 1
|
||||
if next_node not in d:
|
||||
d.append(next_node)
|
||||
if count[next_node] == n: # 如果某个点松弛了n次,说明有负回路
|
||||
flag = True
|
||||
if flag:
|
||||
break
|
||||
|
||||
if flag:
|
||||
print("circle")
|
||||
else:
|
||||
if min_dist[-1] == inf:
|
||||
print("unconnected")
|
||||
else:
|
||||
print(min_dist[-1])
|
||||
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
### Rust
|
||||
|
||||
@ -702,7 +702,129 @@ public class Main {
|
||||
|
||||
```
|
||||
|
||||
```java
|
||||
class Edge {
|
||||
public int u; // 边的端点1
|
||||
public int v; // 边的端点2
|
||||
public int val; // 边的权值
|
||||
|
||||
public Edge() {
|
||||
}
|
||||
|
||||
public Edge(int u, int v) {
|
||||
this.u = u;
|
||||
this.v = v;
|
||||
this.val = 0;
|
||||
}
|
||||
|
||||
public Edge(int u, int v, int val) {
|
||||
this.u = u;
|
||||
this.v = v;
|
||||
this.val = val;
|
||||
}
|
||||
}
|
||||
|
||||
/**
|
||||
* SPFA算法(版本3):处理含【负权回路】的有向图的最短路径问题
|
||||
* bellman_ford(版本3) 的队列优化算法版本
|
||||
* 限定起点、终点、至多途径k个节点
|
||||
*/
|
||||
public class SPFAForSSSP {
|
||||
|
||||
/**
|
||||
* SPFA算法
|
||||
*
|
||||
* @param n 节点个数[1,n]
|
||||
* @param graph 邻接表
|
||||
* @param startIdx 开始节点(源点)
|
||||
*/
|
||||
public static int[] spfa(int n, List<List<Edge>> graph, int startIdx, int k) {
|
||||
// 定义最大范围
|
||||
int maxVal = Integer.MAX_VALUE;
|
||||
// minDist[i] 源点到节点i的最短距离
|
||||
int[] minDist = new int[n + 1]; // 有效节点编号范围:[1,n]
|
||||
Arrays.fill(minDist, maxVal); // 初始化为maxVal
|
||||
minDist[startIdx] = 0; // 设置源点到源点的最短路径为0
|
||||
|
||||
// 定义queue记录每一次松弛更新的节点
|
||||
Queue<Integer> queue = new LinkedList<>();
|
||||
queue.offer(startIdx); // 初始化:源点开始(queue和minDist的更新是同步的)
|
||||
|
||||
|
||||
// SPFA算法核心:只对上一次松弛的时候更新过的节点关联的边进行松弛操作
|
||||
while (k + 1 > 0 && !queue.isEmpty()) { // 限定松弛 k+1 次
|
||||
int curSize = queue.size(); // 记录当前队列节点个数(上一次松弛更新的节点个数,用作分层统计)
|
||||
while (curSize-- > 0) { //分层控制,限定本次松弛只针对上一次松弛更新的节点,不对新增的节点做处理
|
||||
// 记录当前minDist状态,作为本次松弛的基础
|
||||
int[] minDist_copy = Arrays.copyOfRange(minDist, 0, minDist.length);
|
||||
|
||||
// 取出节点
|
||||
int cur = queue.poll();
|
||||
// 获取cur节点关联的边,进行松弛操作
|
||||
List<Edge> relateEdges = graph.get(cur);
|
||||
for (Edge edge : relateEdges) {
|
||||
int u = edge.u; // 与`cur`对照
|
||||
int v = edge.v;
|
||||
int weight = edge.val;
|
||||
if (minDist_copy[u] + weight < minDist[v]) {
|
||||
minDist[v] = minDist_copy[u] + weight; // 更新
|
||||
// 队列同步更新(此处有一个针对队列的优化:就是如果已经存在于队列的元素不需要重复添加)
|
||||
if (!queue.contains(v)) {
|
||||
queue.offer(v); // 与minDist[i]同步更新,将本次更新的节点加入队列,用做下一个松弛的参考基础
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
// 当次松弛结束,次数-1
|
||||
k--;
|
||||
}
|
||||
|
||||
// 返回minDist
|
||||
return minDist;
|
||||
}
|
||||
|
||||
public static void main(String[] args) {
|
||||
// 输入控制
|
||||
Scanner sc = new Scanner(System.in);
|
||||
System.out.println("1.输入N个节点、M条边(u v weight)");
|
||||
int n = sc.nextInt();
|
||||
int m = sc.nextInt();
|
||||
|
||||
System.out.println("2.输入M条边");
|
||||
List<List<Edge>> graph = new ArrayList<>(); // 构建邻接表
|
||||
for (int i = 0; i <= n; i++) {
|
||||
graph.add(new ArrayList<>());
|
||||
}
|
||||
while (m-- > 0) {
|
||||
int u = sc.nextInt();
|
||||
int v = sc.nextInt();
|
||||
int weight = sc.nextInt();
|
||||
graph.get(u).add(new Edge(u, v, weight));
|
||||
}
|
||||
|
||||
System.out.println("3.输入src dst k(起点、终点、至多途径k个点)");
|
||||
int src = sc.nextInt();
|
||||
int dst = sc.nextInt();
|
||||
int k = sc.nextInt();
|
||||
|
||||
// 调用算法
|
||||
int[] minDist = SPFAForSSSP.spfa(n, graph, src, k);
|
||||
// 校验起点->终点
|
||||
if (minDist[dst] == Integer.MAX_VALUE) {
|
||||
System.out.println("unreachable");
|
||||
} else {
|
||||
System.out.println("最短路径:" + minDist[n]);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### Python
|
||||
|
||||
Bellman-Ford方法求解单源有限最短路
|
||||
|
||||
```python
|
||||
def main():
|
||||
# 輸入
|
||||
@ -736,6 +858,48 @@ def main():
|
||||
|
||||
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
```
|
||||
|
||||
SPFA方法求解单源有限最短路
|
||||
|
||||
```python
|
||||
from collections import deque
|
||||
from math import inf
|
||||
|
||||
|
||||
def main():
|
||||
n, m = [int(i) for i in input().split()]
|
||||
graph = [[] for _ in range(n+1)]
|
||||
for _ in range(m):
|
||||
v1, v2, val = [int(i) for i in input().split()]
|
||||
graph[v1].append([v2, val])
|
||||
src, dst, k = [int(i) for i in input().split()]
|
||||
min_dist = [inf for _ in range(n+1)]
|
||||
min_dist[src] = 0 # 初始化起点的距离
|
||||
que = deque([src])
|
||||
|
||||
while k != -1 and que:
|
||||
visited = [False for _ in range(n+1)] # 用于保证每次松弛时一个节点最多加入队列一次
|
||||
que_size = len(que)
|
||||
temp_dist = min_dist.copy() # 用于记录上一次遍历的结果
|
||||
for _ in range(que_size):
|
||||
cur_node = que.popleft()
|
||||
for next_node, val in graph[cur_node]:
|
||||
if min_dist[next_node] > temp_dist[cur_node] + val:
|
||||
min_dist[next_node] = temp_dist[cur_node] + val
|
||||
if not visited[next_node]:
|
||||
que.append(next_node)
|
||||
visited[next_node] = True
|
||||
k -= 1
|
||||
|
||||
if min_dist[dst] == inf:
|
||||
print("unreachable")
|
||||
else:
|
||||
print(min_dist[dst])
|
||||
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
```
|
||||
|
||||
@ -424,6 +424,71 @@ floyd算法的时间复杂度相对较高,适合 稠密图且源点较多的
|
||||
|
||||
### Java
|
||||
|
||||
- 基于三维数组的Floyd算法
|
||||
|
||||
```java
|
||||
public class FloydBase {
|
||||
|
||||
// public static int MAX_VAL = Integer.MAX_VALUE;
|
||||
public static int MAX_VAL = 10005; // 边的最大距离是10^4(不选用Integer.MAX_VALUE是为了避免相加导致数值溢出)
|
||||
|
||||
public static void main(String[] args) {
|
||||
// 输入控制
|
||||
Scanner sc = new Scanner(System.in);
|
||||
System.out.println("1.输入N M");
|
||||
int n = sc.nextInt();
|
||||
int m = sc.nextInt();
|
||||
|
||||
System.out.println("2.输入M条边");
|
||||
|
||||
// ① dp定义(grid[i][j][k] 节点i到节点j 可能经过节点K(k∈[1,n]))的最短路径
|
||||
int[][][] grid = new int[n + 1][n + 1][n + 1];
|
||||
for (int i = 1; i <= n; i++) {
|
||||
for (int j = 1; j <= n; j++) {
|
||||
for (int k = 0; k <= n; k++) {
|
||||
grid[i][j][k] = grid[j][i][k] = MAX_VAL; // 其余设置为最大值
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// ② dp 推导:grid[i][j][k] = min{grid[i][k][k-1] + grid[k][j][k-1], grid[i][j][k-1]}
|
||||
while (m-- > 0) {
|
||||
int u = sc.nextInt();
|
||||
int v = sc.nextInt();
|
||||
int weight = sc.nextInt();
|
||||
grid[u][v][0] = grid[v][u][0] = weight; // 初始化(处理k=0的情况) ③ dp初始化
|
||||
}
|
||||
|
||||
// ④ dp推导:floyd 推导
|
||||
for (int k = 1; k <= n; k++) {
|
||||
for (int i = 1; i <= n; i++) {
|
||||
for (int j = 1; j <= n; j++) {
|
||||
grid[i][j][k] = Math.min(grid[i][k][k - 1] + grid[k][j][k - 1], grid[i][j][k - 1]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
System.out.println("3.输入[起点-终点]计划个数");
|
||||
int x = sc.nextInt();
|
||||
|
||||
System.out.println("4.输入每个起点src 终点dst");
|
||||
|
||||
while (x-- > 0) {
|
||||
int src = sc.nextInt();
|
||||
int dst = sc.nextInt();
|
||||
// 根据floyd推导结果输出计划路径的最小距离
|
||||
if (grid[src][dst][n] == MAX_VAL) {
|
||||
System.out.println("-1");
|
||||
} else {
|
||||
System.out.println(grid[src][dst][n]);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### Python
|
||||
|
||||
基于三维数组的Floyd
|
||||
|
||||
@ -257,6 +257,54 @@ public class Main {
|
||||
|
||||
|
||||
### Python
|
||||
#### 深搜版
|
||||
```python
|
||||
position = [[1, 0], [0, 1], [-1, 0], [0, -1]]
|
||||
count = 0
|
||||
|
||||
def dfs(grid, x, y):
|
||||
global count
|
||||
grid[x][y] = 0
|
||||
count += 1
|
||||
for i, j in position:
|
||||
next_x = x + i
|
||||
next_y = y + j
|
||||
if next_x < 0 or next_y < 0 or next_x >= len(grid) or next_y >= len(grid[0]):
|
||||
continue
|
||||
if grid[next_x][next_y] == 1:
|
||||
dfs(grid, next_x, next_y)
|
||||
|
||||
n, m = map(int, input().split())
|
||||
|
||||
# 邻接矩阵
|
||||
grid = []
|
||||
for i in range(n):
|
||||
grid.append(list(map(int, input().split())))
|
||||
|
||||
# 清除边界上的连通分量
|
||||
for i in range(n):
|
||||
if grid[i][0] == 1:
|
||||
dfs(grid, i, 0)
|
||||
if grid[i][m - 1] == 1:
|
||||
dfs(grid, i, m - 1)
|
||||
|
||||
for j in range(m):
|
||||
if grid[0][j] == 1:
|
||||
dfs(grid, 0, j)
|
||||
if grid[n - 1][j] == 1:
|
||||
dfs(grid, n - 1, j)
|
||||
|
||||
count = 0 # 将count重置为0
|
||||
# 统计内部所有剩余的连通分量
|
||||
for i in range(n):
|
||||
for j in range(m):
|
||||
if grid[i][j] == 1:
|
||||
dfs(grid, i, j)
|
||||
|
||||
print(count)
|
||||
```
|
||||
|
||||
#### 广搜版
|
||||
```python
|
||||
from collections import deque
|
||||
|
||||
@ -293,17 +341,22 @@ def bfs(r, c):
|
||||
|
||||
|
||||
for i in range(n):
|
||||
if g[i][0] == 1: bfs(i, 0)
|
||||
if g[i][m-1] == 1: bfs(i, m-1)
|
||||
if g[i][0] == 1:
|
||||
bfs(i, 0)
|
||||
if g[i][m-1] == 1:
|
||||
bfs(i, m-1)
|
||||
|
||||
for i in range(m):
|
||||
if g[0][i] == 1: bfs(0, i)
|
||||
if g[n-1][i] == 1: bfs(n-1, i)
|
||||
if g[0][i] == 1:
|
||||
bfs(0, i)
|
||||
if g[n-1][i] == 1:
|
||||
bfs(n-1, i)
|
||||
|
||||
count = 0
|
||||
for i in range(n):
|
||||
for j in range(m):
|
||||
if g[i][j] == 1: bfs(i, j)
|
||||
if g[i][j] == 1:
|
||||
bfs(i, j)
|
||||
|
||||
print(count)
|
||||
```
|
||||
|
||||
@ -413,6 +413,81 @@ if __name__ == "__main__":
|
||||
```
|
||||
|
||||
### Go
|
||||
```go
|
||||
package main
|
||||
|
||||
import (
|
||||
"os"
|
||||
"fmt"
|
||||
"strings"
|
||||
"strconv"
|
||||
"bufio"
|
||||
)
|
||||
|
||||
var directions = [][]int{{0, -1}, {0, 1}, {-1, 0}, {1, 0}} // 四个方向的偏移量
|
||||
|
||||
func main() {
|
||||
scanner := bufio.NewScanner(os.Stdin)
|
||||
|
||||
scanner.Scan()
|
||||
lineList := strings.Fields(scanner.Text())
|
||||
N, _ := strconv.Atoi(lineList[0])
|
||||
M, _ := strconv.Atoi(lineList[1])
|
||||
|
||||
grid := make([][]int, N)
|
||||
visited := make([][]bool, N) // 用于标记是否访问过
|
||||
for i := 0; i < N; i++ {
|
||||
grid[i] = make([]int, M)
|
||||
visited[i] = make([]bool, M)
|
||||
scanner.Scan()
|
||||
lineList = strings.Fields(scanner.Text())
|
||||
|
||||
for j := 0; j < M; j++ {
|
||||
grid[i][j], _ = strconv.Atoi(lineList[j])
|
||||
}
|
||||
}
|
||||
|
||||
// 遍历每个单元格,使用DFS检查是否可达两组边界
|
||||
for i := 0; i < N; i++ {
|
||||
for j := 0; j < M; j++ {
|
||||
canReachFirst, canReachSecond := dfs(grid, visited, i, j)
|
||||
if canReachFirst && canReachSecond {
|
||||
fmt.Println(strconv.Itoa(i) + " " + strconv.Itoa(j))
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
func dfs(grid [][]int, visited [][]bool, startx int, starty int) (bool, bool) {
|
||||
visited[startx][starty] = true
|
||||
canReachFirst := startx == 0 || starty == 0 || startx == len(grid)-1 || starty == len(grid[0])-1
|
||||
canReachSecond := startx == len(grid)-1 || starty == len(grid[0])-1 || startx == 0 || starty == 0
|
||||
|
||||
if canReachFirst && canReachSecond {
|
||||
return true, true
|
||||
}
|
||||
|
||||
for _, direction := range directions {
|
||||
nextx := startx + direction[0]
|
||||
nexty := starty + direction[1]
|
||||
|
||||
if nextx < 0 || nextx >= len(grid) || nexty < 0 || nexty >= len(grid[0]) {
|
||||
continue
|
||||
}
|
||||
|
||||
if grid[nextx][nexty] <= grid[startx][starty] && !visited[nextx][nexty] {
|
||||
hasReachFirst, hasReachSecond := dfs(grid, visited, nextx, nexty)
|
||||
if !canReachFirst {
|
||||
canReachFirst = hasReachFirst
|
||||
}
|
||||
if !canReachSecond {
|
||||
canReachSecond = hasReachSecond
|
||||
}
|
||||
}
|
||||
}
|
||||
return canReachFirst, canReachSecond
|
||||
}
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
|
||||
@ -491,6 +491,54 @@ func main() {
|
||||
|
||||
### JavaScript
|
||||
|
||||
```javascript
|
||||
const rl = require('readline').createInterface({
|
||||
input:process.stdin,
|
||||
output:process.stdout
|
||||
})
|
||||
|
||||
let inputLines = []
|
||||
|
||||
rl.on('line' , (line)=>{
|
||||
inputLines.push(line)
|
||||
})
|
||||
|
||||
rl.on('close',()=>{
|
||||
let [n , edgesCount]= inputLines[0].trim().split(' ').map(Number)
|
||||
|
||||
let graph = Array.from({length:n+1} , ()=>{return[]})
|
||||
|
||||
for(let i = 1 ; i < inputLines.length ; i++ ){
|
||||
let [from , to] = inputLines[i].trim().split(' ').map(Number)
|
||||
graph[from].push(to)
|
||||
}
|
||||
|
||||
let visited = new Array(n + 1).fill(false)
|
||||
|
||||
let dfs = (graph , key , visited)=>{
|
||||
if(visited[key]){
|
||||
return
|
||||
}
|
||||
|
||||
visited[key] = true
|
||||
for(let nextKey of graph[key]){
|
||||
dfs(graph,nextKey , visited)
|
||||
}
|
||||
}
|
||||
|
||||
dfs(graph , 1 , visited)
|
||||
|
||||
for(let i = 1 ; i <= n;i++){
|
||||
if(visited[i] === false){
|
||||
console.log(-1)
|
||||
return
|
||||
}
|
||||
}
|
||||
console.log(1)
|
||||
|
||||
})
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
@ -27,11 +27,16 @@
|
||||
|
||||
**那我们就将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。**
|
||||
|
||||
如何标记呢,**就是要处理的节点放入栈之后,紧接着放入一个空指针作为标记。** 这种方法也可以叫做标记法。
|
||||
如何标记呢?
|
||||
|
||||
* 方法一:**就是要处理的节点放入栈之后,紧接着放入一个空指针作为标记。** 这种方法可以叫做`空指针标记法`。
|
||||
|
||||
* 方法二:**加一个 `boolean` 值跟随每个节点,`false` (默认值) 表示需要为该节点和它的左右儿子安排在栈中的位次,`true` 表示该节点的位次之前已经安排过了,可以收割节点了。**
|
||||
这种方法可以叫做`boolean 标记法`,样例代码见下文`C++ 和 Python 的 boolean 标记法`。 这种方法更容易理解,在面试中更容易写出来。
|
||||
|
||||
### 迭代法中序遍历
|
||||
|
||||
中序遍历代码如下:(详细注释)
|
||||
> 中序遍历(空指针标记法)代码如下:(详细注释)
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -70,6 +75,45 @@ public:
|
||||
|
||||
可以看出我们将访问的节点直接加入到栈中,但如果是处理的节点则后面放入一个空节点, 这样只有空节点弹出的时候,才将下一个节点放进结果集。
|
||||
|
||||
> 中序遍历(boolean 标记法):
|
||||
```c++
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> inorderTraversal(TreeNode* root) {
|
||||
vector<int> result;
|
||||
stack<pair<TreeNode*, bool>> st;
|
||||
if (root != nullptr)
|
||||
st.push(make_pair(root, false)); // 多加一个参数,false 为默认值,含义见下文注释
|
||||
|
||||
while (!st.empty()) {
|
||||
auto node = st.top().first;
|
||||
auto visited = st.top().second; //多加一个 visited 参数,使“迭代统一写法”成为一件简单的事
|
||||
st.pop();
|
||||
|
||||
if (visited) { // visited 为 True,表示该节点和两个儿子位次之前已经安排过了,现在可以收割节点了
|
||||
result.push_back(node->val);
|
||||
continue;
|
||||
}
|
||||
|
||||
// visited 当前为 false, 表示初次访问本节点,此次访问的目的是“把自己和两个儿子在栈中安排好位次”。
|
||||
|
||||
// 中序遍历是'左中右',右儿子最先入栈,最后出栈。
|
||||
if (node->right)
|
||||
st.push(make_pair(node->right, false));
|
||||
|
||||
// 把自己加回到栈中,位置居中。
|
||||
// 同时,设置 visited 为 true,表示下次再访问本节点时,允许收割。
|
||||
st.push(make_pair(node, true));
|
||||
|
||||
if (node->left)
|
||||
st.push(make_pair(node->left, false)); // 左儿子最后入栈,最先出栈
|
||||
}
|
||||
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
此时我们再来看前序遍历代码。
|
||||
|
||||
### 迭代法前序遍历
|
||||
@ -105,7 +149,7 @@ public:
|
||||
|
||||
### 迭代法后序遍历
|
||||
|
||||
后续遍历代码如下: (**注意此时我们和中序遍历相比仅仅改变了两行代码的顺序**)
|
||||
> 后续遍历代码如下: (**注意此时我们和中序遍历相比仅仅改变了两行代码的顺序**)
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
@ -136,6 +180,42 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
> 迭代法后序遍历(boolean 标记法):
|
||||
```c++
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> postorderTraversal(TreeNode* root) {
|
||||
vector<int> result;
|
||||
stack<pair<TreeNode*, bool>> st;
|
||||
if (root != nullptr)
|
||||
st.push(make_pair(root, false)); // 多加一个参数,false 为默认值,含义见下文
|
||||
|
||||
while (!st.empty()) {
|
||||
auto node = st.top().first;
|
||||
auto visited = st.top().second; //多加一个 visited 参数,使“迭代统一写法”成为一件简单的事
|
||||
st.pop();
|
||||
|
||||
if (visited) { // visited 为 True,表示该节点和两个儿子位次之前已经安排过了,现在可以收割节点了
|
||||
result.push_back(node->val);
|
||||
continue;
|
||||
}
|
||||
|
||||
// visited 当前为 false, 表示初次访问本节点,此次访问的目的是“把自己和两个儿子在栈中安排好位次”。
|
||||
// 后序遍历是'左右中',节点自己最先入栈,最后出栈。
|
||||
// 同时,设置 visited 为 true,表示下次再访问本节点时,允许收割。
|
||||
st.push(make_pair(node, true));
|
||||
|
||||
if (node->right)
|
||||
st.push(make_pair(node->right, false)); // 右儿子位置居中
|
||||
|
||||
if (node->left)
|
||||
st.push(make_pair(node->left, false)); // 左儿子最后入栈,最先出栈
|
||||
}
|
||||
|
||||
return result;
|
||||
}
|
||||
};
|
||||
```
|
||||
## 总结
|
||||
|
||||
此时我们写出了统一风格的迭代法,不用在纠结于前序写出来了,中序写不出来的情况了。
|
||||
@ -234,7 +314,7 @@ class Solution {
|
||||
|
||||
### Python:
|
||||
|
||||
迭代法前序遍历:
|
||||
> 迭代法前序遍历(空指针标记法):
|
||||
```python
|
||||
class Solution:
|
||||
def preorderTraversal(self, root: TreeNode) -> List[int]:
|
||||
@ -257,7 +337,7 @@ class Solution:
|
||||
return result
|
||||
```
|
||||
|
||||
迭代法中序遍历:
|
||||
> 迭代法中序遍历(空指针标记法):
|
||||
```python
|
||||
class Solution:
|
||||
def inorderTraversal(self, root: TreeNode) -> List[int]:
|
||||
@ -282,7 +362,7 @@ class Solution:
|
||||
return result
|
||||
```
|
||||
|
||||
迭代法后序遍历:
|
||||
> 迭代法后序遍历(空指针标记法):
|
||||
```python
|
||||
class Solution:
|
||||
def postorderTraversal(self, root: TreeNode) -> List[int]:
|
||||
@ -306,6 +386,61 @@ class Solution:
|
||||
return result
|
||||
```
|
||||
|
||||
> 中序遍历,统一迭代(boolean 标记法):
|
||||
```python
|
||||
class Solution:
|
||||
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
|
||||
values = []
|
||||
stack = [(root, False)] if root else [] # 多加一个参数,False 为默认值,含义见下文
|
||||
|
||||
while stack:
|
||||
node, visited = stack.pop() # 多加一个 visited 参数,使“迭代统一写法”成为一件简单的事
|
||||
|
||||
if visited: # visited 为 True,表示该节点和两个儿子的位次之前已经安排过了,现在可以收割节点了
|
||||
values.append(node.val)
|
||||
continue
|
||||
|
||||
# visited 当前为 False, 表示初次访问本节点,此次访问的目的是“把自己和两个儿子在栈中安排好位次”。
|
||||
# 中序遍历是'左中右',右儿子最先入栈,最后出栈。
|
||||
if node.right:
|
||||
stack.append((node.right, False))
|
||||
|
||||
stack.append((node, True)) # 把自己加回到栈中,位置居中。同时,设置 visited 为 True,表示下次再访问本节点时,允许收割
|
||||
|
||||
if node.left:
|
||||
stack.append((node.left, False)) # 左儿子最后入栈,最先出栈
|
||||
|
||||
return values
|
||||
```
|
||||
|
||||
> 后序遍历,统一迭代(boolean 标记法):
|
||||
```python
|
||||
class Solution:
|
||||
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
|
||||
values = []
|
||||
stack = [(root, False)] if root else [] # 多加一个参数,False 为默认值,含义见下文
|
||||
|
||||
while stack:
|
||||
node, visited = stack.pop() # 多加一个 visited 参数,使“迭代统一写法”成为一件简单的事
|
||||
|
||||
if visited: # visited 为 True,表示该节点和两个儿子位次之前已经安排过了,现在可以收割节点了
|
||||
values.append(node.val)
|
||||
continue
|
||||
|
||||
# visited 当前为 False, 表示初次访问本节点,此次访问的目的是“把自己和两个儿子在栈中安排好位次”
|
||||
# 后序遍历是'左右中',节点自己最先入栈,最后出栈。
|
||||
# 同时,设置 visited 为 True,表示下次再访问本节点时,允许收割。
|
||||
stack.append((node, True))
|
||||
|
||||
if node.right:
|
||||
stack.append((node.right, False)) # 右儿子位置居中
|
||||
|
||||
if node.left:
|
||||
stack.append((node.left, False)) # 左儿子最后入栈,最先出栈
|
||||
|
||||
return values
|
||||
```
|
||||
|
||||
### Go:
|
||||
|
||||
> 前序遍历统一迭代法
|
||||
|
||||
@ -240,14 +240,14 @@ class Solution {
|
||||
# 前序遍历-迭代-LC144_二叉树的前序遍历
|
||||
class Solution:
|
||||
def preorderTraversal(self, root: TreeNode) -> List[int]:
|
||||
# 根结点为空则返回空列表
|
||||
# 根节点为空则返回空列表
|
||||
if not root:
|
||||
return []
|
||||
stack = [root]
|
||||
result = []
|
||||
while stack:
|
||||
node = stack.pop()
|
||||
# 中结点先处理
|
||||
# 中节点先处理
|
||||
result.append(node.val)
|
||||
# 右孩子先入栈
|
||||
if node.right:
|
||||
@ -262,25 +262,27 @@ class Solution:
|
||||
# 中序遍历-迭代-LC94_二叉树的中序遍历
|
||||
class Solution:
|
||||
def inorderTraversal(self, root: TreeNode) -> List[int]:
|
||||
|
||||
if not root:
|
||||
return []
|
||||
stack = [] # 不能提前将root结点加入stack中
|
||||
stack = [] # 不能提前将root节点加入stack中
|
||||
|
||||
result = []
|
||||
cur = root
|
||||
while cur or stack:
|
||||
# 先迭代访问最底层的左子树结点
|
||||
# 先迭代访问最底层的左子树节点
|
||||
if cur:
|
||||
stack.append(cur)
|
||||
cur = cur.left
|
||||
# 到达最左结点后处理栈顶结点
|
||||
# 到达最左节点后处理栈顶节点
|
||||
else:
|
||||
cur = stack.pop()
|
||||
result.append(cur.val)
|
||||
# 取栈顶元素右结点
|
||||
# 取栈顶元素右节点
|
||||
cur = cur.right
|
||||
return result
|
||||
```
|
||||
```python
|
||||
```python
|
||||
|
||||
# 后序遍历-迭代-LC145_二叉树的后序遍历
|
||||
class Solution:
|
||||
@ -291,7 +293,7 @@ class Solution:
|
||||
result = []
|
||||
while stack:
|
||||
node = stack.pop()
|
||||
# 中结点先处理
|
||||
# 中节点先处理
|
||||
result.append(node.val)
|
||||
# 左孩子先入栈
|
||||
if node.left:
|
||||
@ -303,6 +305,44 @@ class Solution:
|
||||
return result[::-1]
|
||||
```
|
||||
|
||||
#### Python 后序遍历的迭代新解法:
|
||||
* 本解法不同于前文介绍的`逆转前序遍历调整后的结果`,而是采用了对每个节点直接处理。这个实现方法在面试中不容易写出来,在下一节,我将改造本代码,奉上代码更简洁、更套路化、更容易实现的统一方法。
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
|
||||
values = []
|
||||
stack = []
|
||||
popped_nodes = set() # 记录值已经被收割了的 nodes,这是关键,已经被收割的节点还在树中,还会被访问到,但逻辑上已经等同于 null 节点。
|
||||
current = root
|
||||
|
||||
while current or stack:
|
||||
if current: # 一次处理完一个节点和他的左右儿子节点,不处理孙子节点,孙子节点由左右儿子等会分别处理。
|
||||
stack.append(current) # 入栈自己
|
||||
|
||||
if current.right:
|
||||
stack.append(current.right) # 入栈右儿子
|
||||
|
||||
if current.left: # 因为栈是后进先出,后序是‘左右中’,所以后加左儿子
|
||||
stack.append(current.left) # 入栈左儿子
|
||||
|
||||
current = None # 会导致后面A处出栈
|
||||
continue
|
||||
|
||||
node = stack.pop() # A处,出的是左儿子,如果无左儿子,出的就是右儿子,如果连右儿子也没有,出的就是自己了。
|
||||
|
||||
# 如果 node 是叶子节点,就可以收割了;如果左右儿子都已经被收割了,也可以收割
|
||||
if (node.left is None or node.left in popped_nodes) and \
|
||||
(node.right is None or node.right in popped_nodes):
|
||||
popped_nodes.add(node)
|
||||
values.append(node.val)
|
||||
continue
|
||||
|
||||
current = node # 不符合收割条件,说明 node 下还有未入栈的儿子,就去入栈
|
||||
|
||||
return values
|
||||
```
|
||||
|
||||
### Go:
|
||||
|
||||
> 迭代法前序遍历
|
||||
|
||||
@ -75,7 +75,7 @@ for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target;
|
||||
|
||||
除了这些难点,**本题还有细节,例如:切割过的地方不能重复切割所以递归函数需要传入i + 1**。
|
||||
|
||||
所以本题应该是一个道hard题目了。
|
||||
所以本题应该是一道hard题目了。
|
||||
|
||||
**本题的树形结构中,和代码的逻辑有一个小出入,已经判断不是回文的子串就不会进入递归了,纠正如下:**
|
||||
|
||||
|
||||
@ -107,7 +107,7 @@ cd a/b/c/../../
|
||||
设计单调队列的时候,pop,和push操作要保持如下规则:
|
||||
|
||||
1. pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
|
||||
2. push(value):如果push的元素value大于入口元素的数值,那么就将队列出口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
|
||||
2. push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
|
||||
|
||||
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
|
||||
|
||||
|
||||
@ -78,7 +78,7 @@
|
||||
* 求解每一个子问题的最优解
|
||||
* 将局部最优解堆叠成全局最优解
|
||||
|
||||
这个四步其实过于理论化了,我们平时在做贪心类的题目 很难去按照这四步去思考,真是有点“鸡肋”。
|
||||
这个四步其实过于理论化了,我们平时在做贪心类的题目时,如果按照这四步去思考,真是有点“鸡肋”。
|
||||
|
||||
做题的时候,只要想清楚 局部最优 是什么,如果推导出全局最优,其实就够了。
|
||||
|
||||
|
||||
Reference in New Issue
Block a user