mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-12 13:36:33 +08:00
0051.N皇后:优化排版,补充Swift版本
This commit is contained in:
@ -33,7 +33,7 @@ n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,
|
||||
**如果对回溯算法基础还不了解的话,我还特意录制了一期视频:[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/)** 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
|
||||
|
||||
|
||||
都知道n皇后问题是回溯算法解决的经典问题,但是用回溯解决多了组合、切割、子集、排列问题之后,遇到这种二位矩阵还会有点不知所措。
|
||||
都知道n皇后问题是回溯算法解决的经典问题,但是用回溯解决多了组合、切割、子集、排列问题之后,遇到这种二维矩阵还会有点不知所措。
|
||||
|
||||
首先来看一下皇后们的约束条件:
|
||||
|
||||
@ -43,7 +43,7 @@ n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,
|
||||
|
||||
确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。
|
||||
|
||||
下面我用一个3 * 3 的棋牌,将搜索过程抽象为一颗树,如图:
|
||||
下面我用一个 3 * 3 的棋盘,将搜索过程抽象为一颗树,如图:
|
||||
|
||||
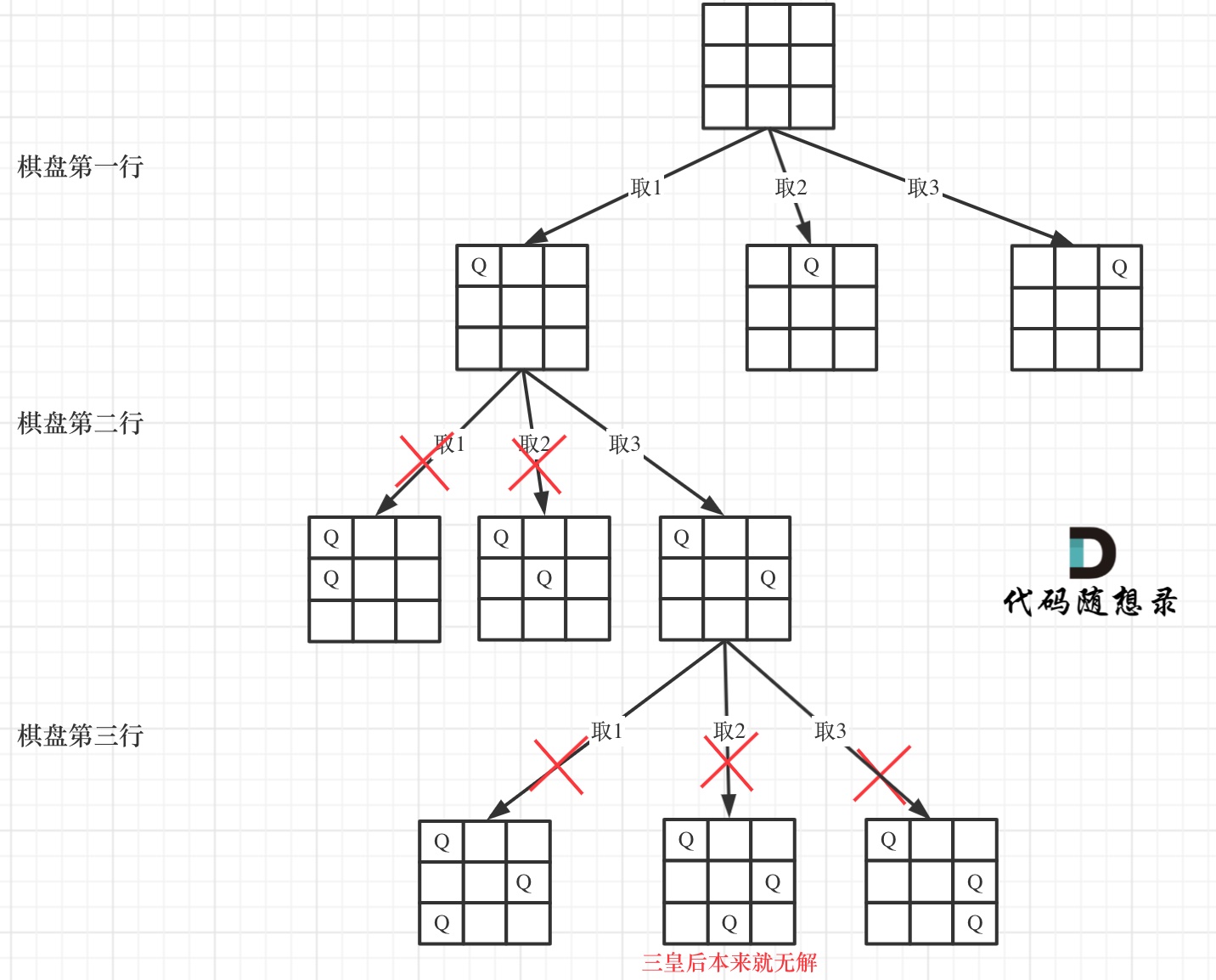
|
||||
|
||||
@ -73,11 +73,11 @@ void backtracking(参数) {
|
||||
|
||||
我依然是定义全局变量二维数组result来记录最终结果。
|
||||
|
||||
参数n是棋牌的大小,然后用row来记录当前遍历到棋盘的第几层了。
|
||||
参数n是棋盘的大小,然后用row来记录当前遍历到棋盘的第几层了。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
```cpp
|
||||
vector<vector<string>> result;
|
||||
void backtracking(int n, int row, vector<string>& chessboard) {
|
||||
```
|
||||
@ -92,7 +92,7 @@ void backtracking(int n, int row, vector<string>& chessboard) {
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
```cpp
|
||||
if (row == n) {
|
||||
result.push_back(chessboard);
|
||||
return;
|
||||
@ -107,7 +107,7 @@ if (row == n) {
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
```cpp
|
||||
for (int col = 0; col < n; col++) {
|
||||
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
|
||||
chessboard[row][col] = 'Q'; // 放置皇后
|
||||
@ -117,7 +117,7 @@ for (int col = 0; col < n; col++) {
|
||||
}
|
||||
```
|
||||
|
||||
* 验证棋牌是否合法
|
||||
* 验证棋盘是否合法
|
||||
|
||||
按照如下标准去重:
|
||||
|
||||
@ -163,7 +163,7 @@ class Solution {
|
||||
private:
|
||||
vector<vector<string>> result;
|
||||
// n 为输入的棋盘大小
|
||||
// row 是当前递归到棋牌的第几行了
|
||||
// row 是当前递归到棋盘的第几行了
|
||||
void backtracking(int n, int row, vector<string>& chessboard) {
|
||||
if (row == n) {
|
||||
result.push_back(chessboard);
|
||||
@ -470,7 +470,56 @@ var solveNQueens = function(n) {
|
||||
};
|
||||
```
|
||||
|
||||
### Swift
|
||||
|
||||
```swift
|
||||
func solveNQueens(_ n: Int) -> [[String]] {
|
||||
var result = [[String]]()
|
||||
// 棋盘,使用Character的二维数组,以便于更新元素
|
||||
var chessboard = [[Character]](repeating: [Character](repeating: ".", count: n), count: n)
|
||||
// 检查棋盘是否符合N皇后
|
||||
func isVaild(row: Int, col: Int) -> Bool {
|
||||
// 检查列
|
||||
for i in 0 ..< row {
|
||||
if chessboard[i][col] == "Q" { return false }
|
||||
}
|
||||
|
||||
var i, j: Int
|
||||
// 检查45度
|
||||
i = row - 1
|
||||
j = col - 1
|
||||
while i >= 0, j >= 0 {
|
||||
if chessboard[i][j] == "Q" { return false }
|
||||
i -= 1
|
||||
j -= 1
|
||||
}
|
||||
// 检查135度
|
||||
i = row - 1
|
||||
j = col + 1
|
||||
while i >= 0, j < n {
|
||||
if chessboard[i][j] == "Q" { return false }
|
||||
i -= 1
|
||||
j += 1
|
||||
}
|
||||
|
||||
return true
|
||||
}
|
||||
func backtracking(row: Int) {
|
||||
if row == n {
|
||||
result.append(chessboard.map { String($0) })
|
||||
}
|
||||
|
||||
for col in 0 ..< n {
|
||||
guard isVaild(row: row, col: col) else { continue }
|
||||
chessboard[row][col] = "Q" // 放置皇后
|
||||
backtracking(row: row + 1)
|
||||
chessboard[row][col] = "." // 回溯
|
||||
}
|
||||
}
|
||||
backtracking(row: 0)
|
||||
return result
|
||||
}
|
||||
```
|
||||
|
||||
-----------------------
|
||||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>
|
||||
|
||||
Reference in New Issue
Block a user