Update

problems/0257.二叉树的所有路径.md

@@ -69,15 +69,15 @@ if (cur->left == NULL && cur->right == NULL) {
 
 再来看一下终止处理的逻辑。
 
-这里使用vector<int> 结构path来记录路径，所以要把vector<int> 结构的path转为string格式，再把这个string 放进 result里。
+这里使用`vector<int>` 结构path来记录路径，所以要把`vector<int>` 结构的path转为string格式，再把这个string 放进 result里。
 
-**那么为什么使用了vector<int> 结构来记录路径呢？**  因为在下面处理单层递归逻辑的时候，要做回溯，使用vector方便来做回溯。
+**那么为什么使用了`vector<int>` 结构来记录路径呢？**  因为在下面处理单层递归逻辑的时候，要做回溯，使用vector方便来做回溯。
 
 可能有的同学问了，我看有些人的代码也没有回溯啊。
 
 **其实是有回溯的，只不过隐藏在函数调用时的参数赋值里**，下文我还会提到。
 
-这里我们先使用vector<int>结构的path容器来记录路径，那么终止处理逻辑如下：
+这里我们先使用`vector<int>`结构的path容器来记录路径，那么终止处理逻辑如下：
 
 ```CPP
 if (cur->left == NULL && cur->right == NULL) { // 遇到叶子节点

problems/0509.斐波那契数.md

@@ -151,7 +151,7 @@ public:
 * 时间复杂度：O(2^n)
 * 空间复杂度：O(n)，算上了编程语言中实现递归的系统栈所占空间
 
-这个递归的时间复杂度大家画一下树形图就知道了，如果不清晰的同学，可以看这篇：[通过一道面试题目，讲一讲递归算法的时间复杂度！](https://programmercarl.com/前序/通过一道面试题目，讲一讲递归算法的时间复杂度！.html)
+这个递归的时间复杂度大家画一下树形图就知道了，如果不清晰的同学，可以看这篇：[通过一道面试题目，讲一讲递归算法的时间复杂度！](./前序/递归算法的时间复杂度.md)
 
 
 ## 总结

problems/kamacoder/0103.水流问题.md

@@ -162,16 +162,17 @@ int main() {
 
 同样从第二组边界的边上节点 逆流而上，将遍历过的节点也标记上。 
 
-然后**两方都标记过的节点就是既可以流太平洋也可以流大西洋的节点**。
+然后**两方都标记过的节点就是既可以流向第一组边界也可以流向第二组边界的节点**。
 
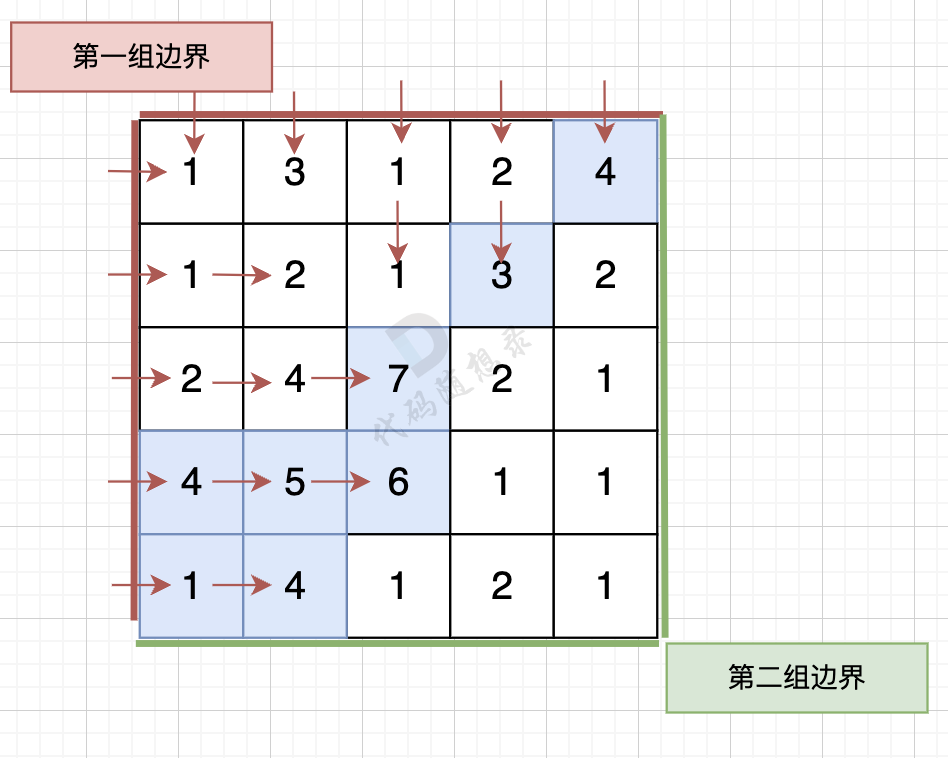
-从第一组边界边上节点出发，如图：  
+从第一组边界边上节点出发，如图：  （图中并没有把所有遍历的方向都画出来，只画关键部分）
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240522120036.png)
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20250304174747.png)
 
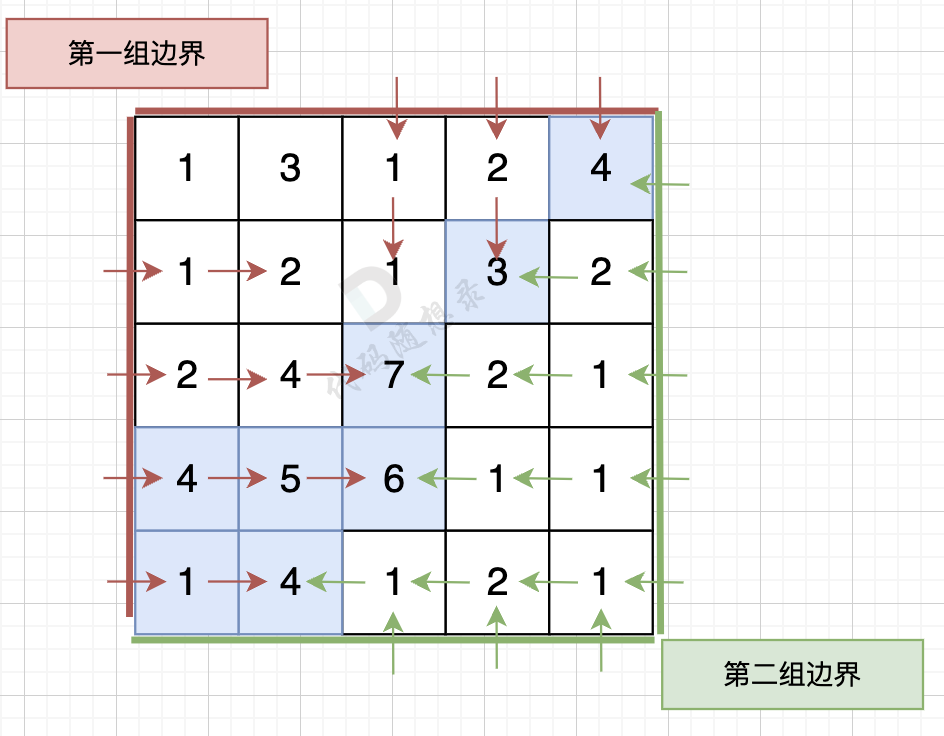
+从第二组边界上节点出发，如图： （图中并没有把所有遍历的方向都画出来，只画关键部分） 
 
-从第二组边界上节点出发，如图：  
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20250304174801.png)
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240522120122.png)
+最后，我们得到两个方向交界的这些节点，就是我们最后要求的节点。
 
 按照这样的逻辑，就可以写出如下遍历代码：（详细注释）
 

problems/kamacoder/0104.建造最大岛屿.md

@@ -72,7 +72,7 @@
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829104834.png)
 
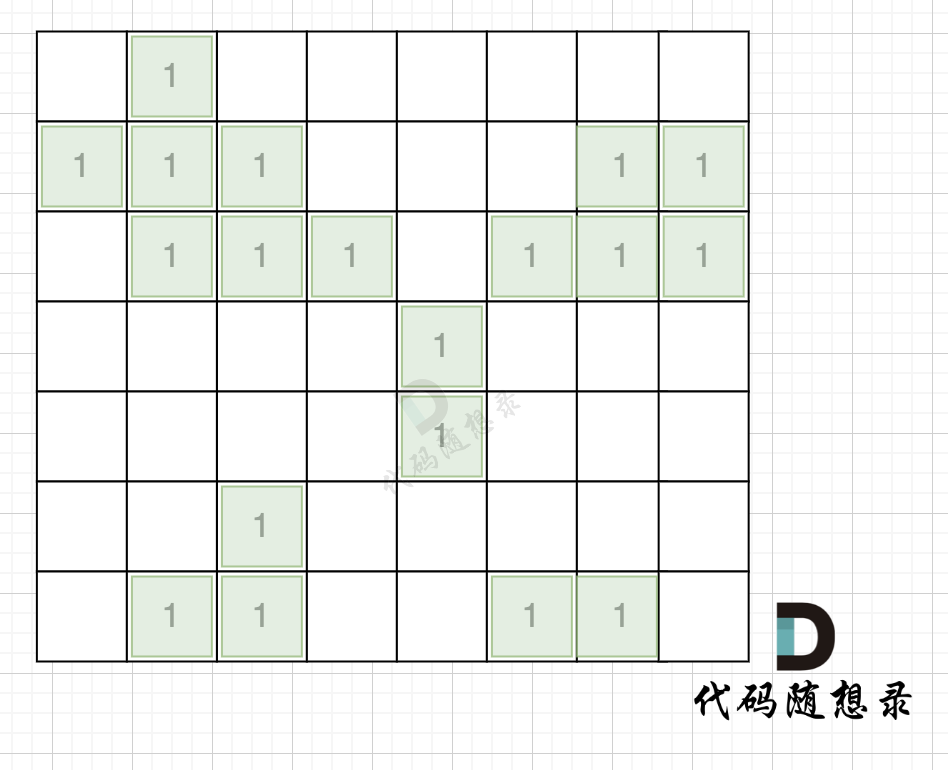
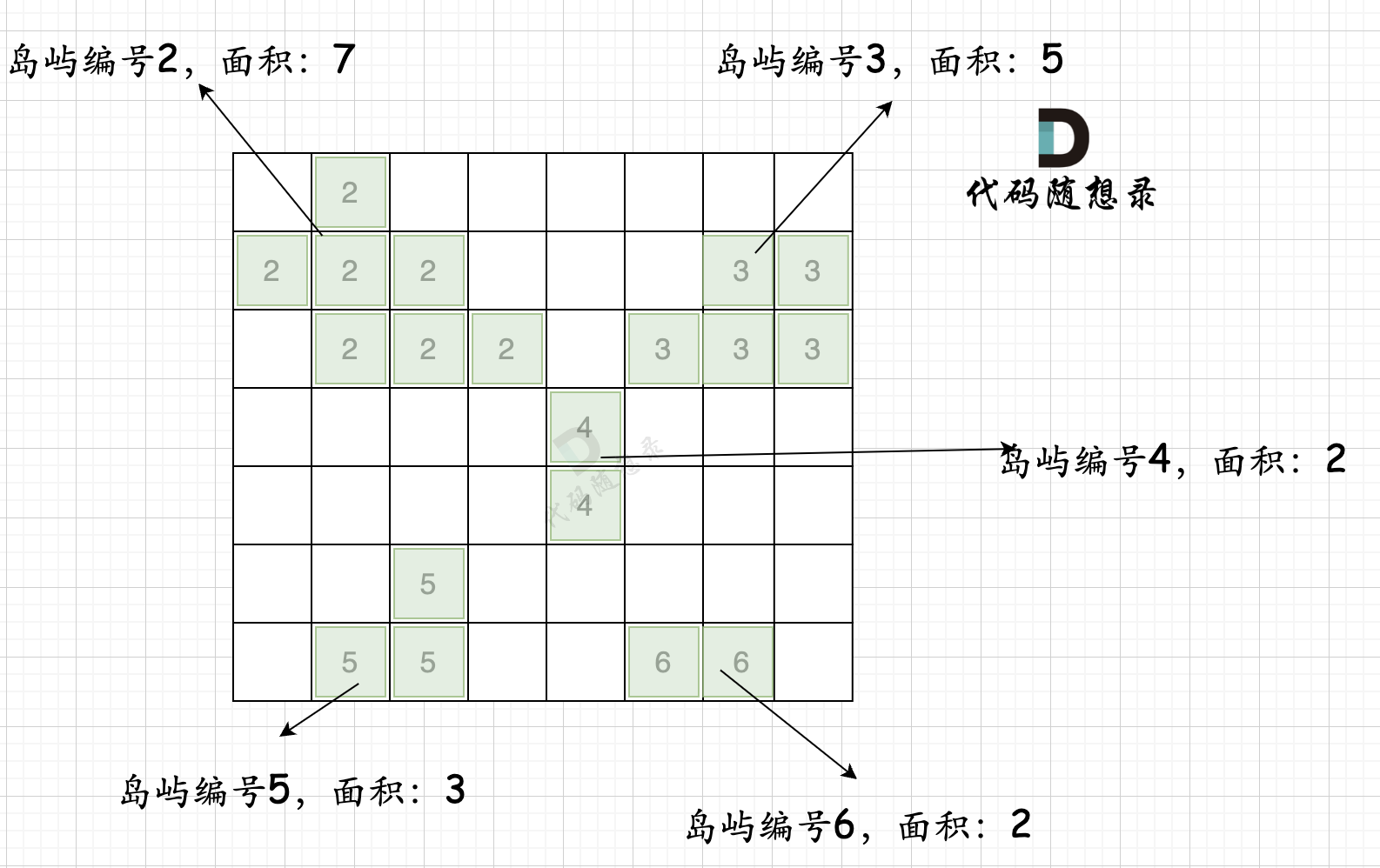
-第一步，则遍历题目，并将岛屿到编号和面积上的统计，过程如图所示： 
+第一步，则遍历地图，并将岛屿的编号和面积都统计好，过程如图所示： 
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829105644.png)