mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-08 00:43:04 +08:00
Update
This commit is contained in:
Binary file not shown.
|
Before Width: | Height: | Size: 127 KiB After Width: | Height: | Size: 142 KiB |
@ -48,7 +48,7 @@
|
||||
|
||||
按照左边界排序,就要从右向左遍历,因为左边界数值越大越好(越靠右),这样就给前一个区间的空间就越大,所以可以从右向左遍历。
|
||||
|
||||
如果按照左边界排序,还从左向右遍历的话,要处理各个区间右边界的各种情况,就很复杂了。
|
||||
如果按照左边界排序,还从左向右遍历的话,其实也可以,逻辑会有所不同。
|
||||
|
||||
一些同学做这道题目可能真的去模拟去重复区间的行为,这是比较麻烦的,还要去删除区间。
|
||||
|
||||
@ -126,7 +126,67 @@ public:
|
||||
|
||||
**所以我把本题的难点也一一列出,帮大家不仅代码看的懂,想法也理解的透彻!**
|
||||
|
||||
# 补充
|
||||
|
||||
本题其实和[贪心算法:用最少数量的箭引爆气球](https://mp.weixin.qq.com/s/HxVAJ6INMfNKiGwI88-RFw)非常像,弓箭的数量就相当于是非交叉区间的数量,只要把弓箭那道题目代码里射爆气球的判断条件加个等号(认为[0,1][1,2]不是相邻区间),然后用总区间数减去弓箭数量 就是要移除的区间数量了。
|
||||
|
||||
把[贪心算法:用最少数量的箭引爆气球](https://mp.weixin.qq.com/s/HxVAJ6INMfNKiGwI88-RFw)代码稍做修改,别可以AC本题。
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
// 按照区间右边界排序
|
||||
static bool cmp (const vector<int>& a, const vector<int>& b) {
|
||||
return a[1] < b[1];
|
||||
}
|
||||
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
|
||||
if (intervals.size() == 0) return 0;
|
||||
sort(intervals.begin(), intervals.end(), cmp);
|
||||
|
||||
int result = 1; // points 不为空至少需要一支箭
|
||||
for (int i = 1; i < intervals.size(); i++) {
|
||||
if (intervals[i][0] >= intervals[i - 1][1]) {
|
||||
result++; // 需要一支箭
|
||||
}
|
||||
else { // 气球i和气球i-1挨着
|
||||
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]); // 更新重叠气球最小右边界
|
||||
}
|
||||
}
|
||||
return intervals.size() - result;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
这里按照 作弊案件遍历,或者按照右边界遍历,都可以AC,具体原因我还没有仔细看,后面有空再补充。
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
// 按照区间左边界排序
|
||||
static bool cmp (const vector<int>& a, const vector<int>& b) {
|
||||
return a[0] < b[0];
|
||||
}
|
||||
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
|
||||
if (intervals.size() == 0) return 0;
|
||||
sort(intervals.begin(), intervals.end(), cmp);
|
||||
|
||||
int result = 1; // points 不为空至少需要一支箭
|
||||
for (int i = 1; i < intervals.size(); i++) {
|
||||
if (intervals[i][0] >= intervals[i - 1][1]) {
|
||||
result++; // 需要一支箭
|
||||
}
|
||||
else { // 气球i和气球i-1挨着
|
||||
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]); // 更新重叠气球最小右边界
|
||||
}
|
||||
}
|
||||
return intervals.size() - result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
循序渐进学算法,认准「代码随想录」就够了,值得介绍给身边的朋友同学们!
|
||||
|
||||
> 我是[程序员Carl](https://github.com/youngyangyang04),组队刷题可以找我,本文[leetcode刷题攻略](https://github.com/youngyangyang04/leetcode-master)已收录,更多[精彩算法文章](https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzUxNjY5NTYxNA==&action=getalbum&album_id=1485825793120387074&scene=173#wechat_redirect)尽在:[代码随想录](https://img-blog.csdnimg.cn/20200815195519696.png),期待你的关注!
|
||||
|
||||
|
||||
是不是尽可能重叠,其实它都在那里,没有尽可能这一说
|
||||
|
||||
@ -70,33 +70,68 @@ public:
|
||||
|
||||
## 动态规划
|
||||
|
||||
使用背包要明确dp[i]表示的是什么,i表示的又是什么?
|
||||
如何转化为01背包问题呢。
|
||||
|
||||
填满i(包括i)这么大容积的包,有dp[i]种方法。
|
||||
假设加法的总和为x,那么减法对应的总和就是sum - x。
|
||||
|
||||
所以我们要求的是 x - (sum - x) = S
|
||||
|
||||
x = (S + sum) / 2
|
||||
|
||||
此时问题就转化为,装满容量为x背包,有几种方法。
|
||||
|
||||
大家看到(S + sum) / 2 应该担心计算的过程中向下取整有没有影响。
|
||||
|
||||
这么担心就对了,例如sum 是5,S是2的话其实就是无解的,所以:
|
||||
|
||||
```
|
||||
if ((S + sum) % 2 == 1) return 0; // 此时没有方案,两个int相加的时候要各位小心数值溢出的问题
|
||||
```
|
||||
|
||||
看到这种表达式,应该本能的反应,两个int相加数值可能溢出的问题,当然本题并没有溢出。
|
||||
|
||||
在回归到01背包问题,
|
||||
|
||||
这次和之前遇到的背包问题不一样了,之前都是求容量为j的背包,最多能装多少。
|
||||
|
||||
本题是装满有几种方法。
|
||||
|
||||
* 确定dp数组以及下标的含义
|
||||
|
||||
dp[j] 表示:填满j(包括j)这么大容积的包,有dp[i]种方法
|
||||
|
||||
* 确定递推公式
|
||||
|
||||
有哪些来源可以推出dp[j]呢,只有dp[j - nums[i]]。
|
||||
|
||||
那么dp[j] 应该是 dp[j] + dp[j - nums[i]] (**这块需要好好讲讲**)
|
||||
|
||||
* dp数组如何初始化
|
||||
* 确定遍历顺序
|
||||
|
||||
```
|
||||
// 时间复杂度O(n^2)
|
||||
// 空间复杂度可以说是O(n),也可以说是O(1),因为每次申请的辅助数组的大小是一个常数
|
||||
class Solution {
|
||||
public:
|
||||
int findTargetSumWays(vector<int>& nums, int S) {
|
||||
int sum = 0;
|
||||
for (int i = 0; i < nums.size(); i++) sum += nums[i];
|
||||
if (S > sum) return 0; // 此时没有方案
|
||||
if ((S + sum) % 2) return 0; // 此时没有方案,两个int相加的时候要各位小心数值溢出的问题
|
||||
if ((S + sum) % 2 == 1) return 0; // 此时没有方案,两个int相加的时候要各位小心数值溢出的问题
|
||||
|
||||
int bagSize = (S + sum) / 2;
|
||||
int dp[1001] = {1};
|
||||
for (int i = 0; i < nums.size(); i++) {
|
||||
for (int j = bagSize; j >= nums[i]; j--) {
|
||||
if (j - nums[i] >= 0) dp[j] += dp[j - nums[i]];
|
||||
dp[j] += dp[j - nums[i]];
|
||||
}
|
||||
}
|
||||
return dp[bagSize];
|
||||
}
|
||||
};
|
||||
```
|
||||
* 时间复杂度O(n * m),n为正数个数,m为背包容量
|
||||
* 空间复杂度:O(n),也可以说是O(1),因为每次申请的辅助数组的大小是一个常数
|
||||
|
||||
dp数组中的数值变化:(从[0 - 4])
|
||||
|
||||
```
|
||||
|
||||
@ -1,22 +1,46 @@
|
||||
## 题目链接
|
||||
https://leetcode-cn.com/problems/partition-labels/
|
||||
> 看起来有点难,看仅仅是看起来难而已
|
||||
|
||||
## 思路
|
||||
# 763.划分字母区间
|
||||
|
||||
一想到分割字符串就想到了回溯,但本题其实不用那么复杂。
|
||||
题目链接: https://leetcode-cn.com/problems/partition-labels/
|
||||
|
||||
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
|
||||
|
||||
示例:
|
||||
输入:S = "ababcbacadefegdehijhklij"
|
||||
输出:[9,7,8]
|
||||
解释:
|
||||
划分结果为 "ababcbaca", "defegde", "hijhklij"。
|
||||
每个字母最多出现在一个片段中。
|
||||
像 "ababcbacadefegde", "hijhklij" 的划分是错误的,因为划分的片段数较少。
|
||||
|
||||
提示:
|
||||
|
||||
* S的长度在[1, 500]之间。
|
||||
* S只包含小写字母 'a' 到 'z' 。
|
||||
|
||||
# 思路
|
||||
|
||||
一想到分割字符串就想到了回溯,但本题其实不用回溯去暴力搜索。
|
||||
|
||||
题目要求同一字母最多出现在一个片段中,那么如何把同一个字母的都圈在同一个区间里呢?
|
||||
|
||||
如果没有接触过这种题目的话,还挺有难度的。
|
||||
|
||||
在遍历的过程中相当于是要找每一个字母的边界,**如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了**。此时前面出现过所有字母,最远也就到这个边界了。
|
||||
|
||||
可以分为如下两步:
|
||||
|
||||
* 统计每一个字符最后出现的位置
|
||||
* 从头遍历字符,如果找到之前字符最大出现位置下标和当前下标相等,则找到了分割点
|
||||
* 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
|
||||
|
||||
如图:
|
||||
|
||||
<img src='../pics/763.划分字母区间.png' width=600> </img></div>
|
||||
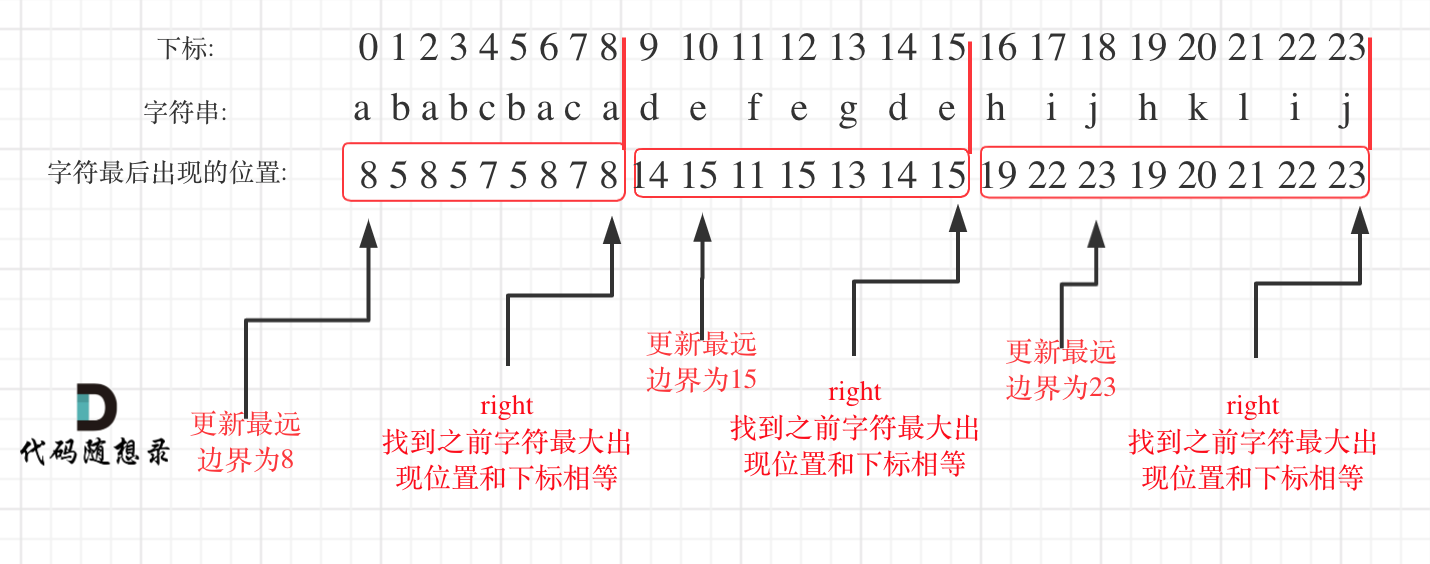
|
||||
|
||||
明白原理之后,代码并不复杂,如下:
|
||||
|
||||
```
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
vector<int> partitionLabels(string S) {
|
||||
@ -38,4 +62,16 @@ public:
|
||||
}
|
||||
};
|
||||
```
|
||||
> 更多算法干货文章持续更新,可以微信搜索「代码随想录」第一时间围观,关注后,回复「Java」「C++」 「python」「简历模板」「数据结构与算法」等等,就可以获得我多年整理的学习资料。
|
||||
|
||||
* 时间复杂度:O(n)
|
||||
* 空间复杂度:O(1) 使用的hash数组是固定大小
|
||||
|
||||
# 总结
|
||||
|
||||
这道题目leetcode标记为贪心算法,说实话,我没有感受到贪心,找不出局部最优推出全局最优的过程。就是用最远出现距离模拟了圈字符的行为。
|
||||
|
||||
但这道题目的思路是很巧妙的,所以有必要介绍给大家做一做,感受一下。
|
||||
|
||||
就酱,循序渐进寻算法,认准「代码随想录」,直接介绍给身边的朋友同学们!
|
||||
|
||||
|
||||
|
||||
@ -37,10 +37,11 @@ dp[j]有两个来源方向,一个是dp[j]自己,一个是dp[j - stones[i]]
|
||||
|
||||
for循环遍历石头的数量嵌套一个for循环遍历背包容量,且因为是01背包,每一个物品只使用一次,所以遍历背包容量的时候要倒序。
|
||||
|
||||
具体原因我在
|
||||
具体原因我在[01背包一维数组实现](https://github.com/youngyangyang04/leetcode-master/blob/master/problems/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-2.md)详细讲解过了。大家感兴趣可以去看一下。
|
||||
|
||||
|
||||
```
|
||||
最后C++代码如下:
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int lastStoneWeightII(vector<int>& stones) {
|
||||
|
||||
Reference in New Issue
Block a user