mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-12 21:50:49 +08:00
Update
This commit is contained in:
@ -3,6 +3,8 @@
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1170)
|
||||
|
||||
[力扣题目讲解以及题目链接(核心代码模式)](https://programmercarl.com/0797.%E6%89%80%E6%9C%89%E5%8F%AF%E8%83%BD%E7%9A%84%E8%B7%AF%E5%BE%84.html#%E6%80%9D%E8%B7%AF)
|
||||
|
||||
【题目描述】
|
||||
|
||||
给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个函数,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
|
||||
@ -19,6 +21,8 @@
|
||||
|
||||
如果不存在任何一条路径,则输出 -1。
|
||||
|
||||
注意输出的序列中,最后一个节点后面没有空格! 例如正确的答案是 `1 3 5`,而不是 `1 3 5 `, 5后面没有空格!
|
||||
|
||||
【输入示例】
|
||||
|
||||
```
|
||||
@ -81,7 +85,7 @@
|
||||
|
||||
我在讲解[二叉树理论基础](https://programmercarl.com/二叉树理论基础.html)的时候,提到过,**二叉树的前中后序遍历其实就是深搜在二叉树这种数据结构上的应用**。
|
||||
|
||||
那么回溯算法呢,**其实 回溯算法就是 深搜,只不过 我们给他一个更细分的定义,叫做回溯算法**。
|
||||
那么回溯算法呢,**其实 回溯算法就是 深搜,只不过针对某一搜索场景 我们给他一个更细分的定义,叫做回溯算法**。
|
||||
|
||||
那有的录友可能说:那我以后称回溯算法为深搜,是不是没毛病?
|
||||
|
||||
@ -91,45 +95,110 @@
|
||||
|
||||
## 图的存储
|
||||
|
||||
在[图论理论基础篇]()
|
||||
在[图论理论基础篇](./图论理论基础.md) 中我们讲到了 两种 图的存储方式:邻接表 和 邻接矩阵。
|
||||
|
||||
本题我们将带大家分别实现这两个图的存储方式。
|
||||
|
||||
### 邻接矩阵
|
||||
|
||||
邻接矩阵 使用 二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图,有多少节点就申请多大的二维数组。
|
||||
|
||||
本题我们会有n 个节点,因为节点标号是从1开始的,为了节点标号和下标对齐,我们申请 n + 1 * n + 1 这么大的二维数组。
|
||||
|
||||
```CPP
|
||||
vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0));
|
||||
```
|
||||
|
||||
输入m个边,构造方式如下:
|
||||
|
||||
```CPP
|
||||
while (m--) {
|
||||
cin >> s >> t;
|
||||
// 使用邻接矩阵 ,1 表示 节点s 指向 节点t
|
||||
graph[s][t] = 1;
|
||||
}
|
||||
```
|
||||
|
||||
### 邻接表
|
||||
|
||||
邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图,有多少边 才会申请对应大小的链表。
|
||||
|
||||
邻接表的构造相对邻接矩阵难理解一些。
|
||||
|
||||
我在 [图论理论基础篇](./图论理论基础.md) 举了一个例子:
|
||||
|
||||
|
||||

|
||||
|
||||
这里表达的图是:
|
||||
|
||||
* 节点1 指向 节点3 和 节点5
|
||||
* 节点2 指向 节点4、节点3、节点5
|
||||
* 节点3 指向 节点4
|
||||
* 节点4指向节点1
|
||||
|
||||
我们需要构造一个数组,数组里的元素是一个链表。
|
||||
|
||||
C++写法:
|
||||
|
||||
```CPP
|
||||
// 节点编号从1到n,所以申请 n+1 这么大的数组
|
||||
vector<list<int>> graph(n + 1); // 邻接表,list为C++里的链表
|
||||
```
|
||||
|
||||
输入m个边,构造方式如下:
|
||||
|
||||
```CPP
|
||||
while (m--) {
|
||||
cin >> s >> t;
|
||||
// 使用邻接表 ,表示 s -> t 是相连的
|
||||
graph[s].push_back(t);
|
||||
}
|
||||
```
|
||||
|
||||
本题我们使用邻接表 或者 邻接矩阵都可以,因为后台数据并没有对图的大小以及稠密度做很大的区分。
|
||||
|
||||
以下我们使用邻接矩阵的方式来讲解,文末我也会给出 使用邻接表的整体代码。
|
||||
|
||||
**注意邻接表 和 邻接矩阵的写法都要掌握**!
|
||||
|
||||
## 深度优先搜索
|
||||
|
||||
接下来我们使用深搜三部曲来分析题目:
|
||||
本题是深度优先搜索的基础题目,关于深搜我在[图论深搜理论基础](./图论深搜理论基础.md) 已经有详细的讲解,图文并茂。
|
||||
|
||||
关于本题我会直接使用深搜三部曲来分析,如果对深搜不够了解,建议先看 [图论深搜理论基础](./图论深搜理论基础.md)。
|
||||
|
||||
深搜三部曲来分析题目:
|
||||
|
||||
1. 确认递归函数,参数
|
||||
|
||||
首先我们dfs函数一定要存一个图,用来遍历的,还要存一个目前我们遍历的节点,定义为x
|
||||
首先我们dfs函数一定要存一个图,用来遍历的,需要存一个目前我们遍历的节点,定义为x。
|
||||
|
||||
至于 单一路径,和路径集合可以放在全局变量,那么代码是这样的:
|
||||
还需要存一个n,表示终点,我们遍历的时候,用来判断当 x==n 时候 标明找到了终点。
|
||||
|
||||
(其实在递归函数的参数 不容易一开始就确定了,一般是在写函数体的时候发现缺什么,参加就补什么)
|
||||
|
||||
至于 单一路径 和 路径集合 可以放在全局变量,那么代码是这样的:
|
||||
|
||||
```CPP
|
||||
vector<vector<int>> result; // 收集符合条件的路径
|
||||
vector<int> path; // 0节点到终点的路径
|
||||
// x:目前遍历的节点
|
||||
// graph:存当前的图
|
||||
void dfs (vector<vector<int>>& graph, int x)
|
||||
// n:终点
|
||||
void dfs (const vector<vector<int>>& graph, int x, int n) {
|
||||
```
|
||||
|
||||
2. 确认终止条件
|
||||
|
||||
什么时候我们就找到一条路径了?
|
||||
|
||||
当目前遍历的节点 为 最后一个节点的时候 就找到了一条 从出发点到终止点的路径。
|
||||
|
||||
-----------
|
||||
当前遍历的节点,我们定义为x,最后一点节点 就是 graph.size() - 1(因为题目描述是找出所有从节点 0 到节点 n-1 的路径并输出)。
|
||||
|
||||
所以 但 x 等于 graph.size() - 1 的时候就找到一条有效路径。 代码如下:
|
||||
|
||||
-------
|
||||
当目前遍历的节点 为 最后一个节点 n 的时候 就找到了一条 从出发点到终止点的路径。
|
||||
|
||||
```CPP
|
||||
// 要求从节点 0 到节点 n-1 的路径并输出,所以是 graph.size() - 1
|
||||
if (x == graph.size() - 1) { // 找到符合条件的一条路径
|
||||
result.push_back(path); // 收集有效路径
|
||||
// 当前遍历的节点x 到达节点n
|
||||
if (x == n) { // 找到符合条件的一条路径
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
```
|
||||
@ -138,224 +207,82 @@ if (x == graph.size() - 1) { // 找到符合条件的一条路径
|
||||
|
||||
接下来是走 当前遍历节点x的下一个节点。
|
||||
|
||||
首先是要找到 x节点链接了哪些节点呢? 遍历方式是这样的:
|
||||
首先是要找到 x节点指向了哪些节点呢? 遍历方式是这样的:
|
||||
|
||||
```c++
|
||||
for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点
|
||||
for (int i = 1; i <= n; i++) { // 遍历节点x链接的所有节点
|
||||
if (graph[x][i] == 1) { // 找到 x指向的节点,就是节点i
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
接下来就是将 选中的x所连接的节点,加入到 单一路径来。
|
||||
接下来就是将 选中的x所指向的节点,加入到 单一路径来。
|
||||
|
||||
```C++
|
||||
path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
|
||||
path.push_back(i); // 遍历到的节点加入到路径中来
|
||||
|
||||
```
|
||||
|
||||
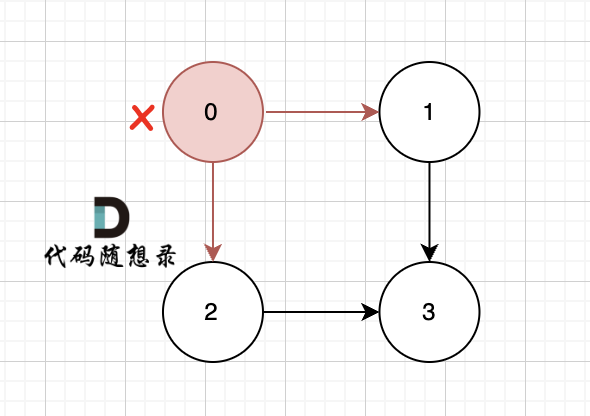
一些录友可以疑惑这里如果找到x 链接的节点的,例如如果x目前是节点0,那么目前的过程就是这样的:
|
||||
|
||||
|
||||
|
||||
二维数组中,graph[x][i] 都是x链接的节点,当前遍历的节点就是 `graph[x][i]` 。
|
||||
|
||||
进入下一层递归
|
||||
|
||||
```CPP
|
||||
dfs(graph, graph[x][i]); // 进入下一层递归
|
||||
dfs(graph, i, n); // 进入下一层递归
|
||||
```
|
||||
|
||||
最后就是回溯的过程,撤销本次添加节点的操作。 该过程整体代码:
|
||||
最后就是回溯的过程,撤销本次添加节点的操作。
|
||||
|
||||
为什么要有回溯,我在[图论深搜理论基础](./图论深搜理论基础.md) 也有详细的讲解。
|
||||
|
||||
该过程整体代码:
|
||||
|
||||
```CPP
|
||||
for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点
|
||||
path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
|
||||
dfs(graph, graph[x][i]); // 进入下一层递归
|
||||
path.pop_back(); // 回溯,撤销本节点
|
||||
}
|
||||
```
|
||||
|
||||
本题整体代码如下:
|
||||
|
||||
```CPP
|
||||
class Solution {
|
||||
private:
|
||||
vector<vector<int>> result; // 收集符合条件的路径
|
||||
vector<int> path; // 0节点到终点的路径
|
||||
// x:目前遍历的节点
|
||||
// graph:存当前的图
|
||||
void dfs (vector<vector<int>>& graph, int x) {
|
||||
// 要求从节点 0 到节点 n-1 的路径并输出,所以是 graph.size() - 1
|
||||
if (x == graph.size() - 1) { // 找到符合条件的一条路径
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点
|
||||
path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
|
||||
dfs(graph, graph[x][i]); // 进入下一层递归
|
||||
for (int i = 1; i <= n; i++) { // 遍历节点x链接的所有节点
|
||||
if (graph[x][i] == 1) { // 找到 x链接的节点
|
||||
path.push_back(i); // 遍历到的节点加入到路径中来
|
||||
dfs(graph, i, n); // 进入下一层递归
|
||||
path.pop_back(); // 回溯,撤销本节点
|
||||
}
|
||||
}
|
||||
public:
|
||||
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
|
||||
path.push_back(0); // 无论什么路径已经是从0节点出发
|
||||
dfs(graph, 0); // 开始遍历
|
||||
return result;
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
## 总结
|
||||
## 打印结果
|
||||
|
||||
本题是比较基础的深度优先搜索模板题,这种有向图路径问题,最合适使用深搜,当然本题也可以使用广搜,但广搜相对来说就麻烦了一些,需要记录一下路径。
|
||||
ACM格式大家在输出结果的时候,要关注看看格式问题,特别是字符串,有的题目说的是每个元素后面都有空格,有的题目说的是 每个元素间有空格,最后一个元素没有空格。
|
||||
|
||||
而深搜和广搜都适合解决颜色类的问题,例如岛屿系列,其实都是 遍历+标记,所以使用哪种遍历都是可以的。
|
||||
有的题目呢,压根没说,那只能提交去试一试了。
|
||||
|
||||
至于广搜理论基础,我们在下一篇在好好讲解,敬请期待!
|
||||
很多录友在提交题目的时候发现结果一样,为什么提交就是不对呢。
|
||||
|
||||
## 其他语言版本
|
||||
例如示例输出是:
|
||||
|
||||
### Java
|
||||
`1 3 5` 而不是 `1 3 5 `
|
||||
|
||||
```Java
|
||||
// 深度优先遍历
|
||||
class Solution {
|
||||
List<List<Integer>> ans; // 用来存放满足条件的路径
|
||||
List<Integer> cnt; // 用来保存 dfs 过程中的节点值
|
||||
即 5 的后面没有空格!
|
||||
|
||||
public void dfs(int[][] graph, int node) {
|
||||
if (node == graph.length - 1) { // 如果当前节点是 n - 1,那么就保存这条路径
|
||||
ans.add(new ArrayList<>(cnt));
|
||||
return;
|
||||
}
|
||||
for (int index = 0; index < graph[node].length; index++) {
|
||||
int nextNode = graph[node][index];
|
||||
cnt.add(nextNode);
|
||||
dfs(graph, nextNode);
|
||||
cnt.remove(cnt.size() - 1); // 回溯
|
||||
}
|
||||
}
|
||||
|
||||
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
|
||||
ans = new ArrayList<>();
|
||||
cnt = new ArrayList<>();
|
||||
cnt.add(0); // 注意,0 号节点要加入 cnt 数组中
|
||||
dfs(graph, 0);
|
||||
return ans;
|
||||
这是我们在输出的时候需要注意的点。
|
||||
|
||||
有录友可能会想,ACM格式就是麻烦,有空格没有空格有什么影响,结果对了不就行了?
|
||||
|
||||
ACM模式相对于核心代码模式(力扣) 更考验大家对代码的掌控能力。 例如工程代码里,输出输出都是要自己控制的。这也是为什么大公司笔试,都是ACM模式。
|
||||
|
||||
以上代码中,结果都存在了 result数组里(二维数组,每一行是一个结果),最后将其打印出来。(重点看注释)
|
||||
|
||||
```CPP
|
||||
// 输出结果
|
||||
if (result.size() == 0) cout << -1 << endl;
|
||||
for (const vector<int> &pa : result) {
|
||||
for (int i = 0; i < pa.size() - 1; i++) { // 这里指打印到倒数第二个
|
||||
cout << pa[i] << " ";
|
||||
}
|
||||
cout << pa[pa.size() - 1] << endl; // 这里再打印倒数第一个,控制最后一个元素后面没有空格
|
||||
}
|
||||
```
|
||||
|
||||
### Python
|
||||
## 本题代码
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def __init__(self):
|
||||
self.result = []
|
||||
self.path = [0]
|
||||
### 邻接矩阵写法
|
||||
|
||||
def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
|
||||
if not graph: return []
|
||||
|
||||
self.dfs(graph, 0)
|
||||
return self.result
|
||||
|
||||
def dfs(self, graph, root: int):
|
||||
if root == len(graph) - 1: # 成功找到一条路径时
|
||||
# ***Python的list是mutable类型***
|
||||
# ***回溯中必须使用Deep Copy***
|
||||
self.result.append(self.path[:])
|
||||
return
|
||||
|
||||
for node in graph[root]: # 遍历节点n的所有后序节点
|
||||
self.path.append(node)
|
||||
self.dfs(graph, node)
|
||||
self.path.pop() # 回溯
|
||||
```
|
||||
|
||||
|
||||
### JavaScript
|
||||
```javascript
|
||||
var allPathsSourceTarget = function(graph) {
|
||||
let res=[],path=[]
|
||||
|
||||
function dfs(graph,start){
|
||||
if(start===graph.length-1){
|
||||
res.push([...path])
|
||||
return;
|
||||
}
|
||||
for(let i=0;i<graph[start].length;i++){
|
||||
path.push(graph[start][i])
|
||||
dfs(graph,graph[start][i])
|
||||
path.pop()
|
||||
}
|
||||
}
|
||||
path.push(0)
|
||||
dfs(graph,0)
|
||||
return res
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
### Go
|
||||
|
||||
```go
|
||||
func allPathsSourceTarget(graph [][]int) [][]int {
|
||||
result := make([][]int, 0)
|
||||
|
||||
var dfs func(path []int, step int)
|
||||
dfs = func(path []int, step int){
|
||||
// 从0遍历到length-1
|
||||
if step == len(graph) - 1{
|
||||
tmp := make([]int, len(path))
|
||||
copy(tmp, path)
|
||||
result = append(result, tmp)
|
||||
return
|
||||
}
|
||||
|
||||
for i := 0; i < len(graph[step]); i++{
|
||||
next := append(path, graph[step][i])
|
||||
dfs(next, graph[step][i])
|
||||
}
|
||||
}
|
||||
// 从0开始,开始push 0进去
|
||||
dfs([]int{0}, 0)
|
||||
return result
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
|
||||
```rust
|
||||
impl Solution {
|
||||
pub fn all_paths_source_target(graph: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
|
||||
let (mut res, mut path) = (vec![], vec![0]);
|
||||
Self::dfs(&graph, &mut path, &mut res, 0);
|
||||
res
|
||||
}
|
||||
|
||||
pub fn dfs(graph: &Vec<Vec<i32>>, path: &mut Vec<i32>, res: &mut Vec<Vec<i32>>, node: usize) {
|
||||
if node == graph.len() - 1 {
|
||||
res.push(path.clone());
|
||||
return;
|
||||
}
|
||||
for &v in &graph[node] {
|
||||
path.push(v);
|
||||
Self::dfs(graph, path, res, v as usize);
|
||||
path.pop();
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
|
||||
邻接矩阵
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
@ -365,13 +292,11 @@ vector<vector<int>> result; // 收集符合条件的路径
|
||||
vector<int> path; // 1节点到终点的路径
|
||||
|
||||
void dfs (const vector<vector<int>>& graph, int x, int n) {
|
||||
|
||||
// 要求从节点 1 到节点 n 的路径并输出,所以是 graph.size()
|
||||
// 当前遍历的节点x 到达节点n
|
||||
if (x == n) { // 找到符合条件的一条路径
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
|
||||
for (int i = 1; i <= n; i++) { // 遍历节点x链接的所有节点
|
||||
if (graph[x][i] == 1) { // 找到 x链接的节点
|
||||
path.push_back(i); // 遍历到的节点加入到路径中来
|
||||
@ -382,10 +307,7 @@ void dfs (const vector<vector<int>>& graph, int x, int n) {
|
||||
}
|
||||
|
||||
int main() {
|
||||
|
||||
|
||||
int n, m, s, t;
|
||||
|
||||
cin >> n >> m;
|
||||
|
||||
// 节点编号从1到n,所以申请 n+1 这么大的数组
|
||||
@ -393,27 +315,26 @@ int main() {
|
||||
|
||||
while (m--) {
|
||||
cin >> s >> t;
|
||||
// 使用临近矩阵 表示无线图,1 表示 s 与 t 是相连的
|
||||
// 使用邻接矩阵 表示无线图,1 表示 s 与 t 是相连的
|
||||
graph[s][t] = 1;
|
||||
}
|
||||
path.push_back(1); // 无论什么路径已经是从0节点出发
|
||||
|
||||
path.push_back(1); // 无论什么路径已经是从0节点出发
|
||||
dfs(graph, 1, n); // 开始遍历
|
||||
|
||||
// 输出结果
|
||||
if (result.size() == 0) cout << -1 << endl;
|
||||
for (const vector<int> &pa : result) {
|
||||
for (int i = 0; i < pa.size(); i++) {
|
||||
for (int i = 0; i < pa.size() - 1; i++) {
|
||||
cout << pa[i] << " ";
|
||||
}
|
||||
cout << endl;
|
||||
cout << pa[pa.size() - 1] << endl;
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
|
||||
|
||||
邻接表
|
||||
### 邻接表写法
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
@ -426,12 +347,11 @@ vector<int> path; // 1节点到终点的路径
|
||||
|
||||
void dfs (const vector<list<int>>& graph, int x, int n) {
|
||||
|
||||
// 要求从节点 1 到节点 n 的路径并输出,所以是 graph.size()
|
||||
if (x == n) { // 找到符合条件的一条路径
|
||||
result.push_back(path);
|
||||
return;
|
||||
}
|
||||
for (int i : graph[x]) { // 找到 x链接的节点
|
||||
for (int i : graph[x]) { // 找到 x指向的节点
|
||||
path.push_back(i); // 遍历到的节点加入到路径中来
|
||||
dfs(graph, i, n); // 进入下一层递归
|
||||
path.pop_back(); // 回溯,撤销本节点
|
||||
@ -439,10 +359,7 @@ void dfs (const vector<list<int>>& graph, int x, int n) {
|
||||
}
|
||||
|
||||
int main() {
|
||||
|
||||
|
||||
int n, m, s, t;
|
||||
|
||||
cin >> n >> m;
|
||||
|
||||
// 节点编号从1到n,所以申请 n+1 这么大的数组
|
||||
@ -455,17 +372,37 @@ int main() {
|
||||
}
|
||||
|
||||
path.push_back(1); // 无论什么路径已经是从0节点出发
|
||||
|
||||
dfs(graph, 1, n); // 开始遍历
|
||||
|
||||
// 输出结果
|
||||
if (result.size() == 0) cout << -1 << endl;
|
||||
for (const vector<int> &pa : result) {
|
||||
for (int i = 0; i < pa.size(); i++) {
|
||||
for (int i = 0; i < pa.size() - 1; i++) {
|
||||
cout << pa[i] << " ";
|
||||
}
|
||||
cout << endl;
|
||||
cout << pa[pa.size() - 1] << endl;
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
## 总结
|
||||
|
||||
本题是一道简单的深搜题目,也可以说是模板题,和 [力扣797. 所有可能的路径](https://leetcode.cn/problems/all-paths-from-source-to-target/description/) 思路是一样一样的。
|
||||
|
||||
很多录友做力扣的时候,轻松就把代码写出来了, 但做面试笔试的时候,遇到这样的题就写不出来了。
|
||||
|
||||
在力扣上刷题不用考虑图的存储方式,也不用考虑输出的格式。
|
||||
|
||||
而这些都是 ACM 模式题目的知识点(图的存储方式)和细节(输出的格式)
|
||||
|
||||
所以我才会特别制作ACM题目,同样也重点去讲解图的存储和遍历方式,来帮大家去练习。
|
||||
|
||||
对于这种有向图路径问题,最合适使用深搜,当然本题也可以使用广搜,但广搜相对来说就麻烦了一些,需要记录一下路径。
|
||||
|
||||
而深搜和广搜都适合解决颜色类的问题,例如岛屿系列,其实都是 遍历+标记,所以使用哪种遍历都是可以的。
|
||||
|
||||
至于广搜理论基础,我们在下一篇在好好讲解,敬请期待!
|
||||
|
||||
|
||||
|
||||
|
||||
186
problems/kamacoder/0099.岛屿的数量广搜.md
Normal file
186
problems/kamacoder/0099.岛屿的数量广搜.md
Normal file
@ -0,0 +1,186 @@
|
||||
|
||||
# 99. 岛屿数量
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1171)
|
||||
|
||||
[力扣题目讲解以及题目链接(核心代码模式)](https://programmercarl.com/0200.%E5%B2%9B%E5%B1%BF%E6%95%B0%E9%87%8F.%E5%B9%BF%E6%90%9C%E7%89%88.html)
|
||||
|
||||
题目描述:
|
||||
|
||||
给定一个由 1(陆地)和 0(水)组成的矩阵,你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
|
||||
|
||||
输入描述:
|
||||
|
||||
第一行包含两个整数 N, M,表示矩阵的行数和列数。
|
||||
|
||||
后续 N 行,每行包含 M 个数字,数字为 1 或者 0。
|
||||
|
||||
输出描述:
|
||||
|
||||
输出一个整数,表示岛屿的数量。如果不存在岛屿,则输出 0。
|
||||
|
||||
输入示例:
|
||||
|
||||
```
|
||||
4 5
|
||||
1 1 0 0 0
|
||||
1 1 0 0 0
|
||||
0 0 1 0 0
|
||||
0 0 0 1 1
|
||||
```
|
||||
|
||||
输出示例:
|
||||
|
||||
3
|
||||
|
||||
提示信息
|
||||
|
||||
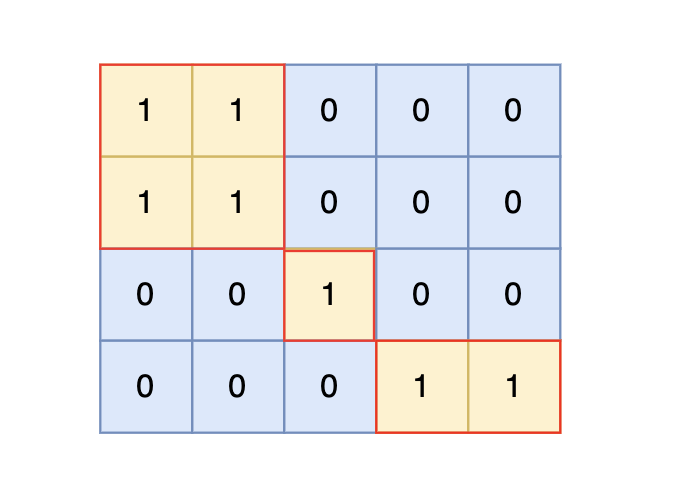
|
||||
|
||||
根据测试案例中所展示,岛屿数量共有 3 个,所以输出 3。
|
||||
|
||||
数据范围:
|
||||
|
||||
* 1 <= N, M <= 50
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
注意题目中每座岛屿只能由**水平方向和/或竖直方向上**相邻的陆地连接形成。
|
||||
|
||||
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
|
||||
|
||||

|
||||
|
||||
这道题题目是 DFS,BFS,并查集,基础题目。
|
||||
|
||||
本题思路,是用遇到一个没有遍历过的节点陆地,计数器就加一,然后把该节点陆地所能遍历到的陆地都标记上。
|
||||
|
||||
在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。
|
||||
|
||||
那么如果把节点陆地所能遍历到的陆地都标记上呢,就可以使用 DFS,BFS或者并查集。
|
||||
|
||||
### 广度优先搜索
|
||||
|
||||
不少同学用广搜做这道题目的时候,超时了。 这里有一个广搜中很重要的细节:
|
||||
|
||||
根本原因是**只要 加入队列就代表 走过,就需要标记,而不是从队列拿出来的时候再去标记走过**。
|
||||
|
||||
很多同学可能感觉这有区别吗?
|
||||
|
||||
如果从队列拿出节点,再去标记这个节点走过,就会发生下图所示的结果,会导致很多节点重复加入队列。
|
||||
|
||||
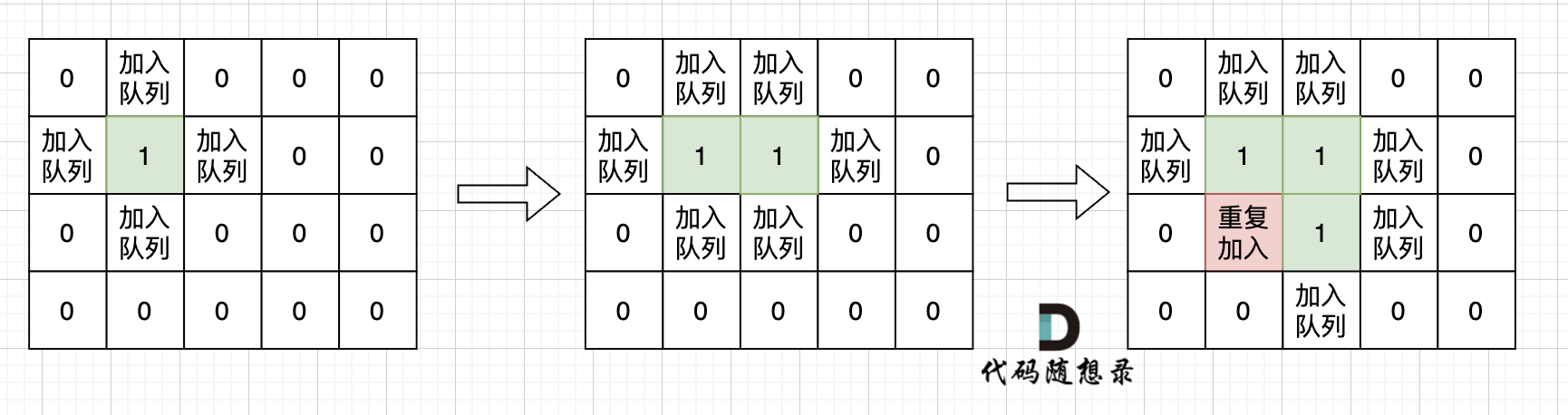
|
||||
|
||||
超时写法 (从队列中取出节点再标记)
|
||||
|
||||
```CPP
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
|
||||
queue<pair<int, int>> que;
|
||||
que.push({x, y});
|
||||
while(!que.empty()) {
|
||||
pair<int ,int> cur = que.front(); que.pop();
|
||||
int curx = cur.first;
|
||||
int cury = cur.second;
|
||||
visited[curx][cury] = true; // 从队列中取出在标记走过
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = curx + dir[i][0];
|
||||
int nexty = cury + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
|
||||
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
|
||||
que.push({nextx, nexty});
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
加入队列 就代表走过,立刻标记,正确写法:
|
||||
|
||||
```CPP
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
|
||||
queue<pair<int, int>> que;
|
||||
que.push({x, y});
|
||||
visited[x][y] = true; // 只要加入队列,立刻标记
|
||||
while(!que.empty()) {
|
||||
pair<int ,int> cur = que.front(); que.pop();
|
||||
int curx = cur.first;
|
||||
int cury = cur.second;
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = curx + dir[i][0];
|
||||
int nexty = cury + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
|
||||
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
|
||||
que.push({nextx, nexty});
|
||||
visited[nextx][nexty] = true; // 只要加入队列立刻标记
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
以上两个版本其实,其实只有细微区别,就是 `visited[x][y] = true;` 放在的地方,这取决于我们对 代码中队列的定义,队列中的节点就表示已经走过的节点。 **所以只要加入队列,立即标记该节点走过**。
|
||||
|
||||
本题完整广搜代码:
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
#include <queue>
|
||||
using namespace std;
|
||||
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void bfs(const vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
|
||||
queue<pair<int, int>> que;
|
||||
que.push({x, y});
|
||||
visited[x][y] = true; // 只要加入队列,立刻标记
|
||||
while(!que.empty()) {
|
||||
pair<int ,int> cur = que.front(); que.pop();
|
||||
int curx = cur.first;
|
||||
int cury = cur.second;
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = curx + dir[i][0];
|
||||
int nexty = cury + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
|
||||
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) {
|
||||
que.push({nextx, nexty});
|
||||
visited[nextx][nexty] = true; // 只要加入队列立刻标记
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
|
||||
vector<vector<bool>> visited(n, vector<bool>(m, false));
|
||||
|
||||
int result = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (!visited[i][j] && grid[i][j] == 1) {
|
||||
result++; // 遇到没访问过的陆地,+1
|
||||
bfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
cout << result << endl;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
179
problems/kamacoder/0099.岛屿的数量深搜.md
Normal file
179
problems/kamacoder/0099.岛屿的数量深搜.md
Normal file
@ -0,0 +1,179 @@
|
||||
|
||||
# 99. 岛屿数量
|
||||
|
||||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1171)
|
||||
|
||||
[力扣题目讲解以及题目链接(核心代码模式)](https://programmercarl.com/0200.%E5%B2%9B%E5%B1%BF%E6%95%B0%E9%87%8F.%E6%B7%B1%E6%90%9C%E7%89%88.html)
|
||||
|
||||
题目描述:
|
||||
|
||||
给定一个由 1(陆地)和 0(水)组成的矩阵,你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
|
||||
|
||||
输入描述:
|
||||
|
||||
第一行包含两个整数 N, M,表示矩阵的行数和列数。
|
||||
|
||||
后续 N 行,每行包含 M 个数字,数字为 1 或者 0。
|
||||
|
||||
输出描述:
|
||||
|
||||
输出一个整数,表示岛屿的数量。如果不存在岛屿,则输出 0。
|
||||
|
||||
输入示例:
|
||||
|
||||
```
|
||||
4 5
|
||||
1 1 0 0 0
|
||||
1 1 0 0 0
|
||||
0 0 1 0 0
|
||||
0 0 0 1 1
|
||||
```
|
||||
|
||||
输出示例:
|
||||
|
||||
3
|
||||
|
||||
提示信息
|
||||
|
||||

|
||||
|
||||
根据测试案例中所展示,岛屿数量共有 3 个,所以输出 3。
|
||||
|
||||
数据范围:
|
||||
|
||||
* 1 <= N, M <= 50
|
||||
|
||||
## 思路
|
||||
|
||||
注意题目中每座岛屿只能由**水平方向和/或竖直方向上**相邻的陆地连接形成。
|
||||
|
||||
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
|
||||
|
||||

|
||||
|
||||
这道题题目是 DFS,BFS,并查集,基础题目。
|
||||
|
||||
本题思路,是用遇到一个没有遍历过的节点陆地,计数器就加一,然后把该节点陆地所能遍历到的陆地都标记上。
|
||||
|
||||
在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。
|
||||
|
||||
那么如何把节点陆地所能遍历到的陆地都标记上呢,就可以使用 DFS,BFS或者并查集。
|
||||
|
||||
### 深度优先搜索
|
||||
|
||||
以下代码使用dfs实现,如果对dfs不太了解的话,**建议按照代码随想录的讲解顺序学习**。
|
||||
|
||||
C++代码如下:
|
||||
|
||||
```CPP
|
||||
// 版本一
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void dfs(const vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = x + dir[i][0];
|
||||
int nexty = y + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
|
||||
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 没有访问过的 同时 是陆地的
|
||||
|
||||
visited[nextx][nexty] = true;
|
||||
dfs(grid, visited, nextx, nexty);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
|
||||
vector<vector<bool>> visited(n, vector<bool>(m, false));
|
||||
|
||||
int result = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (!visited[i][j] && grid[i][j] == 1) {
|
||||
visited[i][j] = true;
|
||||
result++; // 遇到没访问过的陆地,+1
|
||||
dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
|
||||
很多录友可能有疑惑,为什么 以上代码中的dfs函数,没有终止条件呢? 感觉递归没有终止很危险。
|
||||
|
||||
其实终止条件 就写在了 调用dfs的地方,如果遇到不合法的方向,直接不会去调用dfs。
|
||||
|
||||
当然也可以这么写:
|
||||
|
||||
```CPP
|
||||
// 版本二
|
||||
#include <iostream>
|
||||
#include <vector>
|
||||
using namespace std;
|
||||
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
|
||||
void dfs(const vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
|
||||
if (visited[x][y] || grid[x][y] == 0) return; // 终止条件:访问过的节点 或者 遇到海水
|
||||
visited[x][y] = true; // 标记访问过
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextx = x + dir[i][0];
|
||||
int nexty = y + dir[i][1];
|
||||
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
|
||||
dfs(grid, visited, nextx, nexty);
|
||||
}
|
||||
}
|
||||
|
||||
int main() {
|
||||
int n, m;
|
||||
cin >> n >> m;
|
||||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
cin >> grid[i][j];
|
||||
}
|
||||
}
|
||||
|
||||
vector<vector<bool>> visited(n, vector<bool>(m, false));
|
||||
|
||||
int result = 0;
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (!visited[i][j] && grid[i][j] == 1) {
|
||||
result++; // 遇到没访问过的陆地,+1
|
||||
dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
|
||||
}
|
||||
}
|
||||
}
|
||||
cout << result << endl;
|
||||
}
|
||||
```
|
||||
|
||||
这里大家应该能看出区别了,无疑就是版本一中 调用dfs 的条件判断 放在了 版本二 的 终止条件位置上。
|
||||
|
||||
**版本一的写法**是 :下一个节点是否能合法已经判断完了,传进dfs函数的就是合法节点。
|
||||
|
||||
**版本二的写法**是:不管节点是否合法,上来就dfs,然后在终止条件的地方进行判断,不合法再return。
|
||||
|
||||
**理论上来讲,版本一的效率更高一些**,因为避免了 没有意义的递归调用,在调用dfs之前,就做合法性判断。 但从写法来说,可能版本二 更利于理解一些。(不过其实都差不太多)
|
||||
|
||||
很多同学看了同一道题目,都是dfs,写法却不一样,**有时候有终止条件,有时候连终止条件都没有,其实这就是根本原因,两种写法而已**。
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
其实本题是 dfs,bfs 模板题,但正是因为是模板题,所以大家或者一些题解把重要的细节都很忽略了,我这里把大家没注意的但以后会踩的坑 都给列出来了。
|
||||
|
||||
本篇我只给出的dfs的写法,大家发现我写的还是比较细的,那么后面我再单独给出本题的bfs写法,虽然是模板题,但依然有很多注意的点,敬请期待!
|
||||
|
||||
@ -1,9 +1,3 @@
|
||||
<p align="center">
|
||||
<a href="https://www.programmercarl.com/xunlian/xunlianying.html" target="_blank">
|
||||
<img src="../pics/训练营.png" width="1000"/>
|
||||
</a>
|
||||
<p align="center"><strong><a href="./qita/join.md">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!</strong></p>
|
||||
|
||||
# 并查集理论基础
|
||||
|
||||
接下来我们来讲一下并查集,首先当然是并查集理论基础。
|
||||
@ -460,8 +454,3 @@ void join(int u, int v) {
|
||||
|
||||
敬请期待 并查集题目精讲系列。
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
@ -1,9 +1,3 @@
|
||||
<p align="center">
|
||||
<a href="https://www.programmercarl.com/xunlian/xunlianying.html" target="_blank">
|
||||
<img src="../pics/训练营.png" width="1000"/>
|
||||
</a>
|
||||
<p align="center"><strong><a href="./qita/join.md">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!</strong></p>
|
||||
|
||||
# 广度优先搜索理论基础
|
||||
|
||||
|
||||
@ -156,8 +150,3 @@ def bfs(grid, visited, x, y):
|
||||
|
||||
```
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
@ -16,6 +16,8 @@
|
||||
|
||||
深搜注意事项
|
||||
|
||||
同样是深搜模板题,会有两种写法,
|
||||
|
||||
广搜注意事项
|
||||
|
||||
## 并查集
|
||||
|
||||
@ -1,8 +1,3 @@
|
||||
<p align="center">
|
||||
<a href="https://www.programmercarl.com/xunlian/xunlianying.html" target="_blank">
|
||||
<img src="../pics/训练营.png" width="1000"/>
|
||||
</a>
|
||||
<p align="center"><strong><a href="./qita/join.md">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!</strong></p>
|
||||
|
||||
# 深度优先搜索理论基础
|
||||
|
||||
@ -199,7 +194,3 @@ for (选择:本节点所连接的其他节点) {
|
||||
后面我也会给大家安排具体练习的题目,依旧是代码随想录的风格,循序渐进由浅入深!
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
</a>
|
||||
|
||||
Reference in New Issue
Block a user