Merge branch 'youngyangyang04:master' into leetcode-modify-the-code-of-the-dp

problems/0017.电话号码的字母组合.md

@@ -16,11 +16,16 @@
 ![17.电话号码的字母组合](https://img-blog.csdnimg.cn/2020102916424043.png)
 
 示例:
-输入："23"
-输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
+* 输入："23"
+* 输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
 
 说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[还得用回溯算法！| LeetCode：17.电话号码的字母组合](https://www.bilibili.com/video/BV1yV4y1V7Ug)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
+
 # 思路
 
 从示例上来说，输入"23"，最直接的想法就是两层for循环遍历了吧，正好把组合的情况都输出了。

problems/0024.两两交换链表中的节点.md

@@ -154,24 +154,25 @@ class Solution {
 ```
 
 ```java
-// 虚拟头结点
 class Solution {
   public ListNode swapPairs(ListNode head) {
-
-    ListNode dummyNode = new ListNode(0);
-    dummyNode.next = head;
-    ListNode prev = dummyNode;
-
-    while (prev.next != null && prev.next.next != null) {
-      ListNode temp = head.next.next; // 缓存 next
-      prev.next = head.next;          // 将 prev 的 next 改为 head 的 next
-      head.next.next = head;          // 将 head.next(prev.next) 的next，指向 head
-      head.next = temp;               // 将head 的 next 接上缓存的temp
-      prev = head;                    // 步进1位
-      head = head.next;               // 步进1位
+        ListNode dumyhead = new ListNode(-1); // 设置一个虚拟头结点
+        dumyhead.next = head; // 将虚拟头结点指向head，这样方面后面做删除操作
+        ListNode cur = dumyhead;
+        ListNode temp; // 临时节点，保存两个节点后面的节点
+        ListNode firstnode; // 临时节点，保存两个节点之中的第一个节点
+        ListNode secondnode; // 临时节点，保存两个节点之中的第二个节点
+        while (cur.next != null && cur.next.next != null) {
+            temp = cur.next.next.next;
+            firstnode = cur.next;
+            secondnode = cur.next.next;
+            cur.next = secondnode;       // 步骤一
+            secondnode.next = firstnode; // 步骤二
+            firstnode.next = temp;      // 步骤三
+            cur = firstnode; // cur移动，准备下一轮交换
+        }
+        return dumyhead.next;  
     }
-    return dummyNode.next;
-  }
 }
 ```
 

problems/0039.组合总和.md

@@ -19,25 +19,27 @@ candidates 中的数字可以无限制重复被选取。
 * 解集不能包含重复的组合。 
 
 示例 1：
-输入：candidates = [2,3,6,7], target = 7,
-所求解集为：
+* 输入：candidates = [2,3,6,7], target = 7,
+* 所求解集为：
 [
   [7],
   [2,2,3]
 ]
 
 示例 2：
-输入：candidates = [2,3,5], target = 8,
-所求解集为：
+* 输入：candidates = [2,3,5], target = 8,
+* 所求解集为：
 [
   [2,2,2,2],
   [2,3,3],
   [3,5]
 ]
 
-# 思路
+# 算法公开课
 
-[B站视频讲解-组合总和](https://www.bilibili.com/video/BV1KT4y1M7HJ)
+**《代码随想录》算法视频公开课：[Leetcode:39. 组合总和讲解](https://www.bilibili.com/video/BV1KT4y1M7HJ)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+ 
+# 思路
 
 
 题目中的**无限制重复被选取，吓得我赶紧想想 出现0 可咋办**，然后看到下面提示：1 <= candidates[i] <= 200，我就放心了。

problems/0053.最大子序和（动态规划）.md

@@ -25,7 +25,7 @@
 
 1. 确定dp数组（dp table）以及下标的含义
 
-**dp[i]：包括下标i之前的最大连续子序列和为dp[i]**。
+**dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]**。
 
 2. 确定递推公式
 

problems/0115.不同的子序列.md

@@ -33,6 +33,8 @@ s 和 t 由英文字母组成
 
 dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
 
+为什么i-1，j-1 这么定义我在 [718. 最长重复子数组](https://programmercarl.com/0718.最长重复子数组.html) 中做了详细的讲解。
+
 2. 确定递推公式
 
 这一类问题，基本是要分析两种情况
@@ -42,11 +44,11 @@ dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为d
 
 当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。
 
-一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。
+一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母，所以只需要 dp[i-1][j-1]。
 
 一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。
 
-这里可能有同学不明白了，为什么还要考虑 不用s[i - 1]来匹配，都相同了指定要匹配啊。
+**这里可能有录友不明白了，为什么还要考虑 不用s[i - 1]来匹配，都相同了指定要匹配啊**。
 
 例如： s：bagg 和 t：bag ，s[3] 和 t[2]是相同的，但是字符串s也可以不用s[3]来匹配，即用s[0]s[1]s[2]组成的bag。
 
@@ -54,13 +56,19 @@ dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为d
 
 所以当s[i - 1] 与 t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
 
-当s[i - 1] 与 t[j - 1]不相等时，dp[i][j]只有一部分组成，不用s[i - 1]来匹配，即：dp[i - 1][j]
+当s[i - 1] 与 t[j - 1]不相等时，dp[i][j]只有一部分组成，不用s[i - 1]来匹配（就是模拟在s中删除这个元素），即：dp[i - 1][j]
 
 所以递推公式为：dp[i][j] = dp[i - 1][j];
 
+这里可能有录友还疑惑，为什么只考虑 “不用s[i - 1]来匹配” 这种情况， 不考虑 “不用t[j - 1]来匹配” 的情况呢。 
+
+这里大家要明确，我们求的是 s 中有多少个 t，而不是 求t中有多少个s，所以只考虑 s中删除元素的情况，即 不用s[i - 1]来匹配 的情况。
+
 3. dp数组如何初始化
 
-从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][0] 和dp[0][j]是一定要初始化的。
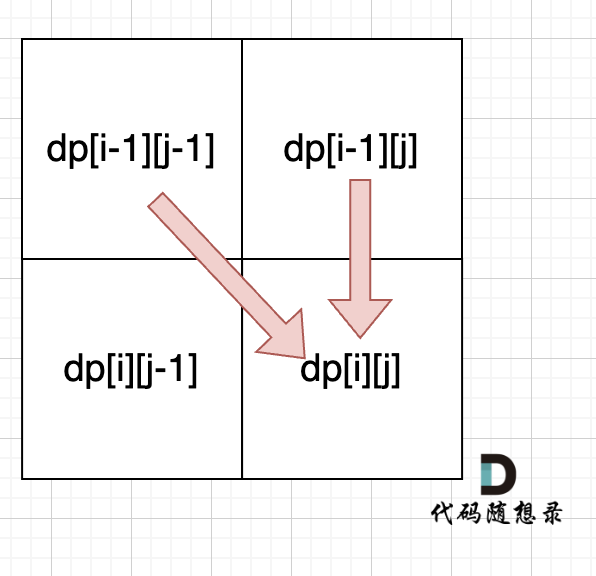
+从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来，如图：，那么 dp[i][0] 和dp[0][j]是一定要初始化的。
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20221222165412.png)
 
 每次当初始化的时候，都要回顾一下dp[i][j]的定义，不要凭感觉初始化。
 
@@ -91,6 +99,8 @@ for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 其实这行代码可以和
 
 从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根据左上方和正上方推出来的。
 
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20221222165412.png)
+
 所以遍历的时候一定是从上到下，从左到右，这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
 
 代码如下：

problems/0216.组合总和III.md

@@ -27,6 +27,10 @@
 输入: k = 3, n = 9
 输出: [[1,2,6], [1,3,5], [2,3,4]]
 
+# 算法公开课
+
+**《代码随想录》算法视频公开课：[和组合问题有啥区别？回溯算法如何剪枝？| LeetCode：216.组合总和III](https://www.bilibili.com/video/BV1wg411873x)，相信结合视频再看本篇题解，更有助于大家对本题的理解**。
+
 
 # 思路
 

problems/0235.二叉搜索树的最近公共祖先.md

@@ -429,6 +429,67 @@ object Solution {
 }
 ```
 
+## rust
+
+递归：
+
+```rust
+impl Solution {
+    pub fn lowest_common_ancestor(
+        root: Option<Rc<RefCell<TreeNode>>>,
+        p: Option<Rc<RefCell<TreeNode>>>,
+        q: Option<Rc<RefCell<TreeNode>>>,
+    ) -> Option<Rc<RefCell<TreeNode>>> {
+        let q_val = q.as_ref().unwrap().borrow().val;
+        let p_val = p.as_ref().unwrap().borrow().val;
+        let root_val = root.as_ref().unwrap().borrow().val;
+
+        if root_val > q_val && root_val > p_val {
+            return Self::lowest_common_ancestor(
+                root.as_ref().unwrap().borrow().left.clone(),
+                p,
+                q,
+            );
+        };
+
+        if root_val < q_val && root_val < p_val {
+            return Self::lowest_common_ancestor(
+                root.as_ref().unwrap().borrow().right.clone(),
+                p,
+                q,
+            );
+        }
+        root
+    }
+}
+```
+
+迭代：
+
+```rust
+impl Solution {
+    pub fn lowest_common_ancestor(
+        mut root: Option<Rc<RefCell<TreeNode>>>,
+        p: Option<Rc<RefCell<TreeNode>>>,
+        q: Option<Rc<RefCell<TreeNode>>>,
+    ) -> Option<Rc<RefCell<TreeNode>>> {
+        let p_val = p.unwrap().borrow().val;
+        let q_val = q.unwrap().borrow().val;
+        while let Some(node) = root.clone() {
+            let root_val = node.borrow().val;
+            if root_val > q_val && root_val > p_val {
+                root = node.borrow().left.clone();
+            } else if root_val < q_val && root_val < p_val {
+                root = node.borrow().right.clone();
+            } else {
+                return root;
+            }
+        }
+        None
+    }
+}
+```
+
 
 <p align="center">
 <a href="https://programmercarl.com/other/kstar.html" target="_blank">

problems/0392.判断子序列.md

@@ -31,11 +31,11 @@
 
 ## 思路
 
-（这道题可以用双指针的思路来实现，时间复杂度就是O(n)）
+（这道题也可以用双指针的思路来实现，时间复杂度也是O(n)）
 
 这道题应该算是编辑距离的入门题目，因为从题意中我们也可以发现，只需要计算删除的情况，不用考虑增加和替换的情况。
 
-**所以掌握本题也是对后面要讲解的编辑距离的题目打下基础**。
+**所以掌握本题的动态规划解法是对后面要讲解的编辑距离的题目打下基础**。
 
 动态规划五部曲分析如下：
 
@@ -47,7 +47,9 @@
 
 有同学问了，为啥要表示下标i-1为结尾的字符串呢，为啥不表示下标i为结尾的字符串呢？
 
-用i来表示也可以！
+为什么这么定义我在 [718. 最长重复子数组](https://programmercarl.com/0718.最长重复子数组.html) 中做了详细的讲解。
+
+其实用i来表示也可以！
 
 但我统一以下标i-1为结尾的字符串来计算，这样在下面的递归公式中会容易理解一些，如果还有疑惑，可以继续往下看。
 
@@ -64,6 +66,8 @@ if (s[i - 1] == t[j - 1])，那么dp[i][j] = dp[i - 1][j - 1] + 1;，因为找
 
 if (s[i - 1] != t[j - 1])，此时相当于t要删除元素，t如果把当前元素t[j - 1]删除，那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了，即：dp[i][j] = dp[i][j - 1];
 
+其实这里 大家可以发现和 [1143.最长公共子序列](https://programmercarl.com/1143.最长公共子序列.html) 的递推公式基本那就是一样的，区别就是 本题 如果删元素一定是字符串t，而 1143.最长公共子序列 是两个字符串都可以删元素。
+
 
 3. dp数组如何初始化
 
@@ -79,7 +83,6 @@ if (s[i - 1] != t[j - 1])，此时相当于t要删除元素，t如果把当前
 
 dp[i][0] 表示以下标i-1为结尾的字符串，与空字符串的相同子序列长度，所以为0. dp[0][j]同理。 
 
-**其实这里只初始化dp[i][0]就够了，但一起初始化也方便，所以就一起操作了**，代码如下：
 
 ```CPP
 vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
@@ -127,10 +130,12 @@ public:
 
 ## 总结
 
-这道题目算是编辑距离的入门题目（毕竟这里只是涉及到减法），也是动态规划解决的经典题型。
+这道题目算是编辑距离的入门题目（毕竟这里只是涉及到减法），也是动态规划解决的经典题型。 
 
 这一类题都是题目读上去感觉很复杂，模拟一下也发现很复杂，用动规分析完了也感觉很复杂，但是最终代码却很简短。
 
+在之前的题目讲解中，我们讲了 [1143.最长公共子序列](https://programmercarl.com/1143.最长公共子序列.html)，大家会发现 本题和 1143.最长公共子序列 的相似之处。
+
 编辑距离的题目最能体现出动规精髓和巧妙之处，大家可以好好体会一下。