algorithm/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2025-07-06 15:09:40 +08:00
Code Issues Packages Projects Releases Wiki Activity

Update

Browse Source
This commit is contained in:
programmercarl
2023-02-13 11:28:33 +08:00
parent 6884c44f72
commit 78afbd2412
3 changed files with 19 additions and 17 deletions
Download Patch File Download Diff File Expand all files Collapse all files

4
problems/0127.单词接龙.md
View File

@ -35,7 +35,7 @@
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20210827175432.png)
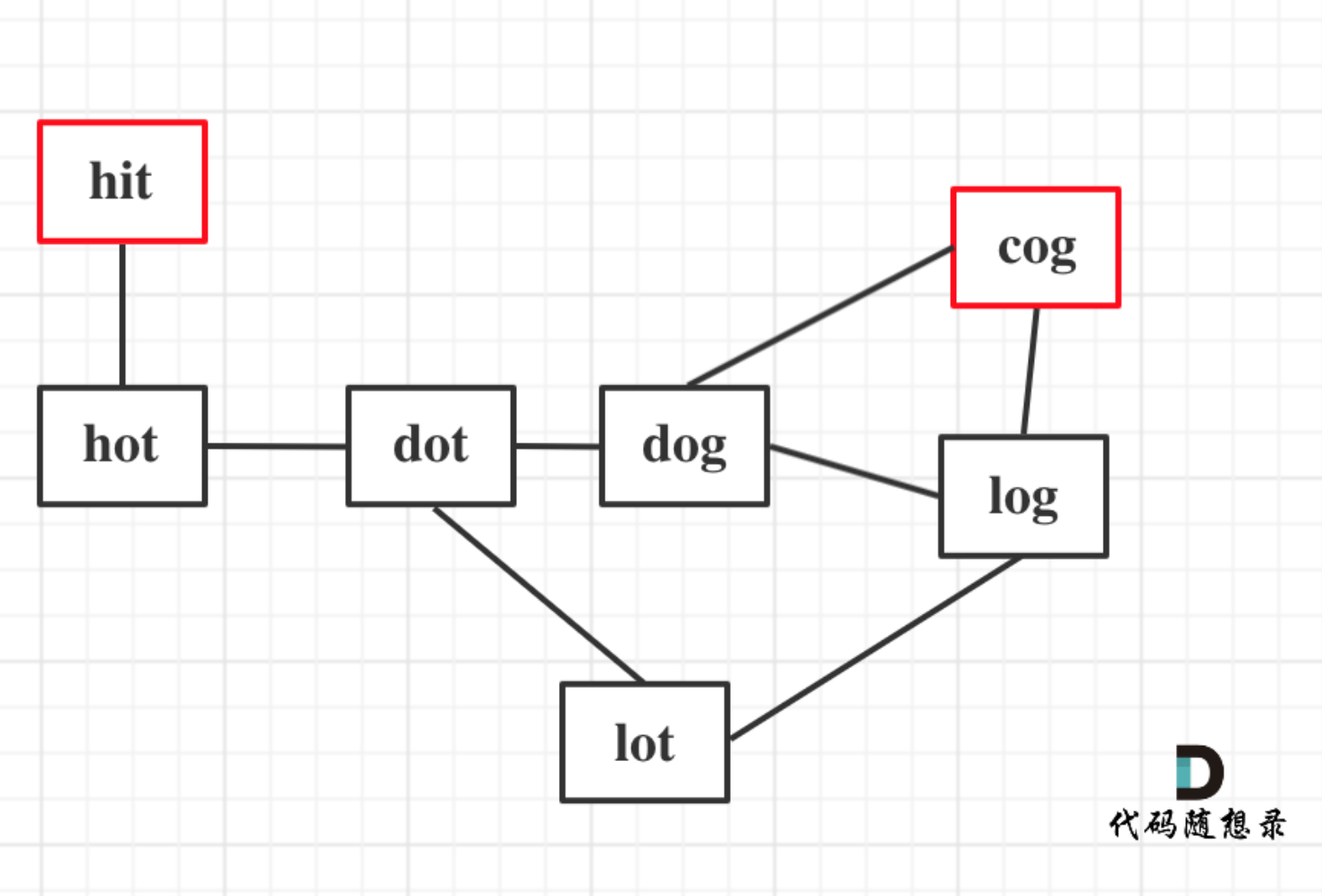
本题只需要求出最短长度就可以了，不用找出路径。
本题只需要求出最短路径的长度就可以了，不用找出路径。
所以这道题要解决两个问题：
@ -46,7 +46,7 @@
然后就是求起点和终点的最短路径长度，**这里无向图求最短路，广搜最为合适，广搜只要搜到了终点，那么一定是最短的路径**。因为广搜就是以起点中心向四周扩散的搜索。
本题如果用深搜，会比较麻烦，要在到达终点的不同路径中选则一条最短路。 而广搜只要达到终点，一定是最短路。
**本题如果用深搜，会比较麻烦，要在到达终点的不同路径中选则一条最短路**。 而广搜只要达到终点，一定是最短路。
另外需要有一个注意点：

4
problems/0309.最佳买卖股票时机含冷冻期.md
View File

@ -148,12 +148,12 @@ public:
vector<vector<int>> dp(n, vector<int>(4, 0));
dp[0][0] -= prices[0]; // 持股票
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
}
return max(dp[n - 1][3], dp[n - 1][1], dp[n - 1][2]);
return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));
}
};
```

28
problems/0739.每日温度.md
View File

@ -24,19 +24,13 @@
那有同学就问了，我怎么能想到用单调栈呢？ 什么时候用单调栈呢？
**通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了**。
**通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了**。时间复杂度为O(n)。
时间复杂度为O(n)。
例如本题其实就是找找到一个元素右边第一个比自己大的元素。
此时就应该想到用单调栈了。
例如本题其实就是找找到一个元素右边第一个比自己大的元素，此时就应该想到用单调栈了。
那么单调栈的原理是什么呢？为什么时间复杂度是O(n)就可以找到每一个元素的右边第一个比它大的元素位置呢？
单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素，优点是只需要遍历一次。
**单调栈的本质是空间换时间**，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素，优点是整个数组只需要遍历一次。
在使用单调栈的时候首先要明确如下几点：
@ -46,10 +40,9 @@
2. 单调栈里元素是递增呢？ 还是递减呢？
**注意一下顺序为 从栈头到栈底的顺序**，因为单纯的说从左到右或者从前到后，不说栈头朝哪个方向的话，大家一定会越看越懵。
**注意以下讲解中，顺序的描述为 从栈头到栈底的顺序**，因为单纯的说从左到右或者从前到后，不说栈头朝哪个方向的话，大家一定比较懵。
这里我们要使用递增循序（再强调一下是指从栈头到栈底的顺序），因为只有递增的时候，加入一个元素i，才知道栈顶元素在数组中右面第一个比栈顶元素大的元素是i。
这里我们要使用递增循序（再强调一下是指从栈头到栈底的顺序），因为只有递增的时候，栈里要加入一个元素i的时候，才知道栈顶元素在数组中右面第一个比栈顶元素大的元素是i。
文字描述理解起来有点费劲，接下来我画了一系列的图，来讲解单调栈的工作过程。
@ -64,9 +57,13 @@
接下来我们用temperatures = [73, 74, 75, 71, 71, 72, 76, 73]为例来逐步分析，输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
首先先将第一个遍历元素加入单调栈
![739.每日温度1](https://img-blog.csdnimg.cn/20210219124434172.jpg)
加入T[1] = 74，因为T[1] > T[0]（当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况），而我们要保持一个递增单调栈（从栈头到栈底），所以将T[0]弹出，T[1]加入，此时result数组可以记录了，result[0] = 1，即T[0]右面第一个比T[0]大的元素是T[1]。
加入T[1] = 74，因为T[1] > T[0]（当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况）。
我们要保持一个递增单调栈（从栈头到栈底），所以将T[0]弹出，T[1]加入，此时result数组可以记录了，result[0] = 1，即T[0]右面第一个比T[0]大的元素是T[1]。
![739.每日温度2](https://img-blog.csdnimg.cn/20210219124504299.jpg)
加入T[2]，同理，T[1]弹出
@ -78,6 +75,7 @@
![739.每日温度4](https://img-blog.csdnimg.cn/20210219124610761.jpg)
加入T[4]，T[4] == T[3] （当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况），此时依然要加入栈，不用计算距离，因为我们要求的是右面第一个大于本元素的位置，而不是大于等于！
![739.每日温度5](https://img-blog.csdnimg.cn/20210219124633444.jpg)
加入T[5]，T[5] > T[4] （当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况），将T[4]弹出，同时计算距离，更新result
@ -87,12 +85,15 @@ T[4]弹出之后， T[5] > T[3] （当前遍历的元素T[i]大于栈顶元素T[
![739.每日温度7](https://img-blog.csdnimg.cn/20210219124726613.jpg)
直到发现T[5]小于T[st.top()]，终止弹出，将T[5]加入单调栈
![739.每日温度8](https://img-blog.csdnimg.cn/20210219124807715.jpg)
加入T[6]，同理，需要将栈里的T[5]，T[2]弹出
![739.每日温度9](https://img-blog.csdnimg.cn/2021021912483374.jpg)
同理，继续弹出
![739.每日温度10](https://img-blog.csdnimg.cn/2021021912490098.jpg)
此时栈里只剩下了T[6]
@ -100,6 +101,7 @@ T[4]弹出之后， T[5] > T[3] （当前遍历的元素T[i]大于栈顶元素T[
![739.每日温度11](https://img-blog.csdnimg.cn/20210219124930156.jpg)
加入T[7]， T[7] < T[6] 直接入栈，这就是最后的情况，result数组也更新完了。
![739.每日温度12](https://img-blog.csdnimg.cn/20210219124957216.jpg)