mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2025-07-11 04:54:51 +08:00
Merge pull request #972 from gaoyangu/master
修改 0188.买卖股票的最佳时机IV 中动规五部曲步骤2的递推公式错误 和 动态规划股票系列,子序列系列的部分笔误
This commit is contained in:
@ -42,7 +42,7 @@ dp[i]只有两个方向可以推出来:
|
||||
|
||||
dp[0]应该是多少呢?
|
||||
|
||||
更具dp[i]的定义,很明显dp[0]因为为nums[0]即dp[0] = nums[0]。
|
||||
根据dp[i]的定义,很明显dp[0]应为nums[0]即dp[0] = nums[0]。
|
||||
|
||||
4. 确定遍历顺序
|
||||
|
||||
|
||||
@ -51,6 +51,7 @@
|
||||
1. 确定dp数组以及下标的含义
|
||||
|
||||
一天一共就有五个状态,
|
||||
|
||||
0. 没有操作
|
||||
1. 第一次买入
|
||||
2. 第一次卖出
|
||||
@ -82,6 +83,7 @@ dp[i][j]中 i表示第i天,j为 [0 - 4] 五个状态,dp[i][j]表示第i天
|
||||
同理可推出剩下状态部分:
|
||||
|
||||
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
|
||||
|
||||
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
|
||||
|
||||
|
||||
|
||||
@ -58,7 +58,7 @@ j的状态表示为:
|
||||
|
||||
所以二维dp数组的C++定义为:
|
||||
|
||||
```
|
||||
```CPP
|
||||
vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
|
||||
```
|
||||
|
||||
@ -89,7 +89,7 @@ for (int j = 0; j < 2 * k - 1; j += 2) {
|
||||
}
|
||||
```
|
||||
|
||||
**本题和[动态规划:123.买卖股票的最佳时机III](https://programmercarl.com/0123.买卖股票的最佳时机III.html)最大的区别就是这里要类比j为奇数是买,偶数是卖剩的状态**。
|
||||
**本题和[动态规划:123.买卖股票的最佳时机III](https://programmercarl.com/0123.买卖股票的最佳时机III.html)最大的区别就是这里要类比j为奇数是买,偶数是卖的状态**。
|
||||
|
||||
3. dp数组如何初始化
|
||||
|
||||
@ -160,7 +160,7 @@ public:
|
||||
|
||||
当然有的解法是定义一个三维数组dp[i][j][k],第i天,第j次买卖,k表示买还是卖的状态,从定义上来讲是比较直观。
|
||||
|
||||
但感觉三维数组操作起来有些麻烦,我是直接用二维数组来模拟三位数组的情况,代码看起来也清爽一些。
|
||||
但感觉三维数组操作起来有些麻烦,我是直接用二维数组来模拟三维数组的情况,代码看起来也清爽一些。
|
||||
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
@ -49,13 +49,13 @@
|
||||
|
||||
3. dp[i]的初始化
|
||||
|
||||
每一个i,对应的dp[i](即最长上升子序列)起始大小至少都是是1.
|
||||
每一个i,对应的dp[i](即最长上升子序列)起始大小至少都是1.
|
||||
|
||||
4. 确定遍历顺序
|
||||
|
||||
dp[i] 是有0到i-1各个位置的最长升序子序列 推导而来,那么遍历i一定是从前向后遍历。
|
||||
|
||||
j其实就是0到i-1,遍历i的循环里外层,遍历j则在内层,代码如下:
|
||||
j其实就是0到i-1,遍历i的循环在外层,遍历j则在内层,代码如下:
|
||||
|
||||
```CPP
|
||||
for (int i = 1; i < nums.size(); i++) {
|
||||
|
||||
@ -8,8 +8,6 @@
|
||||
|
||||
[力扣题目链接](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/)
|
||||
|
||||
[https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/)
|
||||
|
||||
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
|
||||
|
||||
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
|
||||
@ -90,7 +88,7 @@ dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
|
||||
|
||||
* 操作一:昨天卖出了股票(状态三)
|
||||
|
||||
p[i][3] = dp[i - 1][2];
|
||||
dp[i][3] = dp[i - 1][2];
|
||||
|
||||
综上分析,递推代码如下:
|
||||
|
||||
@ -105,7 +103,7 @@ dp[i][3] = dp[i - 1][2];
|
||||
|
||||
这里主要讨论一下第0天如何初始化。
|
||||
|
||||
如果是持有股票状态(状态一)那么:dp[0][0] = -prices[0],买入股票所省现金为负数。
|
||||
如果是持有股票状态(状态一)那么:dp[0][0] = -prices[0],买入股票所剩现金为负数。
|
||||
|
||||
保持卖出股票状态(状态二),第0天没有卖出dp[0][1]初始化为0就行,
|
||||
|
||||
@ -124,7 +122,7 @@ dp[i][3] = dp[i - 1][2];
|
||||
|
||||
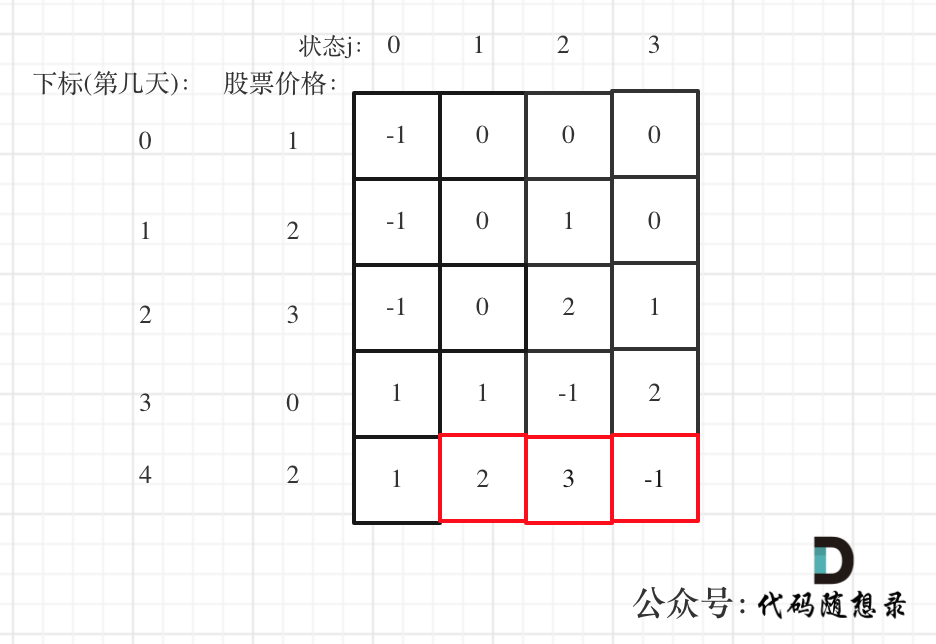
|
||||
|
||||
最后结果去是 状态二,状态三,和状态四的最大值,不少同学会把状态四忘了,状态四是冷冻期,最后一天如果是冷冻期也可能是最大值。
|
||||
最后结果是取 状态二,状态三,和状态四的最大值,不少同学会把状态四忘了,状态四是冷冻期,最后一天如果是冷冻期也可能是最大值。
|
||||
|
||||
代码如下:
|
||||
|
||||
|
||||
@ -81,13 +81,13 @@ if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前
|
||||
|
||||
**其实这里只初始化dp[i][0]就够了,但一起初始化也方便,所以就一起操作了**,代码如下:
|
||||
|
||||
```
|
||||
```CPP
|
||||
vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
|
||||
```
|
||||
|
||||
4. 确定遍历顺序
|
||||
|
||||
同理从从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],那么遍历顺序也应该是从上到下,从左到右
|
||||
同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],那么遍历顺序也应该是从上到下,从左到右
|
||||
|
||||
如图所示:
|
||||
|
||||
|
||||
@ -18,7 +18,7 @@
|
||||
|
||||
## 思路
|
||||
|
||||
本题和[动态规划:115.不同的子序列](https://programmercarl.com/0115.不同的子序列.html)相比,其实就是两个字符串可以都可以删除了,情况虽说复杂一些,但整体思路是不变的。
|
||||
本题和[动态规划:115.不同的子序列](https://programmercarl.com/0115.不同的子序列.html)相比,其实就是两个字符串都可以删除了,情况虽说复杂一些,但整体思路是不变的。
|
||||
|
||||
这次是两个字符串可以相互删了,这种题目也知道用动态规划的思路来解,动规五部曲,分析如下:
|
||||
|
||||
|
||||
@ -43,7 +43,7 @@
|
||||
|
||||
那么我们再来看看是使用动规的方法如何解题。
|
||||
|
||||
相对于[动态规划:122.买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II.html),本题只需要在计算卖出操作的时候减去手续费就可以了,代码几乎是一样的。
|
||||
相对于[动态规划:122.买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II(动态规划).html),本题只需要在计算卖出操作的时候减去手续费就可以了,代码几乎是一样的。
|
||||
|
||||
唯一差别在于递推公式部分,所以本篇也就不按照动规五部曲详细讲解了,主要讲解一下递推公式部分。
|
||||
|
||||
@ -67,7 +67,7 @@ dp[i][1] 表示第i天不持有股票所得最多现金
|
||||
|
||||
所以:dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
|
||||
|
||||
**本题和[动态规划:122.买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II.html)的区别就是这里需要多一个减去手续费的操作**。
|
||||
**本题和[动态规划:122.买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II(动态规划).html)的区别就是这里需要多一个减去手续费的操作**。
|
||||
|
||||
以上分析完毕,C++代码如下:
|
||||
|
||||
|
||||
@ -173,6 +173,7 @@ public:
|
||||
【动态规划】
|
||||
|
||||
一天一共就有五个状态,
|
||||
|
||||
0. 没有操作
|
||||
1. 第一次买入
|
||||
2. 第一次卖出
|
||||
@ -199,6 +200,7 @@ dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);
|
||||
同理可推出剩下状态部分:
|
||||
|
||||
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
|
||||
|
||||
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
|
||||
|
||||
代码如下:
|
||||
@ -279,14 +281,14 @@ j的状态表示为:
|
||||
* 操作一:第i天买入股票了,那么dp[i][1] = dp[i - 1][0] - prices[i]
|
||||
* 操作二:第i天没有操作,而是沿用前一天买入的状态,即:dp[i][1] = dp[i - 1][1]
|
||||
|
||||
dp[i][1] = max(dp[i - 1][0] - prices[i], dp[i - 1][0]);
|
||||
dp[i][1] = max(dp[i - 1][0] - prices[i], dp[i - 1][1]);
|
||||
|
||||
同理dp[i][2]也有两个操作:
|
||||
|
||||
* 操作一:第i天卖出股票了,那么dp[i][2] = dp[i - 1][1] + prices[i]
|
||||
* 操作二:第i天没有操作,沿用前一天卖出股票的状态,即:dp[i][2] = dp[i - 1][2]
|
||||
|
||||
dp[i][2] = max(dp[i - 1][i] + prices[i], dp[i][2])
|
||||
dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])
|
||||
|
||||
同理可以类比剩下的状态,代码如下:
|
||||
|
||||
@ -320,7 +322,7 @@ public:
|
||||
};
|
||||
```
|
||||
|
||||
当然有的解法是定义一个三维数组dp[i][j][k],第i天,第j次买卖,k表示买还是卖的状态,从定义上来讲是比较直观。但感觉三维数组操作起来有些麻烦,直接用二维数组来模拟三位数组的情况,代码看起来也清爽一些。
|
||||
当然有的解法是定义一个三维数组dp[i][j][k],第i天,第j次买卖,k表示买还是卖的状态,从定义上来讲是比较直观。但感觉三维数组操作起来有些麻烦,直接用二维数组来模拟三维数组的情况,代码看起来也清爽一些。
|
||||
|
||||
## 最佳买卖股票时机含冷冻期
|
||||
|
||||
@ -462,7 +464,7 @@ public:
|
||||
|
||||
至此,股票系列正式剧终,全部讲解完毕!
|
||||
|
||||
从买买一次到买卖多次,从最多买卖两次到最多买卖k次,从冷冻期再到手续费,最后再来一个股票大总结,可以说对股票系列完美收官了。
|
||||
从买卖一次到买卖多次,从最多买卖两次到最多买卖k次,从冷冻期再到手续费,最后再来一个股票大总结,可以说对股票系列完美收官了。
|
||||
|
||||
「代码随想录」值得推荐给身边每一位学习算法的朋友同学们,关注后都会发现相见恨晚!
|
||||
|
||||
|
||||
@ -3,11 +3,11 @@
|
||||
|
||||
## 周一
|
||||
|
||||
[动态规划:买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II(动态规划).html)中股票可以买买多了次!
|
||||
[动态规划:买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II(动态规划).html)中股票可以买卖多次了!
|
||||
|
||||
这也是和[121. 买卖股票的最佳时机](https://programmercarl.com/0121.买卖股票的最佳时机.html)的唯一区别(注意只有一只股票,所以再次购买前要出售掉之前的股票)
|
||||
|
||||
重点在于递推公式公式的不同。
|
||||
重点在于递推公式的不同。
|
||||
|
||||
在回顾一下dp数组的含义:
|
||||
|
||||
@ -40,6 +40,7 @@ dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
|
||||
1. 确定dp数组以及下标的含义
|
||||
|
||||
一天一共就有五个状态,
|
||||
|
||||
0. 没有操作
|
||||
1. 第一次买入
|
||||
2. 第一次卖出
|
||||
@ -117,7 +118,7 @@ for (int j = 0; j < 2 * k - 1; j += 2) {
|
||||
}
|
||||
```
|
||||
|
||||
**本题和[动态规划:123.买卖股票的最佳时机III](https://programmercarl.com/0123.买卖股票的最佳时机III.html)最大的区别就是这里要类比j为奇数是买,偶数是卖剩的状态**。
|
||||
**本题和[动态规划:123.买卖股票的最佳时机III](https://programmercarl.com/0123.买卖股票的最佳时机III.html)最大的区别就是这里要类比j为奇数是买,偶数是卖的状态**。
|
||||
|
||||
3. dp数组如何初始化
|
||||
|
||||
@ -131,7 +132,7 @@ for (int j = 1; j < 2 * k; j += 2) {
|
||||
}
|
||||
```
|
||||
|
||||
**在初始化的地方同样要类比j为偶数是买、奇数是卖的状态**。
|
||||
**在初始化的地方同样要类比j为奇数是买、偶数是卖的状态**。
|
||||
|
||||
4. 确定遍历顺序
|
||||
|
||||
@ -162,9 +163,9 @@ for (int j = 1; j < 2 * k; j += 2) {
|
||||
|
||||
j的状态为:
|
||||
|
||||
* 1:持有股票后的最多现金
|
||||
* 2:不持有股票(能购买)的最多现金
|
||||
* 3:不持有股票(冷冻期)的最多现金
|
||||
* 0:持有股票后的最多现金
|
||||
* 1:不持有股票(能购买)的最多现金
|
||||
* 2:不持有股票(冷冻期)的最多现金
|
||||
|
||||
2. 确定递推公式
|
||||
|
||||
@ -179,7 +180,7 @@ dp[i][2] = dp[i - 1][0] + prices[i];
|
||||
可以统一都初始为0了。
|
||||
|
||||
代码如下:
|
||||
```
|
||||
```CPP
|
||||
vector<vector<int>> dp(n, vector<int>(3, 0));
|
||||
```
|
||||
|
||||
|
||||
Reference in New Issue
Block a user